Regularized Coulomb gauge

Regularized Coulomb gauge

Laurent Baulieu^I; Daniel Zwanziger^II

^IUniversit Pierre et Marie Curie, 75005 Paris, France

^IINew York University, New York, NY 10003, USA

ABSTRACT

We define a regularization for the energy divergences in Coulomb gauge. It gives a perturbative algorithm for well-defined computations for the pure non-Abelian Yang-Mills theory in this gauge.

Keywords: Yang-Mills theories; Coulomb gauge; Confinement

I. INTRODUCTION

The Coulomb gauge is a very useful physical gauge at the classical level. It also sheds light for understanding purely quantum effects such has the confinement. However, because it leaves ungauge-fixed the purely residual time-dependant gauge transformations, it lacks of precise renormalization prescription in perturbation quantum field theory, due to energy divergences. Here, we indicate a way to fix-this residual gauge symmetry, and define a perturbative algorithm that allows one to do well-defined computations in the Coulomb gauge for the pure non-Abelian Yang-Mills theory.

II. UNREGULARIZED PHASE-SPACE ACTION IN THE COULOMB GAUGE

The local Euclidean action in Coulomb gauge in phase-space or first-order formalism is

where B_i = ¶_jA_k = ¶_kA_j + gA_j × A_k, for i, j, k cyclic, is the color-magnetic field, and we use the notation for the Lie bracket (A × B)ª º f^abcA^bB^c. The elementary fields, , , bª, cª, ^a carry an upper (lower case) Latin color-index that takes values in the adjoint representation of the non-Abelian Lie algebra and that is generally suppressed, with a sum over color indices implied to form the action. Lower Latin indices take 3 values, i = 1, 2, 3 while greek indices take 4, µ = 0, 1, ... 3. Here c and are the Faddeev-Popov ghost pair, and D_i = D_i(A) is the gauge covariant derivative, D_ic = ¶_ic + gA_i × c, while p_i is an auxiliary field that represents an independent color-electric field. The fields b and A₀ are Lagrange multiplier fields that enforce the Coulomb gauge condition ¶_iA_i = 0 and the color-Gauss law, D_ip_i = 0.

The Euclidean phase-space measure is

If one integrates out p_i, one gets the second-order or Lagrangian Euclidean action in Coulomb gauge,

where

F

_0i = ¶

₀

A_i – ¶

_i

A

₀ +

g(

A

₀ ×

A_i).

A. BRST-invariance and ghost equation of motion

The phase-space action is invariant, sS = 0, under the familiar BRST operator defined by

while p_i transforms gauge-covariantly,[38]

This operator is nil-potent, s² = 0, and the action may be written as the classical phase-space action plus an s-exact piece,

Observables O are in the cohomology of s (namely s-invariant operators sO = 0, modulo s-exact operators O ~ O + sX).

Because the Coulomb gauge condition is linear in the field A, its BRST transformation is linear in the BRST transformation of A. As a consequence, there is the ghost equation of motion that can be enforced as a Ward identity.

Indeed, the action S, Eq. (1), depends only on the spatial derivative of the antighost ¶_i, which makes S trivially invariant under a time-dependent translation of the antighost field ^a(x) ® ª(x) + ^a(x₀). In Coulomb gauge, as in Landau gauge, there is a symmetry between ghost and anti-ghost, and S is also invariant under a time-dependent translation of the ghost field cª(x) ® cª(x) + wª(x₀), provided that there is a compensating transformation of the Lagrange multiplier field b. Here w^a = wª(t) is an infinitesimal c-number element of the Lie algebra that is an arbitrary function of time. As we have chosen wª(t) to be bosonic, the transformation changes bosons into fermions and vice versa.

We implement this transformation by a fermionic symmetry operator

_w that acts according to

It is nilpotent = 0, reduces ghost number by unity, and leaves the action invariant,

Note that the spatial derivatives ¶_ic of c are invariant under this transformation

and this symmetry will imply a Ward identity that is satisfied when the loop corrections to the quantum effective action G depends only on the spatial derivatives ¶_ic of the ghost field, but not on c itself nor its time derivative ¶₀c. There is a corresponding symmetry operator in Landau gauge where however e is a constant (global symmetry) and the loop corrections to G will depend on any derivative ¶_mc of c. This Ward identity corresponds diagrammatically to the well-known factorization of external ghost momentum p_µ in Landau gauge. In Coulomb gauge the spatial components p_i of external ghost momentum factorize, which means loop corrections depend only on ¶_ic.

B. Remnant gauge invariance and energy divergencies

The Coulomb gauge condition ¶_iA_i = 0 is an incomplete gauge fixing because it allows time-dependent but space-independent gauge transformations g(t), which we call ''remnant" gauge transformations, and the Coulomb-gauge action S, Eq. (1) is invariant under them. Under an infinitesimal gauge transformation g(t) = 1 + w(t), with infinitesimal generator G_w the fields transform according to

where A₀ transforms inhomogeneously, while all other fields transform homogeneously,

for X_a = (A_i, p_i, c, , b). Here w^a = w^a(t) is an arbitrary time-dependent element of the Lie algebra. The Coulomb-gauge action is invariant under these gauge transformations,

If this symmetry is preserved, it implies that elementary correlators such as the gluon propagator,

vanish at unequal times. Here dF represents integration over all fields. Indeed, by making the above gauge transformation we obtain

which implies = 0 for x₀¹ y₀. However this behavior is not seen in any finite order of perturbation theory. Indeed at tree level the Coulomb-gauge gluon propagator in momentum space is given by D_ij(k) = (d_ij – _i

_j)/k² and its Fourier transform does not vanish at unequal times, D(x – y) ¹ 0 for x₀¹ y₀. (However the perturbative expansion of gauge-invariant observables may not be as misleading.)

One is tempted to conclude that the symmetry under remnant gauge transformations w(t) must be gauge-fixed or spontaneously broken. However it turns out that the corresponding symmetry operator G_w may be expressed as the anti-commutator

of the two symmetry operators considered previously, the BRST operator s and the operator

_w of translation of the ghost field by a time-dependent function w(t). This is easily checked by applying the anti-commutator to all fields, for example

as asserted. Thus, the remnant gauge invariance cannot be fixed or spontaneously broken without fixing or breaking either BRST-symmetry or ghost-translation symmetry, or both. However we wish to preserve BRST symmetry as an expression of the geometric character of a gauge theory, and the ghost-translation symmetry is trivially maintained in every order of perturbation theory, because of factorization of external ghost momentum p_i for i = 1, 2, 3 from every perturbative diagram.

It thus appear that the Coulomb gauge cannot be used as a gauge in the perturbative quantum field theory regim. The way the remaining ungauged-fixed symmetry manifests itself is that many Feynman diagrams suffer from the energy divergences. These occur in ghost loops because the ghost propagator 1/k² is independent of k₀, so the integration over k₀ diverges. For example, one loop ghost loops contain energy divergences under the following form

This divergence is not regularized by dimensional regularization. It was suggested that energy divergences in ghost loops systematically cancel against corresponding scalar bose loops in the phase-space formalism [2]. However it has recently been found that additional energy divergences occur in Coulomb gauge when a quark loop is inserted into a two-loop (transverse) gluon self-energy [24]. In dimensional regularization, these new energy divergences come from the subtraction term which is introduced to cancel the divergences of the one-loop sub-diagrams, and moreover they cancel among themselves when all one-loop quark insertions are summed [24].

A regularization of the energy divergences and an unambiguous renormalization scheme are thus required in order to give meaning to the perturbative Coulomb gauge in QCD.

For instance, using the gauge condition ¶_iA_i + a¶₀A₀ was proposed [35]. Computations are perfectly defined when the regularizing parameter a ® 0, in a way that preserves the BRST symmetry. However, it was found that, within this class of renormalizable gauges, there is no way to isolate in a practical way the terms that are singular in a, neither for individual diagrams, nor for collection of distinguished diagrams, and to understand the above mentioned cancellations of energy divergencies between ghost loops and unphysical degrees of freedom of the gauge field and its momentum. As it is often the case, ambiguities arise at the 2-loop level. In fact, within this energy divergency regularization, computations must done for a ¹ 0, with no approximation, and the limit a ® 0, can only done afterward. Thus, this regularization sheds not much light on the nature of the Coulomb gauge, and, moreover, the computations are much harder that for the case of Feynman-landau gauge when a = 1.

In what follows we propose a new type of regularization for the energy divergencies of the Coulomb-gauge.

III. MINIMALLY REGULARIZED COULOMB-GAUGE THEORY

A. Color-Coulomb potential as a local field

In classical gauge theory one can solve the constraints in Coulomb gauge by eliminating the longitudinal fields, so the canonical variables are the transverse pair A_i = and . Here is the transverse part of p_i obtained from p_i = –¶_if + , where f is the color-Coulomb potential defined to be the solution of f = –¶_ip_i. The color-Coulomb f will be useful when we regularize the energy divergences, which we shall do shortly.

However in local quantum theory all information must be encoded in a local action. To introduce f, while keeping within the framework of local quantum field theory, we could add to the action the term

where v is an auxiliary local Lagrange multiplier field that imposes the desired equation as a constraint. However we also wish to maintain BRST invariance. Recall that an s-exact term in the action does not change the expectation values of observables (s-invariant quantities), so we are free to add to the action S an auxiliary term S_aux that is s-exact, S_aux = sX. We shall choose S_aux so that its bosonic part agrees with (19). For this purpose we expand the f-v pair into a quartet of auxiliary fields on which s acts trivially,

where f and v are real bosonic fields, while c and are fermionic. For the s-exact auxiliary action we take

whose bosonic part does agree with (19). It gets added to the action

The presence of S_aux does not change the dynamics because it merely introduces a pair of new fields f and c that are fixed by time-independent constraints which are imposed by the Lagrange multiplier fields v and . Moreover because s acts trivially on the quartet f, c, , v, the set of observables, which is the cohomology of s is not enlarged. We note finally that the field c does not appear in any vertex, and appears only in the transition vertex ¶_i(p_i × c), so can only be an external leg of a proper (i. e. one-particle irreducible) diagram.

The auxiliary action S_aux, Eq. (21), is also invariant under the transformation 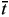_w of translation of the ghost field c(x) by a bosonic time-dependent element of the Lie algebra w(x₀), defined in (8), provided that the new quartet of fields is transformed according to

and we have

The anti-commutator G_w = 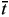_ws + s

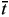_w of the BRST transformation and _w produces an infinitesimal time-dependent gauge transformation that acts covariantly on the new quartet,

for X_a = (, v, f, c), as one may verify by explicit calculation, and we have

where the action of G_w on the other fields is defined in (11).

The free propagators are partially diagonalized by making the change of variable,

with dp_i = d, and sp' = g( – ¶_if) × c + ¶_ic, so the auxiliary action becomes

The Lagrange multiplier field v now imposes the simple constraint that the field be transverse, ¶_i = 0, so and –¶_if are effectively the transverse and longitudinal parts of p_i. In terms of the shifted fields the action S₁ reads

After partial integration cross terms are eliminated by shifting b and v according to

and the action becomes

All propagators are now 2 × 2 block diagonal. In particular, the free propagators of the A_i and fields,

are transverse, and don't mix with the scalar fields A₀ and f.

B. Minimally regularized theory

To control energy divergences we add a term

to the action.

It is designed to provide convergence of energy integrals ò dk₀, and involves the color-Coulomb field f, which is why we introduced f as a local field. We shall be interested in the limit h ® 0. It has dimension 4. Therefore, it is compatible with renormalizability. However, it breaks BRST symmetry, and the issue will be to discuss its stability, in the limit h ® 0.

The minimally regularized theory is defined by the action

With this action, the free propagators of the scalar fields are given by

while the other propagators and all vertices remain unchanged. This is clear because S_reg is quadratic in the fields, and thus affects only the free propagators. With these propagators, all energy divergences are regularized.

We may compare this regularization to the above mentioned regularization provided by the ''interpolating" gauge that interpolates between the Landau and Coulomb gauges [35]. It is defined by the action

where (a¶)_m = ( hp₀, p_i). This provides a regularization of the Coulomb gauge that has the advantage that it preserves BRST invariance, whereas S_reg breaks it. However the interpolating gauge contains a vertex h¶₀

g(A₀ × c) where 3 energy-degenerate propagators meet, which greatly complicates the study of the limit h ® 0. (Moreover the limit appears to be singular [33].) In contrast, at most two energy-degenerate propagators enter the vertices of S_mr, so energy divergences appear only in non-overlapping closed loops, and we shall show an exact pairwise cancellation of these loops at finite h.[39]

Although the regularizing action hS_reg breaks BRST invariance we shall also show that BRST-invariance is restored when the regulator is removed, h ® 0.

IV. CANCELLATION OF ENERGY DIVERGENCES AS h ® 0

To demonstrate the cancellation of energy divergences and obtain a practicable scheme, we will using dimensional regularization of ultraviolet divergences. Notice that we only consider the pure Yang-Mills theory, since the coupling to quarks brings further complications. In this section we consider the regularized (but not yet renormalized) theory at finite e, where D = 4 – e. Cancellation of energy divergences for the renormalized theory is more intricate and will be considered later. Energy divergences are controlled by the parameter h.

A. Diagrammatic cancellation of energy divergences

The action contains the ghosts c and at most bilinearly, and likewise for the scalar bosons A₀ and f. Consequently energy divergences are associated with closed ghost or scalar bose loops. Indeed each ghost loop with loop momentum k, consists of the product of ghost propagators (k + p_n), with energy integral

Upon rescaling by

one obtains for the energy integral

which diverges like h^–1/2 as h ® 0. However this loop integral is exactly cancelled at finite h by an equal but opposite loop integral consisting of (k + p_n) propagators, with (k + p_n) = –i(k + p_n).

This argument may be extended to diagrams with several energy-degenerate loops, and we shall give shortly a general algebraic argument.

We note that when a typical energy-divergent integral is integrated over the spatial loop momenta the resulting divergence at h = 0,

is not a polynomial in the external spatial momenta, so familiar subtraction procedures that may be used for the usual ultraviolet divergences are inadequate for energy divergences. Instead we must rely on an exact cancellation of the terms that diverge like h^–1/2, without subtracting them, that is, at the UV-regularized level, prior to the renormalization.

B. Sufficient conditions for finite limit h ® 0

To establish that the renormalized effective action G has a finite limit h ® 0, we claim that it is sufficient to prove that the regularized G, that is the effective action computed before substraction with e ¹ 0, satisfies.

because the operator h annihilates the h-independent limiting term, and gives the leading h-dependence. This statement will hold true because of the exact compensations that hold between all diagrams with energy divergencies, order by order in perturbation theory, and because the insertions of counterterms introduce no further energy divergencies.

We have

which gives

and we obtain as the condition for a finite limit as the regulator is removed,

To avoid inessential complications we have not introduced sources for the BRST transformations of the fields, and the expectation-value is calculated in the presence of the sources J only.

It might be thought that the coefficient h insures that I₁ approaches 0 with h. However the two time derivatives contained in S_reg = ò d^Dx ( + ) become in momentum space. Under the rescaling (40), we obtain = h^–1, which absorbs the coefficient h. As a result, each of the two terms and in S_reg gives rise to a closed loop that diverges like h^–1/2, and, consistent with our previous evaluation, each of these two closed loops precisely cancel each other at finite h.

We also wish to show that BRST-invariance is regained in the limit h ® 0. This is not obvious because a symmetry that is broken by the regulator is not always regained when it is removed. It is shown below, Eq. (103), that the Slavnov-Taylor identity at finite h is given by the term

so the condition for restoration of BRST symmetry is given by

The resemblance to (45) and (46) is clear. One easily finds

where

The term ¶₀D₀c = + (gA × c) that appears in sS_reg contains 3 time derivatives. Each time derivative produces a factor of k₀ in momentum space, which increases the degree of energy divergence. Fortunately this unpleasant term is cancelled by a similar term which appears after one makes the change of variable b = b' – , that was introduced in (30) to diagonalize the free propagators into 2 × 2 blocks. This gives, after an integration by parts,

The terms that contribute to I₂ individually give contributions that diverge like h^–1/2 however, as for I₁, there are systematic cancellations of terms between bose and fermi ghosts that assure that time-dependent BRST invariance is restored in the limit h ® 0. Again we wish to show this cancellation algebraically.

C. Algebraic cancellation of energy divergences

Contemplation of graphs with energy divergences suggests introducing the operator 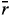defined by

where and v' are defined in (30). It is nilpotent, 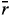² = 0, and decreases ghost number N_gh by unity. This operator is useful because the BRST breaking term is is 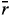-exact, We conclude that the limits of interest, (46) and (47), are determined by the behavior at small h of

for n = 1, 2. (Since lim_{h ® 0}I_2b = 0, for simplicity here and below we have written I₂ instead of I_2a.)

Note that X₁ and X₂ each have half as many terms as S_reg and (s_f S_reg)_a; it is the operator 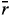acting on X₁ and X₂ that produces the duplicate terms that diverge and cancel each other. To avoid this divergent duplication we take advantage of the fact that 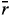is a (grassmannian) operator of differentiation, to perform an integration by parts,

This gives

where

and s_a is a sign factor from commuting 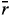through J_a.

Typical graphs that contribute to L₁ and L₂ do not involve any energy-degenerate closed loops and give a contribution that vanishes like h^1/2. We find lim_{h ® 0}L_1,2 = 0.

We next evaluate

S_mr. We have S_mr = S₁ + S_reg = S₁ +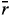 X₁ so, with 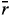² = 0, we have

where S₁ is given in (31). To simplify the calculation we separate an 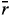-exact piece out of S₁, which may be written,

where

We again use

² = 0, and easily obtain

Typical graphs that contribute to K₁ and K₂ do not involve any energy-degenerate closed loops and give a contribution that vanishes like h^1/2. This is in fact a general property of graphs that contribute to K₁ and K₂ and we find lim_{h ® 0}K_n = 0.

We thus conclude

which shows that G has a finite limit, and

which shows that the limit is BRST-invariant.

We therefore have a perturbation theory whose Feynman diagrams with ultraviolet divergences controlled by dimensional regularization, with D = 4 – e, can be separated in two distinct sets. Those who are singular when h ® 0 sum up exactly to zero, order by order in perturbation theory, while the others are regular in the limit h ® 0. We have shown that in the limit h ® 0 the correlators at finite e are finite and respect BRST-invariance.

V. ENERGY REGULARIZATION WITH SECOND-ORDER ACTION

A. Local action

We would now like to renormalize the theory. However a difficulty arises because the phase-space action S that we used contains only the color-electric terms and p_iF_0i, but one encounters a divergence proportional to e^–1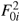 which was not present in S. Such a question also arises when one renormalizes the YM theory in covariant gauges and in first order formalism. It can be solved, but it complicates a lot the proof of renormalization.

To circumvent this difficulty, we now integrate out the conjugate-momentum field p_i by gaussian quadrature, and obtain

where

is quadratic in the fields. The action remains local. It assumes a second-order form that is regularized against ultraviolet and energy divergences in D = 4 – e dimensions, at finite e and h. The information that is relevant for our purpose and was obtained in the first order formalism is in fact retained, under the form of a dependence in c,v and f, A₀, which still keeps its role for the energy divergencies of the ghosts.

It may be written

where S' is the standard BRST-invariant Coulomb-gauge action in second-order formalism given in (3). Just as in the first-order formalism, the auxiliary action is s-exact,

and is thus a pure gauge-fixing term. The terms S' and S_aux are separately invariant under the symmetries s, 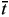_w, G_w of the Coulomb gauge action defined above.

The obvious gain in going from the first to the second-order formalism, is that now the only color-electric term of dimension 4 in the cohomology of s is 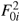. Moreover we shall show shortly that the action at h = 0, is stable under renormalization in the sense that the possible divergences compatible with the Ward identities of sect. III are of the same form as the terms in the second-order action S'.

The field v now appears in vertices, so we will also need its free propagators. One finds, from the action at g = 0,

These propagators contain explicit factors of h or h², which suggests that they vanish in the limit h ® 0. Indeed, when either of these propagators appears in a loop that is not energy-degenerate, it may in fact be neglected at h = 0. However when they appear in an energy-degenerate closed loop, one makes the change of variable k₀ = h^–1/2, and these propagators become independent of h. (The energy-degenerate closed loop, before cancellation, is of order h^–1/2 from ò dk₀ = h^–1/2ò d.)

B. Cancellation of energy divergences in second-order formalism

With ultraviolet and energy regulators in place, corresponding correlators are equal in the first- and second-order formalisms. Thus, since they are finite in the limit h ® 0 in the first-order formalism, they must be finite in the second-order formalism. Moreover the BRST-breaking term has the same value in the first and second order formalism, so the proof that BRST invariance is regained in the limit h ® 0 also holds in the second-order formalism.

One may also show the cancellation of the energy divergences directly in the second-order formalism by the the algebraic method used previously that relies on the 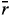transformation (52). For this purpose it is convenient to change variables from v to

so the second-order action may be written

where

The tri-gluon vertex becomes the one term g(A_i × A₀)¶_iu.

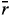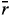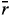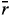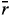We now give an algebraic proof that energy divergences cancel in the second-order formalism, again using the operator. From v' = (v – A₀ + if) = 0, we see that u = if so

We use identities such as

which allow us to express the second-order action as

where

To see the mechanism that is operating, note that the one term,

produces all 3 tri-linear vertices involving more than one scalar field. The algebraic proof of cancellation of energy divergences goes through as in the first-order formalism.

The propagators of u that enter vertices are given by

The propagator D_uu = 1/k² provides no convergence of the k₀ integration, so one might doubt that all energy divergences are in fact regularized. However u appears in the vertex g(A₀ × A_i)¶_iu, so a D_uu propagator in an energy-degenerate loop of a proper (1PI) diagram connects to two vertices from each of which A₀ quanta emerge. Moreover each occurrence of A₀ in a vertex produces a power of h in the denominator, as one sees from and , and all energy-divergent loops are in fact regularized. In the second-order formalism there is also a vertex involving a time derivative, g

_i(A₀ × A_i), which leads to the appearance of the propagator

The first two terms do not provide any convergence of the k₀ integration, but again, the propagator connects to two vertices from each of which A₀ quanta emerge, so the threatened energy divergences are in fact regularized. These terms may contribute to an energy-degenerate loop, and this must cancel against some other energy-degenerate loop. Indeed, the d_ij term cancels against an energy-degenerate loop with a quartic vertex, (A₀ × A_i)², while the k_ik_j/k² term cancels against a D_uu propagator. All energy divergences do in fact cancel, as shown by the preceding algebraic argument, but the cancellation is more intricate in the second-order formulation.

C. Decoupling of auxiliary fields at h = 0

We now add sources K_m, L for the s-transforms that are non-linear to write the Ward identities in a functional way. This yields the extended action

We write F_a = (A_µ, c, , b, f, c, , v) to represent the set of all elementary fields, and J_a = (, J_c, , J_b, J_f, J_c, , J_v) represents the corresponding sources. We next use the equations of motion to determine the dependence on the 4 auxiliary fields (, b, f, c). The partition function Z(J_a, K, L, h) is defined by

The quantum effective action G(F_a, K, L, h) is obtained by the Legendre transformation

Here and below, all derivatives are left derivatives, and s_a = ±1, according as a is a bose or a fermi field.

The auxiliary fields were introduced as a device to regularize the theory while keeping the action local, but we are ultimately interested in the correlators in the absence of sources for these fields namely at

We now express these conditions in terms of the Legendre transforms. We have

which corresponds to the condition = 0. We also have

so J_f = 0 corresponds to

which vanishes with h. Thus we may calculate the correlators of the remaining fields, from (A_m, c, 0, 0, K_m + ¶_i, L).

Suppose now that in the second order action (64) one redefines the auxiliary fields according to

Then the action becomes

where

Apart from the term h in Q, the parameter h appears only in the combination hV and h. We will see shortly, Eq. (96), that the quantum effective action has the same structure,

where the reduced quantum effective action contains the dynamics. In the limit h ® 0, becomes independent of the auxiliary fields V and ,

while retaining the symmetries it inherits from a local action. In particular the Ward identity that expresses BRST symmetry still holds because the contribution of the auxiliary fields to this identity is of the form

which vanishes with h.

However it remains true that in doing calculations we cannot set h = 0 until after the cancellation of energy-divergent diagrams. Thus we cannot neglect the auxiliary fields in the local action while doing calculations.

VI. WARD IDENTITIES IN SECOND-ORDER FORMALISM

A. Linear equations of motion of fields as Ward identities

The equation of motion of the color-Coulomb potential f implies the Ward identity

This has the solution

where G₁ is independent of f.

The equation of motion of implies

This has the solution

where all the dependence on f and is explicit.

The equations of motion of b and c are straightforward, with the result

where

The dependence on the fields , b, f, and c is now explicit. Here (A_m, c, v, , , L, h) depends only on the reduced set of variables indicated, and is called the reduced quantum effective action.

Notice that there is another way to express this result for G. The local extended action (79) has the same dependence on the variables , b, f and c,

where

is independent of h. If we separate the quantum effective action into the tree-level term S plus the set of all loop corrections, G = S + G^loop, it follows that the loop corrections depend only on the reduced set of variables,

Upon making the change of variable (86) in Eq. (96) the promised equations (89) and (90) follow. This establishes the decoupling of the auxiliary fields in , as asserted.

B. Modified Ward identity for the h-broken BRST symmetry

To derive the h-broken BRST Ward identity satisfied by G, we use

This implies an identity satisfied by S,

It implies

for G. We have shown previously that with dimensional regularization the correlators are finite in the limit h ® 0, and that the right-hand side of the last equation vanishes in this limit, and we obtain

C. Ward identity from translation of ghost field

The Ward identity follows from the identity,

which holds because

_w is an operator of differentiation. This gives the Ward identity satisfied by W,

where

The Ward identity satisfied by the effective action is G,

where

which reads

The right-hand side, which represents the breaking of the translation symmetry

_w by G, is linear in the fields.

The right-hand side comes entirely from the tree-level contribution to the quantum effective action G. It is not subject to radiative corrections. If one separates out the tree-level term, G = S +

^loop, one obtains the simple identity satisfied by the loop corrections,

VII. RENORMALISATION AND RESTRICTIONS ON COUNTER-TERMS AT h = 0

We now express the Slavnov-Taylor identity (104) in terms of the reduced quantum effective action (96), and obtain

As shown above, Eq. (91), in the absence of sources for the auxiliary fields, the last term is negligible at h = 0, and the Slavnov-Taylor identity simplifies to

where is now independent of the auxiliary fields,

Likewise, by (23), the contribution of the auxiliary fields to the ghost-translation identity (111) is negligible in the limit h ® 0, and reads,

At finite h the proper (1PI) functions have a Laurent expansion in powers of e, in which the coefficients of the singular terms (negative powers of e) are polynomials in the external momenta.

When h ® 0, at any given order of perturbation theory, all diagrams that contain energy divergencies compensate each other at the regularized level. Therefore no UV counterterms are needed for each one of these diagrams. On the other hand, local counterterms are needed for the rest of the diagrams. Since the later have regular limits for h ® 0, their coefficient can be computed at h ® 0. Moreover, the insertion of counterterms adds no energy divergencies in the diagrams.

In view of this, we will shortly examine properties of the terms at h = 0 that are singular in e and are compatible with the Slavnov-Taylor identity (113) and the ghost-translation identity (115).

The reduced effective action is expanded in powers of , = . We suppose that by a subtraction procedure, in the limit h ® 0, the singular terms are removed to order n – 1, compatible with the two identities. We separate the n-th term into a part that is regular in e and a divergent part that contains inverse powers of e, G⁽ⁿ⁾ = . The n-th order term satisfies the linear identities

where

One may show by standard methods that s is nilpotent,

Since dimensional regularization preserves the BRST symmetry, identities (116) are satisfied separately by the divergent part

Recall that the action of

_w on the sources is given by

(since by definition

_w does not act on the sources), and moreover

The anti-commutator of the symmetries s and

_w acting on the sources yields a time-dependent gauge transformation

just as it does for the fields, under which the sources transform gauge-covariantly,

A. Enumeration of divergences and independent counterterms

We now construct the most general local solution of the identities (119) that is invariant under space-time translations. The mass dimensions of the fields are

and they have ghost number

The only local terms in the cohomology of s are 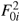and , so the most general solution of = 0 is

where Y is a local function with N_gh(Y) = –1. The most general expression consistent with the dimensions, ghost number, rotational invariance, and global gauge invariance is

We now impose ghost-translation invariance

_w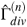 = 0. This is obviously satisfied separately by the terms 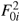and 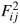since they do not involve the ghost field c(x). For the term with coefficient c₃ in (127) we have

There is no other term in (127) that contains K₀, so we conclude c₃ = 0. Likewise for the term with coefficient c₅ we have

No other term in (127) contains L, so we conclude c₅ = 0. On the other hand, the term with coefficient c₄ is annihilated by 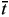_w, for we have

Both Ward identities (119) are now satisfied, and we conclude, that the most general form of divergences compatible with them is

We have not yet imposed Lorentz invariance, which is broken only by the gauge-fixing term. This has been discussed in [35], and we will not repeat that discussion, but note that it yields c₁ = c₂, and we obtain finally

Here c₁ and c₄ are constants that diverge in the limit e = 4 – D ® 0. These are the only possible divergences. Thus in the Coulomb gauge there are only two independent renormalization constants.

B. Multiplicative renormalization constants in the minimally regularized Coulomb gauge

Suppose that the divergences have been cancelled to order n – 1 in an expansion so the divergent constants are of order c₁ ~ ⁿ and c₄ ~ ⁿ. We wish to extend this cancellation to order n by a renormalization of the fields and charges that appear in the reduced extended action,

From the definition of the operator s we have

so, the term with coefficient c₄ in (132) may be cancelled by renormalizing the fields in according to

Recall that S contains and K_i only in the combination K_i + ¶_i, so is implicitly renormalized like K_i,

Now observe by power counting that the Euler differential operator satisfies

Use of this identity gives

because the remaining terms in only involve g in the combination gA_m and Lg, both of which are annihilated by the Euler differential operator. Thus, to order n, the term with coefficient c₁ in (132) may be cancelled by renormalizing the fields in according to

The two renormalizations (135) and (139) together are sufficient to cancel the two divergent terms of (132). However, because ghost number is conserved, we are free to make an additional renormalization of fields with ghost number N by

where a is an arbitrary constant. This constant is frequently chosen so c and renormalize in the same way. However for our purposes it will be convenient instead to choose a, so A₀ and c renormalize in the same way,

This is achieved by a = –c₁. When this choice is combined with the two renormalizations (135) and (139), the complete order n renormalization is given by

In general we write the renormalizations as

where each Z is a power series to arbitrary order in that may be calculated recursively using (142). There are two independent renormalization constants corresponding to the two divergent constants c₁ and c₄. This is the same number as in the Landau gauge. For although manifest Lorentz invariance is lost, on the other hand, in Coulomb gauge ghost-translation invariance 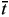_w by an arbitrary function of time w(t) is more powerful than in Landau gauge.

If we choose the two independent renormalization constants to be and , then the others are given by

C. Renormalization-group invariants

The last equations imply the identities

It follows that the following quantities are renormalization-group invariants,

The first one is peculiar to the Coulomb gauge. A direct analog of the second one also occurs in Landau gauge.

[1] V. N. Gribov, ''Quantization Of Non-Abelian Gauge Theories,'' Nucl. Phys. B 139, 1 (1978).

[2] D. Zwanziger, ''Renormalization in the Coulomb gauge and order parameter for confinement in Nucl. Phys. B 518, 237 (1998).

[3] D. Zwanziger, ''No confinement without Coulomb confinement,'' Phys. Rev. Lett. 90, 102001 (2003) [arXiv:hep-lat/0209105].

[4] A. Cucchieri and D. Zwanziger, ''Renormalization group calculation of color Coulomb potential,'' Phys. Rev. D 65, 014002 (2002) [arXiv:hep-th/0008248].

[5] D. Zwanziger, ''Analytic calculation of color-Coulomb potential and color confinement,'' Phys. Rev. D 70 (2004) CORRECT: 094034 [arXiv:hep-ph/0312254].

[6] J. Greensite and S. Olejnik, ''Coulomb energy, vortices, and confinement,'' Phys. Rev. D 67, 094503 (2003) [arXiv:hep-lat/0302018].

[7] R. Alkofer, C. S. Fischer, and F. J. Llanes-Estrada, ''Vertex functions and infrared fixed point in Landau gauge SU(N) Yang-Mills theory,'' Phys. Lett. B 611, 279 (2005) [arXiv:hep-th/0412330].

[30] S. Mandelstam, ''Approximation Scheme For QCD,'' Phys. Rev. D 20, 3223 (1979).

[31] L. von Smekal, R. Alkofer, and A. Hauck, ''The infrared behavior of gluon and ghost propagators in Landau gauge QCD,'' Phys. Rev. Lett. 79, 3591 (1997) [arXiv:hep-ph/9705242].

[32] L. von Smekal, A. Hauck, and R. Alkofer, ''A solution to coupled Dyson-Schwinger equations for gluons and ghosts in Landau gauge,'' Annals Phys. 267, 1 (1998) [Erratum-ibid. 269, 182 (1998)] [arXiv:hep-ph/9707327].

[11] C. Lerche and L. von Smekal, ''On the infrared exponent for gluon and ghost propagation in Landau gauge QCD,'' Phys. Rev. D 65, 125006 (2002) [arXiv:hep-ph/0202194].

[12] C. S. Fischer and R. Alkofer, ''Infrared exponents and running coupling of SU(N) Yang-Mills theories,'' Phys. Lett. B 536, 177 (2002) [arXiv:hep-ph/0202202].

[13] L. Baulieu and D. Zwanziger, ''Renormalizable non-covariant gauges and Coulomb gauge limit,'' Nucl. Phys. B 548, 527 (1999) [arXiv:hep-th/9807024].

[14] A. Cucchieri and F. Karsch, Nucl. Phys. Proc. Suppl. 83, 357 (2000) [arXiv:hep-lat/9909011].

[15] A. Cucchieri, F. Karsch, and P. Petreczky, Phys. Rev. D 64, 036001 (2001) [arXiv:hep-lat/0103009].

[16] J. C. Taylor, ''Ward Identities And Charge Renormalization Of The Yang-Mills Field,'' Nucl. Phys. B 33, 436 (1971).

[17] D. Zwanziger, ''Non-perturbative Landau gauge and infrared critical exponents in QCD,'' Phys. Rev. D 65, 094039 (2002) [arXiv:hep-th/0109224].

[18] A. Cucchieri, T. Mendes, and A. Mihara, ''Numerical study of the ghost-gluon vertex in Landau gauge,'' JHEP 0412, 012 (2004) [arXiv:hep-lat/0408034].

[19] W. Schleifenbaum, A. Maas, J. Wambach, and R. Alkofer, ''Infrared behaviour of the ghost gluon vertex in Landau gauge Yang-Mills theory,'' arXiv:hep-ph/0411052.

[20] R. Alkofer, C. S. Fischer, H. Reinhardt, and L. von Smekal, ''On the infrared behaviour of gluons and ghosts in ghost-antighost symmetric gauges,'' Phys. Rev. D 68, 045003 (2003) [arXiv:hep-th/0304134].

[21] A. P. Szczepaniak and E. S. Swanson, ''Coulomb gauge QCD, confinement, and the constituent representation,'' Phys. Rev. D 65, 025012 (2002) [arXiv:hep-ph/0107078].

[22] C. Feuchter and H. Reinhardt, ''Variational solution of the Yang-Mills Schroedinger equation in Coulomb gauge,'' Phys. Rev. D 70, 105021 (2004) [arXiv:hep-th/0408236]; C. Feuchter and H. Reinhardt, ''Quark and gluon confinement in Coulomb gauge,'' arXiv:hep-th/0402106.

[23] C. Fischer and D. Zwanziger arXiv:hep-ph/0504244

[24] A. Andrasi, J. C. Taylor, "Cancellation of energy-divergences in Coulomb gauge QCD," arXiv:hep-th/0503099

[25] Renormalization of gauge theories, Jean Zinn-Justin (Saclay),. SACLAY-D.PH-T-74-88, Oct 1974. 40pp. Lectures given at Int. Summer Inst. for Theoretical Physics, Jul 29 - Aug 9, 1974, Bonn, West Germany. Published in Bonn Conf.1974:2.

[26] D. Zwanziger, Nucl. Phys. B 518, 237 (1998).

[27] J. Greensite and S. Olejnik, Phys. Rev. D 56, 094503 (2003), arXiv:hep-lat/0209068.

[28] J. Greensite, S. Olejnik, and D. Zwanziger, Phys. Rev. D 69, 074506 (2004), arXiv:heplat/0401003.

[29] A. Nakamura, T. Saito, arXiv: hep-lat/0512042.

[30] S. Mandelstam, ''Approximation Scheme For QCD,'' Phys. Rev. D 20, 3223 (1979).

[31] L. von Smekal, R. Alkofer, and A. Hauck, ''The infrared behaviour of gluon and ghost propagators in Landau gauge QCD,'' Phys. Rev. Lett. 79, 3591 (1997) [arXiv:hep-ph/9705242].

[32] L. von Smekal, A. Hauck, and R. Alkofer, '''A solution to coupled Dyson-Schwinger equations for gluons and ghosts in Landau gauge,'' Annals Phys. 267, 1 (1998) [Erratum-ibid. 269, 182 (1998)] [arXiv:hep-ph/9707327].

[33] C. S. Fischer and D. Zwanziger, Phys. Rev. D 72, 054005 (2005), arXiv: hep-ph/0504244.

[34] J. Greensite, S. Olejnik, and D. Zwanziger, Phys. Rev. D69, 074506 (2004), arXiv: hep-lat/0401003.

[35] L. Baulieu and D. Zwanziger, Nucl. Phys B 548, 527 (1999), arXiv: hep-th/9807024.

[36] " Dimensional renormalization and the action principle", P. Breitenlohner, D. Maison, Commun. Math. Phys. 52, 11 (1977).

[37] "Dimensionally renormalized Green functions for theories with massless particles", P. Breitenlohner, D. Maison, Commun. Math. Phys. 52, 39 (1977).

[38] Alternatively the action of s on p_i may be defined by sp_i = –iF_0i× c, while preserving the invariance of the action sS = 0.

[39] The action S₁ contains the vertex $\partial_i \bar \phi g ( \partial_i \phi \times c)$ which contains 3 fields with energy-degenerate propagators. However the only non-zero propagator of $ \bar \chi $ is D_c['(c)], and c does not appear in any vertex. The precise statement is that in a proper (1pI) diagram no more than two energy-degenerate propagators enter a vertex of S_mr.

Received on 24 March, 2006

Publication Dates

• Publication in this collection
  11 May 2007
• Date of issue
  Mar 2007