Multiple scattering theory for pion-nucleus elastic scattering and the in-medium piN amplitude

Abstract

Elastic scattering of positive and/or negative pions (pi+ and/or pi-) by nuclei has been studied by means of Glauber's multiple scattering theory (GMST). The differential, total and total elastic cross sections using both the full series expansion and the first order correction (called optical limit results, OLA) of the Glauber amplitude, have been calculated. The in-medium pN amplitude (sigmaeff., sigmaeff.) as well as the free piN one (sigmafree, sigmafree) are invoked into the full series calculations of the Glauber amplitude and our results were compared with the corresponding experimental data. These calculations are carried out for the elastic collisions, pi-- 2He4 at incident energy 180 MeV, pi±- 3Li6 at 240 MeV, pi-- 6C12 at incident energies 180, 200 and 260 MeV, pi+- 8O16 at 240 and 270 MeV and pi±- 20Ca40 at energy 292.5 MeV. The comparisons reflect that, except around the minima, the full series calculations with the in-medium pN amplitude are better in describing the scattering data than those using the free piN one and both are better than the optical limit results.

Glauber's multiple scattering theory; Differential cross section; Total cross section; Total elastic cross section; In-medium piN amplitude

REGULAR ARTICLES

Multiple scattering theory for pion-nucleus elastic scattering and the in-medium pN amplitude

A.S. Shalaby^I; M. Y. M. Hassan^II; M. M. H. El-Gogary^II

^IPhysics Department, Faculty of Science, Beni Suef University, Egypt

^IIPhysics Department, Faculty of Science, Cairo University, Egypt

ABSTRACT

Elastic scattering of positive and/or negative pions (p⁺ and/or p^-) by nuclei has been studied by means of Glauber's multiple scattering theory (GMST). The differential, total and total elastic cross sections using both the full series expansion and the first order correction (called optical limit results, OLA) of the Glauber amplitude, have been calculated. The in-medium pN amplitude (s_eff., s_eff.) as well as the free pN one (s_free, s_free) are invoked into the full series calculations of the Glauber amplitude and our results were compared with the corresponding experimental data. These calculations are carried out for the elastic collisions, p^-- ₂He⁴ at incident energy 180 MeV, p^±- ₃Li⁶ at 240 MeV, p^-- ₆C¹² at incident energies 180, 200 and 260 MeV, p⁺- ₈O¹⁶ at 240 and 270 MeV and p^±- ₂₀Ca⁴⁰ at energy 292.5 MeV. The comparisons reflect that, except around the minima, the full series calculations with the in-medium pN amplitude are better in describing the scattering data than those using the free pN one and both are better than the optical limit results.

Keywords: Glauber's multiple scattering theory; Differential cross section; Total cross section; Total elastic cross section; In-medium pN amplitude.

I. INTRODUCTION

The interaction of pions with nuclei has been actively studied for about twenty years [1-4]. The main focus of this effort to date has been to work at energies at or below the pion production threshold, which occurs for the pion-nucleon (pN) interaction at p kinetic energies of ~ 175 MeV. At these energies, the basic pN interaction is completely elastic which is under discussion here. The elastic interaction of pions with finite nuclei and with nuclear matter is of considerable theoretical interest for a number of reasons [5]. We are dealing here with one of the few examples of multiple scattering by a nucleus of an elementary particle projectile, the main other example of which is provided by the nucleon-nucleus interaction. Even as a more repetition of the latter with a different interaction, the p nuclear multiple scattering would therefore be of interest. In particular, the p nuclear interaction is, however, of such a qualitatively different structure compared to the nucleon one, that it must be considered to be of interest in its own right. Also, its connection to the basic processes is clearer and more immediate than in the case of nucleons. Moreover, the absence of poles in the low energy (pN) scattering as well as the short range of the (pN) interaction opens the possibility of establishing a very transparent connection between the elementary scattering and the pN scattering, a connection which unfortunately is not so direct in the case of nucleons. The small recoil corrections in the pion case and the absence of a pion spin are also technical advantages compared to nucleons.

A great deal of low energy pion-nucleus elastic scattering data has been accumulated [6-12]. For the most part, the data were obtained for positive pions scattering from nuclear targets spanning a wide range of the periodic table in order to map out general features of elastic scattering. These experiments indicate that in the low energy region, the pion mean free path is long and pions penetrate to the nuclear interior [13].

Various authors have investigated pion-nucleus scattering for the purpose of studying nuclear structure and the pion-nucleon interaction inside the nucleus [14, 15]. The main purpose of such investigations is to understand the mean field encountered by the pion while traversing the target nucleus. This field is usually described in terms of either multiple scattering processes which depend upon the nuclear charge distributions [16-25] or the complex optical model (OM) potential [26-30]. We will restrict ourselves here to the first one where the projectile undergoes multiple scatterings during its passage through the nucleus. Two independent multiple scattering theories have been used to describe the pion elastic scatterings from nuclei. The first is called Watson's multiple scattering theory (WMST) [31-33], the second is the well known Glauber's multiple scattering theory (GMST) [17-23, 34, 35], which is under discussion here. The theory is based on high-energy Eikonal approximation, in which the interacting particles are almost frozen in their instantaneous positions during the passage of the projectile through the target and the trajectory is nearly straightforward. However, because the Glauber theory is principally derived for the higher energy and the small-angle situations, the reliability of its results may be questioned in the case of low energy and large angle. The GMST has the great advantage of leading to straightforward calculations of the elastic pion-nucleus scattering cross-sections from knowledge of free pion-nucleon scattering amplitude and nuclear densities.

The preliminary applications of GMST were found to have great successes in reproducing the hadron-nucleus scattering data [36-44]. The confidence in this theory encouraged the extension of its application to nucleus-nucleus collisions [45-57].

Following the same procedures as that utilized in our previous works [58, 59] which takes into account the hadron as a projectile, we have studied in our present paper the elastic scattering of positive and/or negative pions (p⁺ and/or p^-) by different nuclei, like, ₂He⁴, ₃ Li⁶, ₆C¹², ₈O¹⁶ and ₂₀Ca⁴⁰ at intermediate energies. We considered here both the full series expansion and the first order correction of the Glauber amplitude.

Correlations within the nucleus are of fundamental theoretical interest but unfortunately they are difficult to study experimentally. In pion-nucleus scattering they manifest themselves through a change of the effective pion-nucleon cross section via the so called in-medium pN amplitude [60-64]. Goldberger [65] suggested that the effective total nucleon-nucleon cross section of a bound nucleon is less than that of free nucleon because the Paula principle forbids momentum transfer, to a bound nucleon, less than a minimum value sufficient to bring it outside the Fermi sea [66]. The relation between and s as quoted by Goldberger is given by = s (1-) where E_F = 38.4 MeV which corresponds to Fermi momentum K_F = 1.38 fm^-1 and E is the kinetic energy of the incident nucleon. Abul-Magd et al. [67] considered that the effective NN scattering amplitude implies that +1 = a²+1/( 1-) . However, Glauber [17] and Faldt et al. [68] argued that the effective nucleon-nucleon cross section should be larger than the free one. It was shown by Glauber that the Pauli correction imply an effective cross section = s^' (1+xs^') [66, 69]. This relation is the golden rule that used in high-energy physics, s' = s(1-ia) is the free pion-nucleon cross section including real and imaginary parts. The actual numerical value of x is very much debated. As a guide one often uses the result of the Fermi-gas model [17] which gives x @ » 0.06 fm^-2. It is helpful to study the effect of the in-medium correction on our results.

The present paper contains three more sections. Section II, contains the theoretical expressions used to calculate the differential, total and total elastic cross sections for the considered reactions. Section III includes the results and their discussions. The conclusion is given in section IV. The orbits, lengths and D-matrices required for carrying out the calculations are exhibited in the ^appendix.

II. THEORETICAL FRAMEWORK

This section is devoted to obtain the expressions for the differential (ds/dW or ds/dt), total (s_T) and total elastic (s_el) cross-sections for the elastic scattering of pion (p⁺ and/or p^-) with light- and medium-weighted nuclei using Glauber's multiple scattering theory. These expressions are developed by using both the full series expansion of the Glauber amplitude and by taking into account the consistent treatment of the center-of-mass (c.m.) correlation.

In this theory, the elastic scattering amplitude between a pion of atomic number ''Z_p'' and a target nucleus of mass number ''B'' and atomic number ''Z_B'' is given as [48]

where, is the momentum transferred from the pion to the target nucleus B, is the incident momentum of the pion, and 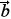is the impact parameter vector. Q() is the center-of-mass correlation function [48]. c_pB(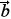) is the phase-shift function resulting from the interaction of the pion with the target nucleus B.

By taking into account the Coulomb phase-shift function in addition to the nuclear one, we can write

where (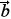) is the point charge correction to the Coulomb phase-shift function, which is equal to 2nln(), a is equal to , n = Z_pZ_Be²/v is the usual Coulomb parameter and (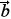) is the extended charge correction to the Coulomb phase shift function. c_n(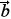) is the nuclear interaction phase-shift function.

From eqs. (1) and (2), we find

In eqs. (1) and (3), the center-of-mass correlation is treated as a global correction (denoted by Q()) multiplied by the scattering amplitude. Because of Q() has an exponential form of q² [48], this leads to unphysical divergence as q goes to high values. The large q-divergence is removed by incorporating the center-of-mass correlation function Q() in the first order calculations [45] or in the fourth order evaluations [47] or in the full series calculations [56], of the Glauber amplitude. Such consistent treatment in the later case [56] has modified the phase-shift functions to new forms, which are simply expressed in terms of the uncorrelated ones.

Thus, eqs. (1) and (3) become

and

where (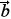) is the modified extended charge correction to the Coulomb phase shift functio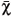n. _n(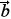) is the modified nuclear interaction phase-shift function. (The bars are introduced to distinguish the modified quantities from their corresponding uncorrelated ones).

Assuming the target ground state wave function has the form:

where x_B(_B) and F_B() are the wave functions describing the center-of-mass motion and the internal motion of the target nucleons, respectively.

Accordingly, the modified optical phase-shift function,

_n(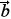), can be written in terms of the uncorrelated phase-shift functio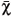n, _n(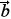), as [47]

where

and

{

^'_j} are the projections of the position vectors {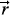^'_j} of the target nucleons on the impact parameter plane. With the definition of the profile function

the phase-shift function is given by

where G_j represents the profile function of scattering between the pion and the jth nucleon in the target nucleus B. It is related to the pion-nucleon (pN) elastic scattering amplitude f_j by

where k_p is the wave number of the incident pion.

Assuming for simplicity that all the pN amplitudes are equal (which is approximately true at high energy) and neglecting further spin effects, f_j can be parameterized by [56]

Here, s is the total pN cross-section, r is the ratio of the real to the imaginary parts of the forward pN scattering amplitude and ''a'' is taken to be complex; the real part is typically the slope parameter (b²) of the pN elastic scattering differential cross section while the imaginary part is a free parameter introducing a phase variation of the pN scattering amplitude, which is taken here to be zero.

Inserting eq. (13) into eq. (12), we obtain

with

To perform the integrations (8) and (9) analytically, consider the approximation in which the nucleons inside the target nucleus are completely uncorrelated, then we can write

where r_B is assumed to be of single-Gaussian type like,

where ''a_B'' is related to the rms radius by

Adopting the wave function (15) with the density (16) and using the same analysis as that utilized in our references [55, 56] with the invoking of the description mentioned above, eq. (8) for Q(q) yield [48]

and eq. (9) after integrating over the variables x and y using the same procedures as that given in Ref. [57] with the canceling out one of the Gaussians, gives the analytic result

where Z_o, has the form

with

where, the indices (m, l _m) characterize an orbit with an order of scattering m and serial index l _m. R_o,W_o,a_o(j),a₁₁(j,1) and C₁(j,1) are independent on j, i.e., they are the same for all j. Obviously, Eq. (18) has an advantage in reducing the computer CPU time spent in the calculations by restoring Z_o at D_1j = 0,1.

In the method of Yin et al.[49], each orbit (m, l _m) is represented by a matrix D(m, l _m) with element D_1j(m, l _m) either equal to ''1'' or ''0''. This matrix D(m, l _m) corresponds to one typical term expressing the multi-cluster elementary collision and its element is equal to ''1'' if G_1j appears in the expansion term and is equal to ''0'' if it is absent. T(m, l _m) is the number of repetitions (length) of the orbit (m, l _m), which is determined by using the properties of the permutation group G₁ = S₁Ä S_B.

Here, ''Ru'' and ''sg'' are the row and column sum vectors of the corresponding orbit, respectively.

Eq. (18) is developed by taking the one-particle system as our cluster particle and hence, N₁ = B (i.e., µ₁:1 ® B), N₂ = 1 (i.e., µ₂ = 1), M_A = M_N = 1, M_B = B.

Incorporating the c.m. correlation, the modified phase-shift function,

_n(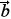) can be expressed as

The form of

_o is obtained by inserting the expressions of Z_o and Q(q) into Eq. (7), yielding

with

Finally, the modified extended charge correction to the Coulomb phase-shift, (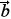), has already been derived analytically in Ref. [47] for a single-Gaussian density where it was found to have the form

where E₁(z) is the exponential integral function and,

With the results of eqs. (19), (20) and (21), the scattering amplitude F_pB(q) can be obtained by performing the integration in Eq. (5) numerically. The angular distribution of the elastic scattering is given by

The total elastic cross section, s_el, is given by subtracting the total reaction cross section ''s_R'' from the total cross section which is related to the forward scattering amplitude of the elastic scattering by the optical theorem as:

The reaction cross section is found to has the form [47, 70, 71]

With the results of Eqs. (23) and (24), the total elastic cross section, s_el, can be easily obtained from Eq. (25).

III. RESULTS AND DISCUSSION

In the framework of the formalisms presented in the above section, we have calculated the differential cross section for a set of elastic nuclear reactions; namely, p^-- ₂He⁴ at incident energy 180 MeV, p^±- ₃Li⁶ at 240 MeV, p^-- ₆C¹² at incident energies 180, 200 and 260 MeV, p⁺- ₈O¹⁶ at 240 and 270 MeV and p^±- ₂₀Ca⁴⁰ at energy 292.5 MeV. Also, we have calculated the total cross section for the elastic collisions, namely; p⁺- ₃Li⁶ at incident energy 128 and 259 MeV, p⁺- ₆C¹² at 89 MeV, p⁺- ₂₀Ca⁴⁰ at 292.5 MeV, p^-- ₃Li⁶ at incident energy 115, 156 and 259 MeV, p^-- ₆C¹² at incident energy 115, 120, 259, 260 and 289 MeV and p^-- ₂₀Ca⁴⁰ at 292.5 MeV. The total elastic cross section is evaluated for the elastic scattering of p^- with ₆C¹² at incident energies 180, 200, 230, 260 and 280. The theoretical results were compared with the available experimental data. The ingredients needed to perform these calculations are the parameters associated with the pN scattering amplitude and the nuclear densities as well as the orbits, lengths and D-matrices of the groups G₁ = S₁Ä S_B and G₂ = S₁Ä S₁. For the above energies, we used the values of the pN parameters given in Table (1).

The values of the rms radii we have used for the present nuclei are given in Table (2).

The structure specific to the considered reactions and the corresponding orbits, lengths and D-matrices are exhibited in the ^appendix. The center-of-mass correlation is treated here in a consistent way in which its expressing function (Q(q)) is incorporated in each order of the optical phase-shift expansion. Such function is found to have an exact form in the case of the employed single-Gaussian density [48]. To show to what extent the inclusion in-medium pN scattering amplitude affects the angular distribution, we first evaluate it with the free pN parameters (s_free, s_free). Second, we calculate it with the effective pN ones (s_eff., s_eff.). The results obtained from these calculations for the considered reactions are shown in Figs. (1-10) as dashed and solid curves, respectively. Fig. 1 contains the results obtained for p^-- ₂He⁴ at 180 MeV. We see from this figure that the predicted angular distribution obtained with the effective pN parameters (referred to as solid curve) is much better than that obtained using the free pN ones (referred to as dashed curve). For p^±- ₃Li⁶ reaction, the results obtained, Figs. 2, 3, show that except around the minima, the angular distributions calculated with (s_eff., s_eff.) are better in comparison with that evaluated with (s_free, s_free) ones. In particular, the dashed curves reproduced well the positions of the minima while the solid curves reproduce more satisfactorily the backward angles in comparison with the results shown by the dashed curves. For p^-- ₆C¹² case, Figs. 4-6, it is shown that the inclusion of the in-medium effect is more comprehensive in fitting the corresponding experimental data, especially at large angles than that neglecting it. Enlarging the mass of the target nucleus as in the p⁺- ₈O¹⁶ reaction, Figs. 7, 8, the improvement shown here in these figures by the solid curves in comparison with the dashed curves reflects the proper account for the full Glauber series calculation in addition to the inclusion of the in-medium pN scattering amplitude. For p^±- ₂₀Ca⁴⁰ reaction, Figs. 9, 10, one can easily see that the in-medium calculations of the angular distributions are still better than that using the free parameters. As we referred before [58, 59] that the use of density distribution more suitable than that employed in our calculations may improve our results. This will be the subject of future work.

To ensure the necessity of accounting for the full multiple scattering series of the Glauber amplitude, comparison has been made with the similar first-order calculations (optical limit result) using Franco and Varma approach [47]. The details of their analysis and the phase-shift expressions developed are quoted in their reference. Figs. (1-10) contain the results of such comparison where the first order calculations are referred to as the dotted curves while the full series evaluations are referred to as the dashed curves. An overall picture of these figures shows that the full series results are relatively better than the optical limit results, especially at large angles. This may ensure the necessity of including the higher order terms at large momentum transfers.

As an additional check, we have calculated the total cross section (s_tot) for the elastic scattering of p⁺ and/or p^- with ₃Li⁶, ₆C¹² and ₂₀Ca⁴⁰, and total elastic cross section (s_el) for p^-- ₆C¹² at different incident energies. The results of the calculated total and total elastic cross-sections and the corresponding experimental data are listed in Tables (3-5). One can easily see from these tables that the full series calculations for the total and total elastic cross-sections are much better than that calculated by the optical limit approach. This ensures the necessity of including the full multiple scattering series of the Glauber amplitude.

IV. CONCLUSION

In the framework of Glauber's multiple scattering theory and taking into account the Coulomb contribution and a consistent treatment of the center-of-mass (c.m.) correlation, we have investigated the elastic scattering of positive and /or negative pions by nuclei, like, ₂He⁴, ₃Li⁶, ₆C¹², ₈O¹⁶, and ₂₀Ca⁴⁰ at intermediate energies. We have calculated the differential, total and total elastic cross sections for the considered reactions. These calculations are carried out by considering the followings; (i) The full series expansion of the Glauber amplitude with free pN parameters (s_free, s_free), (ii) The first order correction of the Glauber amplitude (OLA) with free pN parameters (s_free, s_free), (iii) The full series expansion of the Glauber amplitude with the in-medium pN parameters (s_eff., s_eff.). We compared our results with the corresponding experimental data. It is shown that, except around the minima, the full series results of the differential cross-sections employing the in-medium pN amplitude are more comprehensive in describing the scattering data rather than that using the free pN one. Also, one can easily see that the full series calculations of the Glauber amplitude are relatively better than the optical limit result (OLA), especially at backward angles.

An overall view of the results shown before, we emphasize that the full series expansion of the Glauber amplitude is not sufficient to bring the Glauber theory closer to the experimental data. It must consider some corrections like; in-medium pN amplitude, phase-variation parameter of the pN scattering amplitude which has its strongest effect around the diffraction patterns, more realistic density distribution like harmonic-oscillator density. The last two corrections will be done in our future work.

[1] C. H. Q. Ingram, in proceedings of the Ninth International Conference on High Energy Physics and Nuclear Structure, edited by P. Catillon, P. Radvanyi, and M. Porneuf (North-Holland, Amsterdam, 1982).

[2] R. A. Eisenstein, in proceedings of the Workshop on Nuclear and particle Physics at Energies up to 31 GeV; New and Future Aspects, edited by J. D. Bowman, L. S. Kisslinger, and R. R. Silbar, Los Alamos National Laboratory Report LA-8775-C, 1981.

[3] R. H. Landau, in proceedings of the English International Conference on High Energy Physics and Nuclear Structure, edited by D.F. Measday and A. W. Thomas (North-Holland, Amsterdam, 1979).

[4] D. Marow et al., Phys. Rev. C 30, 1662 (1984).

[5] M. Ericson and T. E. O. Ericson, Ann. Phys. (N.Y.) 36, 323 (1966).

[6] M. Blecher et al., Phys. Rev. C 20, 1884 (1979).

[7] B. M. Preedom et al., Phys. Rev. C 23, 1134 (1981).

[8] S. A. Dytman et al., Phys. Rev. C 19, 971 (1979).

[9] R. R. Johnson et al., Phys. Lett. B 43, 844 (1979).

[10] S. H. Dam et al., Phys. Rev. C 25, 2574 (1982).

[11] M. Blecher et al., in proceedings of the Ninth International Conference on High Energy Physics and Nuclear Structure, Versailles, 1981, edited by P. Catillon, P. Radvanyi, and M. porneuf (North-Holland, Amsterdam, 1982).

[12] F. E. Obenshain et al., in proceedings of the Ninth International Conference on High Energy Physics and Nuclear Structure, Versailles, 1981, edited by P. Catillon, P. Radvanyi, and M. porneuf (North-Holland, Amestrdam, 1982).

[13] M. Blecher et al., Phys. Rev. C 28, 2033 (1983).

[14] D. S. Koltun, Interaction of pions with nuclei, Advances in Nuclear Physics, Vol. 3 (Academic Press, New York, 1970).

[15] H. K. Lee and H. McManus, Nucl. Phys. A 167, 257 (1971).

[16] C. Schmit, Nuovo Cimento Lett. 4, 454 (1970); K. Bjornenak et al., Nucl. Phys. B 22, 179 (1970).

[17] R. J. Glauber, Boulder lectures in theoretical physics (Interscience, New York, 1959) 315; High-Energy Physics and Nuclear Structure (North-Holland, Amsterdam, 1967) 311.

[18] M. M. Sternheim, Phys. Rev. 135, B912 (1964).

[19] G. Faldt and T. E. O. Ericson, Nucl. Phys. B 8, 1 (1964).

[20] G. Faldt, Nucl. Phys. B 10, 597 (1969).

[21] C. Michael and C. Wilkin, Nucl. Phys. B 11, 99 (1969).

[22] T. T. Chou, Phys. Rev. 168, 1594 (1968).

[23] K. Bjornenak et al., Nucl Phys. B 20, 327 (1970).

[24] Li Qing-run, Chen Sheng-zhong, and Zhao En-guang, Physica Energiae Fortis et Physica Nuclearis 5, 531 (1981).

[25] Li Qing-run, Chen Sheng-zhong, and Zhao En-guang, Nucl. Phys. A 384, 466 (1982).

[26] L. S. Kisslinger, Phys. Rev. 98, 761 (1955).

[27] W. F. Baker, H. Byfield, and J. Rainwater, Phys. Rev. 112, 1773 (1958).

[28] E. H. Auerbach, D. M. Fleming, and M. M. Sternheim, Phys. Rev. 162, 1683 (1967).

[29] F. Binon et al., Nucl. Phys. B 17, 168 (1970).

[30] M. Krell and S. Barmo, Nucl. Phys. B 20, 461 (1970).

[31] K. M. Watson, Phys. Rev. 89, 575 (1953).

[32] N. C. Francis and K. M. Watson, Phys. Rev. 92, 291 (1953).

[33] K. M. Watson, Phys. Rev. 105, 1388 (1957).

[34] K. Bjornenak et al., Nucl Phys. B 22, 179 (1970).

[35] W. Czyz, Adv. Nucl. Phys. to be published.

[36] R. J. Glauber and G. Mathiae, Nucl. Phys. B 21, 135 (1970).

[37] C. Wilikin, Nuovo Cimento Lett. 4, 491 (1970).

[38] H. Lesniak and L. Lesniak, Nucl. Phys. B 38, 221 (1972).

[39] J. P. Auger and R. J. Lombard, Phys. Lett. B 45, 115 (1973); G. Igo, in High-Energy Physics and Nuclear Structure edited by D.E. Nagle et al. (AIP, New York, 1975), p. 63.

[40] V. Franco, Phys. Rev. C 8, 1690 (1974).

[41] W. Czyz, Adv. Nucl. Phys. 4, 61 (1971).

[42] R. H. Bassel and C. Wilikin, Phys. Rev. 174, 1179 (1968).

[43] R. J. Glauber, in proceeding of the Second International Conference on High-Energy Physics and Nuclear Structure, Rehovoth, 1967, edited by G. Alexander (North-Holland, Amsterdam, p. 311, 1967).

[44] R.J. Glauber, in proceeding of the Third International Conference on High-Energy Physics and Nuclear Structure, Colubia, 1967, edited by S. Devons (Plenum, New York, p. 207, 1970).

[45] V. Franco and A. Tekou, Phys. Rev. C 16, 658 (1977).

[46] G. K. Varma, Nucl. Phys. A 294, 465 (1978).

[47] V. Franco and G.K. Varma, Phys. Rev. C 18, 349 (1978).

[48] W. Czyz and L.C. Maximon, Ann. Phys. (N.Y.) 52, 59 (1969).

[49] Yichun Yin et al., Nucl Phys. A 440, 685 (1985).

[50] Y. Yin et al., Chinese Phys. 6, 93 (1986); Phys. Ener. Fort. Phys. Nucl. 9, 569 (1985).

[51] V. Franco, Y. Yin, Phys. Rev. C 34, 608 (1986).

[52] Zhen-Qiang Tan, Zheng-Jin Lin, Pan-Ning Yan, and Chong. En Wu, J. Phys. G 16, 1697 (1990).

[53] Zong-Jin Lin, Shu-Xia Yu, Xiang Zhong Huang, and Chong-En Wu, J. Phys. G 17, 1159 (1991).

[54] A. S. Shalaby et al., Phys. Rev. C 56, 2889 (1997).

[55] M. M. H. EL-Gogary et al., Phys. Rev. C 58, 3513 (1998).

[56] M. M. H. EL-Gogary et al., Phys. Rev. C 61, 044604 (2000).

[57] Huang Xiang Zhong, Phys. Rev. C 51, 2700 (1995).

[58] A. S. Shalaby, Egypt. J. Phys. 35, 163 (2004).

[59] A. S. Shalaby, Egypt. J. Phys. 35, 481 (2004).

[60] G. Q. Li and R. Machleidt, Phys. Rev. C 48, 1702 (1993).

[61] G. Q. Li and R. Machleidt, Phys. Rev. C 49, 566 (1994).

[62] T. Alm et al., Nucl. Phys. A 587, 815 (1995).

[63] Cai Xiang-zhou et al., Phys. Rev. C 58, 572 (1998).

[64] E. Friedman et al., Phys. Rev. C 72, 034609 (2005).

[65] M. L. Goldberger, Phys. Rev. 74 (1949) 1269.

[66] I. M. A. Tag Eldin et al., J. Phys. G 16, 1051 (1990).

[67] A. Y. Abul-Magd et al., Can. J. Phys. 58, 1230 (1980).

[68] G. Faldt and A. Ingemarsson, J. Phys. G 9, 261 (1983).

[69] G. Faldt, Nucl. Phys. A 202, 403 (1973).

[70] I. J. Thompson and Y. Suzuki, Nucl. Phys. A 693, 424 (2001).

[71] B. Abu-Ibrahim and Y. Suzuki, Phys. Rev. C 62, 034608 (2000).

[72] M. P. Locher, O. Steinmann, and N. Straumann, Nucl. Phys. B 27, 598 (1971).

[73] A. S. Clough et al., Nucl. Phys. B 76, 15 (1974).

[74] S. A. E. Khallaf and A. A. Ebrahim, Phys. Rev. C 65, 064605 (2002).

[75] Li Qing-Run, Nucl. Phys. A 415, 445 (1984).

[76] Tsung-Shung H. Lee, Soumya Chakravarti, Phys. Rev. C 16, 273 (1977).

[77] L. F. Antonuk et al., Nucl. Phys. A 451, 741 (1996).

[78] J. Frohlich et al., Z. Phys. A 302, 89 (1981).

Received on 5 December, 2006

This appendix contains tables in which we present the orbits, lengths and - matrices employed in our calculations. We obtained them by enumerating and investigating all possible combinations of collisions according to their permutation using the method introduced in Ref. [49]. In the present work, the elastic collisions, p^-- ₂He⁴, p^±- ₃Li⁶, p^-- ₆C¹², p⁺- ₈O¹⁶ and p^±- ₂₀Ca⁴⁰ have been studied. Each reaction according to its assumed cluster structure needs the orbits, lengths and D-matrices of the groups G₁ = S₁Ä S_B and G₂ = S₁Ä S₁ (defined in chapter II). For the sake of brevity, we give only the tables of the non-similar groups.

Total number of orbits (including the orbits not shown) = 4.

Total number of orbits (including the orbits not shown) = 6.

Total number of orbits (including the orbits not shown) = 12.

Total number of orbits (including the orbits not shown) = 16.

Total number of orbits (including the orbits not shown) = 40.

Total number of orbits (including the orbits not shown) = 1.

In these tables, the first column represents the order of multiple scattering which ranges from 1 to 1×n while l _m in the second column represents the serial index used to number the orbits of order µ. The third column represents the length of the orbit T(m, l _m). In the fourth column the 1×n - digit binary numbers give the D-matrices of the group G = S₁Ä S_n. The n-digits are the elements D_1i, i = 1,2,...,n.

By symmetry, the orbits, lengths and D-matrices for µ's which are not shown in our tables could be easily deduced from the Tables. This is carried out by using the results for order µ' = m × n-µ and interchanging the 0's and 1's of D(µ^',l_µ'). The indices l _m and l_µ' are the same and the lengths T(m, l _m) and T(µ',l_µ') are equal. The matrix D(n,1) has elements D_1j equal to 1.

appendix

Publication Dates

• Publication in this collection
  17 July 2007
• Date of issue
  June 2007

History

• Received
  05 Dec 2006