Nonexistence of regular stationary solution in a metric nonsymmetric theory of gravitation

Nonexistence of regular stationary solution in a metric nonsymmetric theory of gravitation

S. Ragusa

Instituto de Física de São Carlos Universidade de São Paulo, C.P. 369 13560-970 São Carlos, SP, Brazil E-mail address: [e-mail]

ABSTRACT

It is proven that the field equations of a previously studied metric nonsymmetric theory of gravitation do not admit any non-singular stationary solution which represents a field of non-vanishing total mass and non-vanishing total fermionic charge.

Keywords: Nonsymmetric; Non-singular

1. INTRODUCTION

In a series of papers [1] we have studied a metric nonsymmetric theory of gravitation. Following the analysis of nonsymmetric theories in the paper of Damour, Deser and McCarthy [2] the theory was shown to be free of ghost-negative energy radiative modes even when expanded about a Riemannian background space. In the Minkowski flat space linear approximation the antisymmetric part g_[αβ] of the metric has been made to obey both of Maxwell-type vacuum equations. This is what guarantied the no-ghost behavior of the theory. The implication for the motion of particles and light was analyzed and the results are consistent with the four classical solar tests of general relativity (GR). Next in [1-III] the electromagnetic field was included in the theory and the solution of the field equations were obtained for a charged point mass. The sources of the field are the energy-momentum-stress tensor T^αβ and the fermionic current density S^α.

Here we study the question of non-singular solutions following the pattern of GR [3,4].

Einstein [3] proved that the gravitational field equations of GR, R_αβ = 0, of a field imbedded in a Minkowski space, do not admit any non-singular stationary (i.e. with the metric independent of time) solution which would represent a field of non-vanishing total mass. Here we show that a similar result is true for the present nonsymmetric theory: the field equations do not admit any non-singular solution which would represent a field of non-vanishing total mass and non-vanishing fermion charge.

Einstein and Pauli (EP) [4] reduced the prove of the Einstein proposition to its necessary elements with a more objective reasoning, which we will follow in our case.

The paper is organized as follows. After presenting the field equations in Sec. 1, we discuss in Sec. 2. the non-singular theorem. In Sec. 3 we draw our conclusions and highlight future work.

2. THE FIELD EQUATIONS

The vacuum field equations of the theory are,

and

The notation () and [] designates symmetric and antisymmetric parts. In the first equation the first term is the analogue of the Ricci tensor. It is symmetric and contains only the symmetric part of the connection,

Here g is the determinant of g_αβ, s the determinant of s_αβ, the inverse of g^(αβ), and we have used the relation . Λ is the cosmological constant. The next two equations involve the symmetric and antisymmetric parts of g^αβ = where g^αβ is the inverse of g_αβ as defined by

The last equation is the null curl of g_[αβ]. The second field equation, (2.2), can be solved for the symmetric part of the connection giving [1-I],

Equations (2.3) and (2.4) are Maxwell-type field equations and that is what have guaranteed the no ghost modes of the field g_[αβ] .

Equation (2.4) came from the relation

where is the vector involving contractions of the antisymmetric part of the connection. We see that Γ_α plays the role of a potential.

Inside the sources the right-hand side of (2.2) will remain the same and equations (2.1), (2.3) and (2.4) would contain, respectively, the source terms 8πG

_(αβ), 4πG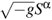 and 8πG

_[αβ,λ] / Λ with 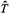_αβ = T_αβ - g_αβ T/2 , where T_αβ is the stress tensor and T = g^µν T_µν.

3. THE PROBLEM OF THE NON-SINGULAR SOLUTION

We will put ourselves in the same frame of work of GR [3,4] setting Λ = 0 in (2.1). Then our starting point, similar to R_αβ = 0, is

For β = 0 in the stationary situation this gives

and (2.2) for γ = 0 gives

because = 0, by the relation mentioned just after (2.5). Contracting (3.2) with g^(αρ) we obtain, after a differentiation by parts and use of (2.2),

where use has been made of time-independence for the first term. Contracting (3.3) with we see that the second term of (3.4) vanishes. Therefore, = 0. For ρ = 0 we have,

This relation corresponds to the GR relation in equation (13) of EP. The method we have used to derive it corresponds to the GR procedure in [5], as a much shorter road to arrive at the one of EP. In ^{Appendix A} we show how to obtain (3.5) by a method similar to the one of EP. Continuing, as reasoned in EP , for a non-singular field this relation holds everywhere. Hence by integrating over a volume V we can go to the surface S that surroundings it. In this way we obtain the condition

nⁱ being the unit vector normal to the spherical S taken at infinity. The field is supposed to be imbedded in a Minkowski field. Therefore, we can use the field equations of the theory of first approximation to calculate (3.6) . We then expand g_αβ around the Minkowskian flat space. Calling h_αβ the deviations from the flat space metric η_αβ = diag. (1,-1,-1,-1) we write

Then,

with h^βα = η ^βµ η^αν h_µν.Therefore,

The inverse to g^(αβ) is then

Thence, to first order, in (2.7) reduces to

because ln(s/g) = h^[µν]h_[µν] / 2, which is of second order. This comes by expanding the relations g^-1 = ε _αβγδ ε _µνρσ g^αµ g^βν g^γρ g^δσ/4! and s^-1 = ε _αβγδ ε _µνρσ g^(αµ)g^(βν)g^(γρ)g^(δσ)/4!. Writing g^αβ = g^(αβ) + g^[αβ] we find, to second order, g^-1 = s^-1 - h^[µν] h_[µν]/ 2. Therefore, s/g = 1 + h^[µν] h_[µν]/ 2 leading to the second order value of ln(s/g). Consequently U_αβ reduces to the first order form of the Ricci tensor. From (3.1) it follows that to first order we have, as in GR,

These are the values of s_αβ as well. As g⁽⁰ⁱ⁾ = 0 the integrand of (3.6) become g⁰⁰

nⁱ = h_00,inⁱ/2 = m/r². Plugging this result into that equation we obtain

as in GR.

In our case this constitutes the first part of the prove of the proposition because, besides the matter stress-tensor we also have the fermionic current as a source of the field. This involves the antisymmetric sector of the field, equations (2.3) and (2.4), which we then start to analyze. The α = 0 component of the first one is

By integrating over a volume V as before we can, for a non-singular field, go to the surface S that surroundings it with radius r and centered at the origin. In this way we obtain the condition

Here use has been made that at infinity we can use (3.9). In that far Minkowski flat space region h_[αβ] obeys, by (2.4), the usual flat space Maxwell-type null curl equation. Therefore, h_[0i] behaves as its electric field counterpart, that is,

where F = S⁰d³x is the fermion charge of the system. Taking this into (3.15) it follows that

This completes the proof of the theorem.

4. CONCLUSION

We have proved that the equations of a previously studied metric nonsymmetric theory of gravitation of a field imbedded in a Minkowski space, do not admit any non-singular static solution which would represent a field of non-vanishing total mass and non-vanishing total fermionic charge. This result is the counterpart of the well know non-singular theorem in general relativity. A topic for future work could be the extension of the present study to the case in which the electromagnetic field is also present. The field equations for the combined gravitational-electromagnetic field have been developed in [1-III] and the study would follow the same steps as described here.

[1] S. Ragusa, Phys. Rev. D 56, 864 (1997).. The term 2Δ_α/3 of equation (6.7) is here replaced by Γ _α; Gen. Relat. Gravit. 31 275 (1999); S. Ragusa and D. Bosquetti, Braz. J. Phys. 30 569, (2000). These papers will be referred to as I, II and III, respectively.

[2] T. Damour, S. Deser, and J. McCarthy, Phys. Rev. D 45, R3289 (1992); 47, 1541 (1993).

[3] A. Einstein Revista (Universidad Nacional de Tucuman), A2 1, (1941).

[4] A. Einstein and W. Pauli, Ann. Math. 44, 131 (1943).

[5] A. Papapetrou, Phys. Rev. 73, 1195 (1948).

[6] A. Papapetrou, Lectures on General Relativity (Dordrecht, Holland, 1974).

Received on 8 July, 2008

We derive here equation (3.5) in a way that corresponds to the one in [4].

Considering the variation δU_αβ we have, after contracting it with g^(αβ) and differentiations by parts of the two first terms,

Now we use equation (2.2) for the third term and for the fourth one the relation, that follows from it,

Then cancellations will take place leaving only the two derivative terms, that is,

where

This corresponds to equation (6) of [4]. If both the original and varied fields satisfy equation (3.1) we have δU_αβ = 0, and, therefore,

This corresponds to equation (6a) of [4]. We calculate now the variation δ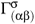 produced by the infinitesimal coordinate transformation

For that purpose we need the transformation property of 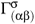under a coordinate transformation to the new system ^µ. The one for even for a nonsymmetric metric can be found in [6]. The result for its αβ- symmetric part is

This result can also be obtained working the transformation of the third order tensor density on the left-hand side of equation (2.1). We show this in ^{Appendix B}.

To first order in the infinitesimal ξ^α we find, from (A7) and from

the result

Choosing ξ^α (x) of the form, not affecting the stationary character of the field,

with a constant c, we find

Inserting this in (A4) we find (noticing that = 0)

In the time independent regime equation (A5) reduces to Bⁱ_,i = 0. Thence, as c is a constant equation (3.5) follows.

Calling the third order tensor density on the left-hand side of equation (2.2) we have for its transformed

where D = det.(∂x^α/∂^λ), the determinant of the coordinate transformation. Making use of

and of its inverse

together with the relation [6]

a little calculation leads to (A1). To see this we start with the contribution of the first, (I), term ∂g^(αβ)/∂x^σ of . After a differentiation by parts and use of the relations above we find

The contribution of the second one is

Those of the third and fourth ones are

and

Adding these contributions and comparing with the explicit expression of on the left-hand side of (B1) equation (A7) follows.

APPENDIX A:  DERIVATION OF EQ. (3.5) BY THE EP METHOD

APPENDIX B:  TRANSFORMATION OF

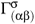
Publication Dates

• Publication in this collection
  22 Sept 2008
• Date of issue
  Sept 2008

History

• Received
  08 July 2008