Optimal paths for minimizing lost available work during heat transfer processes with a generalized heat transfer law

Optimal paths for minimizing lost available work during heat transfer processes with a generalized heat transfer law

Shaojun Xia; Lingen Chen^*; Fengrui Sun

Postgraduate School, Naval University of Engineering, Wuhan 430033, P. R. China

ABSTRACT

A common of finite-time heat transfer processes between high- and low-temperature sides with a generalized heat transfer law [q ∝ (Δ(Tⁿ ))^m] are studied in this paper. The optimal heating and cooling configurations for minimizing lost available work are derived for the fixed initial and final temperatures of the working fluid of the system (low-temperature side). Optimal paths are compared with the common strategies of constant heat flux, constant source (reservoir) temperature and the minimum entropy generation operation by numerical examples. The condition corresponding to the minimum lost available work strategy is that corresponding to a constant rate of lost available work, not only valid for Newton's heat transfer law [q ∝ ΔT] but also valid for the generalized convective heat transfer law [q ∝ (ΔT)^m ]. The obtained results are more general and can provide some theoretical guidelines for the designs and operations of practical heat exchangers.

Keywords: Finite time thermodynamics; Lost available work; Optimal control; Heat transfer process; Heat transfer law

1. INTRODUCTION

Since the mid 1970s, finite-time thermodynamics [1-10] has been applied to optimize the performance of various thermodynamic systems and processes. Heat exchanger is used in modern industry widely. With optimizing the performance of the heat exchanger, the energy utilization efficiency could be improved and the total volume and weight of the heat transfer equipment could be reduced, so the heat exchanger is always one of the main research subjects in finite time thermodynamics. Bejan [11] first analyzed the least combined entropy production induced by the heat transfer and the fluid viscosity as the objective function to optimize the geometry of heat transfer tubes and to find optimum parameters for heat exchangers. Lineskin and Tsirlin [12], Andresen and Gordon [13] showed that the counter-flow heat exchanger could represent the optimal solution for minimizing entropy generation, in which heat transfer between high- and low-temperature sides obeyed Newton's heat transfer law [q ∝ (ΔT)]. Badescu [14] further showed that the counter-flow heat exchanger could also represent the optimal solution for minimizing lost available work. In general, heat transfer is not necessarily Newton's heat transfer law and also obeys other laws. Heat transfer laws not only have significant influences on the performance of the given thermodynamic process [15-19], but also have influences on the optimal configurations of thermodynamic process for the given optimization objectives [20-23]. Nummedal and Kjelstrup [24] considered the reciprocal temperature difference Δ(1/T) as the driving force for heat transfer in irreversible thermodynamics (i.e. the linear phenomenological heat transfer law [q ∝Δ(T^-1)]), and optimized the heat transfer process for minimizing entropy generation. The results show that the reciprocal temperature difference Δ(1/T) is a constant, i.e. the principle of equipartition of forces (EoF). Based on Ref. [24], Johannessen et al. [25] further considered that the heat transfer coefficient is related to the local temperature changes, and showed that the local entropy generation rate is constant, i.e. equipartition of entropy production (EoEP). For a common class of finite-time heat transfer processes between high- and low-temperature sides with generalized radiative heat transfer law [q ∝Δ(Tⁿ)], Andresen and Gordon [26] derived optimal heating and cooling strategies for minimizing entropy generation. Optimal paths are compared with the common strategies of constant heat flux and constant source (reservoir) temperature operation. For a system of uniform temperature in contact with a thermal bath, in which heat transfer between high- and low-temperature sides obeys generalized radiative heat transfer law, Badescu [27] derived optimal heating and cooling strategies for minimizing lost available work. Optimal paths are also compared with the conventional strategies of constant heat-flux, constant source (reservoir) temperature operation and the optimal strategies for minimizing entropy generation. Chen et al. [28] and Li et al. [29,30] investigated the optimal performances of irreversible Carnot heat engine, refrigerator and endoreversible Carnot heat pump with a generalized heat transfer law [q ∝ (Δ(Tⁿ))^m], which included the results with Newton's heat transfer law, the linear phenomenological heat transfer law, the radiative heat transfer law [q ∝Δ(T⁴ )], the Dulong-Petit heat transfer law [q ∝ (ΔT)^1.25][31], the generalized convective transfer law [q ∝ (ΔT)^m] and the generalized radiative transfer law. One of aims of finite time thermodynamics is to pursue generalized rules and results. This paper will extend the previous work [12,13,14,26,27] by using the generalized heat transfer law [q ∝ (ΔTⁿ)^m], in the heat transfer processes between high- and low-temperature sides, to find the optimal heating or cooling strategies for minimizing lost available work. The obtained results are more general and can provide some theoretical guidelines for the designs of practical exchangers.

2. HEAT TRANSFER PROCESS MODEL

The heat transfer process model to be considered in this paper is illustrated in Fig. 1. The following assumptions are made for this model. The only non-negligible thermal resistance is at the heat transfer interface between system and external reservoir, where there is a known thermal conductance k. The practical control variable is the reservoir temperature T₁(t) and the fixed duration of the heat transfer process is τ. Both the initial temperature T₂ (0) and the final temperature T₂(τ) of the system are given. For specificity and clarity of presentation, only the case T₁(t) > T₂ (t) is explicitly considered here (i.e., the system is heated). System cooling involves a change of sign for the heat flux q. Consider that the heat transfer between the system and the reservoir follows a generalized law, including generalized convective heat transfer law and generalized radiative heat transfer law, [q ∝ (ΔTⁿ)^m] [28-30]. Then

As the existence of heat resistance, the entropy generation rate associated with the heat flux q is denoted and is given by:

The total entropy generation for the duration τ of the heat transfer process is:

According to Ref. [27], the lost available work rate is given by:

The total lost available work W_l is obtained by integrating Eq. (4) during the heating process:

In terms of the first law of thermodynamics, the change of system temperature T₂ (t) is governed by

where C is the heat capacity of the working fluid in the system and ₂ = dT₂ /dt.

3 OPTIMAL CONFIGURATION

In a fixed timeτ, the system must be heated from a known initial temperature T₂(0) to a known final temperature T₂(τ). Our problem now is to determine the optimal configuration of the reservoir temperature T₁(t) for minimizing lost available work subjected to the constraint of Eq. (6). Apparently, it is an optimal control problem. Correspondingly, the modified Lagrangian L with a time-dependent Lagrange multiplier λ(t) is given by:

The independent variables are T₁, T₂, and ₂ (and in principle ₁, which does not appear in L). The Euler-Lagrange equations to determine the optimal strategy are then

Substituting Eq. (7) into Eq. (8) yields:

Differentiating Eq. (10) with respect to time t yields:

Eliminating by using Eqs. (9) and (11) yields:

The detailed analytical expressions of the optimal paths will be shown here in dimensionless form. This will make the approach more flexible, increases the generality of the results and allows easy implementation. The following dimensionless variables and constants are defined:

where z is the dimensionless system temperature, u is the ratio of the reservoir temperature to the system temperature, y is the dimensionless reservoir temperature, z_f is the final dimensionless system temperature. A is a special constant, which depends on the parameters k, τ, T₂ (0), m and n. The following relationships exist for the independent and dependent dimensionless variables:

By using the notion Eq. (13), one can define the dimensionless entropy generation rate and the entropy generation , respectively:

Here, Eqs. (2) and (3) are used. Similarly, the dimensionless rate of lost available work

_l and the dimensionless lost available work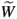 _l are defined, respectively:

Here, Eqs. (4), (5) and (13) are used. By using the notation Eq. (13), the new forms of Eqs. (6) and (12) are, respectively,

Eq. (19) gives through integration:

where C_W is an integration constant, which is determined by T₂ (0) and z_f. From Eqs. (20) and (21) one obtains:

The optimal heating paths are obtained by solving Eqs. (21) and (22). Inputs are the values of m, n, A and z_f .

4. DISCUSSIONS

4.1. Effects of heat transfer laws

When m = 1, the heat transfer law becomes the generalized radiative heat transfer law, Eqs. (21) and (22) become

They are the same results as those obtained in Ref. [27]. If n = 1 further, Equations (23) and (24) are the results of the heat transfer process with Newton's heat transfer law [14, 27]. If n = -1 further, Equations (23) and (24) are the results of the heat transfer process with the linear phenomenological heat transfer law [27]. If n = 4 further, Equations (23) and (24) are the results of the heat transfer process with the radiative heat transfer law [27].

When n = 1, the heat transfer law becomes the generalized convective heat transfer law. Eqs. (21) and (22) take the form

If m = 1 further, Equations (25) and (26) are the results of the heat transfer process with Newton's heat transfer law [14, 27]. If m = 1.25 further, Equations (14) and (15) are the results of the heat transfer process with the Dulong-Petit heat transfer law, which become:

Substituting Eqs. (27) and (28) into Eqs. (17) and (18) yields:

From Eq. (29), it can be concluded that the condition corresponding to the minimum lost available work strategy with the Dulong-Petit heat transfer law is that corresponding to a constant rate of lost available work.

When m = 1.25 and n = 4, the heat transfer law becomes a complex heat transfer law q ∝ (Δ(T⁴))^1.25 . There is no analytical solution for this case, so a numerical approach is necessary.

Salamon et al. [32] proved that for any linear finite-time process, the strategy that minimizes entropy generation was the one that corresponds to a constant rate of entropy generation. Andresen and Gordon [26] further showed that only for the specific cases of Newton's and linear phenomenological transfer laws was the observation of Salamon et al valid. Meanwhile, they proved that for general non-linear problems, a constant rate of entropy generation was not the optimal strategy. Badescu [27] showed that the optimum rate of lost available work is constant over time in the case of the minimum lost available work strategy with Newton's heat transfer law.

When n = 1, Eq. (17) becomes

Evidently, the right side of Eq. (30) is the same as the left side of Eq. (25). Hence, the condition corresponding to the minimum lost available work strategy is that corresponding to a constant rate of lost available work, not only valid for Newton's heat transfer law but also valid for the generalized convective heat transfer law, in which the conclusions in Refs. [14, 27] are included.

4.2. Other heating and cooling strategies

Besides the optimal strategy for minimizing lost available work, there are other cases, such as the optimal strategies for minimizing entropy generation, the strategies of constant heat flux and constant reservoir temperature operation and so on.

4.2.1. Optimal strategies for minimizing entropy generation

According to Ref. [33], the optimal strategies for minimizing entropy generation are:

where C_S is an integration constant, which is determined by T₂ (0) and z_f .

4.2.2. Constant reservoir temperature operation

When y = const, the unknown y is determined by the following implicit equation:

Once y is found from Eq. (33), z(ω) is obtained by substituting y into the following equation:

Finally, The value of u(ω) is obtained by u(ω) = y/z(ω). When m = 1 and n is equal to 1, -1, and 4, respectively, the results with Newton's, the linear phenomenological and radiative heat transfer laws are obtained in Refs. [26, 27]. When m = 1.25 and n = 1, the result with the Dulong-Petit heat transfer law is obtained. In this case, Eqs. (33) and (34) become

When m = 1.25 and n = 4, the result with the complex heat transfer law [q ∝ (Δ(T⁴ ))^1.25 ] is obtained. In this case, Eqs. (33) and (34) become

4.2.3. Constant heat flux operation

When q = const, from Eqs. (1) and (13), one can obtain

When m = 1 and n is equal to 1, -1, and 4, respectively, the results with Newton's, the linear phenomenological and radiative heat transfer laws are obtained in Refs. [26, 27]. When m = 1.25 and n = 1, the result with the Dulong-Petit heat transfer law is obtained. In this case, Eq. (40) becomes

When m = 1.25 and n = 4, the result with the complex heat transfer law [q ∝ (Δ(T⁴))^1.25 ] is obtained. In this case, Eq. (40) becomes

5. NUMERICAL EXAMPLES

For the convenience of analysis, W_l = mindenotes the optimal strategy for minimizing lost available work, S = mindenotes the optimal strategy for minimizing entropy generation, q = const denotes the strategy of constant heat flux operation, and T₁ = const denotes the strategy of constant reservoir temperature operation.

5.1. Numerical example for the Dulong-Petit heat transfer law

In this case, A = 2.5 and z_f = 2 are set. Fig. 2 shows dependence of the dimensionless system temperature z(ω) on the dimensionless time w in case of the Dulong-Petit heat transfer law. The most abrupt variation of z(ω) at the starting time corresponds to the strategy of T₁ = const. It is associated with the highest rate of entropy generation. The other three strategies show an almost linear increase of system temperature over time. Fig. 3 shows dependence of the ratio of the reservoir temperature to the system temperature u(ω) on the dimensionless time ω in case of the Dulong-Petit heat transfer law. The strategies of S = min and W_l = minshow a slight function u(ω) decreasing over time. Both the final reservoir temperature and the final system temperature for the strategies of q = const are equal to those for the strategies of W_l = min, but the initial reservoir temperature for the strategies of q = const is larger than that for the strategies of W_l = min, i.e. the temperature difference between the reservoir and the system for the strategies of q = const is larger than that for the strategies of W_l = min. Hence the entropy generation for the strategies of q = const is larger than that for the strategies of W_l = min. The temperature difference between the reservoir and the system for the strategies of T₁ = // during the heat transfer processes is the largest among various strategies, so the strategies of T₁ = const leads to the largest entropy generation [26, 27, 33].

Fig. 4 shows dependence of the dimensionless rate of lost available work _l on the dimensionless time ω in case of the Dulong-Petit heat transfer law. From Fig. 4, it can be seen that the profiles of _l for various heating strategies are different. The strategy of q = const shows a function _l decreasing over time, while the strategy of S = min shows a function _l increasing over time. The strategy of T₁ = const shows a fast function _l decreasing at the beginning of the heat transfer process, but _l varies little at the end of the heat transfer process. Also from Fig. 4, the rate of lost available work _l for the strategy of W_l = min is constant in the case of the Dulong-Petit heat transfer law, which is the same as the result with Newton's heat transfer law [27]. As is discussed in section 4.1, both Newton's and the Dulong-Petit heat transfer laws belong to special cases of the generalized convective heat transfer law, so the condition corresponding to the minimum lost available work strategy is that corresponding to a constant rate of lost available work, not only valid for Newton's heat transfer law but also valid for the Dulong-Petit heat transfer law. Fig. 5 shows dependence of the dimensionless lost available work 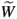_l on the dimensionless system final temperature z_f in case of the Dulong-Petit heat transfer law. The strategies of W_l = min, S = min and q = const show similar results of the lost available work 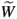_l , i.e. all of the values of 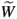_l increases with the increase of z_f . Also from Fig. 5, it can be seen that keeping a constant reservoir temperature is the worst strategy as far as the lost available work is concerned.

5.2. Numerical example for the heat transfer law q ∝ ( Δ (T⁴))^1.25

In this case, A = 0.02 and z_f = 2 are set. Fig. 6 shows dependence of the dimensionless system temperature z(ω) on the dimensionless time w in case of the heat transfer law q ∝ (Δ(T⁴))^1.25 . The highest dimensionless system temperature z(ω) during the whole heat transfer process corresponds to the strategy of T₁ = const, the dimensionless system temperature z(ω) for the strategy of q = const lies between that for the strategy of T₁ = const and that for the strategy of S = min, the lowest dimensionless system temperature z(ω) corresponds to the strategy of W_l = min. Fig. 7 shows dependence of the ratio of the reservoir temperature to the system temperature u(ω) on the dimensionless time w in case of the heat transfer law q ∝ (Δ(T⁴))^1.25 . At the beginning of heat transfer process, the temperature ratio u(ω) for the strategy of W_l = min is larger than that for the other strategies, while at the end of heat transfer process, the temperature ratio u(ω) for the strategy of W_l = min is smaller than those for the other strategies. Also from Fig. 7, the variation of the reservoir temperature for the strategy of S = min is very similar to that for the strategy of W_l = min. Fig. 8 shows dependence of the dimensionless rate of lost available work _l on the dimensionless time w in case of the heat transfer law q ∝ (Δ(T⁴))^1.25 . Compared to the results with the Dulong-Petit heat transfer law, the differences of the time variations of _l among the strategies of q = const, S = min and T₁ = const are smaller. The strategy of W_l = min shows a slow and almost linear time variation of _l , i.e. at the beginning of heat transfer process, the rate of lost available work _l for the strategy of W_l = min is smaller than those for the other strategies, while at the end of heat transfer process, the rate of lost available work _l for the strategy of W_l = min is larger than those for the other strategies.

5.3. Performance comparisons for special heat transfer laws

According to Ref. [27], the parameters in Newton's, the linear phenomenological and radiative heat transfer laws are used. A = 10 and z_f = 2 are set for Newton's heat transfer law. A = -10 and z_f = 2are set for the linear phenomenological heat transfer law, A = 2.5 and z_f = 2 are set for the Dulong-Petit heat transfer law, A = 0.025 and z_f = 2 are set for the radiative heat transfer law, and A = 0.02 and z_f = 2 are set for the heat transfer law q ∝ (Δ(T⁴))^1.25 . Fig. 9 shows dependence of the dimensionless system temperature z(ω) on the dimensionless time ω in case of the minimum lost available work with the special heat transfer laws. The results show that differences between the optimal variation of the system temperature with Newton's heat transfer law and that with the Dulong-Petit heat transfer law are so small that could be negligible. The time variation of the dimensionless system temperature z(ω) with the Dulong-Petit heat transfer law is very similar to that with Newton's heat transfer law, while the time variation of the dimensionless system temperature z(ω) with the radiative heat transfer law is very similar to that with the heat transfer law q ∝ (Δ(T⁴))^1.25. It's evident that the heat transfer laws have effects on the optimal configuration of the system temperature. Fig. 10 shows dependence of the dimensionless reservoir temperature y(ω) on the dimensionless time ω in case of the minimum lost available work with the special heat transfer laws. From Fig. 10, the optimal configuration of the system temperature for Newton's heat transfer law are almost the same as that for the Dulong-Petit heat transfer law, but the optimal configurations of the reservoir temperature for them are different. The reservoir temperature for the Dulong-Petit heat transfer law over the time is smaller than that for Newton's heat transfer law. The variation of the optimal reservoir temperature for Newton's heat transfer law is very similar to that for the Dulong-Petit heat transfer law, while the variation of the optimal reservoir temperature for the radiative heat transfer law is very similar to that for the heat transfer law q ∝ (Δ(T⁴))^1.25. Besides, the variation of the optimal reservoir temperature for the linear phenomenological heat transfer law is different from those for the other heat transfer laws. This shows that the heat transfer laws also have effects on the optimal configuration of the reservoir temperature.

6. CONCLUSION

A common of finite-time heat transfer processes between high- and low-temperature sides with a generalized heat transfer law q ∝ (Δ(Tⁿ))^m is studied in this paper. The optimal heating and cooling configurations for minimizing lost available work are derived for the fixed initial and final temperatures of the low-temperature side working fluid of the system, the obtained results are general, including those results with special heat transfer laws. A more general conclusion is formed: the condition corresponding to the minimum lost available work strategy is that corresponding to a constant rate of lost available work, not only valid for Newton's heat transfer law but also valid for generalized convective heat transfer law q ∝ (ΔT)^m, in which the results in Refs. [14, 27] are included. Numerical examples for minimizing lost available work with the Dulong-Petit heat transfer law and the heat transfer law q ∝ (Δ(T⁴))^1.25 are provided, and the results are also compared with optimal strategy for minimizing entropy generation, and the common strategies of constant heat flux and constant reservoir temperature operation. Numerical calculations show that the constant reservoir temperature strategy leads to the largest lost available work, the strategies of minimum entropy generation and constant heat flux produce less lost available work. Performance comparisons for special heat transfer laws are also provided, and the results show that the heat transfer laws have effects on the optimal time path of heat transfer processes. As has been stated in Refs. [14, 27], optimizing the thermodynamic systems for minimizing lost available work is different from that for minimizing entropy generation when choosing different reference states. Certainly, the two methods are equivalent when the universe environment is chosen to be the reference state. Choosing between the two optimum criteria (i.e. minimum entropy generation and minimum lost available work) depends on the particular implementation of the heating/cooling process. The method based on the entropy generation minimization could be used, for example, in the case of a chemical factory that delivers various products and secondary utilities as flows of heat and power. The entropy generation should be seen in this case as a common measure for the cost of production of all these outputs of different nature, allowing an overall optimization. The method based on lost available work minimization could be used for example during the design of some power plants or in those cases where the main interest is in delivering a maximum output power. The obtained results in this paper are general and can provide some theoretical guidelines for the designs of practical heat exchangers.

Acknowledgements

This paper is supported by the Program for New Century Excellent Talents in University of P. R. China (Project No. 20041006) and The Foundation for the Author of National Excellent Doctoral Dissertation of P. R. China (Project No. 200136).

(Received on 21 December, 2008)

• [1] B. Andresen. Finite-Time Thermodynamics Physics Laboratory II, University of Copen- hagen, 1983.
• [2] B. Andresen, R.S. Berry, M.J. Ondrechen, P. Salamon Thermodynamics for processes in finite time Acc. Chem. Res. 1984, 17 (8): 266-271.
• [3] S. Sieniutycz and P. Salamon (ed.). Advances in Thermodynamics Volume 4: Finite Time Thermodynamics and Thermoeconomics New York: Taylor & Francis, 1990.
• [4] A. De Vos. Endoreversible Thermodynamics of Solar Energy Conversion Oxford: Oxford University, 1992.
• [5] A. Bejan. Entropy generation minimization: The new thermodynamics of finite-size device and finite-time processes J. Appl. Phys., 1996, 79 (3): 1191-1218.
• [6] R.S. Berry, V. A. Kazakov, S. Sieniutycz, Z. Szwast and A.M. Tsirlin. Thermodynamic Optimization of Finite Time Processes. Chichester: Wiley, 1999.
• [7] L. Chen, C. Wu, F. Sun. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J. Non-Equilib. Thermodyn., 1999, 24 (4): 327-359.
• [8] K.H. Hoffman, J. Burzler, A. Fischer, M. Schaller, S. Schubert. Optimal process paths for endoreversible systems. J. Non-Equilib. Thermodyn., 2003, 28 (3): 233-268.
• [9] L. Chen, F. Sun. Advances in Finite Time Thermodynamics: Analysis and optimization. New York: Nova Science Publishers, 2004.
• [10] G. Aragon-Gonzalez, A. Canales-Palma, A. Leon-Galicia, J.R. Morales-Gomez. Maximum power, ecological function and efficiency of an irreversible Carnot cycle. A cost and effectiveness optimization. Brazilian J. Physics, 2008, 38 (4): 1-8.
• [11] A. Bejan. Entropy Generation through Heat and Fluid Flow. New York: Wiley, 1982: 135-145.
• [12] S.B. Linetskii, A.M. Tsirlin. Evaluating thermodynamic efficiency and optimizing heat exchangers. Thermal Engineering, 1988, 35(10): 593-597.
• [13] B. Andresen, J.M. Gordon. Optimal heating and cooling strategies for heat exchanger design. J. Appl. Phys., 1992, 71 (1): 76-80.
• [14] V. Badescu. Optimal strategies for steady state heat exchanger operation. J. Phys. D: Appl. Phys., 2004, 37 (16): 2298-2304.
• [15] A. De Vos. Efficiency of some heat engines at maximum power conditions. Am. J. Phys., 1985, 53(6): 570-573
• [16] L. Chen, F. Sun, C. Wu. The influence of heat transfer law on the endoreversible Carnot refrigerator. J. Institute Energy, 1996, 69 (479): 96-100.
• [17] L. Chen, F. Sun, C. Wu. Effect of heat transfer law on the performance of a generalized irreversible Carnot engine. J. Phys. D: Appl. Phys., 1999, 32 (2): 99-105.
• [18] M. Huleihil, B. Andresen. Convective heat transfer law for an endoreversible engine. J. Appl. Phys., 2006, 100 (1): 014911.
• [19] X. Qin, L. Chen, F. Sun, L. He. Model of real absorption heat pump cycle with a generalized heat transfer law and its performance. Proc. IMechE, Part A: Power & Energy, 2007, 221(A7): 907-916.
• [20] L. Chen, F. Sun, C. Wu. Optimal expansion of a heated working fluid with phenomenological heat transfer. Energy Convers. Mgmt., 1998, 39 (3/4): 149-156.
• [21] S. Sieniutycz, P. Kuran. Modeling thermal behavior and work flux in finite-rate systems with radiation. Int. J. Heat Mass Transfer, 2006, 49 (17-18): 3264-3283.
• [22] H. Song, L. Chen, J. Li, F. Sun, C. Wu. Optimal configuration of a class of endoreversible heat engines with linear phenomenological heat transfer law [q ∝ Δ (T^-1)]. J. Appl. Phys., 2006, 100 (12): 124907
• [23] H. Song, L. Chen, F. Sun. Optimal expansion of a heated working fluid for maximum work output with generalized radiative heat transfer law. J. Appl. Phys., 2007, 102 (9): 094901.
• [24] L. Nummedal, S. Kjelstrup. Equipartition of forces as a lower bound on the entropy production in heat exchange. Int. J. Heat & Mass Transfer, 2001, 44 (15): 2827-2833.
• [25] E. Johannessen, L. Nummedal, S. Kjelstrup. Minimizing the entropy production in heat exchange. Int. J. Heat & Mass Transfer, 2002, 45 (13): 2649-2854.
• [26] B. Andresen, J. M. Gordon. Optimal paths for minimizing entropy generation in a common class of finite time heating and cooling processes. Int. J. Heat & Fluid Flow, 1992, 13 (3): 294-299.
• [27] V. Badescu. Optimal paths for minimizing lost available work during usual heat transfer processes. J. Non-Equilib. Thermodyn., 2004, 29 (1): 53-73.
• [28] L. Chen, J. Li, F. Sun. Generalized irreversible heat-engine experiencing a complex heat-transfer law. Appl. Energy, 2008, 85 (1): 52-60.
• [29] J. Li , L. Chen, F. Sun. Heating load vs. COP characteristic of an endoreversible Carnot heat pump subjected to heat transfer law q ∝ (ΔTⁿ)^m . Appl. Energy, 2008, 85(2-3): 96-100.
• [30] J. Li, L. Chen, F. Sun. Cooling load and coefficient of performance optimizations for a generalized irreversible Carnot refrigerator with heat transfer law q ∝ (ΔTⁿ)^m . Proceedings IMechE, Part E: J. Process Mech. Engineering, 2008, 222 (1): 55-62.
• [31] C .T. O'Sullivan. Newton's law of cooling-A critical assessment. Am. J. Phys., 1990, 58 (12): 956-960.
• [32] P. Salamon, A. Nitan, B. Andresen, R.S. Berry. Minimum entropy production and the optimization of heat engines. Phys. Rev. A, 1980, 21 (6): 2115-2129.
• [33] L. Chen, S. Xia, F. Sun. Optimal paths for minimizing entropy generation during heat transfer processes with a generalized heat transfer law. J. Appl. Phys, in press.

Publication Dates

• Publication in this collection
  15 June 2009
• Date of issue
  Mar 2009

History

• Received
  21 Dec 2008