Abstracts
The aim of this study was to assess the efficiency of the simulated individual BLUP (BLUPIS) method in selecting genotypes within full-sib families of sugarcane in ratoon stage, through comparison with selection using the individual BLUP method. The optimal number of genotypes to be selected in the best families were established for mean stems mass, total soluble solids assay (BRIX), ton of stalks per hectare, and BRIX tons per hectare traits. Seventeen full-sib families were assessed in the Centre for Experimentation in Sugarcane, located in Oratórios, MG, Brazil. Mixed model methodology was used to predict the genotypic effects of each family and the genotypic values of each individual within family. BLUPIS method is efficient for individual selection. The optimal number of genotypes to be selected in the best family for obtaining higher efficiency of the BLUPIS method is 100 in the majority of cases.
Saccharum sp. ; best linear unbiased predictors (BLUP); BLUPIS; selection strategies; sugarcane breeding
A eficiência do método BLUP individual simulado (BLUPIS) na seleção de genótipos dentro de famílias de irmãos germanos de cana-de-açúcar no estágio de cana soca, comparada com a seleção utilizando o método BLUP individual, foi avaliada. O número ótimo de genótipos a serem selecionados na melhor família foi estabelecido para as características massa media de colmos, teor de sólidos solúveis totais (BRIX), tonelada de colmos por hectare e tonelada de BRIX por hectare. Foram avaliadas dezessete famílias de irmãos germanos no Centro de Experimentação em Cana-de-açúcar, localizado em Oratórios, MG, Brasil. A metodologia de modelo misto foi utilizada para predizer os efeitos genotípicos de cada família e os valores genotípicos de cada individuo dentro de família. O método BLUPIS mostrou-se eficiente para a seleção individual. O número ótimo de genótipos a serem selecionados na melhor família para obter a maior eficiência do método BLUPIS foi 100, na maioria dos casos.
Saccharum sp. ; melhor preditor linear não-viesado (BLUP); BLUPIS; estratégias de seleção; melhoramento de cana-de-açúcar
INTRODUCTION
Individual selection at early stages in sugarcane (Saccharum sp.) breeding was initially based on mass selection methods (Mariotti et al. 1999Mariotti JA, Cuenya MI and Salas MBG (1999) Análisis de componentes familiares e intra-familiares em progênies de combinaciones biparentales de cana de azucar (Saccharum spp.). Revista Industrial y Agrícola de Tucumán 76: 52-57.), Australian sequential selection (between families, followed by mass selection) (Kimbeng and Cox 2003Kimbeng CA and Cox MC (2003) Early generation selection of sugarcane families and clones in australia: a review. Journal American Society of Sugarcane Technologists 23: 20-39.), and modified sequential selection (Bressiani et al. 2005Bressiani JA, Vencovsky R and Burnquist WL (2005) Modified Sequential Selection in sugarcane. Proceedings of International Society of Sugarcane Technologists. ISSCT, Guatemala, p.459-467.). These last two methods use family information for selection and, therefore, are superior in relation to mass selection for traits with family mean heritability higher than individual plant heritability. Family selection has been proven to be essential in sugarcane breeding (Barbosa et al. 2004Barbosa MHP, Resende MDV, Peternelli LA, Bressiani JA, Silveira LCI, Silva FL and Figueiredo ICR (2004) Use of REML/BLUP for the selection of sugarcane families specialised in biomass production. Crop Breeding and Applied Biotechnology 4: 218-226., Atkin et al. 2010Atkin FC, Dieters MJ and Stringer JK (2010) Impact of depth of pedigree and inclusion of historical data on the estimation of additive variance and breeding values in a sugarcane breeding program. Theoretical and Applied Genetics 119: 555-565., Stringer et al. 2011Stringer JK, Cox MC, Atkin FC, WEI X and Hogarth DM (2011) Family selection improves the efficiency and effectiveness of selecting original seedlings and parents. Sugar Tech 13: 36-41.).
The optimal strategy for the selection of individuals in the early stages of sugarcane breeding would be through genotypic values predicted by BLUPI (Resende 2002Resende MDV (2002) Genética biométrica e estatística no melhoramento de plantas perenes. Embrapa Informação Tecnológica, Brasília, 975p.). However, this method has not been used in sugarcane breeding due to the practical difficulties and uneconomical aspects of obtaining data from individual plants. Otherwise, sugarcane breeding strategies have relied on family selection (Atkin et al. 2010Atkin FC, Dieters MJ and Stringer JK (2010) Impact of depth of pedigree and inclusion of historical data on the estimation of additive variance and breeding values in a sugarcane breeding program. Theoretical and Applied Genetics 119: 555-565., Stringer et al. 2011Stringer JK, Cox MC, Atkin FC, WEI X and Hogarth DM (2011) Family selection improves the efficiency and effectiveness of selecting original seedlings and parents. Sugar Tech 13: 36-41.).
A practical method that resembles BLUPI was proposed by Resende and Barbosa (2006). This selection method, called simulated individual BLUP (BLUPIS), aims to promote a dynamic allocation of the number of individuals selected per family, considering BLUP as the basis for the genotypic effects of these families. Additionally, according to the authors, by using the mean genotypic value of experimental plots within each progeny, BLUPIS method indicates in which replication the best individuals of each family are. BLUPIS method has been successfully applied in plant breeding (Resende et al. 2006, Oliveira et al. 2008, Farias Neto et al. 2009, Oliveira et al. 2011).
The aim of this study was to assess the efficiency of BLUPIS method in selecting genotypes within sugarcane full-sib families in ratoon stage, through comparison with selection using BLUPI method. In parallel, the optimal number of genotypes to be selected in the best family was established for four assessed traits.
MATERIAL AND METHODS
Experimental details
Seventeen sugarcane full-sib families were assessed. These families derived from crossings performed in 2003 at the Flowering and Crossings Station, located in Serra do Ouro, city of Murici (lat 9° 13' S, long 35° 50' W, and alt 450-500 m asl), AL, Brazil.
Seedlings obtained from each family were transplanted, in March 2004, at the Centre for Experimentation in Sugarcane (CECA), located in Oratórios, MG, Brazil (lat 20o 25' S, long 42o 48' W, and alt 494 m asl), of the Universidade Federal de Viçosa.
The trial was established in a randomized complete block design with six replications. Each experimental plot consisted in two rows spaced 1.40m apart, and plants were spaced 0.5 m apart, totalling 120 genotypes assessed per family. Due to eventual death of genotypes, the total final number of assessed genotypes was 1637.
Traits used to assess the efficiency of BLUPIS selection method were: mean stem mass (MSM), total soluble solids assay (BRIX), tons of stalks per hectare (TSH), and BRIX tons per hectare (TBH), assessed in April 2006, at ratoon stage.
Traits individually assessed in the plot were: mean stalk height (SH) in cm, mean stalk diameter (SD) in cm, number of stalks of each genotype (NS) and total soluble solids (BRIX). Assessment at the individual level was also necessary for the genetic values of each genotype (BLUPI method) to be estimated, providing the selection of the best genotype, as well as a comparison with the selection recommended by BLUPIS method.
By using the assessed traits, it was possible to estimate the MSM variable, expressed
in kg, through the estimator proposed by Chang and
Milligan (1992Chang YS and Milligan SB (1992) Estimating the potential of sugarcane
families to produce elite genotypes using univariate cross prediction methods.
Theoretical and Applied Genetics 84: 662-671.). This estimator is defined by:  ,
,
where d is the stalk specific density, the value of which is 1.0 g cm-³, and π is expressed by approximate dimensionless value of 3.141593.
The TSH estimator of each individual was:  , where tau is the ground
area that each individual explores, expressed in m². In this work, the tau value was
0.7 m².
, where tau is the ground
area that each individual explores, expressed in m². In this work, the tau value was
0.7 m².
For the TBH characteristic, the TSH value of each individual was multiplied by the corresponding BRIX value.
Information at the plot level, necessary for application of BLUPIS method, was obtained through sampling of 14 random individuals of each plot per family. This number of individuals was adopted since the total number of individuals per family was low due to the high mortality rate in the experimental plots. Thus, through the means of the assessed variables in these individuals (SH, SD, NS and BRIX), it was possible to estimate the values at the plot level for MSM, BRIX, TSH and TBH, following previously described estimators.
Procedure for data analysis
Statistical analyses were performed using the mixed linear model methodology (Resende 2002Resende MDV (2002) Genética biométrica e estatística no melhoramento de plantas perenes. Embrapa Informação Tecnológica, Brasília, 975p.) with aid of a computer program in genetics and statistics Selegen-Reml/Blup (Resende 2007Resende MDV (2007a) Matemática e estatística na análise de experimentos e no melhoramento genético. Embrapa Florestas, Colombo, 591p. a and bResende MDV (2007b) Selegen-REML/BLUP: sistema estatístico e seleção genética computadorizada via modelos lineares mistos. Embrapa Florestas, Colombo, 359p.).
The applied linear mixed models were
1.  , where y
is the vector of data; r is the vector of replication effects (assumed as fixed)
summed to the general mean; g is the vector of genotypic effects of family (assumed
as random); and e is the vector of errors or residuals (random effects). Capital
letters represent the incidence matrices for these effects. This model is necessary
for estimating the genotypic effects of each family based on plot means, which are
essential for the usage of BLUPIS selection method.
, where y
is the vector of data; r is the vector of replication effects (assumed as fixed)
summed to the general mean; g is the vector of genotypic effects of family (assumed
as random); and e is the vector of errors or residuals (random effects). Capital
letters represent the incidence matrices for these effects. This model is necessary
for estimating the genotypic effects of each family based on plot means, which are
essential for the usage of BLUPIS selection method.
2.  , where y
is the vector of data; r is the vector of replication effects (assumed as fixed)
summed to the general mean; g the is vector of individual genotypic effects (assumed
as random); p is the vector of random plot effects; and e is the vector of errors or
residuals (random effects). Capital letters represent the incidence matrices for
these effects. This model was used as a mean to obtain the genotypic values (g) of
each individual within the family necessary in the BLUPI selection method. The
individual genotypic values were predicted by adjusting g to the model (2).
, where y
is the vector of data; r is the vector of replication effects (assumed as fixed)
summed to the general mean; g the is vector of individual genotypic effects (assumed
as random); p is the vector of random plot effects; and e is the vector of errors or
residuals (random effects). Capital letters represent the incidence matrices for
these effects. This model was used as a mean to obtain the genotypic values (g) of
each individual within the family necessary in the BLUPI selection method. The
individual genotypic values were predicted by adjusting g to the model (2).
The variance components were obtained by the Restricted Maximum Likelihood (REML) method (Paterson and Thompson 1971Patterson HD and Thompson R (1971) Recovery of inter-block information when block sizes are unequal. Biometrika 58: 545-554.), and were used to calculate the heritability at individual and family means levels, and also for obtaining the BLUP of the genotypic effects.
Simulated individual BLUP selection method (BLUPIS)
The BLUPIS method (Resende and Barbosa 2006Resende MDV and Barbosa MHP (2006) Selection via simulated Blup base on family genotypic effects in sugarcane. Pesquisa Agropecuária Brasileira 41: 421-429.) consists of dynamically determining the number of individuals to be selected in each family, with no individual assessment.
The expression which determines the number nk of individuals to be selected in each
family k is  ,
where: gˆj refers to the genotypic effect of the best family; gˆk refers to the
genotypic effect of the k-th family; and nj equals the number of selected individuals
in the best family. In this paper, it was considered 50, 100, and 120 individuals
selected in the best family, for each characteristic, with the aim of obtaining the
best performance of BLUPIS method in comparison to BLUPI.
,
where: gˆj refers to the genotypic effect of the best family; gˆk refers to the
genotypic effect of the k-th family; and nj equals the number of selected individuals
in the best family. In this paper, it was considered 50, 100, and 120 individuals
selected in the best family, for each characteristic, with the aim of obtaining the
best performance of BLUPIS method in comparison to BLUPI.
The number of individuals (r) to be selected from each plot is obtained from
 , where:
gˆparcr is the genotypic effect of each plot of each family; u is the general mean of
each characteristic; and
, where:
gˆparcr is the genotypic effect of each plot of each family; u is the general mean of
each characteristic; and  refers to the sum of
genotypic values
refers to the sum of
genotypic values  of all plots of family
k.
of all plots of family
k.
Comparison between BLUPIS and BLUPI
For comparison between methods, linear regression analyses were used following the
model:  , where
yi is the number of genotypes selected by BLUPI method in the ith family; xi is the
number of genotypes indicated for selection by the BLUPIS method in the ith family;
β0 is the intercept; β1 is the slope of the regression line; and ei is the random
error of the simple linear regression. Regression analyses were performed using the
software Genes (Cruz 2006Cruz CD (2006) Programa Genes: versão Windows - Biometria. Editora UFV,
Viçosa, 381p.).
, where
yi is the number of genotypes selected by BLUPI method in the ith family; xi is the
number of genotypes indicated for selection by the BLUPIS method in the ith family;
β0 is the intercept; β1 is the slope of the regression line; and ei is the random
error of the simple linear regression. Regression analyses were performed using the
software Genes (Cruz 2006Cruz CD (2006) Programa Genes: versão Windows - Biometria. Editora UFV,
Viçosa, 381p.).
Through these regression analyses, it was possible to verify the efficiency of the BLUPIS selection method when compared to selection performed by the BLUPI method, as well as to verify the optimal number of genotypes to be selected in the best sugarcane family for each assessed characteristic.
RESULTS AND DISCUSSION
The values of the residual variation coefficients (CVe) for MSM, TSH and TBH were of high magnitude, reflecting high plot and within-plot variations (Table 1). For MSM and TSH, similar values were found by Barbosa et al. (2005)Barbosa MHP, Resende MDV, Bressiani JA, Silveira LCI and Peternelli LA (2005) Selection of sugarcane families and parents by Reml/Blup. Crop Breeding and Applied Biotechnology 5: 443-450.. For BRIX, the CVe was of low magnitude, suggesting a high experimental accuracy for this characteristic.
The CVe values are an inadequate parameter for assessing the quality of experiments, since they do not inform the selective accuracy and do not take into account genotypic variation level or number of replications (Resende and Duarte 2007). Resende (2002Resende MDV (2002) Genética biométrica e estatística no melhoramento de plantas perenes. Embrapa Informação Tecnológica, Brasília, 975p.) states that an adequate statistic for assessing the quality of experiments would be that which simultaneously considers the experimental variation coefficient, the number of replications, and the genotypic variation coefficient. Such a parameter is the selective accuracy.
The selective accuracy values (Acfam) obtained were of high magnitude (> 0.74) (Table 1), according to the limiting values suggested by Resende and Duarte (2007)Resende MDV and Duarte JB (2007) Precisão e controle de qualidade em experimentos de avaliação de cultivares. Pesquisa Agropecuária Tropical 37: 182-194., which provide family selection with great precision. Family selectivee accuracy values were 0.77, 0.79, 0.74, and 0.75, for MSM, BRIX, TSH, and TBH, respectively.
Santos et al. (2014) to study the genetic control of resistance to rust in Eucalyptus pellita through inoculations under controlled conditions four full-sib families, found a high magnitude of the value of selective accuracy, concluding that it would be possible to obtain genetic gain with selection of resistant families for this disease.
Estimates of the narrow-sense individual heritabilities (hˆ 2 a) were of low magnitude, as expected for quantitative traits. However, their standard errors were of low magnitude, indicating that these heritability values were statistically different from zero, enabling the selection of superior individuals. This significance in genetic effect was also confirmed by the deviance analysis using the likelihood ratio test (Peternelli et al. 2011Peternelli LA, Resende MDVand Paula TO (2011) Experimentação e análise estatística em cana-de-açúcar. In Santos F, Borém A, Caldas C (Org.) Cana-de-Açúcar: bioenergia, açúcar e etanol - tecnologias e perspectivas. 2nd ed., Editora UFV, Viçosa, p. 333-353.). Estimates of hˆ 2 a were 0.05; 0.09; 0.03 and 0.03, for MSM, BRIX, TSH and TBH, respectively. After adjustment (as done by the BLUP procedure) of the individual phenotypic values for environmental plot effects, the heritability for within-family selection was higher.
Selection via BLUPIS and BLUPI procedures
The selection of individuals via BLUPI procedure was carried out from the classification of the predicted genotypic value of all the assessed individuals, taking as a basis the same number of genotypes indicated for selection via the BLUPIS method (Tables 2 and 3).
Genotypic effects (gˆj), number of genotypes to be selected (nk) by the BLUPIS method, and the number of genotypes selected through individual genotypic values predicted via BLUPI, for mean stalks mass (MSM) and total soluble solids assay (BRIX), considering the number of genotypes to be selected in the best family (nj), equal to 50, 100 and 120, of sugarcane at the ratoon stage
Genotypic effects (gˆj), number of genotypes to be selected (nk) by the BLUPIS method and the number of genotypes selected through individual genotypic values predicted via BLUPI, for ton of stalks per hectare (TSH) and BRIX tons per hectare, considering the number of genotypes to be selected in the best family (nj), equal to 50, 100 and 120, of sugarcane at the ratoon stage
For MSM, and considering the total number of selected genotypes, selection rates (total number of selected individuals in the best families divided by 1637) were approximately 13, 27, and 32% for nj equal to 50, 100, and 120, respectively. For BRIX, selection rates were 16, 32, and 39%, respectively (Table 2).
For TSH and TBH, families 14, 19, 48, 82, 98, 109, and 112 had negative values for the genotypic effect (Table 3). Therefore, these families did not contribute to the indication of genotypes to be selected by the BLUPIS method. This method automatically eliminates families with a negative genotypic effect, i.e., those which present genotypic effect lower than the general mean of the experiment. This is reasonable when the very low probability of obtaining a superior clone in these families is considered (Resende and Barbosa 2006Resende MDV and Barbosa MHP (2006) Selection via simulated Blup base on family genotypic effects in sugarcane. Pesquisa Agropecuária Brasileira 41: 421-429.).
Selection rates for nj equal to 50, 100, and 120 for TSH were approximately 16, 32, and 39%, respectively, and for TBH, these rates were 19, 38, and 45%.
The number of selected individuals by family decreased progressively and slowly from 100 or 120 for the best family, to zero for the null genetic-effect family. These results reflect the importance of the BLUPIS procedure in dynamically allocating the number of selected individuals per family, at the expense of the acceptance, a priori, of fixed selection proportions within families, as practiced in Australia (Kimbeng and Cox 2003Kimbeng CA and Cox MC (2003) Early generation selection of sugarcane families and clones in australia: a review. Journal American Society of Sugarcane Technologists 23: 20-39.).
For TSH and TBH, family 44 indicated the maximum number of selected individuals (nk), as a result of its outstanding genotypic effect in relation to other families. This fact suggests indication of the parents involved in this crossing for performing a recurrent selection program aimed at the accumulation of alleles favorable for these traits.
The distribution of the numbers of individuals to be selected from each family via BLUPIS and BLUPI methods were similar (Table 4). This result reveals that the methods are close in this respect; thus, BLUPIS is efficient for showing the number of individuals to be selected in each plot. For other traits, this distribution was performed in the same manner, considering the mean genotypic values of experimental plots within each family (data not shown).
Distribution of the number of genotypes to be selected (nk) by the BLUPIS method, and selected through individual genotypic values predicted via BLUPI within repetitions, for mean stalks mass (MSM) considering the number of individuals to be selected in the best family (nj), equal to 50, 100 and 120, of sugarcane at the ratoon stage
Efficiency of the BLUPIS selection method
BLUPIS was compared to BLUPI through linear regression  as defined before. These
methods will be considered equivalent if
as defined before. These
methods will be considered equivalent if  and
and  statistically, and if the
determination coefficient is above 70%. This enables the same number of individuals
selected by BLUPI to be selected by this alternative method.
statistically, and if the
determination coefficient is above 70%. This enables the same number of individuals
selected by BLUPI to be selected by this alternative method.
All regression parameter estimates (β0 and β1), except in three situations, were not statistically different from zero and from unity, respectively (Table 5). There was optimal concordance between the BLUPI and BLUPIS methods for all equations in all traits. Therefore, values of nj equal to or higher than 50 are adequate for efficient use of the BLUPIS method.
Estimates of the regression constant (βˆ0) and linear regression coefficient (βˆ1), and p-values (P) associated with the hypotheses
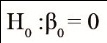 and
and
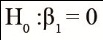 ,
and determination coefficients (R²), associated with regressions between the
total number of genotypes selected in each full-sib family of sugarcane
through the individual genotypic value via BLUPI, and the total number of
genotypes to be selected in each family via BLUPIS, for the assessed traits,
considering the number of individuals to be selected in the best family
(nj), equals to 50, 100 and 120, of sugarcane at the ratoon
stage
,
and determination coefficients (R²), associated with regressions between the
total number of genotypes selected in each full-sib family of sugarcane
through the individual genotypic value via BLUPI, and the total number of
genotypes to be selected in each family via BLUPIS, for the assessed traits,
considering the number of individuals to be selected in the best family
(nj), equals to 50, 100 and 120, of sugarcane at the ratoon
stage
For the dataset considered in this work, the selection of 100 genotypes in the best family provided the best results for β0, β1 and R² statistics, considered simultaneously. So, nj equal to 100 maximized the efficiency of the BLUPIS method.
According to results presented by Vencovsky (1978Vencovsky R (1978) Effective size of monoecious populations submitted to artificial selection. Brazilian Journal of Genetics 1: 181-191.), with an nj equal to 100, it is possible to reach 99% of the maximum representation of a full-sib family. For a nj equal to 50, this representation would be 98%. Resende and Barbosa (2006)Resende MDV and Barbosa MHP (2006) Selection via simulated Blup base on family genotypic effects in sugarcane. Pesquisa Agropecuária Brasileira 41: 421-429. stated that increasing sampling within the family from nj equal to 50 contributed nearly nothing to adding different genotypes in the sample. This means that many genotype means and few extreme genotypes (including superior genotypes) are added when increasing the sample from this nj value. Thus, these authors stated that 50 individuals from the best family, mass-selected for several restrictive traits, are sufficient to retain the best individuals of the progeny.
Considering the results presented in Table 5 and in Figure 1, it can be verified that the higher efficiency of the BLUPIS selection method, as compared to the BLUPI selection of the best individuals via predicted genotypic values, occurred when there was selection of 100 genotypes in the best family. In other words, the maximum concordance between genotypes selected by the two methods occurred when nj equaled 100 in six situations out of eight cases (four traits in two growth stages).
BLUPIS was efficient in the indication of the number of individuals to be selected by each experimental plot (Table 4). Such results were also reported in Stylosanthes (Resende et al. 2006Resende RMS, Resende MDV, Laura VA, Jank L and Valle CB (2006) Genotypic evaluation of accessions and individual selection in Stylosanthes spp. by simulated BLUP method. Crop Breeding and Applied Biotechnology 6: 253-260.) and coconut (Farias Neto et al. 2009Farias Neto JT, Lins PMP, Resende MDVand Muller AA (2009) Seleção genética em progênies híbridas de coqueiro. Revista Brasileira de Fruticultura 31: 190-196.). However, the results obtained in this work are relevant only for this research, and it is necessary to assess a larger number of experiments for possible indications of the optimal number of individuals to be selected in the best full-sib family. If using BLUPIS suggests an optimal sample size of 100, then it would be a great misuse of time and resources, as 50 seedlings can give 98% of the variation within a family. Thus, the use of nj equal to 50 or 100 should be studied in other experiments with a larger number of families.
The present study used the number of selected individuals from selected families as a criterion to compare BLUPIS and BLUPI, as these numbers might imply different sets of clones. For BLUPI, the clones are selected by their own predicted genetic effects, so all selected clones are determined; for BLUPIS, the number only determines how many clones should be selected, and the clones still have to be chosen based on individual phenotypes of the main correlated trait with production. Such an approach approximately coincides with the within-family selection component for BLUPI, thus, the methods can, in fact, lead to the selection of almost the same set of clones.
Obviously, the accuracy of all traits in individual seedlings is not high; therefore, BLUPI itself needs to be validated. However, there is no other option for quantitative traits; one must rely on within-family phenotypes to predict the within-family component of the genotypic value of an individual. It is therefore reasonable to select potential clones to enter into clone trials when there is high accuracy and sufficient precision to identify the best clones for commercial planting.
ACKNOWLEDGEMENTS
To the National Council of Technological and Scientific Development (CNPq) and to the Research Foundation of the State of Minas Gerais (FAPEMIG) for financial support to the Sugarcane Genetic Breeding Program of the Universidade Federal de Viçosa.
- Atkin FC, Dieters MJ and Stringer JK (2010) Impact of depth of pedigree and inclusion of historical data on the estimation of additive variance and breeding values in a sugarcane breeding program. Theoretical and Applied Genetics 119: 555-565.
- Barbosa MHP, Resende MDV, Bressiani JA, Silveira LCI and Peternelli LA (2005) Selection of sugarcane families and parents by Reml/Blup. Crop Breeding and Applied Biotechnology 5: 443-450.
- Barbosa MHP, Resende MDV, Peternelli LA, Bressiani JA, Silveira LCI, Silva FL and Figueiredo ICR (2004) Use of REML/BLUP for the selection of sugarcane families specialised in biomass production. Crop Breeding and Applied Biotechnology 4: 218-226.
- Bressiani JA, Vencovsky R and Burnquist WL (2005) Modified Sequential Selection in sugarcane. Proceedings of International Society of Sugarcane Technologists. ISSCT, Guatemala, p.459-467.
- Chang YS and Milligan SB (1992) Estimating the potential of sugarcane families to produce elite genotypes using univariate cross prediction methods. Theoretical and Applied Genetics 84: 662-671.
- Cruz CD (2006) Programa Genes: versão Windows - Biometria. Editora UFV, Viçosa, 381p.
- Farias Neto JT, Lins PMP, Resende MDVand Muller AA (2009) Seleção genética em progênies híbridas de coqueiro. Revista Brasileira de Fruticultura 31: 190-196.
- Kimbeng CA and Cox MC (2003) Early generation selection of sugarcane families and clones in australia: a review. Journal American Society of Sugarcane Technologists 23: 20-39.
- Mariotti JA, Cuenya MI and Salas MBG (1999) Análisis de componentes familiares e intra-familiares em progênies de combinaciones biparentales de cana de azucar (Saccharum spp.). Revista Industrial y Agrícola de Tucumán 76: 52-57.
- Oliveira RA, Daros E, Bespalhok-Filho JC, Zambon JLC, Ido OT, Weber H, Resende MDVand Zeni-Neto H (2008) Selecao de familias de cana-de-acucar via modelos mistos. Scientia Agraria 9: 269-274.
- Oliveira RA, Daros E, Resende MDV, Bespalhok-Filho JC, Zambon JLC, Souza TR and Lucius ASF (2011) Procedimento Blupis e selecao massal em cana-de-acucar. Bragantia 70: 796-800.
- Patterson HD and Thompson R (1971) Recovery of inter-block information when block sizes are unequal. Biometrika 58: 545-554.
- Peternelli LA, Resende MDVand Paula TO (2011) Experimentação e análise estatística em cana-de-açúcar. In Santos F, Borém A, Caldas C (Org.) Cana-de-Açúcar: bioenergia, açúcar e etanol - tecnologias e perspectivas. 2nd ed., Editora UFV, Viçosa, p. 333-353.
- Resende MDV (2002) Genética biométrica e estatística no melhoramento de plantas perenes. Embrapa Informação Tecnológica, Brasília, 975p.
- Resende MDV (2007a) Matemática e estatística na análise de experimentos e no melhoramento genético. Embrapa Florestas, Colombo, 591p.
- Resende MDV (2007b) Selegen-REML/BLUP: sistema estatístico e seleção genética computadorizada via modelos lineares mistos. Embrapa Florestas, Colombo, 359p.
- Resende MDV and Barbosa MHP (2006) Selection via simulated Blup base on family genotypic effects in sugarcane. Pesquisa Agropecuária Brasileira 41: 421-429.
- Resende MDV and Duarte JB (2007) Precisão e controle de qualidade em experimentos de avaliação de cultivares. Pesquisa Agropecuária Tropical 37: 182-194.
- Resende RMS, Resende MDV, Laura VA, Jank L and Valle CB (2006) Genotypic evaluation of accessions and individual selection in Stylosanthes spp. by simulated BLUP method. Crop Breeding and Applied Biotechnology 6: 253-260.
- Santos MR, Guimarães LMS, Resende MDV, Rosse LN, Zamprogno KC and Alfenas AC (2014) Resistance of Eucalyptus pellita to rust (Puccinia psidii). Crop Breeding and Applied Biotechnology 14: 244-250.
- Stringer JK, Cox MC, Atkin FC, WEI X and Hogarth DM (2011) Family selection improves the efficiency and effectiveness of selecting original seedlings and parents. Sugar Tech 13: 36-41.
- Vencovsky R (1978) Effective size of monoecious populations submitted to artificial selection. Brazilian Journal of Genetics 1: 181-191.
Publication Dates
-
Publication in this collection
Mar 2015
History
-
Received
02 Nov 2013 -
Accepted
09 Feb 2014



 ; selection
accuracy of families (Acfam); coefficient of genotypic
variation (CVgi %) and coefficient of residual variation
(CVe %).
; selection
accuracy of families (Acfam); coefficient of genotypic
variation (CVgi %) and coefficient of residual variation
(CVe %).


