A study of the drop size distributions and hold-up in short Kühni columns

FLUID DYNAMICS; HEAT AND MASS TRANSFER; AND OTHER TOPICS

A study of the drop size distributions and hold-up in short Kühni columns

N. S. Oliveira^I; D. Moraes Silva^I; M. P. C. Gondim^I; M. Borges Mansur^II,*

^IEscola de Engenharia, UFMG, Rua Espírito Santo 35, CEP 30160-030, Belo Horizonte - MG, Brazil

^IIDepartamento de Engenharia Metalúrgica e de Materiais, UFMG, Phone: +(55) (31) 3409-1810, Fax: +(55) (31) 3409-1815, Rua Espírito Santo 35, 2° andar, CEP 30160-030, Belo Horizonte - MG, Brazil E-mail: [e-mail]

ABSTRACT

The hydrodynamic behaviour of a short Kühni column was investigated under no mass transfer conditions using the binary system water (continuous phase) and Exxsol D-80 (dispersed phase). The counter-current flow pattern of the liquid phases was characterised regarding the Sauter mean drop diameter, drop size distribution and hold-up; a photographic method was used to assess drop sizes. The following operating variables were studied: rotor speed, flow rate of both liquid phases and column stage. The log-normal probability density function was found to be adequate to fit the experimental drop size distributions along the column. As expected, smaller drops and more uniform drop size distributions were obtained with the increase of rotor speed and column stage number, thus indicating the predominance of drop breakage phenomena in short columns. The total hold-up was influenced mainly by rotor speed and flow rate of the dispersed phase. Recommended correlations available in the literature were found to be inadequate for predicting experimental drop sizes and hold-up, so alternative expressions, valid only for short Kühni columns, were proposed.

Keywords: Liquid-liquid extraction; Kühni column; Hydrodynamics; Drop size distributions; Short columns.

INTRODUCTION

Pilot-plant testing is an expensive and time-consuming procedure that still remains an almost inevitable preliminary step in order to obtain a full-scale design for liquid-liquid extraction columns. In such equipment, extraction kinetics and mass transfer rates between liquid phases are closely related to the interfacial area (Ji et al., 2006), which, in turn, is very susceptible to contaminants and depends upon the column geometry, hydrodynamics, mass transfer direction, turbulence level, physical properties of liquid phases, column height, flow rates, temperature, etc. The knowledge of the mean drop size and drop size distributions along the equipment is fundamental to get a realistic description of column performance, but is still to complex to be predicted based solely on theory. As recently pointed out by Grinbaum (2006), there is still a wide gap between the development of new models by academia and their application by industrial R&D personnel, so column piloting is, at present, the easiest, fastest, and most accurate method to supply data for industrial column design.

In this context, considerable effort has been made over the years aiming at reducing piloting. It has focused on the development of: (1) cheaper alternative experimental procedures using single drops (Bahmanyar et al., 1990; Cabassud et al., 1990; Seikova et al., 1992; Fang et al., 1995; Modes et al., 1999) and/or short columns (Fan et al., 1987; Mansur et al., 2003) to get reliable design data, and (2) mathematical models incorporating the complex nature of the macroscopic dispersed phase interaction as well as the microscopic interphase mass transfer occurring in the continuously turbulent flow field, which results in a distributed population of drops (Valentas, 1966; Gourdon et al., 2004; Kronberger et al., 1995; Sechremeli et al., 2006; Attarakih et al., 2006). Empirical correlations to predict single operating variables (Kumar and Hartland, 1994, 1995, 1996), neural networks for control purposes (Boger and Haim, 1993) and computational fluid dynamics (CFD) modelling of both hydrodynamics and/or mass transfer along a given column geometry (Nabli et al., 1998; Mate et al., 2000; Bardin-Monnier et al., 2003) have been applied to simulate liquid-liquid extraction column operation.

As a general trend, the Sauter mean diameter decreases everywhere in the extraction column with agitation, while the drop size distribution becomes narrower. On the other hand, an increase in the flow rates results in larger drops, an effect which has been found to be more significant for the dispersed phase flow rate in comparison with the continuous one (Tsouris et al., 1990). In the absence of turbulence or for low agitation levels (Re_R< 10,000), the average size of drops is controlled by the balance between buoyancy and interfacial tensions and is given by the following equation (Bailes et al., 1986):

where C₁ is an empirical parameter depending on the column geometry, mass transfer direction, temperature and physical properties. For a rotating disc contactor, similar values for C₁ have been found by Chang-Kakoti et al. (1985) and Moreira et al. (2005) for drops of n-butyl alcohol (C₁ = 1.3) and n-heptane (C₁ = 1.4 ± 0.2) in water, respectively. More turbulent conditions (Re_R > 10,000) will result in smaller drops that can be conveniently predicted by empirical or semi-empirical correlations such as those proposed by Fischer (1973) and Kumar and Hartland (1996) for the Kühni column. Experimental investigations carried out in a rotating disc contactor have shown that mean drop sizes are strongly influenced by rotor speed, column height and dispersed phase flow rate when Re_R > 10,000 (Yamaguchi et al., 2002; Moreira et al., 2005).

With respect to drop size distributions, experimental studies with agitated columns have shown that distributions of rising organic drops dispersed in a continuous aqueous phase are broad in the first stages, becoming narrower and shifting toward smaller drop sizes along the column until a steady-state distribution is achieved (Tsouris et al., 1990; Moreira et al., 2005). On the other hand, a contrary behaviour, resulting in relatively larger drops, has been observed in the upper stages of the column due to the continuous phase feed effect, thus indicating that drop breakage dominates in the base of the column, whereas coalescence and breakage rates reach equilibrium in the upper stages (Tsouris et al., 1990). Consequently, a variation in drop size distribution produces a hold-up profile exhibiting a maximum value along the column depending on the operating conditions, which can be used to determine the column flooding. A unified correlation for the prediction of total hold-up of the dispersed phase in columns has been proposed by Kumar and Hartland (1995) for engineering calculations. This correlation predicted the experimental hold-up obtained by Kentish (1996) in a Kühni column (72mm diameter, 25 stages) to within a deviation of 17.7% for the system acetic acid-water-MIBK (methyl isobutyl ketone).

Despite the obvious importance of knowledge of drop size for the theoretical description of extraction operation in columns, Grimbaum (2006) points out that this is a far more problematic variable than hold-up. In some practical situations, drops are quite difficult to observe and sometimes just impossible to be measured as no dispersion is clearly identified. Moreover, when dispersion is observed, drops are not spherical at all but form big bulges or lumps. In the case of agitated columns, however, drops are practically spherical for a broad range of operational conditions, so CFD or drop-population balances can describe their behaviour with satisfactory accuracy. Therefore, at the current stage of knowledge, piloting and modelling contributions are both important (and also complementary) for improving the design procedure for extraction columns.

In the present work, experimental drop size distributions and hold-up have been measured in a short Kühni column (150 mm diameter and 5 stages) using the binary system water (continuous phase) and kerosene Exxsol D-80 (dispersed phase) at room temperature in order to investigate the hydrodynamic behaviour of ascending drops in short columns under normal operating conditions in the range of 7225 < ReR < 21675. According to Fan et al. (1987), the main difficulties to be recognised in a short column are the end effects and inlet drops being of uncharacteristic size for a given geometry and degree of agitation, so the aim of this work is to gain a better understanding of drop behaviour in short columns in order to provide basic data required for column design at reduced cost.

EXPERIMENTAL

Kühni Pilot Scale Unit

The current experimental work was carried out in a short Kühni column of 5 stages and 150 mm diameter which was built in a cylindrical precision bore glass section. Each stage was equipped with a six-blade turbine agitator (rotor diameter = 85 mm and rotor height = 10 mm) with accurate speed control, and stator plate (fractional free cross-sectional area = 30 %) spacing of 70 mm. All the internal parts of the column were constructed in AISI 316 stainless steel. Teflon annular gaskets were fixed on the stators to prevent any liquid from passing between the stators and the column wall.

The dispersed phase was introduced into the column using a conical distributor of 92 mm diameter made of AISI 316 stainless steel centrally located in the base of the column. In the distributor, a total of 170 holes of 1 mm diameter each are distributed into five concentrical circles. The diameter of the smaller circle of holes is 37 mm and the distance between each circle of holes is 9 mm; in each circle, the distance between holes is around 6-7 mm.

In the unit, all piping was constructed of resistant plastic and pumps were helicoidal provided with a PID system for precise flow rate control. Tanks were made of polypropylene. A scheme of the experimental pilot scale unit used in this work is shown in Figure 1.

Reagents

Runs were carried out in the absence of mass transfer using water as the continuous phase and commercial kerosene Exxsol D-80 (Exxon Mobil, predominantly aliphatic, aromatic max. of 0.5%wt.) as the dispersed phase, at room temperature. Distilled water and Exxsol D-80 were mutually saturated before being fed into the column in order to prevent miscibility effects from interfering with drop size measurements. The physicochemical properties of saturated liquids at 25°C are given in Table 1. After each run, the column was cleaned using a solution of non-surface-active detergent, then thoroughly rinsed with tap water and finally cleaned with distilled water. All joints and pipes were washed to ensure thorough removal of the detergent.

Experimental and Image Analysis Procedures

The same experimental methodology and image analysis procedure proposed by Moreira et al. (2005) for the photographic determination of drop size distributions in a rotating disc contactor has been adopted in this study. The following operating variables and range levels were investigated in this work: rotor speed (60, 90, 120, 150 and 180 rpm), flow rate of the continuous phase (1.24 and 2.00 L/min), flow rate of the dispersed phase (1.24 and 2.00 L/min) and stage number from the bottom of the column (0 or distributor, 1, 3 and 5). These variables and levels have been chosen based on a previous study (Mansur et al., 2003). Under this range of operating variables, the short Kühni column described in Section 2.1 operates at 7225 < Re_R< 21675 conditions.

Firstly, the column was filled with the continuous aqueous phase until it reached a previously set level (1-2 mm above the top stage); this was done carefully in order to avoid the formation of small bubbles below the plates. The rotor motor was started and agitation speed adjusted. Then both phases were fed to the column at a specified throughput and allowed to circulate in the unit for 30 minutes according to Figure 1 (closed system) to assure that the hydrodynamic steady-state condition has been reached.

A digital camera (Nikon® Coolpix 990) was suitably placed 200 mm from the column wall to provide photographs of the two-phase mixture at a given operating condition for drop size measurements. A graduated scale was fixed by the side of the column as a size reference. In the photographs obtained from runs at 150 and 180 rpm, drops of stages 3 and 5 were photographed using the zoom mode of the camera in order to obtain clearer pictures of the fine drops. The photographs were analysed with the aid of the software Quantikov Image Analyser (version 5.1 for Windows®) for drop size determination. All drops were assumed to be spherical because they did not exhibit very significant deviations from spherical shape for the operating conditions evaluated in this work. Drops were measured in the vertical position only according to Moreira et al. (2005) and measured drop values were multiplied by a factor of 0.8 in order to correct the parallax deformation of drops photographed inside the column. A minimum of 400 drops was analysed for each experimental condition in order to guarantee the statistical significance of the determined size distributions (Colella et al., 1999).

The total hold-up of the dispersed phase was assessed using the shut-down method (Gayler et al., 1951). Measurements were done in triplicate to verify experimental reproducibility.

RESULTS AND DISCUSSION

Drop Size Distributions in a Short Kühni Column

The drop diameters determined in the analysis of the photographs of the two-phase mixture were used to establish the corresponding drop size distributions considering 18 equally spaced size classes in the range 0.0 < d (mm) < 9.0 for all analyzed operating conditions.

The effect of rotor speed on the experimental drop size distributions at different positions along the short Kühni column (stages 0, 1, 3 and 5) is shown in Figure 2 at constant flow rates of both phases (Q_c = 1.24 L/min and Q_d = 2.00 L/min). It was observed that drop size distributions shifted to the left with the increase of agitation, thus evidencing that smaller drops and more homogeneous distributions are obtained in more turbulent conditions, as verified also for other types of liquid-liquid columns (Tsouris et al., 1990; Moreira et al., 2005). It was also observed that, for a given stage, the distribution became narrower as the rotor speed increased (this is rather evident in Figure 2 for stage 5). Furthermore, for a given rotor speed, the drop size distribution was broader at the bottom of the column than at the top. Such behaviour was attributed to an increase in the frequency of drop collisions with the internals of the column due to the increase in the shear force produced by the rotors to break the dispersed phase into smaller drops. The effect of rotors in order to enhance drop breakage was not significant at stage 0, which contains no rotor, and the small shift to the left observed in the drop size distribution at 180 rpm could be attributed to the turbulence effect from stage 1.

Figure 3 shows the influence of the stage number on the experimental drop size distributions measured in a short Kühni column at changing rotor speeds and fixed flow rates of both phases. The measured drop sizes ranged from 0.5 to 8.5 mm for the operational conditions investigated. Broader distributions were found at lower rotor speeds and at stages near to the bottom of the column, thus evidencing how inaccurate the use of a representative mean drop size is for these populations. According to Figure 3, drop size distributions did not change significantly at stages 0, 1 and 3 if rotor speeds were lower than (or equal to) 120 rpm. Actually, for these slow rotor speeds, the breakage frequency was too small to bring about significant changes in the size distribution for the small differences in column stages 0, 1 and 3. The same behaviour was verified for the other flow rate levels investigated as well.

The effect of flow rates of the continuous and dispersed phases on the experimental drop size distributions at changing rotor speeds and at stages 3 and 5 of the short Kühni column is shown in Figure 4. No significant effect was observed for the flow rate of the dispersed phase for the operational conditions investigated. On the contrary, the flow rate of the continuous phase affected significantly the drop size distributions at higher levels of agitation, e.g., 150 and 180 rpm. Again, for rotor speeds lower than 120 rpm, a small breakage frequency might explain the lack of an effect of the flow rate of the continuous phase on the drop size distributions. In fact, the increase of the flow rate of the continuous phase led to an increase in the drag force, which then resulted in a reduction in the ascending velocity of the drop and thus to an increase in the drop residence time in the column. Consequently, the frequency of drop collisions with the internals of the column is increased, so smaller drops were then obtained. In addition, no significant effect was identified on the drop size distributions measured at stages 0 and 1 for the flow rate levels studied.

Apart from the qualitative analysis of the effects of the considered operating variables upon the drop size distributions, an attempt was made to enable some quantitative representation of these effects. In this study, the log-normal probability density function (Eq. 2) was chosen for representing the experimental drop size distributions:

in which d is the drop diameter and m and s are parameters to be fitted. It should be emphasised that the log-normal function was already found to be adequate for describing drop size distributions in extraction columns (Giles et al., 1971; Tsouris et al., 1990; Moreira et al., 2005). For a given diameter d_i, the corresponding cumulative frequency F_i is expressed as follows:

For each diameter d_i, the experimental cumulative frequency was estimated as the number of drops with a diameter equal to or smaller than d_i divided by the total number of analysed drops plus two. The values of d_i as a function of F_i were used in the fitting of the inverse cumulative log-normal distribution to the data set with the aid of the software Statistica®, thereby determining the parameters µ and σ for each set of studied operating conditions.

As far as the fitting determination coefficient (R²) is concerned, the log-normal function represented the data well within the investigated range of operating parameters, as most of the fittings exhibited values of R² greater than 0.970, the minimum value being equal to 0.927. No significant correlation between µ and σ was found (p-level < 0.05), whose values were thus chosen to represent the drop size distributions in the short Kühni column.

The parameters µ and σ were fitted in order to obtain empirical correlations that related these parameters to the corresponding values of flow rates of the continuous and dispersed phases, rotor speed and stage number. After a series of trial-and-error tests, the following functions, whose linear coefficients were adjusted by multiple linear regression, were found to be adequate to estimate the parameters of the log-normal drop size distribution in the short Kühni column for 7225 < Re_R< 21675 including 95% confidence interval (p-value < 0.05; R² equal to 0.96 and 0.67, respectively) for the operational conditions investigated in this work:

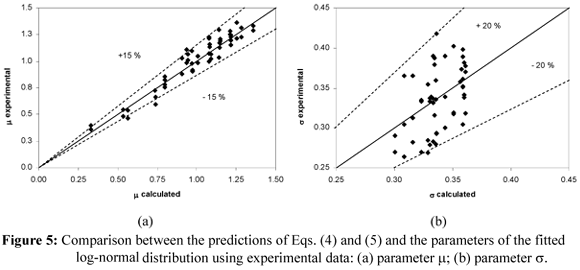
in which Q_d and Q_c are given in L/min and N_R in rps. According to Eq. (4), the increase of the operating variables rotor speed, stage number and flow rate of the continuous phase results in smaller drops, as verified experimentally. The effect of variable rotor speed was found to be statistically more significant for the conditions investigated. The effect of the flow rate of the dispersed phase was found to be non-significant from the statistical point of view. Comparative plots shown in Figure 5 indicated that Eq. (4) suitably reproduced the parameter µ with a deviation lower than 15% while Eq. (5) reproduced the parameter σ with 20% deviation. However, the use of Eqs. (4) and (5) is restricted to the operational conditions (1.24 < Q_c< 2.00 L/min; 1.24 < Q_d< 2.00 L/min; 60 < N_R< 180 rpm), chemical system and column characteristics (short Kühni column, 150 mm diameter and 5 stages) investigated in this work. It is important to emphasise that, for both fitted functions, the analysis of residuals did not show any evidence against the adequacy of the least squares method employed in the regression (Montgomery, 1991).

Sauter Mean Drop Diameter in a Short Kühni Column

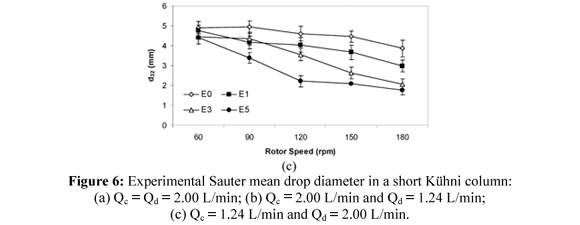
The effect of the operating variables rotor speed and stage number on the Sauter mean drop diameter in a short Kühni column is shown in Figure 6. As expected, smaller drops were found at higher rotor speeds and along the column height. The explanation for both effects is related to the increase in the frequency of drop collisions against the internal parts of the column in more turbulent environments during their ascending path inside the equipment. But the significance of the combined effect of these variables changed considerably depending on the column stage. At stages 0 and 1, for instance, drops sizes were found to be practically unchanged, independent of rotor speed. This occurred because there is no rotor in stage 0 and also because drops still did not reach a stable size at stage 1. However, at stages 3 and 5, drops became smaller and smaller with the increase of agitation and this effect was found to be more significant when rotor speed changed from 120 to 150 rpm, as shown in Figures 6(a) and 6(b). The effect was less pronounced when the flow rate of the continuous phase was diminished, as can be seen from Figures 6(b) and 6(c). Actually, the effect of flow rates of the continuous and dispersed phases on the Sauter mean drop diameter were less significant for the operational range studied in comparison to the variables rotor speed and stage number. In the case of the flow rate of the dispersed phase, no significant change in drop size was verified for the operating range investigated.

As shown in Figure 6, the Sauter mean drop diameter is practically constant at 60 rpm (Re_R = 7225), independent of the operating variables number of the stage and flow rates of both liquid phases, so all experimental drop sizes measured at 60 rpm (16 points) were fit to Eq. (1), resulting in C₁ = 1.5 ± 0.1 (error 7.1%), a value similar to previous results obtained by Chang-Kakoti et al. (1985) and Moreira et al. (2005) in a rotating disc contactor. In the case of drops measured at stage 0, the average drop size was found to be d₃₂ = (4.6 ± 0.4) mm (13 points, error 8.7%); this value could be predicted by using Eq. (1), e.g., d₃₂ = 4.5 mm.

The correlations proposed by Fischer (1973) and Kumar and Hartland (1996) underpredicted the experimental Sauter mean drop diameters with 66% and 75% error, so these correlations seem to be inadequate for describing drop sizes in a short Kühni column. So, the following empirical correlation was derived, which is valid for 1.24 < Q_c< 2.00 L/min, 1.24 < Q_d< 2.00 L/min and 60 < N_R< 180 rpm conditions (p-level < 0.05 including 95% of confidence level, R² = 0.92):

in which d₃₂ is given in mm, Q_c in L/min and N_R in rps. According to Eq. (6), the Sauter mean drop size diminishes with the increase of the operating variables rotor speed and stage number, thus corroborating the experimental observation (Figure 6). No significant statistical effect was found for the flow rate of the dispersed phase. As shown in Figure 7, the experimental data was suitably predicted by Eq. (6) with a relative deviation within 10% on average.

Total Hold-up in a Short Kühni Column

Figure 8 shows the behaviour of the experimental total hold-up measured in a short Kühni column. As expected, a higher hold-up was obtained upon increasing the operating variables rotor speed and flow rate of the dispersed phase. In the former effect, the increase of agitation results in smaller drops that exhibit relatively higher residence times, while in the latter one, the greater the volume of the organic phase fed to the column, the larger the hold-up. On the other hand, a slightly smaller hold-up was measured with the increase of the continuous phase. Such a trend was not expected and is probably due to experimental errors in the measurement of hold-up, which were done in triplicate. As shown in Figure 8, the experimental changes in the measured hold-up with the flow rate of the continuous phase are within the interval of 95% confidence level.

The correlation by Kumar and Hartland (1995) overpredicted the total hold-up values measured in the short Kühni column by 60%. Therefore, the following equation was derived including 95% of confidence level (p-level < 0.05 and R² = 0.97):

in which Q_d is given in L/min and N_R in rps. According to Eq. (7), the combined effect of the operating variables rotor speed and flow rate of the dispersed phase was predominant, as shown in Figure 8. It is interesting to note that total hold-up was found to be statistically constant at low agitation conditions (N_R < 120 rpm), independent of flow rate levels of both phases. A comparison between experimental and calculated hold-up is shown in Figure 9.

CONCLUSIONS

The use of short columns to obtain design data for extraction columns is an alternative way to reduce costs in piloting investigations. As verified in this work, short columns exhibit similar hydrodynamic behaviour with regard to drop size, drop size distribution and total hold-up as those found in longer columns. However, empirical correlations valid for longer columns should be adapted; expressions were proposed in this work valid for a short Kühni column (150 mm diameter, 5 stages) with operational conditions ranging from 7225 < Re_R< 21675, e.g., 60 < N_R< 180 rpm, 1.24 < Q_c< 2.00 L/min, 1.24 < Q_d< 2.00 L/min. It was also verified that the effect of drop breakage dominates in the whole short Kühni column for the range of operating conditions investigated, similarly to what is commonly verified in the bottom section of long extraction columns. Further investigations using short columns, including mass transfer effects to hydrodynamics, are suggested.

ACKNOWLEDGEMENTS

The authors are grateful to Dr. Lúcio C.M. Pinto (Centro de Desenvolvimento da Tecnologia Nuclear, CDTN/CNEN) for providing the software Quantikov image analyzer, to Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG, Project TEC 304/02) for the financial support to build the Kühni column unit at UFMG, to CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) for the research grants to undergraduate students and especially to Dr. Michael John Slater (Department of Chemical Engineering, University of Bradford, UK) for his lovely enthusiasm and for the short Kühni column that made possible this research work in Belo Horizonte, MG, Brazil.

NOMENCLATURE

C₁

parameter of Eq. (1)

dimensionless

d

drop diameter

m

d₃₂

Sauter mean drop diameter

m

D_R

rotor diameter

m

E

stage number

dimensionless

F_i

cumulative frequency function defined by Eq. (3)

dimensionless

g

acceleration due to gravity

m.s^-2

N_R

rotor speed

s^-1

p_lg(d)

log-normal probability density function defined by Eq. (2)

dimensionless

Q

flow rate

m³.s^-1

Re_R

Reynolds number of rotor

dimensionless

x

spatial coordinate

m

Greeks Letters

γ

interfacial tension

N.m^-1

µ

median of the probability density function,

dimensionless

ρ

density

kg.m^-3

ø

volume fraction hold-up of the dispersed phase

dimensionless

σ

standard deviation of the probability density function

dimensionless

Δρ

density difference between phases

kg.m^-3

υ

viscosity

Pa.s

Subscripts

c

continuous phase

(-)

d

dispersed phase

(-)

(Received: May 18, 2007 ; Accepted: May 05, 2008)

• Attarakih, M. M., Bart, H.-J. and Faqir, N. M., Numerical solution of the bivariate population balance equation for the interacting hydrodynamics and mass transfer in liquid-liquid extraction columns, Chem. Eng. Sci. 61, p. 113 (2006).
• Bahmanyar, H., Chang-Kakoti, D. K., Garro, L., Liang, T.-B. and Slater, M.J., Mass transfer from single drops in rotating disc, pulsed sieve plate and packed liquid-liquid extraction columns, Chem. Eng. Res. Des., 68, p. 74 (1990).
• Bailes, P. J., Gledhill, J., Godfrey, J. C. and Slater, M. J., Hydrodynamic behavior of packed, rotating disc and Kühni liquid/liquid extraction columns, Chem. Eng. Res. Des., 64, p. 43 (1986).
• Bardin-Monnier, N., Guiraud, P. and Gourdon, C., Residence time distribution of droplets within discs and doughnuts pulsed extraction columns via Lagrangian experiments and simulations, Chem. Eng. J., 94, p. 241 (2003).
• Boger, Z. and Haim, M.B., Application of neural networks for SX, In: Solvent Extraction in the Process Industries, Longsdail, D. H. and Slater, M. J. (Eds.), Elsevier, London, p. 1198 (1993).
• Cabassud, M., Gourdon, C. and Casamatta, G., Single drop break-up in a Kühni column, Chem. Eng. J., 44, p. 27 (1990).
• Chang-Kakoti, D. K., Fei, W-.Y., Godfrey, J. C. and Slater, M. J., Drop sizes and distributions in RDC's used for liquid-liquid extraction, J. Sep. Process. Technol., 6, p. 40 (1985).
• Colella, D., Vinci, D., Bagatin, R., Masi, M. and Bakr, E.A., A study on coalescence and breakage mechanisms in three different bubble columns, Chem. Eng. Sci., 54, p. 4767 (1999).
• Fan, Z., Oloidi, J. O. and Slater, M. J., Liquid-liquid extraction column design data acquisition from short columns, Chem. Eng. Res. Des., 65, p. 243 (1987).
• Fang, J., Godfrey, J. C., Mao, Z.-Q., Slater, M. J. and Gourdon, C., Single liquid drop breakage probabilities and characteristic velocities in Kühni columns, Chem. Eng. Technol., 18, p. 41 (1995).
• Fischer, A., Hydrodynamik und Stoffaustausch in einer Flüssig-Flüssig-Rührextraktionskolonne, PhD. Thesis, n. 5016, ETH Zurich, Switzerland (1973).
• Gayler, R., Roberts, N. M., Pratt, H. R. C., Holdup and pressure drop in packed columns, Trans. Inst. Chem. Eng., 29, p. 110 (1951).
• Giles, J. W., Hanson, C. and Marsland, J. G., Drop size distributions in agitated liquid-liquid systems with simultaneous interface mass transfer and chemical reaction, In: Proc. of the Int. Solvent Extraction Conference, 94 (1971).
• Gourdon, C., Casamata, G. and Muratet, G., Population balance based modelling of solvent extraction columns, In: Godfrey, J.C., Slater, M.J. (Eds.), Liquid-liquid extraction equipment. John Wiley & Sons, p. 137 (1994).
• Grinbaum, B., The Existing models for simulation of pulsed and reciprocating columns How well do they work in the real world?, Solv. Extr. and Ion Exch., 24, p. 795 (2006).
• Ji, J., Mensforth, K. H., Perera, J. M. and Stevens, G. W., The role of kinetics in the extraction of zinc with D2EHPA in a packed column, Hydrometallurgy, 84, p. 139 (2006).
• Kentish, S., Forward mixing in a countercurrent solvent extraction contactor, PhD Thesis, University of Melbourne, Australia (1996).
• Kronberger, T., Ortner, A., Zulehner, W. and Bart, H.-J., Numerical simulation of extraction columns using a drop population model, Computers Chem. Eng., 19, p. S639 (1995).
• Kumar, A. and Hartland, S., A unified correlation for the prediction of dispersed-phase hold-up in liquid-liquid extraction columns, Ind. Eng. Chem. Res., 34, p. 3925 (1995).
• Kumar, A. and Hartland, S., Empirical prediction of operating variables, In: Godfrey, J.C., Slater, M.J. (Eds.), Liquid-liquid extraction equipment. John Wiley & Sons, p. 625 (1994).
• Kumar, A. and Hartland, S., Unified correlations for the prediction of drop size in liquid-liquid extraction columns, Ind. Eng. Chem. Res., 35, p. 2682 (1996).
• Mansur, M. B., Slater, M. J., Biscaia Jr. and E. C., Reactive extraction of zinc sulphate with D2EHPA in a short Kühni column used in batch mode, Ind. Eng. Chem. Res., 72, p. 4068 (2003).
• Mate, A., Masbernat, O. and Gourdon, C., Detachment of a drop from an internal wall in a pulsed liquid-liquid column, Chem. Eng. Sci., 55, p. 2073 (2000).
• Modes, G., Bart, H.-J., Rodriguez-Perancho D. and Bröder, D., Simulation of the fluid dynamics of solvent extraction columns from single droplet parameters, Chem. Eng. Technol., 22, v. 3, p. 231 (1999).
• Montgomery, D. C., Design and analysis of experiments, 3rd ed, John Wiley & Sons, Singapore (1991).
• Moreira, E., Pimenta, L. M., Carneiro, L. L., Faria, R.C.L., Mansur, M.B. and Ribeiro Jr., C. P., Hydrodynamic behaviour of a rotating disc contactor under low agitation conditions, Chem. Eng. Commun., 192, p. 1017 (2005).
• Nabli, M. S. A., Guiraud, P. and Gourdon, C., CFD contribution to a design procedure for discs and doughnuts extraction columns, Trans. IChemE., 76, p. 951 (1998).
• Sechremeli, D., Stampouli, A. and Stamatoudis, M., Comparison of mean drop sizes and drop size distributions in agitated liquidliquid dispersions produced by disk and open type impellers, Chem. Eng. J., 117, p. 117 (2006).
• Seikova, I., Gourdon, C. and Casamatta, G., Single-drop transport in a Kühni extraction column, Chem. Eng. Sci., 47, v. 15-16, p. 4141 (1992).
• Tsouris, C., Ferreira, R. and Tavlarides, L. L., Characterization of hydrodynamic parameters in a multistage column contactor, Can. J. Chem. Eng., 68, p. 913 (1990).
• Valentas, K. J., Bilous, O. and Amundson, N. R., Breakage and coalescence in dispersed phase systems, Ind. Eng. Chem. Fundam., 5, p. 271 (1966).
• Yamaguchi., M., Yamashita H. and Noda, H., Hydrodynamics and mass transfer of a rotating disc column, In: Sole, K.C., Cole, P.M., Preston, J.S. and Robinson, D.J. (Eds.), Proc. of the Int. Solvent Extraction Conference p. 1334 (2002).

*

To whom correspondence should be addressed

Publication Dates

• Publication in this collection
  24 Nov 2008
• Date of issue
  Dec 2008

History

• Accepted
  05 May 2008
• Received
  18 May 2007