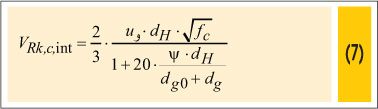Abstracts
The use of column capitals is one way to increase the punching strength of slab-column connections. Recommendations presented by codes of practice for defining the geometry and checking the resistance of slab-column connections with capitals are not comprehensive, with few experimental studies available on the topic. This paper discusses important aspects of the historical development of mushroom slabs and also presents experimental results of 4 tests, with 1 test in a reference flat slab and 3 tests in mushroom slabs with circular column capitals. These results are compared with theoretical results estimated using Eurocode 2 (2004) and NBR 6118 (2007). They were also compared with a series of non-linear finite element analysis in order to get insight of the stress distribution and of the failure mechanism of mushroom slabs.
mushroom slab; punching shear; reinforced concrete; column capitals
O uso de capitéis é uma das formas de se aumentar a resistência à punção de ligações laje-pilar. As recomendações normativas para a definição da geometria e verificação da resistência última de ligações com capitéis são pouco abrangentes, sendo poucas as pesquisas experimentais disponíveis sobre o tema. Este artigo discute aspectos relevantes do desenvolvimento histórico das lajes cogumelo e apresenta resultados de 4 ensaios experimentais, sendo 1 laje lisa de referência e 3 lajes cogumelo com capitéis de seção circular. Estes resultados são comparados com as estimativas das normas EUROCODE 2 (2004) e NBR 6118 (2007) e com modelos numéricos não-lineares a fim de se compreender melhor a distribuição das tensões e o mecanismo de ruptura de lajes cogumelo.
lajes cogumelo; punção; concreto armado; capitel
Experimental and numerical analysis of reinforced concrete mushroom slabs
A. F. Lima NetoI; M. P. FerreiraII; D. R. C. OliveiraIII; G. S. S. A. MeloIV
IProfessor, Faculdade de Engenharia Civil, Universidade Federal do Pará, Campus de Tucurui, aaraon@ufpa.br, Tucurui, Pará, Brasil
IIProfessor, Faculdade de Engenharia Civil, Universidade Federal do Pará, mpina@ufpa.br, Belém, Pará, Brasil
IIIProfessor, Faculdade de Engenharia Civil, Universidade Federal do Pará, denio@ufpa.br, Belém, Pará, Brasil
IVProfessor, Departamento de Engenharia Civil e Ambiental, Universidade de Brasília, melog@unb.br, Brasília, Distrito Federal, Brasil
ABSTRACT
The use of column capitals is one way to increase the punching strength of slab-column connections. Recommendations presented by codes of practice for defining the geometry and checking the resistance of slab-column connections with capitals are not comprehensive, with few experimental studies available on the topic. This paper discusses important aspects of the historical development of mushroom slabs and also presents experimental results of 4 tests, with 1 test in a reference flat slab and 3 tests in mushroom slabs with circular column capitals. These results are compared with theoretical results estimated using Eurocode 2 (2004) and NBR 6118 (2007). They were also compared with a series of non-linear finite element analysis in order to get insight of the stress distribution and of the failure mechanism of mushroom slabs.
Keywords: mushroom slab, punching shear, reinforced concrete, column capitals.
1. Introduction
Flat slabs are distinguished from conventional beam-and-slab floors because they are supported directly on columns. This structural system is easier to be constructed because forms and reinforcement are simple, which may generate economic gains due to reductions in the construction time. The main disadvantage of this structural system is the possibility of punching shear, which is a brittle local failure that may spread and lead the whole structure to ruin through progressive collapse. To improve the ductility and to increase the bearing capacity of a slab-column connection it is common the use of shear reinforcements like stud rails, bent-up bars or double-headed studs. Another alternative is to increase the effective depth of the slab by using column capitals or drop panels, what reduces the shear stresses in slab-column connections. These elements may also increase its ductility as the punching strength approaches the flexural resistance of the slab. Figure 1 shows some possibilities for slab-column connections and Figure 2 presents a mushroom slab used in a garage building in Brazil.
1.1 Historic
Flat slabs were developed probably independently in the early XX century by different engineers. In the U.S.A. C. A. P. Turner was responsible for demonstrating the efficiency and reliability of the system (Gasparini [1]). In Europe Robert Maillart, a Swiss engineer more famous for his works with bridges, is believed to be the inventor of flat slabs (Furst and Marti [2]),but credits are also given to Arthur F. Loleit, a Russian engineer (Kierdorf [3]).
At that time one of the biggest challenges was to determinate the stresses in floors with slabs supported directly on columns, without any beams. It was common to observe significant variations in the flexural reinforcement ratio between different patented systems. According to Melo [4], in 1911 the first structural accident was registered in a building with flat slabs. It was the collapse of Prest-o-Lite building in the U.S.A., where a local punching failure led the whole building to ruin, evidencing the need for research on the behavior and resistance of slab-column connections.
The first experimental study that provided information for the design of slab-column connections was performed by Talbot [5], which in fact tested concrete footings and observed that in many cases they failed by punching forming a truncated failure cone with faces tilted around 45 degrees(influenced by the high thickness of the footings). He also noticed at that time that the flexural reinforcement ratio could significantly influence the ultimate punching strength, which was later observed by Richart [6].
Only in 1960 it was presented the first theoretical model to explain the punching failure mechanism and predict the ultimate strength of slab-column connections. This model was presented by Kinnunen and Nylander [7] and was based on experimental observations obtained after conducting an extensive experimental program. The authors observed that the portion of the slab outside the failure surface showed rigid body rotations and created a model aiming to satisfy the forces equilibrium (see Figure 3a). In this model, the slab segments are treated as rigid bodies supposedly supported on a conical imaginary shell confined between the column and the shear crack.
Under load, each segment rotates around a point of rotation (CR) and is supported by the forces shown in Figure 3b, with the internal forces being a function of rotation (ψ) of the slab. According to the authors failure occurs when a point in the bottom surface of the slab, located vertically below the root of the shear crack reaches a critical radial strain (εcto) at the same time that the tangential strains in concrete and in the imaginary conical shell reach characteristic ultimate strain for concrete. This model was initially developed for the case of axisymmetric reinforcement, but as in practice flexural reinforcement are arranged orthogonally, Kinnunen and Nylander [7] presented changes to the model. The method was always considered difficult to use in practice, due to its high level of complexity. Also, the quality of predicted results didn't justified its use instead of the simpler empirical methods presented by codes of practice. Yet this method is still one of the most significant contributions ever made to the subject.
1.2 Research significance
Many experimental researches have been developed, mostly focused at evaluating the contribution of different types of shear reinforcement in the punching resistance of flat slabs. Few experimental results are available about the contribution of column capitals or drop panels (Wey [8] and Hueste at al. [9]) and those available are more focused in evaluating the ductility of slab-column connections in case of earthquakes (cyclic loading). Design recommendations presented by codes of practice for mushroom slabs are superficial and strongly influenced by tests on footings. Thus, it is evident the importance of providing experimental results on the behavior and strength of mushroom slabs.
1.3 Methodology
This paper presents the results of four experimental tests, one of a flat slab tested as reference and three tests in mushroom slabs with circular column capitals. Experimental results are compared with theoretical values obtained using recommendations of NBR 6118 [10], EUROCODE 2 [11] and of the Critical Shear Crack Theory as presented by Muttoni [12]. Results of a computational analysis using nonlinear FEA commercial software MIDAS are also presented in order to better understand the behavior and failure mechanism of mushroom slabs.
2. Theoretical methods for estimation of punching resistance
2.1 NBR 6118 (2007)
NBR 6118 [10] recommends that the punching resistance of mushroom slabs must be checked in three regions of the slab-column connection. The maximum resistance of the connection should be checked using Equation 1 which evaluates the strength of the compression strut around the column, using the control perimeter u0. It should also be checked the diagonal tensile strength of concrete in the area inside and outside the column capital, in control perimeters u1 and uout, using Equations 2 and 3, with the effective depth of the slab in each case considered as shown in Figure 4.
Where:
 , with fc in MPa;
, with fc in MPa;
u0 is the column perimeter in mm;
dH is the effective depth of the slab in the ends of the column in mm (see Figure 4).
Where:
ρ is the geometric flexural reinforcement ratio expressed by  ;
;
ρx and ρy are the flexural reinforcement ratios in orthogonal directions x and y;
fc is the compressive strength of concrete in MPa (fc< 50 MPa);
u1 is the length of a control perimeter taken 2·d from the column faces, in mm. For slabs without column capitals it is calculated as  and for slabs with column capitals it is calculated as
and for slabs with column capitals it is calculated as  ;
;
da is the effective depth as shown in Figure 4 in mm.
Where:
d is the effective depth of the slab in mm;
uout is the length of a control perimeter taken 2·d from the ends of capital and calculated as  ;
;
lH is the distance between the edge of the capital and the column face, in mm.
In cases where lH< 2·(dH - d), designers have to check only the resistance in the control perimeter uout. When 2·(dH - d) < lH< 2·dH, resistance should be checked only in the control perimeter u1. If lH > 2·dH it is necessary to check the resistance in both uout and u1.
2.2 Eurocode 2
EUROCODE 2 [11] assumes that the punching strength of flat slabs with column capitals or drop panels must be checked in three control perimeters as shown in Figure 5. This means that it must be checked the maximum shear strength of the slab-column connection, using Equation 4, and that the tensile diagonal strength inside and outside the capital or drop panel should be checked using Equations 5 and 6.
Where:
fc is the compressive strength of (fc< 90 MPa);
u0 is the column perimeter in mm;
d is the effective depth of the slab, in mm.
Where:
ξH is the size effect, taken as  for a failure surface inside the column capital, with d and hH in mm;
for a failure surface inside the column capital, with d and hH in mm;
ρ is the geometric flexural reinforcement ratio expressed by  , where ρx and ρy are the flexural reinforcement ratios in orthogonal directions x and y, considering only bars within a region away 3∙d from the faces of the column;
, where ρx and ρy are the flexural reinforcement ratios in orthogonal directions x and y, considering only bars within a region away 3∙d from the faces of the column;
u1 is the length of a control perimeter taken 2·d from the column faces, in mm;
dH is the effective depth of the slab in the ends of the column faces, in mm;
hH is the thickness of the capital, in mm.
Where:
uout is the length of a control perimeter taken 2·d from the ends of capital, in mm.
2.3 Critical shear crack theory (CSCT)
Muttoni [12] idealized his theory based on the idea that the punching resistance decreases with increasing rotation of the slab. Such behavior may be attributed to formation of a critical shear crack that propagates along the slab thickness cutting the compression strut, which transmits shear forces to the column (see Figure 6). With increasing load the shear crack trends to open, reducing the efficiency of the shear transfer mechanisms and eventually leading to a punching shear failure. According Muttoni and Schwartz [13] the opening of this crack is proportional to the product ψ·d (see Figure 6), but the transmission of shear forces along the critical crack depend on the roughness of the concrete failure surface. The influence of the roughness of concrete surface can be assessed in terms of the maximum aggregate size used in concrete. Based on these concepts Muttoni [12] proposed that the punching strength of a slab failing by diagonal tensile can be obtained using Equation 7.
Where:
u1 is the length of a control perimeter taken d/2 from the column faces, in mm;
dH is the effective depth of the slab in the ends of the column faces, in mm;
fc is the compressive strength of concrete, in MPa;
ψ is the slab rotation;
dg0 is a reference diameter of the aggregate admitted as 16mm;
dg is the maximum diameter of the aggregate used in the concrete slab, in mm.
The rotation ψ of the slab is expressed by Equation 8.
Where:
rs is the distance between the axis of the column and the line of contra flexure of moments;
rq is the distance between the axis of the column and the load line;
rc is the radius of the circular column or the equivalent radius of a rectangular column;
fys is the yield stress of the tensile flexural reinforcement;
Es is the modulus of elasticity of the tensile flexural reinforcement;
VE is the applied force;
It is also necessary to check the strength for the case of a failure occurring in the outside of the column capitals, calculated using Equation 9.
Where:
uout is the length of a control perimeter taken d/2 from the ends of the capital, in mm;
d is the effective depth of the slab, in mm.
With VE, ψ and VR,c is possible to draw a graph with two curves. The first is a curve that expresses the theoretical load-rotation behavior of the slab. The second curve expresses the strength reduction of the slab due to the increase of rotation. The point of intersection of these two curves express the punching strength of a slab-column connection. Figure 10 illustrates this graph.
3. Experimental program
A series of four experimental tests was carried in the civil engineering laboratory of Federal University of Para in order to evaluate the behavior and strength of reinforced concrete flat slabs with column capitals (mushroom slabs). One was a reference flat slab and the other three slabs had circular column capitals. The slabs were square with sides of 2,600 mm and were 140 mm thick supported on circular central column stubs with diameter of 250 mm. The flexural reinforcement used was the same for all the slabs being formed by 12.5 mm bars spaced at each 105 mm in x direction and 12.5 mm bars spaced at each 115 mm in the y direction. The concrete cover was 15 mm in the upper face and 10 mm the bottom of the slabs. This series of tests has as main variable the slope of the column capitals, adopting relations between hH:lH of 1:2, 1:3 and 1:4, in order to assess their influence on the behavior and strength of slabs. Table 1 shows the characteristics of the tested slabs. The slabs were subjected to symmetrical loading as shown in Figure 8.
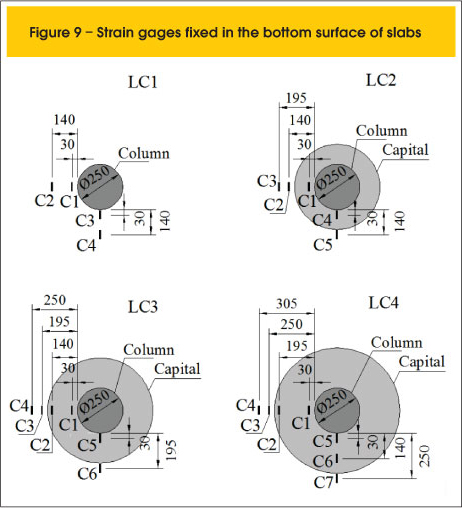
Compressive strains in the concrete surface were measured using strain gauges placed in the region around the slab-column connection. The gauges were positioned in tangential and radial directions, as shown in Figure 9, in which it is possible to notice that the gauges position varied according to the geometry (slope) of the capitals. The monitoring of strains was more intense in the edges of the capitals which are critical areas in terms of stress concentration.
Table 2 shows test results where it is possible to observe a variation in the failure load of slabs up to 58.5% (LC1 to LC3). This variation can be attributed to the addition and the subsequent increase in capitals, once the slab LC1 has capital and the slabs LC2, LC3 and LC4 had their capitals added and varying its thickness/length ratio of 1:2 to 1:4. Tests showed an increase of 30% of the failure load of slab LC1 to LC2, which had the smaller column capital, with 1:2 ratio, as recommended by the EUROCODE 2 [11] and NBR 6118 [10].In the case of slab LC3, which had a ratio of 1:3 between the thickness and the length of the capital, the increase in the failure load was of 21% in comparison to slab LC2 and 58% if compared to slab LC1. However, slab LC4, which had the biggest column capital, didn't show improvements in the ultimate punching strength if compared to slab LC3.
Regarding the strains in concrete, it is observed that near the column face, slabs LC3 and LC4 presented higher compressive strains than slab LC2.This behavior was different considering the compressive strains in the outside of the column capitals, where slabs LC2 presented higher strains than the others. These differences are in agreement with the position of the failure surface observed after tests. Slab LC2 failed in the outside of the columns capital whereas slabs LC3 and LC4 failed inside the capitals. The use of column capitals was also beneficial in terms of ductility. Tensile strains measured in the flexural bars showed that in the case of slab LC1 only two bars yielded before failure, which results in a yield radius (rys) of 3.23·d. For slabs LC2 and LC3 the yield radius rys was of 5.02·dand for slab LC4 almost all monitored bars yielded before failure, resulting in a yield radius rys of 6.95·d.
4. Computational analysis
Experimental tests are fundamental for the development and improvement of theoretical methods. However, the complete understanding of the behavior and failure mechanisms may be hampered because of displacements and strains results are restricted to the points of the experimental model in which gauges were installed. An efficient methodology to complement the analysis of experimental results and is to carry computational non-linear finite element analysis, which after calibration may return comprehensive results. This topic presents results from nonlinear finite element analysis carried using commercial software MIDAS FEA. Axisymmetric computational models were generated using as reference analyzes made by Ferreira [14], Menétrey [15] and Trautwein [16]. In these analyses authors adapted the geometry and the reinforcement of slabs in order to use axisymmetric models. Flexural reinforcement which were originally placed in orthogonal arrangements were adjusted and changed to axisymmetric reinforcement formed by rings and by radial bars, as shown in the Figure 10.
Comparisons between experimental and computational results presented by Ferreira [14] and Menétrey [15] indicate that the axisymmetric theoretical models present load-displacement response stiffer than what is observed in tests with experimental models with orthogonal reinforcement. According to the authors, these results indeed describe the expected behavior once axisymmetric reinforcement are more effective than orthogonal reinforcement in terms of bending and cracking. They use results from Kinnunen and Nylander [7] as experimental evidence and show that, despite the significantly different flexural behavior, the ultimate punching resistance of slabs with orthogonal or axisymmetric reinforcement are similar. Therefore, axisymmetric computational analyses are valid and may provide a better understanding of the punching shear failure mechanism.
Based on literature, the input data used in the computational non-linear analysis to define the properties of concrete and steel were: Poisson's ratio of the concrete νc = 0,15; compressive strength of concrete fc = 32 MPa; modulus of elasticity of concrete Ec = 27 GPa; Fixed Total Strain Crack Model; Effect of lateral cracking according to Vecchio and Collins [17];Confinement effect neglected; basic value of fracture energy for a maximum aggregate size of 9.5 mm Gf0 N.mm/mm2 = 0.0259; compressive fracture energy Gc = 10 N.mm/mm2 ; modulus of elasticity of steel Es = 200 GPa, Poisson's ratio of the steel νs = 0.30; Yield stress of steel fys = 550 N/mm2. The fracture energy was calculated using Equation 10.
Where:
Gf0 is the basic value of fracture energy determined as a function of the aggregate size;
fcm is the average compressive strength of concrete (Equation 11);
fcm0 is assumed as 10 MPa.
The load was considered as a 50 mm displacement applied at 100 mm from the edges of the slab into 160 load steps. The equilibrium between external and internal force vectors was verified using the Newton-Raphson method, which is an incremental iterative procedure. An energy based convergence criterion was used with a tolerance value of 1∙10-3. The concrete compressive behavior was described with a parabolic hardening and softening relationship proposed by Feenstra[18]. The unconfined uniaxial tensile stress - strain diagram was assumed to be linear in tension until cracking. After cracking it was assumed that the tensile stress decreases exponentially as a function of strain in the direction normal to the crack. More details are available in Lima Neto [19].
4.1 Slab without column capital
A parametric investigation was performed in order to establish the ideal refinement for the finite elements mesh, for the tensile strength of concrete (fct) and for the shear retention factor (βc). Figure 11 presents the optimal finite elements mesh used in the computational models of tested slabs. For the tensile strength of concrete and the shear retention factor were used values of 1.85 MPa and 0.12, respectively. Figure 12a presents the load-displacement curves for experimental and computational models. As expected, the computational models were stiffer in terms of flexural response but the ultimate punching shear strength for both models were similar. The ultimate strength of experimental model was 327 kN and the computational failed with 309 kN (difference of 5.5% as shown in Table 3). The distribution of the normal stresses of Figure 13a show the formation of 2 strut compressed, the most significant being that may have generated the tensile stresses which allowed the opening of the rupture surface. Just as concentrated compressive stresses near the binding slab-column value above the compressive strength of the concrete, that may have generated the crushing of concrete at this point and thus made possible rupture by punching. Note also that the approximated radius to appearance of rupture supposed cone on the upper face of the slab, from the face of the column would be close to that found experimentally (2.8·d).
Figure 14a shows radial tangential cracks in 3 different areas of the slab. The first crack is in the projection of the column edges and is formed in the early load stages mainly due to stresses caused by flexure. The second tangential crack appears in advanced load stages and is supposed to be formed by flexure and shear stresses. This crack develops towards the column edges and may eventually divide the original fan strut into two mains prism struts. The third radial crack was observed immediately after the peak load during the computational analysis and may indicate the formation of the critical shear cracks that leads to a punching shear failure. Assuming that this third radial crack represents the failure surface, it is possible to see that it would form a 24º angle with the horizontal, similar to inclination of the failure surface observed after test, which was of 23º.
Figure 15a and 15b present comparisons between computational and experimental results for strains in the concrete surface of slab LC1. It is possible to observe that in case of tangential strains there is consistency between computational (C1N and C2N) and experimental (C1 and C2) results. However, for the case of radial strains, computational (C3N and C4N) and experimental results (C3 and C4) were consistent only for initial load stages but differed significantly for the ultimate load stage. In experimental tests radial strain gauges registered tensile strains, what in fact was not observed in the computational analyzes.
4.2 Slabs with column capitals
The finite elements mesh was refined for analyzes of slabs with column capitals as shown in Figure 11. Minor changes in the adopted values of the tensile strength of concrete and of the shear retention factor were also necessary in order to improve the quality of computational results. Therefore, for slab LC2 were adopted fct = 1.75 MPa and βc = 0.15. For slab LC3 were adopted fct = 1.72 MPa and βc = 0.16 and for the slab LC4 were used fct = 1.85 MPa and βc = 0.15.Computational models of slabs with column capitals also showed a stiffer load-displacement response if compared to experimental results. However, peak loads of computational models were similar to failure loads observed on tests as show in Table 3.
The LC3 slab, with a slope of 1:3, showed a rupture of 518.5 kN experimental and numerical analysis model of a loading capacity of 456.5 kN, namely, a difference of 12%, but with proper behavior and rupture mode close to what was observed in laboratory. It also highlights that there was a gain in load capacity compared to previous slabs, provided by the increase of the capital, and was also observed a surface of rupture inside the capital, as happened with the slabs tested. The loading to slab LC4 was 513.5 kN experimental and numerical of 457.3 kN, namely, the strength capacity of the slab shaped was 11% lower than experimental. Note that the slab with a 1:4 slope capital did not present improvement in load capacity when compared with the slab slope of 1:3 (LC3), as was observed experimentally.
In Figure 13b it is observed to the slab LC2 in the last step load, forming a compressed strut, starting from the outer edge of the capital on the underside of the slab to the top surface of the same. Probably this strut compressed generated tensile stresses which enable the opening of the collapse cone, since the underside of the slab, the edge of the slab with capital realizes a compressive stress values above the compressive strength of the concrete adopted for the slab. Thus, there is an indication that this rupture, as was observed in the laboratory, has been starting at outside edge of the capital with the slab. Figures 13c and 13d is perceived, as in the previous model, which models of the slabs LC3 and LC4 present the development of a strut compressed with tensile stress on your back.
However unlike of LC2, it is noted that these models which high concentration of compressive stresses are spread from the external limit of the capital, with slightly higher stress, up to this connection with the column. Because of this fact, it is possible be considered that the surface rupture passed the limit of the capital and probably started in connection of the capital with the column. It is observed that the rupture surface, starting at the column face, may have reached a radius of approximately 489 mm, the LC3 slab model, near to 3.2·(d + hH) found in the laboratory, and 558 mm, the LC4 model slab, this being also near the experimental (4·(d+hH)).
In Figure 14b is noted tangential cracks in the upper face of the LC2 slab model, already stabilized more or less the same locations were observed where the higher radial strain and the appearance of probable rupture surface, with an inclination of approximately 22º, noting that the experimental presented variation between 20º and 24º. In Figures 14c and 14d is observed the tangential cracks of the LC3 slab model, on the upper face, already stabilized more or less the same locations were observed where the higher radial strains on LC2, and the appearance of probable rupture surface, with an inclination of approximately 22°, highlighting that the experimental presented variation between 20º and 24º. The model slab LC4 has a greater amount of tangential cracks compared to previous models, including cracks occurring in the internal regions capital. These internal cracks can be attributed to the greater length of the capital used in this model, causing cracks that before appeared just at the end, entered the boundaries thereof. It is observed that the tangential cracks occurred in the same regions where appeared high tangential strains, as observed in previous slabs, even the rupture surface, showing a projection with an inclination of approximately 19°.
In Figure 15 there is a comparison between the strains of the concrete, experimental (C1, C2, C3, C4, C5, C6 and C7) and numerical models (C1N, C2N, C3N, C4N, C5N, C6N and C7N) for slabs with capital (LC2, LC3 and LC4). In general, it is clear that the tangential strain (see Figures 15c, 15e and 15g) of numerical models approached the experimental, thus confirming the good behavior of the models in the analysis of slabs. Thus, there is again a tendency of the slabs present higher values of strain at the points where the appearance of the identified rupture surface. Note also that the strain of the numerical models tend to be slightly smaller than the experimental for the same loading level, which can be attributed to the axisymmetric distribution of the reinforcement, which makes models stiffer in relation to the slabs. For radial strain (see Figures 15d, 15f and 15h), as observed in the slab without capital (LC1), are perceived near deformations, between the experimental and numerical modeling, in the early stages of loading, but with discordant values for the same level of loading in the last steps of load. Except for radial strains in the slab LC2 which showed similar between the numerical models (C5N and C4N) and experimental (C4 and C5), for the same load level, especially in relation to strain inside the capital, near the face column.
5. Evaluation of calculus methods
The Table 3 shows the rupture loads seen in the experiments (Pu) and the rupture loads estimated by the recommendations of EUROCODE 2 [11] and NBR 6118 [10] (VRc), and the location of the rupture surface, since these could occur inside (internal) or outside (external) of the area corresponding to the capitals. For experimental rupture loads observes values near of the rupture loads estimated by the recommendations of ECUROCODE 2 [11]. The slab LC4 has a higher difference between the experimental and the estimated loads, since the code considers the contribution of the capital, and it was revealed experimentally that capitals with inclination above of 1:3 has its contribution to the punching strength reduced. Almost all slabs had a relation Pu/VRc near to 1.0, with the exception of the slab LC4. Regarding the NBR 6118 [10], there is rupture loads, mostly the loads near encountered by estimates EUROCODE 2 [11], with the exception of the loads concerning slabs that have capitals with inclination higher than 1:2 (LC3, LC4). In spite of recommendations presented similar formulations, it is noted that the limits for the use thereof are different, when referring to the control perimeter after all NBR 6118 [10] is independent of the perimeter length of the capital, and must be always respected the ratio 1:2 on the thickness thereof, thereby forcing an angle of 26.6º from the column face. Therefore, applying the limits found in the code, it is noticed that the slabs with capital inclination of 1:3 and 1:4, the control perimeter to be used has a length of 2·dH and thickness with effective depth d, and thus the estimated values are presented somewhat conservative. Regarding the rupture surfaces was observed that the NBR 6118 [10] showed good results, because their estimates coincide with the rupture surfaces observed experimentally (see Figure 16). The estimates by EUROCODE 2 [11], to the rupture site was determined using the equality between formulations VRc,int and VRc,ext. With this equality is possible to determine the equivalent value of lH (circular capital) that has the limit between these two rupture modes. Thus, experimentally, the slabs had to rupture just outside the capital with inclination 1:2, initially agreeing with the code (EUROCODE 2 [11]), however, for slabs an inclination higher than 1:2, the rupture occurred in an internal region of the capital, diverging from what was estimated.
The Table 3 shows a comparison between the experimental rupture loads and the estimated rupture loads by the CSCT. It is observed that the estimated loads presented in all the slabs, some conservative values regarding experimental loads, the ratio Pu/Vcsct shows an average of 1.32. It is noticed that the more conservative value was observed in the slab LC3, with capital of 165 mm in length, and less conservative in slabs without capital or capital with inclination 1:2. Related to the place of rupture is observed that the estimates showed good results. It is emphasized that the slab LC2, with an inclination of 1:2, although the rupture mode assigned thereto, the slab has a proximity between the two rupture modes possible with difference of about 5 kN between the internal rupture load and external rupture load of the capital.
6. Conclusions
In the analysis of experimental rupture loads was used normative and theoretical recommendations developed about it. In the present work were used the recommendations of EUROCODE 2 [11], the NBR 6118 [10] and the Critical Shear Crack Theory. Then we observe that the estimates for the rupture load EUROCODE 2 [11] (VRc) had good results, with values close to the experimental relation with Pu/VRc around 1.0, except for the slab LC4. Once the code in question considers the contribution the increase in load capacity the capital, even to inclination the capital above of 1:3, a fact that has not been verified experimentally. Regarding the estimate for the rupture site, the slabs with an inclination of 1:2 showed external rupture, whichever is provided by the code, but for the slabs with capitals ratio hH:lH of 1:3 and 1:4 showed rupture internal, starting from the face of the column, differing from what was estimated. The NBR 6118 [10] also showed good results for slabs LC1 and LC2, but with conservative values in relation to slabs LC3 and LC4. As for the location of the rupture surface appearance the code showed good estimates for all slabs. Regarding the CSCT was observed conservative results, because of the theory that uses a perimeter of control with a radius of 0.5·d from the column face and the capital limit. The ratio between the experimental and rupture loads estimated by the CSCT (Pu/Vcsct) had an average of 1.32. It is observed that the estimated for LC3 was close to slab LC4, which indicates a better assessment as to the contribution the capital for relations hH:lH of 1:3 and 1:4. One can also be seen that in relation to the rupture surface, this theory had good results, but it is observed in the slab LC2 a balance between the internal and external rupture loads, with a difference of about 5 kN.
The computational models showed greater stiffness compared to experimental, with lower displacements for the same loading level, as expected, since the reinforcement of the numerical model was axisymmetric and the experimental arranged orthogonally. However, regarding the rupture surface, the strains in the concrete and the rupture loads realize good results in computer models of experimental relation to mainly the slabs LC1 and LC2, that showed 5% difference between the experimental and numerical loads. Also shown as approaching to the inclination of rupture surface computational with what was observed experimentally, thus confirming the efficiency of the model. For the slabs LC3 and LC4 presented differences in average by 10% from numerical and experimental rupture loads, as well as good approximation for rupture surface.
7. Acknowledgements
The authors would like to thank the CNPq and CAPES for financial support.
8. References
- [01] GASPARINI D. A., Contributions of C. A. P. Turner to development of reinforced concrete flat slabs 1905 - 1999. Journal of Structural Engineering, 2002, 128, No. 10, 1243 - 1252.
- [02] FURST, A., MARTI, D., Robert Maillart's design approach for flat slabs. Journal of Structural Engineering, 1997, No. 123(8), 1102 - 1110.
- [03] KIERDORF, A., Early Mushroom Slab Construction in Switzerland, Russia and the U.S.A. - A Study in Parallel Technological Development, In: Proceedings of the Second International Congress on Construction History, vol II, pp 1793 - 1807. Cambridge Construction History Society, Cambridge University, 2006.
- [04] MELO, G. S. S. A., Behavior of Reinforced Concrete Flat Slabs after Local Failure. PhD Thesis, Polytechnic of Central London, London, England, 1990, 214p.
- [05] TALBOT, A. N., Reinforced Concrete Wall Footings and Column Footings. Engineering Experiment Station, University of Illinois, Urbana, Bulletin No. 67, Mar. 1913, 114p.
- [06] RICHART, F. E., Reinforced Concrete Wall and Column Footings. ACI Journal, Proceedings, V. 45, No. 10, Oct. 1948, pp. 97-127.
- [07] KINNUNEN, S., NYLANDER, H., Punching of Concrete Slabs Without Shear Reinforcement. Transactions of the Royal Institute of Technology, No. 158, Stockholm, Sweden, 1960, 112 pp.
- [08] WEY, E. H., 1991. Seismic response of slab-column connections with shear capitals.PhD Thesis, Rice University. Houston, Texas.
- [09] HUESTE, M. B. D., BROWNING, J., LEPAGE, A. and WALLACE, J. W., Seismic Design Criteria for Slab-Column Connections, ACI Structural Journal, 2007; 104(4): 448 - 11.
- [10] ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118 - Projeto de Estruturas de Concreto. Rio de Janeiro, 2007.
- [11] EUROCODE 2, Design of Concrete Structures - Part 1-1: General Rules and Rules for Buildings, CEN, EN 1992-1-1, Brussels, Belgium, 2004, 225 pp.
- [12] MUTTONI, A., Punching Shear Strength of Reinforced Concrete Slabs without Transverse Reinforcement, ACI Structural Journal, V. 105, No. 4, July-Aug. 2008, pp. 440-450.
- [13] MUTTONI, A., and SCHWARTZ, J., Behaviour of Beams and Punching in Slabs without Shear Reinforcement, IABSE Colloquium, V. 62, Zurich, Switzerland, 1991, pp. 703-708.
- [14] FERREIRA, M. P. (2010). Punção em Lajes Lisas de Concreto Armado com Armaduras de Cisalhamento e Momentos Desbalanceados. Tese de Doutorado em Estruturas e Construção Civil, Publicação E.TD - 007 A/10 Departamento de Engenharia Civil e Ambiental, Universidade de Brasília, Brasília, DF, 275p.
- [15] MENETREY, Ph., Relationship between flexural and punching failure. ACI StructuralJournal, 1998; 95(4): 412 - 9.
- [16] TRAUTWEIN, L. M., 2001. Punção em Lajes Cogumelo de Concreto Armado com Armadura de Cisalhamento Tipo "Stud Interno" e Tipo "Estribo Inclinado". Dissertação de Mestrado, Publicação 001 A/2001, Departamento de Engenharia Civil e Ambiental, Universidade de Brasília, Brasília, DF, 165p.
- [17] VECCHIO, F. J., COLLINS, M.P., The Modified Compression Field Theory for Reinforced Concrete Elements Subjected To Shear. Proceedings V. 83, No. 2, Mar.-Apr. 1986, pp. 219-231
- [18] FEENSTRA, P. H., Computational Aspects of Civil Engineering, Delft University of Technology, Delft, Netherlands, 1993, 149 p.
- [19] LIMA NETO, A. F., 2012. Punção em Lajes Cogumelo de Concreto Armado com Capitéis. Tese de Doutorado em Estruturas e Construção Civil. Publicação E.TD. - 003 A/12 Departamento de Engenharia Civil e Ambiental, Universidade de Brasília. Brasília, DF. 164p.
Publication Dates
-
Publication in this collection
17 Apr 2013 -
Date of issue
Apr 2013
History
-
Received
06 June 2012 -
Accepted
12 Nov 2012