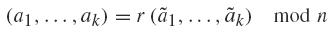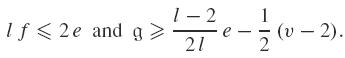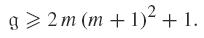ABSTRACT.
The genus graphs have been studied by many authors, but just a few results concerning in special cases: Planar, Toroidal, Complete, Bipartite and Cartesian Product of Bipartite. We present here a general lower bound for the genus of a abelian Cayley graph and construct a family of circulant graphs which reach this bound.
Keywords:
Abelian Cayley Graphs; Genus of a graph; Flat torus; Tessellations
RESUMO.
O gênero de grafos têm sido estudados por muitos autores, mas existem resultados apenas para casos especiais: Planar, Toroidal, Completo, Bipartido e Produto cartesiano de Bipartidos. Apresentamos aqui um limite inferior para o gênero de um grafo de Cayley de um grupo abeliano e construímos uma família de grafos circulantes que atingem esse limitante.
Palavras-chave:
Grafos de Cayley abelianos; Gênero de grafos; Toro plano; Tesselações
1 INTRODUCTION
The genus of a graph, defined as the minimum genus of a 2-dimensional surface4 4 The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along nonintersecting closed simple curves without rendering the resultant manifold disconnected. It is equal to the number of handles on it. on which this graph can be embedded without crossings 77 J.E. Gross & T.W. Tucker. Topological graph theory. Dover Publications Inc., Mineola, NY (2001).), (2121 R.J. Trudeau. Introduction to graph theory. Dover Publications Inc., New York, 1993. Corrected reprint of the 1976 original., is well known as being an important measure of the graph complexity and it is related to other invariants.
A circulant graph, Cn (a 1 , . . . , ak ), is an homogeneous graph which can be represented (with crossings) by n vertices ({v 0 , . . .vn −1}) on a circle, with two vertices being connected if only if there is jump of ai from one to the other, ∀i = 1, . . . , k, where a jump is an edge between vj and vmod ( j ± ai, n ) (Figure 1). A circulant graph is particular case of abelian Cayley graph. Different aspects of circulant graphs have been studied lately, either theoretically or through their applications in telecommunication networks and distributed computation 1010 X. Lin, Y. Yang, J. L¨u & X. Hao. The crossing number of C(mk; {1, k}). Graphs Combin., 21(1) (2005), 89-96.), (1212 D. Matthew. On Hamilton cycle decomposition of 6-regular circulant graphs. Graphs Combin., 22(3) (2006), 331-340.), (1111 V. Liskovets & R. P¨oschel.Counting circulant graphs of prime-power order by decomposing into orbit enumeration problems. Discrete Math., 214(1-3) (2000), 173-191.), (1515 M. Muzychuk. Ádám's conjecture is true in the square-free case. J. Combin. Theory Ser. A, 72(1) (1995), 118-134.), (1313 F.P. Muga II. Undirected Circulant Graphs, International Symposium on Parallel Architectures. Algorithms and Networks, (1994), 113-118.), (99 C. Heuberger. On planarity and colorability of circulant graphs. Discrete Math., 268(1-3) (2003), 153-169..
The circulant graph C 13(1, 6) represented in the standard form (left) and on a 2-dimensional flat torus (right).
Concerning specifically to the genus of circulant graphs few results are known up to now. We quote 33 F. Boesch & R. Tindell. Circulants and their connectivities. J. Graph Theory, 8(4) (1984), 487-499. for a small class of toroidal (genus one) circulant graphs, 99 C. Heuberger. On planarity and colorability of circulant graphs. Discrete Math., 268(1-3) (2003), 153-169. which establish a complete classification of planar circulant graphs, 55 M. Conder & R. Grande. On Embeddings of Circulant Graphs. The Eletronic Journal of Combinatorics, 22(2) (2015), 1-27. which establish a complete classification of minimum genus 1 and 2 for circulant graphs, and the cases where the circulant graph is either complete or a bipartite complete graph 44 L. W. Beineke & F. Harary. The Genus of the n-Cube. Canad. J. Math., 17 (1965), 494-496.), (88 F. Harary, Graph Theory. Reading,MA: Addison-Wesley, (1994).), (1717 G. Ringel. Das Geschlecht des vollst¨andiger Paaren Graphen. Abh. Math. Sem. Univ. Hamburg, 28 (1965), 139-150.), (1818 G. Ringel, Der vollst¨andige paare Graph auf nichtorientierbaren Fl¨achen. J. Reine Angew. Math., 220 (1965), 88-93.), (2020 G. Ringel & J.W.T. Youngs. Solution of the Heawood Map-Coloring Problem. Proc. Nat. Acad. Sci. USA, 60 (1968), 438-445..
In 66 S.I.R Costa, J.E Strapasson, M.Muniz & T.B. Carlos. Circulant graphs and tessellations on flat tori. Linear Algebra and Appl, 432(1) (2010), 369-382. the authors show how any circulant graph can be viewed as a quotient of lattices and obtain as consequences that: i) for k = 2, any circulant graph must be either genus one or zero (planar graph) and ii) for k = 3, there are circulant graphs of arbitrarily high genus.
We derive a general lower bound for the genus of abelian Cayley graph Cn
(a
1
, . . . , ak
) as  (Proposition 1), and construct a family of abelian Cayley graphs which reach this bound (Corollary 4).
(Proposition 1), and construct a family of abelian Cayley graphs which reach this bound (Corollary 4).
This note is organized as follows. In Section 2 we introduce concepts and previous results concerning circulant graphs, abelian Cayley graphs and genus.
In Section 3 we derive a lower bound for the genus of an n-circulant graph of order 2 k (Proposition 1) and construct families of graphs reaching this bound for arbitrarily k (Corollary 4).
2 NOTATION AND PREVIOUS RESULTS
In this section we recall concepts and results used in this paper concerning circulant graphs. We also fix the notations which will be followed later on.
Let G = ({e = g 1 , . . . gn },+) be a finite abelian group. Given a subset S = {a 1 , . . . , ak } of G, the associated Cayley graph (G, S) is an undirected graph whose vertices are the elements of G, and where two vertices gi and gj are connected if and only if gi − gj = ±al for some al ∈ S. We remark that (G, S) is connected if and only if S generates G as a group, and that this graph is 2k-regular if ai + ai ≠ 0, ∀i = 1, 2, . . . k, and (2k − l)-regular otherwise, where l is a number of ai such that ai + ai = 0.
A circulant graph Cn (a 1 , . . . , ak ) with n vertices v 0 , . . .vn − 1 and jumps a 1 , . . . , ak , 0 < aj ≤ ⌊n/2⌋, ai ≠ aj , is an undirected graph such that each vertex vj, 0 ≤ j ≤ n − 1, is adjacent to all the vertices vj ± ai mod n, for 1 ≤ i ≤ k. A circulant graph is homogeneous: any vertex has the same degree (number of incident edges), with is 2k except when aj = n/2 for some j, when the degree is 2k − 1, a circulant graph is a particular case of abelian Cayley graph (G = ℤn, S = {a 1 , . . . , ak }).
The n-cyclic graph and the complete graph of n vertices are examples of circulant graphs denoted by Cn (1) and Cn(1, . . . , ⌊n/2⌋), respectively. Figure 1 shows on the left the standard picture of the circulant graph C 13(1, 6).
In what follows we write (a 1 , . . . , ak ) = (ã 1 , . . . , ãk) mod n to indicate that for each i, there is j such that ai = ±ãj mod n. Two circulant graphs, Cn (a 1 , . . . , ak ) and Cn (ã 1 , . . . , ãk ) are said to satisfy the Ádám's relation if there is r, with gcd(r, n) = 1, such that
An important result concerning circulant graphs isomorphisms is that circulant graphs satisfying the Ádám's relation are isomorphic 11 A. Ádám. Research problem 2-10. J. Combinatorial Theory, (1967).. The reciprocal of this statement was also conjectured by Ádám. It is false for general circulant graphs but it is true in special cases such as k = 2 or n = p or n = pq (p and q prime) (see 1111 V. Liskovets & R. P¨oschel.Counting circulant graphs of prime-power order by decomposing into orbit enumeration problems. Discrete Math., 214(1-3) (2000), 173-191.), (22 B. Alspach & T.D. Parsons. Isomorphism of circulant graphs and digraphs. Discrete Math., 25(2) (1979), 97-108.). In this paper we will not distinguish between isomorphic graphs.
Without loss of generality we will always consider a 1 < · ·· < ak ≤ n/2 for a circulant graph Cn (a 1 , . . . , ak ).
A circulant graph Cn (a 1 , . . . , ak ) is connected if, and only if, gcd(a 1 , . . . , ak , n) = 1 33 F. Boesch & R. Tindell. Circulants and their connectivities. J. Graph Theory, 8(4) (1984), 487-499.. In this paper we just consider connected circulant graphs.
The genus of a graph is defined as the minimum genus, 𝔤, of a 2-dimensional orientable compact surface ℳ𝔤 onwhich this graph can be embeddedwithout crossings 77 J.E. Gross & T.W. Tucker. Topological graph theory. Dover Publications Inc., Mineola, NY (2001).), (2121 R.J. Trudeau. Introduction to graph theory. Dover Publications Inc., New York, 1993. Corrected reprint of the 1976 original.. This number, besides being a measure of the graph complexity, is related to other invariants. Let G a graph of the genus 𝔤, defines p
𝔤 as p
𝔤 = 5
5
The algebraic connectivity is the second-smallest eigenvalue of the Laplacian matrix of G.
of G, μ(G), , satisfies μ(G) < p𝔤 − 1 for all noncomplete graphs G if p𝔤(p𝔤 − 7) = 12(𝔤 − 1), see (1414 J.J. Molitierno. On the algebraic connectivity of graphs as a function of genus. Linear Algebra and its Applications, 419(2-3) (2006), 519-531.). , so: the chromatic number of G is γ(G) = p𝔤 (Heawood conjecture) and the algebraic connectivity
, so: the chromatic number of G is γ(G) = p𝔤 (Heawood conjecture) and the algebraic connectivity
A graph E is a subdivision of H if it is constructed from H by possibly adding new vertices on the edges of H. Finally, if there is a subdivision E of H which is a subgraph of G we say G is supergraph of H. From this definition follows that
if G is a supergraph of H, genus(G) ≥ genus(H).
When a connected graph G is embedded on a surface, ℳ𝔤, of minimum genus 𝔤 it splits the surface in regions called faces, each one homeomorphic to an open disc surrounded by the graph edges, giving rise to a tessellation on this surface. Denoting the number of faces, edges and vertices by f, e, and v respectively, those numbers must satisfy the well known Euler's second relation:
We quote next other known relations those numbers must satisfy 77 J.E. Gross & T.W. Tucker. Topological graph theory. Dover Publications Inc., Mineola, NY (2001).), (2121 R.J. Trudeau. Introduction to graph theory. Dover Publications Inc., New York, 1993. Corrected reprint of the 1976 original.:
If G is a graph of genus 𝔤 with v ≥ l such that any face in ℳ𝔤 has at least l sides in its boundary,
In the above expressions we have equalities if, only if, all the faces have l sides.
An upper bound for the genus of a connected graph of n vertices is given by the genus of the complete graph, Cn
(1, . . . , ⌊n/2⌋), which is  . Combining the lower bound above with a minimum of three edges for each face, we can write the following inequality, for n ≥ 3:
. Combining the lower bound above with a minimum of three edges for each face, we can write the following inequality, for n ≥ 3:
where ⌈x⌉ is the ceiling (smallest integer which is greater or equal to) of x.
For a circulant graph Cn (a 1 , . . . , ak ), a 1 < a 2 < · ·· < ak we can replace e by e = n k when ak < n/2 , or e = n(2k −1)/2 when ak = n/2 . We can then rewrite the lower bound in last expression as ⌈n/6 (k − 3) + 1⌉ or ⌈n/6 (k − 4) + 1⌉, respectively.
2.1 Previous results on genus of circulant graphs and abelian Cayley graphs
• Theorem (Ringel, Beineke and Harary, 1965 ( 1919 G. Ringel, ¨Uber drei kombinatorische Problem am n-dimensionalen W¨urfel und Wurfelgitter. Abh. Math. Sem. Univ. Hamburg, 20 (1965), 10-19.), (44 L. W. Beineke & F. Harary. The Genus of the n-Cube. Canad. J. Math., 17 (1965), 494-496.)). The genus of the n-cube graph Qn is 1 + 2n −3(n − 4).
• Theorem (Ringel, 1965 (
1717 G. Ringel. Das Geschlecht des vollst¨andiger Paaren Graphen. Abh. Math. Sem. Univ. Hamburg, 28 (1965), 139-150.), (1818 G. Ringel, Der vollst¨andige paare Graph auf nichtorientierbaren Fl¨achen. J. Reine Angew. Math., 220 (1965), 88-93.)). The genus of the complete bipartite graph Km,n is − 1), the genus of this one-parameter family is
− 1), the genus of this one-parameter family is  .
. . Since Kn,n is the circulant graph C2n(1, 3, . . . , 2
. Since Kn,n is the circulant graph C2n(1, 3, . . . , 2
• Theorem (White, 1970 (2222 A.T. White. The genus of repeated cartesian products of bipartite graphs. Trans. Amer. Math. Soc., 151 (1970), 393-404.)). Let G = Cm1□Cm2 · ··□Cmr6 6 The Cartesian product G 1□G 2 of the graphs G 1 and G 2 is a graph such that the vertex set of G 1□G 2 is the Cartesian product of the set of vertices of G 1 with the set of vertices G 2(V(G 1) × V(G 2)) and any two vertices (u,u') and (v,v') are adjacent in G 1□G 2 if and only if either u = v and u is adjacent with v in G 2, or u = v and u is adjacent with v in G 1. , where Cmi is even cycle, r > 1 and mi > 3 for all i . Then the genus of G is 1 + v(r − 2)/4, where v = m1m2, · · ·mr.
• Theorem (Pisanski, 1980 (1616 T. Pisanski.Genus of Cartesian products of regular bipartite graphs. J. Graph Theory, 4 (1980), 31-42.)) Let G and H be connected r-regular bipartites graphs. Then the Cartesian product G□H of G and H has genus 1+ pm(r − 2)/4 where p and m are the number of vertices of G and H, respectively.
• Theorem (Heuberger, 2003 (99 C. Heuberger. On planarity and colorability of circulant graphs. Discrete Math., 268(1-3) (2003), 153-169.)). A planar circulant graph is either the graph Cn(1), or Cn(a1, a2), where i) a2 = ±2a1 mod n and n is even, ii) a2 = n/2, and a2 is even.
• For k = 2, and general (a1, a2), we have shown that circulant graphs Cn(a1, a2) are very far for from reaching the upper bound for the genus given in (4), as it was shown in (66 S.I.R Costa, J.E Strapasson, M.Muniz & T.B. Carlos. Circulant graphs and tessellations on flat tori. Linear Algebra and Appl, 432(1) (2010), 369-382.):
Proposition 1 (66 S.I.R Costa, J.E Strapasson, M.Muniz & T.B. Carlos. Circulant graphs and tessellations on flat tori. Linear Algebra and Appl, 432(1) (2010), 369-382.). Any circulant graph Cn(a1, a2), a1 < a2 ≤ n/2, has genus one, except for the cases of planar graphs: i) a2 = ±2a1 mod n, and n is even, ii) a2 = n/2, and a2 is even.
• For k = 3 and n ≠ 2a3 we can assert that the genus of Cn(a1, a2, a3) satisfies:
The genus of the complete graph C 7(1, 2, 3) achieves the minimum value one (4). However, in opposition to the case k = 2, the genus of a circulant graph Cn (a 1, a 2, a 3) can be arbitrarily high:
Proposition 2 66 S.I.R Costa, J.E Strapasson, M.Muniz & T.B. Carlos. Circulant graphs and tessellations on flat tori. Linear Algebra and Appl, 432(1) (2010), 369-382.. There are circulant graphs Cn (a 1, a 2, a 3) of arbitrarily high genus. A family of such graphs is given by: n = (2m + 1) (2m + 2) (2m + 3), m ≥ 2; a 1 = (2m + 2) (2m + 3), a 2 = (2m + 1) (2m + 2) (m + 1), a 3 = (2m + 2) (2m + 3) (m + 1), with the correspondent genus satisfying
In the next section we dealwith the more general class of abelian Cayley graphs and establish a lower bound for their genus.
3 QUADRANGULAR EMBEDDING OF ABELIAN CAYLEY GRAPHS
In this section we consider Cayley graphs of abelian groups, a more general class of graphs of which circulant graphs form a very particular subclass, the Cayley graphs of cyclic groups. Nevertheless, an important feature of circulant graphs, their embeddings in k-dimensional tori, is shared by the whole class of Cayley graphs of abelian groups. We will see in the following that k is associated to the number of elements of the generating set of the edges of the Cayley graph. We will determine a subclass of these graphs that has quadrangular embeddings, and hence a subclass where we know the genus of each graph.
It is known that graphs that have 3-cycles may have embeddings with triangular faces, and some easy calculations establish a lower bound for the genus. In general we can also establish a lower bound that depends on the girth l of the graph. If (G, S) is a Cayley graph and there are no solutions of ah = ±(ai ± aj ) for h, i, j ∈ {1, 2, . . . k} (not necessarily distinct), the girth is always 4 (a typical 4-cycle is 0, ai, ai + aj, aj , 0), which implies at least four edges for each face.
If the graph is 2k-regular, then
Hence, we get the following lemma, which establishes a lower bound for circulant graphswith no triangular faces.
Lemma 1. The genus, 𝔤, of the circulant graph Cn (a 1 , . . . , ak ), such that ai ≠ aj + al, ∀i, j, l ≤ k and n ≠ 2 ai, ∀i satisfy:
In what follows the (additive) subgroup of G = ℤn 1 × ℤn 2 ×· · ·× ℤnl generated by a 1 , . . . , ak ∈ G is denoted by 〈a 1 , . . . , ak 〉, and let Gs = 〈a 1 , a 2 , . . . , as 〉 ⊲ G. Define Ls as the group order of as , 1 ≤ s ≤ k, where L 1 = o(a 1) is the group order of a1, and Ls = o(as + Gs −1) = [Gs : Gs −1] is the index of the quotient group 1 < s ≤ k.
Under the above conditions we can assert that x ∈ G can be expressed uniquely as a linear combination, x = m 1 a 1 + m 2 a 2 + . . .mkak , where 0 ≤ mi < Li . This fact is stated in the next a lemma.
Lemma 2. Given x ∈ G and Gs ⊲ G, 1 ≤ s < k then there exist a unique mi ∈ ℕ and Rs,x such that
x = m 1 a 1 + ···+msas + Rs,x and Rs,x = R(ms +1 , . . . ,mk ) = ms +1 as +1 + ·· ·mkak
with 0 ≤ mi < Li for all i.
Through the Lemma 2 we can show that not only the circulant graphs 66 S.I.R Costa, J.E Strapasson, M.Muniz & T.B. Carlos. Circulant graphs and tessellations on flat tori. Linear Algebra and Appl, 432(1) (2010), 369-382. but any Cayley graph of an abelian group can be embedded in a k-dimensional torus. The construction of such embedding, for k = 2, is illustrade in Figure 2.
We consider the mapping:
Therefore G and ker φ is lattice. The Cayley graph associated to G, as a quotient of lattices, is then naturally embedded in flat torus which a polytope generated by basis of this lattice, with the parallel faces identified. ~
~
To proceed in a uniform way we can use the standard Hermite basis for ker φ, as it done for circulant graphs in 99 C. Heuberger. On planarity and colorability of circulant graphs. Discrete Math., 268(1-3) (2003), 153-169..
We remark that Hermite basis of ker φ, {U 1 , . . . ,Uk }, is given as columns of a upper triangular matrix (bi, j )k × k , where bi,i = Li and 0 ≤ bi, j < Li .
In Figure 2, we consider the Cayley graph of G = ℤ2 × ℤ8 and a 1 = (1, 2) and a 2 = (0, 1), therefore o(a 1) = 4 and o(a 2 + 〈a 1〉) = 4 and Hermite basis is {(4, 0), (2, 4)}.
We will construct the embedding of Cayley graphs (G, S) by induction on k = #S (#S is equal to the cardinality of S). Note that (G, S − {ak }) may be disconnected: it is well known that this graph has d = gcd(n, a 1 , . . . , ak −1) components, where Lk = [G = Gk : Gk −1] = o(ak + Gk −1), and that each component is isomorphic to the Cayley graph (Gk −1 , S − {ak }). Since x and y are linked by a path if and only if x − y = m 1 a 1 + ·· ·+mk −1 ak −1 in G, it follows that x and y are in the same component if and only if x ≡ y ∈ Gk −1. Hence, each 0 ≤ js < Lk determines a component and the numbers,
Rk,mk + m 1 a 1 +· · ·+mk −1 ak −1
describe all vertices of the component of (G, S − ak ) associated to mk , where 0 ≤ mk < Lk and Rk,mk is a fixed element of this component.
Proposition 3. Let (G, {a
1
, . . . , ak
}), where n = #G = 2l, and Li
= 2li , 1 ≤ i ≤
k, and l
1
> 1 and ai
≠ ±(aj
± ah), 1 ≤ i, j, h < k. Hence, the genus of G is .
.
Proof. The proof will be done by induction on k. For k = 2 it is trivial (vide Figure 2). Assume that the result holds for k −1. The graph (G, {a1, . . . , ak−1}) is a disconnectedCayley graph with an even number of connected components (Lk = 2lk ), Hmk = Rk,mk + Gk−1, 0 ≤ mk < 2lk, where 2lk = [G : Gk−1].
Each component Hmk can be embedded on a surface Smk giving to a rise tessellation where every face has 4 edges. As in Figure 3, we reverse the orientation of the components that contain the odd multiples of ak.
The construction of the C32(8, 2, 3) embedding. Tubes are added on the two connected components of C32(8, 2) considered with reversal orientation.
We wish to add tubes that, topologically, are prisms with squared bases.
Let x ∈ Hmk, then x = mkak + m1a1 + ··· +mk−1ak−1 where 0 ≤ mk < 2lk and 0 ≤ mi < 2li as in Lemma 2. Given 0 < j < k − 1, we can also express
with g =  miai and δj , δk−1 ∈ {0, 1}.
miai and δj , δk−1 ∈ {0, 1}.
Three possibilities should be considered:
i) Each vertex of Hmk , mk even, is a vertex of a square determined by {P, P + ak−1, P + ak−1 + aj, P + aj}, where P is of the form
where 0 ≤ 2 pj < Lj , 2 pk −1 < Lk −1. Just as Figure 3, each such square is then connected to the square {P + ak, P + ak + ak −1 , P + ak + ak −1 + aj, P + ak + aj } (which lies on Hmk +1) by a prism which contains the edges [P, P + ak ], [P + ak −1 , P + ak + ak −1], [P + ak −1 + aj, P + ak + ak −1 + aj ] and [P + aj, P + ak + aj ]; and then we cut out both squares. Doing this for every j ∈ {1, 2, . . . , k−2} we construct a surface where each edge of the form [x, x + ak ] is embedded without crossings.
ii) Each vertex of Hmk , mk odd and mk ≠ 2lk − 1, is a vertex of a square determined by {Q, Q + ak −1 , Q + ak −1 + aj, Q + aj }, where Q is of the form
where 2 ≤ 2qj ≤ Lj , 2 qk −1 < Lk −1. The same reasoning as above can be applied by replacing P by Q.
iii) Each vertex, x of H
2
lk
−1, x + ak
∈ H
0. This case requires special care, since we need to choose a face in H
2
lk
−1 and another in H
0, once that some faces have been excluded. This choice depends on how 2lk ak
is described in Gk
, since 2lk ak
= mj
are not both even, and mk
−1 is not odd. We then repeat the procedure of item (i), replacing P by  such that
such that  choose
choose  and
and  .
.
Therefore, under restrictions considered in this proposition we always can connect the excluded squares by prisms and construct a surface which is tessellated by (G, S), and each face of this tessellation is a square, by Lemma 1 the genus is greater than or equal to  , remember that equality is achieved if all faces have the same number of sides, and this concludes the proof. □
, remember that equality is achieved if all faces have the same number of sides, and this concludes the proof. □
Corollary 4. Let G = Cn(a1, . . . , ak), where n = 2rl, ai = 2ri li , i = 1, . . . k − 1, where l, li, ak odd, 0 < ri+1 < ri < r and ai+1 ≠ ±2 ai, 1 ≤ i < k. Hence, the genus of G is  .
.
The next example shows that there are more circulant graphs than the ones considered in Proposition 3 which also can be embedded giving rise to a quadrilateral tessellation.
Example 3.1. For the graph C32(8, 2, 3, 7), if we consider C32(8, 2, 3) as in last proposition, we note that just half the faces of the tessellation of C32(8, 2) are excluded to add tubes. We can also exclude the other faces adding tubes to support the edges ±a4. Hence this is an embedding generating quadrilateral faces and since there are no cycles of size 3, the expression for the genus still holds.
Figure 4 shows all the circulant graphs of 32 vertices for which the genus can be given by Proposition 2.1 (Heuberger), 1 and Corollary 4
All circulant graphs of 32 vertices satisfying Propositions 2.1 (Heuberger), 1 and 4 (I = {±1,±3, . . . ,±15}).
We note that some graphs satisfying the hypotheses of the last proposition belong to the class of graphs with given genus. For some of those graphs we could have used the results ofWhite and Pisanski (see 2222 A.T. White. The genus of repeated cartesian products of bipartite graphs. Trans. Amer. Math. Soc., 151 (1970), 393-404.), (1616 T. Pisanski.Genus of Cartesian products of regular bipartite graphs. J. Graph Theory, 4 (1980), 31-42.) to determine their genus namely. The particular class of Cartesian product of bipartite graphs which satisfy the proposition hypothesis. However, many of the graphs considered in the last proposition are not Cartesian product of bipartite graphs.
For example the Cayley graphs G 1 = (ℤ2 × ℤ8 , {(1, 2), (0, 1)}) and G 2 = C 16(1, 4).
We can assert that the G 1 is not a product of de bipartite graphs, since as G 1 = G□H, a regular graph, to be such a product, each graph factor needed to be also a regular graph. There are few possibilities to be considered here: #G = 2 or 4 and #H = 8 or 4, respectively. That is, either i) G = P 2 and H is a 3-regular complete bipartite graph (hypothesis of White and Pisanski results), what is not possible since H is bipartite and therefore it should be 4-regular, or ii) G = H = K 2 , 2 what again cannot be true, since K 2 , 2□K 2 , 2 = (ℤ4×ℤ4 , {(1, 0), (0, 1)}),which has spectrum{8, 6, 6, 6, 6, 4, 4, 4, 4, 4, 4, 2, 2, 2, 2, 0} and G 1 has spectrum {8, 6, 6, 4+√2, 4+√2, 4+√2, 4+√2, 4, 4, 4−√2, 4−√2, 4−√2, 4−√2, 2, 2, 0}.
G2 also is not a product of bipartite graphs since it has odd size cycles (ex: 0, 1, 2, 3, 4, 0) what does not occur for bipartite graphs.
4 ACKNOWLEDGMENTS
This work was partially supported by FAPESP-Brazil 2007/56052-8, 2007/00514-3, 2011/01096-6 and 2013/25977-7 and CNPq 309561/2009-4 and 304705/2010-1.
REFERENCES
-
1A. Ádám. Research problem 2-10. J. Combinatorial Theory, (1967).
-
2B. Alspach & T.D. Parsons. Isomorphism of circulant graphs and digraphs. Discrete Math., 25(2) (1979), 97-108.
-
3F. Boesch & R. Tindell. Circulants and their connectivities. J. Graph Theory, 8(4) (1984), 487-499.
-
4L. W. Beineke & F. Harary. The Genus of the n-Cube. Canad. J. Math., 17 (1965), 494-496.
-
5M. Conder & R. Grande. On Embeddings of Circulant Graphs. The Eletronic Journal of Combinatorics, 22(2) (2015), 1-27.
-
6S.I.R Costa, J.E Strapasson, M.Muniz & T.B. Carlos. Circulant graphs and tessellations on flat tori. Linear Algebra and Appl, 432(1) (2010), 369-382.
-
7J.E. Gross & T.W. Tucker. Topological graph theory. Dover Publications Inc., Mineola, NY (2001).
-
8F. Harary, Graph Theory. Reading,MA: Addison-Wesley, (1994).
-
9C. Heuberger. On planarity and colorability of circulant graphs. Discrete Math., 268(1-3) (2003), 153-169.
-
10X. Lin, Y. Yang, J. L¨u & X. Hao. The crossing number of C(mk; {1, k}). Graphs Combin., 21(1) (2005), 89-96.
-
11V. Liskovets & R. P¨oschel.Counting circulant graphs of prime-power order by decomposing into orbit enumeration problems. Discrete Math., 214(1-3) (2000), 173-191.
-
12D. Matthew. On Hamilton cycle decomposition of 6-regular circulant graphs. Graphs Combin., 22(3) (2006), 331-340.
-
13F.P. Muga II. Undirected Circulant Graphs, International Symposium on Parallel Architectures. Algorithms and Networks, (1994), 113-118.
-
14J.J. Molitierno. On the algebraic connectivity of graphs as a function of genus. Linear Algebra and its Applications, 419(2-3) (2006), 519-531.
-
15M. Muzychuk. Ádám's conjecture is true in the square-free case. J. Combin. Theory Ser. A, 72(1) (1995), 118-134.
-
16T. Pisanski.Genus of Cartesian products of regular bipartite graphs. J. Graph Theory, 4 (1980), 31-42.
-
17G. Ringel. Das Geschlecht des vollst¨andiger Paaren Graphen. Abh. Math. Sem. Univ. Hamburg, 28 (1965), 139-150.
-
18G. Ringel, Der vollst¨andige paare Graph auf nichtorientierbaren Fl¨achen. J. Reine Angew. Math., 220 (1965), 88-93.
-
19G. Ringel, ¨Uber drei kombinatorische Problem am n-dimensionalen W¨urfel und Wurfelgitter. Abh. Math. Sem. Univ. Hamburg, 20 (1965), 10-19.
-
20G. Ringel & J.W.T. Youngs. Solution of the Heawood Map-Coloring Problem. Proc. Nat. Acad. Sci. USA, 60 (1968), 438-445.
-
21R.J. Trudeau. Introduction to graph theory. Dover Publications Inc., New York, 1993. Corrected reprint of the 1976 original.
-
22A.T. White. The genus of repeated cartesian products of bipartite graphs. Trans. Amer. Math. Soc., 151 (1970), 393-404.
-
4
The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along nonintersecting closed simple curves without rendering the resultant manifold disconnected. It is equal to the number of handles on it.
-
5
The algebraic connectivity is the second-smallest eigenvalue of the Laplacian matrix of G.
-
6
The Cartesian product G 1□G 2 of the graphs G 1 and G 2 is a graph such that the vertex set of G 1□G 2 is the Cartesian product of the set of vertices of G 1 with the set of vertices G 2(V(G 1) × V(G 2)) and any two vertices (u,u') and (v,v') are adjacent in G 1□G 2 if and only if either u = v and u is adjacent with v in G 2, or u = v and u is adjacent with v in G 1.
Publication Dates
-
Publication in this collection
Sep-Dec 2016
History
-
Received
03 Jan 2016 -
Accepted
21 Oct 2016