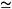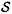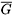Abstract

LARRION, F.; NEUMANN-LARA, V.  and  PIZANA, M. A.. On the homotopy type of the clique graph. J. Braz. Comp. Soc. [online]. 2001, vol.7, n.3, pp.69-73. ISSN 0104-6500.  http://dx.doi.org/10.1590/S0104-65002001000200010.

If G is a graph, its clique graph K(G) is the intersection graph of all its (maximal) cliques. The complex G^­ of a graph G is the simplicial complex whose simplexes are the vertex sets of the complete subgraphs of G. Here we study a sufficient condition for G^­ and K(G)^­ to be homotopic. Applying this result to Whitney triangulations of surfaces, we construct an infinite family of examples which solve in the affirmative Prisner's open problem 1 in Graph Dynamics (Longman, Harlow, 1995): Are there finite connected graphs G that are periodic under K and where the second modulo 2 Betti number is greater than 0?

Keywords : clique graphs; clique convergence; Whitney triangulations; clean triangulations; simplicial complexes; modulo 2 Betti numbers.

        · text in English     · English ( pdf epdf )