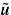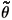In this paper, a strongly nonlinear coupled elliptic-parabolic system modelling a class of engineering problems with heat effect is studied. Existence of a weak solution is first established by Schauder fixed point theorem, where the coupled functions σ(s), k(s) are assumed to be bounded. The uniqueness of the solution is obtained by applying Meyers' theorem and assuming that σ(s), k(s) are Lipschitz continuous. The regularity of the solution is then analyzed in dimension d < 2 under the assumptions on σ(s), k(s) ∈ C2(R) and the boundedness of their derivatives of second order. Finally, the blow-up phenomena of the system are studied. Mathematical subject classification: 35J60, 35K55.
elliptic-parabolic system; existence; uniqueness; regularity; blow-up