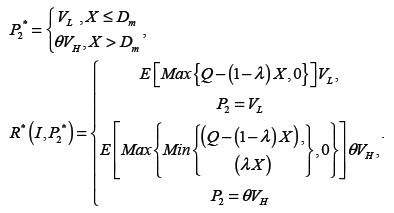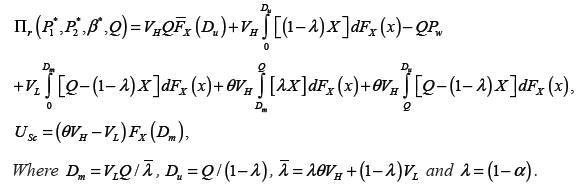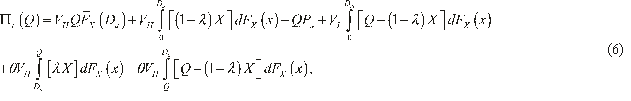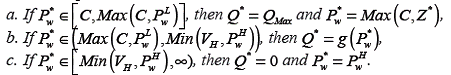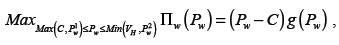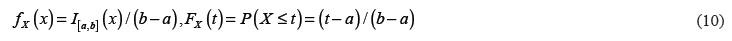ABSTRACT
This paper studying the impact of strategic customer behavior on decentralized supply chain gains and decisions, which includes a supplier, and a monopoly firm as a retailer who sells a single product over a finite two periods of selling season. We consider three types of customers: myopic, strategic and low-value customers. The problem is formulated as a bi-level game where at the second level (e.g. horizontal game), the retailer determines his/her equilibrium pricing strategy in a non-cooperative simultaneous general game with strategic customers who choose equilibrium purchasing strategy to maximize their expected surplus. At the first level (e.g. vertical game), the supplier competes with the retailer as leader and follower in the Stackelberg game. They set the wholesale price and initial stocking capacity to maximize their profits. Finally, a numerical study is presented to demonstrate the impacts of strategic behavior on supply chain gain and decisions; subsequently the effects of market parameters on decision variables and total profitability of supply chain's members is studied through a sensitivity analysis.
key words:
pricing and revenue management; strategic customer; supply chain management; game theory.
INTRODUCTION
Retailer's decision variables are always affected by supply situations and sale policies, so they are the two most important challenges influencing the retailers. However, the complexity of these challenges has considerably increased by various factors such as customer awareness, economic variables, technological development, and competitive environment. For instance, internet development has inspired suppliers to sell their products or services directly to target consumers or those customers looking for some opportunities at lower prices because of growing global awareness. If retailers cannot overcome these challenges, their benefits will be significantly compromised. Therefore, supplying and selling policies are retailer's two major concerns.
In the real context, there are many applications, which help us better understand this issue; for example, travel agencies must book airline tickets and hotel rooms (e.g. supply side) and determine sales policies (e.g. demand side) based on their demand estimations; or style goods retailers should simultaneously consider supplying constraints and market behavior. Therefore, it seems imperative for firms to simultaneously focus on both sides of supply and demand.
On the demand side, nowadays, customers have largely learned to follow buying opportunities at fair prices. During the last decade, many research projects have emphasized on increasing the number of customers who buy their required goods during season sales. Change in the customer behavior as well as other factors such as competitive pressures or supplying constraints, have forced retailers to modify their pricing and stocking strategies (see e.g., Byrnes and Zellner (2004)Byrnes N and Zellner W. 2004. Playing the discount game. Bus Week, December 13., Silverstein and Butman (2006))Silverstein MJ and Butman J. 2006. Treasure Hunt: Inside the Mind of the New Consumer, Portfolio, New York. of future prices and this strategic behavior has resulted in a plethora of studies in this area (for example, see, e.g., Su and Zhang (2008))Su X and Zhang F. 2008. Strategic customer behavior, commitment, and supply chain performance. Management Sci 54(10): 1759-1773..
According to strategic customer behavior in recent literature, customer purchasing decisions depend on their expectations of the market conditions. Specifically, some studies have focused on strategic customers with future price-depended purchasing time. Such papers have examined optimal markdowns pricing strategies in the presence of strategic customers. Shen and Su (2007)Shen ZJ and Su X. 2007. Customer behavior modeling in revenue management and auctions: A review and new research opportunities. Prod Oper Management 16(6): 713-728. have presented a comprehensive review of these studies. Desai et al. (2004)Desai P, Koenigsberg O and Purohit D. 2004. Strategic decentralization and channel coordination. Quant Marketing Economic 2: 5-22. compared centralized and decentralized distribution channels for durable goods and demonstrated that strategic decentralization could increase the manufacturer's profits under some specific conditions. Arya and mittendorf (2006)Arya A and Mittendorf B. 2006. Benefits of channel discord in the sale of durable goods. Marketing Sci 25(1): 91-96. proved that the benefits of decentralization are robust against fluctuations of manufacturer's commitments ability. Aviv and Pazgal (2008)Aviv Y and Pazgal A. 2008. Optimal pricing of seasonal products in the presence of forward-looking customers. Manuf Service Oper Manage 10(3): 339-359. proposed optimal pricing of a seasonal product at the market with forward-looking customers. Elmaghraby et al. (2008)Elmaghraby W, Gulcu A and Keskinocak P. 2008. Designing optimal pre-announced markdowns in the presence of rational customers with multi-unit demands. Manuf Service Oper Manage 10(1): 126-148. investigated optimal markdown pricing in the presence of multi-unit rational demands. Gallien (2006)Gallien G. 2006. Dynamic mechanism design for online commerce. Oper Res 54(2): 291-310. proved that when we sell a finite inventory to infinite strategic customer, the optimal prices should increase over time horizon. Su (2007)Su X. 2007. Inter-temporal pricing with strategic customer behavior. Manage Sci 53(5): 726-741. examined a market with heterogeneous myopic and strategic customers and demonstrated that the optimal pricing strategy is one of the two markup or markdown mechanisms, based on the customer composition.
Also, Yu et al. (2007)Yu M, Kapuscinski R and Ahn HS. 2007. Advance selling with limited capacity and customers' dependent valuations. Working paper. Ross School of Business. University of Michigan. Ann Arbor. compared different demand scenarios by using advance selling with limited capacity. Some other studies have focused on the models in which strategic customers decide about their buy-or-wait decisions based on products availability as driven by firms' inventory decisions. yin et al. (2009)Yin R, Aviv Y , Pazgal A and Tang C. 2009. Optimal markdown pricing: Implications of inventory display formats in the presence of strategic customers. Management Sci 55(8): 1391-1408. determined the optimal pricing strategies, in the presence of strategic customers, by developing a game-theoretical model for a retailer who sells a limited inventory of a product by using either display all format (dA) or display one format (dO), over a finite horizon time. They also supposed that strategic customers arrive at the store according to a Poisson process with a constant rate. Liu and van Ryzin (2008)Liu Q and Van Ryzin G. 2008. Strategic capacity rationing to induce early purchases. Manage Sci 54(6): 1115-1131. developed quantity decisions instead of price decisions for a firm with a single product in a capacityrationing model in the presence of strategic customers with heterogeneous valuations, identical risk preferences, and knowledge of the price path and fill rate. Anily and Hassin (2013)Anily S and Hassin R. 2013. Pricing, replenishment, and timing of selling in a market with heterogeneous customers. Int J Prod Economics 145(2): 672-682. studied a deterministic pricing and replenishment model in which the retailer advertised a fixed price and the selling schedule, and the strategic customers incurred holding or shortage costs. Jie et al. (2015)Jie D, Juliang Z and Guowei H. 2015. Pricing and inventory management in the presence of strategic customers with risk preference and decreasing value. I J Prod Economics 164: 160-166. studied the impacts of the risk preference and the decreasing value of strategic customers on the ordering quantity, the sale price and the total profit in a single-period joint inventory pricing problem. They also compared the results with the classical newsvendor model. They found that strategic behavior leads to a lower ordering quantity, a lower price and a lower total profit. Besbes (2015)Besbes O. 2015. Intertemporal Price Discrimination: Structure and Computation of Optimal Policies. Manage Sci 61(1): 92-110. developed a dynamic programming approach to determine firm's optimal pricing policy under commitment and in presence of strategic heterogeneous customers. He studied the class of monotone pricing policies.
On the supply side, there are many related papers focusing on pricing strategies in supply chain framework with demand uncertainty. Cardenas-Barron et al. (2014)Cardenas-Barron LE, Chung KJ and Treviño-Garza G. 2014. Celebrating a century of the economic order quantity model in honor of Ford Whitman Harris, I. J. Prod Economics 155: 1-7. presented a comprehensive introduction to inventory management and supply chain scopes, and provided a basis for new directions in inventory management research. Chen et al. (2012)Chen Y, Su X and Zhao X. 2012. Modeling Bounded Rationality in Capacity Allocation Games with the Quantal Response Equilibrium. Manage Sci 58(10): 1952-1962. considered a supply chain with a single supplier and two retailers who competed with each other under a capacity allocation to determine the ordering strategy. Lai et al. (2012)Lai G, Xiao W and Yang J. 2012. Supply Chain Performance Under Market Valuation: An Operational Approach to Restore Efficiency. Manage Sci 58(10): 1933-1951. studied the stocking decision of a downstream buyer with some private demand information under a general, single buyback contract as a supply chain framework. using rational expectations framework, Tereyağoğlu and veeraraghavan (2012)Tereyağoğlu N and Veeraraghavan S. 2012. Selling to Conspicuous Consumers: Pricing, Production, and Sourcing Decisions. Manage Sci 58(12): 2168-2189. proposed a model that addressed pricing and production decisions for a firm under uncertain market demand including strategic consumers. Swinney (2011)Swinney R. 2011. Selling to Strategic Consumers When Product Value Is Uncertain: The Value of Matching Supply and Demand. Manage Sci 57(10): 1737-1751. examined the value of quick response production practices in the presence of forward-looking customers with uncertain, heterogeneous valuations who could have chosen between purchasing early and delaying the purchase decision until resolving valuation uncertainty. The market size is also uncertain to the firm and it may commit either to a single production run at a low unit cost or to a quick response strategy. katsifou et al. (2014)Katsifou A, Seifert RW and Tancrez JS. 2014. Joint product assortment, inventory and price optimization to attract loyal and non-loyal customers. Omega 46: 36-50. presented an optimization model and an iterative heuristic to analyze the trade-offs between three decisions that are reliater a rof laicurc׳s commercial success: the product assortment, the inventory levels, and the pricing.
Cachon and Swinney (2009)Cachon GP and Swinney R. 2009. Purchasing, pricing, and quick response in the presence of strategic consumers. Manage Sci 55(3): 497-511. considered a retailer who sells a product with uncertain demand including myopic, bargain-hunting, and strategic customers, over a finite selling season. They also determined retailer's initial stocking quantity and markdown pricing strategy. Cachon and Swinney (2011)Cachon GP and Swinney R. 2011. The Value of Fast Fashion: Quick Response, Enhanced Design, and Strategic Consumer Behavior. Manage Sci 57(4): 778-795. also examined the performance of fast fashion system in comparison with three different systems: quick-response-only systems, enhanced-design-only systems, and traditional systems. They paid attention to the impact of each system on the strategic customer purchasing behavior. Levin et al. (2009)Levin Y, McGill J and Nediak M. 2009. Optimal dynamic pricing of perishable items by a monopolist facing strategic consumers. Prod Oper Manage 19(1): 40-60. considered a monopolist seller who contingently prices a fixed stock of items over a finite time horizon. They proposed a dynamic pricing model for a finite population of strategic customers in a stochastic market by using a stochastic dynamic game. Hua et al. (2010)Hua Q, Wei Y and Xia Y. 2010. Revenue management for a supply chain with two streams of customers. E J Oper Research 200: 582-598. studied a service supply chain including a supplier and a retailer in which both of them face customers who have strategic behavior in choosing a purchasing channel. They assumed that a supplier has a limited capacity of a perishable product. They examined pricing and purchasing strategies under two alternative supply chain systems: centralized and decentralized. Su (2010)Su X. 2010. Optimal Pricing with Speculators and Strategic Consumers. Manage Sci 56(1): 25-40. considered a monopolist seller with a finite capacity at the two-period season for determining pricing and the long-run capacity decisions in uncertain aggregate market included strategic customers, bargain hunters, and speculators with different valuations. Daojian et al. (2015)Daojian Y, Ershi Q and Yajiao L. 2015. Quick response and supply chain structure with strategic consumers. Omega 52: 1-14. determined pricing and inventory decisions on decentralized supply chains with revenue-sharing contracts and centralized supply chains, and explored the impact of quick response on supply chain performance in presence of strategic customer. They found that if the extra cost of quick response is relatively low, the value of quick response would be greater in centralized systems than in decentralized ones. They also showed that revenue-sharing contracts can improve decentralized supply chain performance in comparison with centralized supply chain. Nita and Cardenas-Barron (2015)Nita HS and Cardenas-Barron LE. 2015. Retailer's decision for ordering and credit policies for deteriorating items when a supplier offers order-linked credit period or cash discount. Applied Math Compute 259: 569-578. studied ordering and credit policies in a supply chain with a supplier who offers its retailer either a cash discount or a fixed credit period for enough great ordering quantity, and a retailer who offers credit period to its customer. They also assumed deteriorating constant rate for the retailer's inventory system.
As you can see, although many studies have distinctly investigated the strategic customer behavior and pricing strategies in a supply chain framework, few have probed into the performance of supply chain in the presence of strategic customers. The main purpose of this study, according to the literature, is to develop a modeling framework to study the strategic behavior of customers on supply chain gain and decisions and subsequently, supply chain members' decisions on strategic customer buying behavior. in this paper, the model is somewhat similar to the newsvendor problem, with the effects of supplier's decisions and the presence of strategic customers as the two major differences between them. Indeed, this model indicates the interaction among supplier, retailer, and strategic customers. Perhaps, Su and Zhang (2008)Su X and Zhang F. 2008. Strategic customer behavior, commitment, and supply chain performance. Management Sci 54(10): 1759-1773. is the closest research to the model proposed in this paper. They developed a rational expectation to study the impact of capacity information on strategic customer purchase behavior by using a game-theoretical framework. They examined two seller strategies: commitment to a particular level of initial inventory, and providing customers with guarantees on product availability. The main differences between their model and this model are represented in supplier and his/her competition with retailer, and two-period pricing policies.
This study attempts to contribute to the earlier works in the following ways:
-
1
. many existing methods only consider a fixed and given initial capacity, while the model in this study analyzes pricing and ordering decisions in a decentralized supply chain.
-
2
.As a new contribution to the field, the proposed model considers vertical and horizontal relationships among supplier, retailer, and customers.
-
3
.This paper considers a two-segment market: certain and uncertain market with three myopic, strategic, and low-value customers.
This study also introduces the model with its assumptions, notations, and applications; develops a bilevel game approach to analyze the model and extracts results; presents a numerical example and reports the results. The model and its computational results are instantiated in a case with uniform distribution as uncertain demand function. Finally, concluding remarks summarize the contribution of the study. Also, Appendix A provides the evidence of all technical results.
MODEL DESCRIPTION
Consider a decentralized two-echelon supply chain with a supplier and a retailer in an uncertain market with myopic and strategic customers. The retailer makes an order for a single durable product (i.e. stylish goods) from a particular supplier and sells it to customers. The following describes these three groups of agents with their characteristics and other relevant assumptions,
-
1
.The supplier supplies or produces a single durable product and wishes to maximize its total profit by determining the optimal wholesale pricing strategy with respect to its unit supply costs and retailer's ordering quantities. However, the wholesale price cannot be less than unit supply cost or more than customers' high valuation. We introduce C and QMax as unit supply costs (included purchasing, ordering and holding costs for each product) and supply constraint, respectively.
-
2
.The monopolist retailer determines ordering quantity and pricing policies over two time periods, t =1, 2, to maximize his/her total expected profit. We assume there is only one purchasing opportunity because supply lead times are too long and also any inventory remaining at the end of the second period is equal to zero (Cachon and Swinney (2009))Cachon GP and Swinney R. 2009. Purchasing, pricing, and quick response in the presence of strategic consumers. Manage Sci 55(3): 497-511.. Let Pt be the unit retail price in period t called as fullprice and sale-price in the rest of the paper. meanwhile, Pt must be between the wholesale price and customer high valuation in each period (it is a rational and obvious assumption).
-
3
.Demand in the market is divided into two distinct segments, with three different types of customers (referred to as strategic, myopic, and low-value consumers in the rest of this paper). Each customer demands at most one unit of product but may have different valuations for it. Customer's valuations are either VH (i.e. high-value) or VL (i.e. low-value); in other words, it refers to their utility from using the product so it can also be interpreted as the maximum willingness to pay for buying the product (Su (2010))Su X. 2010. Optimal Pricing with Speculators and Strategic Consumers. Manage Sci 56(1): 25-40..
Uncertain Demand: First, the retailer faces uncertain demand segment where there is a non-negative random number X of customers who arrive at the first period into the market. Let f and F denote the probability density and cumulative distribution function of X, respectively. Also we assume that X satisfies the following property (Cachon and Swinney (2009))Cachon GP and Swinney R. 2009. Purchasing, pricing, and quick response in the presence of strategic consumers. Manage Sci 55(3): 497-511..
Definition 1. A continuous, nonnegative random variable X with density f satisfies the monotone scaled likelihood ratio (MSLR) property if, for all λ≤1 and x in the support of X, fX (λx)/ fX (x) is monotonic in x.
This segment actually has two types of high-value customers: strategic and myopic. A fraction α∈[0 ,1 ] of these customers are myopic and the rest of them are strategic (Su (2010))Su X. 2010. Optimal Pricing with Speculators and Strategic Consumers. Manage Sci 56(1): 25-40.. All these customers have high valuations V H , but the strategic customer valuation in the second period is èVH , where θ∈[0 ,1 ] is fixed non-increasing rate of strategic customers' valuation in the second period. They are also homogeneous in their valuations, their purchasing and their waiting risks. myopic customers will just purchase at the first period if the retail price is less than their valuations (their surplus is positive) and their numbers are always less than Q. Strategic customers rationally decide about purchasing opportunities at both of the two periods and they will buy a product when price is sufficiently attractive. in other words, they consider their surplus from purchasing the product in each period and choose between them to maximize their expected surplus. But, there are two major points which influence on the strategic customers' decision: achieving the product and declining their valuations at the second period. Also, we assume that the customers, who wait, have the highest priority to receive the product at the second period. This is reasonable because customers who are interested in a particular product are more likely to get the product when the sale actually takes place.
Certain or Low-value demand: The certain demand segment includes infinite low-value customers (even greater than initial capacity) who just enter into the market at the second period. They have the lowest priority compared with other customers to buy the product (equivalently, we can consider that low-value consumers show up only at the end of the second period). Hence, at a sufficiently low price (e.g., below VL ), the retailer can always sell all remaining capacity. It should also be noted that VL can be lower than supplier wholesale price.
The problem is modeled as a bi-level game. At the second level, retailer and strategic customers play together in a two-person non-cooperative simultaneous general game to determine their pricing and purchasing equilibrium strategies. The retailer does not exactly know about the customers' valuation, but s/he could estimate about customers low and high valuation based on his/her experiences so that we can assume s/he has enough knowledge about customers' valuation. each strategic customer has also private knowledge of his/her own second-period valuation at the start of the game. While, at the first level, a supplier (as a leader) competes with a retailer (as a follower) to detect optimal pricing and ordering policies based on the Stackelberg game.
MODEL NOTATIONS
The table Ι summarizes the model notations and their definitions.
CHRONOLOGY OF EVENTS
In this section, we briefly describe the sequence and the timeline of the proposed model. At the beginning of the season, a supplier sets the wholesale price Pw . Then, the retailer determines and orders the initial stocking quantity Q based on his/her prediction about the demand and the supplier's wholesale price. We suppose there is only one purchasing opportunity because production lead times are long enough. At the beginning of the first period, the retailer sets the full-price P 1 before that high-value random demand X is realized. After that, myopic customers buy the product and leave the market whereas strategic consumers must decide whether to buy or to wait until the sale period.
At t=2, low-value customers enter into the market and the retailer determines sale-price P 2 based on remaining capacity and market demand in the second period. Finally, trades take place at this price. Figure 1 presents the sequence of events in our model and also summarizes some key terms that will be used later.
IMPLICATIONS OF THE PROPOSED MODEL
There are several practical Implications of the proposed model such as tourism and fashion industries. In the tourism industry, Travel agencies always deal with customers in the demand side, and hotels and airlines in the supply side. Travel agencies can be never sure about the demand because customers' willingness about a special tour is always affected by many factors (such as tour's facilities and attractions of destination). Furthermore, they become aware of customers' price sensitivity. usually, they expect that a relatively insensitive group of diehard tourists exist, and it is reasonably assumed to be myopic customers. There is also another price sensitive segment which has reliance on tour's price changes. This segment is known to be strategic customers in our model. Now, in regards to the uncertain and price sensitive demand, travel agencies must decide about tour's capacity which depends not only on demand but also on many other factors in suppliers' side such as airlines' ticket price or hotels' room price.
Our model can also be applied to study the fashion market or newly introduced products, such as electronic gadgets. In both of them normally there are some constraints such as production capacity or uncertain demand.
EQUILIBRIUM ANALYSIS
Now, by using a standard backward induction, a bi-level game among supplier, retailer, and strategic costumers is studied. At the second level, we model the game between the retailer and the strategic customers as non-zero sum simultaneous non-cooperative. in this situation retailer's gain/ loss of utility is not exactly balanced by the losses/gains of the utility of the strategic customers, and players make decisions independently without any enforcement to have cooperative behavior. Each player in this game has some beliefs about the actions of the other players. In other words, we look for a sub game perfect Nash equilibrium with a backward approach under rational expectations as the best solution which means that each player chooses optimal actions based on their beliefs about how others will play.
Finally, at the first level, the supplier and the retailer compete with each other in the Stackelberg game as a leader and a follower, respectively, to extract optimal pricing and ordering policies. In fact, in the Stackelberg game with a backward procedure, firstly, the retailer's (i.e. follower) problem must be solved to determine his/her decision variables as a function of the supplier's decision variables. in the next step, the supplier's decision problem is solved by attending the follower's possible reaction to maximize its utility. The retailer's optimal decisions can be determined by considering the supplier's decisions as input parameters in retailer's problem. Finally, the leader (i.e. supplier) finds its optimal decisions by assuming that the follower takes the optimal response.
SECOND LEVEL: A TWO-PERSON NON-COOPERATIVE SIMULTANEOUS GENERAL GAME
Second period
The retailer's optimal sale price must now be derived. in the first period, we suppose that the retailer has sold αX and β α(1− )X units to myopic and strategic customers, respectively (let β ∈[0,1 ], however, this assumption will be modified). Let I =[Q−(α+β (1− α)) X ] denote the retailer's on-hand inventory at the start of the second period. Therefore, the number of strategic consumers who have chosen to wait is [(1−α)(1− β)X ]. Further, we know that the infinite number of low-value customers are entered into the market at t=2. Thus, we have [(1−α)(1− β)X ]. high-value and infinite low-value customers at the sale market. Furthermore, it is obvious that the sale-price P2 could never be less than VL (P 2 =VL always yields greater profit) or greater than èVH (if P 2 >θVH , the strategic customer surplus will be negative so they will not buy any product). Therefore, if we consider that the retailer sets P2 as sale-price, then his/her expected revenue function at the second period is equals to:
where P 2 ∈[VL , θVH ].
The following lemma demonstrates the set of the sale-prices given by revenue function.
Lemma 1. In equilibrium, P2 ∈{VL , θVH }
Proof. The proofs of all lemmas appear in the technical appendix. □
By attending to lemma 1, we can rewrite R (I, P 2 ) in (1),
In other words, if the retailer chooses vL as sale-price, s/he could absolutely sell all remaining capacity, otherwise, the strategic customer is only able to buy the product. Now, the retailer's equilibrium salepricing policy characterized by the following lemma can be determined:
Lemma 2. Letand be critical minimum demand level where
be critical minimum demand level where 
. Therefore, based on demand's random variable X, equilibrium sale-price (P2*) and expected revenue ( R* (I, P
2
* )
) at the second period are equal to:
The form of the equilibrium policy shown at lemma 2 seems natural. Based on the results of lemma 2, there are two possible outcomes at the second period, corresponding to uncertain high-demand realizations. If uncertain demand is low or X ≤ Dm , retailer's expected revenue for P2 = vL is greater than when P 2 =θVH , because sometimes, clearing all remaining inventory by the lowest sale-price will be more beneficial than just selling some products (not all) by highest sale-price. But, when demand is high or X > Dm , the retailer sets the highest sale-price to sell the product only to the high-value strategic customers who had not bought at the first period. However there may be some unsold remaining inventory at the end of the season.
First period
At the beginning of the first period, the retailer proposes to maximize expected total profit by determining his/her pricing and ordering policies. in this section, primarily, the retailer's equilibrium pricing policy can be extracted, and then his/her optimal ordering policy which is set by competing with supplier is specified. The full-price is the most important point in the second level game because it not only influences strategic consumer decisions, but also, determines sale-price as described above. But before answering the question "what is the retailer's equilibrium full-price?" Therefore, the retailer total expected profit function and strategic customer surplus need to be introduced.
Retailer total expected profit function
Retailer total expected profit function consists of three parts: revenue in both of the first and second period, and the products' total purchase or supply cost. Suppose Pw and Q are supplier's unit wholesale price and retailer's ordering quantity, respectively. Therefore, P wQ is the products' total supply cost that should be paid by the retailer. Then, with respect to lemma 2, Πr (P 1, P 2 *,Q) is equals to:
Or to put it another way,
Strategic customers' surplus
As mentioned before, the strategic customer's valuations at the first and second period are VH and θ VH , respectively. Now, consider a particular customer who beliefs that s/he will get V H − P 1 surplus, if s/he buys the product at the first period; but if s/he waits for the second period, s/he will obtain the product with
 surplus. Based on these expectations, the strategic customer's surplus is:
surplus. Based on these expectations, the strategic customer's surplus is:
Availability probability of the product can be calculated as follows. Consider an individual strategic customer who does not buy a product at the first period and waits instead. Because this customer is infinitesimal compared with the remaining customers, s/he will face a stockout if X > Q. In other words, when s/he waits, s/he will obtain the product if X ≤ Q or with probability FX (Q). Of course, we implicitly know that the customers, who wait, have the highest priority to receive the product at the sale-price. Thus, we can rewrite the strategic customer's surplus as follows:
Now, we can solve the second level game and specify retailer's equilibrium full-price and strategic customer's equilibrium purchasing decision.
EQUILIBRIUM STRATEGIES OF RETAILER AND STRATEGIC CUSTOMER
According to customers' valuation at the first period (VH
) and supplier's unit wholesale price (Pw
), we can derive Pw
≤ P
1 ≤VH
because if the full-price is greater than VH
or less than Pw
, customers' surplus or retailer's profit, respectively, will be negative. Now, based on the above description and by attending to (4) and (5), the following theorem demonstrates the existence of an equilibrium solution. But before considering theorem 1, we should explain lemma 3 to introduce 
 as the strategic customer's indifferent full-price.
as the strategic customer's indifferent full-price.
Lemma 3. There exists a full-price 
 = VH −(θVH
−VL
)FX
(Dm
)∈[P w
, V H
] so that if retailer chooses one, all strategic consumers with first and second-period value VH and θVH are indifferent between purchasing in the first or second period.
= VH −(θVH
−VL
)FX
(Dm
)∈[P w
, V H
] so that if retailer chooses one, all strategic consumers with first and second-period value VH and θVH are indifferent between purchasing in the first or second period.
Actually, lemma 3 declares that strategic customers will purchase in the first period if P
1 ≤ 
 , otherwise they wait for the second period.
, otherwise they wait for the second period.
Theorem 1. In a two-person non-cooperative simultaneous general game between the retailer and strategic consumers, there is a subgame perfect Nash equilibrium so that,
The equilibrium full-price, P1*, and strategic customers' purchasing decision, β* , satisfy the following situations:
In equilibrium, retailer's total expected profit function and strategic customers' surplus equal to:
As we can observe from Theorem 1, at the first period, the retailer should charge a high full-price P 1 * =VH which is a reasonable result. One obvious reason is that the myopic customers stand in the market at this period and if retailer charges P 1 * <VH , they will yield less benefit compared with P 1 * =VH . But, at the second period, if uncertain demand is big enough or on the other hand, the number of strategic customers waited until second period are significant, the retailer should maintain the same strategy and charges high sale-price P 2 * =θVH ; otherwise, a markdown to VL is preferable because of his clear policy at the end of season. This type of pricing format is commonly observed in practice.
Having extracted equilibrium retailer pricing and strategic customer purchasing strategies, the research analyzes first level game between retailer and supplier to specify the optimal initial stocking capacity and wholesale price in the next section.
First level: The Stackelberg game
This section models competition between the supplier and the retailer as a non-cooperative Stackelberg game in which the supplier acts as the leader and the retailer as the follower. Their net profits are considered as the players' payoff/utility functions for maximization. As mentioned before, the supplier produces or supplies a single product at the wholesale price according to the retailer's ordering quantity, while the retailer determines and orders his/her required initial stocking capacity based on market demand and supplier's wholesale price. However, according to the model assumptions, we know that Pw ≥ C and Q ≤ QMax . The payoff function (i.e. net profit) for each player equals to its revenue minus total cost where these functions to the retailer (obtained in theorem 1) and the supplier are given, respectively, by
The Stackelberg equilibrium is obtained using a backward procedure. According to this procedure, at the first step, the retailer's (i.e. follower) problem must be solved to determine his/her initial stocking capacity as a function of the supplier's wholesale price (suppose that the supplier's wholesale price, in this step, is Pw ). in the next step, the supplier's decision problem is solved by attending the follower's possible reaction to maximize its net profit. The retailer's optimal initial stocking capacity can be determined by considering the supplier's wholesale price as its input parameter. Finally, the leader (i.e. supplier) finds its optimal wholesale price by assuming that the follower takes the optimal response.
At the first step, based on rational expectations, both the supplier and the retailer know that there are some Pw 1 and Pw 2, so that Max (C, Pw 1)≤ Pw ≤ Pw 2 and the retailer ordering quantity will always be QMax or 0, if the supplier chooses some Pw less than Pw 1 or more than Pw 2, respectively. Therefore, we can write the retailer's and supplier's maximization problems as follows,
According to above descriptions, theorem 2 demonstrates the retailer's response based on his/her estimation from the supplier's wholesale price, Pw .
Theorem 2. Consideras the retailer best response ordering quantity. Let 
 w1and
w1and
 w2be retailer's low-erbond and upperbond estimations about Pw1and Pw2. Define
w2be retailer's low-erbond and upperbond estimations about Pw1and Pw2. Define where
where 
 Therefore,
Therefore,
There are some Q L, QH ∈[0, Qmax] so that QL and QH are minimum and maximum points of Z (Q), respectively. Then, Z * and Z ** can be defined as follows,
a. If Pw ∈[C, max (C, Z * )], then Πr (Q) is a non-decreasing function of Q, and QMax, =
=
b. If Pw
∈(max C, Z( * ), Min V( H ,Z** )), then Πr (Q) is quasiconcave in Q andis determined by the unique solution to the first-order derivatives' equation of Π r (Q),

c. If Pw ∈[Min (V H ,Z** ), ∞ ) then Πr (Q) is a non-increasing function of Q, and . = 0
= 0
Now, as mentioned above, the retailer supposes Pw
∈[Max (C, Z
* ), Z
**] because s/he beliefs that the ordering quantity for Pw
>Z
** is the same as Pw
= Z
**. Similarly, there is also no difference between ordering quantity at Pw
< Max (C, Z
*) and Pw
= Max (C, Z
* ). So, consider g (Pw ) as the solution of equation dΠr (Q)/ dQ = 0 from theorem 2 which g (P w ) is decreasing and reversible function of Pw
. Further, let g
−1 (Q =QMax = Pw
L
and g
−1 (Q =0 = Pw
H
(where g
−1 ( =
=  )
)  )
)  ) is reverse function). By substituting
) is reverse function). By substituting  , PwL, and PwH by the supplier's maximization problem in (9), we will be able to find the supplier's wholesale price decision and subsequently, the retailer's optimal ordering quantity.
, PwL, and PwH by the supplier's maximization problem in (9), we will be able to find the supplier's wholesale price decision and subsequently, the retailer's optimal ordering quantity.
Theorem 3. Consider the supplier's maximization problem in (9),
Therefore,
2. If g(P w ) is a concave function, Πw (Pw ) will be quasiconcave in Pw and the optimal wholesale price (Pw*) is determined by solving the equation dΠw (Pw )/ dPw = 0. Otherwise, the optimal wholesale price (Pw*) is obtained by comparing the value of Πw (Pw ) in critical points and boundaries.
3. The optimal initial stocking quantity can be calculated based on different values of the optimal wholesale price,
Indeed, theorem 3 demonstrates that the wholesale price Pw* acts as a lever for persuading the supply chain to achieve a particular equilibrium ordering quantity because we know that the ordering quantity Q is decreasing in Pw and depends on it. So the supplier based on his/her capacity and his/her strategy can control the retailer's demand. in other words, by varying Pw between Max (C, Z * ) and Min (V H ,PwH ), the system adjusts itself to appropriate equilibrium quantity within the corresponding range. Interestingly, as observed from the theorem 3, it is possible Pw* >θVH but the retailer chooses the equilibrium pricing strategy according to theorem 2 despite of gaining negative profit at the second period.
DISCUSSION
in this section, firstly, in order to demonstrate the proposed model and the emphasis of the analytical results presented in the previous sections a numerical example is presented. In fact, this example helps us practically analyze and explain the results of the proposed bi-level game and its solutions. Secondly, a sensitivity analysis is also performed for some market-related parameters to study the model results' sensitivity in comparison with parameters' volatility. Finally we extract some meaningful managerial insights.
NUMERICAL EXAMPLE
Suppose that the market's uncertain demand follows up continues uniform distribution with a and b as distribution's parameters and following density and cumulative distribution functions,
Moreover, suppose strategic customers account for 80% of uncertain demand with VH = 250$ and θ= 85% as high-value and discount factor valuation, respectively. The low-value customers' valuation is also 150$. The supplier's maximum capacity is 50 with 80$ as a supply unit cost. The values of our example's input parameters are given in Table II.
By using the model results and with respect to input parameters, the optimal decision variables for the retailer, supplier, and strategic customer are presented in Table III .
In other words, the equilibrium retailer's full-price and supplier's wholesale price are 250$ and 175$, respectively, and the equilibrium profits are obtained in Q=16.52. Furthermore, as much as E (X)= 35 > Dm =12.39, we can consider P2 = 212.5$ as the equilibrium retail's sale-price, however, for uncertain demand less than 12.39, it is 150$.
SENSITIVITY ANALYSIS
In this section, sensitivity analysis is also performed for market-related parameters (α, θ ). In other words, we compare the effects of Parameters' volatility on the supplier's total profit, retailer's total expected profit and ordering quantity. initially, the strategic customers' portion in the market (1−α) is considered. It is supposed that it varies in [0%, 95%]. Figure 2 shows the variations of supplier's profit, retailer's profit and ordering quantity with respect to (1−α).
As we can observe in Fig 2a, variations of supplier's total profit is more than the retailer's total expected profit and both of them are non-increasing with respect to (1−α)'s fluctuations. But, the interesting point is decreasing the trend of ordering quantity's variations compared with (1−α)'s fluctuations shown in Fig 2b.
As we can observe in Fig 2a, variations of supplier's total profit is more than the retailer's total expected profit and both of them are non-increasing with respect to (1−α)'s fluctuations. But, the interesting point is decreasing the trend of ordering quantity's variations compared with (1−α)'s fluctuations shown in Fig 2b.
Next, we evaluate the variations of supplier's profit, retailer's profit and ordering quantity with respect to variations of strategic customers' valuation discount factor, θ which is shown in Figure 3.
According to Fig 3a, by increasing θ, supplier's total profit and retailer's total expected profit raise, and vice versa, any decrease of θ will reduce the profit of supply chain members. The most important reason is the existence of direct relationship between ordering quantity and strategic customer valuation discount factor. In other words, any increase of θ influences positively on retailer's ordering quantity and subsequently, supplier's and retailer's profit will grow up.
As it can be observed in numerical example and sensitivity analysis sections, our achievements can be summarized in two important points:
-
1
.more strategic behavior in the market, results in less retailer ordering quantity. However, practically, this happens when strategic customers buy a product earlier and as result, retailer's profit increases.
-
2
.There is direct relationship between ordering quantity and strategic customer valuation discount factor. In other words, any increase of θ influences retailer's ordering quantity positively; subsequently, supplier's and retailer's profit will grow up.
However, this result is reasonable because strategic customer valuation discount factor enhancement will stimulate the retailer to force strategic customers to buy later and without having to reduce his/her fullprice. Generally, it is observed that customer strategic behavior has more affected on the supplier's decision in compare to the retailer.
CONCLUSIONS
In this paper, we presented a comprehensive study of the customers' behavior (i.e. myopic, strategic, and low value) in a two-echelon supply chain with a supplier and a monopolist retailer. The study attempted to bridge the existing gap, based on how customers' strategic behaviors influence supply chain's decision variable. The proposed model of this paper has been studied in two segments market including three types of customers. The first section presented a high-value uncertain demand with myopic and strategic customers who realized at the beginning of season, while there were infinite certain low-value customers at the second section who entered into the market at the end of the second period. We analyzed the model as a bi-level game where at the second level (horizontal game), the retailer competed with strategic customers in a non-cooperative simultaneous general game to determine the equilibrium pricing and purchasing strategy. While, at the first level (vertical game), the supplier and the retailer competed together as leader and follower in a Stackelberg game to set the optimal wholesale price and initial stocking capacity. In the other hand, by doing so, strategic customers had to decide about their purchasing time based on their expectations of the retailer's pricing strategies as well as reducing their valuation discount factor because of accessing late to the product in the season. Similarly, on the other hand, competitive environment, uncertain demand, and market's strategic behavior motivated retailers to compete with suppliers on ordering and pricing policies. Finally, the proposed model was also analyzed numerically using a uniform distribution demand and some managerial implications were derived.
As we can observe from the model results, the retailer's equilibrium pricing strategy is occurred in maximum valuation of strategic customer at the both period (based on uncertain demand's population). in other words, the retailer charges a high full-price (P1* = VH ) at the first period which is a reasonable because of the presence of myopic customers in the market at this period. At the second period, the retailer keeps its previous strategy (charges high sale-price P2* =θVH ); if remaining uncertain demand in the market is big enough; otherwise, a markdown price (P2* =VL ) is preferable because of retailer clear policy at the end of season. This type of pricing format is commonly observed in practice. As a result of retailer's decision in equilibrium, the strategic customer prefers to wait and purchase at the second period, hoping to reduce the price.
On the other hand, the results of proposed model demonstrates that the reverse dependence between wholesale price and ordering quantity can act as a leverage to control the retailer's demand, and consequently helps the supply chain to achieve a particular equilibrium. Particularly, at supplier's wholesale price that is the low/high enough, the retailer prefers to order maximum capacity or zero, respectively (QMax / 0).
We can also see that customer strategic behavior influences the supplier's decision more than the retailer's decision. in other words, a market with strategic behavior has negative effects on the retailer's ordering policies; therefore, this situation brings about decrease in supplier's profit. moreover, there is a direct relationship between ordering quantity and strategic customer valuation discount factor so that any increase of θ results in increasing the retailer's ordering quantity and supplier's and retailer's profit.
This study could be developed for more complicated situations such as multi supplier, oligopoly market, heterogeneous strategic customers with uncertain valuation, as well as market with Bargainhunting customers. The model can also be modified and tailored for real implications such as tourism management problems.
REFERENCES
- Anily S and Hassin R. 2013. Pricing, replenishment, and timing of selling in a market with heterogeneous customers. Int J Prod Economics 145(2): 672-682.
- Arya A and Mittendorf B. 2006. Benefits of channel discord in the sale of durable goods. Marketing Sci 25(1): 91-96.
- Aviv Y and Pazgal A. 2008. Optimal pricing of seasonal products in the presence of forward-looking customers. Manuf Service Oper Manage 10(3): 339-359.
- Besbes O. 2015. Intertemporal Price Discrimination: Structure and Computation of Optimal Policies. Manage Sci 61(1): 92-110.
- Byrnes N and Zellner W. 2004. Playing the discount game. Bus Week, December 13.
- Cachon GP and Swinney R. 2009. Purchasing, pricing, and quick response in the presence of strategic consumers. Manage Sci 55(3): 497-511.
- Cachon GP and Swinney R. 2011. The Value of Fast Fashion: Quick Response, Enhanced Design, and Strategic Consumer Behavior. Manage Sci 57(4): 778-795.
- Cardenas-Barron LE, Chung KJ and Treviño-Garza G. 2014. Celebrating a century of the economic order quantity model in honor of Ford Whitman Harris, I. J. Prod Economics 155: 1-7.
- Chen Y, Su X and Zhao X. 2012. Modeling Bounded Rationality in Capacity Allocation Games with the Quantal Response Equilibrium. Manage Sci 58(10): 1952-1962.
- Daojian Y, Ershi Q and Yajiao L. 2015. Quick response and supply chain structure with strategic consumers. Omega 52: 1-14.
- Desai P, Koenigsberg O and Purohit D. 2004. Strategic decentralization and channel coordination. Quant Marketing Economic 2: 5-22.
- Elmaghraby W, Gulcu A and Keskinocak P. 2008. Designing optimal pre-announced markdowns in the presence of rational customers with multi-unit demands. Manuf Service Oper Manage 10(1): 126-148.
- Gallien G. 2006. Dynamic mechanism design for online commerce. Oper Res 54(2): 291-310.
- Hua Q, Wei Y and Xia Y. 2010. Revenue management for a supply chain with two streams of customers. E J Oper Research 200: 582-598.
- Jie D, Juliang Z and Guowei H. 2015. Pricing and inventory management in the presence of strategic customers with risk preference and decreasing value. I J Prod Economics 164: 160-166.
- Katsifou A, Seifert RW and Tancrez JS. 2014. Joint product assortment, inventory and price optimization to attract loyal and non-loyal customers. Omega 46: 36-50.
- Lai G, Xiao W and Yang J. 2012. Supply Chain Performance Under Market Valuation: An Operational Approach to Restore Efficiency. Manage Sci 58(10): 1933-1951.
- Levin Y, McGill J and Nediak M. 2009. Optimal dynamic pricing of perishable items by a monopolist facing strategic consumers. Prod Oper Manage 19(1): 40-60.
- Liu Q and Van Ryzin G. 2008. Strategic capacity rationing to induce early purchases. Manage Sci 54(6): 1115-1131.
- Nita HS and Cardenas-Barron LE. 2015. Retailer's decision for ordering and credit policies for deteriorating items when a supplier offers order-linked credit period or cash discount. Applied Math Compute 259: 569-578.
- Rusnock P and Kerr-Lawson A. 2005. Bolzano and uniform continuity. Historia Mathematica 32(3): 303-311.
- Shen ZJ and Su X. 2007. Customer behavior modeling in revenue management and auctions: A review and new research opportunities. Prod Oper Management 16(6): 713-728.
- Silverstein MJ and Butman J. 2006. Treasure Hunt: Inside the Mind of the New Consumer, Portfolio, New York.
- Su X. 2007. Inter-temporal pricing with strategic customer behavior. Manage Sci 53(5): 726-741.
- Su X. 2010. Optimal Pricing with Speculators and Strategic Consumers. Manage Sci 56(1): 25-40.
- Su X and Zhang F. 2008. Strategic customer behavior, commitment, and supply chain performance. Management Sci 54(10): 1759-1773.
- Swinney R. 2011. Selling to Strategic Consumers When Product Value Is Uncertain: The Value of Matching Supply and Demand. Manage Sci 57(10): 1737-1751.
- Tereyağoğlu N and Veeraraghavan S. 2012. Selling to Conspicuous Consumers: Pricing, Production, and Sourcing Decisions. Manage Sci 58(12): 2168-2189.
- Yin R, Aviv Y , Pazgal A and Tang C. 2009. Optimal markdown pricing: Implications of inventory display formats in the presence of strategic customers. Management Sci 55(8): 1391-1408.
- Yu M, Kapuscinski R and Ahn HS. 2007. Advance selling with limited capacity and customers' dependent valuations. Working paper. Ross School of Business. University of Michigan. Ann Arbor.
APPENDIX

Publication Dates
-
Publication in this collection
07 June 2016 -
Date of issue
Apr-Jun 2016