Abstract
In this paper we treat the question of the existence of solutions of boundary value problems for systems of nonlinear elliptic equations of the form - deltau = f (x, u, v,<FONT FACE="Symbol">Ñ</FONT>u,<FONT FACE="Symbol">Ñ</FONT>v), - deltav = g(x, u, v, <FONT FACE="Symbol">Ñ</FONT>u, <FONT FACE="Symbol">Ñ</FONT>v), in omega, We discuss several classes of such systems using both variational and topological methods. The notion of criticality takes into consideration the coupling, which plays important roles in both a priori estimates for the solutions and Palais-Smale conditions for the associated functional in the variational case.
elliptic equations; variational methods; palais-smale conditions; leray-schauder degree; a priori bounds
Nonlinear Elliptic Systems * * Invited paper ** Member of the Academia Brasileira de Ciências E-mail: djairo@ime.unicamp.br
DJAIRO G. DEFIGUEIREDO** * Invited paper ** Member of the Academia Brasileira de Ciências E-mail: djairo@ime.unicamp.br
Departamento de Matemática, UNICAMP, Cx. Postal 6065 - 13081-970 Campinas, SP.
Manuscript received on May 2, 2000; accepted for publication on May 9, 2000.
ABSTRACT
In this paper we treat the question of the existence of solutions of boundary value problems for systems of nonlinear elliptic equations of the form
- Du = f (x, u, v, Ñu, Ñv), - Dv = g(x, u, v, Ñu, Ñv), in W,
We discuss several classes of such systems using both variational and topological methods. The notion of criticality takes into consideration the coupling, which plays important roles in both a priori estimates for the solutions and Palais-Smale conditions for the associated functional in the variational case.
Key words: elliptic equations, variational methods, palais-smale conditions, leray-schauder degree, a priori bounds.
1. INTRODUCTION
Systems of nonlinear elliptic equations present some new and interesting phenomena, which are not present in the study of a single equation. In general, the systems are coupled, or even strongly coupled, in the dependent variables. So, the notions of superlinearity or sublinearity, and that of criticality have to take into consideration such a coupling. In this survey we explain how these notions have been properly defined in the framework of systems. We discuss several types of systems in an attempt to provide results that apply to large classes of problems. As usual, nonlinear problems present such a diversity of features that general theories, even if ever possible, are far from being produced. The classification we propose here is motivated mostly by the methods employed to solve the problems. Our main concern is on establishing the existence of solutions of boundary value problems for the systems under consideration. In order to keep the exposition lighter, but still emphasizing the real essential points, we restrict ourselves to second order systems with two dependent variables (unknows) u(x) and v(x), that in some places we use u1(x) and u2(x), where x 
 . Here
. Here  is some domain in
is some domain in  N, with N
N, with N  3. The case N = 2 is also interesting, but presents different features, due to the type of Imbedding Theorems in Sobolev Spaces. Indeed, in dimension N
3. The case N = 2 is also interesting, but presents different features, due to the type of Imbedding Theorems in Sobolev Spaces. Indeed, in dimension N  3, we use Sobolev and Kondracov Imbedding Theorems, which imerge the Sobolev Spaces into Lp spaces. On the other hand, in order to treat properly the case N = 2 we should exploit the Trudinger-Moser results on imbedding of the corresponding Sobolev spaces into some Orlicz spaces.
3, we use Sobolev and Kondracov Imbedding Theorems, which imerge the Sobolev Spaces into Lp spaces. On the other hand, in order to treat properly the case N = 2 we should exploit the Trudinger-Moser results on imbedding of the corresponding Sobolev spaces into some Orlicz spaces.
Systems that are Euler-Lagrange equations of some functional are called Variational. They can be treated using the Theory of Critical Points, since the solutions of these systems are precisely the critical points of the functional that originates them. The spaces where the functional is studied depend on the boundary conditions that the solutions have to satisfy. The method in this case is usually called the Direct Method of the Calculus of Variations, whose origin remounts to Gauss and Thompson in the middle 1850's, and which was used by Dirichlet and also by Riemann to "solve'' the Dirichlet problem for the Laplace equation. However, there were gaps in the proof, mathematical rigour needed, as pointed out by Weierstrass in the 1870's. So this procedure had to wait until the turn of the century, when Hilbert revived the method and put in the right tracks what was called the Dirichlet Principle. Today the same sort of ideas is used to other boundary value problems for more general elliptic equations and systems. In the simpler case of Dirichlet problem for Laplace equation, the critical point is a minimum of the associated functional. The problems we treat today present a wider variety of critical points. As a consequence, some new Critical Point Theory had to be developed. Already in the 1930's, Ljusternik and Schnierelmann developed a theory of critical points of the min-max type for functionals presenting a Z2 symmetry. In the 1970's Ambrosetti and Rabinowitz established several results on critical points of the min-max type for functionals without symmetry.
We restrict to second order elliptic systems whose principal part is given by the differential operator - 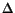 , where
, where 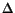 : =
: =  + ... +
+ ... +  , and we will discuss systems of the form
, and we will discuss systems of the form
We say that the system above is of gradient type if there exists a function F :  x
x  x
x 
 of class C1 such that
of class C1 such that
 = f,
= f,  = g.
= g.
The above system is said to be of Hamiltonean type if there exists a function H :  x
x  x
x 
 of class C1 such that
of class C1 such that
 = f,
= f,  = g.
= g.
Using variational methods we discuss Gradient systems in Section 2 and Hamiltonean systems in Section 3. What to do if the system (1) does not fall in one of those categories? Or if the functions in the right side of the equations depend also on the gradients
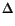
(1.2)
In this case we must recourse to other tools. For the treatment of superlinear problems, the most adequate one is the Leray-Schauder topological degree. In Section 4, we discuss systems by this method.
2. GRADIENT SYSTEMS
The theory of gradient systems is sort of similar to that of scalar equations
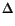
(2.1)
This theory could also be presented in the context of the p-Laplacians,
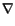 u|p - 2u), p > 1.
u|p - 2u), p > 1.
We consider the system of equations
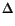
(2.2)
subject to Dirichlet boundary condition. The variational method consists in looking for the solutions of (2.2) as critical points of the functional
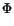 (
(
(2.3)
whose Euler-Lagrange equations are precisely the weak form of equations (2.2). The functional (2.3) is to be defined in the Cartesian product E = W1, 20( ) x W1, 20(
) x W1, 20( ). So, due to Sobolev imbeddings, we require
). So, due to Sobolev imbeddings, we require
F1) F :  x
x  x
x 
 is C1 and
is C1 and
 C(1 + | u|2* - 1 + | v|2* - 1)
C(1 + | u|2* - 1 + | v|2* - 1) C(1 + | v|2* - 1 + | u|2* - 1).
C(1 + | v|2* - 1 + | u|2* - 1).where 2* =  , N
, N  3, which comes from the continuous imbedding W1, 20(
3, which comes from the continuous imbedding W1, 20( )
) 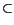 L2*(
L2*( ). Condition (F1) implies that
). Condition (F1) implies that  is well defined and a functional of class, C1in E. In most variational methods some sort of compactness is required, like a Palais-Smale condition (for short, PS condition). In this survey we treat only subcritical problems. So we require
is well defined and a functional of class, C1in E. In most variational methods some sort of compactness is required, like a Palais-Smale condition (for short, PS condition). In this survey we treat only subcritical problems. So we require
 C(1 + | u|r + | v|s),
C(1 + | u|r + | v|s),where 0 < r < 2* and 0 < s < 2*. Here a variety of problems have been studied. We single out three non-critical cases, although many other combinations are of interest:
(I) r, s < 2,("sublinear"),
(II) r, s > 2,("superlinear"),
(III) r = s = 2,("resonant type").
Systems (2.1) satisfying one of the above conditions, as well as other problems, have been discussed in Boccardo-deFigueiredo (1997), Boccardo et al. (2000), Vélin & de Thélin (1993). Let us mention three of those results, in order to show the sort of techniques used in this area.
THEOREM 2.1. (The coercive case). Assume (F1) and (F2) with r and s as in (I). Then  achieves a global minimum at some point (u0, v0)
achieves a global minimum at some point (u0, v0)  E, which is then a weak solution of (2.2).
E, which is then a weak solution of (2.2).
REMARK. This result is a consequence of the theorem on the minimization of coercive weakly lower semicontinuous functionals, which is exactly what is used today to prove the existence of the minimum of the Dirichlet integral as explained in the Introduction. This is a result from General Topology:
AUXILIARY THEOREM NO1. Let X be a compact topological space. Let  : X
: X 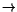
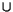 +
+ 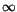 be a lower semi-continuous function. Then (i)
be a lower semi-continuous function. Then (i)  is bounded below, and (ii) the infimum of
is bounded below, and (ii) the infimum of  is achieved, i.e., there exists x0X such that
is achieved, i.e., there exists x0X such that 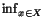
 (x) =
(x) =  (x0).
(x0).
For the proof of Theorem 2.1 we observe that  is weakly lower semicontinuous in the Hilbert space E, so the Auxiliary Theorem no1 applies.
is weakly lower semicontinuous in the Hilbert space E, so the Auxiliary Theorem no1 applies.
Next, if we assume
(F3) F(x, 0, 0) = Fu(x, 0, 0) = Fv(x, 0, 0) = 0,  x
x 
 ,
,
then u = v = 0 is a solution of (2.2). The next result gives conditions for the existence of non-trivial solutions.
THEOREM 2.2. (The coercive case, non-trivial solutions). Assume (F1), (F3) and (F2) with r and s as in (I). Then  achieves a global minimum at a point (u0, v0)
achieves a global minimum at a point (u0, v0) (0, 0), provided that there are positive constants R and
(0, 0), provided that there are positive constants R and  < 1, and a continuous function K :
< 1, and a continuous function K :  x
x  x
x 
 such that
such that
(F4) F(x, t
u, tv) tK(x, u, v),
tK(x, u, v),
for x 
 , | u|,| v|
, | u|,| v|  R and small t > 0.
R and small t > 0.
REMARK. As in Theorem 2.1,  achieves its infimum. All we have to do is to show that there is a point (u1, v1)
achieves its infimum. All we have to do is to show that there is a point (u1, v1)  E where
E where  (u1, v1) < 0. Let
(u1, v1) < 0. Let 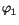 be a first eigenfunction of the Laplacian subject to Dirichlet data. The function
be a first eigenfunction of the Laplacian subject to Dirichlet data. The function 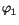 can be taken > 0 in
can be taken > 0 in  . So we can use u1, v1 = t
. So we can use u1, v1 = t
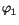 , and t > 0 small.
, and t > 0 small.
Now let us go to the "superlinear cases". Viewing the need of a Palais-Smale condition we assume a sort of Ambrosetti-Rabinowitz condition
(F5) 0 < F(x, u, v) 
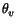 vFv(x, u, v),
vFv(x, u, v),
for all x 
 and | u|,| v|
and | u|,| v|  R, where R is some positive number and
R, where R is some positive number and
 <
<  ,
,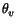 <
<  .
.
THEOREM 2.3. Assume (F1), (F3), (F5) and (F2) with r and s as in (II). Assume also that there are positive constants C and  , and numbers
, and numbers  ,
, > 2 such that
> 2 such that
(F6) | F(x, u, v)|  C(| u|
C(| u| + | v|
+ | v| ),
),
for | u|,| v| 
 , x
, x 
 . Then
. Then  has a non- trivial critical point.
has a non- trivial critical point.
REMARK. The proof goes by an application of the Mountain-Pass Theorem, Ambrosetti & Rabinowitz 1973. This is a result from the Theory of Critical Points for functionals that are not bounded below, and whose critical points appear as saddles. For easy reference let us state this result.
AUXILIARY THEOREM NO2. Let X be a Banach space, and  : X
: X 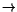
 which is of class C1 and satisfying the PS condition. Suppose that
which is of class C1 and satisfying the PS condition. Suppose that  (0) = 0, and
(0) = 0, and
(i) There exists 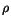 > 0 and
> 0 and 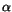 > 0 such that
> 0 such that  (u)
(u) 
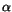 for all u
for all u  Xwith || u || =
Xwith || u || = 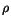 .
.
(ii) There exists an u1
X such that || u1 || >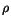 and
and  (u1) <
(u1) < 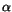 .
.
Then  has a critical point u0
has a critical point u0 0, which is at the level c given by
0, which is at the level c given by
c : =
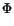 (u),
(u),
where  : = {
: = {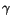
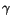 (0) = 0,
(0) = 0,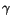 (1) = u1}.
(1) = u1}.
We recall that  : X
: X 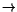
 satisfies the (PS) condition if every sequence (xn)
satisfies the (PS) condition if every sequence (xn) 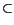 X such that (i) |
X such that (i) | (un)|
(un)|  const, and (ii)
const, and (ii)  (un)
(un) 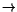 0 contains a convergent subsequence.
0 contains a convergent subsequence.
The Condition (F6) essentially implies that the origin in E is a local minimum of the functional  . Condition (F5) implies that the problem is superlinear and so condition (ii) of the Mountain Pass Theorem is satisfied.
. Condition (F5) implies that the problem is superlinear and so condition (ii) of the Mountain Pass Theorem is satisfied.
The analysis of the resonant case requires the study of some eigenvalue problem for systems, and this can be done even for systems involving p-Laplacians, see Boccardo & DeFigueiredo 1997.
3. HAMILTONEAN SYSTEMS
In this section we study elliptic systems of the form
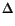
(3.1)
where H :  x
x  x
x 
 is a C1- function and
is a C1- function and  N, N
N, N  3, is a smooth bounded domain. One can consider the case when
3, is a smooth bounded domain. One can consider the case when  =
=  N, and in this case, the system takes the form
N, and in this case, the system takes the form
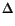
(3.2)
In the bounded case, we look for solutions of (3.1) subject to Dirichlet boundary conditions, u = v = 0 on 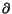
 . This kind of problems has been object of intensive research recently, starting with the work of Clément et al. 1992, Hulshof & van der Vorst 1993.
. This kind of problems has been object of intensive research recently, starting with the work of Clément et al. 1992, Hulshof & van der Vorst 1993.
In the case when  =
=  N, we will assume some symmetry with respect to x to hold; for instance, that the x-dependence of H is radial, or that H is invariant with respect to certain subgroups of O(N) acting on RN, see, for instance, DeFigueiredo & Yang 1998, Bartsch & DeFigueiredo 1999. We have obtained both radial and non-radial solutions in the radial symmetric case, thus observing a symmetry breaking effect.
N, we will assume some symmetry with respect to x to hold; for instance, that the x-dependence of H is radial, or that H is invariant with respect to certain subgroups of O(N) acting on RN, see, for instance, DeFigueiredo & Yang 1998, Bartsch & DeFigueiredo 1999. We have obtained both radial and non-radial solutions in the radial symmetric case, thus observing a symmetry breaking effect.
One simple case of an elliptic Hamiltonean system appears in Clément et al. 1992, where it is proved the existence of a positive solution of the system below subject to Dirichlet boundary conditions:
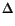
(3.3)
In this case the Hamiltonean is H(u, v) = F(v) + G(u), where F(t) =  f (s)ds, and similarly G is a primitive of g. However, the treatment given there of system (3.3) was via a Topological argument, using a theorem of Krasnoselskii on Fixed Point Index for compact mappings in cones in Banach spaces, see Auxiliary Theorem no4. We will come back to that method in section 4. The model of a superlinear system as in (3.3) is
f (s)ds, and similarly G is a primitive of g. However, the treatment given there of system (3.3) was via a Topological argument, using a theorem of Krasnoselskii on Fixed Point Index for compact mappings in cones in Banach spaces, see Auxiliary Theorem no4. We will come back to that method in section 4. The model of a superlinear system as in (3.3) is
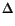
(3.4)
By analogy with the scalar case one would guess that the subcritical case occurs when 1
p - 1, q - 1 <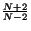 . However, if p = 2, system (3.4) is equivalent to the biharmonic equation
. However, if p = 2, system (3.4) is equivalent to the biharmonic equation 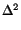 u = | u|q - 2u, and the Dirichlet problem for the system becomes the Navier problem for the biharmonic, that is u =
u = | u|q - 2u, and the Dirichlet problem for the system becomes the Navier problem for the biharmonic, that is u = 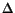 u = 0, on
u = 0, on 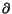
 . Since the biharmonic is a fourth order operator the critical exponent is (N + 4)/(N - 4), which is greater than (N + 2)/(N - 2). So this raises the suspicion (!) that for systems the notion of criticality should carefully take into consideration the fact that the system is coupled. It appeared in Clément et al. 1992 and independently in Peletier & van der Vorst 1992 the notion of the Critical Hyperbola, which replaces the notion of the critical exponent of the scalar case:
. Since the biharmonic is a fourth order operator the critical exponent is (N + 4)/(N - 4), which is greater than (N + 2)/(N - 2). So this raises the suspicion (!) that for systems the notion of criticality should carefully take into consideration the fact that the system is coupled. It appeared in Clément et al. 1992 and independently in Peletier & van der Vorst 1992 the notion of the Critical Hyperbola, which replaces the notion of the critical exponent of the scalar case:
 +
+ 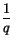 = 1 -
= 1 - 
associated to system (3.3), and in general to systems (3.2) when Hv grows like vp - 1 as v 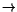 +
+ 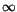 , and Hu grows like uq - 1 as u
, and Hu grows like uq - 1 as u 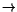 +
+ 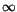 , and the dependence on the other variables is of some lower orders.
, and the dependence on the other variables is of some lower orders.
If the growths of H with respect to u and v as u, v 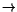 +
+ 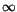 are both less that (N + 2)/(N - 2) one could consider the functional
are both less that (N + 2)/(N - 2) one could consider the functional
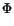 (
(
(3.5)
which is then well defined in E = H01( ) x H01(
) x H01( ). (We use indistinctly the notations H01(
). (We use indistinctly the notations H01( ) and W01, 2.) However the possibility of using powers larger than (N + 2)/(N - 2) calls for the use of fractional Sobolev spaces. They are defined using Fourier expansions on the eigenfunctions of (-
) and W01, 2.) However the possibility of using powers larger than (N + 2)/(N - 2) calls for the use of fractional Sobolev spaces. They are defined using Fourier expansions on the eigenfunctions of (- 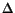 , H10(
, H10( )); it is well-known that the eigenvalue problem
)); it is well-known that the eigenvalue problem
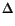
(3.6)
has an increasing sequence of eigenvalues  , and a corresponding sequence of eigenfunctions (
, and a corresponding sequence of eigenfunctions (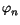 ),
), 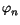
 ),
),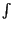 |
|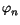 |2 = 1, with the properties
|2 = 1, with the properties
(i) is a positive and simple eigenvalue, and
is a positive and simple eigenvalue, and 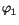 (x) > 0 for x
(x) > 0 for x 
 ,
,
(ii)
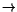 +
+  ,
,
(iii)
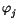 =
= 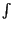
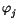 = 0, for ij.
= 0, for ij.
It is well known that (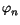 ) is an orthonormal system in L2(
) is an orthonormal system in L2( ) and an orthogonal system in H01(
) and an orthogonal system in H01( ).
).
DEFINITION. For s  0, we define
0, we define

(3.7)
Here an = 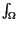 u
u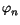 . Es is a Hilbert space with the inner-product given by
. Es is a Hilbert space with the inner-product given by
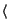
(3.8)
Associated with these spaces we have the following maps, which are isometric isomorphisms:

(3.9)

(3.10)
The Sobolev imbedding theorem says that "Es
Lp continuously if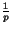
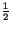 -
- 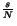 , and compactly if the previous inequality is strict''.
, and compactly if the previous inequality is strict''.
Instead of the functional (3.5), we have to construct one defined in these fractional Sobolev spaces, which will be chosen depending on the growths of the Hamiltonean. Assume the following conditions on the Hamiltonean:
(H.1) H :  x
x  x
x 
 is C1 and H
is C1 and H  0.
0.
(H.2)There exist positive constants p, q and c1 with
 +
+
(3.11)
such that

(3.12)
and

(3.13)
for all (x, u, v) 
 x
x  .
.
The first inequality in (3.11) expresses a superlinearity of the system, and the second one the fact that the system is subcritical.
Choose s, t > 0, such that s + t = 2 and
 >
>  -
-  ,
, 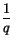 >
>  -
-  .
.
Thus Es
Lp( ), and EtLq(
), and EtLq( ), with compact immersions.
), with compact immersions.
Let now E = Esx Et. If z = (u, v)  E, then H(x, u, v)
E, then H(x, u, v)  L1. So the functional below
L1. So the functional below
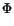 (
(
(3.14)
is well defined for z = (u, v)  E and it is of class C1. Its derivative is given by the following expression
E and it is of class C1. Its derivative is given by the following expression
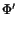 (z),
(z),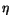
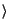 =
= 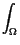 AsuAt
AsuAt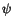 + AsAtv -
+ AsAtv - 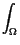 Hu
Hu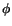 + Hv
+ Hv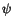 ,
,
where 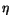 = (
= (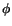 ,
,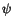 ). So the critical points of the functional
). So the critical points of the functional  given by (3.14) are the weak solutions (u, v)
given by (3.14) are the weak solutions (u, v)  Esx Et of the system
Esx Et of the system
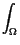
(3.15)
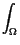
(3.16)
REMARK. The following regularity theorem was proved in DeFigueiredo & Felmer 1994a:
"these weak solutions (u, v) are indeed u  W01,
W01, (
( )
) 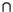 W2,
W2, and v
and v  W01,
W01, (
( )
) 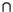 W2,
W2, , which we call strong solutions of (3.2)''.
, which we call strong solutions of (3.2)''.
In the same paper the following result was proved:
THEOREM 3.1. Assume (H1), (H2) with p, q > 0 satisfying (3.11). In addition, assume
(H3) There exists R > 0 such that
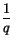 Hv(x, u, v)v
Hv(x, u, v)v  H(x, u, v) > 0
H(x, u, v) > 0
for all x 
 and |(u, v)|
and |(u, v)|  R.
R.
(H4) There exist r > 0 and c > 0 such that
| H(x, u, v)|  c(| u|p + | v|q),
c(| u|p + | v|q),
for all x 
 and |(u, v)|
and |(u, v)|  r.
r.
Then, system (3.2) has a strong solution.
REMARKS ON THE PROOF OF THEOREM 3.1. The proof consists in obtaining a critical point of the functional (3.14). First we observe that  is strongly indefinite. This means that the space E decomposes into the direct sum of two infinite dimensional subspaces, with the property that the functional is positive definite in one of them and negative definite in the other. In fact, the space E decomposes into E = E+
is strongly indefinite. This means that the space E decomposes into the direct sum of two infinite dimensional subspaces, with the property that the functional is positive definite in one of them and negative definite in the other. In fact, the space E decomposes into E = E+
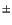 are infinite dimensional subspaces and the quadratic part
are infinite dimensional subspaces and the quadratic part
Q(z) = 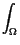 AsuAtv, for z = (u, v)
AsuAtv, for z = (u, v)
is positive definite in E+ and negative definite in E-. This fact and (H5) induce a geometry on the functional  that calls for the use of some linking theorem. For example in DeFigueiredo & Felmer 1994a we used the Linking Theorem of Benci-Rabinowitz 1979 in a version due to Felmer 1992.
that calls for the use of some linking theorem. For example in DeFigueiredo & Felmer 1994a we used the Linking Theorem of Benci-Rabinowitz 1979 in a version due to Felmer 1992.
REMARK. Condition (H4) in the previous theorem excludes cases when Hu and Hv have linear terms. Indeed, on one hand the superlinearity condition in (3.11) implies that pq > 1. And on the other hand, linear terms would imply that (H4) should hold with p = q = 1, which then is not possible. Let us now treat this case.
Suppose now that H has a quadratic part, namely 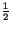 cu2 +
cu2 + 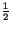 bv2 + auv. In this case the system becomes
bv2 + auv. In this case the system becomes
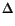
(3.17)
where H satisfies the assumption of the previous theorem. This situation has been studied in special cases in Hulshof-van der Vorst 1993 and in deFigueiredo-Magalhães 1996. The result we present below is one of the most general result in this line and it is due to deFigueiredo-Ramos 1998. We need some extra assumptions on the Hamiltonean, namely.
(H5) There exist c1 and c2 such that, for all x, u, v one has
c1(| u|p + | v|q - 1)  H(x, u, v)
H(x, u, v)  c2(| u|p + | v|q + 1).
c2(| u|p + | v|q + 1).
(H6)
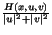 = 0, uniformly in x
= 0, uniformly in x 
 .
.
(H7) There exists r > 0 such that one of the conditions below hold
 0,
0,
(3.18)
 0,
0,
(3.19)
Finally, the next condition is a "non-quadraticity'' condition at infinite introduced in Costa-Magalhães (1994, 1996). It is related to the so-called Ambrosetti-Rabinowitz condition and it is devised to get some sort of Palais-Smale condition for the functionals involved.
(H8) There exists R > 0 such that for any x 
 and | u| + | v|
and | u| + | v|  R
R
 (uHu(x, u, v) + vHv(x, u, v)) - H(x, u, v)
(uHu(x, u, v) + vHv(x, u, v)) - H(x, u, v)  const(| u|p| v|q).
const(| u|p| v|q).
THEOREM 3.2. Let a, b, c be real constants. Suppose that H satisfies (H1),(H2), (H5)-(H8). Then system (3.17) admits a nonzero strong solution.
REMARK. In both DeFigueiredo & Felmer 1994a and DeFigueiredo & Ramos 1998 one allows more general Hamiltoneans H. In fact, the growth at 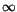 can be different from the its behavior at zero. The proof of both above theorems, 3.1 and 3.2, requires a Linking Theorem for Strongly Indefinite Functionals. We have used in Theorem 3.2 the following result in Li & Willem 1995. One could alse use the results in Silva 1988, 1991. Before stating it we give some definitions. We work in a Hilbert space E, which is supposed to decompose into two subspaces E+ and E-, with E = E+
can be different from the its behavior at zero. The proof of both above theorems, 3.1 and 3.2, requires a Linking Theorem for Strongly Indefinite Functionals. We have used in Theorem 3.2 the following result in Li & Willem 1995. One could alse use the results in Silva 1988, 1991. Before stating it we give some definitions. We work in a Hilbert space E, which is supposed to decompose into two subspaces E+ and E-, with E = E+
E1
E2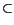 ... and
... and 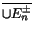 = E
= E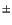 .
.
DEFINITION. A C1 functional  : E
: E
 satisfies the (PS)*-condition if every sequence (zn)
satisfies the (PS)*-condition if every sequence (zn) 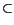 En : = E+nE-n such that
En : = E+nE-n such that
|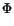 (zn)|
(zn)|  Const, and |
Const, and |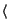
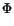 (zn),
(zn),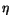
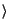 |
| 
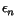 ||
|| 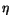
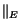 ,
, 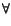 En, and
En, and 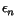
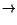 0,
0,
possesses a subsequence converging to a critical point of  .
.
DEFINITION. A functional  has a local linking at the origin if for some r > 0 one has
has a local linking at the origin if for some r > 0 one has
AUXILIARY THEOREM NO3. [Li & Willem 1995] Let  : E
: E 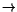
 be a functional of class C1 satisfying the following conditions:
be a functional of class C1 satisfying the following conditions:
B1)  has a local linking at the origin,
has a local linking at the origin,
(B2)  satisfies the (PS)*-condition,
satisfies the (PS)*-condition,
(B3)  maps bounded sets into bounded sets,
maps bounded sets into bounded sets,
(B4)
n
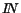 ,
,  (z)
(z)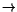 -
- 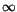 as || z ||
as || z || 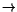
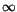 , z
, z  E+nE-.
E+nE-.
Then  has a nontrivial critical point.
has a nontrivial critical point.
4. NONVARIATIONAL SYSTEMS
In this section we propose to treat system (1.1) of the Introduction, in the case that it is not variational. For that matter, we have to recourse to other methods in order to prove the existence of solutions. It seems that the only available technique to treat such systems with nonlinearities f (x, u, v) and g(x, u, v) behaving eventually as powers of u, v at 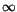 is topological; explicitely, the Topological Degree of Leray-Schauder. Let us then set to solve the problem on the existence of positive solutions of the Dirichlet problem for system (1.1). We assume
is topological; explicitely, the Topological Degree of Leray-Schauder. Let us then set to solve the problem on the existence of positive solutions of the Dirichlet problem for system (1.1). We assume
(NV1) f, g :  x
x 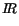 +x
+x 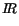 +
+
We shall work here with the Banach space C00( ) endowed with the norm of the maximum. Our notation is
) endowed with the norm of the maximum. Our notation is
C00( ) = {u :
) = {u : 
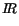 , continuous and u = 0 on
, continuous and u = 0 on 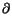
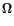 }.
}.
Let E : = C00( ) x C00(
) x C00( ), and K : = {(u, v)
), and K : = {(u, v)  E : u
E : u  0, v
0, v  0}. Condition (NV1) implies that, if u, v
0}. Condition (NV1) implies that, if u, v  C00(
C00( ), and u, v
), and u, v  0, then the system
0, then the system
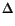
(4.1)
has a positive solution in the space C1( )
) 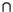 C00(
C00( ). These assertions come from the maximum principle and the theory of solvability of elliptic equations; the solutions
). These assertions come from the maximum principle and the theory of solvability of elliptic equations; the solutions 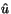 ,
,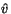 are not classical, but what matters is that the weak solvability of (4.1) defines a mapping T : K
are not classical, but what matters is that the weak solvability of (4.1) defines a mapping T : K
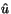 ,
,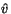 ). So a fixed point of T is a solution of system (1.1). In this way, one obtains a weak solution in C1(
). So a fixed point of T is a solution of system (1.1). In this way, one obtains a weak solution in C1( )
) 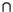 C00(
C00( ), and after, by the regularity theory the solution is in fact in C2,
), and after, by the regularity theory the solution is in fact in C2,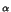 . The operator T is compact, in view of the compact imbedding of C00(
. The operator T is compact, in view of the compact imbedding of C00( ) into C1(
) into C1( )
) 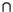 C00(
C00( ). So we can use topological degree through and Index Point Theorem, cf Amann 1976, Benjamin 1971.
). So we can use topological degree through and Index Point Theorem, cf Amann 1976, Benjamin 1971.
THEOREM 4.1. AUXILIARY THEOREM NO4. [Krasnosel'skii 1964]. Let 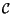 be a cone in Banach space X and T :
be a cone in Banach space X and T : 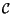
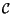 a compact map such that T(0) = 0. Suppose that there exists 0 < r < R, t > 0 such that
a compact map such that T(0) = 0. Suppose that there exists 0 < r < R, t > 0 such that
(i) x  tTx for 0
tTx for 0  t
t  1, x
1, x 
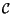 , || x || = r,
, || x || = r,
(ii)  compact map H :
compact map H :  x [0,
x [0,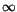 )
)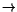
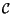 such that
such that
(a) H(x, 0) = Tx for || x || = R,
(b) H(x, t)  x for || x || = R and t
x for || x || = R and t  0,
0,
(c) H(x, t) = x has no solution x 
 for t
for t  t0.
t0.
Then i (T, Br) = 1, i
(T, Br) = 1, i (T, BR) = 0, i
(T, BR) = 0, i (T, U) = - 1, where U = {x
(T, U) = - 1, where U = {x 
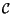 : r < || x || < R}. So T has a fixed point in U.
: r < || x || < R}. So T has a fixed point in U.
Let us illustrate the use of the Auxiliary Theorem no4 to system (1.1) of the Introduction under some further conditions. So let us assume
(NV2) f (x, u, v) = o(| u| + | v|), g(x, u, v) = o(| u| + | v|), as | u| + | v|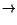 0,
0,
uniformly in x 
 .
.
(NV3) There are positive real numbers  ,
, and a constant C > 0 such that
and a constant C > 0 such that 
 >
>  , and
, and
We recall that  is the first eigenvalue of (-
is the first eigenvalue of (- 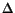 , H01(
, H01( )).
)).
THEOREM 4.2. Assume (NV1),(NV2) and (NV3). And suppose that there is an a priori bound for all eventual positive solutions of the one-parameter family of Dirichlet problems
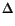
(4.2)
Then system (1.1) has a nonnegative nontrivial solution (u, v).
Condition (NV2) implies that condition (i) in the Auxiliary Theorem no4 is satisfied. System (4.2) enables us to construct the homotopy required in the Auxiliary Theorem no4. Condition (NV3) gives us condition (ii)(c). And of course the assumption that the eventual solutions of system (4.2) are uniformly bounded with respect to the parameter, gives (ii)(b). So Theorem 4.1 is a simple application of the Auxiliary Theorem no4.
Now the interesting question is under which further assumptions in the functions f, g the system (4.2) has its solutions bounded. Here we mean bounded in L (
( ). Such a priori bounds have been proved by three different methods.
). Such a priori bounds have been proved by three different methods.
A) In Clément et al. 1992, it was used the Method of Moving Planes (see Berestycki & Nirenberg 1991) in order to estimate the solutions near the boundary. We remark that condition (NV3) implies that the projections of the eventual solutions (u, v) over the first eigenspace are bounded. That is, there is a constant C > 0 such that 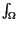 u
u
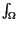 vC. In this way it was proved (see Clément et al. 1992 for more general results) that the positive solutions of
vC. In this way it was proved (see Clément et al. 1992 for more general results) that the positive solutions of
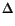
(4.3)
are bounded in L (
( ) provided
) provided
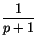 +
+
(4.4)
where p > 1 is the growth of f at 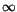 , and q > 1 is the growth of g at
, and q > 1 is the growth of g at 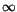 . So we have considered subcritical problems. Recall that equality in (4.3) is the critical hyperbola. This method had been used before in the scalar case to prove a priori bounds of positive solutions of superlinear scalar equations, DeFigueiredo et al. 1982.
. So we have considered subcritical problems. Recall that equality in (4.3) is the critical hyperbola. This method had been used before in the scalar case to prove a priori bounds of positive solutions of superlinear scalar equations, DeFigueiredo et al. 1982.
B) In Clément et al. 1996, we used inequalities of the Hardy type to prove the a priori bounds.This method had been used before in Brézis & Turner 1977. It is based in an inequality of Hardy, which essentially says the following: any function u  H01(
H01( ) has a vanishing at the boundary
) has a vanishing at the boundary 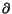
 of an order related to the order of vanishing of the first eigenfunction
of an order related to the order of vanishing of the first eigenfunction 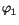 of (-
of (- 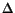 , H01(
, H01( )), in the sense that u/
)), in the sense that u/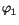 is an L2(
is an L2( )-function. More precisely the Hardy inequality says: there is a constant C > 0 such that
)-function. More precisely the Hardy inequality says: there is a constant C > 0 such that
||
C ||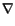 u
u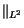 ,
, 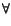 u
u  H01.
H01.
As in the previous method, the Hardy inequality essentially helps to estimating u, v near the boundary 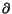
 . In order to state the result in Clément et al 1996 we need two further conditions
. In order to state the result in Clément et al 1996 we need two further conditions
(NV4) There exist q  1 and
1 and 
 0 such that | f (x, u, v)|
0 such that | f (x, u, v)|  C(| u|q + | v|q
C(| u|q + | v|q + 1) uniformly in x
+ 1) uniformly in x 
 .
.
(NV5) There exist p  1 and
1 and 
 0 such that | g(x, u, v)|
0 such that | g(x, u, v)|  C(| v|p + | u|p
C(| v|p + | u|p + 1) uniformly in x
+ 1) uniformly in x 
 .
.
THEOREM 4.3. Let N  4. Assume conditions (NV1), (NV3), (NV4) and (NV5) with p, q,
4. Assume conditions (NV1), (NV3), (NV4) and (NV5) with p, q, and
and  satisfying
satisfying
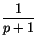 +
+
(4.5)
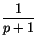
(4.6)
and
 =
= 
 =
= 
where
K =  -
-  > 0 and L =
> 0 and L =  -
-  > 0.
> 0.
Let (u, v) be a positive solution of (1.1). Then there exists a constant C > 0 such that || u || L
C and || v || LC.REMARK. Observe that the conditions on p and q described in inequalities (4.5)-(4.6) express the fact that these parameters are below two hyperbolas in the plane (p, q). These two hyperbolas are below the critical hyperbola, which indicates that this result is not the best possible. However, it is what can be expected by this method since, the intersection of those two hyperbolas is precisely the Brézis-Turner exponent:  .
.
C) The last technique is the so-called Blow-up Method. This technique seems to have been introduced in Gidas and Spruck in 1981a to obtain a priori bounds for positive solutions of scalar equations whose nonlinearities behave like powers at +  . The method was first used in the case of systems in Souto 1992, 1995, and he was able to treat some special systems. In Montenegro 1997, it were treated more general systems, including even systems with more than two equations. We now present some results essentially due to him in a form given in the survey paper DeFigueiredo 1998. For that matter, viewing some symmetry present in the conditions, we write the system in the following form,
. The method was first used in the case of systems in Souto 1992, 1995, and he was able to treat some special systems. In Montenegro 1997, it were treated more general systems, including even systems with more than two equations. We now present some results essentially due to him in a form given in the survey paper DeFigueiredo 1998. For that matter, viewing some symmetry present in the conditions, we write the system in the following form,

(4.7)
The functions and parameters involved in the above system satisfy the following set of conditions:
(A1) The coefficients a, b, c, d : 
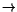 [0,
[0,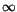 ) are continuous functions.
) are continuous functions.
(A2) The exponents
 0 i, j = 1, 2.
0 i, j = 1, 2.
(A3) There exist positive constants c1 and c2 such that
| h1(x, u1, u2)|  c1(1 + | u1|
c1(1 + | u1| + | u2|
+ | u2| )
)
| h2(x, u1, u2)|  c2(1 + | u1|
c2(1 + | u1| + | u2|
+ | u2| )
)
where
0
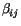 <
< 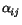 i, j = 1, 2.
i, j = 1, 2.
The blow-up method goes by a contradiction argument. One supposes that there is no L a priori bound and after a procedure of "blowing'' the independent variable, see DeFigueiredo 1998, one obtains statements on the existence of solutions of certain systems in the whole of
a priori bound and after a procedure of "blowing'' the independent variable, see DeFigueiredo 1998, one obtains statements on the existence of solutions of certain systems in the whole of  N or in halfspaces of the same. Such results are known as Liouville theorems. Gidas-Spruck (1991b) studied the scalar case -
N or in halfspaces of the same. Such results are known as Liouville theorems. Gidas-Spruck (1991b) studied the scalar case - 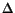 u = f (u), where f (u)
u = f (u), where f (u)  up as u
up as u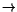 +
+ 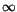 , for some p > 1. The blow-up yielded to the assertion that the following problem has a solution:
, for some p > 1. The blow-up yielded to the assertion that the following problem has a solution:
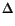
(4.8)
Problem (4.7) does not have a solution if 0 < p < (N + 2)/(N - 2). As it is well known, problem (4.7) has a solution for p = (N + 2)/(N - 2), a whole 2-parameter family of solutions, the so-called instantons. So an a priori bound for the positive solutions of the superlinear problem holds if 0 < p < (N + 2)/(N - 2).
The blow-up method used to the system (4.6) yields to similar statements, Liouville theorems for systems. Depending on some relations on the exponents we come to different systems in the whole of
N. We single out two classes of systems: (i) weakly coupled, (ii) strongly coupled, whose definitions we give next.DEFINITION 1. System (4.5) is weakly coupled if there are positive numbers  ,
, such that
such that
 + 2 -
+ 2 -
(4.9)
DEFINITION 2. System (4.5) is strongly coupled if there are positive numbers  ,
, such that
such that
 + 2 -
+ 2 -
(4.10)
This terminology comes from the fact that the limiting equations in the case of a weakly coupled system is decoupled. Namely, assuming that a(x0) and d (x0) are positive, it follows after the blow-up and a scaling that there are functions w1 and w2 of class C2 defined in the whole of  N with w1
N with w1 0, w1
0, w1 0, w2
0, w2 0 satisfying
0 satisfying
If the maximum of the eventual solutions migrate to the boundary, one obtains a similar statement in a halfspace. So in the case of a weakly coupled system, a priori bounds exist if 0 <  ,
, < (N + 2)/(N - 2).
< (N + 2)/(N - 2).
In the case of a strongly coupled system the limiting systems are
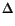
(4.11)
or
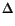
(4.12)
with
w1(x', 0) = w2(x', 0) = 0
So one obtains the a priori bounds if the above systems do not have a solution as especified. One expects that this would be the case if p, q are below the critical hyperbola. However this is not yet proved in this generality. There are partial results of Souto 1992, 1995, DeFigueiredo & Felmer 1994b, several results of Serrin & Zou 1994, 1996, 1997. Some more details can be seen in DeFigueiredo 1998.
SERRIN J & ZOU H. 1997. Existence of Positive Solutions of Lane-Emden System, to appear in Atti del Sem. Mat Univ Modena.
- AMANN H. 1976. Fixed Point Equation and nonlinear Eigenvalue Problems in Ordered Banach Spaces, S.I.A.M. Review 18: 630-709.
- AMBROSETTI A & RABINOWITZ PH. 1973. Dual variational methods in critical point theory and applications, J Fctl Anal 14: 349-381.
- BARTSCH T & DEFIGUEIREDO DG. 1999. Infinitely many solutions of nonlinear elliptic systems, Progress in Nonlinear Differential Equations and their Applications, (The Herbert Amann Anniversary Volume) 35: 51-68.
- BENJAMIN TB. 1971. A Unified Theory of Conjugate Flows, Phil Trans Royal Soc 269(A): 587-643.
- BENCI V & RABINOWITZ PH. 1979. Critical Point Theorems for Indefinite Functionals, Invent Math 241-273.
- BERESTYCKI H & NIRENBERG L. 1991. On the method of moving planes and the sliding method, Bull Soc Bras Mat 22: 1-22.
- BOCCARDO L & DEFIGUEIREDO DG. 1997. Some remarks on a system of quasilinear elliptic equations. Relatório de Pesquisa, RP 51, IMECC-UNICAMP.
- BOCCARDO L, FLECKINGER J & DE THÉLIN F. 2000. Elliptic Systems with various growths. Preprint.
- BRÉZIS H & TURNER REL. 1977. On a Class of Superlinear Elliptic Problems, Comm Part Diff Eq 2: 601-614.
- CLÉMENT PH, DEFIGUEIREDO DG & MITIDIERI E. 1992. Positive Solutions of Semilinear Elliptic Systems, Comm Part Diff Eq 17: 923-940.
- CLÉMENT PH, DEFIGUEIREDO DG & MITIDIERI E. 1996. A priori estimates for positive solutions of semilinear elliptic systems via Hardy-Sobolev inequalities. Pitman Res Notes in Math, 73-91.
- COSTA DG & MAGALHĂES CA. 1994. A Variational Approach to Subquadratic Perturbations of Elliptic Systems, J Diff Eq 111: 103-122.
- COSTA DG & MAGALHĂES CA. 1996. A Unified Approach to a Class of Strongly Indefinite Functionals, J Diff Eq 122: 521-547.
- DEFIGUEIREDO DG. 1998. Semilinear Elliptic Systems, Proceedings of the Second School on Nonlinear Functional Analysis and Applications to Differential Equations, Ed. A. AMBROSETTI, K.-C. CHANG, I. EKELAND.World Scientific, 122-154.
- FELMER PL. 1992. Periodic Solutions of "Superquadratic'' Hamiltonean Systems, J Diff Eq 17: 923-940.
- DEFIGUEIREDO DG & FELMER PL. 1994a. On Superquadratic Elliptic Systems, Trans Amer Math Soc 343: 119-123.
- DEFIGUEIREDO DG & FELMER PL. 1994b. A Liouville-type Theorem for Systems, Ann Sc Norm Sup Pisa, XXI: 387-397.
- DEFIGUEIREDO DG & MAGALHĂES CA. 1996. On Nonquadratic Hamiltonean Elliptic Systems, Advances in Diff Eq 1: 881-898.
- DEFIGUEIREDO DG & RAMOS M. 1998. On Linear Perturbations of Superquadratic Elliptic Systems, Reaction Diffusion Systems, Lecture Notes in Pure and Applied Math. vol 194, Editors G. CARISTI & E. MITIDIERI, Marcel Dekker Publ.
- DEFIGUEIREDO DG & YANG J. 1998. Decay, Symmetry and Existence of positive solutions of semilinear elliptic Systems, Nonl Anal, TMA, 33: 211-234.
- DEFIGUEIREDO DG, LIONS P-L & NUSSBAUM R. 1982. A priori Estimates and Existence of Positive Solutions of Semilinear Elliptic of Positive Solutions of Semilinear Elliptic Equations, J Math Pures et Appl 61: 41-63.
- GIDAS B & SPRUCK J. 1981a. A priori bounds for positive solutions of nonlinear elliptic equations, Comm Part Diff Eq 6: 883-901.
- GIDAS B & SPRUCK J. 1981b. Global and Local Behaviour of Positive Solutions of Nonlinear Elliptic Equations, Comm Pure Appl Math 34: 525-598.
- HULSHOF J & VAN DER VORST RCAM. 1993. Differential Systems with Strongly Indefinite Variational Structure, J Fctl Anal 114: 32-58.
- KRASNOSELS'KII MA. 1964. "Positive Solutions of Operator Equations''. P. Noordhoff Groningen.
- LI SHUJIE & WILLEM M. 1995. Application of local linking to critical point theory, J Math Anal Appl 189: 6-32.
- MONTENEGRO MS. 1997. Criticalidade, superlinearidade e sublinearidade para sistemas elíptico semilineares, Tese de Doutoramento, Unicamp.
- PELETIER LA. & VAN DER VORST RCAM. 1992. Existence and Non-existence of Positive Solutions of Non-linear Elliptic Systems and the Biharmonic Equation, Diff Int Eq 5: 747-767.
- SOUTO MAS. 1992. Sobre a existęncia de soluçőes positivas para sistemas cooperativos năo-lineares, Tese de doutorado 1992, UNICAMP.
- SOUTO MAS. 1995. A priori estimates and existence of positive solutions of nonlinear cooperative elliptic systems. Diff Int Eq 8: 1245-1258.
- SERRIN J & ZOU H. 1994. Nonexistence of Positive Solutions of Semilinear Elliptic Systems, Discourses in Mathematics and Its Applications 3, Dept. of Mathematics, Texas A-M University, 55-68.
- SERRIN J & ZOU H. 1996. Non-existence of Positive Solutions of Lane-Emden System, Diff Int Eq 9: 635-653.
- SILVA EAB. 1988. Critical point Theorems and Applications to differential equations, PhD thesis at the University of Wisconsin-Madison.
- SILVA EAB. 1991. Linking Theorems and applications to nonlinear elliptic equations at resonance, Nonlinear Anal. TMA 16: 455-477.
- VÉLIN J & DE THÉLIN F. 1993. Existence and Non-existence of non-trivial solutions for some nonlinear elliptic systems. Rev Math Univ Compl Madrid 6: 153-194.
Publication Dates
-
Publication in this collection
05 Jan 2001 -
Date of issue
Dec 2000
History
-
Received
02 May 2000 -
Accepted
09 May 2000














 , in
, in 