Abstracts
Electrostatic phenomena in insulators have been known for the past four centuries, but many related questions are still unanswered, for instance: which are the charge-bearing species in an electrified organic polymer, how are the charges spatially distributed and which is the contribution of the electrically charged domains to the overall polymer properties? New scanning probe microscopies were recently introduced, and these are suitable for the mapping of electric potentials across a solid sample thus providing some answers for the previous questions. In this work, we report results obtained with two of these techniques: scanning electric potential (SEPM) and electric force microscopy (EFM). These results were associated to images acquired by using analytical electron microscopy (energy-loss spectroscopy imaging in the transmission electron microscope, ESI-TEM) for colloid polymer samples. Together, they show domains with excess electric charges (and potentials) extending up to hundreds of nanometers and formed by large clusters of cations or anions, reaching supramolecular dimensions. Domains with excess electric charge were also observed in thermoplastics as well as in silica, polyphosphate and titanium oxide particles. In the case of thermoplastics, the origin of the charges is tentatively assigned to their tribochemistry, oxidation followed by segregation or the Mawell-Wagner-Sillars and Costa Ribeiro effects.
electrostatics of solids; electric charge excess; scanning electric potential microscopy; electric force microscopy; polymer electrostatic behavior
A eletrificação de sólidos é conhecida há quatro séculos, mas há muitas questões importantes sobre este assunto, ainda não respondidas: por exemplo, quais são as espécies portadoras de cargas em um polímero isolante eletrificado, como estas cargas estão espacialmente distribuídas e qual é a contribuição destas cargas para as propriedades do polímero? Técnicas microscópicas introduzidas recentemente são apropriadas para o mapeamento de potenciais elétricos ao longo de uma superfície sólida, portanto podem responder a uma destas questões, contribuindo para a resolução das outras. Este trabalho resenha resultados obtidos combinando-se as microscopias de varredura de potencial elétrico (SEPM) e de força elétrica (EFM) com a microscopia eletrônica analítica baseada na espectroscopia de perda de energia de elétrons (ESI-TEM). Os materiais examinados são colóides poliméricos (látexes), polímeros termoplásticos, nanopartículas e híbridos. Nos materiais particulados foram observados domínios com excesso de cargas elétricas, estendendo-se por dezenas e centenas de nanômetros, formados por grandes acúmulos de cátions ou ânions atingindo dimensões supramoleculares. No caso dos termoplásticos, a formação dos domínios elétricos ainda não está bem compreendida, sendo tentativamente atribuída a efeitos triboquímicos no processamento do plástico, à formação de domínios oxidados, à ação de radiação de alta energia no ambiente ou aos efeitos Mawell-Wagner-Sillars e Costa Ribeiro.
eletrostática de sólidos; excesso de carga elétrica; microscopia de varredura de potencial elétrico; microscopia de força elétrica; polímeros; eletrostática
Supramolecular ionics: electric charge partition within polymers and other non-conducting solids
FERNANDO GALEMBECK1, CARLOS A. R. COSTA1, ANDRÉ GALEMBECK2
and MARIA DO CARMO V. M. SILVA1
1Universidade Estadual de Campinas, IQ, Cx. Postal 6154, 13083-970 Campinas, SP.
2Universidade Federal de Pernambuco, Recife, PE.
Manuscript received on September 14, 2001; accepted for publication on September 21, 2001;
contributed by FERNANDO GALEMBECK
ABSTRACT
Electrostatic phenomena in insulators have been known for the past four centuries, but many related questions are still unanswered, for instance: which are the charge-bearing species in an electrified organic polymer, how are the charges spatially distributed and which is the contribution of the electrically charged domains to the overall polymer properties? New scanning probe microscopies were recently introduced, and these are suitable for the mapping of electric potentials across a solid sample thus providing some answers for the previous questions. In this work, we report results obtained with two of these techniques: scanning electric potential (SEPM) and electric force microscopy (EFM). These results were associated to images acquired by using analytical electron microscopy (energy-loss spectroscopy imaging in the transmission electron microscope, ESI-TEM) for colloid polymer samples. Together, they show domains with excess electric charges (and potentials) extending up to hundreds of nanometers and formed by large clusters of cations or anions, reaching supramolecular dimensions. Domains with excess electric charge were also observed in thermoplastics as well as in silica, polyphosphate and titanium oxide particles. In the case of thermoplastics, the origin of the charges is tentatively assigned to their tribochemistry, oxidation followed by segregation or the Mawell-Wagner-Sillars and Costa Ribeiro effects.
Key words: electrostatics of solids, electric charge excess, scanning electric potential microscopy, electric force microscopy, polymer electrostatic behavior.
ELECTRIC CHARGES IN INSULATORS: A HISTORICAL NOTE AND SOME OPEN QUESTIONS
Electric charges are easily transferred, accumulated and dissipated in contacting dielectrics, and many related observations are very well known to the layperson. In the year 1600 William Gilbert already described observations made on sulfur, wax, resins, glasses and precious stones, as described in the first edition of the Encyclopedia Britannica. Francis Bacon, Boyle and many others were interested in this topic and published catalogues of electrical bodies. A large number of experimental and theoretical efforts followed them, with contributions from Faraday, Volta, Ampère, Coulomb, Maxwell, Rutherford and Bohr among many other scientists, leading to the current understanding of electricity and electrical phenomena. However, even considering this long history and the large array of resources available and widely used in the study of electric phenomena in dielectrics, there is still a number of open questions related to them.
A few statements represent the current difficulties in understanding electricity in non-conducting solids. First, it is experimentally more difficult to measure electric potentials in dielectrics than in conductors, even though techniques have been devised for this purpose more than one century ago. There are now practical, commercial electrometers, but these do not have the same high resolution reached by the meters used in the study of electrochemical systems, or electronics. Second, the fundamental equations relating electric potentials and charge densities are all very well established, but their application is difficult in any real systems. For instance, the analytical solution of the Poisson-Boltzmann equation is achieved only in specific cases, often under rather drastic simplifications (Hunter 1991). Another more specific open question is the following: which is the distribution of electric potentials across the bulk or surface of any given object made out of an organic polymer or ionic non-conducting material, and how does it contribute to the mechanical, optical, adhesion and electrically insulating properties of the solid? This question is usually neglected, and almost all the literature on plastics, rubbers and glasses normally assumes that dielectrics are electrically neutral, not only in the macroscopic scale but also at the micro- and nanometric scales. Still another problem is the speciation pattern of the excess charges in an electrified dielectric, this means, are these charges better described as ions, or as free electrons and holes?
ELECTROSTATIC PHENOMENA
On the other hand, there is now a large literature on many important topics related to the questions stated in the previous section. For instance, electrostatic discharges (ESD) have been intensely studied (Davidson et al. 2001), as they are strongly damaging for personnel, materials and property safety. Searching the Web of Science and the Derwent Innovations Index, from the year 1992 to this date (early September 2001) we obtain respectively 100 and 94 references on "electrostatic discharges", evidencing a significant activity on this topic. A related subject is dielectrophoresis (Pohl and Schwar 1959), the electric field-driven mass transfer in non-conducting media. This was described many years ago and it is now finding many applications due to the recent surge of interest in the nanostructures and microelectromechanical actuators (MEMS) (Jones et al. 2001, Jones 2001). Electrets are another important subject; a recent review (Eberle et al. 1996) on piezoelectric polymer electrets addresses the problem of the nature and origin of the trapped charges and their role in the stabilization of molecular dipole orientation (Bihler et al. 1987), in electrets. These authors exclude the possibility of polymer ionization by accelerated electrons ejected by the electrodes, and they conclude that only the direct contact of the electrode structure to the polymer surface can lead to charge injection. The detection of gases emitted by polymers subjected to polarization between electrodes shows the formation of C2H4+, which is a strong indirect evidence for transient polymer macro-ion formation, but direct evidence for the existence of macro-ions was not obtained.
Another review article (Bauer-Gogonea and Gerhard-Multhaupt 1996) on the non-linear optical polymer electrets acknowledges that a corona discharge produces and carries chemically active species which tend to attack and modify the surface and subsurface layers of organic materials, but the spatial distribution and chemical identity of the resulting charged species responsible for polymer polarization is not described. The high stability of electret charge is predicted by a theory involving a competition between the rate of current-carrier creation in activation processes and the rate of annihilation due to recombination and carrier capturing on the electrodes as well as by free, implanted charge already present in electrets (Malecki 1999). The existence of ionic carriers was considered, but this author did not identify these.
A current text on dielectrics (Robert 1988) emphasizes a fourth component of the electrical polarization of a dielectric, beyond the usual three (orientation, atomic and electronic) acknowledged in the more basic texts treating the electrical polarization of matter. This component is the interfacial polarization, the result of local accumulation of charges due to the migration phenomena, and concentrated around imperfections such as impurities, vacancies, grain boundaries and others. This author does not describe the nature and detailed location of these mobile charges. The current difficulties for the fundamental understanding of electrically charged entities within dielectrics are summed up in the "almost total impossibility of using models based on fundamental theories" to understand partial discharges phenomena (Robert 1988). Of course, these difficulties have not prevented the use of thermally stimulated discharge currents in polymers, in the study of polymer relaxations (Lacabanne et al. 1980, Shrivastava et al. 1980, Mudarra et al. 1999).
The formation of double-layers of opposite electrical charges by two dielectric contacting phases was recognized (Skinner et al. 1953, Skinner 1955), as well as the existence of a double layer at the polymer-metal interface (Possart and Roder 1984). An essential role in adhesion was assigned to the ensuing electrostatic attraction (Derjaguin and Smilga 1967), but later on two groups determined the electrostatic component of adhesion quantitatively, and the values obtained indicate that it amounts to a few percent only of the actual work of adhesion. For this reason, the electrostatic contribution to adhesion does not receive great attention, currently (Lee 1991).
Indeed, the formation of an electrical double layer at an interface is expected, considering the Maxwell-Wagner-Sillars effect (Ilavsky et al. 2001). Since most crystalline polymers are multiphase systems, they should intrinsically display internal charge separation. This idea is supported by evidence showing that the crystalline-amorphous interface plays an important role not only as a charge-trapping site but also in carrying an important amount of the total polarization in PVDF. The differences in dielectric constants of e.g. crystalline and amorphous polyethylene (and other partially crystalline thermoplastics) are probably small, but their electronic polarization component is sufficient to impair the transparency of the partially crystalline polymer. The polarization of a solid-liquid interface during crystal growth was discovered many years ago by J. da Costa Ribeiro in Brazil (Ribeiro 1950, Eyerer 1972) and it is the basis of the use of an electric field to promote crystal growth in solution.
Beyond the differences of dielectric constant between amorphous and crystalline polymer domains, there are other factors for the formation of differentiated domains within a polymer: oxidized chains are segregated, as well as the immiscible catalyst residues and contaminants introduced during fabrication and shaping of a polymer material.
An important topic concerning electrical polarization in dielectrics are the space charges. These and injection effects in bulk polymer were examined in detail, due to their relevance for electrical aging of extruded dielectric cables (Dang et al. 1996). The concept of a critical field above which charge injection (Hibma and Zeller 1986) occurs is in agreement with the observation that below 1.6 x 107 V/m there is no charge injection in XLPE. PE has a dark non-ohmic conductivity (Suh et al. 1994) and it is electroluminescent under large electrical fields (Jonsson et al. 1995), which is an evidence for the formation of chemical species in high-energy states trapped within the inert polyolefin; but these have not been identified or mapped. However, the development of theories and phenomenological relations between conduction activation energies, electric field, pressure (Crine 1982) and other variables was quite successful.
Mechanical and electromechanical stresses induce the formation of submicrocavities within polymer materials (Crine 1997). Electrons can then move without scattering within the submicrocavities and this may lead to further degradation. The formation of free radicals and end-groups of scission molecules formed in polyethylene, polypropylene and polycaprolactam under axial tension was already investigated many years ago, and their association with sub-microcrack generation in stressed polymers was well established (Zhurkov et al. 1972). The number of scission chains may reach 1019 cm 3, three orders of magnitude larger than the number of free radicals detected in the stressed polymer, which is in turn about of the same order of magnitude as the detected sub-microcracks. This raises the possibility of the formation of significant amounts of carbon and oxygen anions and cations following polymer stressing, which would then be trapped in the dielectric.
Free radicals are conveniently identified even at very small amounts by electron spin resonance (ESR), but the same is not true for macro-cations and anions, due to the absence of a suitable experimental technique. The studies on ion beam effects in polymer films show that polymer conductivity increases by as much as 1015 in ion beam-implanted polymers, and there is rather detailed information on depth distribution of the implanted species as well as on free-radical formation. However, the existence of polymer-derived ionic species has not been considered, and the conductivity changes are assigned to the formation of carbonization as well as to an associated degenerated quasi-two-dimensional electron gas (Popok et al. 1997).
To conclude, all this literature does not give information on the overall spatial distribution of electric charges in insulators, neither it addresses the problem of charge speciation, even though it provides many answers on the macroscopic characteristics of polymer behavior, under electric fields or under conditions leading to charge accumulation.
SCANNING ELECTRIC PROBE MICROSCOPIES
A new possibility to address these questions was created recently, thanks to the progress in scanning probe microscopy and analytical electron microscopy. The advent of the scanning probe microscopes made available techniques for sensing charges, dielectric constants, film thickness of insulating layers, photo-voltage and electric potentials (Nonnenmacher et al. 1991) and ferroelectric domain imaging (Saurenbach and Terris 1990). For instance, the electrostatic force microscope (EFM) maps the spatial variation and potential energy difference between a tip and a sample, arising from non-uniform charge distributions and local variations in surface work function (Nyffenegger et al. 1997). A tapping mode AFM coupled to electrostatic force modulation was used to image a polystyrene latex layer deposited on silicon, showing a large and intriguing contrast between neighboring latex particles (Hong et al. 1996). Localized charges were detected on PMMA samples following charge implantation (Terris et al. 1990).
In this laboratory, scanning electric potential microscopy (SEPM) and electric force microscopy (EFM) produced a wealth of information on electric charge distribution throughout insulating solids. This information was coupled to other information obtained by analytical electron microscopy, to help establishing the speciation patterns of electric charges in insulators. The results obtained in the past few years are reviewed in this work.
SCANNING ELECTRIC POTENTIAL MICROSCOPY (SEPM) AND ELECTRIC FORCE MICROSCOPY (EFM)
The SEPM technique uses the standard non-contact AFM set-up, but the sample is scanned with Pt-coated silicon nitride tips. An AC signal is fed 10 kHz below the frequency of the normal AFM oscillator, which matches the natural frequency of mechanical oscillation of the cantilever-tip system (40-70 kHz). During a measurement, the mechanical oscillation of the tip is tracked by the four-quadrant photodetector and analysed by two feedback loops. The first loop is used in the conventional way to control the distance between tip and sample surface, while scanning the sample at constant oscillation amplitude. The second loop is used to minimize the electric field between tip and sample: a second lock-in amplifier measures the tip vibration at the AC frequency oscillation while scanning, and adds a DC bias to the tip, to cancel the phase displacement in the mechanical oscillation component at the AC frequency. A schematic description is in Fig. 1. This technique differs from that used by Terris (Terris et al. 1990), who measures the phase displacement of the AC voltage, while in the Topometrix set up we cancel the phase displacement by DC biasing. The image is built using the DC voltage fed to the tip, at every pixel, thus detecting spatially resolved electric potentials throughout the scanned area. This technique is reminiscent of the oscillating electrode technique for monolayer study: both use an oscillating electrode separated from the sample by an air gap.
The major difference between both is the detection technique used, since SEPM uses a phase detection of the mechanic oscillation generated in the frequency of the applied voltage. The system is calibrated and the electric potential measurements are verified using two procedures: i) measuring electric potentials in the air 10-nm above thin strips of metal deposited on an insulator sheet, to which known voltages were applied; ii) changing the voltage applied to a metal holder beneath the sample, and acquiring images at different sample holder voltages.
The electric potential sensed by the tip at 10 nm from the surface is measured at each pixel, and all the electric potentials for a given sample area are displayed as a gray-level (or eventually color-coded) image. Since the information acquired derives from electrostatic interactions, the effect of buried charges has a quadratic dependence on distance. The sampling depth is dependent on the sample dielectric constant and also on the charge distribution normal to the sample. Consequently, charges buried up to 100 nm beneath the sample-air interface can still interfere in the measurements. However, the effect of a charge at the interface will be respectively four and nine times as large as that of the same charge but 10 or 20 nm beneath the surface.
Figure 2 presents AFM and SEPM images of titanium dioxide particles laying close to a step in a mica crystal surface. In the AFM image we observe the small particles, smaller than the step height. In this case, contrast is due to the topography, this means, the higher parts are brighter. The SEPM image does not show any contrast for the height difference across the mica step, but the particle borders appear much brighter than the particle cores. This means, the particles are made out of positive shells enclosing a negative core.
ELECTRIC FORCE MICROSCOPY (EFM)
In the EFM measurements, the dependence of electrostatic and van der Waals forces with distance is used and it provides information on the local accumulation of electric charges. The non-contact AFM setup is used, but each sample line is scanned at two heights above the surface: 10 nm and then 60 nm. In the first scan (10 nm) the tip response is dominated by short-distance van der Waals forces. In the second scan (60 nm) the electrostatic interactions predominate, due to their slower dependence on distance. As the tip crosses over an electrically charged region, charge is induced in the tip resulting in changes in the tip-to-surface force gradient, causing a change in the effective cantilever spring constant and in the resonance frequency of the tip. This change in the resonance frequency modifies the signal phase detected by a lock-in amplifier, as described in Fig. 3 (Dang et al. 1996). In our experiments, both EFM and AFM measurements are made simultaneously, by monitoring the detector signal amplitude at 300 x 300-pixel resolution, using silicon nitride tips coated with platinum with 20 nm nominal radius (resonance frequency = 70 - 99 kHz, stiffness constant = 1.8 - 5.2 N/m).
ANALYTICAL TRANSMISSION ELECTRON MICROSCOPY AND ELEMENTAL MAP IMAGES
Elemental mapping by energy-loss spectroscopy imaging in the transmission electron microscope (ESI-TEM) has been available for the past twenty years. In this laboratory, we use a Carl Zeiss CEM 902 transmission electron microscope equipped with a Castaing-Henry energy filter spectrometer within the column, a Proscan Slow Scan CCD camera and controlled by a microcomputer running the AnalySis 3.0 system. The spectrometer uses inelastic scattered electrons to form energy-loss and element-specific images. When the electron beam passes through the sample, interaction with electrons of different elements results in characteristic energy losses. A prism-mirror system deflects electrons with different energies to different angles so that only electrons with a well-defined energy are selected. If elastic electrons only are chosen (
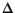
E = 0eV) a transmission image with reduced chromatic aberration is obtained. When monochromatic inelastic scattered electrons are selected, electron spectroscopic images (ELSI, or ESI) are formed, in which contrast is dependent on the local energy-loss spectrum and thus on the concentration fluctuations of a particular chosen element. (Amalvy et al. 2001).
Clear areas in the elemental distribution maps correspond to element-rich domains. The following procedure is used to acquire spectral images: a set of 38 to 42 images is acquired, around the absorption border for each element of interest. The energy window used is 6 eV, and the energy step between images is 2.5 eV. This set of images is used to define the three energy windows used for elemental mapping. Two images are recorded at energy windows below the absorption threshold, and they are used for fitting the background with a chosen function. The third image is obtained using an energy window set at the absorption band. The elemental map is obtained by subtracting the background from the image acquired in the third image, and it is checked for signal saturation, using the R-map macro from the AnalySis software. Each elemental map is validated by three independent checks: i) contrast inversion in the plasmon region, ii) spectral verification, by acquisition of the energy-loss spectra and iii) absence of signal saturation.
A specific attractive feature of this technique is the possibility to identify nanocrystallites by plasmon imaging, but with a much higher quality than usual diffractive dark-field imaging. (Leite and Galembeck 2001).
RESULTS ON LATEX PARTICLES
The majority of our results were obtained for latex particles (Cardoso et al. 1999a,b). Latexes are polymer colloids widely used in the fabrication of paints, adhesives, rubbers and thermoplastics. Beyond their exceptional technological importance, they are also good model systems for the study of particulate matter, because of their nanometer-to-micrometer size range and their accurate characterization by many other techniques. Latex synthesis proceeds in aqueous emulsion media in the presence of ions and surfactants, often using ionic peroxodisulfate initiators. Consequently, it is not surprising that these polymers contain ionic charges, but current thinking on all polymers and most other solids is based on the idea of prevalence of electroneutrality (Wu et al. 1999), following which charges should be present as ion pairs or small ion clusters, and larger domains with opposite charges could be found but only as electrical double layers.
This is not confirmed by microscopy results; Figure 4 shows AFM, SEPM and elemental maps of the poly (styrene-co-hydroxiethylmethacrylate) latex. Following the SEPM and EFM maps, the particles have negative cores and positive shells, with significant potential variations within the cores and the shells. The elemental maps show that the latex constituent associated to the negative charges (sulfur, from the sulfate chain-heads created by polymerization peroxodisulfate initiator) is absent from the particle outermost layers, where the (positive) potassium counter-ions are concentrated. Consequently, these completely independent sets of images provide essentially the same picture: latex particles are core-and-shell, with negative charges distributed throughout the particle core and enclosed within a positive shell. This picture is in considerable disagreement with many previous assumptions in the literature, following which the sulfate groups should concentrate at the particle borders, in close mixing with the potassium counter-ions. However, since these previous assumptions have not yet been substantiated by objective results, we shall not discuss them any further.
There are many important details on these images, which are discussed in our other publications, but two details are especially important. First, the particles appear circular in the TEM images, but they appear as deformed, packed hexagons in the AFM, SEPM and EFM images as well as in scanning electron micrographs (Galembeck et al. 2001a). This difference is easily explained: TEM micrograph was acquired from a sub-monolayer prepared on an evaporated carbon hydrophobic film, while the electric images are from a self-arrayed macrocrystal. In the later, the particles are strongly deformed by capillary adhesion forces, which do not operate in the former. Another important detail is the low significance of the central region of each particle elemental map, due to the excessive thickness for the ESI-TEM technique. However, we have also examined ultra-microtome thin cuts, which confirm the sulfur distribution throughout the particle cores (Cardoso et al. 1998).
Results obtained for a polystyrene (PS) latex are in Figure 5, showing some differences with the PS-HEMA latex: first, the PS particles do not form well-organized arrays; second, the patterns for cation (K) and anion (S) distribution are not sharply different as in the PS-HEMA, but S (associated to sulfate negative charges) is again excluded from the dry particle surfaces. This is in agreement with the observed negative cores and positive shells, in the SEPM image.
The examination of self-arrayed PS-HEMA film surfaces using SEPM (and SEM in a field-emission scanning microscope) shows an accumulation of hydrophobic particles around point and line macrocrystal defects. Defects in self-arrayed latex films are thus largely due to latex particle chemical heterogeneities (Cardoso et al. 2001). This result is consistent with the models for macrocrystal formation dependent on capillary adhesion, and it shows the importance of latex purification prior to macrocrystallization (Cardoso et al. 1999 a,b, Teixeira-Neto et al. 2000).
Electric potencial and force microscopies associated to electron microscopies have provided many other results, which are giving us a completely new view on polymer latex particles and films, as well as on the events relevant to particle coalescence and film formation. Some examples are in the following paragraphs.
Thin films made out of PS particles coagulated at the latex liquid surface under exposure to chloroform vapors are transparent, showing that the particles are well coalesced. However, large electric potential differences are observed between the microscope probe and adjacent domains in the films; domain sizes range from a few nanometers to hundreds of nanometers (Braga et al. 2001).
Sub-monolayers of PS-AAM latex particles examined by SEPM, AFM and FESEM show domains of positive or negative potentials within the individual particles and aggregates, forming multipoles. All the particle multipoles have the same relative orientation in the image plane and they are aligned with the mica a crystallographic axis. Particle alignment is interpreted considering the polarization anisotropy in the mica (001) plane: the deposited particles rotate, until the particle dipole-mica induced dipole interaction energy is minimum (Teixeira-Neto et al. submitted).
SEPM images from coalesced poly (styrene-butyl acrylate-acrylic acid) low-Tg latex films show the particle boundaries even in transparent films (transmittance > 99%), and the boundaries appear as positive domains, relative to the particle cores. Aging, annealing and exposure to toluene or chloroform vapors modify electric domain patterns, evidencing the mobility of charges within the films (Keslarek et al. in the press).
CHARGE SEPARATION IN THERMOPLASTICS
A typical model thermoplastic chain adequate for the study of polymers such as polyethylene, polystyrene and many others is a neutral linear or branched array of carbon and hydrogen atoms. However, species bearing electric charges are also expected in thermoplastics, due to: i) contaminants, including catalyst residues, ii) high-energy species produced tribochemically, especially during processing, iii) other high-energy species, but due to background energy radiation including the omnipresent cosmic rays and iv) oxidation and photo-oxidation products due to exposure to air and sunlight.
The distribution of electric potentials in thermoplastics was recently reported for the first time by this group (Galembeck et al. 2001b), even though some images published by other authors already suggested the existence of electric domains, e.g. in acrylic thin films. However, the existence of these domains was not explicitly acknowledged, perhaps due to the suspicion that these observations could be distorted by instrumental noise and also to the prevailing ideas on electroneutrality.
In our work, we showed images with two main results: i) sharp electric potential gradients were observed in most samples of the usual thermoplastics examined; ii) the degree of correlation of topographic and electric potential line-scans across the samples examined is highly variable: in some cases it is very high, while in others there is a great independence between sample surface topography and electric features. Usual thermoplastic polymers are thus irregular electric mosaics, a hitherto ignored but probably important feature for the mechanical, optical, thermal and electric properties of these important materials. Perhaps, this new information will help developing new polymer compounds.
OTHER MATERIALS
So far, we have examined few non-polymer systems. Two different samples of monodisperse Stöber silica particles were examined using SEPM as well as EFTEM and FESEM. Upon drying the silica dispersions, the larger ( ca. 141 nm) particles are only partially deformed by capillary adhesion, while the smaller particles ( ca. 36 nm) are strongly deformed and closely packed into dense films of a low porosity, which is an evidence of their larger plasticity, or superplasticity. Electric potential distribution maps obtained by SEPM show a significant interparticle as well as intra-particle contrast, especially in the case of the smaller particles. Examination by electron backscattering also reveals a larger contrast among the smaller particles, thus evidencing a non-uniformity of chemical composition. The results were interpreted considering the changes in the synthetic medium and other aspects of the particle growth mechanism, and they point towards the possibility to exploit the plasticity of the nanosized silica particles, in the making of silica monoliths (Costa et al. 2001, Leite et al. 2001). Other results were on aluminum polyphosphate nanoparticles, revealing a complex core-and-shell distribution of the particle constituents. (Monteiro et al. 1999).
A sodium polyphosphate-latex hybrid was also examined, showing an important contribution of the charged domains to this hybrid adhesion to glass. These results were presented to the Gordon Conference on Polymer Colloids, July 2001, and they are now being submitted for publication.
CONCLUSIONS
The new microscopy tools described in this work are revealing some previously unsuspected electric patterns in solids, formed by nano- to micron-sized domains bearing excess electrical charges and thus appearing as ion-like entities of supra-molecular dimensions.
Further exploration of these techniques should bring two kinds of results: a better understanding of the structure of non-conducting solids (and perhaps also of some liquids), and new ways to modify these solids, thus achieving new and desirable properties.
Two major challenges should be faced now: the acquisition of quantitative data on electric charge densities, beyond voltages, and the speciation of ionic chain entities.
ACKNOWLEDGEMENTS
FG acknowledges the continuing support of CNPq, Fapesp and Pronex/Finep/MCT. CARC is a Fapesp pre-doctoral fellow, and AG was supported by a Serrana-Unicamp contract.
RESUMO
A eletrificação de sólidos é conhecida há quatro séculos, mas há muitas questões importantes sobre este assunto, ainda não respondidas: por exemplo, quais são as espécies portadoras de cargas em um polímero isolante eletrificado, como estas cargas estão espacialmente distribuídas e qual é a contribuição destas cargas para as propriedades do polímero?
Técnicas microscópicas introduzidas recentemente são apropriadas para o mapeamento de potenciais elétricos ao longo de uma superfície sólida, portanto podem responder a uma destas questões, contribuindo para a resolução das outras. Este trabalho resenha resultados obtidos combinando-se as microscopias de varredura de potencial elétrico (SEPM) e de força elétrica (EFM) com a microscopia eletrônica analítica baseada na espectroscopia de perda de energia de elétrons (ESI-TEM). Os materiais examinados são colóides poliméricos (látexes), polímeros termoplásticos, nanopartículas e híbridos. Nos materiais particulados foram observados domínios com excesso de cargas elétricas, estendendo-se por dezenas e centenas de nanômetros, formados por grandes acúmulos de cátions ou ânions atingindo dimensões supramoleculares. No caso dos termoplásticos, a formação dos domínios elétricos ainda não está bem compreendida, sendo tentativamente atribuída a efeitos triboquímicos no processamento do plástico, à formação de domínios oxidados, à ação de radiação de alta energia no ambiente ou aos efeitos Mawell-Wagner-Sillars e Costa Ribeiro.
Palavras-chave: eletrostática de sólidos, excesso de carga elétrica, microscopia de varredura de potencial elétrico, microscopia de força elétrica, polímeros, eletrostática.
Correspondence to: Fernando Galembeck
E-mail: fernagal@iqm.unicamp.br
- AMALVY JI, ASUA JM, LEITE CAP AND GALEMBECK F. 2001. Elemental mapping by ESI-TEM, during styrene emulsion polymerization. Polymer 42: 2479-2489.
- BAUER-GOGONEA S AND GERHARD-MULTHAUPT R. 1996. Nonlinear optical polymer electrets current practice. IEEE Trans Dielectr Electr Insul 3: 677-705.
- BIHLER E, HOLDIK K AND EISENMENGER W. 1987. Electric field-induced gas emission from PVDF films. IEEE T Electr Insul 22: 207-210.
- BRAGA M, COSTA CAR, LEITE CAP AND GALEMBECK F. 2001. Scanning electric potential microscopy imaging of polymer latex films: detection of supramolecular domains with nonuniform electrical characteristics. J Phys Chem 105: 3005-3011.
- CARDOSO AH, LEITE CAP AND GALEMBECK F. 1998. Elemental distribution within single latex particles: Determination by electron spectroscopy imaging. Langmuir 14: 3187-3194.
- CARDOSO AH, LEITE CAP AND GALEMBECK F. 1999a. Latex particle self-assembly and particle microchemical symmetry: PS/HEMA latex particles are intrinsic dipoles. Langmuir 15: 4447-4453.
- CARDOSO AH, LEITE CAP AND GALEMBECK F. 1999b. PS-HEMA latex fractionation by sedimentation and colloidal crystallization. J Braz Chem Soc 10: 497-504.
- CARDOSO AH, LEITE CAP AND GALEMBECK F. 2001. Latex macrocrystal self-assembly dependence on particle chemical heterogeneity. Colloids Surf A 181: 49-55.
- COSTA CAR, LEITE CAP, DE SOUZA EF AND GALEMBECK F. 2001. Size effects on the microchemistry and plasticity of Stober silica particles: A study using EFTEM, FESEM, and AFM-SEPM microscopies. Langmuir 17: 189-194.
- CRINE JP. 1982. Influence of electric-field and low-pressure on the activation-energy for conduction in polyethylene. Phys Status Solidi A 72: 789-797.
- CRINE JP. 1997. Molecular model to evaluate the impact of aging on space charges in polymer dielectrics. IEEE T Dielect El In 4: 487-495.
- DANG C, PARPAL JL AND CRINE JP. 1996. Electrical aging of extruded dielectric cables - review of existing theories and data. IEEE T Dielect El In 3: 237-247.
- DAVIDSON JL, WILLIAMS TJ, BAILEY AG AND HEARN GL. 2001. Characterisation of electrostatic discharges from insulating surfaces. J Electrostat 51: 374-380.
- DERJAGUIN BV AND SMILGA VP. 1967. Electronic theory of adhesion. J Appl Phys 38: 4609.
- EYERER P. 1972. Electric charge separation and charge storage during phase changes in the absence of external electric fields. Adv Colloid Interface Sc 3: 223-273.
- EBERLE G, SCHMIDT H AND EISENMENGER W. 1996. Piezoelectric polymer electrets. IEEE T Dielect El 3: 624-646.
- GALEMBECK A, GALEMBECK F, COSTA CAR AND SILVA MCVM. 2001a. Macrocrystal swelling: AFM in situ observation of particle and film deformation and motion. J Colloid Interface Sci 234: 393-399.
- GALEMBECK A, COSTA CAR, SILVA MCVM, SOUZA EF AND GALEMBECK F. 2001b. Scanning electric potential microscopy imaging of polymers: electrical charge distribution in dielectrics. Polymer 42: 4845-4851.
- HIBMA T AND ZELLER HR. 1986. Direct measurement of space-charge injection from a needle electrode into dielectrics. J Appl Phys 59: 1614-1620.
- HONG JW, KHIM ZG, HOU AS AND PARK S. 1996. Tapping mode atomic force microscopy using electrostatic force modulation. Appl Phys Lett 69: 2831-2833.
- HUNTER RJ. 1991. Foundations of Colloid Science, vol 1, OUP, Oxford.
- ILAVSKY M, SOKOL R, NEDBAL J, FAHNRICH J AND KOLARIK J. 2001. Dielectric behaviour of polycarbonate/ poly(styrene-co-acrylonitrile) and polycarbonate/ poly(methyl methacrylate) two-phase blends. Macromol Symp 170: 79-89.
- JONES TB. 2001. Liquid dielectrophoresis on the microscale. J Electrostat 51: 290-299.
- JONES TB, GUNJI M, WASHIZU M AND FELDMAN MJ. 2001. Dielectrophoretic liquid actuation and nanodroplet formation. J Appl Phys 89: 1441-1448.
- JONSSON J, RANBY B, MARY D, LAURENT C AND MAYOUX C. 1995. Electroluminescence from polyolefins subjected to a homogeneous AC field. IEEE T Dielect El In 2: 107-113.
- LACABANNE C, GOYAUD P AND BOYER RF. 1980. Thermally stimulated currente (TSC) study of the T-G and T-11 transitions in anionic polystyrenes. J Polym Sci Polym Phys 18: 277-284.
- LEE L-H. 1991. Adhesive bonding. Plenum. New York.
- LEITE CAP AND GALEMBECK F. 2001. Nanocrystalline domain identification in gold films, by backscattered electron imagin and energy-filtered transmission electron microscopy. J Colloid Interface Sci 235: 4-8.
- LEITE CAP, SOUZA EF AND GALEMBECK F. 2001. Core- and shell nature of Stober silica particles. J Braz Chem Soc 12: 519-525.
- MALECKI JA. 1999. Linear decay of charge in electrets. Phys Rev B 59: 9954-9960.
- MONTEIRO VAR, SOUZA EF, AZEVEDO MMM AND GALEMBECK F. 1999. Aluminum polyphosphate nanoparticles: preparation, particle size determination and microchemistry. J Colloid Interface Sci 217: 237-248.
- MUDARRA M, BELANA J, CANADAS JC AND DIEGO JA. 1999. Windowing polarization: considerations for the study of the space charge relaxation in poly(methyl methacrylate) by thermally stimulated depolarization currents. Polymer 40: 2659-2665.
- NONNENMACHER M, O'BOYLE MP AND WICKRAMASINGHE HK. 1991. Kelvin probe force microscopy. Appl Phys Lett 58: 2921-2923.
- NYFFENEGGER RM, PENNER RM AND SCHIERLE R. 1997. Electrostatic force microscopy of silver nanocrystals with nanometer-scale resolution. Appl Phys Lett 71: 1878-1880.
- POHL HA AND SCHWAR JP. 1959. Factors affecting separations of suspensions in nonuniform electric fields. J Appl Phys 30: 69-73.
- POPOK VN, ODZHAEV VB, KOZLOV IP, AGARKO II, KARPOVICH IA AND SVIRIDOV DV. 1997. Ion beam effects in polymer films: structure evolution of the implanted layer. Nucl Instrum Meth B 129: 60-64.
- POSSART W AND RODER A. 1984. Measurement of electrical potential distribution in a polymer near the contact to a metal by means of scanning electron-microscopy. Phys Status Solidi A 84: 319-325.
- RIBEIRO JC. 1950. On the thermo-dielectric effect. An Acad Bras Cienc 22: 325-347.
- ROBERT P. 1988. Electrical and magnetic properties of materials. Norwood: Artech House, 300 p.
- SAURENBACH F AND TERRIS BD. 1990. Imaging of ferroelectric domain-walls by force microscopy. Appl Phys Lett 56: 1703-1705.
- SHRIVASTAVA SK, RANADE JD AND SRIVASTAVA AP. 1980. Thermally stimulated discharge currents in polystyrene films. Thin Solid Films 67: 201-206.
- SKINNER SM. 1955. Diffusion, static charges, and the conduction of electricity in nonmetallic solids by a single charge carrier: solution of the rectifier equations for insulating layers. J Appl Phys 26: 509-518.
- SKINNER SM, SAVAGE RL AND RUTZLER JE. 1953. Electrical phenomena in adhesion: electron atmospheres in dielectrics. J Appl Phys 24: 438-450.
- SUH KS, LEE CR, NOH JS, TANAKA J AND DAMON DH. 1994. Electrical-conduction in polyethylene with semiconductive electrodes. IEEE T Dielect El In 1: 224-230.
- TEIXEIRA-NETO E, LEITE CAP, CARDOSO AH, SILVA MCVM AND GALEMBECK F. 2000. Latex fractionation by sedimentation and colloidal crystallization: the case of poly(styrene-co-acrylamide. J Colloid Interface Sci 231: 182-189.
- TERRIS BD, STERN JE, RUGAR D AND MAMIN HJ. 1990. Localized charge force microscopy J Vac Sci Technol A 8: 374-377.
- WU K, IEDEMA MJ AND COWIN JP. 1999. Ion penetration of the water-oil interface. Science 286: 2482-2485.
- ZHURKOV SN, ZAKREVSK VA, KORSUKOV VE AND KUKSENKO VS. 1972. Mechanism of submicrocrack generation in stressed polymers. J Polym Sci A2 10: 1509-1520.
Publication Dates
-
Publication in this collection
12 Dec 2001 -
Date of issue
Dec 2001
History
-
Accepted
21 Sept 2001 -
Received
14 Sept 2001







