Abstracts
The generator coordinate Hartree-Fock method is used to generate adapted Gaussian basis sets for the atoms from Li (Z=3) through Xe (Z=54). In this method the Griffin-Hill-Wheeler-Hartree-Fock equations are integrated through the integral discretization technique. The wave functions generated in this work are compared with the widely used Roothaan-Hartree-Fock wave functions of Clementi and Roetti (1974), and with other basis sets reported in the literature. For all atoms studied, the errors in our total energy values relatively to the numerical Hartree-Fock limits are always less than 7.426 mhartree.
generator coordinate Hartree-Fock method; Gaussian basis sets; atomic total energy values
Utiliza-se o método coordenada geradora Hartree-Fock para gerar bases Gaussianas adaptadas para os átomos de Li (Z=3) até Xe (Z=54). Neste método, integram-se as equações de Griffin-Hill-Wheeler-Hartree-Fock através da técnica de discretização integral. Comparam-se as funções de ondas geradas neste trabalho com as funções de ondas Roothaan-Hartree-Fock de Clementi e Roetti (1974) e com outros conjuntos de bases relatados na literatura. Para os átomos estudados aqui, os erros em nossas energias totais relativos aos limites numéricos Hartree-Fock são sempre menores que 7,426 milihartree.
método coordenada geradora Hartree-Fock; conjuntos de bases de Gaussianas; energias totais atômicas
Adapted Gaussian basis sets for atoms from Li through Xe generated with the generator coordinate Hartree-Fock method
EUSTÁQUIO V. R. DE CASTRO1 and FRANCISCO E. JORGE2
1Departamento de Química, Universidade Federal do Espírito Santo, 29060-900 Vitória, ES, Brazil
2Departamento de Física, Universidade Federal do Espírito Santo, 29060-900 Vitória, ES, Brazil
Manuscript received on March 8, 2001; accepted for publication on August 28, 2001;
presented by FERNANDO GALEMBECK
ABSTRACT
The generator coordinate Hartree-Fock method is used to generate adapted Gaussian basis sets for the atoms from Li (Z=3) through Xe (Z=54). In this method the Griffin-Hill-Wheeler-Hartree-Fock equations are integrated through the integral discretization technique. The wave functions generated in this work are compared with the widely used Roothaan-Hartree-Fock wave functions of Clementi and Roetti (1974), and with other basis sets reported in the literature. For all atoms studied, the errors in our total energy values relatively to the numerical Hartree-Fock limits are always less than 7.426 mhartree.
Key words: generator coordinate Hartree-Fock method, Gaussian basis sets, atomic total energy values.
1 INTRODUCTION
Hartree-Fock (HF) wave functions for atoms may be computed numerically by standard methods (Froese Fischer 1977). Algebraic approximations to HF wave functions in which the radial orbitals are expanded by the Roothaan procedure (Roothaan 1960) in a set of basis functions such as Slater-type functions (STFs) or Gaussian-type functions (GTFs), are known as Roothaan-HF wave functions. Roothaan-HF wave functions are convenient for many purposes, as indicated by the large impact of the work of Clementi and Roetti (CR) (1974).
An alternative to the Roothaan-HF method is the generator coordinate HF (GCHF) method developed by Mohallem et al. (1986). In the last years, this method has been used with success to generate atomic and molecular wave functions (Jorge et al. 1998, Jorge and Martins 1998, Jorge and Fantin 1999, Jorge and Franco 2000, Jorge and Aboul Hosn 2001, Centoducatte et al. 2001, de Castro and Jorge 1998, Pinheiro et al. 1997a, b, da Costa et al. 1991, Custodio et al. 1992a, b).
In this paper we present accurate adapted Gaussian basis sets (AGBSs - a specific basis set for each atom studied here) for the atoms from Li through Xe, generated with the GCHF method (Mohallem et al. 1986). These basis sets are appropriate to be contracted and enriched with polarization functions and, then, can be used in nonrelativistic molecular calculations.
2 METHOD
The GCHF method (Mohallem et al. 1986) is based in choosing the one-electron functions as the continuous superpositions
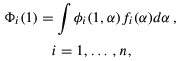
where n is the number of one-electron functions of the system,  are the generator functions (GTFs - in our case), fi are the weight functions and
are the generator functions (GTFs - in our case), fi are the weight functions and  is the generator coordinate. Using Eq. (1) to build a Slater determinant for the multi-electronic wave functions, and minimizing the total energy E with respect to the fi(
is the generator coordinate. Using Eq. (1) to build a Slater determinant for the multi-electronic wave functions, and minimizing the total energy E with respect to the fi( ), one arrives at the Griffin-Hill-Wheeler-HF (GHWHF) equations (Mohallem et al. 1986)
), one arrives at the Griffin-Hill-Wheeler-HF (GHWHF) equations (Mohallem et al. 1986)
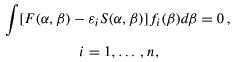
where F and S are Fock and overlap kernels, respectively (for more details about these kernels see Mohallem et al. (1986)).
The GHWHF equations are integrated using a procedure known as integral discretization (ID) (Mohallem 1986). The ID technique is implemented through a relabelling of the generator coordinate space, i.e.,
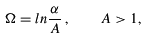
where A is a scaling factor determined numerically. In the new generator coordinate space 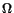 , an equally spaced N-point mesh {
, an equally spaced N-point mesh { } is selected, and the integration range is characterized by a starting point
} is selected, and the integration range is characterized by a starting point  , an increment
, an increment 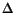
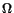 , and the number of discretization points N. The highest value (
, and the number of discretization points N. The highest value ( ) for the generator coordinate is given by
) for the generator coordinate is given by
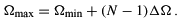
The choice of the discretization points determines the exponents of the GTFs.
3 RESULTS AND DISCUSSION
Self-consistent-field ground state total energy calculations are performed for the atoms from Li (Z=3) through Xe (Z=54), using the GCHF method (Mohallem et al. 1986) presented in the last section. Throughout the calculations we used the scaling factor A [see Eq. (3)] equal to 6.0. For all atoms studied here, we searched the best discretization parameters (
and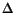
 ) values for each s, p and d symmetry. The AGBS exponents generated in this work for the above atoms can be easily reproduced by using Eqs. (3) and (4) and the discretization parameters showed in Table I. All calculations were carried out using a modified version of the ATOMSCF program (Chakravorty et al. 1989). For each atom, the optimization process is repeated until the total energy stabilize within ten significant figures.
) values for each s, p and d symmetry. The AGBS exponents generated in this work for the above atoms can be easily reproduced by using Eqs. (3) and (4) and the discretization parameters showed in Table I. All calculations were carried out using a modified version of the ATOMSCF program (Chakravorty et al. 1989). For each atom, the optimization process is repeated until the total energy stabilize within ten significant figures.
From Table II we can see that our total energies for Li, Be, and Na-Kr are worse than the CR (1974) results, while for the fourth-row atoms the opposite occurs. For B, C and Ne the two approaches give the same energy values. These results are surprising since the CR wave functions have been regarded for a long time as having near NHF quality. It is known that STFs have the correct functional forms to describe the nonrelativistic wave functions of atomic species at the origin, but they are not particularly suitable for self-consistent field molecular calculations. On the other hand, GTFs are useful in the evaluation of multicenter integrals in molecules, but they do not possess the correct functional behavior at the origin. Thus, for an atomic system, to obtain equivalent results for any physical or chemical property it is necessary to use GTFs basis set greater in size than STFs basis set. The CR (1974) result for Rh is wrong, because it is below the HF limit.
Koga et al. (1993) improved the widely used wave functions of CR (1974) by reoptimization of the STF exponents. They used exactly the same number and type of STFs (see the discussion about STFs and GTFs presented in the last paragraph) as CR. However, for Sr and Zr-Cd our energy results are better than those obtained by them (see Table II). Clearly, greater number of STFs are needed to improve the wave function (Koga et al. 1993) accuracy for Sr and Zr-Cd.
In summary, the AGBSs generated in this work are appropriate to be used in nonrelativistic atomic and molecular calculations of physical and chemical properties. An application of these basis sets in HF calculations of some properties of third- and fourth-row diatomic molecules is in progress. We recall that AGBSs generated with the GCHF method (Mohallem et al. 1986) were used with success to calculate various properties of first- and second-row diatomic molecules (Pinheiro et al. 1997a, b).
For the atoms from Li to Ar, the error in our total energies is not more than 1 mhartree. For the third- and fourth-row atoms the error is always larger than 1 mhartree (see Table II). The largest error (7.426 mhartree) occurs for In.
4 CONCLUSIONS
The present work shows that a specific and careful numerical evaluation of the GHWHF equations for each of those atoms studied here, is capable of generating accurate AGBSs to be used in HF atomic and molecular calculations.
When we compare our ground state total energies with the benchmark results obtained by CR (1974), who used fully-optimized basis sets of STFs, we find that the results for first-, second- ant third-row atoms are in general worse, while those for fourth-row atoms are better than theirs. Besides this, the largest difference between our energy results and the corresponding values computed with a NHF method (Bunge et al. 1992) is equal to 7.426 mhartree for In.
ACKNOWLEDGEMENTS
We acknowledge the financial support of CNPq (Brazilian Research Agency).
RESUMO
Utiliza-se o método coordenada geradora Hartree-Fock para gerar bases Gaussianas adaptadas para os átomos de Li (Z=3) até Xe (Z=54). Neste método, integram-se as equações de Griffin-Hill-Wheeler-Hartree-Fock através da técnica de discretização integral. Comparam-se as funções de ondas geradas neste trabalho com as funções de ondas Roothaan-Hartree-Fock de Clementi e Roetti (1974) e com outros conjuntos de bases relatados na literatura. Para os átomos estudados aqui, os erros em nossas energias totais relativos aos limites numéricos Hartree-Fock são sempre menores que 7,426 milihartree.
Palavras-chave: método coordenada geradora Hartree-Fock, conjuntos de bases de Gaussianas, energias totais atômicas.
Correspondence to: Eustáquio V.R. de Castro
E-mail: castro@cce.ufes.br
- BUNGE CF, BARRIENTOS JA, BUNGE AV AND COGORDAN JA. 1992. Hartree-Fock and Roothaan- Hartree-Fock energies for the ground states of He through Xe. Phys Rev A 46: 3691-3696.
- CENTODUCATTE R, JORGE FE AND PEIXOTO LT. 2001. Adapted Gaussian basis sets for ions with N< 54. J Mol Structure (Theochem) 539: 35-43.
- CHAKRAVORTY SJ, CORONGIU G, FLORES JR, SONNAD V, CLEMENTI E, CARRAVETTA V AND CACELLI I. 1989. Modern techniques in computational chemistry: MOTECC-89; Clementi E., Ed., Leiden: ESCOM.
- CLEMENTI E AND ROETTI C. 1974. Roothaan- Hartree-Fock atomic wave functions. At Data Nucl Data Tables 14: 177-478.
- CUSTODIO R, GODDARD JD, GIORDAN M AND MORGAN NH. 1992a. The application of an optimization technique to the development of universal basis sets. Can J Chem 70: 580-588.
- CUSTODIO R, GIORDAN M, MORGAN NH AND GODDARD JD. 1992b. Application of an optimization technique to the discretized version of the Griffin-Hill-Wheeler-Hartree-Fock equations. Int J Quantum Chem 42: 411-423.
- DA COSTA HFM, DA SILVA ABF, MOHALLEM JR, SIMAS AM AND TRSIC M. 1991. The generator coordinate Hartree-Fock method for molecular systems. Formalism and first applications to H2, LiH and Li2 Chem Phys 154: 379-384.
- DE CASTRO EVR AND JORGE FE. 1998. Accurate universal Gaussian basis set for all atoms of the periodic table. J Chem Phys 108: 5225-5229.
- FROESE FISCHER C. 1977. The Hartree-Fock Method for Atoms. New-York: Wiley.
- JORGE FE AND MARTINS RF. 1998. Accurate universal Gaussian basis set for H through Xe for Hartree-Fock calculations. Chem Phys 233: 1-7.
- JORGE FE AND FANTIN PA. 1999. A universal basis set for cations and anions generated with the generator coordinate Hartree-Fock method. Chem Phys 249: 105-111.
- JORGE FE AND FRANCO ML. 2000. A universal Gaussian basis set for positive and negative ions from H through Xe. Chem Phys 253: 21-26.
- JORGE FE AND ABOUL HOSN HM. 2001. Gaussian basis sets for isoelectronic series of the He to Ne. Chem Phys 264: 255-265.
- JORGE FE, LIBRELON PR AND CANAL NETO A. 1998. Adapted Gaussian basis sets for atoms Cs to Lr based on the generator coordinate Hartree-Fock method. J Comp Chem 19: 858-865.
- KOGA T, TATEWAKI H AND THAKKAR AJ. 1993. Roothaan- Hartree-Fock wave functions for atoms with Z< 54. Phys Rev A 47: 4510-4512.
- MOHALLEM JR. 1986. A further study on the discretisation of the Griffin-Hill-Wheeler equation. Z Phys D 3: 339-344.
- MOHALLEM JR, DREIZLER RM AND TRSIC M. 1986. A Griffin-Hill-Wheeler version of the Hartree-Fock equations. Int J Quantum Chem Symp 20: 45-55.
- PINHEIRO JC, DA SILVA ABF AND TRSIC M. 1997a. The generator coordinate Hartree-Fock method applied to the choice of a contracted Gaussian basis for first-row atoms. J Mol Structure (Theochem) 394: 107-115.
- PINHEIRO JC, DA SILVA ABF AND TRSIC M. 1997b. Generator coordinate Hartree-Fock method applied to the choice of a contracted Gaussian basis for the second-row atoms. Int J Quantum Chem. 63: 927-934.
- ROOTHAAN CCJ. 1960. Self-consistent field theory for open shells of electronic systems. Rev Mod Phys 32: 179-185.
Publication Dates
-
Publication in this collection
12 Dec 2001 -
Date of issue
Dec 2001
History
-
Accepted
28 Aug 2001 -
Received
08 Mar 2001



