Abstracts
In this work are studied periodic perturbations, depending on two parameters, of quadratic planar polynomial vector fields having an infinite heteroclinic cycle, which is an unbounded solution joining two saddle points at infinity. The global study envolving infinity is performed via the Poincaré compactification. The main result obtained states that for certain types of periodic perturbations, the perturbed system has quadratic heteroclinic tangencies and transverse intersections between the local stable and unstable manifolds of the hyperbolic periodic orbits at infinity. It implies, via the Birkhoff-Smale Theorem, in a complex dynamical behavior of the solutions of the perturbed system, in a finite part of the phase plane.
heteroclinic cycles; periodic perturbations; polynomial systems
Neste trabalho são estudadas perturbações periódicas, dependendo de dois parâmetros, de campos vetoriais polinomiais planares que possuem um ciclo heteroclínico infinito, que consiste de uma solução ilimitada, que conecta dois pontos de sela no infinito. O estudo global do campo vetorial, envolvendo o infinito, foi elaborado utilizando-se a compactificação de Poincaré. O resultado principal estabelece que, para certo tipo de perturbação periódica, o sistema apresenta tangências heteroclínicas e intersecção transversal das variedades invariantes de órbitas periódicas no infinito, o que implica, via o Teorema de Birkhoff-Smale, em um comportamento dinâmico bastante complexo das soluções do sistema perturbado, em uma região finita do plano de fase.
ciclos heteroclínicos; perturbações periódicas; sistemas polinomiais
Periodic perturbations of quadratic planar polynomial vector fields
MARCELO MESSIAS
Departamento de Matemática - Faculdade de Ciências e Tecnologia - UNESP, Caixa Postal 467
19060-900 Presidente Prudente, SP, Brazil
Manuscript received on September 13, 2001; accepted for publication on November 22, 2001;
presented by J. SOTOMAYOR
ABSTRACT
In this work are studied periodic perturbations, depending on two parameters, of quadratic planar polynomial vector fields having an infinite heteroclinic cycle, which is an unbounded solution joining two saddle points at infinity. The global study envolving infinity is performed via the Poincaré compactification. The main result obtained states that for certain types of periodic perturbations, the perturbed system has quadratic heteroclinic tangencies and transverse intersections between the local stable and unstable manifolds of the hyperbolic periodic orbits at infinity. It implies, via the Birkhoff-Smale Theorem, in a complex dynamical behavior of the solutions of the perturbed system, in a finite part of the phase plane.
Key words: heteroclinic cycles; periodic perturbations; polynomial systems.
1. INTRODUCTION
The study of periodic perturbations of vector fields in the plane having homoclinic or heteroclinic trajectories have been widely developed due to the great interest of such systems as mathematical models for natural phenomena as well as for their intrinsic theoretic importance. In this subject, some of the systems studied are Duffing's equation subject to an external force, the forced Van der Pol equation, Hill's equation, forced pendulum, among others. Due to the existence of transverse homoclinic (or heteroclinic) fixed points for the Poincaré Map associated to the periodic perturbed systems, the solutions of them may present a complex dynamical behavior, called "chaotic'' by some authors.
The studies mentioned above are, in general, concerned with bounded periodic perturbations of planar vector fields restricted to a compact region of the plane, which contains the homoclinic and heteroclinic trajectories. In the special case in which the vector field is polynomial, it can be studied in the entire plane by means of a compactification procedure. In these cases, the compactfied polynomial vector field may present symmetric and nonsymmetric infinite heteroclinic cycles (see Figure 1).
Bifurcations of codimension one, due to autonomous perturbations of polynomial systems having these type of cycles were considered in (Sotomayor and Paterlini 1987). In the present work are studied bifurcations derived from periodic perturbations of such infinite heteroclinic cycles, for quadratic polynomial vector fields. It is proved that certain types of periodic perturbations imply in a complex dynamical behavior of the solutions of the perturbed system in the compact region of the plane, similar to the "horseshoe-like'' dynamics. It's a consequence of the Birkhoff-Smale Theorem (Guckenheimer and Holmes 1983) and is due to the quadratic tangencies and transversal intersections of the stable and unstable manifolds of two periodic orbits at infinity, originated from the periodic perturbation of the system. Although the results obtained are true for degree n polynomial vector fields having an infinite heteroclinic cycle (Messias 2000), the quadratic case will be considered here, since it can be applied to the study of several natural phenomena (Coppel 1966 and Taboas 1987).
2. STATEMENT OF THE MAIN RESULTS
Consider in
2 a quadratic polynomial vector field having an invariant straight line, free from singularities. Without lost of generality, such straight line can be taken as the y-axis, and the system of differential equations associated to this vector field has the following form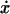
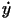
Making an affine change of variables it becomes, after renaming constants and variables,
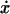
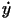
with n2 - 4ac < 0.
Vector fields like this arise in the study of several applied problems (Coppel 1966). Here, we shall consider periodic perturbations of them. The invariant straight line of the system will play the role of the heteroclinic trajectory joining the saddles at infinity, on the Poincaré disk, after compactification. Translating the straight line to the point (1, 0), to prevent that the origin (0, 0) be on the heteroclinic trajectory, the system takes the form,
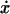
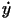
Then, we have the following result (Messias 2000), which gives the normal form of the quadratic systems that have a symmetric infinite heteroclinic cycle (nonsymmetric case is also treated in (Messias 2000)).
PROPOSITION 1. Suppose that the following hypothesis hold
H1) (b + n)2 - 4(a + m + a)c < 0 and m2 - 4aa > 0;
H2) 0 < c < 1;
H3) b2 - 4a(c - 1) < 0;
Then, (1)-(2) has exactly two hyperbolic saddle points (q1, 0) and (q2, 0) at infinity, connected by an heteroclinic solution g(s), given by a reparametrization of the solution j(t), contained in the straight line {x=1}. The solution j(s) gives rise to the symmetric infinite heteroclinic cycle g(s) È q1 È a (s) È q2 (Figure 1a).
Consider now the following periodic perturbation of the system (1)-(2):
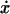
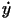
where g is a Ck periodic function, k ³ 2, with period T = 2p/w.
The following theorem holds:
THEOREM 2. Suppose that for m = A = 0 the system (3)-(4) satisfies the hypothesis (H1)-(H3) in Proposition 1. Then (3)-(4) has two hyperbolic periodic orbits at infinity, q1(s) and q2(s), having invariant manifolds  and
and  and, for m sufficiently small, there exist differentiable functions AM(m) and Am(m) such that (see Figure 2):
and, for m sufficiently small, there exist differentiable functions AM(m) and Am(m) such that (see Figure 2):
a)if A = AM(m) or A = Am(m), the invariant manifolds  and
and  , are quadraticaly tangent;
, are quadraticaly tangent;
b)if m > 0 (m < 0, respectively) and Am(m) < A < AM(m) (AM(m) < A < Am(m), respectively), then  Ç
Ç  ;
;
c)if m > 0 and A > AM(m) or A < Am(m), then  and
and  intersect transversely in at least one point;
intersect transversely in at least one point;
d)if m < 0 and A > Am(m) or A < AM(m), the same result stated in c) holds.
The proof appears in (Messias 2000), and is carried out in the following way: using polar coordinates, we compactify equations (3)-(4) to obtain a system defined on the solid torus, D2´ S1. This system has two hyperbolic periodic orbits, q1(s) and q2(s), at infinity, which is represented by the border of the solid torus, S1´ S1. Such periodic orbits have invariant manifolds  and
and  which coincides, for m = A = 0. Then, we define a separation function that gives the distance of these manifolds, for (m, A) in a neighborhood of (0, 0). Taylor expanding the separation function and using the Implicit Function Theorem, we prove the existence of the differentiable functions AM(m) and Am(m) that appears in Theorem 2.
which coincides, for m = A = 0. Then, we define a separation function that gives the distance of these manifolds, for (m, A) in a neighborhood of (0, 0). Taylor expanding the separation function and using the Implicit Function Theorem, we prove the existence of the differentiable functions AM(m) and Am(m) that appears in Theorem 2.
3. CONCLUSIONS
From the theorem above, one can sketch the bifurcation diagram of the perturbed system, in a neighborhood of the origin in the parameter plane (Figure 2): there exist two types of regions, S1 and S2, separated by the curves AM(m) and Am(m), such that, if the pair (m, A) belongs to these curves, the system presents heteroclinic tangencies; if (m, A) belongs to the regions S1, the intersection of the manifolds  and
and  is empty; if (m, A) belongs to the region S2, the manifolds intersect transversely in at least one point.
is empty; if (m, A) belongs to the region S2, the manifolds intersect transversely in at least one point.
The periodic perturbation considered is the most natural possible, since it is orthogonal to the heteroclinic trajectory g(s). The parameter m was used "to split'' (or to disconnect) the manifolds  and
and  , while the parameter A represents the amplitude of the periodic perturbation. The theorem gives the values of A, depending on m, for which the manifolds are tangent, intersect transversely or are separated.
, while the parameter A represents the amplitude of the periodic perturbation. The theorem gives the values of A, depending on m, for which the manifolds are tangent, intersect transversely or are separated.
An important consequence of the theorem is that, although the periodic orbits belong to infinity, quadratic tangencies and transverse intersections of the manifolds will happen in a compact portion of the plane (interior of the Poincaré disk - Figure 2), thus affecting the dynamics of the solutions in a finite region of the plane. In fact, numerical simulations indicate that the complex behavior of the solutions will happen in a limited region, containing the origin of the phase plane (see Messias 2000). This phenomenon may well be called the chaos that arises from infinity.
ACKNOWLEDGMENTS
This communication is part of the author's PhD thesis (Messias 2000), developed at IME-USP-Brazil, under the supervision of Prof. Jorge Sotomayor, to whom the author is grateful. The work was supported by the CAPES Conv. PICDT 047/95.
RESUMO
Neste trabalho são estudadas perturbações periódicas, dependendo de dois parâmetros, de campos vetoriais polinomiais planares que possuem um ciclo heteroclínico infinito, que consiste de uma solução ilimitada, que conecta dois pontos de sela no infinito. O estudo global do campo vetorial, envolvendo o infinito, foi elaborado utilizando-se a compactificação de Poincaré. O resultado principal estabelece que, para certo tipo de perturbação periódica, o sistema apresenta tangências heteroclínicas e intersecção transversal das variedades invariantes de órbitas periódicas no infinito, o que implica, via o Teorema de Birkhoff-Smale, em um comportamento dinâmico bastante complexo das soluções do sistema perturbado, em uma região finita do plano de fase.
Palavras-chave: ciclos heteroclínicos; perturbações periódicas; sistemas polinomiais.
Correspondence to: Marcelo Messias
E-mail: marcelo@prudente.unesp.br
- COPPEL WA. 1966. A survey of quadratic systems. J Differ Equations 2: 293-304.
- GUCKENHEIMER J AND HOLMES P. 1983. Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Applied Mathematical Series, 42. Springer-Verlag, New York.
- MESSIAS M. 2000. Perturbaçőes periódicas de ciclos heteroclínicos infinitos de campos vetoriais polinomiais planares. PhD Thesis - IME-USP, Săo Paulo, Brazil.
- SOTOMAYOR J AND PATERLINI R. 1987. Bifurcations of polynomial vector fields in the plane. Canadian Mathematical Society - Conference Proceedings 8: 665-685.
- TABOAS P. 1987. Periodic solutions of a forced Lotka-Volterra equation. J Math Anal Appl 124: 82-97.
Publication Dates
-
Publication in this collection
17 July 2002 -
Date of issue
June 2002
History
-
Accepted
22 Nov 2001 -
Received
13 Sept 2001




