Abstracts
In this paper, we prove that if a Nemytskii operator maps Lp(omega, E) into Lq(omega, F), for p, q greater than 1, E, F separable Banach spaces and F reflexive, then a sequence that converge weakly and a.e. is sent to a weakly convergent sequence. We give a counterexample proving that if q = 1 and p is greater than 1 we may not have weak sequential continuity of such operator. However, we prove that if p = q = 1, then a weakly convergent sequence that converges a.e. is mapped into a weakly convergent sequence by a Nemytskii operator. We show an application of the weak continuity of the Nemytskii operators by solving a nonlinear functional equation on W1,p(omega), providing the weak continuity of some kind of resolvent operator associated to it and getting a regularity result for such solution.
weak continuity; nonlinearities; Nemytskii operator
Neste artigo, provamos que se um operador de Nemytskii aplica Lp(ômega, E) no Lq(ômega , F), para p, q maiores do que 1, E, F espaços de Banach separáveis e F reflexivo, então uma seqüência que converge fracamente e q.t.p. é transformada em uma seqüência fracamente convergente. Fornecemos um contra-exemplo mostrando que se q = 1 e p é maior do que 1, podemos não ter continuidade seqüêncial de tal operador. Contudo provamos que se p = q = 1, então seqüências fracamente convergentes que convergem q.t.p. são aplicadas em seqüências fracamente convergentes por um operador de Nemytskii. Mostramos uma aplicação da continuidade fraca dos operadores de Nemytskii resolvendo uma equação funcional não linear no W1,p(ômega), provando a continuidade fraca de um tipo de operador resolvente associado ao operador de Nemytskii e obtendo um resultado de regularidade de tal solução.
continuidade fraca; não linearidades; operador de Nemytskii
Weak convergence under nonlinearities
DIEGO R. MOREIRAI; EDUARDO V. O. TEIXEIRAII
IDepartamento de Matemática, Universidade Federal do Ceará, Campus do Pici
60455-760 CE, Brazil
IIDepartment of Mathematics, University of Texas at Austin, RLM 9.136
Austin, Texas, 78712-1082 U.S.A.
Correspondence Correspondence to Eduardo V.O. Teixeira E-mail: teixeira@math.utexas.edu
ABSTRACT
In this paper, we prove that if a Nemytskii operator maps Lp(W, E) into Lq(W, F), for p, q greater than 1, E, F separable Banach spaces and F reflexive, then a sequence that converge weakly and a.e. is sent to a weakly convergent sequence. We give a counterexample proving that if q = 1 and p is greater than 1 we may not have weak sequential continuity of such operator. However, we prove that if p = q = 1, then a weakly convergent sequence that converges a.e. is mapped into a weakly convergent sequence by a Nemytskii operator. We show an application of the weak continuity of the Nemytskii operators by solving a nonlinear functional equation on W1,p(W), providing the weak continuity of some kind of resolvent operator associated to it and getting a regularity result for such solution.
Key words: weak continuity, nonlinearities, Nemytskii operator.
RESUMO
Neste artigo, provamos que se um operador de Nemytskii aplica Lp(W, E) no Lq(W , F), para p, q maiores do que 1, E, F espaços de Banach separáveis e F reflexivo, então uma seqüência que converge fracamente e q.t.p. é transformada em uma seqüência fracamente convergente. Fornecemos um contra-exemplo mostrando que se q = 1 e p é maior do que 1, podemos não ter continuidade seqüêncial de tal operador. Contudo provamos que se p = q = 1, então seqüências fracamente convergentes que convergem q.t.p. são aplicadas em seqüências fracamente convergentes por um operador de Nemytskii. Mostramos uma aplicação da continuidade fraca dos operadores de Nemytskii resolvendo uma equação funcional não linear no W1,p(W), provando a continuidade fraca de um tipo de operador resolvente associado ao operador de Nemytskii e obtendo um resultado de regularidade de tal solução.
Palavras-chave: continuidade fraca, não linearidades, operador de Nemytskii.
1. INTRODUCTION
A very important question in Functional Analysis is how to decide if an operator in a Banach space is weakly continuous. Frequently, we meet this issue in variational problems when we have to check the main assumptions of the classical theorems, especially if we are searching for some kind of compactness results. This question becomes more difficult when we deal with nonlinearities. Among the nonlinear operators, there is an outstanding group called Nemytskii operators. We are interested in the weak sequential continuity of these operators. In order to develop these ideas, we consider the notion of a.e. and weak convergence (a.e.w.) and formulate the problem ap,q where p, q ³ 1 to be: Let f be a Caratheodory function and suppose that the Nemytskii operator associated to f maps Lp(W, ) intoLq(W,
) intoLq(W, ). Does Nf map a.e.w. convergent sequences into a.e.w. convergent sequences? Our goal in this paper is to study under what conditions the problem ap,q is affirmatively answered.
). Does Nf map a.e.w. convergent sequences into a.e.w. convergent sequences? Our goal in this paper is to study under what conditions the problem ap,q is affirmatively answered.
Our paper is organized as follows. In the section 2, we treat the heart of the matter. We start providing a uniqueness result of convergence in the a.e.w sense for Lp(W, ) spaces (Lemma 1). Afterwards, we construct an example which shows the affirmative answer for the problem ap, 1 fails to p > 1 (Example 2) and we establish the solvability of the problem ap,q under the following assumptions: q > 1 and reflexivity of
) spaces (Lemma 1). Afterwards, we construct an example which shows the affirmative answer for the problem ap, 1 fails to p > 1 (Example 2) and we establish the solvability of the problem ap,q under the following assumptions: q > 1 and reflexivity of  (Theorem 2). At the end of this section, we prove the counterpart of the example 2 which says that the problem a1, 1 is solvable on bounded domains (Theorem 4). In the section 3, the last section, we are concerned about studying the solvability on W1, p(W) of the equation
(Theorem 2). At the end of this section, we prove the counterpart of the example 2 which says that the problem a1, 1 is solvable on bounded domains (Theorem 4). In the section 3, the last section, we are concerned about studying the solvability on W1, p(W) of the equation
f (x, u(x)) - lu(x) = y(x)
for l Î  and y Î W1, p(W) given. We also provide conditions to the weak sequential continuity of the resolvent operator Rl = (Nf - l I )-1 on W1, p(W) and we observe a regularity result for such solutions. In the study of the problems ap,q, surprisingly, the cases q = 1 and q > 1 have been shown very different. Some of these facts turned out to be known, mainly in particular cases; however not in such a generality. We think it is worthwhile to formulate them in a more general form and make them more available. We believe the ideas developed in this paper may be applied in quite different problems.
and y Î W1, p(W) given. We also provide conditions to the weak sequential continuity of the resolvent operator Rl = (Nf - l I )-1 on W1, p(W) and we observe a regularity result for such solutions. In the study of the problems ap,q, surprisingly, the cases q = 1 and q > 1 have been shown very different. Some of these facts turned out to be known, mainly in particular cases; however not in such a generality. We think it is worthwhile to formulate them in a more general form and make them more available. We believe the ideas developed in this paper may be applied in quite different problems.
2. WEAK CONTINUITY OF THE NEMYTSKII OPERATOR
DEFINITION 1. Let W be a domain in  N. Let
N. Let  and
and  be separable Banach spaces. A function f : W x
be separable Banach spaces. A function f : W x  ®
®  is said to be a Caratheodory function if:
is said to be a Caratheodory function if:
(a) for each fixed v Î  the function x
the function x  f (x, v) is Lebesgue measurable in W;
f (x, v) is Lebesgue measurable in W;
(b) for almost everywhere fixed x Î W the function f (x,.) :  ®
®  is continuous.
is continuous.
In this case we denote f Î (C). Let  (W,
(W, ) be all measurable functions u : W ®
) be all measurable functions u : W ®  . It is easy to prove that if f Î (C) then f defines a mapping Nf :
. It is easy to prove that if f Î (C) then f defines a mapping Nf :  (W,
(W, ) ®
) ®  (W,
(W, ) by Nf(u)(x) : = f (x, u(x)). This mapping is called the Nemytskii operator associated to f. The first result we would like to state is an extention to separable Banach spaces of the remarkable theorem due to Vainberg concerning about the Nemytskii operator theory.
) by Nf(u)(x) : = f (x, u(x)). This mapping is called the Nemytskii operator associated to f. The first result we would like to state is an extention to separable Banach spaces of the remarkable theorem due to Vainberg concerning about the Nemytskii operator theory.
THEOREM 1 (Lucchetti and Patrone 1980). Let  ,
,  be separable Banach spaces. The Nemytskii operator Nf maps Lp(W,
be separable Banach spaces. The Nemytskii operator Nf maps Lp(W, ) into Lq(W,
) into Lq(W, ), 1 £ p, q < +
), 1 £ p, q < +  , if and only if there exist a constant a > 0 and b(x) Î Lq+(W) such that
, if and only if there exist a constant a > 0 and b(x) Î Lq+(W) such that
In this case, the operator Nf is continuous and bounded, in the sense that maps bounded sets in bounded sets
DEFINITION 2. Let (X, ,m) be a measure space,
,m) be a measure space, 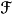 (X,
(X, ) a topological vector space of
) a topological vector space of  -valued functions defined on X and (fn)n ³ 1Ì
-valued functions defined on X and (fn)n ³ 1Ì 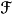 (X,
(X, ) . We said fn ® (f, g) a.e.w.(almost everywhere and weakly) in
) . We said fn ® (f, g) a.e.w.(almost everywhere and weakly) in 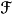 (X,
(X, ) if fn ® f a.e. in X and fn
) if fn ® f a.e. in X and fn
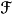 (X,
(X, ). If f = g we just say fn ® f a.e.w. in
). If f = g we just say fn ® f a.e.w. in 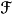 (X,
(X, ).
).
The next Lemma gives a kind of uniqueness of the limit in the above convergence in Lp(X,m, ) spaces.
) spaces.
LEMMA 1 (Moreira 2001, Teixeira 2001). Let (X, ,m) be a
,m) be a  -finite measure space and (un)n ³ 1Ì Lp(X,m,
-finite measure space and (un)n ³ 1Ì Lp(X,m, ), 1 £ p < +
), 1 £ p < + 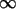 . Suppose that un ® (u, v) a.e.w. in Lp(X,m,
. Suppose that un ® (u, v) a.e.w. in Lp(X,m, ). Then u = v, and therefore un ® u a.e.w. in Lp(X,m,
). Then u = v, and therefore un ® u a.e.w. in Lp(X,m, ).
).
PROOF. There exists a sequence {Xj}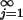 of measurable subsets of X such that:
of measurable subsets of X such that:
Let j ³ 1 be fixed. Given e1 = 1, by Egorov's theorem, there is a subset A1 of Xj,m(A1) < 1 such that un® u in L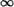 (Xj \ A1,
(Xj \ A1, ), in particular,
), in particular,
Thus we have u = v a.e. in Xj \ A1. Taking now e2 =  and applying Egorov's theorem again, we obtain a subset A2 of A1, m(A2) <
and applying Egorov's theorem again, we obtain a subset A2 of A1, m(A2) <  such that un ® u in L
such that un ® u in L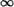 (A1 \ A2,
(A1 \ A2, ) hence un ® u in Lp(Xj \ A2,
) hence un ® u in Lp(Xj \ A2, ) and therefore, we have u = v a.e. in Xj \ A2. Carry on this process we get a decreasing sequence {An}
) and therefore, we have u = v a.e. in Xj \ A2. Carry on this process we get a decreasing sequence {An} , m(An) <
, m(An) <  and u = v a.e. in Xj \ An. Set AXj =
and u = v a.e. in Xj \ An. Set AXj =  An. This way m(AXj) = 0 and u = v a.e. in Xj \ AXj. To finish, we define
An. This way m(AXj) = 0 and u = v a.e. in Xj \ AXj. To finish, we define
thus
This concludes the Lemma.
EXAMPLE 1 (Teixeira 2001).Let 1 < p < + 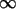 , m Î
, m Î  and let W be a domain in
and let W be a domain in  N. Every bounded sequence in Wm, p(W) contains a subsequence that converges a.e.w. to some function in Wm, p(W). Indeed, suppose (un)n ³ 1Ì Wm, p(W), || un||Wm, p(W)£ C. Since Wm, p(W) is reflexive, we can suppose that un
N. Every bounded sequence in Wm, p(W) contains a subsequence that converges a.e.w. to some function in Wm, p(W). Indeed, suppose (un)n ³ 1Ì Wm, p(W), || un||Wm, p(W)£ C. Since Wm, p(W) is reflexive, we can suppose that un
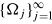 be a nested sequence of relatively compact open sets exhausting W. For all j ³ 1 let vj Î C
be a nested sequence of relatively compact open sets exhausting W. For all j ³ 1 let vj Î C (
( N;
N; ) be a function holding the following properties: 0 ³ vj ³ 1, vj
) be a function holding the following properties: 0 ³ vj ³ 1, vj 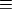 1 in
1 in 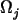 , vj
, vj 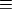 0 in
0 in  N \
N \ 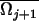 . By Sard's theorem, there exists a regular value 0 < a < 1 of vj. Let
. By Sard's theorem, there exists a regular value 0 < a < 1 of vj. Let 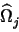 =
= 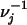 (a, +
(a, + 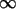 ). So {
). So {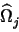 }
}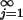 is a nested sequence of C
is a nested sequence of C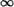 relatively compact open sets of W. Since the embedding Wm, p(
relatively compact open sets of W. Since the embedding Wm, p(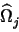 )
) 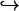 Lp(
Lp(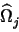 ) is compact, un® u in Lp(
) is compact, un® u in Lp(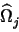 ); therefore, for each j ³ 1, (un)n ³ 1 has a subsequence converging a.e. to u in
); therefore, for each j ³ 1, (un)n ³ 1 has a subsequence converging a.e. to u in 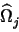 . Using the Cantor Diagonal Argument, we build a subsequence of (un)n ³ 1 that converges a.e. in W to u.
. Using the Cantor Diagonal Argument, we build a subsequence of (un)n ³ 1 that converges a.e. in W to u.
We are interested in the following problem: When does the Nemytskii operator map a.e.w. convergent sequences into a.e.w. convergent sequences? This question is a way of asking about the weak sequential continuity of the Nemytskii operator. More precisely, our problem is
Of course, a.e. convergent sequences are mapped into a.e. convergent sequences by a Nemytskii operator. Actually, what we want to know is when this class of operator maps a.e.w. convergent sequences into weakly convergent sequences.
It is reasonable to suspect that the problem ap, 1, 1 < p < + 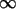 , cannot be affirmatively answered because if it were solvable, we would automatically get, without domain dependence, that the embedding W1, p(W)
, cannot be affirmatively answered because if it were solvable, we would automatically get, without domain dependence, that the embedding W1, p(W) 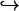 Lp(W) would be compact. However, there exist many domains where we have lack of compactness of such an embedding. The next example shows this directly.
Lp(W) would be compact. However, there exist many domains where we have lack of compactness of such an embedding. The next example shows this directly.
EXAMPLE 2.Let 1 < p < + 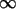 and W be a domain in
and W be a domain in  N. Then answer of the problem ap, 1 is negative. Indeed, without lost generality we may assume 0 Î W. Set f : W x
N. Then answer of the problem ap, 1 is negative. Indeed, without lost generality we may assume 0 Î W. Set f : W x  ®
®  , f (x, t) = |t|p . v0, where v0Î
, f (x, t) = |t|p . v0, where v0Î  \ {0}. The Nemytskii operator Nf applies Lp(W) into L1(W,
\ {0}. The Nemytskii operator Nf applies Lp(W) into L1(W, ). Set (un)n³1Ì Lp(W), un = |Bn|-1/p
). Set (un)n³1Ì Lp(W), un = |Bn|-1/p , where Bn = {x Î
, where Bn = {x Î  N;|x| < 1/n}. Since un ® 0 a.e. in W, ||un||p = 1 and Lp(W) is reflexive, we may assume un ® 0 a.e.w. It is easy to check that Nf(un)
N;|x| < 1/n}. Since un ® 0 a.e. in W, ||un||p = 1 and Lp(W) is reflexive, we may assume un ® 0 a.e.w. It is easy to check that Nf(un)  0 in L1 (W,
0 in L1 (W, ). In fact, from Hahn-Banach theorem, there exists a y Î
). In fact, from Hahn-Banach theorem, there exists a y Î  * such that y(v0) = 1. Define
* such that y(v0) = 1. Define  Î [L1(W,
Î [L1(W, )]*, setting
)]*, setting
we obtain
But if we have the presence of the reflexivity, the situation changes and we get the following very useful result. The next theorem is an improvement of the result found in (Moreira 2001, Teixeira 2001).
THEOREM 2 (Moreira 2001, Teixeira 2001). Let 1 ³ p, q < + 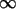 with q
with q  1 and W be a domain in
1 and W be a domain in  N. If
N. If  is reflexive, then answer of the problem ap,q is affirmative.
is reflexive, then answer of the problem ap,q is affirmative.
PROOF. By theorem 1, the Nemytskii operator Nf : Lp(W, ) ® Lq(W,
) ® Lq(W, ) is a bounded map. Suppose um® u a.e.w. in Lp(W,
) is a bounded map. Suppose um® u a.e.w. in Lp(W, ). Since (um) is bounded in Lp(W,
). Since (um) is bounded in Lp(W, ), (Nf(um)) is bounded in Lq(W,
), (Nf(um)) is bounded in Lq(W, ). By reflexivity, we can extract a subsequence Nf(umk)
). By reflexivity, we can extract a subsequence Nf(umk)  v Î Lq(W,
v Î Lq(W, ). Clearly, Nf(umk) ® Nf(u) a.e. in W. Therefore, by Lemma 1, Nf(umk) ® Nf(u) a.e.w. in Lq(W,
). Clearly, Nf(umk) ® Nf(u) a.e. in W. Therefore, by Lemma 1, Nf(umk) ® Nf(u) a.e.w. in Lq(W, ). So far, we have proven that if um® u a.e.w. in Lp(W,
). So far, we have proven that if um® u a.e.w. in Lp(W, ) there exists a subsequence (umk) of (um) such that Nf(umk) ® Nf(u) a.e.w. in Lq(W,
) there exists a subsequence (umk) of (um) such that Nf(umk) ® Nf(u) a.e.w. in Lq(W, ). We claim that
). We claim that
In fact, as we have already observed, we only need to show that Nf(um)  Nf(u) in Lq(W,
Nf(u) in Lq(W, ). Suppose, by a contradiction, this is not the case. Thus there is a weak neighborhood Nw(Nf(u)) of Nf(u) and a subsequence (umj), Nf(umj)
). Suppose, by a contradiction, this is not the case. Thus there is a weak neighborhood Nw(Nf(u)) of Nf(u) and a subsequence (umj), Nf(umj)  Nw(Nf(u))
Nw(Nf(u))  j ³ 1. Naturally, umj® u a.e.w., then applying the first step of this proof, we obtain a subsubsequence (umjk) of (umj), Nf(umjk) ® Nf(u) a.e.w. in Lq(W,
j ³ 1. Naturally, umj® u a.e.w., then applying the first step of this proof, we obtain a subsubsequence (umjk) of (umj), Nf(umjk) ® Nf(u) a.e.w. in Lq(W, ), a contradiction, since Nf(umjk)
), a contradiction, since Nf(umjk)  Nf(u) because Nf(umjk)
Nf(u) because Nf(umjk)  Nw(Nf(u))
Nw(Nf(u))  k ³ 1.
k ³ 1. 
COROLLARY 1. If W is a domain in  N and um ® u a.e.w. in Lp(W), 1 < p < +
N and um ® u a.e.w. in Lp(W), 1 < p < + 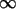 . Then um+ ® u+, um- ® u-, | um| ® | u| all these convergences being in the a.e.w. sense in Lp(W).
. Then um+ ® u+, um- ® u-, | um| ® | u| all these convergences being in the a.e.w. sense in Lp(W).
COROLLARY 2. If W is a domain in  N, m Î
N, m Î  and Nf maps the Lp(W) into Lq(W), 1 < p, q < +
and Nf maps the Lp(W) into Lq(W), 1 < p, q < + 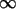 , the operator Nf : Wm, p(W) ® Lq(W) is weakly sequentially continuous.
, the operator Nf : Wm, p(W) ® Lq(W) is weakly sequentially continuous.
COROLLARY 3. Let W be a bounded domain in  N. If un ® u a.e.w in Lp(W) with p > 1, then for all 1 £ q < p, un ® u in Lq(W). Consequently, W1, p(W) is compactly embedded in Lq(W), for all 1 £ q < p, without any regularity condition on
N. If un ® u a.e.w in Lp(W) with p > 1, then for all 1 £ q < p, un ® u in Lq(W). Consequently, W1, p(W) is compactly embedded in Lq(W), for all 1 £ q < p, without any regularity condition on  W.
W.
PROOF. Let us fix 0 < 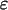 < p - 1. Since Lp(W)
< p - 1. Since Lp(W) 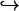 Lp - e(W) we have that un
Lp - e(W) we have that un
 ®
®  given by f (t) = | t|p - e. Nf maps Lp(W) into Lp/p - e(W). From theorem 2, f (un)
given by f (t) = | t|p - e. Nf maps Lp(W) into Lp/p - e(W). From theorem 2, f (un)  f (u) in Lp/p - e(W). In particular
f (u) in Lp/p - e(W). In particular
So we have that un
u in Lp - e(W) and ||un||Lp - e(W)® ||u||Lp - e(W). Once Lp - e is uniformly convex, it implies that un® u in Lp - e(W). Moreover, using again the fact that Lr(W) is continuosly embedded into Ls(W) for r ³ s, we are able to conclude that un® u in Lq(W) for all q Î [1, p -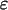 ]. Letting
]. Letting 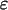 ® 0, we get the result. The second part of the corollary follows from the first part added with example 1.
® 0, we get the result. The second part of the corollary follows from the first part added with example 1. 
It is worthwhile to stand out that the corollary 3 is sharp. In general, W1, p(W)  Lq(W) for q ³ p. This fact can be found in (Adams 1975).
Lq(W) for q ³ p. This fact can be found in (Adams 1975).
We remark that weak convergence in Lp(W) is not suffice to conclude the thesis of theorem 2. In fact, let W = (0, ), un(x) = sin(nx)
), un(x) = sin(nx)  0 in L2(0,
0 in L2(0, ), and let f : (0,
), and let f : (0, ) x
) x  ®
®  be given by: f (x, s) = s+. Now we note that:
be given by: f (x, s) = s+. Now we note that:  1, f (x, un(x))
1, f (x, un(x))  =
= 
 (sin(y))+dy, so:
(sin(y))+dy, so:
It remains to study the problem a1, 1. In order to start analyzing this problem, we shall state the general version of Dunford-Pettis theorem, obtained by Talagrand in 1984.
THEOREM 3 (Talagrand 1984). Let W be a bounded domain in  N and
N and  be a weak complete Banach space. Let
be a weak complete Banach space. Let 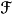 Ì L1(W,
Ì L1(W, ) be a bounded convex subset. Then
) be a bounded convex subset. Then 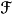 is weakly relatively compact, if and only if it satisfies the following two conditions:
is weakly relatively compact, if and only if it satisfies the following two conditions:
-
{||
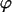 ||
|| W ®
W ® 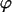 Î
Î 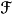 } Ì
} Ì L
1(W)
is weakly precompact;
-
for each sequence (
 )
) in
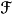 ,
,the set of
x Î W
such that there is a
k for which the sequence (
 )
)n³k is equivalent to the vector basis of l1 has measure zero.
Let us point out that from Dunford-Pettis's theorem, the condition 1 above is equivalent to the equiintegrability of {||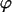 ||
||
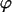 Î
Î 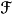 }. The next theorem is the counterpart of example 2.
}. The next theorem is the counterpart of example 2.
THEOREM 4. Let W be a bounded domain in  N. If
N. If  is reflexive, then the answer of the problem a1, 1 is affirmative.
is reflexive, then the answer of the problem a1, 1 is affirmative.
PROOF. Let um® u a.e.w. in L1(W, ). Defining u0 = u, by the Eberlein-Smulian theorem (Brito 1998) the set K = {um;m ³ 0} is weakly compact, since it is weakly sequentially compact. Let us denote X =
). Defining u0 = u, by the Eberlein-Smulian theorem (Brito 1998) the set K = {um;m ³ 0} is weakly compact, since it is weakly sequentially compact. Let us denote X =  (K). From Krein's theorem (Brito 1998) we get that X is weakly compact, thus, in particular theorem 3 says that X is equiintegrable. The equiintegrability means that if
(K). From Krein's theorem (Brito 1998) we get that X is weakly compact, thus, in particular theorem 3 says that X is equiintegrable. The equiintegrability means that if 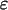 > 0 is given; there exists d1 > 0 such that
> 0 is given; there exists d1 > 0 such that
By theorem 1, the Caratheodory function f satisfies the following growth condition:
where a > 0 and b(x) Î L (W). Let Y =
(W). Let Y =  (Nf(K)). If v Î co(Nf(K)), there exist functions u1,..., unÎ K and positive numbers
(Nf(K)). If v Î co(Nf(K)), there exist functions u1,..., unÎ K and positive numbers  ,...,
,..., fufilling
fufilling  lj = 1 such that v =
lj = 1 such that v =  lj . uj. In this way
lj . uj. In this way
Since
b(x)dx = 0 there exists l2 > 0, such that | A| < l2b(x)dx <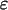 ; therefore
; therefore
Thus, we obtain
We have just verified the condition 1 of theorem 3, for Y. However, by hypothesis, the condition 2 we get for free, since  being reflexive, it does not contain a copy of l1; therefore by theorem 3, the set Y is weakly compact, and thus so is Nf(K) = {Nf(um) : m ³ 0}. Using again the Eberlein-Smulian theorem, we can extract a subsequence umk, such that, Nf(umk)
being reflexive, it does not contain a copy of l1; therefore by theorem 3, the set Y is weakly compact, and thus so is Nf(K) = {Nf(um) : m ³ 0}. Using again the Eberlein-Smulian theorem, we can extract a subsequence umk, such that, Nf(umk)  v in L1(W,
v in L1(W, ). Since Nf(umk) ® Nf(u) a.e. in W, by the Lemma 1, v = Nf(u) and then Nf(umk)
). Since Nf(umk) ® Nf(u) a.e. in W, by the Lemma 1, v = Nf(u) and then Nf(umk)  Nf(u) in L1(W,
Nf(u) in L1(W, ). So far, we have proven that if um® u a.e.w in L1(W,
). So far, we have proven that if um® u a.e.w in L1(W, ) there exists a subsequence (umk) of (um) such that Nf(umk)
) there exists a subsequence (umk) of (um) such that Nf(umk)  Nf(u) in L1(W,
Nf(u) in L1(W, ). We can repeat the same argument used in the proof of theorem 2 and obtain Nf(um)
). We can repeat the same argument used in the proof of theorem 2 and obtain Nf(um)  Nf(u) in L1(W,
Nf(u) in L1(W, ).
). 
It is interesting to notice that follows immediately from theorem 4 if un® u a.e.w. in L1(W, ) then un® u in the L1(W,
) then un® u in the L1(W, )-norm topology.
)-norm topology.
3. AN APPLICATION
We shall provide an application of theorem 2 by solving a general nonlinear equation on the Sobolev spaces W1, p(W). The problem studied here is a very natural question for the Nemytskii operator on Sobolev spaces. Indeed, the problem we shall work on is:
Let 1 < p < 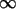 , let W be a bounded domain in
, let W be a bounded domain in  N and let f : W x
N and let f : W x  ®
®  be a Lipschitzian function (In this paper, the Lipschtz norm is defined using the sum norm in euclidean space, i.e, |(x, s)|
be a Lipschitzian function (In this paper, the Lipschtz norm is defined using the sum norm in euclidean space, i.e, |(x, s)| N x
N x  = |x|
= |x| N + |s|
N + |s| ), such that
), such that
for some a > 0 and some b Î Lp+(W). Given a y Î W1, p(W), and given a l Î  we are interested in finding u Î W1, p(W) such that
we are interested in finding u Î W1, p(W) such that

(P)
DEFINITION 3. Let f:W x  ®
®  be a Caratheodory function such that the Nemytskii operator Nf maps Lp(W,
be a Caratheodory function such that the Nemytskii operator Nf maps Lp(W, ) into Lq(W,
) into Lq(W, ). We define
). We define  (f)= inf{a > 0
(f)= inf{a > 0
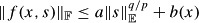 }.
}.
Let us remark that the infimum on this definition actually is a minimum. Indeed, let an be a minimizing sequence for  (f ), and let bnÎ Lp(W) be functions such that the following inequality || f (x, s)||
(f ), and let bnÎ Lp(W) be functions such that the following inequality || f (x, s)|| £ an|| s||
£ an|| s|| + bn(x) holds for all n Î
+ bn(x) holds for all n Î  , s Î
, s Î  and a.e. x Î W. Taking the lim infn, we find || f (x, s)||
and a.e. x Î W. Taking the lim infn, we find || f (x, s)|| £
£  (f )|| s||
(f )|| s|| +
+  (x) where
(x) where  (x) = lim infnbn(x).
(x) = lim infnbn(x).
THEOREM 5. The problem above is answered affirmatively for all l > ||f||Lip. Moreover the solution is unique and the operator (Nf - lId)-1 : W1, p(W) ® W1, p(W) is sequentially weakly continuous.
PROOF. Initially, we remark that  (f) ³ ||f||Lip. In fact, since
(f) ³ ||f||Lip. In fact, since
we get
Let us start by estimating || f (x, (x))||W1, p(W):
(x))||W1, p(W):
This estimative above tell us Nf : W1, p(W) ® W1, p(W) is a bounded operator. Therefore, from the same argument found on the final step of theorem 2, we conclude Nf is sequentially weak continuous.
Let us define  : W1, p(W) ® W1, p(W) by
: W1, p(W) ® W1, p(W) by
We observe that once Nf is sequentially weak continuous, so is  . Moreover, to solve (P) is equivalent to find a fixed point of
. Moreover, to solve (P) is equivalent to find a fixed point of  .
.
Let us fix M >  . For such a M we see that if ||
. For such a M we see that if || ||W1, p(W) < M
||W1, p(W) < M
In other words,  maps the ball of radius M in W1, p(W) into itself, i.e.,
maps the ball of radius M in W1, p(W) into itself, i.e.,  : BW1, p[M] ® BW1, p[M]. Let X denote BW1, p[M] endowed with the weak topology. So X is a compact convex subset of a locally convex space. In additional, as we pointed out before,
: BW1, p[M] ® BW1, p[M]. Let X denote BW1, p[M] endowed with the weak topology. So X is a compact convex subset of a locally convex space. In additional, as we pointed out before,  : X ® X is a continuous map.
: X ® X is a continuous map.
Finally, we can use the Leray-Schauder-Tychonoff fixed point theorem (Dunford and Schwartz 1964), and conclude that  has a fixed point which is precisely a solution of (P). Now, let us suppose that there exist u1, u2Î W1, p(W) such that
has a fixed point which is precisely a solution of (P). Now, let us suppose that there exist u1, u2Î W1, p(W) such that
Subtracting these equations we find f (x, u1(x)) - f (x, u2(x)) = l(u1(x) - u2(x)). Therefore
If u1(x) - u2(x)  0, we would be able to cancel this expression at the inequality above and we would find, l ³ ||f||Lip. Hence the solution of (P) is unique.
0, we would be able to cancel this expression at the inequality above and we would find, l ³ ||f||Lip. Hence the solution of (P) is unique.
In order to study the weak continuity of  = (Nf - lId )-1 : W1, p(W) ® W1, p(W), we shall use the same idea found in the final step of theorem 2. Since all weakly convergent sequence in W1, p(W) has a subsequence converging a.e., to prove
= (Nf - lId )-1 : W1, p(W) ® W1, p(W), we shall use the same idea found in the final step of theorem 2. Since all weakly convergent sequence in W1, p(W) has a subsequence converging a.e., to prove  is sequentially weakly continuous, it is enough to show that
is sequentially weakly continuous, it is enough to show that  is bounded. Suppose
is bounded. Suppose  (y) = u,
(y) = u,
Then
Writing in a better way,
This estimative shows the operator  is bounded.
is bounded. 
The main information given by theorem 5 is the regularization of the solution. We observe that if we see the map  , defined on the proof of this theorem, as
, defined on the proof of this theorem, as  : Lp(W) ® Lp(W), it is easy to verify that it is a contraction; therefore from the Banach Fixed Point theorem, the problem (P) has, for all y Î Lp(W), always a unique solution u Î Lp(W), provided l > ||f||Lip. The main point of theorem 5 is that u Î W1, p(W) whenever y Î W1, p(W).
: Lp(W) ® Lp(W), it is easy to verify that it is a contraction; therefore from the Banach Fixed Point theorem, the problem (P) has, for all y Î Lp(W), always a unique solution u Î Lp(W), provided l > ||f||Lip. The main point of theorem 5 is that u Î W1, p(W) whenever y Î W1, p(W).
Let us point out that in a special case when f(x, s) = A|s| + b(x), b Î Lip(W), we can improve theorem 5, saying that (P) is solvable for all l >  (f ). However we cannot expect to solve (P) if l ³
(f ). However we cannot expect to solve (P) if l ³  (f) as the following simple situation show us: Let f : W x
(f) as the following simple situation show us: Let f : W x  ®
®  be defined by f(x, s) = |s|. In this case,
be defined by f(x, s) = |s|. In this case,  (f)= ||f||Lip = 1. Suppose l ³ 1, then f(x, u(x)) - lu(x) = |u(x)| - lu(x) ³ 0. Hence if y Î W1, p(W), with y(x) < 0, it is impossible to solve the equation (P).
(f)= ||f||Lip = 1. Suppose l ³ 1, then f(x, u(x)) - lu(x) = |u(x)| - lu(x) ³ 0. Hence if y Î W1, p(W), with y(x) < 0, it is impossible to solve the equation (P).
From these comments, a interesting question arises in this problem: What can we say when  (f) < l ³ ||f||Lip?
(f) < l ³ ||f||Lip?
4. ACKNOWLEDGMENTS
The second author would like to thank professor Haskell Rosenthal (University of Texas - Austin) for bringing the Talagrand's paper to his attention. The authors are grateful for the financial support by CAPES and CNPq, respectively, which are brazilian government agencies that finance the development of science and technology.
Manuscript received on May 31, 2002;
accepted for publication on October 25, 2002;
presented by JOÃO LUCAS BARBOSA
- ADAMS RA. 1975. Sobolev Spaces. Academic Press, New York, p. 122-161.
- BRITO W. 1998. Compacidad debil en espacios de Banach y aplicaciones de un teorema de R.C. James. Universidad de los Andes, Faculdad de Ciencias, Notas de Matematica, Serie Pre-Print, p. 2-42.
- DUNFORD N AND SCHWARTZ J. 1964. Linear operator, 2nd ed., Interscience Publishers, New York, p. 456.
- LUCCHETTI R AND PATRONE, F. 1980. On Nemytskii's operator and its application to the lower semicontinuity of integral functionals, Indiana Univ Math J 29(5), p. 703-735.
- MOREIRA D. 2001. Soluçőes positivas de equaçőes elípticas năo lineares na presença de expoentes críticos, Universidade Federal do Ceará, Master degree manuscript, p. 12-15.
- TALAGRAND M. 1984. Weak Cauchy sequence in L1(E). Amer J Math 106: 703-724.
- TEIXEIRA E. 2001. O princípio de concentraçăo e compacidade e aplicaçőes, Universidade Federal do Ceará, Master degree manuscript, p. 36-43.
Publication Dates
-
Publication in this collection
17 Apr 2003 -
Date of issue
Mar 2003
History
-
Accepted
25 Oct 2002 -
Received
31 May 2002


































