Abstracts
In this paper we prove a tangency principle (see Fontenele and Silva 2001) related with the length of the second fundamental form, for hypersurfaces of an arbitrary ambient space. As geometric applications, we make radius estimates of the balls that lie in some component of the complementary of a complete hypersurface into Euclidean space, generalizing and improving analogous radius estimates for embedded compact hypersurfaces obtained by Blaschke, Koutroufiotis and the authors. The basic tool established here is that some operator is elliptic at points where the second fundamental form is positive definite.
hypersurfaces; tangency principle; second fundamental form; balls; radius estimates
Neste trabalho nós provamos um princÍpio de tangência (veja Fontenele and Silva 2001) para hipersuperfícies de um espaço ambiente arbitrário e relacionado com o comprimento da segunda forma fundamental. Como aplicações geométricas, nós fazemos estimativas dos raios das bolas contidas em uma determinada componente conexa do complemento de uma hipersuperfÍcie completa do espaço Euclidiano, generalizando e melhorando estimativas de raios análogas obtidas por Blaschke, Koutroufiotis e os autores. O fato básico estabelecido aqui é que um determinado operador é elÍptico nos pontos onde a segunda forma fundamental é positiva definida.
hipersuperfícies; princípio de tangência; segunda forma fundamental; bolas; estimativas de raios
MATHEMATICAL SCIENCES
The length of the second fundamental form, a tangency principle and applications
Francisco X. FonteneleI; Sérgio L. SilvaII
IUniversidade Federal Fluminense, Instituto de Matemática, Departamento de Geometria 24020-140 Niterói, RJ, Brasil
IIUniversidade Estadual do Rio de Janeiro-UERJ, Departamento de Estruturas Matemáticas-IME 20550-013 RJ, Brasil
Correspondence Correspondence to Francisco X. Fontenele E-mail: fontenele@mat.uff.br
ABSTRACT
In this paper we prove a tangency principle (see Fontenele and Silva 2001) related with the length of the second fundamental form, for hypersurfaces of an arbitrary ambient space. As geometric applications, we make radius estimates of the balls that lie in some component of the complementary of a complete hypersurface into Euclidean space, generalizing and improving analogous radius estimates for embedded compact hypersurfaces obtained by Blaschke, Koutroufiotis and the authors. The basic tool established here is that some operator is elliptic at points where the second fundamental form is positive definite.
Key words: hypersurfaces, tangency principle, second fundamental form, balls, radius estimates.
RESUMO
Neste trabalho nós provamos um princÍpio de tangência (veja Fontenele and Silva 2001) para hipersuperfícies de um espaço ambiente arbitrário e relacionado com o comprimento da segunda forma fundamental. Como aplicações geométricas, nós fazemos estimativas dos raios das bolas contidas em uma determinada componente conexa do complemento de uma hipersuperfÍcie completa do espaço Euclidiano, generalizando e melhorando estimativas de raios análogas obtidas por Blaschke, Koutroufiotis e os autores. O fato básico estabelecido aqui é que um determinado operador é elÍptico nos pontos onde a segunda forma fundamental é positiva definida.
Palavras-chave: hipersuperfícies, princípio de tangência, segunda forma fundamental, bolas, estimativas de raios.
1 INTRODUCTION
In (Fontenele and Silva 2001), the same authors proved that if an n-dimensional embedded compact hypersurface Mn into (n+1)-dimensional Euclidean space satisfies |Hk| >  , for some k-mean curvature Hk, 1 < k < n, and some positive constant l, then the greatest ball that fits inside Mn has radius less than l unless Mn is a sphere of radius l, generalizing results of (Blaschke 1956) and (Koutroufiotis 1973) for surfaces. Our basic tool for the proof of the above result was a tangency principle stated in (Fontenele and Silva 2001) as Theorem 1.1. This tangency principle turned out to be very useful to obtain other geometric applications. In this work we obtain a tangency principle (see Fontenele and Silva 2001) related with the length of the second fundamental form and improve (see Remark 3.1) the radius estimate for the greatest ball that fits inside a suitable component of the complementary of an n-dimensional complete hypersurface into (n+1)-dimensional Euclidean space. In order to state our results we need the following.
, for some k-mean curvature Hk, 1 < k < n, and some positive constant l, then the greatest ball that fits inside Mn has radius less than l unless Mn is a sphere of radius l, generalizing results of (Blaschke 1956) and (Koutroufiotis 1973) for surfaces. Our basic tool for the proof of the above result was a tangency principle stated in (Fontenele and Silva 2001) as Theorem 1.1. This tangency principle turned out to be very useful to obtain other geometric applications. In this work we obtain a tangency principle (see Fontenele and Silva 2001) related with the length of the second fundamental form and improve (see Remark 3.1) the radius estimate for the greatest ball that fits inside a suitable component of the complementary of an n-dimensional complete hypersurface into (n+1)-dimensional Euclidean space. In order to state our results we need the following.
As in (Fontenele and Silva 2001), given a hypersurface Mn of a complete Riemannian manifold Nn+1 with metric á , ñ and exponential mapping exp: TN ® N, we parametrize a neighborhood of Mn containing p and contained in a normal ball of Nn+1 putting
where x varies in a neighborhood W of zero in TpM (the tangent space to Mn at p), ho is a fixed unitary vector normal to Mn at p and m is an unique real function defined in W with m(0) = 0. Let h: W ®  M be a local orientation of Mn with h(0) = ho . Denote by Ah(x) the second fundamental form of Mn in the direction h(x) and by s the vector valued second fundamental form of Mn. The length of the second fundamental form at x is given by
M be a local orientation of Mn with h(0) = ho . Denote by Ah(x) the second fundamental form of Mn in the direction h(x) and by s the vector valued second fundamental form of Mn. The length of the second fundamental form at x is given by
If l1 (x) < l2 (x) < ¼ <l n (x) are the principal curvatures of Mn at x Î W, we have that
Given hypersurfaces  and
and  of Nn+1 with TpM1 = TpM2 (tangent at p), parametrize
of Nn+1 with TpM1 = TpM2 (tangent at p), parametrize  and
and  as in (1) obtaining correspondent functions m1 and m2. As in (Fontenele and Silva 2001), we say that
as in (1) obtaining correspondent functions m1 and m2. As in (Fontenele and Silva 2001), we say that  remains above
remains above  in a neighborhood of p with respect to ho if m1 (x) > m 2 (x) in a neighborhood of zero.
in a neighborhood of p with respect to ho if m1 (x) > m 2 (x) in a neighborhood of zero.
Following the ideas in (Fontenele and Silva 2001), we obtain the following tangency principle:
THEOREM 1.1. Consider hypersurfaces
and of Nn+1 tangent at p and ho a unitary vector normal to at p. Denote by |s1|2(x) and |s2|2(x) the length of the second fundamental form of respectively and at x Î W. Assume that remains above in a neighborhood of p with respect to ho , |s1|2(x)< |s2|2(x) in a neighborhood of zero and that the principal curvatures of M2 at zero are all positive. Under these conditions, and must coincide in a neighborhood of p.For hypersurfaces with boundaries and as a consequence of proof of Theorem 1.1, we obtain the following tangency principle:
THEOREM 1.2. Let
and be hypersurfaces of Nn+1 with boundaries ¶M1 and ¶M2 respectively. Suppose that and as well as ¶M1 and ¶M2 are tangent at p Î ¶M1ǶM2 and let ho be normal to at p. Denote by |s1|2(x) and |s2|2(x) the length of the second fundamental form of respectively and at x Î W. Assume that remains above in a neighborhood of p with respect to ho , |s1|2(x)< |s2|2(x) in a neighborhood of zero and that the principal curvatures of M2 at zero are all positive. Under these conditions, and must coincide in a neighborhood of p. When the ambient is the (n+1)-dimensional Euclidean space and the hypersurfaces  and
and  have the same constant length of the second fundamental form, Theorems 1.1 and 1.2 are the analogous of the well known maximum principles for hypersurfaces with the same constant k-mean curvature in the Euclidean space.
have the same constant length of the second fundamental form, Theorems 1.1 and 1.2 are the analogous of the well known maximum principles for hypersurfaces with the same constant k-mean curvature in the Euclidean space.
For enunciate our geometric applications let us fix some notation. Given an oriented hypersurface Mn of the (n+1) - dimensional Euclidean space 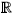 n+1, the k-mean curvature Hk(p) of Mn at p is given by
n+1, the k-mean curvature Hk(p) of Mn at p is given by
where l1< l2< ¼ < l n are the principal curvatures of Mn at p. In particular, H1(p) is denoted by h(p) and called the mean curvature of M at p and H2(p) is denoted by R(p) and called the scalar curvature of M at p.
The Ricci curvature of Mn at a point p in the direction of an unitary vector u is given by
where w1 = u, w2,... ,wn is an orthonormal basis of TpM and K(u,wi) is the sectional curvature of the plane generated by u and wi.
DEFINITION 1.3. If U is an open subset of the Euclidean space 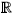 n+1, we define
n+1, we define
ru := sup{ r >0, such that  contains a closed ball in
contains a closed ball in 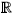 n+1 of radius r},
n+1 of radius r},
where  denotes the closure of U in
denotes the closure of U in 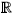 n+1.
n+1.
CONDITION I. Mn is a complete connected euclidean hypersurface that splits 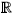 n+1 into two disjoint regions of which Mn is the common boundary.
n+1 into two disjoint regions of which Mn is the common boundary.
THEOREM 1.4. Suppose that Mn satisfies Condition I. Assume further that |s|2 >  and |h| >
and |h| >  over Mn, where l is a positive constant. Under these conditions, if we denote by U the component of
over Mn, where l is a positive constant. Under these conditions, if we denote by U the component of
COROLLARY 1.5. Suppose that Mn satisfies Condition I. Assume further that |s|2>
and R > over Mn, where l is a positive constant. Then, the mean curvature function h is positive for some suitable orientation of Mn and, denoting by U the component of n+1\M that contains the normals for which h is positive, we have rU< l. Moreover, if in the closure of U there exists a closed ball of radius l, then Mn must be a sphere in n+1 of radius l.COROLLARY 1.6. Suppose that Mn satisfies Condition I and that |Hk| >
on Mn for some k, 1 < k < n, and some positive constant l > 0. For k > 2, assume further that there exists at least one point in Mn where the second fundamental form is definite. Then there exists a component U of n+1\M such that rU< l. Moreover, if UÈM contains a closed ball of radius l, then Mn coincides with a sphere in n+1 of radius l.THEOREM 1.7. Suppose that Mn satisfies Condition I and is oriented. Assume that h > 0 and that |s|2>
over Mn, where l is a positive constant. Assume further that n > 3 and RicM> . Then, if we denote by U the component of n+1\M that contains the normals, we have rU<l. Moreover, if UÈMn contains a closed ball of radius l then either n must be even or Mn coincides with a sphere in n+1 of radius l.COROLLARY 1.8. Suppose that Mn satisfies Condition I and that |s|2>
over Mn, for some positive constant l. Consider also that RicM > 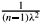 . Then, the mean curvature function h is positive for some suitable orientation of Mn and denoting by U the component of
. Then, the mean curvature function h is positive for some suitable orientation of Mn and denoting by U the component of 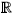 n+1\M that contains the normals for which h is positive, we have rU<l. Furthermore, if in the closure of U there exists a closed ball of radius l, then Mn must be a sphere in n+1 of radius l.
n+1\M that contains the normals for which h is positive, we have rU<l. Furthermore, if in the closure of U there exists a closed ball of radius l, then Mn must be a sphere in n+1 of radius l.
In the following result, Mn is a connected and complete manifold isometrically immersed in 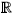 n+1.
n+1.
COROLLARY 1.9. Assume that KM> 0 and |s|2>
over Mn, for some positive constant l. If Mn is not compact, assume further that there exists at least one point in Mn where all sectional curvatures are positive. Then there exists a component U of n+1\M such that rU<l. Moreover, if UÈM contains a closed ball of radius l then Mn coincides with a sphere in n+1 of radius l.2 SKETCH OF PROOF OF THEOREM 1.1
Fix an orthonormal basis e1,e2,... ,en in TpM1 = TpM2 and introduce coordinates, for x in TpM1, setting x =  xi ei. As in , parametrize M1 and M2 in a neighborhood of p by respectively j1 and j2 , obtaining respectively functions m1 and m2. Let hl : W®
xi ei. As in , parametrize M1 and M2 in a neighborhood of p by respectively j1 and j2 , obtaining respectively functions m1 and m2. Let hl : W®  Ml, l = 1,2, be a local orientation of Ml with hl(0) = ho and denote by
Ml, l = 1,2, be a local orientation of Ml with hl(0) = ho and denote by  the second fundamental form of Ml in the direction hl(x). Denote by
the second fundamental form of Ml in the direction hl(x). Denote by  (x) the vector
(x) the vector  (x) and by Al(x) the matrix of
(x) and by Al(x) the matrix of  in the basis
in the basis  (x), 1 < i < n. In (Fontenele and Silva 2001), it is proved the existence of a matrix valued function à defined in
(x), 1 < i < n. In (Fontenele and Silva 2001), it is proved the existence of a matrix valued function à defined in  , where
, where  is a connected open set of
is a connected open set of 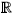 n+1 containing the origin, such that
n+1 containing the origin, such that
where ( (x),
(x), (x),ml(x),x), 1 < i < j < n, is a point of
(x),ml(x),x), 1 < i < j < n, is a point of 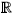 d, d =
d, d =  +2n+1. We write an arbitrary point of
+2n+1. We write an arbitrary point of 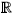 d as (rij,ri,z,x), 1 < i < j < n, and x = (x1,¼,xn). Define a function F:
d as (rij,ri,z,x), 1 < i < j < n, and x = (x1,¼,xn). Define a function F:  ®
® 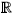 by
by
Now using the derivatives of Ã, with respect to the rkl's, given in (Fontenele and Silva 2001), we obtain that
where At(0) = Ã( (1-t)  (0)+t
(0)+t  (0) , 0 , 0 , 0 ). Using that
(0) , 0 , 0 , 0 ). Using that  remains above
remains above  in a neighborhood of p with respect to ho , |s1|2(x) < |s2|2(x) in a neighborhood of zero and that the principal curvatures of M2 at zero are all positive, one can prove that F is elliptic in ((1-t)
in a neighborhood of p with respect to ho , |s1|2(x) < |s2|2(x) in a neighborhood of zero and that the principal curvatures of M2 at zero are all positive, one can prove that F is elliptic in ((1-t)  (0)+t
(0)+t  (0) , 0 , 0 , 0 ) for t Î [0,1], and, restricting W if necessary, conclude that F is elliptic with respect to the functions (1-t)m2+ tm1, t Î [0,1] (see Fontenele and Silva 2001).
(0) , 0 , 0 , 0 ) for t Î [0,1], and, restricting W if necessary, conclude that F is elliptic with respect to the functions (1-t)m2+ tm1, t Î [0,1] (see Fontenele and Silva 2001).
Recalling that |sl|2(x) = trace [Al(x)]2, it follows from (2), (3) and our assumptions that
Now the conclusion of the theorem is obtained from the following maximum principle (Alexandrov 1962):
MAXIMUM PRINCIPLE. Let f, g: U ® 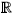 be C2-functions defined in an open set U of
be C2-functions defined in an open set U of 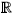 n and let F: G Ì
n and let F: G Ì 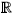 d®
d® 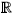 be a function of class C1 . Suppose that F is elliptic with respect to the functions (1-t)f+tg, t Î [0,1]. Assume also that
be a function of class C1 . Suppose that F is elliptic with respect to the functions (1-t)f+tg, t Î [0,1]. Assume also that
and that f < g on U. Then, f < g on U unless f and g coincide in a neighborhood of any point xo Î U such that f (xo ) = g(xo).
Now we will prove Theorem 1.7 for give an idea of how one can use Theorem 1.1 to obtain geometric applications.
3 PROOF OF THEOREM 1.7
PROOF OF THEOREM 1.7. Consider in
n+1 an arbitrary closed ball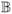 r[po], centered at po and radius r, contained in U È M. Move
r[po], centered at po and radius r, contained in U È M. Move 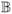 r[po] until its boundary
r[po] until its boundary 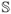 r [po] touches Mn the first time. Let p be a tangency point between Mn and
r [po] touches Mn the first time. Let p be a tangency point between Mn and 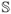 r [po]. Denote by l1< l2< ¼< l n the principal curvatures of Mn at p. It is well known that li <
r [po]. Denote by l1< l2< ¼< l n the principal curvatures of Mn at p. It is well known that li <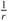 for all i. Since l1 +l2+¼+ln> 0 by assumption, we have
for all i. Since l1 +l2+¼+ln> 0 by assumption, we have
where  means that li has been omitted on the sum. Therefore, for a negative li, we deduce that
means that li has been omitted on the sum. Therefore, for a negative li, we deduce that
where ei stands for an unitary eigenvector with eigenvalue li. The above inequality, gives - < l i < 0 for a negative li. We consider two possibilities:
< l i < 0 for a negative li. We consider two possibilities:
P.1. There exists at p at least one negative li. Denoting by t the number of li's that are negative and using our assumption on the length of the second fundamental form, we get
Thus, l> r. In case r = l, we have that l1 = l2 = ¼ = lt = - and lt+1 = ¼ = ln =
and lt+1 = ¼ = ln =  . Since h > 0, we obtain that n > 2 t. On the other hand, we have
. Since h > 0, we obtain that n > 2 t. On the other hand, we have
which implies that n < 2t. Hence, n = 2 t and n is even. Notice also that Mn is minimal at p and the Ricci curvature at p is constant and equal to -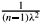 .
.
P.2. At p, all li's are nonnegative. In this case,
Thus l> r. If r = l, it follows easily that l1 = l2 = ¼ = ln =  . Using Theorem 1.1 and noting that
. Using Theorem 1.1 and noting that  is the constant value of the length of the second fundamental form of a sphere having radius r, we obtain that Mn and
is the constant value of the length of the second fundamental form of a sphere having radius r, we obtain that Mn and 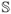 r [po] coincide in a neighborhood of p. By an argument of connectness, we conclude that Mn is equal to
r [po] coincide in a neighborhood of p. By an argument of connectness, we conclude that Mn is equal to 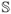 r [po].
r [po].
REMARK 3.1. We point out that Corollary 1.6 extends to complete hypersurfaces Theorem 1.3 in (Fontenele and Silva 2001) and that its hypothesis are stronger than those in Theorem 1.4. In fact, for k = 1, this follows from the well known inequality |s|2> n h2 and, for k > 1, this follows from Lemma 1 in (Montiel and Ros 1991). Furthermore, the estimate for rU in Theorem 1.4 improves the one given by Corollary 1.6. For if inf|h| =  > 0 and inf|s|2 =
> 0 and inf|s|2 =  with |h|>
with |h|>  , the upper bound given for rU in Theorem 1.4 is lo and the one given by Corollary 1.6 is Ho. That lo< Ho follows from the well known inequality |s|2> n h2. For example, in the cilinder C =
, the upper bound given for rU in Theorem 1.4 is lo and the one given by Corollary 1.6 is Ho. That lo< Ho follows from the well known inequality |s|2> n h2. For example, in the cilinder C = 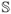 1 ×
1 × 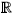 in
in 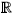 3, oriented by the normals pointing to the component U of
3, oriented by the normals pointing to the component U of 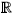 3 \C containing the origin,where
3 \C containing the origin,where 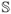 1 is the unitary circle, the mean curvature and length of the second fundamental form are given respectively by
1 is the unitary circle, the mean curvature and length of the second fundamental form are given respectively by  and 1. The estimate given by Theorem 1.4 is rU <
and 1. The estimate given by Theorem 1.4 is rU <  , while the estimate given by Corollary 1.6 is rU< 2.
, while the estimate given by Corollary 1.6 is rU< 2.
Manuscript received on September 5, 2003;
Accepted for publication on November 21, 2003;
Presented by Manfredo do Carmo
The first author dedicates this work to his parents José (in memoriam) and Herondina
- ALEXANDROV AD. 1962. Uniqueness theorems for surfaces in the large I-V, Amer Math Soc Transl, Ser. 2, 21: 341-416.
- BLASCHKE W. 1956. Kreis und Kugel. 2. Auflage, Berlin.
- FONTENELE F AND SILVA SL. 2001. A tangency principle and applications, Illinois J Math, 45: 213-228.
- KOUTROUFIOTIS D. 1973. Elementary geometric applications of a maximum principle for nonlinear elliptic operators, Arch Math, 24: 97-99.
- MONTIEL S AND ROS A. 1991. Compact hypersurfaces: the Alexandrov theorem for higher order mean curvatures, Differential Geometry (Lawson B and Tenenblat K, eds.), 52, Pitman Monographs, Essex, Longman: 1-13.
Correspondence to
Publication Dates
-
Publication in this collection
17 Feb 2004 -
Date of issue
Mar 2004
History
-
Accepted
21 Nov 2003 -
Received
05 July 2003


















