Abstracts
We show how to compute the number of reducible cubic scrolls of codimension 2 in (math blackboard symbol P)n incident to the appropriate number of linear spaces.
cubic scrolls; enumerative geometry
Mostramos como calcular o número de rolos cúbicos redutíveis de codimensão 2 em (math blackboard symbol P)n incidentes a espaços lineares apropriados.
rolos cúbicos; geometria enumerativa
MATHEMATICAL SCIENCES
Numbers for reducible cubic scrolls
Israel VainsencherI; Fernando XavierII
IICEX - Departamento de Matemática - UFMG, Cx. Postal 702 Belo Horizonte 30123-970 Belo Horizonte, MG, Brasil
IIDepartamento de Matemática - UFPb, Cidade Universitária - 58051-900 João Pessoa, PB, Brasil
Correspondence Correspondence to Israel Vainsencher E-mail: israel@mat.ufmg.br
ABSTRACT
We show how to compute the number of reducible cubic scrolls of codimension 2 in (math blackboard symbol P)n incident to the appropriate number of linear spaces.
Key words: cubic scrolls, enumerative geometry.
RESUMO
Mostramos como calcular o número de rolos cúbicos redutíveis de codimensão 2 em (math blackboard symbol P)n incidentes a espaços lineares apropriados.
Palavras-chave: rolos cúbicos, geometria enumerativa.
1 INTRODUCTION
A cubic rational normal scroll of codimension 2 in
n is the residual intersection of 2 quadric hypersurfaces containing a codimension 2 plane. It is also equal to the locus of rank 1 of a 2 x 3 matrix
(cf. (Harris 1992) where the Li, Mj denote sufficiently general linear forms in the homogeneous coordinates x0,...,xn of  n. For n = 3, this is a twisted cubic. Enumeration of such curves has attracted some attention in the last two decades, and is now but an example in Gromov-Witten theory, cf. (Fulton and Pandharipande 1997), (Kock and Vainsencher 1999). No such general technique is known yet for higher dimension. For the case of cubic scrolls, a procedure to determine some of these numbers was explained in (Vainsencher and Xavier 2002).
n. For n = 3, this is a twisted cubic. Enumeration of such curves has attracted some attention in the last two decades, and is now but an example in Gromov-Witten theory, cf. (Fulton and Pandharipande 1997), (Kock and Vainsencher 1999). No such general technique is known yet for higher dimension. For the case of cubic scrolls, a procedure to determine some of these numbers was explained in (Vainsencher and Xavier 2002).
The purpose of this note is to show an application of Bott's residual formula for the calculation of the number of reducible (n-2)-dimensional cubic scrolls in  n satisfying suitable incidence conditions to linear subspaces. The whole point is the simple observation that, just as in the case of twisted cubics, a general reducible cubic scroll of dimension (n-2)- is the union of an (n-2)-plane with an (n-2)-dimensional quadric meeting along an (n-3)-plane.
n satisfying suitable incidence conditions to linear subspaces. The whole point is the simple observation that, just as in the case of twisted cubics, a general reducible cubic scroll of dimension (n-2)- is the union of an (n-2)-plane with an (n-2)-dimensional quadric meeting along an (n-3)-plane.
2 THE PARAMETER SPACE
As customary in enumerative questions, we take the lead from the previous observation and consider the incidence variety
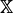 is naturally obtained as a tower of fiber bundles. Start with the grassmannian,
is naturally obtained as a tower of fiber bundles. Start with the grassmannian,
of projective (n-3)-dimensional subspaces of  n. It carries a tautological exact sequence
n. It carries a tautological exact sequence
where rank  = 3 and
= 3 and 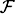 denotes the trivial bundle with fiber the dual space
denotes the trivial bundle with fiber the dual space  . The homogeneous coordinates x0,...,xn form a basis for the latter space. The fiber of
. The homogeneous coordinates x0,...,xn form a basis for the latter space. The fiber of  over p = [n-3] Î
over p = [n-3] Î 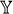 is the 3-dimensional space of linear forms vanishing on p. The choice of a space
is the 3-dimensional space of linear forms vanishing on p. The choice of a space 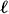 = [n-2] containing a fixed p = [n-3] is tantamount to picking a 2-dimensional vector subspace of the fiber
= [n-2] containing a fixed p = [n-3] is tantamount to picking a 2-dimensional vector subspace of the fiber  p, i.e., a point in the dual space
p, i.e., a point in the dual space  . Thus, the set of pairs p Ì
. Thus, the set of pairs p Ì 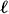 is the total space of the
is the total space of the  2-bundle,
2-bundle,  . Likewise, hyperplanes h through p form the total space of the
. Likewise, hyperplanes h through p form the total space of the  2-bundle,
2-bundle,  . The choice of a quadric k Ì h containing p yields the
. The choice of a quadric k Ì h containing p yields the  2n-2- bundle,
2n-2- bundle,
Here  stands for the rank-(2n-1) vector bundle over
stands for the rank-(2n-1) vector bundle over  (
( ) obtained as follows. Let
) obtained as follows. Let  be the kernel of
be the kernel of  . Since 3n =
. Since 3n =  , this is the rank-3n bundle of quadrics vanishing at the varying p Î
, this is the rank-3n bundle of quadrics vanishing at the varying p Î 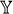 . Let
. Let 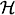 =
=  (-1)
(-1) 
 be the line bundle over
be the line bundle over  (
( ) with fiber over h given by the scalar multiples of the linear form h. Put
) with fiber over h given by the scalar multiples of the linear form h. Put  =
= 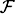 /
/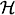 . Then
. Then  fits into the diagram of natural vector bundle maps,
fits into the diagram of natural vector bundle maps,
We may summarize the previous discussion as follows.
LEMMA 2.1. Notation as above, the parameter space 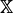 is isomorphic to the fiber product,
is isomorphic to the fiber product,
and dim 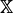 = 5n-4.
= 5n-4.
REMARK 2.2. Let
It should be noted that  ®
® 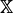 is not a flat family. It can be rendered flat by a single blowup along a suitable smooth subvariety of
is not a flat family. It can be rendered flat by a single blowup along a suitable smooth subvariety of 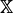 using techniques as in (Vainsencher and Xavier 2002), but this is not needed in the sequel.
using techniques as in (Vainsencher and Xavier 2002), but this is not needed in the sequel.
3 CYCLE CLASSES
Now we define the divisors corresponding to the relevant incidence conditions.
Fix a line
0 = 1Ì
1Ì  n and a plane p0 =
n and a plane p0 =  2Ì
2Ì  n. We define
n. We define
We also need a bit more of notation. We write
for the tautological sequence over  (
( ), where rank
), where rank  =2.
=2.
PROPOSITION 3.1. The cycle classes of the divisors defined above can be expressed as follows in terms of Chern classes of the natural bundles:
PROOF. Let 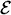 = áx3,...,xnñ Ì
= áx3,...,xnñ Ì 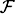 be the space of n-2 linear forms cutting p0 =
be the space of n-2 linear forms cutting p0 =  2Ì
2Ì  n. Let
n. Let  =
= 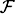 /
/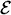 denote the rank-3 quotient. Studying the diagram of vector bundles over
denote the rank-3 quotient. Studying the diagram of vector bundles over 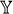 ,
,
it can be seen that p Î 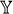 meets p0 if and only if the slant arrow s:
meets p0 if and only if the slant arrow s:  ®
®  is not injective at p. Hence Dp0,p is the divisor of zeros of
is not injective at p. Hence Dp0,p is the divisor of zeros of  s. It follows that Dp0,p = c1(
s. It follows that Dp0,p = c1(
 ) = c1(
) = c1( ). The proof of 2. is similar. The last formula is slightly trickier. It suffices to establish it over an open subset the complement of which contains no divisor. Thus, we may restrict to the locus of h transversal to
). The proof of 2. is similar. The last formula is slightly trickier. It suffices to establish it over an open subset the complement of which contains no divisor. Thus, we may restrict to the locus of h transversal to 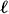 0. Let
0. Let 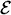 = áx3,...,xnñ Ì
= áx3,...,xnñ Ì 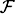 be now the space of equations for
be now the space of equations for 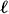 0 =
0 =  1Ì
1Ì  n. Let
n. Let  =
= 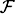 /
/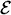 be the rank 2 quotient. The composition
be the rank 2 quotient. The composition 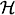 ®
® 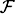 ®
® 
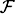
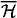 =
= 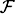 /
/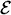 +
+ 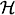 can be thought of as evaluation of linear forms at the point of intersecion of
can be thought of as evaluation of linear forms at the point of intersecion of 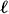 0 with a varying, transversal hyperplane. It yields an evaluation map for quadratic forms, S2
0 with a varying, transversal hyperplane. It yields an evaluation map for quadratic forms, S2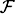 ® S2
® S2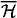 and induces S2(
and induces S2(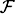 /
/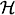 ) ® S2
) ® S2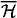 . Composing with
. Composing with 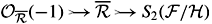 , we find
, we find 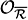 (-1) ® S2
(-1) ® S2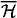 . The latter vanishes precisely over
. The latter vanishes precisely over 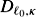 (along the transversal locus). Since c1(S2
(along the transversal locus). Since c1(S2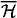 ) = 2c1(
) = 2c1(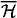 ) = -2c1(
) = -2c1(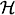 ), the formula follows .
), the formula follows . 
4 NUMBERS
We shall abuse notation and keep writing
for the pullback of these divisors to 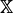 . The intersection of general translates is transversal by standard Bertini-Kleiman-Sard arguments (applied to (2.2)
. The intersection of general translates is transversal by standard Bertini-Kleiman-Sard arguments (applied to (2.2)  ®
®  n). Taking i1+i2+i3 = 5n-4 = dim
n). Taking i1+i2+i3 = 5n-4 = dim 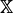 such translates, we may find the number of elements (p,
such translates, we may find the number of elements (p, 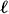 , k) of
, k) of 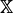 such that the subspace p = [n-3] meets i1
such that the subspace p = [n-3] meets i1
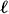 = [n-2] meets i21's and the (n-2)-quadric k meets i31's. This is done by evaluating Ni1,i2: =
= [n-2] meets i21's and the (n-2)-quadric k meets i31's. This is done by evaluating Ni1,i2: =
For the specific task of enumerating the reducible cubic scrolls, we take translates of the divisors Dp0,p and  : =
: =  . We are now asked to compute
. We are now asked to compute
for i+j = dim 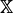 . This is a purely mechanical matter with the help of either Schubert calculus (e.q., as implemented in (Katz and Strømme 1992) or Bott's residue formula (cf. (Bott 1967), (Meurer 1996)). Here are the ingredients for the latter. First find the fixed points of a
. This is a purely mechanical matter with the help of either Schubert calculus (e.q., as implemented in (Katz and Strømme 1992) or Bott's residue formula (cf. (Bott 1967), (Meurer 1996)). Here are the ingredients for the latter. First find the fixed points of a  -action on
-action on 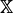 , induced by an action xi
, induced by an action xi
 n. Choosing the integral weights wi sufficiently general, it can be checked that all fixed points are isolated, starting at
n. Choosing the integral weights wi sufficiently general, it can be checked that all fixed points are isolated, starting at 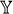 , then climbing up the tower
, then climbing up the tower
Pick p1 = áx0, x1, x2ñ Î 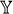 =
=  r[n-3n], among the
r[n-3n], among the  fixed points in
fixed points in 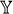 . There are just three fixed points on the fiber
. There are just three fixed points on the fiber  2 =
2 =  (
( p1). Choose one, say p1,1 = áx0ñ (a hyperplane through p1). The fiber of
p1). Choose one, say p1,1 = áx0ñ (a hyperplane through p1). The fiber of  (
( ) over p1,1 is
) over p1,1 is
with the obvious 2n-1 fixed points. Pick p1,1,1 = á ñ. By the same token, the fiber of
ñ. By the same token, the fiber of 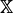 ®
®  (
( ) over p1,1,1 is
) over p1,1,1 is  2 =
2 =  (á
(á 0,
0,  1,
1,  2ñ), with
2ñ), with  i = áx0, x1, x2ñ/áxj, xkñ. We obtain thus the fixed point p1,1,1,1 =
i = áx0, x1, x2ñ/áxj, xkñ. We obtain thus the fixed point p1,1,1,1 =  0 (among a total of
0 (among a total of  .3.(2n-1)·3 possible ones). The contribution of this fixed point to Bott's formula is given by evaluating the indicated Chern classes in the equivariant cohomology ring at the point. Explicitly, c1(
.3.(2n-1)·3 possible ones). The contribution of this fixed point to Bott's formula is given by evaluating the indicated Chern classes in the equivariant cohomology ring at the point. Explicitly, c1( ) evaluates to
) evaluates to  wi, because the fiber
wi, because the fiber  p1 = áx3,...,xnñ decomposes into eigenspaces with weights wi, i = 3... n. The term c1(
p1 = áx3,...,xnñ decomposes into eigenspaces with weights wi, i = 3... n. The term c1( ) evaluates to -w1-w2. Next, the fiber of
) evaluates to -w1-w2. Next, the fiber of  (-1) is the line spanned by the equation of the hyperplane áx0ñ; dualizing, we see that c1(
(-1) is the line spanned by the equation of the hyperplane áx0ñ; dualizing, we see that c1( (1)) yields -w0. The fiber of
(1)) yields -w0. The fiber of 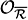 (1) is dual to the line á
(1) is dual to the line á ñ hence contributes with -2w1. We also need the weights of the fiber of the tangent bundle of
ñ hence contributes with -2w1. We also need the weights of the fiber of the tangent bundle of 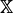 . Starting at Tp1
. Starting at Tp1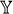 , we write the eigenspace decomposition Hom(áx3,...,xn,ñ
, we write the eigenspace decomposition Hom(áx3,...,xn,ñ 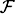 áx3,...,xnñ) = åxi/xj, with i Î {0,1,2}, j Î {3,...,n}. Add to this the (decomposition of the) tangent along the fiber of
áx3,...,xnñ) = åxi/xj, with i Î {0,1,2}, j Î {3,...,n}. Add to this the (decomposition of the) tangent along the fiber of  (
( ) ®
) ® 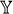 , at áx0ñ, namely, x1/x0+x2/x0. Continuing, get the tangent along the fiber of
, at áx0ñ, namely, x1/x0+x2/x0. Continuing, get the tangent along the fiber of  (
( ) ®
) ®  (
( ), to wit, (x1x2+···+x1xn+
), to wit, (x1x2+···+x1xn+ +···+x2xn)/
+···+x2xn)/ . At last, add the fiber of T(
. At last, add the fiber of T( (
( ) /
) /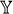 ) at ,á
) at ,á 0ñ x0/x1+x0/x2. The top Chern class needed is the product of weights (wi-wj), i Î {0,1,2}, j Î {3,...,n}, times (w1-w0)(w2-w0), times (w2-w1)···(wn-w1)(2w2-2w1)···(w2+wn-2w1), times (w0-w1)(w0-w2); call this product w. The total contribution of the present fixed point is the fraction
0ñ x0/x1+x0/x2. The top Chern class needed is the product of weights (wi-wj), i Î {0,1,2}, j Î {3,...,n}, times (w1-w0)(w2-w0), times (w2-w1)···(wn-w1)(2w2-2w1)···(w2+wn-2w1), times (w0-w1)(w0-w2); call this product w. The total contribution of the present fixed point is the fraction
Quite miraculously, adding up the contributions over all fixed points, we get an integer.
The table below compiles some examples for 3 < n < 6.
Thus we find in
4 the numbers N3 = 7484880 of reducible cubic scrolls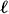 È k « (p,
È k « (p, 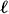 , k) such that the line p =
, k) such that the line p =  1Ì
1Ì  4 meets 3 general given
4 meets 3 general given  2Ì
2Ì  4 and p Í
4 and p Í 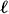 Ç k and the union
Ç k and the union 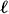 È k meets dim
È k meets dim 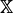 -3 = 5·4-4-3 = 13 general lines. On the same row of the table we read N5,2 = 1570, the number of configurations (p,
-3 = 5·4-4-3 = 13 general lines. On the same row of the table we read N5,2 = 1570, the number of configurations (p, 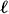 , k) Î
, k) Î 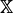 with the line p meeting i1 = 5 general
with the line p meeting i1 = 5 general  2's, the plane
2's, the plane 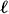 meeting i2 = 2 general lines and the quadric surface k meeting i3 = 16-i1-i2 = 9 other general lines. The entries have been computed employing Greuel et al. 2001. A script can be downloaded from Vainsencher 2004.
meeting i2 = 2 general lines and the quadric surface k meeting i3 = 16-i1-i2 = 9 other general lines. The entries have been computed employing Greuel et al. 2001. A script can be downloaded from Vainsencher 2004.
CLOSING REMARKS
As kindly pointed out by the referee, for n > 5 all rational normal cubic scrolls of codimension 2 in  n are cones (cf. XXX 1957). For n = 4,5, the irreducible singular cubic scrolls not contained in a hyperplane are cones over a scroll in a hyperplane. The enumeration of such cones satisfying suitable incidence conditions can be pursued by means of a natural fibration. We hope to report on this elsewhere.
n are cones (cf. XXX 1957). For n = 4,5, the irreducible singular cubic scrolls not contained in a hyperplane are cones over a scroll in a hyperplane. The enumeration of such cones satisfying suitable incidence conditions can be pursued by means of a natural fibration. We hope to report on this elsewhere.
ACKNOWLEDGMENTS
We thank the referees for several suggestions and corrections. This work was partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq).
Manuscript received on January 19, 2004; accepted for publication on July 6, 2004; contributed by ISRAEL VAINSENCHER* * Member Academia Brasileira de Ciências
- BOTT R. 1967. A residue Formula for Holomorphic Vector Fields. J Diff Geom 1: 311-330.
- FULTON W AND PANDHARIPANDE R. 1997. Notes on Stable Maps and Quantum Cohomology. Proc Symp Purę Math 62(II): 45-96 (alg-geom/9608011).
- GREUEL G-M, PFISTER G AND SCHÖNEMANN H. 2001. Singular 2.0. A Computer Álgebra System for Polynomial Computations. Centre for Computer Álgebra, University of Kaiserslautern. http://www.singular.uni-kl.de
- HARRIS J. 1992. Algebraic geometry. A first course, Texts in Matematics, 133. Springer-Verlag, New York.
- KATZ S AND STRŘMME SA. 1992. Schubert. A maple package for Intersection Theory. http://www.mi.uib.no/schubert/
- KOCK J AND VAINSENCHER I. 1999. Kontsevich's formula for rational plane curves, book, to appear, http://www.mat.ufmg.br/ israel/kontsevich.html,
- MEURER P. 1996. The number of rational quartics on Calabi-Yau hypersurfaces in weighted projective space P(2,14) Math Scandin 78: 63-83 (alg-geom/9409001).
- VAINSENCHER I AND XAVIER F. 2002. A compactification of the space of twisted cubics. Math Scand 91: 221-243.
- VAINSENCHER I. 2004. http://www.mat.ufmg.br/ israel/sing.html
- XXX (ANONYMOUS) 1957. Correspondence. Am J Math 79: 951-952.
Publication Dates
-
Publication in this collection
22 Nov 2004 -
Date of issue
Dec 2004
History
-
Received
19 Jan 2004 -
Accepted
06 June 2004
























