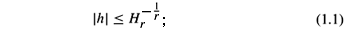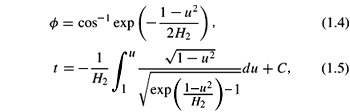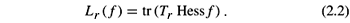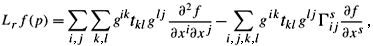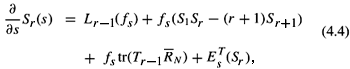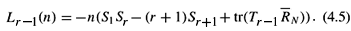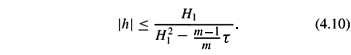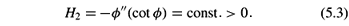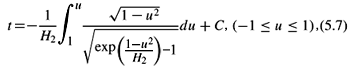Embedded positive constant r-mean curvature hypersurfaces in Mm × R

Abstracts

Let M be an m-dimensional Riemannian manifold with sectional curvature bounded from below. We consider hypersurfaces in the (m + 1)-dimensional product manifold M × R with positive constant r-mean curvature. We obtain height estimates of certain compact vertical graphs in M × R with boundary in M × {0}. We apply this to obtain topological obstructions for the existence of some hypersurfaces. We also discuss the rotational symmetry of some embedded complete surfaces in S² × R of positive constant 2-mean curvature.

product manifold; hypersurface; r-mean curvature

Seja M uma variedade riemanniana de dimensão m, de curvatura seccional limitada de abaixo. Consideramos as hipersuperfícies na variedade produto M × R de dimensão m+1, com curvatura r-média constante positiva. Obtemos uma estimativa para altura das alguns gráficos verticais em M × R com seus fronteiras em M × {0}. Aplicamos isto para obter as obstruções topológicas sobre existência das algumas hipersuperfícies. Também discutimos a simetria rotacional das algumas superfícies completas em S² × R de curvatura 2-média constante positiva.

variedade produto; hipersuperfície; curvatura r-média

MATHEMATICAL SCIENCES

Embedded positive constant r-mean curvature hypersurfaces in M^m × R

Xu Cheng^I; Harold Rosenberg^II,*

^IInstituto de Matemática, Universidade Federal Fluminense-UFF, Centro, 24020-140 Niterói, RJ, Brasil

^IIUniversité Paris 7, Institut de Mathématiques, 2 Place Jussieu, 75251 Paris cedex 05, France

^{Correspondence}

ABSTRACT

Let M be an m-dimensional Riemannian manifold with sectional curvature bounded from below. We consider hypersurfaces in the (m + 1)-dimensional product manifold M × R with positive constant r-mean curvature. We obtain height estimates of certain compact vertical graphs in M × R with boundary in M × {0}. We apply this to obtain topological obstructions for the existence of some hypersurfaces. We also discuss the rotational symmetry of some embedded complete surfaces in S² × R of positive constant 2-mean curvature.

Key words: product manifold, hypersurface, r-mean curvature.

RESUMO

Seja M uma variedade riemanniana de dimensão m, de curvatura seccional limitada de abaixo. Consideramos as hipersuperfícies na variedade produto M × R de dimensão m+1, com curvatura r-média constante positiva. Obtemos uma estimativa para altura das alguns gráficos verticais em M × R com seus fronteiras em M × {0}. Aplicamos isto para obter as obstruções topológicas sobre existência das algumas hipersuperfícies. Também discutimos a simetria rotacional das algumas superfícies completas em S² × R de curvatura 2-média constante positiva.

Palavras-chave: variedade produto, hipersuperfície, curvatura r-média.

1 INTRODUCTION

If

^m+1 is an (m+1)-dimensional oriented Riemannian manifold and S^m is a hypersurface in , the r-mean curvature of S, denoted by H_r, is the weighted r'th symmetric function of the second fundamental form (see Definition 2.1). The hypersurfaces with constant r-mean curvature include those of constant mean curvature, and of constant Gauss-Kronecker curvature. In some situations, for example, = ^m+1, ^m+1, ^m+1(–1), a hypersurface of constant r-mean curvature is a critical point for a certain variational problem (See the related works in (Reilly 1973), (Rosenberg 1993), (Barbosa and Colares 1997) and (Elbert 2002)).

Heinz discovered that a compact graph S in

^m+1 with zero boundary values, of constant mean curvature H ¹ 0, is at most a height from its boundary. A hemisphere in ^m+1 of radius shows this estimate is optimal. Using Alexandrov reflection techniques, it follows that a compact embedded hypersurface with constant mean curvature H ¹ 0 and boundary contained in x_m+1 = 0, is at most a distance from the hyperplane x_m+1 = 0.

Height estimates have been obtained by the second author (Rosenberg 1993) for compact graphs S in

^m+1 with zero boundary values and with a higher order positive constant r-mean curvature. He also obtained such height estimates in space forms. For example, in ³, such a graph of positive constant Gauss curvature can rise at most from the plane containing the boundary. In general, the maximum height is . For r = 1, this result in hyperbolic space ^m+1(–1) was proved by Korevaar, Kusner, Meeks and Solomon (Korevaar et al. 1992). We refer the reader to (Rosenberg 1993) for applications of these height estimates.

In (Hoffman et al. 2005), Hoffman, Lira and Rosenberg obtained height estimates for some vertical graphs in M² × of nonzero constant mean curvature, where M is a Riemannian surface.

In this paper, we will consider orientable hypersurfaces in an (m + 1)-dimensional oriented product manifold M × with positive constant r-mean curvature. Here M is an m-dimensional Riemannian manifold with sectional curvature bounded below. The typical models are when M = ^m, ^m, ^m(–1). We will obtain height estimates for such compact vertical graphs with boundary in M × {0}. A significant difference between this case and the previous cases we discussed is the nature of the linearized operator. It is no longer a divergence form operator and we do not have a flux formula. We prove that,

THEOREM 1.1. (Th. 4.1). Let M be an m-dimensional oriented Riemannian manifold. Let S be a compact vertical graph in the (m+1)-dimensional product manifold M × with positive constant H_r, for some 1< r < m, with boundary in M × {0}. Let h: S ® denote the height function of S.

(i) If the sectional curvature of M satisfies K > 0, then on S,

(ii) When r = 2, if the sectional curvature of M satisfies K > –t (t > 0), and H₂ > t, then on S,

(iii) When r = 1, if the sectional curvature of M satisfies K > –t (t > 0), and , then on S,

We give some applications of Theorem 1.1 using the Alexandrov reflection technique. First we give the extrinsic vertical diameter estimate of compact embedded surfaces in M × with positive constant r-mean curvature (under the same curvature assumptions as in Theorem 1.1. See Th.4.2); Secondly, we prove that if M is an m-dimensional compact Riemannian manifold and S is a noncompact properly embedded hypersurface in M^m × with positive constant r-mean curvature (under the same curvature assumptions as in Theorem 1.1), then the number of ends of S is not one (Th.4.3). Thus we give a topological obstruction for the existence of such a hypersurface. For example, if S is a noncompact properly embedded hypersurface in ^m × of positive constant r-mean curvature for 1 < r < m, then the number of ends of S is more than one (Cor.4.1).

In this paper, we also consider the properties of symmetry of certain embedded hypersurfaces of positive constant r-mean curvature. Alexandrov (Alexandrov 1962) showed an embedded constant mean curvature hypersurface in the Euclidean space must be a standard round hypersurface. The symmetric properties of hypersurfaces (with or without boundary) in the Euclidean space and the other space forms with constant mean curvature or higher order constant r-mean curvatures have been studied in varied degrees. We discuss the rotational symmetry of a complete embedded surface in ² × of positive constant 2-mean curvature and obtain that,

THEOREM 1.2. (Th. 5.1; Cor. 5.1). Let ² be the unit sphere in ³ and be the open upper hemisphere in ². Let S be a complete orientable embedded surface in ² × with H₂ = constant > 0. If S Ì × , then S has the following properties:

(i) S is topologically a sphere; and

(ii) S is a compact surface of revolution about o' × , o' Î , that is, S is foliated by round circles in × {t}, the centers of which are o' × t, where t Î (h_min,h_max) and h_min,h_max are the maximum and minimum of the height of S respectively. Moreover, there exists a horizontal level × {t₀}, t₀ = , such that S divides into two (upper and lower) symmetric parts; and

(iii) Let f₀Î [0,) denote the polar angle between the north pole of the open upper hemisphere and o'. Then H₂ > –(if f₀ = 0,H₂ > 0) and the generating curve of the rotational surface S can be denoted by l(u) = (f(u), t(u)) where –1< u < 1, and f denotes the polar coordinate (about o') of ², and:

where C is a real constant.

We conjecture a compact immersed surface in

² × of positive constant 2-mean curvature is rotationally symmetric about a vertical line. Moreover, such a surface in ² × is rotational when it is topologically a sphere.

2 PRELIMINARIES

Let

^m+1 be an (m + 1)-dimensional oriented Riemannian manifold and let S^m be an m-dimensional orientable Riemannian manifold. Suppose x : S ® is an isometric immersion. We choose a unit normal field N to S and define the shape operator A associated with the second fundamental form of S, i.e., for any p Î S,

A : T_pS ® T_pS, áA(X),Yñ = – á_X N,Yñ , X,Y Î T_pS,

where is the Riemannian connection in .

Let l₁,...,l_m denote the eigenvalues of A. The r-th symmetric function of l₁,...,l_r, denoted by S_r, is defined as

DEFINITION 2.1. With the above notations, H_r = S_r, r = 1,...,m, is called the r-mean curvature of x.

Particularly, H₁ = H is the mean curvature; H_m is the Gauss-Kronecker curvature. H₂ is , modulo a constant, the scalar curvature of S, when the ambient space ^m+1 is Einstein (Elbert 2002).

We also introduce endomorphisms of T(S), the Newton transformations, defined by

T₀ = I,

T_r = S_rI – S_r–1A + ... + (–1)^r A^r, r = 1, ... , m.

It is obvious that T_r, r = 0,1,...,m are symmetric linear operators and T_r = S_rI – AT_r–1.

Let e₁,...,e_m be the principal directions corresponding respectively to the principal curvatures l₁,..., l_m. For i = 1,...,m, let A_i denote the restriction of the transformation A to the (m – 1)-dimensional subspace normal to e_i, and let S_r(A_i) denote the r-symmetric function associated to A_i.

One has the following properties of T_r and S_r.

PROPOSITION 2.1. For 0< r < m, 1< i < m,

(i) T_r(e_i) = e_i = S_r(A_i);

(ii) (m – r)S_r = trace(T_r) = S_r(A_i);

(iii) (r + 1)S_r+1 = trace(AT_r) = l_iS_r(A_i);

(iv)

> H₂.

Proposition 2.1 can been verified directly.

PROPOSITION 2.2. For each r (1< r < m), if H₁, H₂,...,H_r are nonnegative, then

(i) H₁> > > ... > ;

(ii) H_r–1 H_r+1< ;

(iii) H₁H_r > H_r+1, where, H₀ = 1, H_m+1 = 0.

See the proof of (i) and (ii) of Proposition 2.2 in (Hardy et al. 1989. p.52). The inequality in (iii) can be obtained from (ii).

Given a function f in C²(S) for p Î S, the linear operator Hessian of f is defined as Hess f(X) = Ñ_X(Ñf), X Î T_pS, where Ñ is the induced connection on S.

With T_r and Hess, we can define a differential operator L_r as follows:

DEFINITION 2.2. Given f Î C²(S), 0< r < m,

Given a local coordinate frame of S at p, by direct computation, we have locally the expression of L_r,

where

are the connection coefficients of Ñ.

From the above local expression, we know that the linear operator L_r is elliptic if and only if T_r is positive definitive. Clearly, L₀ = tr(Hess f) = div(Ñ f) is elliptic.

In this paper, the ambient space which we study is an (m + 1)-dimensional product manifold M^m × , where M is an m-dimensional Riemannian manifold. S will be a hypersurface in M × with positive constant r-mean curvature, i.e, H_r = constant > 0.

We use t to denote the last coordinate in M × .

The height function, denoted by h, of S in M × is defined as the restriction of the projection t : M × ® to S , i.e., if p Î S,x(p) Î M × {t}, then h(p) = t. We have = h.

3 THE ELLIPTIC PROPERTIES OF THE OPERATOR L_r

The following Prop. 3.1 is known (cf. Elbert 2002. Lemma 3.10). For completeness, we give its proof.

PROPOSITION 3.1. Let

^m+1 be an (m + 1)-dimensional oriented Riemannian manifold and let S^m be a connected m–dimensional orientable Riemannian manifold. Suppose x : S ® is an isometric immersion. If H₂ > 0, then the operator L₁ is elliptic.

PROOF. Since L₁ is elliptic if and only if T₁ is positive definite, we will prove that T₁ is positive definite.

By H₂ > 0 and > H₂, H₁ is nonzero and has the same sign on S. We may choose the normal N such that H₁ is positive. So S₁ = mH₁ > 0.

By = å + 2S₂ > , we have S₁ > l_i. Then S₁(A_i) = S₁ – l_i > 0. Since T₁e_i = S₁(A_i)e_i (Prop. 2.1 (i)), T₁ is positive definite.

In Prop. 3.2, we will prove the ellipticity of L_r when the hypersurface S with positive r-mean curvature has an elliptic or parabolic point.

PROPOSITION 3.2. Let

^m+1 be an (m + 1)-dimensional oriented Riemannian manifold and let S^m be a connected m–dimensional orientable Riemannian manifold (with or without boundary). Suppose x : S ® is an isometric immersion with H_r > 0 for some 1< r < m. If there exists an interior point p of S such that all the principle curvatures at p are nonnegative, then for all 1< j < r – 1, the operator L_j is elliptic, and the j-mean curvature H_j is positive.

PROOF. Since L_j is elliptic if and only if T_j is positive definite, it is sufficient to prove that the eigenvalues of T_j are positive, that is S_j(A_i) > 0 on S, for all 1 < j < r – 1, 1 < i < m.

In the following proof, the ranges of j and i are 1 < j < r – 1, 1 < i < m respectively.

Since S_r > 0 and the principal curvatures of x at p are nonnegative, we have that at p, at least r principal curvatures are positive. For simplicity, we suppose that l₁, l₂,..., l_r are positive.

Then, by direct verification, at p, S_j(A_i) > 0.

By continuity, there exists an open intrinsic ball B(p) Ì S with center p such that the functions S_j(A_i) > 0 on B(p).

For any q Î S, since S is connected, there exists a path g(t) (t Î [0,1]) in S, joining p to q with g(0) = p and g(1) = q.

Define J = {t Î [0,1]|S_j(A_i) > 0 on g|_[0,t]}. Let t₀ = sup J.

Note S_j(A_i) > 0 on B(p) so t₀ > 0. By continuity, at t₀, S_j(A_i) > 0.

We will prove that S_j(A_i) > 0 at t₀ and hence t₀Î J.

We first show that S_r–1(A_i) > 0 at t₀. Otherwise, there exists 1 < i < r – 1 such that S_r–1(A_i) = 0 at t₀. For this i, by S_r = l_iS_r–1(A_i) + S_r(A_i), we have S_r(A_i) = S_r > 0 at t₀. So, at t₀, S_j(A_i) > 0, 1 < j < r – 1 and S_r(A_i) > 0. By (ii) in Prop. 2.2, at t₀, the following inequality holds,

H₁(A_i) >H2> ... > H_r–1> Hr.

Then at t₀, H_r–1(A_i) > 0, i.e., S_r–1(A_i) > 0, which is a contradiction. Thus, we have S_r–1(A_i) > 0 at t₀.

Next, by S_r–1(A_i) > 0 and H₁(A_i) > H₂

> ... > H_r–1 at t₀, we have that S_j(A_i) > 0 at t₀. Hence t₀Î J.

If t₀ < 1, by continuity, there exists an open intrinsic ball B(g(t₀)) of center g(t₀) such that S_j(A_i) > 0 on B(g(t₀)), which contradicts our choice of t₀ = sup J. Hence, t₀ = 1.

So we obtain that at q, S_j(A_i) > 0. Hence the L_j, for all 1 < j < r – 1 are elliptic.

By Prop. 2.1 (ii), H_j (for all 1 < j < r – 1) are positive.

4 THE HEIGHT ESTIMATES OF THE VERTICAL GRAPH

In this section, we will consider hypersurfaces in an (m + 1)-dimensional product manifold M^m × of positive constant r-mean curvature.

LEMMA 4.1. Let M be an m–dimensional oriented Riemannian manifold and let S be an immersed orientable hypersurface in M × (with or without boundary). Then

where 1 < r < m + 1, h denotes the height function of S, and n = áN,ñ.

PROOF. Fix p Î S. Let {e_i} be a geodesic orthonormal frame of S at p. So at p, e_j(p) = 0. We can assume {e_i} are the principal directions at p, that is, Ae_i(p) = l_ie_i, where l_i are the eigenvalues (principal curvatures) of A at p (this frame can been obtained by rotating {e_i}).

Observe that the vertical translation in M × is an isometry. Hence h = is a Killing vector field, and

h = 0, for i = 1,...,m.

We have

where the T denotes the tangent part of the vector of T(M × ) to S.

Then

Hence

Since rS_rn is independent of the choice of the frame, we obtain that, on S

In order to prove the following Lemma 4.2, we first recall some known results.

Let S Ì

^m+1 be an oriented hypersurface. Let D be a compact domain of S. Consider a variation of D, denoted by f. f:(–,) × ® M × , > 0, such that for each s Î (–,) , the map f_s : {s} × ® M × , f_s(p) = f(s, p) is an immersion, and f₀ = .

Let A_t(p) be the shape operator of S(t) at p and for 0 < r < m, let S_r(t)(p) be the r-th symmetric function of the eigenvalues of A_t(p). We are interested in the first variation of S_r. To calculate this one may differentiate the equation rS_r = tr(T_r–1A). We refer the reader to (Rosenberg 1993) for details of this calculation in space forms. In general ambient spaces, Elbert (Elbert 2002. Proposition 3.2) proved the following result.

Set E_s(p) = (p, s) and f_s = < E_s, N_s > , where N_s is the unit normal to f_s(D). We have

where

_N is defined as _N(X) = (N, X)N, the curvature operator of , and denotes the tangent part of E_s.

LEMMA 4.2. With M and S as in Lemma 4.1, assume H_r of S is constant, for some r, 1< r < m + 1. Then, on S,

PROOF. We may choose the variation f_s : (–, ) × D Ì (–, ) × S ® M × given by vertical translation of M × , (x, t₀) ® (x, t₀ + s), (x, t₀) Î M × R.

Under this variation, S_r(s) is constant, i.e., S_r(s) = 0. Also by the hypothesis S_r = constant on S, we have (S_r) = 0, for s = 0. Hence, when s = 0, we have f₀ = áE₀, N₀ñ = á, Nñ = n and

Thus (4.6) holds on S.

We will express tr(T₁

_N) using the sectional curvature of M in order to prove Theorem 4.1.

Given p = (x, t) Î M × . For X Î T_pM × , let X^h denote the horizontal component of X. If {e_i} denotes a geodesic frame of S at p and N denotes the unit normal to S at p, we have, by direct calculation,

(e_i, N, e_i, N) = (, N^h, , N^h) = K(, N^h) × |Ù N^h|²,

where K is the sectional curvature of M.

If e_i are also the principal directions of A. We have T_re_i = S_r(A_i)e_i. Then

THEOREM 4.1. Let M be an m-dimensional oriented Riemannian manifold. Let S be a compact vertical graph in the product manifold M × with boundary in M × {0} and with positive constant H_r, for some 1< r < m. Let h : S ® denote the height function of S.

(i) If the sectional curvature of M satisfies K > 0, then on S,

(ii) When r = 2, if the sectional curvature of M satisfies K > –t (t > 0), and H₂ > t, then on S,

(iii) When r = 1, if the sectional curvature of M satisfies K > –t (t > 0), and > t, then on S,

PROOF. At a highest point, all the principal curvatures have the same sign. Since we assume that H_r > 0, we know that at this point, all the principal curvatures are nonnegative and the unit normal N to S is downward pointing. Since S is a vertical graph, we may choose the smooth unit normal field N to S to be downward pointing (i.e.,n = áN,ñ < 0 on S). Hence we can apply Prop. 3.1 and Prop. 3.2 to obtain that, L_r–1 is elliptic, and H_i(1 < i < r – 1) are positive.

Define j = ch + n on S, where c is a positive constant to be determined. On ¶S, j = n < 0.

Since L_r–1 is an elliptic operator, we have, by the maximum principle, that if L_r–1j > 0, then j < 0 on S. Then h < –< .

Now we will choose c such that L_r–1j > 0. By Lemma 4.1 and 4.2,

L_r–1(j) = crS_rn – (S₁S_r – (r + 1)S_r+1 + tr(T_r–1

_N))n.

So L_r–1(j) > 0 is equivalent to

–rS_rc + S₁S_r – (r + 1)S_r+1 + tr(T_r–1

_N) > 0.

If K > a (a < 0), we have

So we may choose c such that

–rS_rc + S₁S_r – (r + 1)S_r+1 + (m – r + 1)aS_r–1> 0.

When H₁,...,H_r are nonnegative, H₁H_r> H_r+1, that is, S₁S_r> (r + 1)S_r+1. So it is sufficient to choose c such that

–rS_rc + S₁S_r + (m – r + 1)aS_r–1> 0.

Then, .

(i) Take a = 0 and choose c < . Hence h < .

(ii) Take a = –t(t > 0). Then c < H₁ – t · .

When r = 2, c < H₁ – t · = H₁(1 – ).

By H₁> , we may choose c < (1 – ) = . Hence h < .

(iii) When K > a (a < 0) and r = 1, we have a better estimate. Note

Similar to the above, we may choose c < . Take a = –t(t > 0). We have h < .

REMARK 4.1. The height estimate in Theorem 4.1 is sharp. Consider a hemisphere of the unitary round sphere

^m in ^m+1. It is a vertical graph on ^m = ^m × {0} of H_r = 1 with boundary ^m–1 × {0} and has the maximum height 1.

REMARK 4.2. In the case m = 2 and r = 1, (i) and (iii) of Theorem 4.1 was proved in (Hoffman et al. 2005).

THEOREM 4.2. Let M be an m-dimensional Riemannian manifold and let S be a compact orientable embedded hypersurface in M × with H_r = constant > 0, for some 1< r < m. Then S is symmetric about some horizontal surface M × {t₀}, t₀Î . Moreover,

(i) If the sectional curvature of M satisfies K > 0, then the extrinsic vertical diameter of S is no more than 2;

(ii) When r = 2, if the sectional curvature of M satisfies K > –t and H₂ > t(t > 0), then the extrinsic vertical diameter of S is no more than .

(iii) When r = 1, if the sectional curvature of M satisfies K > –t(t > 0), and > t, then the extrinsic vertical diameter of S is no more than .

PROOF. We will prove that S has a horizontal surface of symmetry M(t₀) = M × {t₀}, for some t₀Î .

Note that vertical translation is an isometry, as well as reflection through each horizontal M(t). Hence we can use the Alexandrov reflection technique. One comes down from above S with the horizontal surfaces M(t). For t slightly smaller than the highest value of the height of S, the part of S above M(t) is a vertical graph of bounded gradient over a domain in M(t). The symmetry through M(t) of this part of S, is below M(t), contained in the domain bounded by S, and meets S only along the boundary. One continues to do these reflections through the M(t) translated downwards, until a first accident occurs. This plane is a plane of symmetry of S, and the part of S above this plane is a graph with zero boundary values. This proves the Theorem.

Remark 4.3. Consider the case m = 2 and r = 2 in Theorem 4.1 or Theorem 4.2. From the Gauss equation, we obtain that the intrinsic sectional curvature of S has a positive lower bound H₂. So Bonnet-Myers theorem yields the intrinsic diameter estimate of S and hence the vertical height or the extrinsic vertical diameter estimate. That is, (a) when S is a vertical graph with zero boundary values, a geodesic on S from the highest point to ¶S (and hence the vertical height) is at most ; (b) when S is a compact embedded surface, a geodesic on S from the highest point to the lowest point (and hence extrinsic vertical diameter) is at most . But our estimates (a) and (b) are better. Moreover our estimate works for any dimension m and any r, for which Bonnet-Myers theorem indeed doesn't apply.

THEOREM 4.3. Let M be an m-dimensional compact Riemannian manifold and let S be a noncompact properly embedded hypersurface in × with H_r = constant > 0, for some 1< r < m. If the sectional curvature of M and the r-mean curvature of S satisfy the conditions in (i), (ii) or (iii) of Theorem 4.1, then the number of ends of S is not one.

PROOF. Suppose on the contrary, that S has exactly one end E. Since S is properly embedded, E must go up or down, but not both. Assume E goes down. Then S has a highest point so we can do Alexandrov reflection coming down from above S with horizontal surfaces M(t).

Since S is not invariant by symmetry in any M(t), there is no first point of contact of the symmetry of the part of S above M(t), with the part of S below M(t). But by the Alexandrov reflection technique, the part of S above each M(t) is always a vertical graph. This contradicts the height estimate for such vertical graphs.

COROLLARY 4.1. Let S be a noncompact properly embedded hypersurface in ^m × with H_r = constant > 0, for some 1< r < m. Then the number of ends of S is not one.

5 ROTATIONAL SYMMETRY OF SOME SURFACES IN

² × OF CONSTANT 2-MEAN CURVATURE

If M is the unit sphere ² in ³, an embedded surface in ² × of positive constant 2-mean curvature has another symmetry under some restriction. If we demand the vertical projection of such a surface on ² × {0} is contained in an open hemisphere, then it is also rotational about a vertical line parallel to the vertical -axis.

We now give some definitions which are modifications of the related concepts in

³ (cf. Hopf 1983. p.147-148).

Let be the open hemisphere in ² and ¶ be the boundary of . Let {p,–p} denote a pair of antipodal points on ¶, and g denote a semi-circle on joining p and –p. We call the surface P = g × in ² × a vertical geodesic strip.

DEFINITION 5.1. For a point q Î × , a point q' Î × is called a point of symmetry of q about a vertical geodesic strip P = g × if, for a geodesic l passing through q and perpendicular to P, we have q' Î l, lies on the opposite part of l divided by P, and dist(q, P) = dist(q', P). This means q' is the image of q by the isometry of S × which is reflection of each S(t) through g × {t}.

A vertical geodesic strip P = g × in ² × is called a vertical strip of symmetry for a set W Ì ² × if, for every point q Î W, its point of symmetry q' is also in W.

We will obtain the following:

Theorem 5.1. Let

² be the unit sphere in ³ and be an open hemisphere in ². Let S be a complete oriented embedded surface in ²× with H₂ = constant > 0. If S Ì × , then S has the following properties:

(i) S is topologically a sphere; and

(ii) S is a surface of revolution about a vertical line parallel to the vertical -axis, that is, S is foliated by round circles in × {t}, the centers of which are the same point on modulo t, where t Î (h_min,h_max ) Ì , and h_min, h_max are the maximum and minimum of vertical height of S respectively; and

(iii) there exists t₀ = such that × {t₀} divides S into two (upper and lower) symmetric parts.

PROOF. By the Gauss equation, the sectional curvature of S is bounded below by a positive constant, hence S is compact by the Bonnet-Myers theorem. By the Gauss-Bonnet theorem, S is topologically a sphere. By Corollary 4.2, we know there exists t₀ = such that the horizontal level × {t₀} divides S into two (upper and lower) symmetric parts.

We prove S is rotational in two steps 1) and 2).

1) S has a vertical strip of symmetry about every pair of antipodal points.

Fix a pair of antipodal points {p,–p} on ¶. Then ¶ is divided into two semi-circles joining p and –p. Let q denote the rotational angle from one semi-circle to the other (0 < q < p), and g(q) denote the semi-circle on joining p and –p, with the rotational angle q.

Since S Ì × and S is compact, the vertical strip P(q) = g(q) × is disjoint from S for sufficiently small q. Note the rotation on ² is an isometry. We may do the Alexander reflection through P(q), as q moves from 0 to p, to obtain a vertical strip of symmetry P(q₀) such that S is divided into two graphs of symmetry over a domain of P(q₀).

By the arbitrariness of p on ¶, we have proved 1).

2) Since any two such vertical strips of symmetry intersect in a line parallel to the vertical -axis, it is sufficient to prove all of these lines coincide.

Choose a horizontal surface (t) = × {t} whose intersection with S has at least two points.

Fix this t. Let S(t) = (t)Ç S. Since S is embedded and compact, S(t) is a simple closed curve on (t). Any vertical strip of symmetry P = g × of S corresponds to a semi-circle of symmetry g(t) = g × {t} of S(t) on (t). By 1), we know that every pair of antipodal points {p, –p} on ¶(t) determines a semi-circle of symmetry g of S(t).

We will look into the relation of all the semi-circles of symmetry {g(t)}. For simplification of notation, we omit t in g(t). Fix a semi-circle of symmetry g₀ on (t). Let g₁ be any other one, and b denote the angle between g₀ and g₁ (we may choose the direction of the angle such that, if the rotation from the oriented g₀ to the oriented g₁ is anti-clockwise, b is positive). Then the reflection of S(t) by g₁, followed by a reflection of S(t) by g₀, corresponds to a rotation of S(t) through an angle 2b about the intersection of g₀ and g₁, and leaves S(t) invariant. By this property of rotation and the arbitrariness of p Î ¶, we know all of the rotations of g are about the same point. Hence S(t) contains a circle and thus must be this circle. Thus we have proved that all of g intersect at the same point, and S(t) is rotational about this point on (t).

Therefore we have proved that S is a surface of revolution (rotational about a vertical line parallel to the -axis).

In the following, we discuss complete (hence compact) smooth surfaces of revolution, about a vertical line, in

² × of positive constant 2-mean curvature. We will give the parameterized equation of such surfaces.

Given o' Î ². Then {o'} × is a vertical line. Let S denote a complete surface of revolution about {o'} × , in ² × (that is to say that S is rotational about the vertical line {o'} × ).

Let p Î ² × , and let (f,q,t) (0 < f < p, 0 < q < 2p) denote the local coordinate of p where t denotes the -coordinate of and (f,q) denotes the spherical coordinate of ² about o', that is, f and q are the polar coordinate and azimuthal coordinate respectively. Then p = (sin f cos q, sin f sin q,cos f, t).

The generating curve l(s) of the rotational surface S is l(s) = (f(s),t(s)), where s is the arc-length parameter.

S can be denoted by (sin f(s) cos q,sin f(s) sin q,cos f(s), t(s)).

Take the unit normal N of S as N = (t' cos f cos q, t' cos f sin q, –t' sin f, –f'). Then the two principle curvatures of S are

and the 2-mean curvature of S is

Since s is the arc-length parameter, t'² + f'² = 1. Then t't" + f'f" = 0. So

Suppose y is the lowest point of S. We may choose s positive with y = l(0). We have t'(0) = 0. From l₂ = t' cot f, we know that f = 0, or p at y. Without loss of generality, we assume that f = 0 at y. This implies y = o' × {t_y} for some t_y Î .

Since H₂ > 0, f ¹ . Hence the domain of f is contained either in [0,) or in (,p]. Since we assume f(0) = 0, we have f Î [0,). This means that S stays in × , where is the open hemisphere of ² of the center o'.

Since y = l(0) is the lowest point, we have t'(s) > 0 and hence l₂(s) > 0 for sufficiently small positive s. But l₂ must have the same sign, so t'(s) > 0 for all s. Hence t increases as s increases and S must be embedded.

Suppose z = l(s₁) is the highest point S. Also we have f = 0 at z (i.e., z = o' × {t_z} for some t_z Î .

Hence the domain of s is [0,s₁], and f(0) = f(s₁) = 0; t'(0) = t'(s₁) = 0; f'(0) = 1, f'(s₁) = –1.

Since H₂ = –f"(cot f), we have f" < 0. This implies f' decreases from f(0) = 1 to f'(s₁) = –1. So as s increases from 0 to s₁, f first increases from 0 to f_max then decreases from f_max to 0.

By equation (5.3),

where C₁ is a constant to be determined by the boundary conditions.

By f(0) = 0 and f'(0) = 1, we have C₁ = 1. So

We have f_min = 0, f_max = f|_{f' = 0} = cos^–1exp(–).

Let u = f'(|u| < 1). We will give the equation of the generating curve l.

By equation (5.5), we have

Since u = f', = f" = –, we have

Then

where C is a real constant.

We have

Therefore, we obtain the equations (5.6) and (5.7) of f and t. As u decreases from 1 to –1, t increases from t_min to t_max, and f first increases from 0 to f_max then decreases from f_max to 0. Also S is symmetric about × {t₀}.

From the above analysis, we obtain that

PROPOSITION 5.1. Let S be a complete immersed surface of revolution (about a vertical line o' × , o' Î ²) in ² × with H₂ = constant > 0. Then S has the following characters:

(i) S is topologically a sphere and embedded; and

(ii) S stays in × , where denotes the open hemisphere of ² of the center o'; and

(iii) the generating curve of S can be denoted by l(u) = (f(u), t(u)) with parameter u (–1< u < 1), where t denotes the -coordinate of and f denotes the polar coordinate (about o') of ², as follows:

where C is a real constant.

The equation of l implies that there exists a horizontal level × {t₀}, t₀Î such that S divides into two (upper and lower) symmetric parts.

By Theorem 5.1 and Proposition 5.1, we can determine the generating curvature of S satisfying the conditions of Th. 5.1 as follows:

COROLLARY 5.1. Let

² be the unit sphere in ³ and be the open upper hemisphere in ². Let S be a complete orientable embedded surface in ² × with H₂ = constant > 0. If S Ì × , then S has the following properties:

The 2-mean curvature H₂ satisfies

(where f₀Î [0,) denotes the polar angle between the north pole of the open upper hemisphere and o').

Moreover, the generating curve of the rotational surface S can be denoted by l(u) = (f(u), t(u)) where –1< u < 1, and f denotes the polar coordinate (about o') of ², and:

where C is a real constant.

PROOF. We just need to prove H₂ > –. Since S Ì ² × , f₀ + f_max < . Here f_max denotes the maximum of f. Of course, we have f_max = f|_{f' = 0} = cos^–1 exp(–). By it, H₂ > –.

REMARK 5.1. We have proved that if S is a complete embedded surface in

² × Ì ² × of positive constant 2-mean curvature, S is rotationally symmetric about a vertical line. We conjecture this is true for immersed such S in ² × (also in ² × ). This is true if one assumes that the mean curvature is constant instead of positive constant H₂ under the condition that the genus of S is zero (Abresch and Rosenberg 2005).

ACKNOWLEDGMENTS

This work was done when the first author was visiting Université Paris 7 (Institut de Mathématiques de Jussieu), supported by a post-doctoral fellowship by Centre Nationale de la Recherche Scientifique (CNRS), France. She would like to thank Université Paris 7 for support and hospitality.

HOFFMAN D, LIRA J AND ROSENBERG H. 2005. Constant mean curvature surfaces in M × R. Trans Amer Math Soc. (In press).

Manuscript received on September 20, 2004; accepted for publication on January 14, 2005; contributed by HAROLD ROSENBERG*

• ABRESCH U AND ROSENBERG H. 2005. A Hopf differential for constant mean curvature surfaces in S × R and H × R Acta Math. (In press).
• ALEXANDROV AD. 1962. Uniqueness theorems for surfaces in the large, V. (Russian) Vestnik Leningrad. Univ. 13 1958 19: 5-8; English translation: Amer Math Soc Transl 21: 412-416.
• BARBOSA JL AND COLARES AG. 1997. Stability of hypersurfaces with constant r-mean curvature. Ann Global Anal Geom 15: 277-297.
• ELBERT MF. 2002. Constant positive 2-mean curvature hypersurfaces. Illinois. J Math 46: 247-267.
• HARDY G, LITTLEWOOD J AND POLYA G. 1989. Inequalities, 2nd. Ed., Cambridge, Univ. Press.
• HOPF H. 1983. Differential geometry in the large, Lecture Notes in Mathematics, 1000. Springer-Verlag, Berlin.
• KOREVAAR N, KUSNER R, MEEKS W AND SOLOMON B. 1992. Constant mean curvature surfaces in hyperbolic space. Amer J Math 114: 1-43.
• REILLY R. 1973. Variational properties of functions of the mean curvatures for hypersurfaces in space forms. J Differ Geom 8: 465-477.
• ROSENBERG H. 1993. Hypersurfaces of constant curvature in space forms. Bull Sci Math 117: 211-239.

*

Member Academia Brasileira de Ciências

Publication Dates

• Publication in this collection
  09 May 2005
• Date of issue
  June 2005

History

• Accepted
  14 Jan 2005
• Received
  20 Sept 2004