Abstracts
In this work we deal with surfaces immersed in R³ with constant mean curvature and circular boundary. We improve some global estimates for area and volume of such immersions obtained by other authors. We still establish the uniqueness of the spherical cap in some classes of cmc surfaces.
surfaces with boundary; constant mean curvature; spherical caps; area; volume
Neste artigo, estudamos superfícies imersas em R³ com curvatura média constante e bordo circular. Melhoramos algumas estimativas globais para área e volume destas imersões obtidas por outros autores. Estabelecemos, além disso, a unicidade da calota esférica em algumas classes de superfícies cmc.
Superfícies com bordo; Curvatura média constante; calota esférica; área; volume
MATHEMATICAL SCIENCES
Constant mean curvature surfaces with circular boundary in R3
Pedro A. Hinojosa
Universidade Federal da Paraíba (UFPB), CCEN - Departamento de Matemática, Cidade Universitária, 58051-900 João Pessoa, PB, Brasil
ABSTRACT
In this work we deal with surfaces immersed in R3 with constant mean curvature and circular boundary. We improve some global estimates for area and volume of such immersions obtained by other authors. We still establish the uniqueness of the spherical cap in some classes of cmc surfaces.
Key words: surfaces with boundary, constant mean curvature, spherical caps, area, volume.
RESUMO
Neste artigo, estudamos superfícies imersas em R3 com curvatura média constante e bordo circular. Melhoramos algumas estimativas globais para área e volume destas imersões obtidas por outros autores. Estabelecemos, além disso, a unicidade da calota esférica em algumas classes de superfícies cmc.
Palavras-chave: Superfícies com bordo, Curvatura média constante, calota esférica, área, volume.
1 INTRODUCTION AND STATEMENT OF RESULTS
The global structure and classification of compact surfaces immersed in a three space form with constant mean curvature (cmc-surfaces) had been the subject of a plenty of research papers in the last decades.
In contrast with the case of closed cmc surfaces, the structure and classification of cmc compact surfaces with nonempty boundary are almost unknown, also in the simplest case of circular boundary. The only known examples are the umbilical ones and some non embedded examples with genus bigger than two, constructed by Kapouleas (Kapouleas 1993). Barbosa (Barbosa 1990) studied the case where the surface is contained in a sphere of radius  and proved that such a surface must be a spherical cap. Later (Barbosa 1991) extended this result to the case where the surface is contained in a cylinder of radius
and proved that such a surface must be a spherical cap. Later (Barbosa 1991) extended this result to the case where the surface is contained in a cylinder of radius  . Barbosa and Jorge (Barbosa and Jorge 1994) and Alias, López and Palmer (Alias et al. 1999) proved that if the surface is stable then it must be a spherical cap.
. Barbosa and Jorge (Barbosa and Jorge 1994) and Alias, López and Palmer (Alias et al. 1999) proved that if the surface is stable then it must be a spherical cap.
The lack of examples and the analogy with the case without boundary become natural the question of the uniqueness of the umbilical examples under the following hypothesis (a problem nowadays known as spherical cap conjecture).
CONJECTURE. Let S be a compact surface with boundary ¶S and y: S ®
3 be an isometric immersion with non zero constant mean curvature H such that y(¶S) is a circle. If S has genus zero, then y(S) is a spherical cap.
If S is embedded, then y(S) is a spherical cap.
If M is a compact surface, with planar boundary, embedded in  3 with non zero constant mean curvature H and it is contained in one of the half spaces determined by the plane of the boundary, then the Alexandrov's method of reflection (Alexandrov 1958) shows that M has all the symetries of its boundary. Thus, if ¶M is a circle, M is a surface of revolution and therefore a spherical cap (Darboux 1914). In this way, the conjecture above is true for the subclass of embedded surfaces that are contained in one of the half spaces determined by the plane of the boundary.
3 with non zero constant mean curvature H and it is contained in one of the half spaces determined by the plane of the boundary, then the Alexandrov's method of reflection (Alexandrov 1958) shows that M has all the symetries of its boundary. Thus, if ¶M is a circle, M is a surface of revolution and therefore a spherical cap (Darboux 1914). In this way, the conjecture above is true for the subclass of embedded surfaces that are contained in one of the half spaces determined by the plane of the boundary.
In this work, we will consider the first item of the previous conjecture, that is, we will be interested in the case where S has genus zero. As usual we define the area and the volume of y respectively as:
and
where N represents the Gauss map of y, yu =  and yv =
and yv =  .
.
Notice that if y : S®
3 is an isometric immersion with constant mean curvature H ¹ 0 and y(¶S) is a plane curve of length L that limits a region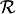 of area
of area 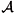 (
(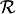 ), then, using the flux formula (Kusner 1985), it is easy to show that |H| <
), then, using the flux formula (Kusner 1985), it is easy to show that |H| < 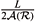 . In particular if y(¶S) is an unitary circle, we have |H| < 1. The initial demonstration of this fact was made by H. Heinz (Heinz 1969) and it doesn't use the flux formula. The equality |H| =
. In particular if y(¶S) is an unitary circle, we have |H| < 1. The initial demonstration of this fact was made by H. Heinz (Heinz 1969) and it doesn't use the flux formula. The equality |H| = 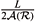 is characterized by the author in (Hinojosa 2002) without the hypothesis that the curve of the boundary is a circle.
is characterized by the author in (Hinojosa 2002) without the hypothesis that the curve of the boundary is a circle.
Now we will consider spherical caps of mean curvature H, whose boundary is an unitary circle. Let us denote, respectively, for A- and A+ the areas of the small and big caps. It is easy to see that:
López and Montiel (López and Montiel 1995) showed that if the immersion y is not umbilical, then
From this result and by using the Minkowski formula, the same authors (López and Montiel 1996) obtained estimates for the volume which do not depend on the mean curvature H. More precisely, they showed that if y is not umbilical, then
Our first result is an improvement of the estimates cited above establishing the following result.
THEOREM 1. If y is not umbilic, then A >  p and V >
p and V >  p.
p.
The estimates in the above theorem allow us to show uniqueness of the spherical caps in the class of immersions of the type above in which two of the three numbers A,V and H are fixed. In other terms, given real numbers A,V and H we define the following sets in the class of immersions y : S ®  3 such that y(¶S) is a circle and S has genus zero
3 such that y(¶S) is a circle and S has genus zero
CA,H
: =
{ y has constant mean curvature H and area A}.
CA,V
: =
{ y has area A and volume V}.
CH,V
: =
{ y has constant mean curvature H and volume V}.
We then are able to prove
THEOREM 2. If there is some spherical cap S Î CA,H or S Î CA,V, then S is the unique element of this set. Moreover, if |H| > 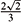 , the same conclusion is true for CH,V.
, the same conclusion is true for CH,V.
2 PROOF OF THEOREM 1
Let S be a genus zero oriented compact surface and y : S ®
3 be an isometric immersion with non zero constant mean curvature H. We suppose that y(¶S) is a circle which, without loss of generality, we may assume as being x2 + y2 = 1 in the plane z = 0. Let A and V be the area and the volume of y as defined respectively by the equations (1) and (2). Under these conditions, it is easy to verify thatD|y|2 = 4 (1 + H áN, yñ),
where N is the Gauss map of y. Using Stoke's Theorem we then obtain the so-called Minkowski formula
where n denotes the unit positively oriented co-normal vector field along ¶S. Since the geodesic curvature of y(¶S) is given by kg = -áy, nñ, we may write down the equation (4) in the form
However by using twice the Cauchy-Schwarz inequality it follows that
Now, by the flux formula (see Kusner 1985) we have that
Therefore we conclude that
and the equality occurs if and only if the immersion y is totally umbilical. Now, using the fact that |s|2 = 4H2 - 2K we obtain by integration that
By the Gauss-Bonnet theorem and equation (5) we obtain
Therefore
On the other hand, a result of Barbosa and Jorge (see Barbosa and Jorge 1994) establishes that if òS|s|2< 8p, then y is totally umbilical. From this, we conclude that if y is not totally umbilical, then
4H2A - 4p + 4(A - 3HV) > 8p.
So, 3p- H2A < A - 3HV and by equation (6) we have that if y is not totally umbilical, then
We now consider the following function g : (0,1] ® 
It is easy to see that this function has an absolute minimum at the point H0 =  and
and
Therefore,
This proves the first part of Theorem 1.
Now, the equations (6) and (8) imply that
In order to prove the second part of Theorem 1, we define the function
We verify easily that f has an absolute minimum at the point H1 =  and that f(H1) >
and that f(H1) >  p. This completes the proof of Theorem 1.
p. This completes the proof of Theorem 1.
3 PROOF OF THEOREM 2
We begin by studying the class CA,H. If there exists a spherical cap S in S Î CA,H, then A = A- or A = A+. Thus, by the equation (3) (Lopez and Montiel 1995) we conclude that any element of CA,H is totally umbilical.
Now, suppose that there exists a spherical cap S Î CA,V. We must prove that any y Î CA,V is totally umbilical. If this is not the case, then Theorem 1 implies that V >  p. Then, we may suppose that S is the larger cap. Let H and h be respectively the mean curvatures of y and S. If y is not umbilical, then by Theorem 1 we have
p. Then, we may suppose that S is the larger cap. Let H and h be respectively the mean curvatures of y and S. If y is not umbilical, then by Theorem 1 we have
Therefore H > h. On the other hand, A - 3hV = -p and, for the equation (4) we have A - 3HV = -
and, for the equation (4) we have A - 3HV = -
Now, it follows from equations (4) and (6) that
we conclude that 3V (H - h) < p - p
- p and since that H > h we have 3V(H - h) < 0. So, H < h, which contradicts the former inequality. From this contradiction, we have that y should be totally umbilical.
and since that H > h we have 3V(H - h) < 0. So, H < h, which contradicts the former inequality. From this contradiction, we have that y should be totally umbilical.
Finally, we consider the class CH,V. We suppose that there exists a spherical cap S Î CH,V with |H| > 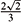 . If there exists a non totally umbilical y Î CH,V, then
. If there exists a non totally umbilical y Î CH,V, then
Since y is not totally umbilical, then y is not stable. Therefore,
S|s|2> 8p. Then, using formula (7), we obtain 4A(H2-1) - 4p + 12HV > 8p. Using the fact that A > A+, we have that 4H2A+ - 4p - 4(A+ - 3HV) > 8p. Now, replacing the value of A+ in the equation above, we obtain |H| <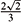 . However, by hypothesis, |H| >
. However, by hypothesis, |H| > 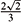 . From this contradiction, we conclude that y is totally umbilical.
. From this contradiction, we conclude that y is totally umbilical.
ACKNOWLEDGMENTS
I want to thank my advisor, Professor J. Lucas Barbosa, and also Professor A. G. Colares, by the encouragement and many helpful conversations. Special gratefulness to my colleage J. Herbert S. de Lira for the innumerable conversations and help.
Work partially supported by Programa de Apoio ao Desenvolvimento Científico e Tecnológico (PADCT) /CT-INFRA/Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) /Ministério da Ciência e Tecnologia (MCT) Grant # 620120/2004-5.
Manuscript received on July 27, 2005; accepted for publication on October 3, 2005; presented by JOÃO L.M. BARBOSA
E-mail: hinojosa@mat.ufpb.br
- ALEXANDROV AD. 1958. Uniqueness Theorems for Surfaces in the Large V. Vestnik Leningrad Univ 13(19): 5-8.
- ALIAS L, LÓPEZ R AND PALMER B. 1999. Stable Constant Mean Curvature Surfaces with Circular Boundary. Proc Amer Math Soc 127: 1195-1200.
- BARBOSA JLM. 1990. Hipersurfaces of Constant Mean Curvature on Rn+1 Bounded by an Euclidean Sphere. Geometry and Topology II, World Scientific Publishing Co Pte Ltd., p. 1-9.
- BARBOSA JLM. 1991. Constant Mean Curvature Surface Bounded by a Planar Curve. Mat Contemp 1: 3-15.
- BARBOSA JLM AND DO CARMO MP. 1984. Stability of Hypersurfaces with Constant Mean Curvature. Math Z 185: 339-353.
- BARBOSA JLM AND JORGE LP. 1994. Stable H-Surfaces Whose Boundary is S1(1). An Acad Bras Cienc 66: 259-263.
- DARBOUX G. 1914. Leçons sur la théorie générale des surfaces et les applications géometriques du calcul infinitésimal. Paris: Gauthier-Villars 1 part, 2 ed.
- HEINZ H. 1969. On the Nonexistence of a Surface of Constant Mean Curvature with Finite Area and Prescribed Rectifiable Boundary. Arch Rational Mech Anal 35: 249-252.
- HINOJOSA PA. 2002. Surfaces of Constant Mean Curvature in Euclidean 3-space Orthogonal to a Plane along its Boundary. An Acad Bras Cienc 74: 33-35.
- HOPF H. 1983. Differential Geometry in the Large. Lectures Notes in Mathematics, 1000, Springer-Verlag, Berlin.
- KAPOULEAS N. 1991. Compact Constant Mean Curvature Surfaces in Euclidean Three-Space. J Diff Geom 33: 683-715.
- KUSNER RB. 1985. Global Geometry of Extremal Surfaces in the Three-Space. Doctoral Thesis, University of California, Berkeley.
- LÓPEZ R AND MONTIEL S. 1995. Constant Mean Curvature Disc with Bounded Area. Proc Amer Math Soc 123: 1555-1558.
- LÓPEZ R AND MONTIEL S. 1996. Constant Mean Curvature Surfaces with Planar Boundary. Duke Math J 85: 583-604.
- WENTE HC. 1986. Counterexample to a Conjecture of H. Hopf. Pacific J Math 121: 193-243.
Publication Dates
-
Publication in this collection
08 Mar 2006 -
Date of issue
Mar 2006
History
-
Received
27 July 2005 -
Accepted
03 Oct 2005

























