Abstracts
We establish a method for giving lower bounds for the fundamental tone of elliptic operators in divergence form in terms of the divergence of vector fields. We then apply this method to the Lr operator associated to immersed hypersurfaces with locally bounded (r + 1)-th mean curvature Hr + 1 of the space forms Nn+ 1(c) of constant sectional curvature c. As a corollary we give lower bounds for the extrinsic radius of closed hypersurfaces of Nn+ 1(c) with Hr + 1 > 0 in terms of the r-th and (r + 1)-th mean curvatures. Finally we observe that bounds for the Laplace eigenvalues essentially bound the eigenvalues of a self-adjoint elliptic differential operator in divergence form. This allows us to show that Cheeger's constant gives a lower bounds for the first nonzero Lr-eigenvalue of a closed hypersurface of Nn+ 1(c).
fundamental tone; Lr operator; r-th mean curvature; extrinsic radius; Cheeger's constant
Estabelecemos um método para obter limites inferiores para o tom fundamental de operadores elípticos em forma divergente em termos do divergente de campos de vetores. Aplicamos esse método para os operadores Lr associados a hipersuperfícies imersas nas formas espaciais Nn(c) de curvatura seccional constante c com (r + 1)-curvatura média Hr + 1 localmente limitada. Obtemos como corolário limites inferiores para o raio extrínseco de hipersuperfícies compactas das formas espaciais Nn(c) com Hr + 1 > 0 em termos das r-ésima e r + 1-ésima curvatura médias. Finalmente, observamos que limites para os autovalores do Laplaciano essencialmente limitam os autovalores dos operadores elípticos em forma divergente. Isso permite mostrar que a constante de Cheeger limita inferiormente o primeiro autovalor não-nulo dos operadores Lr em hypersuperfícies compactas de Nn(c).
tom fundamental; operador Lr; r-curvatura média; raio extrínseco; constante de Cheeger
MATHEMATICAL SCIENCES
Fundamental tone estimates for elliptic operators in divergence form and geometric applications
Gregório P. BessaI; Luquésio P. JorgeI; Barnabé P. LimaII; José F. MontenegroI
IUniversidade Federal do Ceará - UFC, Departamento de Matemática - Campus do Pici, 60455-760 Fortaleza, CE, Brasil
IIUniversidade Federal do Piauí - UFPi, Departamento de Matemática - Campus Petrônio Portela, 64049-550 Teresina, PI, Brasil
ABSTRACT
We establish a method for giving lower bounds for the fundamental tone of elliptic operators in divergence form in terms of the divergence of vector fields. We then apply this method to the Lr operator associated to immersed hypersurfaces with locally bounded (r + 1)-th mean curvature Hr + 1 of the space forms Nn + 1(c) of constant sectional curvature c. As a corollary we give lower bounds for the extrinsic radius of closed hypersurfaces of Nn + 1(c) with Hr + 1 > 0 in terms of the r-th and (r + 1)-th mean curvatures. Finally we observe that bounds for the Laplace eigenvalues essentially bound the eigenvalues of a self-adjoint elliptic differential operator in divergence form. This allows us to show that Cheeger's constant gives a lower bounds for the first nonzero Lr-eigenvalue of a closed hypersurface of Nn + 1(c).
Key words: fundamental tone, Lr operator, r-th mean curvature, extrinsic radius, Cheeger's constant.
RESUMO
Estabelecemos um método para obter limites inferiores para o tom fundamental de operadores elípticos em forma divergente em termos do divergente de campos de vetores. Aplicamos esse método para os operadores Lr associados a hipersuperfícies imersas nas formas espaciais Nn(c) de curvatura seccional constante c com (r + 1)-curvatura média Hr + 1 localmente limitada. Obtemos como corolário limites inferiores para o raio extrínseco de hipersuperfícies compactas das formas espaciais Nn(c) com Hr + 1 > 0 em termos das r-ésima e r + 1-ésima curvatura médias. Finalmente, observamos que limites para os autovalores do Laplaciano essencialmente limitam os autovalores dos operadores elípticos em forma divergente. Isso permite mostrar que a constante de Cheeger limita inferiormente o primeiro autovalor não-nulo dos operadores Lr em hypersuperfícies compactas de Nn(c).
Palavras-chave: tom fundamental, operador Lr, r-curvatura média, raio extrínseco, constante de Cheeger.
INTRODUCTION
Let W be a domain in a smooth Riemannian manifold M and let F : W ® End (TW) be a smooth symmetric and positive definite section of the bundle of all endomorphisms of TW. Each section F is associated to a second order self-adjoint elliptic operator LF(f) = div (F grad f), f Î C2(W). Observe that when F is the identity section then LF = D, the Laplace operator. Recall that the LF-fundamental tone of W is given by
If W is bounded with smooth boundary ¶W ¹ Æ, the LF-fundamental tone of W coincides with the first eigenvalue  (W) of the Dirichlet eigenvalue problem LF u + l u = 0 on W, with u|¶W = 0, u Î C2(W) Ç Cº
(W) of the Dirichlet eigenvalue problem LF u + l u = 0 on W, with u|¶W = 0, u Î C2(W) Ç Cº \ {0}. If W is bounded with empty boundary ¶W = Æ then
\ {0}. If W is bounded with empty boundary ¶W = Æ then  (W) = 0.
(W) = 0.
A basic problem in Riemannian geometry is what lower and upper bounds for  (W) can be obtained in terms of Riemannian invariants. In this paper we show that the method established by Bessa and Montenegro (Bessa and Montenegro 2004) that gives lower bounds for the D-fundamental tone can be extended for self-adjoint elliptic operators LF, (Theorem 2.1). Then we consider immersed hypersurfaces j : M ®
(W) can be obtained in terms of Riemannian invariants. In this paper we show that the method established by Bessa and Montenegro (Bessa and Montenegro 2004) that gives lower bounds for the D-fundamental tone can be extended for self-adjoint elliptic operators LF, (Theorem 2.1). Then we consider immersed hypersurfaces j : M ® 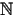 n+1(c) of the (n + 1)-dimensional simply connected space form
n+1(c) of the (n + 1)-dimensional simply connected space form 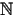 n+1(c) of constant sectional curvature c Î {1,0,-1} with locally bounded (r + 1)-th mean curvature such that the differential operators Lr, r Î { 0,1,..., n} are elliptic. We give lower bounds for the Lr-fundamental tone of domains W Ì j-1 (
n+1(c) of constant sectional curvature c Î {1,0,-1} with locally bounded (r + 1)-th mean curvature such that the differential operators Lr, r Î { 0,1,..., n} are elliptic. We give lower bounds for the Lr-fundamental tone of domains W Ì j-1 (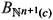 (p, R)), in terms of the r-th and (r + 1)-th mean curvatures Hr, Hr + 1, (Theorem 3.2), where
(p, R)), in terms of the r-th and (r + 1)-th mean curvatures Hr, Hr + 1, (Theorem 3.2), where 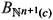 (p, R) is the geodesic ball of
(p, R) is the geodesic ball of 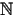 n+1(c) centered at p with radius R. From these estimates we derive three geometric corollaries 3.4, 3.5 and 3.8 that should be viewed as an extension of a result of Jorge and Xavier (Jorge and Xavier 1981). It should be mentioned that these corollaries are related to results due to Vlachos (Vlachos 1997) and to Fontenele and Silva (Fontenele and Silva 2001), see Remark 3.7. In Theorem 3.10 we consider immersed hypersurfaces M of
n+1(c) centered at p with radius R. From these estimates we derive three geometric corollaries 3.4, 3.5 and 3.8 that should be viewed as an extension of a result of Jorge and Xavier (Jorge and Xavier 1981). It should be mentioned that these corollaries are related to results due to Vlachos (Vlachos 1997) and to Fontenele and Silva (Fontenele and Silva 2001), see Remark 3.7. In Theorem 3.10 we consider immersed hypersurfaces M of 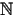 n+1(c) such that the operators Lr and Ls, 0 < r, s < n are elliptic and we compare the Lr and Ls fundamental tones
n+1(c) such that the operators Lr and Ls, 0 < r, s < n are elliptic and we compare the Lr and Ls fundamental tones 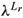 (W)
(W) (W) of domains W Ì M Ì
(W) of domains W Ì M Ì 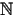 n+1(c). In section 4 we observe (Theorem 4.1) that in order to get bounds for the eigenvalues of a self-adjoint elliptic differential operator LF we essentially need bounds for the Laplace operator eigenvalues. This allows us to use Cheeger's constant to give lower bounds for the first nonzero Lr-eigenvalue of a closed hypersurface of
n+1(c). In section 4 we observe (Theorem 4.1) that in order to get bounds for the eigenvalues of a self-adjoint elliptic differential operator LF we essentially need bounds for the Laplace operator eigenvalues. This allows us to use Cheeger's constant to give lower bounds for the first nonzero Lr-eigenvalue of a closed hypersurface of 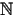 n+1(c). The results are stated and discussed in Sections 2, 3 and 4 and the proofs are given in Section 5.
n+1(c). The results are stated and discussed in Sections 2, 3 and 4 and the proofs are given in Section 5.
LF-FUNDAMENTAL TONE ESTIMATES
Our main estimate is the following method for giving lower bounds for LF-fundamental tone of arbitrary domains of Riemannian manifolds. It extends the version of Barta's theorem (Barta 1937) proved by Cheng-Yau in (Cheng and Yau 1977). It is the same proof (with proper modifications) of a generalization of Barta's theorem proved in (Bessa and Montenegro 2004).
THEOREM 2.1. Let W be a domain in a Riemannian manifold and let F : W® End (TW) be a smooth symmetric and positive definite section of End (TW). Then the LF-fundamental tone of W has the following lower bound
If W is bounded and with piecewise smooth boundary ¶W ¹ Æ then we have equality in (2).
Where  (W) is the set of all smooth vector fields on W.
(W) is the set of all smooth vector fields on W.
GEOMETRIC APPLICATIONS
Consider the linearized operator Lr of the (r + 1)-mean curvature
arising from normal variations of a hypersurface M immersed into the (n + 1)-dimensional simply connected space form 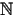 n+1(c) of constant sectional curvature c Î {1,0,-1}, where Sr + 1 is the (r + 1)-th elementary symmetric function of the principal curvatures k1, k2,..., kn, see (Reilly 1973) and (Rosenberg 1993) for details. Recall that the elementary symmetric function of the principal curvatures are given by
n+1(c) of constant sectional curvature c Î {1,0,-1}, where Sr + 1 is the (r + 1)-th elementary symmetric function of the principal curvatures k1, k2,..., kn, see (Reilly 1973) and (Rosenberg 1993) for details. Recall that the elementary symmetric function of the principal curvatures are given by
Letting A = - ( h) be the shape operator of M, where
h) be the shape operator of M, where  is the Levi-Civita connection of
is the Levi-Civita connection of 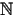 n+1(c) and h a globally defined unit vector field normal to M, we can recursively define smooth symmetric sections Pr : M ® End (TM), for r = 0, 1,..., n, called the Newton operators, setting P0 = I and Pr = Sr Id - APr - 1 so that Pr(x) : Tx M ® Tx M is a self-adjoint linear operator with the same eigenvectors as the shape operator A. The operator Lr is the second order self-adjoint differential operator
n+1(c) and h a globally defined unit vector field normal to M, we can recursively define smooth symmetric sections Pr : M ® End (TM), for r = 0, 1,..., n, called the Newton operators, setting P0 = I and Pr = Sr Id - APr - 1 so that Pr(x) : Tx M ® Tx M is a self-adjoint linear operator with the same eigenvectors as the shape operator A. The operator Lr is the second order self-adjoint differential operator
associated to the section Pr. However, the sections Pr may be not positive definite and then the operators Lr may not be elliptic. However, there are geometric hypothesis that imply the ellipticity of Lr, see for instance, Reilly 1973, Caffarelli et al. 1985, Korevaar 1988 or Barbosa and Colares 1997. Here we will not impose geometric conditions to guarantee ellipticity of the Lr, except in corollary 3.5. Instead we will ask the ellipticity on the set of hypothesis. It is known the ordered eigenvalues { (x) < ... <
(x) < ... <  (x)} of Pr (x) depend continuously on x Î M. (Kato 1976 pages 106-109). In fact, this proof can be pushed to prove that they are Lipschitz thus differentiable almost everywhere. In addition, the respective eigenvectors {e1(x),..., en(x)} form a smooth orthonormal frame in a neighborhood of every point. Set n(Pr) = supxÎ M{
(x)} of Pr (x) depend continuously on x Î M. (Kato 1976 pages 106-109). In fact, this proof can be pushed to prove that they are Lipschitz thus differentiable almost everywhere. In addition, the respective eigenvectors {e1(x),..., en(x)} form a smooth orthonormal frame in a neighborhood of every point. Set n(Pr) = supxÎ M{ (x)} and µ(Pr) = infx Î M{
(x)} and µ(Pr) = infx Î M{ (x)} . Observe that if µ(Pr) > 0 then Pr is positive definite, thus Lr is elliptic.
(x)} . Observe that if µ(Pr) > 0 then Pr is positive definite, thus Lr is elliptic.
We need the following definition of locally bounded (r + 1)-th mean curvature hypersurface in order to state our next result.
DEFINITION 3.1. An oriented immersed hypersurface j : M  N of a Riemannian manifold N is said to have locally bounded (r + 1)-th mean curvature Hr + 1 if for any p Î N and R > 0, the number
N of a Riemannian manifold N is said to have locally bounded (r + 1)-th mean curvature Hr + 1 if for any p Î N and R > 0, the number
is finite. Here BN(p, R) Ì N is the geodesic ball of radius R with center at p Î N.
Our next result generalizes in some aspects the main application of (Bessa and Montenegro 2003). There the first and fourth authors give lower bounds for D-fundamental tone of domains in submanifolds with locally bounded mean curvature in complete Riemannian manifolds.
THEOREM 3.2. Let j : M
n+1(c) be an oriented hypersurface immersed with locally bounded (r + 1)-th mean curvature Hr + 1 for some r < n - 1 and with µ(Pr ) > 0. Let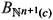 (p, R) be the geodesic ball centered at p Î
(p, R) be the geodesic ball centered at p Î 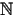 n+1(c) with radius R and W Ì j-1
n+1(c) with radius R and W Ì j-1 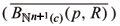 be a connected component. Then the Lr-fundamental tone
be a connected component. Then the Lr-fundamental tone 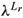 (W) of W has the following lower bounds.
(W) of W has the following lower bounds.
i. For c = 1 and 0 < R < cot-1
we have that
ii. For c < 0, hr + 1(p, R) ¹ 0 and 0 < R <  we have that
we have that
iii. If c < 0, hr + 1(p, R) = 0 and R > 0 we have that
DEFINITION 3.3. Let j : M  N be an isometric immersion of a closed Riemannian manifold into a complete Riemannian manifold N. For each x Î N, let r(x) = supy Î MdistN(x, j(y)). The extrinsic radius Re(M) of M is defined by
N be an isometric immersion of a closed Riemannian manifold into a complete Riemannian manifold N. For each x Î N, let r(x) = supy Î MdistN(x, j(y)). The extrinsic radius Re(M) of M is defined by
Moreover, there is a point x0Î N called the barycenter of j(M) in N such that Re(M) = r(x0).
COROLLARY 3.4. Let j : M 
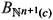 (R) Ì
(R) Ì 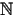 n+1(c) be a complete oriented hypersurface with bounded (r + 1)-th mean curvature Hr + 1 for some r < n - 1, R chosen as in Theorem (3.2). Suppose that µ(Pr ) > 0 so that the Lr operator is elliptic. Then M is not closed.
n+1(c) be a complete oriented hypersurface with bounded (r + 1)-th mean curvature Hr + 1 for some r < n - 1, R chosen as in Theorem (3.2). Suppose that µ(Pr ) > 0 so that the Lr operator is elliptic. Then M is not closed.
COROLLARY 3.5. Let j : M
n+1(c)1 1 If c = 1 suppose that n+1( c) is the open hemisphere of . , c Î {1,0,-1} be an oriented closed hypersurface with Hr + 1 > 0. Then there is an explicit constant Lr = Lr (c, infM Sr , supM Sr + 1) > 0 such that the extrinsic radius Re(M) > Lr.i. For c = 1, Lr = cot-1 .
.
ii. For c Î {0, -1}, Lr =  .
.
REMARK 3.6. The hypothesis Hr + 1 > 0 implies that Hj > 0 and Lj are elliptic for j = 0, 1,...r, see Barbosa and Colares 1997, Caffarelli et al. 1985 or Korevaar 1988. Thus in fact have that Re > max{L0,..., Lr}.
REMARK 3.7. Jorge and Xavier, (Jorge and Xavier 1981) proved the inequalities of Corollary 3.5 when r = 0 for complete submanifolds with scalar curvature bounded from below contained in a compact ball of a complete Riemannian manifold. Moreover, for c = -1 their inequality is slightly better. It is possible to give sharp estimates for the extrinsic radius of a closed hypersurface of 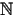 n+1(c) in terms of supM|Hr| alone. Vlachos (Vlachos 1997) proved a result that implies that, for each
n+1(c) in terms of supM|Hr| alone. Vlachos (Vlachos 1997) proved a result that implies that, for each
if c = 0, c = 1 or c = -1 respectively, and that in any case the equality holds if and only if M is a geodesic sphere of the ambient space. The result of Vlachos was extended to any ambient space by Fontenele and Silva (Fontenele and Silva 2001).
REMARK 3.8. An interesting question is: Is it true that any closed oriented hypersurface with  (M) > 0 and Hr + 1 = 0 intersect every great circle? For r = 0 it is true and it was proved by T. Frankel, (Frankel 1966).
(M) > 0 and Hr + 1 = 0 intersect every great circle? For r = 0 it is true and it was proved by T. Frankel, (Frankel 1966).
We now consider immersed hypersurfaces j : M 
THEOREM 3.9. Let j : M
n+1(c) be an oriented n-dimensional hypersurface M immersed into the (n + 1)-dimensional simply connected space form of constant sectional curvature c and µ(Pr ) > 0 and µ(Ps ) > 0, 0< s, r < n - 1. Let W Ì M be a domain with compact closure and piecewise smooth nonempty boundary. Then the Lr and Ls fundamental tones satisfies the following inequalities
From (9) we have in particular that
CLOSED EIGENVALUE PROBLEM
Let M be a closed hypersurface of a simply connected space form 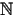 n+1(c). The interesting problem is what bounds can one obtain for the first nonzero Lr-eigenvalue
n+1(c). The interesting problem is what bounds can one obtain for the first nonzero Lr-eigenvalue  (M) in terms of the geometries of M and of the ambient space. Upper bounds for the first nonzero D-eigenvalue or even for the first nonzero Lr-eigenvalue, r > 1 have been obtained by many authors in contrast with lower bounds that are rare. For instance, Reilly (Reilly 1977) extending earlier result of Bleecker and Weiner (Bleecker and Weiner 1976) obtained upper bounds for
(M) in terms of the geometries of M and of the ambient space. Upper bounds for the first nonzero D-eigenvalue or even for the first nonzero Lr-eigenvalue, r > 1 have been obtained by many authors in contrast with lower bounds that are rare. For instance, Reilly (Reilly 1977) extending earlier result of Bleecker and Weiner (Bleecker and Weiner 1976) obtained upper bounds for  (M) of a closed submanifold M of
(M) of a closed submanifold M of 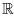 m in terms of the total mean curvature of M. Reilly's result applied to compact submanifolds of the sphere M Ì
m in terms of the total mean curvature of M. Reilly's result applied to compact submanifolds of the sphere M Ì  m+1(1), this latter viewed as a hypersurface of the Euclidean space
m+1(1), this latter viewed as a hypersurface of the Euclidean space  m+1(1) Ì
m+1(1) Ì 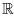 m+2 obtains upper bounds for
m+2 obtains upper bounds for  (M), see Alencar, Do Carmo and Rosenberg in Alencar et al. 1993. Heintze (Heintze 1988) extended Reilly's result to compact manifolds and Hadamard manifolds
(M), see Alencar, Do Carmo and Rosenberg in Alencar et al. 1993. Heintze (Heintze 1988) extended Reilly's result to compact manifolds and Hadamard manifolds  . In particular for the hyperbolic space
. In particular for the hyperbolic space  n+1. The best upper bounds for the first nonzero D-eigenvalue of closed hypersurfaces M of
n+1. The best upper bounds for the first nonzero D-eigenvalue of closed hypersurfaces M of  n+1 in terms of the total mean curvature of M was obtained by El Soufi and Ilias (Soufi and Ilias 1992). Regarding the Lr operators, Alencar, Do Carmo and Rosenberg (Alencar et al. 1993) obtained sharp (extrinsic) upper bound the first nonzero eigenvalue
n+1 in terms of the total mean curvature of M was obtained by El Soufi and Ilias (Soufi and Ilias 1992). Regarding the Lr operators, Alencar, Do Carmo and Rosenberg (Alencar et al. 1993) obtained sharp (extrinsic) upper bound the first nonzero eigenvalue  (M) of the linearized operator Lr of compact hypersurfaces M of
(M) of the linearized operator Lr of compact hypersurfaces M of 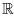 m+1 with Sr+1 > 0. Upper bounds for
m+1 with Sr+1 > 0. Upper bounds for  (M) of compact hypersurfaces of
(M) of compact hypersurfaces of  n+1,
n+1,  n+1 under the hypothesis that Lr is elliptic were obtained by Alencar, Do Carmo, Marques in (Alencar et al. 2001) and by Alias and Malacarne in (Alias and Malacarne 2004) see also the work of Veeravalli (Veeravalli 2001). On the other hand, lower bounds for
n+1 under the hypothesis that Lr is elliptic were obtained by Alencar, Do Carmo, Marques in (Alencar et al. 2001) and by Alias and Malacarne in (Alias and Malacarne 2004) see also the work of Veeravalli (Veeravalli 2001). On the other hand, lower bounds for  (M) of closed hypersurfaces M Ì
(M) of closed hypersurfaces M Ì 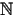 n+1(c) are not so well studied as the upper bounds, except for r = 0 in which case L0 = D. In this paper we make a simple observation (Theorem 4.1) that to obtain lower and upper bounds for the LF-eigenvalues (Dirichlet or Closed eigenvalue problem) it is enough to obtain lower and upper bounds for the eigenvalues of F and for the eigenvalues for the Laplacian in the respective problem. When applied to the Lr operators (supposing them elliptic) we obtain lower bounds for closed hypersurfaces of the space forms via Cheeger's lower bounds for the first D-eigenvalue of closed manifolds. Let {µ1(x) < ... < µn(x)} be the ordered eigenvalues of F(x). Setting n(F) = supx Î W{µn(x)} and µ(F) = infx Î W{µ1(x)} we have the following theorem.
n+1(c) are not so well studied as the upper bounds, except for r = 0 in which case L0 = D. In this paper we make a simple observation (Theorem 4.1) that to obtain lower and upper bounds for the LF-eigenvalues (Dirichlet or Closed eigenvalue problem) it is enough to obtain lower and upper bounds for the eigenvalues of F and for the eigenvalues for the Laplacian in the respective problem. When applied to the Lr operators (supposing them elliptic) we obtain lower bounds for closed hypersurfaces of the space forms via Cheeger's lower bounds for the first D-eigenvalue of closed manifolds. Let {µ1(x) < ... < µn(x)} be the ordered eigenvalues of F(x). Setting n(F) = supx Î W{µn(x)} and µ(F) = infx Î W{µ1(x)} we have the following theorem.
THEOREM 4.1. Let  (W) denote the LF-fundamental tone of W if W is unbounded or ¶W ¹ Æ and the first nonzero LF-eigenvalue
(W) denote the LF-fundamental tone of W if W is unbounded or ¶W ¹ Æ and the first nonzero LF-eigenvalue  (W) if W is a closed manifold. Then
(W) if W is a closed manifold. Then  (W) satisfies the following inequalities,
(W) satisfies the following inequalities,
where lD(W) is the D-fundamental tone of W or the first nonzero D-eigenvalue of W.
Let M be a closed n-dimensional Riemannian manifold, Cheeger (Cheeger 1970) defined the following constant given by
where S Ì M ranges over all connected closed hypersurfaces dividing M in two connected components, i.e. M = W1È W2, W1Ç W2 = Æ such that S = ¶W1 = ¶W2 and he proved that the first nonzero D-eigenvalue  (M) > h(M)2/4.
(M) > h(M)2/4.
COROLLARY 4.2. Let j : M
n+1(c), c Î {1, 0, -1}2 2 If c = 1 suppose that n+1( c) is the open hemisphere of . be an oriented closed hypersurface with Hr + 1 > 0. Then the first nonzero Lr-eigenvalue of M has the following lower bound
PROOF OF THE RESULTS
PROOF OF THEOREM 2.1.
Let W be an arbitrary domain, X be a smooth vector field on W and f Î  (W). The vector field f 2FX has compact support supp (f 2FX) Ì supp (f) Ì W. Let S be a regular domain containing the support of f. We have by the divergence theorem that
(W). The vector field f 2FX has compact support supp (f 2FX) Ì supp (f) Ì W. Let S be a regular domain containing the support of f. We have by the divergence theorem that
Therefore
By the variational formulation (1) of  (W) this inequality above implies that
(W) this inequality above implies that
When W is a bounded domain with smooth boundary ¶W ¹ Æ then  (W) =
(W) =  (W). This proof above shows that
(W). This proof above shows that
Let v Î C2(W) Ç Cº be a positive first LF-eigenfunction3
3
v Î
C
2(W) Ç
(W) if ¶W is not smooth.
of W and if we set X0 = -grad log(v) we have that
be a positive first LF-eigenfunction3
3
v Î
C
2(W) Ç
(W) if ¶W is not smooth.
of W and if we set X0 = -grad log(v) we have that
This proves (3).
PROOF OF THEOREM 3.2 AND COROLLARIES 3.4, 3.5 AND 3.8
We start this section stating few lemmas necessary to construct the proof of Theorem 3.2. The first lemma was proved in (Jorge and Koutrofiotis 1980) for the Laplace operator and for the Lr operator in (Lima 2000). We reproduce its proof to make the exposition complete.
LEMMA 5.1. Let j : M
n+1(c) be a hypersurface immersed in (n + 1)-dimensional simply connected space form n+1(c) of constant sectional curvature c. Let g : n+1(c) ®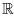 be a smooth function and set f = g
be a smooth function and set f = g 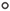 j. Identify X Î TpM with dj(p) X Î Tj(p)j(M) then we have that
j. Identify X Î TpM with dj(p) X Î Tj(p)j(M) then we have that
PROOF. Each Pr is also associated to a second order self-adjoint differential operator defined by  f = Trace (Pr Hess (f)) see (Cheng and Yau 1977, Hartmann 1978). We have that
f = Trace (Pr Hess (f)) see (Cheng and Yau 1977, Hartmann 1978). We have that
Rosenberg (Rosenberg 1993) proved that when the ambient manifold is the simply connected space form
n+1(c) then Trace (ÑPr) grad º 0 , see also (Reilly 1973). Thus one has that Lrf = Trace (Pr Hess (f)). Using Gauss equation to compute Hess (f) we obtain
where áa(X, Y), hñ = áA(X), Yñ. Let {ei} be an orthonormal frame around p that diagonalize the section Pr so that Pr(x)(ei) =  (x)ei. Thus
(x)ei. Thus
Substituting (19) into (20) we have that
Here Hess f (X) = ÑX grad f and Hess f(X, Y) = áÑX grad f, Yñ. The next two lemmas we are gong to present are well known and their proofs are easily found in the literature thus we will omit them here.
LEMMA 5.2 [Hessian Comparison Theorem]. Let M be a complete Riemannian manifold and x0, x1Î M. Let g : [0, r(x1) ] ® M be a minimizing geodesic joining x0 and x1 where r(x) is the distance function distM(x0, x). Let K be the sectional curvatures of M and u(r), defined below.
Let X = X^ + XTÎ TxM, XT = áX, g'ñg' and áX^, g'ñ = 0. Then
See (Schoen and Yau 1994) for a proof.
LEMMA 5.3. Let p Î M and 1< r < n - 1, let {ei} be an orthonormal basis of TpM such that Pr(ei) =  ei and A(ei ) = kiei. Then
ei and A(ei ) = kiei. Then
i. Trace (Pr) = 
 = (n - r)Sr
= (n - r)Sr
ii. Trace (A Pr) =  ki
ki = (r + 1)Sr + 1
= (r + 1)Sr + 1
In particular, if the Newton operator Pr is positive definite then Sr > 0.
To prove Theorem (3.2) set g : B(p, R) Ì 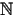 n+1(c) ®
n+1(c) ® 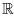 given by g = R2 - r2 , where r is the distance function (r(x) = dist (x, p)) of
given by g = R2 - r2 , where r is the distance function (r(x) = dist (x, p)) of 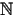 n+1(c). Setting f = g
n+1(c). Setting f = g  j we obtain by (17) that
j we obtain by (17) that
since Trace (A Pr) = (r + 1) · Sr + 1. Letting X = -grad log f we have that
then by Theorem (2.1) we have that
Computing the Hessian of g we have that
Therefore we have that
Setting  = ágrad r, eiñgrad r and
= ágrad r, eiñgrad r and  = ei -
= ei -  , by the Hessian Comparison Theorem we have that
, by the Hessian Comparison Theorem we have that
and
From (28) and (29) we have that
If c < 0 then r · u(r) > 1 thus from (30) we have that
If c > 0 then r · u(r) = r ·  · cot[
· cot[ r] < 1 thus from (30) we have that
r] < 1 thus from (30) we have that
To prove the Corollaries (3.4) and (3.5) observe that the hypotheses µ(Pr)(M) > 0 (in Corollary 3.4) and Hr + 1 > 0 (in Corollary 3.5) imply that the Lr is elliptic. If the immersion is bounded (contained in a ball of radius R, for those choices of R) and M is closed we would have by one hand that the Lr-fundamental tone would be zero and by Theorem (3.2) that it would be positive. Then M can not be closed if the immersion is bounded. On the other hand if M is closed a ball of radius R centered at the barycenter of M could not contain M because the fundamental tone estimates for any connected component W Ì j-1(j(M) Ç 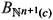 (p, R) is positive. Showing that M ¹ W.
(p, R) is positive. Showing that M ¹ W.
PROOF OF THEOREM 3.9.
Let j : W 
Consider {ei} be an orthonormal basis such that Prei =  ei and Psei =
ei and Psei =  ei. Letting Y =
ei. Letting Y =  yiei then
yiei then
Combining (33) with (34) and by Theorem (2.1) we have that
for every 0 < k <  . This proves (9).
. This proves (9).
PROOF OF THEOREM 4.1.
Recall that for any smooth symmetric section F : W ® End (TW) there is an open and dense subset U Ì W where the ordered eigenvalues {µ1(x) < ... < µn(x)} of F(x) depend continuously in all W. In addition, the respective eigenvectors {e1(x),..., en(x)} form a smooth orthonormal frame in a neighborhood of every point of W, see (Kato 1976). Let f Î  (W) \ {0} (f Î C2(W) with fWf = 0) be an admissible function for (the closed LF-eigenvalue problem if W is a closed manifold) the Dirichlet LF-eigenvalue problem. It is clear that f is an admissible function for the respective D-eigenvalue problem. Writing grad f (x) =
(W) \ {0} (f Î C2(W) with fWf = 0) be an admissible function for (the closed LF-eigenvalue problem if W is a closed manifold) the Dirichlet LF-eigenvalue problem. It is clear that f is an admissible function for the respective D-eigenvalue problem. Writing grad f (x) =  ei(f)ei(x) we have that
ei(f)ei(x) we have that
From (36) we have that
and
Taking the infimum over all admissible functions in (38) we obtain (11).
Manuscript received on October 31, 2005; accepted for publication on April 17, 2006; presented by MANFREDO DO CARMO
Correspondence to: Gregório P. Bessa
E-mail: bessa@mat.ufc.br
- ALENCAR H, DO CARMO M AND ROSENBERG H. 1993. On the first eigenvalue of the linearized operator of the r-th mean curvature of a hypersurface. Ann Global Anal Geom 11: 387-395.
- ALENCAR H, DO CARMO M AND MARQUES FC. 2001. Upper bounds for the first eigenvalue of the operator Lr and some applications. Illinois J of Math 45: 851-863.
- ALIAS L AND MALACARNE M. 2004. Sharp upper bounds for the first positive eigenvalue of the linearized operator of the higher order mean curvature of closed hypersurfaces into a Riemannian space form. Illinois J Math 48: 219-240.
- BARBOSA JL AND COLARES AG. 1997. Stability of hypersurfaces with constant r-mean curvature. Ann Global Anal Geom 15: 277-297.
- BARTA J. 1937. Sur la vibration fundamentale d'une membrane. C R Acad Sci 204: 472-473.
- BESSA GP AND MONTENEGRO JF. 2003. Eigenvalue estimates for submanifolds with locally bounded mean curvature. Ann Global Anal Geom 24: 279-290.
- BESSA GP AND MONTENEGRO JF. 2004. An Extension of Barta's Theorem and Geometric Applications. ArchivX Paper Id: math.DG/0308099.
- BLEECKER D AND WEINER J. 1976. Extrinsic bounds for l1 of D on a compact manifold. Comment Math Helv 51: 601-609.
- CAFFARELLI L, NIRENBERG L AND SPRUCK J. 1985. The Dirichlet problem for nonlinear second order elliptic equations III. Functions of the eigenvalues of the Hessian. Acta Math 155: 261-301.
- CHEEGER J. 1970. A lower bound for the smallest eigenvalue of the Laplacian Problems in Analysis. Princenton University Press, Princenton, New Jersey, p. 195-199.
- CHENG SY AND YAU ST. 1977. Hypersurfacces with Constant Scalar Curvature. Math Ann 225: 195-204.
- FONTENELE F AND SILVA S. 2001. A tangency principle and applications. Illinois J of Math 45: 213-228.
- FRANKEL T. 1966. On the fundamental group of a compact minimal submanifold. Ann of Math 83: 68-73.
- HARTMANN P. 1978. On complete hypersurfaces of nonnegative sectional curvatures and constant m mean curvature. Trans AMS 245: 363-374.
- HEINTZE E. 1988. Extrinsic upper bound for l1 Math Ann 280: 389-402.
- JORGE LP AND KOUTROFIOTIS D. 1980. An estimate for the curvature of bounded submanifolds. Amer J of Math 103: 711-725.
- JORGE LP AND XAVIER F. 1981. An inequality between the exterior diameter and the mean curvature of bounded immersions. Math Z 178: 77-82.
- KATO T. 1976. Perturbation Theory for Linear Operators. Grundlehren der mathematischen Wissenschaften, Springer-Verlag 132: 122-124.
- KOREVAAR N. 1988. Sphere theorems via Alexandrov for constant Weingarten curvature hypersurfaces. Appendix to a Note of A. Ros. J Diff Geom 27: 221-223.
- LIMA BP. 2000. Omori-Yau Maximum Principle for the Operator Lr and its Applications, Doctoral Thesis, Universidade Federal do Ceará-UFC.
- REILLY R. 1973. Variational properties of functions of the mean curvatures for hypersurfaces in space forms. J Differential Geom 8: 465-477.
- REILLY R. 1977. On the first eigenvalue of the Laplacian for compact submanifolds of the Euclidean space. Comment Math Helv 52: 525-533.
- ROSENBERG H. 1993. Hypersurface of Constant curvatures in space forms. Bull Sc Math 117: 211-239.
- SOUFI AE AND ILIAS S. 1992. Une inegalite du type "Reilly" pour les sous-varietes de l'espace hyperbolique. Comm Math Helv 67: 167-181.
- SCHOEN R AND YAU ST. 1994. Lectures on Differential Geometry. Conference Proceedings and Lecture Notes. In: Geometry and Topology 1.
- VEERAVALI A. 2001. On the first Laplacian eigenvalue and the center of gravity of compact hypersurfaces. Comment Math Helv 76: 155-160.
- VLACHOS T. 1997. A characterization for geodesic spheres in space forms. Geom Dedicata 68: 73-78.
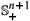 .
. 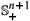 .
.  (W) if ¶W is not smooth.
(W) if ¶W is not smooth. Publication Dates
-
Publication in this collection
18 Aug 2006 -
Date of issue
Sept 2006
History
-
Accepted
17 Apr 2006 -
Received
31 Oct 2005















































