Finitely curved orbits of complex polynomial vector fields

Abstracts

This note is about the geometry of holomorphic foliations. Let X be a polynomial vector field with isolated singularities on C². We announce some results regarding two problems: 1. Given a finitely curved orbit L of X, under which conditions is L algebraic? 2. If X has some non-algebraic finitely curved orbit L what is the classification of X? Problem 1 is related to the following question: Let C <FONT FACE=Symbol>Ì</FONT> C² be a holomorphic curve which has finite total Gaussian curvature. IsC contained in an algebraic curve?

Holomorphic foliations; polynomial vector fields; algebraic curves; finite total curvature

Esta nota versa sobre a geometria de folheações holomorfas. Seja X um campo vetorial polinomial complexo com singularidades isoladas. Anunciamos resultados relacionados a dois problemas: 1. Dada uma órbita L de X finitamente curvada sob quais condições L é algébrica? 2. Se X possui alguma órbita não algébrica finitamente curvada L qual é a classificação de X? O problema 1 está relacionado à seguinte questão: Seja C <FONT FACE=Symbol>Ì</FONT> C² uma curva holomorfa com curvatura Gaussiana total finita. C está contida numa curva algébrica?

Folheações holomorfas; campos de vetores polinomiais; curvas algébricas; curvatura total finita

MATHEMATICAL SCIENCES

Finitely curved orbits of complex polynomial vector fields

Albetã C. Mafra

Instituto de Matemática, Universidade Federal do Rio de Janeiro, Caixa Postal 68530, 21945-970 Rio de Janeiro, RJ, Brasil

ABSTRACT

This note is about the geometry of holomorphic foliations. Let X be a polynomial vector field with isolated singularities on C². We announce some results regarding two problems: 1. Given a finitely curved orbit L of X, under which conditions is L algebraic? 2. If X has some non-algebraic finitely curved orbit L what is the classification of X? Problem 1 is related to the following question: Let C Ì C²be a holomorphic curve which has finite total Gaussian curvature. IsC contained in an algebraic curve?

Key words: Holomorphic foliations, polynomial vector fields, algebraic curves, finite total curvature.

RESUMO

Esta nota versa sobre a geometria de folheações holomorfas. Seja X um campo vetorial polinomial complexo com singularidades isoladas. Anunciamos resultados relacionados a dois problemas: 1. Dada uma órbita L de X finitamente curvada sob quais condições L é algébrica? 2. Se X possui alguma órbita não algébrica finitamente curvada L qual é a classificação de X? O problema 1 está relacionado à seguinte questão: Seja C Ì C² uma curva holomorfa com curvatura Gaussiana total finita. C está contida numa curva algébrica?

Palavras-chave: Folheações holomorfas, campos de vetores polinomiais, curvas algébricas, curvatura total finita.

1 INTRODUCTION

Let X be a holomorphic vector field with isolated singularities on ² and let L Ì ² be a non-singular orbit. Then L is an immersed holomorphic curve in ², and its topology can be very complicated (space of ends not denumerable, infinity genus and so on). It is also a minimal surface in ⁴ to which we can associate a holomorphic Gauss map as in (Lawson 1980, Scárdua 2002). A classical theorem of Osserman states that, for a complete minimal surface in ⁿ, the finiteness of the total curvature is equivalent to algebraicity of its holomorphic Gauss map. See (Lawson 1980). For instance, if L is obtained from an algebraic curve C Ì ² by deleting some points then its holomorphic Gauss map is algebraic. In this work we study, for orbits of polynomial vector fields, the possible converses to this fact. Our main tools are the dynamics of the vector field in a neighborhood of the line at infinity L_¥ = P²\² and the fact that, since L is a holomorphic curve, its corresponding holomorphic Gauss map takes values into P¹ which can be identified with L_¥. This will relate the finiteness of the total curvature of L with the dynamics of X close to L_¥.

Given a polynomial vector field

with isolated singularities on

², the dual 1-form w = Pdy - Qdx defines a holomorphic foliation on ² whose leaves are the non-singular orbits of X and whose singular set is sing(X). This foliation extends naturally to a one-dimensional holomorphic foliation with singularities (X) of the complex projective plane P² and the geometry of its leaves contains important additional information on the orbits of X. Thus we shall work with the foliation (X) in most of our considerations. Let us recall some basic definitions about singularities of holomorphic foliations in dimension two. Let a holomorphic foliation with discrete singular set sing() on a complex surface M. A singularity p Î sing() is called irreducible if there is an open neighborhood U of p in M where is induced by a holomorphic differential 1-form which has one of the following types:

or

See (Camacho and Sad 1982).

An isolated singularity is called a generalized curve if its reduction process exhibits only non-degenerate singularities. It is non-dicritical if the exceptional divisor of this reduction is invariant by the foliation. See (Camacho et al. 1984).

Under suitable non-degeneracy conditions on the singularities of the foliation, a finitely curved orbit is algebraic as it follows from the following theorem:

THEOREM 1. Let X be a polynomial vector field defined on

² and let L be a finitely curved orbit of X. Suppose that the singularities of (X) on P² are non-dicritical generalized curves, then L is contained in an algebraic curve.

A Poincaré-Dulac normal form vector field

has non-algebraic orbits (except for the orbit contained on {y = 0}) but are finitely curved. This situation is described by the following theorem:

THEOREM 2. Let X be a polynomial vector field on

² such that the singularities of (X) are non-dicritical and in the Poincaré domain. If X has a finitely curved non-algebraic orbit then (X) is given by a closed rational 1-form on P². Indeed, either (X) is a logarithmic foliation or there is a rational map f: P² 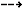P² such that (X) is the pull-back f^*(Y_n,c) where Y_n,c is a Poincaré-Dulac normal form. In particular all orbits of X have finite total curvature.

Complete proofs of Theorems 1 and 2 are given in (A.C. Mafra, unpublished data, Mafra 2006).

2 SKETCH OF THE PROOF OF THEOREMS 1 AND 2

Let us begin with a brief idea of the proof of Theorem 1. First we study the local behavior of a finitely curved orbit L in a neighborhood of a non-degenerated irreducible singularity p Î sing(X) in ².

LEMMA 1. Let X be a holomorphic vector field on

² and p Î sing(X) an irreducible singularity with first jet of the form

If an orbit of X accumulates at p and is not contained in the union of separatrices of X through p then this orbit has infinite total curvature.

This lemma and the hypothesis in the singular set of (X) imply:

LEMMA 2. A finitely curved orbit L of a vector field X as in Theorem 1 is contained in an analytic curve in

². Indeed, we have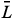 Ì L È sing(X).

The proof of Lemma 2 involves some combinatorial in the reduction of singularities for sing((X)) as in (Mol 2002) in order to exclude the case where L accumulates on two straight lines intersecting at the singular point on ². Indeed, blowing up the singularity which is the intersection of two invariant lines we conclude that the area of the Gauss map is infinite. The second step is to assure the analytical behavior of L in a neighborhood of L_¥. As we have remarked above for a non-singular orbit L Ì ² the holomorphic Gauss map can be identified with a map F: L ® L_¥@ P¹. Moreover, there is a leaf Ì P² of the foliation (X) such that L = \(Ç L_¥). The finiteness of the total curvature of L then implies the following:

LEMMA 3. (i) If L_¥is not invariant by (X) then is analytic in a neighborhood of L_¥. (ii) If L_¥is invariant by (X) then L accumulates only on points in sing((X))Ç L_¥.

In order to finish the proof of Theorem 1 one applies Remmert-Stein Extension Theorem to conclude that Ì P² is an analytic subset of dimension one and then Chow's Theorem.

SKETCH OF THE PROOF OF THEOREM 2. Let L be a nonsingular transcendental orbit of X with finite total curvature. We have two possibilities:

CASE 1. L is closed in ² \ sing((X)). In this first case we can assume that the line L_¥ is invariant by (X). Moreover, given a small transverse disc S to L_¥ at a point q Î L_¥\ sing((X)), L induces in S an orbit which is discrete outside the origin q = S Ç L_¥. According to Nakai's density theorem (Nakai 1994) this implies that the holonomy group of the leaf L_¥ \ sing((X)) is a solvable subgroup of Diff(,0). Now, according to the construction and classification results in Sections 5 and 6 in (Scárdua 1999) this implies, taking into account the hypothesis on the singularities of (X), that the foliation (X) is given by a rational 1-form on P². According then to Section 7 in (Bracci and Scárdua 2007) this implies, always taking into account the nature of the singularities, that (X) is conjugated to a Poincaré-Dulac normal form as stated.

CASE 2. L is not closed in ² and L accumulates in some invariant line E Ì ². The same argumentation of the first case can be applied to E in place of L_¥ to show that (X) must be conjugated to a Poincaré-Dulac normal form.

ACKNOWLEDGMENTS

I would like to thank Bruno Scárdua for valuable conversations during the elaboration of this work.

Manuscript received on October 23, 2006; accepted for publication on October 25, 2006; presented by MARCIO G. SOARES

E-mail: [e-mail]

• BRACCI F AND SCÁRDUA B. 2007. One dimensional holomorphic foliatons transverse to polydiscs. J London Math Soc (in press).
• CAMACHO C AND SAD P. 1982. Invariants varieties through singularities of holomorphic vector fields. Ann Math 115: 579-595.
• CAMACHO C, LINS NETO A AND SAD P. 1984. Topological invariants and equidesingularization for holomorphic vector fields. J Diff Geom 20: 143-174.
• LAWSON HB. 1980. Lectures on minimal submanifolds Vol. 1, 2^nd ed., Mathematics Lecture Series, 9. Publish or Perish, Inc. Wilmington, Del.
• MAFRA AC. 2006. Complex polynomial vector fields having a finitely curved orbit. Pre-print, IM-UFRJ.
• MOL RS. 2002. Meromorphic first integrals: some extension results. Tohoku Math J 54: 85-104.
• NAKAI I. 1994. Separatrices for nonsolvable dynamics on C,0. Ann Inst Fourier (Grenoble) 44: 569-599.
• SCÁRDUA B. 1999. A remark on parabolic projective foliations. Hokkaido Math J 28: 231-252.
• SCÁRDUA B. 2002. Complex vector fields having orbits with bounded geometry. Tohoku Math J 54: 367-392.

Publication Dates

• Publication in this collection
  23 Mar 2007
• Date of issue
  Mar 2007

History

• Received
  23 Oct 2006
• Accepted
  25 Oct 2006