Abstracts
Cesium atomic beam clocks have been the workhorse for many demanding applications in science and technology for the past four decades. Tests of the fundamental laws of physics and the search for minute changes in fundamental constants, the synchronization of telecommunication networks, and realization of the satellite-based global positioning system would not be possible without atomic clocks. The adoption of optical cooling and trapping techniques, has produced a major advance in atomic clock precision. Cold-atom fountain and compact cold-atom clocks have also been developed. Measurement precision of a few parts in 10(15) has been demonstrated for a cold-atom fountain clock. We present here an overview of the time and frequency metrology program based on cesium atoms under development at USP São Carlos. This activity consists of construction and characterization of atomic-beam, and several variations of cold-atom clocks. We discuss the basic working principles, construction, evaluation, and important applications of atomic clocks in the Brazilian program.
atomic clock; cold atoms; time and frequency; metrology
Relógios atômicos de feixe de Césio têm sido a base para diversas aplicações em ciência e tecnologia nas últimas quatro décadas. Testes de leis fundamentais de física, buscas por mínimas variações em constantes fundamentais, sincronização de redes de telecomunicações e o funcionamento do sistema de posicionamento global, baseado em satélites de navegação, não seriam possíveis sem os relógios atômicos. A adoção de técnicas de aprisionamento e resfriamento ópticos tem permitido um grande avanço na precisão dos relógios atômicos. Chafarizes de átomos frios e relógios compactos de átomos frios também têm sido desenvolvidos. Precisões de medida de algumas partes em 1015 foram demonstradas para relógios do tipo chafariz de átomos frios. Apresentamos uma visão geral do programa de metrologia de tempo e freqüência baseado em átomos de césio, em desenvolvimento na USP de São Carlos. Estas atividades consistem na construção e caracterização de relógios do tipo feixe atômico e de outros, utilizando átomos frios. Discutimos os princípios básicos, construção, avaliação e importantes aplicações de relógios atômicos no programa brasileiro.
Relógio atômico; átomos frios; tempo e freqüência; metrologia
PHYSICAL SCIENCES
The Brazilian time and frequency atomic standards program
Mushtaq AhmedI; Daniel V. MagalhãesII; Aida BebeachibuliII; Stella T. MüllerII; Renato F. AlvesII; Tiago A. OrtegaII; John WeinerIII; Vanderlei S. BagnatoII
IOptics Laboratories, P.O. Box 1021, Islamabad, Pakistan
IIInstituto de Física de São Carlos, Universidade de São Paulo, Caixa Postal 369, 13560-970 São Carlos, SP, Brasil
IIIUniversité Paul Sabatier, 118 route de Narbonne, 31062 Toulouse, France
Correspondence to Correspondence to: Vanderlei Salvador Bagnato vander@if.sc.usp.br
ABSTRACT
Cesium atomic beam clocks have been the workhorse for many demanding applications in science and technology for the past four decades. Tests of the fundamental laws of physics and the search for minute changes in fundamental constants, the synchronization of telecommunication networks, and realization of the satellite-based global positioning system would not be possible without atomic clocks. The adoption of optical cooling and trapping techniques, has produced a major advance in atomic clock precision. Cold-atom fountain and compact cold-atom clocks have also been developed. Measurement precision of a few parts in 1015 has been demonstrated for a cold-atom fountain clock. We present here an overview of the time and frequency metrology program based on cesium atoms under development at USP São Carlos. This activity consists of construction and characterization of atomic-beam, and several variations of cold-atom clocks. We discuss the basic working principles, construction, evaluation, and important applications of atomic clocks in the Brazilian program.
Key words: atomic clock, cold atoms, time and frequency, metrology.
RESUMO
Relógios atômicos de feixe de Césio têm sido a base para diversas aplicações em ciência e tecnologia nas últimas quatro décadas. Testes de leis fundamentais de física, buscas por mínimas variações em constantes fundamentais, sincronização de redes de telecomunicações e o funcionamento do sistema de posicionamento global, baseado em satélites de navegação, não seriam possíveis sem os relógios atômicos. A adoção de técnicas de aprisionamento e resfriamento ópticos tem permitido um grande avanço na precisão dos relógios atômicos. Chafarizes de átomos frios e relógios compactos de átomos frios também têm sido desenvolvidos. Precisões de medida de algumas partes em 1015 foram demonstradas para relógios do tipo chafariz de átomos frios. Apresentamos uma visão geral do programa de metrologia de tempo e freqüência baseado em átomos de césio, em desenvolvimento na USP de São Carlos. Estas atividades consistem na construção e caracterização de relógios do tipo feixe atômico e de outros, utilizando átomos frios. Discutimos os princípios básicos, construção, avaliação e importantes aplicações de relógios atômicos no programa brasileiro.
Palavras-chave: Relógio atômico, átomos frios, tempo e freqüência, metrologia.
INTRODUCTION
Precise measurement of time and frequency has great importance in commercial and defense applications as well as in fundamental physics. Each atom or molecule absorbs and emits electromagnetic radiation at characteristic transition frequencies. Some of these frequencies lend themselves to stabilization over time and space and therefore constitute natural frequency standards. The U.S. National Institute for Standard and Technology (NIST) built up its first frequency standard clock based upon an ammonia transition in 1949 (Lyons 1949). The ammonia clock performance, however, was not better than conventional clocks existing at that time. The National Physical Laboratory (NPL) in England built up the first practical cesium atomic clock in 1955 (Essen and Parry 1957), and in 1967 atomic clock technology enabled scientists to define the unit of time, the second, based on atomic measurements (CGPM 1967).
In current primary atomic frequency standards, transitions between ground state hyperfine energy levels in cesium atoms at microwave frequencies form the basis for measuring time. The present definition is: The second is the duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium 133 atom at a temperature of 0 K.
1 second = 9 192 631 770 periods of the Cs133, F = 3, mF = 0 « F = 4, mF = 0 hyperfine transition
The usual stability (precision) of Cs atomic beam clocks is a few parts in 1013, and the uncertainty (accuracy) is of the order of one part in 1014. For the modern cold-atom fountain clock two orders of improvement in stability is possible and about one order in uncertainty. Atomic clocks use natural internal-state transitions within atoms or molecules to keep time. These quantum mechanical oscillators are vastly less sensitive to gross environmental effects such as temperature, pressure, humidity, and vibration, for example, than macroscopic oscillators such as pendulums and quartz crystals. But the most important advantage of atomic clocks is that every atom of a given element and isotope is identical. Therefore an atomic clock standard based on Cs133 transitions is transferable the world over. The atomic clock is the most stable and accurate clock known. Atomic clocks are so good that time and frequency can be measured more precisely than any other physical quantity. Cesium atomic clocks are the primary standard, and rubidium clocks are accepted as a secondary standard.
Modern life depends upon the precise time. Communication, financial transactions, electric power and many other activities have become dependent upon time accuracy. The demand of these technologies will continue to drive research toward more accurate, precise, and transferable time standards. Improvement in the development of the frequency and time standard is continually in progress. Development of the harmonic generating "frequency comb" made the optical frequency regime a prominent candidate for an advanced frequency standard. Cold atoms and cold ions are certainly the most promising systems for the development of a new atomic standard (Bize et al. 2005, Ma et al. 2004, Udem et al. 2002). Any country which aspires to develop and grow technologically must include a serious program of scientific time and frequency metrology.
The official Brazilian time scale is maintained by the Observatório Nacional, located in Rio de Janeiro and associated with the Brazilian institute of metrology, Instituto Nacional de Metrologia, Nomalização e Qualidade Industrial (INMETRO). This service is implemented with commercial cesium and rubidium clocks. In this paper we provide an overview of the scientific time and frequency program at University of São Paulo in São Carlos. The program is composed of different types of atomic clocks based on cesium atoms. Historically the earth's rotation was used as a time standard, and we start by discussing how this standard relates to the atomic standard. We then discuss briefly some of the current applications for atomic clocks followed by a more detailed description of clocks constructed and under development at USP São Carlos.
SYSTEMS OF TIME: UTC AND TAI
Originally, the local time at the Royal Observatory, Greenwich, England was chosen as standard at the 1884 International Meridian Conference, leading to the widespread use of Greenwich Mean Time (GMT) in order to set local clocks. This location was chosen because by 1884 two-thirds of all charts and maps already used it as their Prime Meridian. In 1929, the term Universal Time (UT) was introduced to refer to GMT with the day starting at midnight. Until the 1950s, broadcast time signals were based on UT, and hence on the rotation of the Earth. Coordinated Universal Time (UTC), a high-precision atomic time standard, is an updated variant of UT. As a time scale, UTC divides up time into days, hours, minutes, and seconds. Each day contains 24 hours and each hour contains 60 minutes, but the number of seconds in a minute is slightly variable. UTC has uniform seconds defined by International Atomic Time, referred to as TAI from the French "Temps Atomique International," with leap seconds announced at irregular intervals to compensate for the earth's slowing rotation and other discrepancies. Leap seconds allow UTC to closely track Universal Time (UT), based on the Earth's angular rotation. UTC is derived from TAI, which tracks proper time from atomic standards with no reference to the rotation of the Earth. At any particular time, UTC proceeds as a linear function of TAI, and since 1972 UTC "ticks" at the same rate as TAI. UTC occasionally has discontinuities where it changes from one linear function of TAI to another. These discontinuities take the form of leaps implemented by a UTC day of irregular length. The accuracy and stability of atomic clocks is the effective standard for TAI. Atomic clocks maintain a continuous and stable time scale for TAI, and provide an excellent reference for time and frequency in scientific applications. The UTC, not the TAI, is the time distributed by standard radio stations that broadcast time, such as WWV and WWVH. It can also be obtained readily from the GPS satellites (Audoin and Guinot 2001, Nelson et al. 2001, Riehle 2004, Jesperson and Fitz-Randolph 1999).
APPLICATIONS OF ATOMIC STANDARDS
The precise and accurate measurement of time and frequency plays a fundamental and important role in the success of many fields of technologies and research. Atomic clock technology has several practical applications. On the scientific side, atomic clocks provide a sensitive probe for minute variations in physical constants such as the fine structure constant, a. Clocks can also be used to search for variations in the isotropy of space, preferred frames of reference, charge- parity-time (CPT) symmetry violation and to test the theories of relativity and electrodynamics (Uzan 2003). Precise and accurate clocks may provide the means to revel new phenomena signaling a fundamental change in how we perceive nature (Riehle 2004, Audoin and Guinot 2001). Practical applications include metrology, geodesy, global positioning systems for navigation, communication, electric power networks and defense. We shall briefly discuss these practical applications as well.
FUNDAMENTAL PHYSICS RESEARCH
According to Einstein's Equivalence Principle (Vessot and Levine 1979), fundamental constants should not vary with time, but some modern theories predict the existence of variation. The development of atomic clocks (Cs and Rb) have provided the accuracy necessary to test fundamental constants like the Rydberg constant R and the fine structure constant a and their possible slow variation with respect to time. Recently a stringent upper limit has been set to a possible fractional time variation of the ratio of hyperfine transition frequencies in Rb and Cs atoms.
where µRb and µCs are the magnetic moments of rubidium and cesium respectively. Furthermore it can be shown that the sensitivity of the ratio of nRb/nCs to a variation of a is given by
Combining Eqs. 1 and 2, the upper limit to the fractional time variation of the fine structure constant is
(Marion et al. 2003). In another approach (Peik et al. 2004) measured an optical transition frequency in the Yb+ ion over a period of almost three years and were able to relate the constancy of this frequency to an upper limit on the variability of a of 2.0 × 10-15 yr-1. The advantage of this approach is that it is independent of the assumed constancy of the atomic masses or magnetic moments.
Precise atomic spectroscopy, precision interferometry for gravitational wave detection, and other astrophysical measurements as well as tests for relativity, quantum electrodynamics and CPT invariance can be made possible using ultra-stable atomic clocks (Bize et al. 2005, Flambaum and Tedesco 2006, Uzan 2003, Vessot et al. 1980).
In 1993 the quantity gp(me/mp) was measured by comparing the frequency data of Cs and Mg atomic beam standards (Godone et al. 1993), where gp is the proton gyromagnetic ratio and me, mp are the mass of the electron and proton respectively. The time stability of this quantity is an important subject for theoretical physics as well as for dimensional metrology. The study of time variation of such quantities or its product with fine structure constant plays an important role in definition of international standards (SI).
We list here a few specific examples of important applications in time and frequency measurements.
Time dilation test
U.S. Naval Observatory performed an experiment to test time dilation in 1971, (Hafele and Keating 1972). Airline flights around the world in opposite directions carried four Cs atomic beam clocks. At the end of the flights it was found that the traveling clocks gained about 0.15 µs relative to rest clocks. Measurement of time dilation has been an important test for special relativity.
Pulsar frequency detection
Atomic clocks were used to monitor the frequency variation of pulsars. Repeated radio pulses from stars in our galaxy were discovered in 1960. These pulses called "pulsars" were attributed to rotating neutron stars which emit lighthouse-type sweeping beams as they rotate (Ramsey 1990). The study of such phenomenon advance our understanding of star formation and evolution of the universe.
POSITIONING AND NAVIGATION ON THE EARTH SURFACE
Navigation has continued to be one of the principal applications of accurate clocks. Frequency standards provide enabling technology for satellite navigation systems and at the same time satellite systems distribute time and frequency standards to the whole world. The Global Positioning System (GPS) originally consisted of 24 satellites, placed in the earth orbit in 1989. The GPS constellation of satellites has been continuously updated since the first launch in 1989 of the Block II satellite. Presently with the last launch of Block IIR-M in 2006, it operates with 30 satellites distributed in four categories (Block II, IIA, IIR, and IIR-M). Atomic clocks can be found in all 30 of the satellites. These clocks, together with ground based clocks, enable sailors, pilots, drivers and hikers to know their location on the earth surface within a few meters. Planes navigate using GPS although it is not yet acceptable to land an aircraft by GPS alone since atomic clocks on satellites are still not accurate enough and it takes too long to compute positions. These atomic clocks are periodically updated from the ground primary Cs clock at the U.S. Naval Observatory. These satellites transmit both timing and positioning data. The combination of primary frequency standard (Cs atomic clock) and commercial atomic standards (Cs and Rb clocks) and a stable communication network provide accurate time and frequency. The GPS provides altitude, latitude and longitude with an uncertainty of less than 10 meters. Improvement in the ground-based master clocks that calibrate the GPS atomic clocks along with better satellite clocks will allow transportation systems to locate vehicles with sub-meter precision in real time. It is not only the GPS space system that carries atomic clocks on board. The Russian navigation satellite system, Glonass, is also similarly equipped. Initially implemented in the Soviet Union, this system fell into disrepair, but with the help of the Indian government it is now being restored. Other proposed systems are in development such as COMPASS (China), GALILEO (European Union), and an updated version of GPS called GPS III that is planned to be fully operational in 2013. Communication satellite systems such as Milstar require the robust timekeeping capabilities of atomic clocks in order to provide secure communications. As the competition for radio frequency bandwidth increases, other communication systems, commercial as well as military, may have to rely on atomic clocks to provide accurate frequency and time on board spacecraft. Satellite ranging for deep space will require an accuracy of 1015 to 1017, (Allan et al. 1994, Audoin and Guinot 2001, Bauch 2003, McCaskill et al. 1999, Riehle 2004, Wu and Feess 2000).
SPACE GEODESY
Time and frequency standards have enabled space-based geodesy systems to acquire high accuracy forimportant investigations of earth including open ocean circulation, sea level monitoring, and the measurement of man-made gaseous emissions. Atomic clocks in satellites are important to satellite laser ranging (SLR) and the hydrogen maser reference used in very long baseline interferometry (VLBI). Without the development of these atomic clocks these instrumental techniques would not be possible (Shapiro et al. 2004). The TOPEX/POSEIDON project was initiated to monitor global oceans circulation by satellite.Satellite observations of the oceans are important because they provide long-term, continuous measurements sea surface height, sea surface temperature and other climate conditions over the entire earth. Accuracy of these measurements depends upon the atomic clocks launched in satellites (Cazenave et al. 1997).
LENGTH AND OTHER PHYSICAL PROPERTIES MEASURED AS FREQUENCY
Presently there exists no other quantity measured as precisely as frequency. Due to this unique capability, it is possible to measure more precisely other physical quantities using frequency and time. Considerable efforts are under way to translate the measurement of length, speed, temperature, electric field, magnetic field, voltage, etc. into frequency. The meter (m) is the Système International (SI) unit of length and is now defined as the length of the path traveled by light in vacuum during the time interval of 1/299 792 458 of a second, i.e. 1/c. This new definition replaces two previous definitions of the meter: the original adopted in 1889 based on a platinum-iridium prototype bar, and a definition adopted in 1960 based on a krypton-86 radiation from an electrical discharge lamp. The krypton-86 electrical discharge lamp was designed to produce the Doppler-broadened wavelength of the 2p10-5d5 transition of the unperturbedatom. The two dominant wavelength shifts, one caused by the DC Stark effect and the other by the gas pressure in the discharge lamp, were opposite in sign and could be made equal in magnitude by the proper choice of operating conditions. Different krypton-86 lamps reproduced the same wavelength to about 4 parts in 109, but had the disadvantage that the coherence length of its radiation was shorter than the meter, complicating the changeover from the older standard. Faced with the possibility that further advances in laser spectroscopy would lead to proposals for new length standards based on more precise atoms or molecules, a new concept for the length standard definition was developed. The second (which is equivalent to 9,129,631,770 oscillations of the cesium-133 microwave transition) and the meter are now considered independent base units. Traditionally, the speed of light was measured in terms of their ratio. By contrast, the present standard defines the meter in terms of the SI second and a defined value for the speed of light in vacuum which fixes it to 299 792 458 m s-1 exactly. Thus the meter is determined experimentally based on the cesium-133 frequency standard. Since it is not based on a particular radiation, this definition opens the way to major improvements in the precision with which the meter can be realized using laser techniques without redefining the length standard. As a practical matter the meter can be measured at different, more convenient optical frequencies and referenced back to the cesium-133 standard using frequency chains (Udem et al. 2002).
TIME SYNCHRONIZATION OF COMPUTERS
The discussion in the section is taken from the Wikipedia entry on the Network Time Protocol. The Network Time Protocol (NTP) is a protocol for synchronizing the clocks of computer systems over packet-switched, variable-latency data networks. NTP uses an algorithm with the UTC time scale, including support for features such as leap seconds. NTP v4 can usually maintain time to within 10 milliseconds (1/100 s) over the public Internet, and can achieve accuracies of 200 microseconds (1/5000 s) or better in local area networks under ideal conditions. Atomic clocks are used to synchronize computer clocks. NTP uses a hierarchical system of "clock strata". The stratum levels define the distance from the reference clock and the associated accuracy.
Stratum 0
These are devices such as atomic (cesium, rubidium) clocks, GPS clocks or other radio clocks. Stratum-0 devices are not attached to the network; instead they are locally connected to computers.
Stratum 1
These are computers attached to Stratum 0 devices. Normally they act as servers for timing requests from Stratum 2 servers via NTP. These computers are also referred to as time servers. Many Stratum 1 servers (for NTP v3 and earlier versions) may not actually be operating with Stratum 1 precision. As the NTP protocol is developed, it will become less and less possible for misleading Stratum 1 servers to run - instead the protocol would automatically bump the server Stratum level down to an appropriate level.
Stratum 2
These are computers that send NTP requests to Stratum 1 servers. Normally a Stratum 2 computer will reference a number of Stratum 1 servers and use the NTP algorithm to gather the best data sample, dropping any Stratum 1 servers that seem obviously wrong. Stratum 2 computers will peer with other Stratum 2 computers to provide more stable and robust time for all devices in the peer group. Stratum 2 computers normally act as servers for Stratum 3 NTP requests.
Stratum 3
These computers employ exactly the same NTP functions of peering and data sampling as Stratum 2, and can themselves act as servers for higher strata, potentially up to 16 levels. NTP (depending on what version of NTP protocol in use) supports up to 256 strata. It is hoped that in NTP 5 (a protocol still in development) that only 8 or 16 strata will be permitted.
DEFENSE
Frequency standards and clocks play a major role in military communication, navigation, surveillance, missile guidance, Identification Friend or Foe (IFF) and Electronic Warfare (EW) systems. The major enabling technologies require robustness to environmental disturbances, low input power, long stability, high accuracy, small size and weight. Development of more compact atomic clocks will better meet these requirements. The mobility and robustness of military systems and platforms can be improved by using ultra-miniature time reference units such as chip-scale atomic clocks. The ultra-stable frequency reference provided by atomic clocks will drastically improve channel selectivity and density for all military communications.
IMPLEMENTATION OF ATOMIC FREQUENCY STANDARDS
Atomic frequency standard can be either active or passive. An active atomic standard uses the electromagnetic radiation emitted by atoms themselves as they decay from a higher energy state to a lower energy state. A passive standard matches the frequency of an electronic oscillator or laser to the resonant frequency of the atoms by means of a feedback circuit.
There are different types of atomic clocks, but they are all based on an equivalent basic principle. The differences are the type of atom and detection mechanism. There are three most common types of atomic clocks in use. These are based on the cesium, rubidium and hydrogen atoms. Figure 1 illustrates the working principle of an atomic clock. The oscillatory mechanism of the clock is the atom itself. Atomic energy states and hence the transition frequency n0 = (E2 - E1)/h between them serves as a basis for the clock operation. This transition frequency is intrinsically independent of space and time. When an electronic transition takes place in the atom between two energy levels, it either emits or absorbs an electromagnetic (EM) wave with a center frequency n0.
All the atoms of the same element and isotope absorb or emit electromagnetic radiation of the same frequency. This is the fundamental difference of atomic clocks as compared to other time-keeping devices. The microwave oscillator provides the frequency for the atomic transition which, through the atoms, is corrected until the difference between the frequency of the oscillator and the atoms is minimized. The oscillator is then locked to this transition using a feed back loop. The choice of a specific frequency of a selected atom depends on certain requirements to acquire best accuracy and stability. To obtain high precision, the natural line width of the transition should be as small as possible and the interaction time between the atomic and radiation should be as long as possible. This characteristic implies a high quality factor Q = n0/Dn0 for the atomic transition. Signal to noise ratio (S/N) of the observed resonance transition should be large to minimize statistical fluctuations of the signal controlling the local oscillator (LO). The velocity of the atoms should be low to minimize Doppler shifts. The resonance atomic transition should be insensitive to electric and magnetic fields and to pressure broadening effects.
How to measure the clock transition with minimum external influence?
An ingenious answer to this key question is the idea of Ramsey (Ramsey 1950) known as the two- separated-zones interaction in an atomic beam. In this method, when the atom beam travels down an evacuated tube, the atoms interact with two separated microwave cavities. The probability that an atomic transition in the first and in the second zone occurs depends upon a number of parameters.
RAMSEY METHOD
In the Ramsey method, atoms in the beam pass through two separated zones of length l having two phase-coherent microwave fields that are spatially separated by the distance L, where L >> l. The characteristic signature of the output of an atomic clock is the Ramsey fringe pattern. The Ramsey fringes trace the transition probability between the two atomic states as a function of microwave frequency as the atoms move in two separated microwave interaction zones as shown in Figure 2. The fringes originate from an interference of transition couplings that comes from both interaction zones. With this approach the basic goal is to reduce the transit-time broadening arising from the finite time that the atoms spend within each of the interaction zones.
To understand how the Ramsey technique reduces the line width of a transition, consider a two-level atom with states |0ñ and |1ñ. At time t = 0, this atom enters a microwave region of length l, where it is perturbed by an oscillatory microwave electromagnetic field and as a result an atomic excitation takes place. The probability P of transition between the two states |0ñ and |1ñ is given by the following equation.
with
Here t is the interaction time within the zone l, w0 is the atomic transition frequency, w is the applied microwave frequency, µB is the Bohr magneton, B is the amplitude of the microwave magnetic field and  is Planck's constant divided by 2p. The quantity b is a measure of the strength of the magnetic dipole coupling between the magnetic component of the microwave field and the atom. It is known as the Rabi frequency (Ramsey 1990). The first factor on the right hand side of the expression for P(t) becomes unity when w = w0 (resonance) and the full width at half maximum is Dw = 5.02/t. The second factor is time-dependent. The probability will be maximum at w = w0, when bt = p. The interaction time is t = l/u where u is the velocity of the atomic beam and l is the length of interaction region. The width for such a transition under these conditions can be expressed as Dw = 5.02/t = 5.02u/l.
is Planck's constant divided by 2p. The quantity b is a measure of the strength of the magnetic dipole coupling between the magnetic component of the microwave field and the atom. It is known as the Rabi frequency (Ramsey 1990). The first factor on the right hand side of the expression for P(t) becomes unity when w = w0 (resonance) and the full width at half maximum is Dw = 5.02/t. The second factor is time-dependent. The probability will be maximum at w = w0, when bt = p. The interaction time is t = l/u where u is the velocity of the atomic beam and l is the length of interaction region. The width for such a transition under these conditions can be expressed as Dw = 5.02/t = 5.02u/l.
The above equation implies that the transitions can be made arbitrarily narrow as the length of the interaction zone is increased. However, in practice this cannot be realized due to two limitations: loss of beam intensity and the impossibility to achieve homogenous B-field amplitude throughout the interaction zone. The resonance frequency will differ along the beam path and resulting in broader resonances instead of narrower. Ramsey's ingenious idea of two separated fields not only overcomes the problem of field inhomogeneity but in addition generates resonances much narrower than those arising from a single interaction. The transition probability in the case of the two-zone Ramsey configuration is calculated from the following equation.
Here j is the phase shift and T is the duration of the time interval between the two separated interaction zones.
In the on-resonance case, all of the atoms will undergo transition resulting in maximum signal. Now if the frequency is slightly off resonance, there will be a difference in the phase of the atomic states between the first and second interaction zones, and some of the atoms will be left in the original atomic state.The signal will decrease. In case of one half of the phase difference, none of the atoms will make the transition and the signal will be minimum. If the phase difference is complete integral multiple of cycle then we will observe other maxima signal and in case of half integral multiple phase difference, we will observe other a minima.
The probability will be maximum when j = 0, W0 = 0 and bt = p/2. For W0¹ 0 the motion of the atoms in field free region produces interference effects. The generation of interference fringes is called a Ramsey pattern. The interference pattern arises because of the two separated interrogation regions(Ramsey 1950, 1963, 1990).
The central fringe has the principal importance of providing the atomic frequency reference. Its peak-to-valley height is taken as the amplitude of the resonance profile. The full width at half maximum (FWHM) given as
Here L is separation between two interaction zones. As a numerical example consider u = 200 ms-1 and L = 10 cm, Dn = 6.283 KHz. As bt = p/2 ®, b = 31400 rad s-1 for l = 1 cm, (interaction region). Hence the corresponding amplitude of the microwave magnetic field B = 0.357 µT.
Two extreme cases can be considered separately: The central feature of the Ramsey fringe, W0 << b and the "Rabi Pedestal", W0 >> b (Ramsey 1963, Vanier and Audoin 1989).
For W0 << b
For W0 >> b
Figure 3 illustrates the recorded signal of the Ramsey central fringe and Figure 4 all seven possible Zeeman transitions 6S1/2 (F = 3) ® 6S1/2 (F = 4); DmF = 0. The signal consists of a narrow spectral feature (Ramsey central fringe) superimposed on the broader envelope(Rabi pedestal). The Rabi pedestal is related to the transit time broadening as the atoms pass through the two microwave regions as well as the velocity distribution of the atoms in the thermal beam. This pedestal is much more significant for the atomic-beam frequency standard (20 kHz) than for the atomic fountain (cf. Section 6) using optically cooled atoms (70 Hz). The overall shape of the Rabi pedestal is due to the combined effects of the probability that a transition occurs in the first excitation region but not in the second, plus the probability that it occurs in the second excitation zone but not in the first.
Characteristic parameters such as Rabi frequency, second order Zeeman effect, second-order Doppler shift, and the end-to-end cavity phase shift were quantitatively analyzed. These characteristic parametric measurements are very important to correct the clock frequency, and will be addressed in the next section.
CESIUM BEAM ATOMIC CLOCK
The cesium atom has proved to be a good choice for the development of a clock. Three kinds of cesium clocks are under development in Brazil. These are the cesium atomic beam, the cesium fountain and the cesium "expanding cold atoms" clock. All of these cesium-based atomic clocks have been constructed and evaluated at the University of São Paulo at São Carlos.
The Cs133 atom is a stable element. It is highly electropositive and reactive. The saturating Cs vapor pressure at room temperature and at 100°C is 1.86 × 10-4 and 7.45 × 10-2 Pa, respectively. Cesium has only one valence electron and a 2S1/2 ground-state Russell-Saunders term. The nuclear magnetic spin of Cs133 is 7/2. The ground-state term is split into two hyperfine levels, F = 3 and F = 4. At room temperature, the two hyperfine levels are populated according to their 2F + 1 degeneracies. Figure 5 illustrates the relevant term energy diagram of Cs133. The energy of the Zeeman sublevels, labeled mF, is proportional to the applied magnetic field and is expressed in units of kHz/G. In the absence of an external magnetic field, the mF Zeeman sublevels are degenerate.
The clock transition between between states F = 3, mF = 0 to F = 4, mF = 0 is a magnetic dipole transition. The probability of spontaneous magnetic dipole relaxation from the upper hyperfine state is very low, and therefore atoms in the excited state F = 4, mF = 0 will remain there for a very long time compared to the observation time.
CONSTRUCTION OF THE CESIUM ATOMIC BEAM CLOCK
The Brazilian Cs atomic beam clock was designed and developed following the scheme of the Ramsey two-separated-microwave- interaction zones. The basic advantage of this experimental scheme is the reduction of time-of-flight broadening and increase of the atoms number that participates during the interrogation and detection process. The natural line width of radio frequency and microwave transitions is extremely small because the spontaneous transition probability is proportional to the frequency cubed. Therefore, the spectral line width of these transitions is determined by transit-time broadening Dn = 1/T = u/L. The term T is the atom time of flight between two microwave interaction zones, u is the velocity of the atoms and L is the length between two interaction zones.
CESIUM ATOMIC BEAM APPARATUS
The cesium beam apparatus consists of a stainless steel cylindrical chamber with diameter 20 cm and length 90 cm, Cs oven, microwave cavity, C-field, graphite beam-collimating discs, vacuum pump and optical detection. There are 10 ports on the chamber. Four laser beam ports, one vacuum port, one for the microwave source, two for electrical feeds and two for Cs beam input and output. A schematic view of the Cs beam apparatus is shown in Figure 6. A turbo molecular pump was used to maintain the background pressure at less 10-5 Pa. The cesium oven was operated at 100°C. The beam divergence less than 200µ steradians was obtained using a number of collimating stainless steel and graphite discs having a 2 mm hole diameter. Graphite discs were used to adsorb residual Cs atoms scattered out of the main beam.
The C-field is produced by using four coils as illustrated in Figure 6. This configuration produces a magnetic field perpendicular to the atomic beam and is used to lift the degeneracy of the hyperfine sublevels mF of the Cs ground state. The U-shaped copper microwave cavity consists of two interrogation zones, each having 10 mm length and 5 mm width. The separation between the two zones is 90 mm. The atoms in the two zones interact with microwaves generated by the microwave synthesizer. The quality factor Q (= n/Dn) of the cavity is about 500 at the oscillation frequency of 9.2 GHz. The whole microwave cavity region is shielded with m metal to avoid external magnetic field perturbations.
The Cs atoms are prepared in a selected ground state hyperfine level and detected using laser induced fluorescence before and after the microwave cavity region using a stabilized diode laser (Teles et al. 2000).
Microwave synthesizer, control and comparison
The microwave synthesizer (HR1 #003) used to interrogate the Cs atoms was built in NIST (National Institute of Standards and Technology - Bolder - USA), by Dr. F. Walls team. Depicted in Figure 7, it is constituted of three base high performance quartz oscillators (5 MHz, 100 MHz and 10.7 MHz Wenzell VCXO's). Phase Locked Loops (Phase Detectors and Loops Filters) are implemented in order to extract the best spectral characteristics of each oscillator and synthesize the 9.192 GHz interrogation signal. An external DDS (Direct Digital Synthesizer - SR345 Stanford), driven in external reference by the 5 MHz oscillator, provides the capability to sweep the microwave signal. Once phase locked to the 5 MHz oscillator, the 100 MHz signal is multiplied by a factor of five. The 500 MHz signal is then mixed to the signal from the 10.7 MHz oscillator and feeds a Step Recovery Diode (SRD). This device, based on a nonlinear effect, generates a frequency comb with the harmonics of the 510.7 MHz input signal. With proper filtering, only the 18th harmonic of 510.7 MHz is obtained, producing 9.1926 GHz. The 10.7 MHz oscillator is phase locked to the external DDS, in order to provide a fine-tuning capability in the microwave signal. A LabVIEW computer interface program controls the DDS. The synthesizer has the frequency resolution of 18 × 10-6 Hz and fractional frequency stability better than 3 × 10-14 t-1/2 for 104 seconds of averaging time.
Optical pumping and detection
Initially, for the development of cesium atomic clocks, the magnetic state selection and detection of ground state hyperfine levels using a Stern-Gerlach technique was implemented successfully by a number of workers (Bauch 2003, Vanier and Audoin 1989 and references therein). However, optical pumping schemes can be used effectively for state selection and state detection as well. Optical schemes are more attractive compared to the use of inhomogeneous multipole magnets (Stern-Gerlach technique) because they avoid stray magnetic fields. Optical schemes have the advantage of single-state selection efficiency in which all the population can be pumped into a single state. An external cavity-stabilized, single-mode diode laser (SDL 5412-H1) was used for pumping and detection. A conventional saturation absorption technique was used to stabilize and reference the laser. Wavelength tuning was achieved by varying the current and temperature. The line width of the laser after stabilization was less than 500 KHz. The optical schematic diagram is shown in Figure 6.
The optical pumping scheme involves the transfer of all the atoms to the 62S1/2 (F = 3) ground level before the atoms enter the microwave cavity and fluorescence detection from the transition 62S1/2 (F = 4) ® 62P3/2 (F = 5) after the second microwave interaction zone. To stabilize the laser at a certain atomic line, a part of the laser beam was sent to pass through cesium cell. The laser wavelength was locked at the 62S1/2 (F = 4) ® 62P3/2 (F = 5) transition of the saturation absorption line of the cesium cell to avoid the long term drift. The remaining part of the laser beam was propagated through the acoustic optical modulator (AOM). The AOM modulator was operated at 250 MHz to generate first order diffracted and zero order beams for pumping 62S1/2 (F = 4) ® 62P3/2 (F = 4) and detection 62S1/2 (F = 4) ® 62P3/2 (F = 5) respectively (Teles et al. 2000). Optical pumping for the radiative transitions in alkalies takes about 10µ sec.
EVALUATION OF THE CS ATOMIC BEAM CLOCK
The performance of a time and frequency standards depends on stability, frequency shifts uncertainty and accuracy. The stability criterion can be divided into short and long term stability, both of which are evaluated by the "Allan variance". The frequency shift of true hyperfine transitions can occur due to a number of external and internal perturbations such as black body transitions, Gravitational field, and Doppler and Zeeman effects. These effects manifest themselves as frequency offsets.
Before presenting the clock evaluation, it is worthwhile to introduce the concepts of accuracy, stability, and reproducibility. They are often used to describe an atomic clock quality with respect to its instabilities.
Accuracy is the degree of correctness of a quantity with respect to the true value. It is related to the offset from an ideal value. In the world of time and frequency, accuracy is used to refer to the time offset or frequency offset of a device from the value of the international primary standard.
Stability is the inherent characteristic of a device that determines how well it can produce the same value over a given time interval. Stability does not determine whether the frequency of a clock is right or wrong, but only whether it stays the same. The stability of an oscillator does not necessarily change when the frequency offset changes. One can adjust the frequency of an oscillator by moving either further away from or closer to its nominal frequency without changing its stability.
Reproducibility is the ability of a device to produce the same value, without any adjustment, each time when it is operated.
EVALUATION OF THE FREQUENCY STABILITY AND ALLAN VARIANCE
The frequency stability of an oscillator is the degree to which it maintains the same value throughout the specified time interval. The short-term stability of a well designed beam clock is limited by shot-noise and abrupt changes, whereas long-term stability is limited by changes in the magnetic field environment, velocity distribution changes, cavity temperature change, microwave level change, and other environmental perturbations. The stability is characterized by the "Allan variance" (Allan 1966, 1989). It is defined as one half of the time average of the squares of the differences between consecutive measurements. The Allan variance is expressed as:
where yn is the fractional frequency error, averaged over sampling period t. The normalized frequency is defined as:
where n is the reference clock frequency and dn is the error in frequency, and the average is performed over n sampling periods. The division by two in Eq. 6 causes this variance to be equal to the classical variance if the y's are taken from a random and uncorrelated function, i.e. white noise. The advantage of this variance over the classical variance is that it converges for most of the commonly encountered kinds of noise, whereas the classical variance does not always converge to a finite value. Flicker noise and random walk noise are two examples that commonly occur in macroscopic oscillators where the classical variance does not converge. Allan variance is used as to measure the stability of a number of precision oscillators such as atomic clocks and frequency-stabilized lasers. The stability of the atomic clock is given by the square root of the Allan variance and can be defined as:
where t is the sampling time, Qat is the quality factor of the atomic resonance, S/N is the signal to noise ratio for a sampling time t and t is the cycle time. If we plot the values of square root of Allan variance s(t) as a function of sampling time t on a log-log scale then the slope will characterize the type of noise in the clock. For the Brazilian atomic beam clock, the short-term stability was determined using a commercial atomic standard (Agilent - 5071A) and a computer with a GPIB interface to store the data reading, allowing us to perform a constant evaluation of the atomic beam standard. Figure 8 shows the measured values of s of our Cs133 beam frequency standard versus the sampling time t. For the present evaluation, the short term stability of the Cs clock is s(t) = (6.6 ± 0.2) × 10-10t-0.50+0.1.
FREQUENCY SHIFTS AND UNCERTAINTIES
The frequency of the clock transition is affected by a number of small frequency offsets due to external as well as internal sources. As a result measured frequency differs from the actual value. By definition, the frequency of a clock transition must be determined in the absence of these perturbations. Therefore, the frequency shifts due to perturbation must be estimated, and the measured frequency value be adjusted accordingly. These shifts include relativistic effects, interaction due to external electric and magnetic fields, losses and changes in microwave cavity, effect of neighboring transitions and instrumental drift. Each of these are discussed below:
Determination of the Rabi frequency
From the Ramsey fringes one can obtain important operation parameters. The transition rate for the Ramsey interrogation depends on the Rabi frequency. The Rabi frequency is written as, b = (µB/ )B, where B is the microwave magnetic field amplitude in the interrogation region and can be determined by measuring the power of the microwave signal injected into the cavity. The method that we have used makes it easier to ascertain the Rabi frequency by a mathematical analysis of the experimental Ramsey pattern. This analysis provides greater accuracy of the Ramsey pattern (Makdissi and de Clerq 1997). In order to obtain better precision in the determination of the Rabi frequency, we take the second derivative of Eq. (5) and rewrite it as a sum of three Dirac pulses at different frequencies (Teles et al. 2002). The measured value of b = 49,197 ± 16.21 rad s-1 is consistent with the operational parameters.
)B, where B is the microwave magnetic field amplitude in the interrogation region and can be determined by measuring the power of the microwave signal injected into the cavity. The method that we have used makes it easier to ascertain the Rabi frequency by a mathematical analysis of the experimental Ramsey pattern. This analysis provides greater accuracy of the Ramsey pattern (Makdissi and de Clerq 1997). In order to obtain better precision in the determination of the Rabi frequency, we take the second derivative of Eq. (5) and rewrite it as a sum of three Dirac pulses at different frequencies (Teles et al. 2002). The measured value of b = 49,197 ± 16.21 rad s-1 is consistent with the operational parameters.
Gravitational and second-order Doppler frequency shifts
These shifts are due to the intrinsic nature of time and space. The most important is the gravitational red shift and the second order Doppler shift.
The Gravitational frequency shift is a relativistic correction due to the gravitational potential variation at a given location on the earth. It is independent of the atomic velocity and just produces a translation shift in the Ramsey fringe.
Clocks on the earth or near to the earth surface, by convention (CCDS 1980) origin of gravitational potential is the geoid surface. This follows the gravitational frequency shift as under (Vanier and Audoin 1989):
where n0 is the atomic clock resonance frequency, H is the height difference, g is the acceleration due to gravity and c is the velocity of light. Hence the frequency of a clock is an increasing function of its latitude. The fractional frequency change is 1.09 × 10-13 Km-1. The most precise gravitational measurement has carried been out with a ballistic flight of hydrogen maser. The gravitational effect is red-shifted when the altitude decreases and blue-shifted when altitude increases. The São Carlos altitude, where the atomic beam standard is located, is h = 850 ± 50 m. This was measured with a GPS receiver (9390-6000 Datum). The following is the frequency shift due to the gravitational effect (Teles et al. 2003, Bebeachibuli et al. 2005):
The second-order Doppler shift is one of the major frequency shifts in the atomic beam clock. The Doppler effect is always present whenever there is relative motion between the source, observer and propagating waves. The atom acts as an observer, emitter and detector. The Doppler effect is always present in gaseous atoms due to their motion unless some special techniques are adopted for its reduction or elimination.
The relativistic approach in case of emission or absorption of electromagnetic radiation makes the 2nd order Doppler effect evident. Therefore higher order terms of the Doppler effect have to considered.
Here w0 is the atomic resonance frequency, K is the propagation vector whose magnitude is defined as K =  , uk is the velocity of the atoms, c is the velocity of light,
, uk is the velocity of the atoms, c is the velocity of light,  is Planck's constant divided by 2p and M is the mass of atom. The second and third terms are identified with the 1st order and the 2nd order Doppler effect. The last term represents the recoil effect and it is a function of frequency. Its detection may be possible at high frequencies.
is Planck's constant divided by 2p and M is the mass of atom. The second and third terms are identified with the 1st order and the 2nd order Doppler effect. The last term represents the recoil effect and it is a function of frequency. Its detection may be possible at high frequencies.
Since the microwave field and the laser fields for optical pumping and detection are all applied orthogonal to the atomic beam velocity, the 1st order term can be made negligible. The second-order Doppler effect, however, needs to be considered. The fractional change in the frequency of clock value is expressed as:
The second-order Doppler shift is related to the time dilation predicted by the theory of relativity. For each velocity component the shift is given by,
This is valid for an atom ensemble having the same velocity. Generally atomic ensembles have a velocity distribution. The weighted integral value determined by the above equation will correspond to the frequency shift for an atomic ensemble. Therefore we must determine the velocity distribution. In this respect we have applied two different methods to evaluate the 2nd order Doppler shift for the Brazilian frequency standard (Bebeachibuli et al. 2003, 2005, Teles et al. 2002, 2003). The first method was developed by (Makdissi and de Clercq 1997), where the variation of the shift as a function of modulation amplitude is obtained from the second derivative of the Ramsey fringe. The second method was also developed by (Makdissi 1999), where a general expression for frequency shifts is applicable to the case of any agent displacing the frequency. The 2nd order Doppler shift as a function of modulation amplitude of the microwave field was measured. For the temperature T = 343 K (corresponding to an average atomic velocity of 200 ms-1) and at modulation of 45 Hz of Ramsey fringe the resulting shift is
DC electric field effect on hyperfine states: Stark effect
The DC electric field effect on the hyperfine structure of alkali atoms and ions with S1/2 ground state has been studied by number of workers. The 1st order Stark effect perturbs the energy levels having different parity. Thus in case of ground state hyperfine levels of alkali atoms, the 1st order Stark effect may be interpreted as an admixture of P and higher states in the ground state S. However only the quadratic Stark effect produces the shift in the hyperfine structure and this must be considered for clock evaluation. The differential Stark shift induced by the electric field E on the Cesium clock transition is given by (Simon et al. 1998).
Here a10 and a12 are the contribution to the cesium static polarizability from contact and the spin-dipolar interactions respectively, E is the electric field strength and h is Planck's constant. The value of a12/h is 10-7 smaller than (a10/h), therefore the second term can be neglected. The value of 8/7 × a10/h = 2.273 × 10-10 Hz/(V/m). The measured value of the fractional hyperfine frequency shift for cesium atoms due to applied electric field is given by
where E is the electric field expressed in V/m. This is clearly a very negligible frequency shift. In the atomic frequency standard there exist no sizable electric field that can be detectable. Therefore we have neglected this effect for Cs beam clock evaluation.
DC magnetic field effect on hyperfine states: Zeeman effect
Atomic Cs primary frequency standards are based on the transition between two levels F = 4, mF = 0 « F = 3, mF = 0. In the absence of a magnetic field all the mF sublevels of a given F level are degenerate. So a magnetic field is essential to lift the degeneracy of the mF manifold. The value of the required magnetic field (C-field) is very small, ~ 13µ T. The Zeeman effect is expressed according to the Breit-Rabi equation (Vanier and Audoin 1989)
where x = (gJ - gI)/2p nhfs, gI and gJ are the Landé g factors for angular momentum I and J, µB is the Bohr magneton, B0 the magnetic field, nhfs is the cesium clock transition frequency in the absence of magnetic fields, and mF is the magnetic moment. The first term corresponds to the natural resonance frequency of the atoms and the second and third terms represent the 1st order and the 2nd order Zeeman effect respectively. For mF = 0 states the 1st order effect vanishes and only the 2nd order effect is applicable. The Cs clock operates between the mF = 0 levels as mentioned above, so the 2nd order shift will effect the accuracy of the clock, and it must be measured with the greatest care (Vanier and Audoin 1989):
nhfs, gI and gJ are the Landé g factors for angular momentum I and J, µB is the Bohr magneton, B0 the magnetic field, nhfs is the cesium clock transition frequency in the absence of magnetic fields, and mF is the magnetic moment. The first term corresponds to the natural resonance frequency of the atoms and the second and third terms represent the 1st order and the 2nd order Zeeman effect respectively. For mF = 0 states the 1st order effect vanishes and only the 2nd order effect is applicable. The Cs clock operates between the mF = 0 levels as mentioned above, so the 2nd order shift will effect the accuracy of the clock, and it must be measured with the greatest care (Vanier and Audoin 1989):
Besides the evaluation of transition between mF = 0 other six transitions between mF = ±1, ±2 and ±3 are equally important for determination of clock accuracy. These transitions strongly depend on the magnetic field. We have observed a shift of 7.3 KHz from the spectrum shown in Figure 4. This value corresponds to the magnetic field B0 = 13µ T. A periodic measurement of n+1 and n-1 are necessary to observe temporal dependence of the quadratic Zeeman shift. We have measured them for ten days, five time in a day in normal operating conditions and observed that the daily variation is about 5 mHz. Thus relative uncertainty in the temporal measurement of the 2nd order Zeeman shift is
For details see (Bebeachibuli et al. 2003, 2005, Teles et al. 2002, Santos et al. 2003).
Black body radiation shift
This shift is due to nonresonant excitation of atoms by electromagnetic radiation in thermal equilibrium with the black body at room temperature. The Planck distribution law governs black body radiation. The average electric field and magnetic field energies are proportional to the fourth power of thermodynamic temperature T4 and are given by the following equations (Vanier and Audoin 1989).
These electric and magnetic fields perturb the cesium atoms by an ac Stark effect and an ac Zeeman effect respectively. Perturbation due to the magnetic field can be neglected because it three orders of magnitude less than the electric field. The operational temperature of the clock is T = 296 ± 2 K, resulting in a black body radiation shift of
End-to-end cavity phase shift
This shift is related only to the Ramsey type of configuration, and it occurs when there exists a microwave phase difference in the two regions due to losses in the waveguide. In case of a microwave phase difference between the first and second interaction zones, the peak of the Ramsey signal will be shifted. This shift can be expressed as,
where j is the phase difference between two interaction zones, T is the travel, L is length between the two zones and u is the atom velocity. The phase difference between the two extremes of the cavity, due to a small variation in length DL0 of the arms, is given by,
where L0 is the effective electrical length of the two arms, ag is the attenuation constant and lg the wavelength in the guide. This shift also depends on the velocity of atoms and the measured shift is sensitive to the velocity distribution as expressed in the 2nd order Doppler effect. Taking into account the velocity distribution, we have measured this shift as a function of amplitude modulation directly from the Ramsey pattern. It was observed that the shift increases with decreasing amplitude. The relative shift is-6.8 × 10-12 (Teles et al. 2002).
Inhomogeneity of the magnetic field along the microwave cavity
As already discussed, the characteristic signature of an atomic clock is the Ramsey fringe superimposed on a broader resonance called the Rabi pedestal. In ideal conditions, the Ramsey fringe is exactly centered to the Rabi pedestal. However, if there is any magnetic field inhomogeneity along the atom trajectory through the microwave cavity the Ramsey fringe is no longer centered on the Rabi pedestal and a frequency shift is induced.
For the measurement of the inhomogeneity of the magnetic field we undertook to measure the position of the Ramsey fringe with the Rabi pedestal for the D mF = 0 transitions. The difference between them was computed and written as (Makdissi and de Clerq 2001)
where
1 and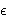 2 are fluctuations of the mean static field in the first and second interaction regions respectively. The slope in the linear curve of D(mF) as a function of mF determines the value of (
2 are fluctuations of the mean static field in the first and second interaction regions respectively. The slope in the linear curve of D(mF) as a function of mF determines the value of (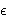 1 +
1 + 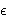 2). As seen in Figure 9, the slope in the experimental curve D(mF) × mF is 11.35 ± 0.05 resulting in (
2). As seen in Figure 9, the slope in the experimental curve D(mF) × mF is 11.35 ± 0.05 resulting in (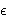 1 +
1 + 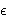 2) = -0.99 ± 0.05 × 10-8. This yields a frequency error on the clock transition due to the field inhomogeneity of nz = 1.08 ± 0.04 × 10-5 Hz. The other Zeeman transitions are also shifted by the same effect, and they are shifted by 0.77µHz. The detailed analysis procedure is given in articles (Bebeachibuli 2003, 2005, Santos et al. 2003). The results are computed in terms of total uncertainty considering the uncertainty measured due the experimental determination of the Zeeman frequency,
2) = -0.99 ± 0.05 × 10-8. This yields a frequency error on the clock transition due to the field inhomogeneity of nz = 1.08 ± 0.04 × 10-5 Hz. The other Zeeman transitions are also shifted by the same effect, and they are shifted by 0.77µHz. The detailed analysis procedure is given in articles (Bebeachibuli 2003, 2005, Santos et al. 2003). The results are computed in terms of total uncertainty considering the uncertainty measured due the experimental determination of the Zeeman frequency,
and the correction due to the field inhomogeneity,
The quadratic sum of these terms results in
with an uncertainty of 0.15 × 10-13.
Rabi Pulling
Besides the chosen clock transition, there are the other six Zeeman transitions whose energies depend linearly on the static magnetic field (C-field), DF = ±1; DmF = 0, as shown in Figure 4. The separation between the neighboring transition and the clock transition is 92 KHz which corresponds to a 13 µT C-field. These transitions have finite line width and hence they overlap the clock transition. Rabi Pulling is due to the superposition of the pedestals between adjacent transitions in the Zeeman spectrum. The transition signal of the first neighbor (mF = 0) is written as,
where P(W0) is the Ramsey probability and P3(W0) is the Rabi pedestal, I(m) is the amplitude of transition m and wz = 2pnz. The probability P3(W0) is given by the equation
Expanding this equation in first order in  , we obtain
, we obtain
If we insert Eqs. 10 into Eq. 9 and rewriting terms we obtain
where
From Eqs. 11 and 12 we see that the effect of the neighbors' transition on the clock transition is expressed by a small even quantity b0 and an odd function b1. The odd function creates a deformation of the clock signal. When the neighbor transitions, mF = I and mF = -I, have the same amplitude the deformation vanishes. The frequency shift induced may be calculated by,
where A(wm, b, t) is the unperturbed transition probability and f(t) is the velocity distribution. The Rabi pulling may shift the Rabi pedestal and the Ramsey fringe. However, this effect is more pronounced for the Rabi pedestal, because the inclination of the pedestal is smaller than the Ramsey fringe, while the amplitude modulation is greater. Thus, with the same method used for the second-order Zeeman effect, we measured the shift between the pedestal and the associated fringe for each of the seven transitions.
The fractional frequency shift of the clock transition was determined in the same way for the field inhomogeneity (Makdissi and de Clercq 2001). From Figure 4, we have observed that there is an asymmetry of 1.3% between the nearest-neighbor transition and the clock transition. We now can estimate the fractional Rabi pulling as 4.4 × 10-11. The corresponding pulling for the Ramsey fringe is smaller by a factor of l/2L; and its magnitude is 1.3 × 10-13 (Bebeachibuli et al. 2003, 2005).
Cavity pulling
Cavity pulling arises from the variation of the microwave amplitude with frequency when the cavity is mistuned. It is nearly independent of mF, but it has a strong dependence on the microwave power and on the modulation amplitude. Our procedure to measure the cavity pulling is the same as was used to measure the magnetic field inhomogeneity. From Figure 9 the measured pedestal shift is 3.76 ± 0.10 Hz and the induced effect on the Ramsey fringe for the cavity detuning is 1.27 × 10-13 for the clock transition (Bebeachibuli et al. 2003, 2005).
GLOBAL ACCURACY BUDGET
The accuracy of an atomic frequency standard is defined as the capacity of the standard to produce a frequency that is in agreement with the definition of the second. It is expressed as a relative uncertainty  , relative to the second definition. Applying the several corrections to our frequency standard, their corresponding uncertainties are tabulated in Table I.
, relative to the second definition. Applying the several corrections to our frequency standard, their corresponding uncertainties are tabulated in Table I.
Finally, the global accuracy of the beam standard results in sC = 6.13 × 10-13. This value means that the precision at which our frequency standard measures the clock transition frequency is 9 192 631 770 Hz. This uncertainty is comparable with the available commercial beam clocks. The constructed device was an important step on the learning curve for the Brazilian team towards the fountain clock development that will be described in the next section.
CONSTRUCTION AND EVALUATION OF THE CESIUM FOUNTAIN CLOCK
Time and frequency metrology is a dynamic field. As the technology advances, new and more precise ways to measure time arise. The fountain clock is an important step with about three orders of magnitude improvement over the current atomic beam clock. In order to master the state-of-the-art in the field of time and frequency standards, we decided to undertake development of an atomic fountain clock.
Why is a fountain clock better than the conventional atomic beam?
The Ramsey two-interaction-zones technique demonstrates that the full-width-half-maximum (FWHM) of the central fringe is proportional to (1/T) or (u/L). This imposes two limits in the achievement of narrower Ramsey fringe and hence improvements over the accuracy of thermal beam clock: the cavity length L increment and the atomic velocity (u) reduction. The thermal atomic beam cannot be made slower than 70 ms-1 due to the intrabeam collisions and velocity distribution. The length of cavity is limited by the beam shape and loss of the atoms. Thus the shape of velocity distribution and correct geometry put an upper limit on the thermal atomic beam clock. A typical tube with a 1 m drift region and velocity of 100 ms-1 results in a 10 ms interaction time or 50 Hz line width.
In the 1950s Zacharias (Ramsey 1963) proposed a device in which slow atoms from a thermal source were directed vertically upwards and then allowed to drop under gravity. This scheme could provide an interaction time of more than 1 second, but initial attempts were unsuccessful due to atomic velocity dispersion at ambient temperature. However, with the advent of laser cooling and trapping techniques (Metcalf and Straaten 1999), with much reduced atomic velocity dispersion, the door was opened to reconsider the Zacharias approach. In the last decade it was successfully implemented with the name of the atomic fountain clock (Kasevich et al. 1989, Clairon et al. 1991). By using laser cooling and trapping techniques such as a Magneto Optical Trap (MOT), one can localize millions of cesium atoms in a very small volume and at a temperature of a few µK. The average velocity of the atoms at this temperature is of the order of 1 cm s-1. In the fountain clock the launching velocity is selected in such way that the atoms reach a height of 1 meter and then fall down along the same path under gravity. While the atoms travel up and down they pass through the same microwave cavity. Each time the atoms pass through the cavity they experience a p/2 pulse of microwave field. A typical height above the cavity is about 20 cm. So the effective interaction of about half a second can be easily achieved and results in reduction of the resonance line width by 100 fold compared to the thermal beam clock. Besides the most advantageous aspect of line width reduction, another benefit of the fountain clock configuration is the trajectory reversal that removes the cavity end-to-end phase shift and eliminates the distributed cavity phase effects. The first fountain clock was developed at the Observatoire de Paris, France and exhibited a relative uncertainty of 1.1 × 10-15 (Clairon et al. 1996, Wynands and Weyers 2005).
CONSTRUCTION
Device description
The construction of a cesium cold atom fountain frequency standard is described in detail in (Magalhães et al. 2003) and shown in Figure 10.
It consists of ultrahigh vacuum pumps, a magneto-optical trap (MOT), stabilized diode lasers, a microwave synthesizer, free-flight cylinder and detection regions. The vacuum system consists of two parts, one for the trapping chamber and another for the free-flight cylinder. The background pressure in the chamber, lower than 10-7 Pa, was maintained by a 60 ls-1 ion pump. The MOT vacuum chamber is made of stainless steel having dimensions 35 cm in length and 20 cm in diameter. The MOT operates with the trapping beams meeting at the center orthogonally and tuned to the D2 line of cesium. In this geometry 3 upper and lower trapping beams make an angle of 35.4° with respect to the horizontal x-y plane. Anti-Helmholtz coils are mounted along the y-direction for the generation of magnetic field. The detection region is about 19 cm below the trapping region as shown in Figure 10. The free-flight cylinder is 90 cm in height and 1.5 cm in diameter. It is made of copper (nonmagnetic) to reduce the effects of residual magnetic fields inherent in stainless steel.
The microwave cavities for the interrogation and preparation regions are made inside the free flight chamber. These cavities couple the TE011 mode of the microwave signal. They are resonant at the clock rf frequency. The unique interrogation cavity acts as the two-interaction-regions in the Ramsey scheme: first when the atoms move upwards and second when they come back down under gravity. In this way atoms pass through the same cavity twice. The preparation microwave cavity is used only for the preparation of the atoms in the selected state. This cavity remains active only at launch time. The quality (Q) factor of the preparation cavity is 1900 and the Ramsey cavity is 8500. The static magnetic field that generates the quantization axes, called the C-field, is produced by an 80 cm long solenoid. To prevent perturbations from stray magnetic fields a cylinder of µ-metal is placed around the free-flight tube.
The cycling process of the atomic fountain is stated with the preparation of cold atoms in the MOT. Then to produce a homogeneous atomic cloud, the magnetic field is turned off and atoms are exposed to a molasses phase. Then the cold atoms cloud is launched using the moving molasses technique. The initial velocity of launched atoms is determined by the frequency detuning between upper and lower laser beams at 852 nm. During this phase the trapped atoms are detuned adiabatically far from the resonance that results in a sub-Doppler cooling of the cloud.
The principal laser source for trapping and cooling the atoms is a diode laser system model TA 100 from TOPTICA. The laser is locked to the reference Cs cell using the conventional saturated absorption technique. In the reference system an acousto-optic modulator (AOM) shifts the laser frequency and provides the detuning control for the MOT and sub-Doppler cooling phase. The optical output from the TA 100 is divided by using polarizing cubes, and each beam passes through separate AOMs. The voltage controlled oscillator (VCO) that supplies RF signal to these two AOMs insures that they are phased-locked for the MOT and optical molasses production. For launching the atoms, a frequency difference is introduced between the upper and lower beams by an external digitally derived synthesizer (DDS) through the two AOMs. A repumper consisting of an external cavity diode laser system is used to pump the atoms from 62S1/2F = 3 ® 62P3/2F = 4. A part of the laser beam is split and propagated through another reference Cs cell while the rest of the repumper maintains stability and correct functioning of the MOT. A third diode laser (SDL5412-H1) is used for the detection of atoms. It is locked to the 62S1/2F = 4 ® 62P3/2F = 5 transition. The detection system is located just below the MOT chamber. Two light beams having 6 mm separation are generated. One is in resonance at the 62S1/2F = 4 ® 62P3/2F = 5 transition and the second beam is a composition of two frequencies: the repumping beam frequency at the 62S1/2F = 3 ® 62P3/2F = 4 transition and the 62S1/2F = 4 ® 62P3/2F = 5 resonance frequency. Therefore atoms in both hyperfine levels can be detected. The fluorescence detection of these two beams is carried out by using two PIN photodiodes with separate collection optics. The Ramsey fringes are observed by the measurements of the ratio
where NF = 3 and NF = 4 are the populations of the atoms in F = 3 and F = 4 levels. Polarization maintaining optical fibers are used to deliver the laser power to the vacuum chamber. The optical power of the beam is about 11 mW and diameter is about 28 mm. Using this cycling process, and launching the cold atoms 10.5 cm above the microwave cavity, we obtained a 1.7 Hz wide Ramsey central fringe. With this signal, the short-term stability was 6.6 × 10-12.
Microwave synthesizer
To produce the interrogation signal to the atomic fountain experiment, a microwave synthesizer was constructed with the valuable collaboration of the LNE-SYRTE (Laboratoire National de Métrologie et d'Essais-Systèmes de Référence Temps-Espaces) time-and-frequency team. This chain, shown in Figure 11 uses a similar topology to some devices already operating with their atomic frequency standards [4]. It has the same core idea used in the NIST chain, that is to generate a signal with the best spectral characteristics of high performance oscillators using phase-locked-loop techniques.
The main parts of the synthesizer are the three oscillators: 4.596 GHz (DRO - Dielectric Resonant Oscillator - 4R596-10SF - Omega Technologies), 10 MHz (BVA - OCXO 8600 - Oven Controlled Crystal Oscillator - Oscilloquartz) and 100 MHz (500-07542A - Wenzel Associates Inc). The 100 MHz crystal oscillator is phase locked to the BVA at low frequencies (below 30 Hz), providing an output signal at 100 MHz with phase noise characteristics superior to each component individually. This 100 MHz signal is then doubled and inserted into a sampling mixer (RF - Reference Frequency input), which performs the subtraction of the 23rd harmonic of this input (4.6 GHz) with the main harmonic signal coming from the DRO at 4.596 GHz (LO - Local Oscillator input). The output signal from the sampling mixer (IF - Intermediate Frequency) is compared with an external 29.5 MHz frequency, supplied by a DDS (SR345 - Stanford Research Systems) that uses the BVA as an external reference. This comparison provides the phase locking of the DRO, allowing modulation through the DDS programming. The other DRO output is connected to a waveguide filter whose band is centered on its first harmonic at 9.192 GHz. The signal output has -15 dBm of output power, that is more than enough to feed the resonant cavity with a quality factor better than 5000 and minimizes spurious fields from connection leakages. The direct modulation of the DRO also provides an excellent way to increase the step resolution of the chain. Since the frequency step in the SR-345 is microhertz, the division by 8 provides a double advantage. The first advantage is that the frequency step resolution is 2.5 × 10-7 Hz. The second is provided by the fact that the signal synthesis is digitally performed, so the phase noise is not increasing with frequency. Using this fact, and since the DDS maximal frequency is 30 MHz, the 29.5 MHz signal is set, and a frequency division by eight also divides the signal phase noise by the same amount, improving the quality of the signal. This synthesizer was compared to other similar chains, and the obtained stability was shown to be 9.7 × 10-14t-1/2. To supply the microwave preparation signal, part of the 200 MHz signal generated in the first synthesizer is used to drive a second high-frequency phase lock, in the same topology used as in the first chain. In this case, a DRO at 9.192 GHz (10.84 dBm) is inserted into a sampling mixer and subtracted from the 46th harmonic of a 200 MHz signal derived from the interrogation chain. The sampling mixer output is compared with a 7.3 MHz signal provided by a DDS (SR345 - Stanford) and phase locks the DRO. In order to avoid perturbing fields during the interrogation phase, after the atoms pass the preparation cavity, the signal is switched off by the temporal sequence controller. This is done by using a switch with 80dB of isolation (F192A - General Microwave).
CONSTRUCTION AND EVALUATION OF THE EXPANDING COLD ATOM CLOCK
There is a need for simple, compact atomic clocks due to their wide applications in defense, communication and space technology. The relevant requirements for a good atomic clock depend significantly on the application. Compactness and robust design are at a premium, and stability dominates over accuracy for space-based systems. Recently compact clocks implemented using microfabrication technology (but not using cold atoms) have been demonstrated by Kitching et al. (2005a, b) and Knappe et al. (2006).In order to minimize the "footprint", weight and power consumption of magnetic traps, surface-mount wire traps and atom chips enable atom traps in various geometries. Robustness and mechanical stability can be achieved by using microfabricated wires (Feenstra et al. 2004 and references therein). NIST scientists demonstrated a chip-scale atomic clock based on coherent population trapping in 2004. Recently interest has been focused on the development of compact clocks where a trade-off between size and performance must be taken into account. In a recent example a trapped cloud of cesium atoms was prepared, interrogated within the microwave cavity. The resulting performance was a 14 Hz width of Ramsey central fringe and 10-12t-1/2 projected stability (Trémine et al. 2004). In the view of the great potential for the development of the cold-atom compact clock, we have also started a research program for the development of compact cesium cold-atom clocks in addition to the cesium beam and fountain clocks.
CONSTRUCTION
The Brazilian compact cold-atom clock is based on a Rabi profile and the Ramsey Method and is made from a freely expanding cloud of cold cesium atoms. Cold cesium atoms are prepared and trapped in a magneto-optical trap (MOT). A microwave antenna is used to provide the microwave radiation for the clock transition, which is detected by the fluorescence from the optically pumped excited states.
Figure 12 illustrates the simplified schematic diagram. A cesium vapor cell can be pumped to a base pressure ~ 10-7 Pa. A temperature-controlled reservoir allows regulating the amount of Cs atoms into the glass cell. Around the glass cell two main coils produce the magnetic field for magneto-optical trapping of the atoms and a set of compensation coils guarantee a field-free environment for the atomic cloud expansion. Atomic densities ~ 1010 cm-3 are typically measured by fluorescence. Two stabilized diode lasers provide the frequencies necessary to produce the cooling and repumping light. The relevant transitions excited by the lasers are the 62S1/2F = 4 ® 62P3/2F = 5 cycling transition and the 62S1/2F = 3 ® 62P3/2F = 4 repumping transition, that prevents atoms from accumulating in the F = 3 ground state during the trapping phase of the experiment. The trapping and repumping beams are spatially overlapped and divided along three orthogonal axes. Two counterpropagating beams intersect in the horizontal x - y plane and the third beam is directed along the z axis, perpendicular to the x-y plane and passing through the point of intersection of the the other two beams. Each laser beam carries about 12 mW of power in a 2.5 cm waist. Fluorescence light from the intersection region is imaged onto a calibrated detector located 10 cm from the cell center. A microwave antenna of quarterwave is positioned perpendicular to the vertical axis, outside the glass cell and about 3 cm from the atoms. The radiation pattern of the antenna was determined so as to position the atoms in the high-intensity region. The antenna was coupled to a microwave chain, generating 9.192 GHz. About 2 × 108 atoms are captured in the MOT and become the sample for performing the microwave transition and to lock the oscillator chain. The time sequence used to observe the microwave resonance is the following: for about 800 ms, the magnetic field of the MOT, as well as the lasers, are turned on, allowing capture and accumulation of atoms. The repumping laser and the MOT coils are then turned off until the end of the sequence. For the next 23.9 ms the trapping laser is still on and will promote optical pumping of the atoms to the 62S1/2F = 3 state, after which it is turned off. At this stage the atomic cloud is in free expansion and remains so for the next few ms. Then the first microwave pulse of duration 2 ms is applied. After a quiescent interval of 8 ms, a second pulse of microwave can be applied or not. At the end, the trapping laser is turned back on for 50 ms and the fluorescence of atoms at 62S1/2F = 4 is detected. The atoms originally populated in 62S1/2F = 3 are transferred to 62S1/2F = 4 by the microwave field. A variable attenuator is placed on the microwave source such that a p-pulse is applied during the Dtp period (Rabi method). In the case of two consecutive pulses Dtp, the microwave power is adjusted to produce two p/2-pulses (Ramsey method). The temporal sequence for the experiment is illustrated in Figure 13. The fluorescence detection system is composed of a collecting lens that images the cloud onto a calibrated photodetector. Once the resonance line is obtained, a modulation of the microwave frequency allows generates the error signal used to lock the oscillator on the atomic resonance. The microwave chain is phase-locked (phase-locked-loop) to the 10 MHz outputof a commercial standard oscillator source (Magalhães et al. 2006, Müller et al. 2005).
EVALUATION
Two experiments were conducted using the cold cloud of atoms interacting with microwave radiation. In the first experiment investigated the Rabi frequency coupling the upper and lower levels by using microwave B-field amplitude 30 µG. The pulse duration (Dtp) was varied 2-20 ms and the growing population of 62S1/2 (F = 4) atoms could be observed, reaching a maximum and then decreasing. This is the first cycle of the Rabi oscillation. The pulse time Dtp has been fixed to produce the maximum transference to the 62S1/2 (F = 4) level, which corresponds to a p-pulse. At 30 µG microwave amplitude, Dtp = 12 ms and fixing the pulse duration, the microwave frequency was swept, generating the resonance curve as shown in Figure 14. Fitting the resonance curve with a Lorentzian shape we obtain a full width at half-maximum (FWHM) of 39 Hz. Comparing with the results reported by (Guillot et al. 1999) for the first evaluation of the atomic clock with cooled atoms in a cell, a factor of 6 improvement is obtained with a freely-expanding cold atom cloud. Our results are however compatible with the results by (Sesko and Wieman 1989), where 44Hz FWHM was observed in an experiment similar to the one here presented.
If our observed line width of 39 Hz is compared to NIST-6 (NBS-6) atomic clock, 26 Hz, which was obtained with a Cs beam and a 4 m long transition region (Glaze et al. 1977), we can appreciate the great potential for the use of the cold-atom Rabi interrogation method as a clock transition. In terms of line width vs. length of transition region, we are three orders of magnitude better than conventional beam clocks. Compared to atomic fountains, whose typical line width is 1 Hz, we see that there is also room for improvement when just a cloud of cold atoms is used.
The resonance observed in Figure 14 was used as a clock transition to lock a local oscillator. The generated error signal was used to evaluate the comparison thus obtaining the Allan variance. The frequency stability of the produced clock is presented in Figure 15, resulting in an Allan standard deviation of s(t) = (9 ± 1) × 10-11 t-1/2, already a good stability considering the simplicity of the device. There is still a lot of room for improvement, and we should be able to obtain a result about one order of magnitude better for short-term stability. It should be straightforward to extend the present demonstration technology to make a compact high performance, all-optical atomic clock, with a long lifetime of Cs supply compared to present Cs tube lifetimes.
In the second experiment, a sequence of two pulses during the interrogation time was used in an attempt to implement the Ramsey method. In this case we have used Dtp = 2 ms and Dtb = 8 ms, with a power level such that a p/2-pulse condition for each interrogation is satisfied. The existence of fringe is quite clear but with very poor contrast. The reason for this poor contrast are not yet entirely understood. It seems that the fringes exhibit a great narrowing of the transition but the poor contrast makes it hard to lock an oscillator as has been done for the single-interaction-zone, Rabi profile. The possible reasons for this poor contrast are under investigation.
CONCLUSION
In this article we have discussed the important applications of atomic clocks, their working principles, based on the two separated microwave interaction zones, and the different types of cesium atomic clocks.We have thoroughly described the cesium-based Brazilian program, construction and evaluation.
We have designed and developed the cesium beam clock, fountain clock and compact cold atom clock under the research program on time and frequency metrology in Brazil. These are the first thermal and cold atoms standards fully constructed in Latin America.
The construction of the Brazilian frequency standards family has been described in detail. It consists of cesium oven, beam chamber, vacuum systems, microwave cavity, C-field, graphite discs, diode laser, diode laser driver and stabilizer, microwave synthesizer, magneto-optical trap (MOT) and free flight cylinder.
Evaluation of the frequency standards was performed and based on experimental data. Short term stability of the clocks was determined from the square root of the Allan variance. The short term stability of the beam clock, fountain clock and compact expanding cold atom clock were determined to be s(t) = (6.6 ± 0.2) × 10-10t0.5±0.1, s(t) = (6.6 ± 0.2) × 10-12t0.5, and s(t) = (9 ± 1) × 10-11t0.5 respectively.
The observed line width in case of Brazilian expanding cold atom clock is 39 Hz with respect to the Rabi profile. With a 0.2 m long transit region the typical line width of the fountain clock is about 1 Hz. This illustrates the great potential of compact cold atomic clocks.
We have discussed and evaluated all the possible frequency offsets due to perturbations. Optimal Rabi frequency, second order Doppler shift, second order Zeeman shift, cavity pulling, end-to-end cavity phase shift and inhomogeneity of the magnetic field along the microwave cavity were all determined from the analysis of Ramsey central fringe and Rabi pedestal. The global accuracy budget of these frequency shifts with corrections and uncertainties was tabulated. Finally the global accuracy of the beam clock is determined to be 6.13 × 10-13. The future program is to extend present demonstrated technology to achieve a high-performance, compact, cold-atom clock with long life and continue efforts toward developing the atomic fountain for use as a high-performance reference as well as to contribute to TAI and perform fundamental physics research.
ACKNOWLEDGMENTS
The authors acknowledge the financial support obtained from Fundação de Amparo à Pesquisa do Estado de São Paulo, Centros de Pesquisa, Inovação e Difusão, Centro de Pesquisa em Óptica e Fotônica (FAPESP/CEPID/CePOF), Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES/COFECUP) and Conselho Nacional de Desenvolvimento Científico e Tecnológico (TIB-CNPq). We also acknowledge the important collaboration with LNE-SYRTE. M.A. also acknowledges support from the higher education commission of Pakistan.
Manuscript received on July 7, 2007; accepted for publication on December 18, 2007; contributed by VANDERLEI S. BAGNATO* * Member Academia Brasileira de Ciências
- ALLAN DW. 1966. Statistics of atomic frequency standards. Proceedings of IEEE 54: 221230.
- ALLAN DW. 1989. In seach of the bet clock: An update in: Frequency standards and metrology. Springer, Berlin, Heidelberg.
- ALLAN DW, KUSTERS J AND GRIFFRED R. 1994. Civil GPS timing application. Proceedings of ION GPS-04, p. 2532.
- AUDOIN C AND GUINOT B.2001. The Measurement of Time: Time, Frequency and The Atomic Clock. Cambridge University Press.
- BAUCH A. 2003. Cesium atomic clock: function, performance and applications. Meas Ci Technol 14: 11591173.
- BEBEACHIBULI A, SANTOS MS, MAGALHÃES DV, TELES F AND BAGNATO VS. 2003. Characterization of the frequency pulling by magnetic field oscillation of the Brazilian Cs atomic frequency standard. Proceedings of the 2003 IEEE International frequency control symposium, p. 9599.
- BEBEACHIBULI A, SANTOS MS, MAGALHÃES DV, MÜLLER ST AND BAGNATO VS. 2005. Characterization of the main frequency shifts for the Brazilian Cs atomic beam frequency standard. Braz J Phys 35: 10101015.
- BIZE S ET AL. 2005. Cold atom clocks and applications. J Phys B 38: S449S468.
- CASENAVE A, BONNEFOND P, DOMINH K AND SCHAEFFER P. 1997. Caspian Sea-Level from TOPEX/ POSEIDON Altimetry Level Now Falling. Geophys Res Lett 24: 881884.
- CCDS. 1980. Proceedings of the Consultive Committee for the Definition of Second Bureau International des Poids et Mesures, Sèvres, France.
- CGPM. 1967. 13th General Conference on Weights and Measures.
- CLAIRON A, SALOMON C, GUELLATI S AND PHILLIPS WD. 1991. Ramsay Resonance in a Zacharias Fountain. Europhys Lett 16: 165170.
- CLAIRON A, GHEZALI S, SANTARELLI G, LAURENT PH, LEA SN, BAHOURA M, SIMON E, WEYERS S AND SZYMANIEC. 1996. Preliminary accuracy evaluation of a cesium frequency standard. Proceeding of the 5th Symposium on Frequency Standards and Metrology, p. 4959.
- ESSEN L AND PARRY JVL. 1957. The cesium resonator as a standard of frequency and time. Phil Trans R Soc A250: 510514.
- FEENSTRA L, ANDERSSON LM AND SCHMIEDMAYER J. 2004. Microtraps and atom chips: Toolboxes for cold atom physics. Gen Rel and Grav 36: 23172329.
- FLAMBAUM VV AND TEDESCO AF. 2006. Dependence of nuclear magnetic moments on quark masses and limits on temporal variation of fundamental constants from atomic clock experiments. Phys Ref C 73: 055501.
- GLAZE DJ, HELLWIG H, ALLAN DW AND JARVIS S. 1977. NBS-4 and NBS-6: The NBS Primary Frequency Standards Metrologia 13: 1728.
- GODONE A, NOVERO C, TEVALLE P AND RAHIMULLAH K. 1993. New experimental limits to the time variations of gp (me/mp) and a. Phys Rev Lett 71: 23642366.
- GUILLOT E, POTTIE PE, VALENTIN C, PRTIT P AND DIMARQ N. 1999. Proceedings of the 1999 Joint meeting of the European Frequency and time forum and the IEEE International frequency control symposium, p. 8184.
- HAFELE JC AND KEATING RE. 1972. Around the worls atomic clocks. Predicted relativistic time gains. Science 177: 166168.
- JESPERSON J AND FITZ-RANDOLPH J. 1999. From sundials to atomic clocks: understanding time and frequency. Dover publications.
- KASEVICH M, RIIS E, CHU S AND DE VOE R. 1989. RF Spectroscop in an Atomic Fountain. Phys Rev Lett 63: 612615.
- KITCHING J. 2005a. An atomic clock on a microchip. The Horological J 147: 5455.
- KITCHING J ET AL. 2005b. Microfabricated Atomic Frequency References Metrologia 42: S100S104.
- KNAPPE S, SCHWINDT PDD, GERGINOV V, SHAH V, LIEW L, MORELAND J, ROBINSON HG, HOLLBERG L AND KITCHING J. 2006. Microfabricated atomic clocks and magnetometers. J Opt A: Pure Appl Opt 8: S318S322.
- LYONS H. 1949. Microwave spectroscopy frequency and time standards. Elec Eng 68: 251.
- MA LS, BI Z, BARTELS A, ROBERTSSOB L. ZYCCI M, WINDELER RS, WILPERS G, OATES C, HOLLBERG L AND DIDDAMS SA. 2004. Optical frequency synthesis and comparison with uncertainty at the 10-19 level. Science 303: 18431845.
- MAGALHÃES DV, SANTOS MS, BEBEACHIBULI A, TELES F AND BAGNATO VS. 2003. Progress towards a Cs fountain as frequency standard in Brazil. Proceedings of the 2003 IEEE International frequency control symposium, p. 132135.
- MAGALHÃES DV, MÜLLER ST, BEBEACHIBULI A, ALVES RF AND BAGNATO VS. 2006. Comparative short-term stability for a Cs beam and an expanding atomic cloud of Cs used as atomic frequency standards. Laser Physics 16: 12681271.
- MAKDISSI A. 1999. PhD Thesis, Université de Paris-Sud, 5844 p.
- MAKDISSI A AND DE CLERCQ E. 1997. A Signal Approach Analysis of the Ramsey Pattern in Cesium Beam Frequency Standards. IEEE Trans Instrum Meas 46: 112116.
- MAKDISSI A AND DE CLERCQ E. 2001. Evaluation of the accuracy of the optical cesium beam primary standard of BNM-LPTF. Metrologia 38: 409425.
- MARION H ET AL. 2003. Search for variation of fundamental constants using atomic fountain clocks. Phys Rev Lett 90: 150801150804.
- MCCASKILL TB, OAKS OJ, LARGAY MM, REID WG, WARREN HE AND BUISSON JA. 1999. Performance of global positioning system block II/IIA/IIR on-orbit Navstar clocks. Proceedings Annual PTTI systes and applications Meeting, p. 7589
- METCALF HJ AND STRAATEN P VAN DER. 1999. Laser cooling and trapping. Springer, Berlin Heidelberg, New York.
- MÜLLER ST, MAGALHÃES DV, BEBEACHIBULI A, SANTOS MS AND BAGNATO VS. 2005. Demonstration and observation of a frequency standard based on expanding cold atoms cloud of cesium. Proceedings of the 2005 IEEE International Frequency control symposium, p. 288291.
- NELSON RA, MCCARTHY DD, MALYS S, LEVINE J, GUINOT B, FLIEGEL HF, BEARD RL AND BARTHOLOMEW TR. 2001. The leap second: its histoy and possible future. Metrologia 38: 509529.
- PEIK E, LIPPHARDT B, SCHNATZ H, SCHNEIDER T AND TAMM CHR. 2004. Limit on the Present Temporal Variation of the Fine Structure Constant. Phys Rev Lett 93: 170801170804.
- RAMSEY NF. 1950. A molecular beam method with separated oscillating fields. Phys Rev 78: 695699.
- RAMSEY NF. 1963. Molecular beams. Oxford University Press, Amen House, London E.C. 4, p. 115144.
- RAMSEY NF. 1990. Experiments with separated oscillatory fields and hydrogen masers. Rev Mod Phys 62: 541552.
- RIEHLE F. 2004. Frequency Standars: Basics and Applications Wiley-VCH, Berlin.
- SANTOS MS, BEBEACHIBULI A, MAGALHÃES DV, TELES F AND BAGNATO VS. 2003. Stability and reproducibility of a Cs beam frequency standard. J Metrology Soc India 18: 139145.
- SESKO DW AND WIEMAN CE. 1989. Observation of the cesium clock transition in laser-cooled atoms. Opt Lett 14: 269271.
- SHAPIRO SS, DAVIS JL, LABACH DE AND GREGORY JS. 2004. Measurement of the solar gravitational deflection of radio waves using geodetic very-long-baseline interferometry data, 1979-1999. Phys Rev Lett 92: 121101(1-4).
- SIMON E, LAURENT P AND CLAIRON A. 1998. Measurement of the Stark shift of the cesium hyperfine splitting in an atomic fountain. Phys Rev A 57: 436439.
- TELES F, MAGALHÃES DV, SANTOS MS, ROVERA GD AND BAGNATO VS. 2000. Construction and evaluation of the first Brazilian atomic clock. IEEE Trans Ultrason Frroele and Freq Contr 47: 11111114.
- TELES F, MAGALHÃES DV, SANTOS MS, BEBEACHIBULI A AND BAGNATO VS. 2002. Characterization of the Brazilian Cs atomic frequency standard: Evaluation of the major shifts. Metrologia 39: 135141.
- TELES F, MAGALHÃES DV, SANTOS MS, BEBEACHIBULI A AND BAGNATO VS. 2003. Optically operated Brazilian atomic clock: Description and evaluation. Laser Physics 13: 175179.
- TRÉMINE S, GUÉRANDEL S, HOLLEVILLE D, CLAIRON A AND DIMARCQ N. 2004. 2004 IEEE International Ultrasonics Ferroelectrics and Frequency Control Joint 50th Anniversary Conference, p. 6570.
- UDEM TH, HOLZWARTH R AND HÄNSCH TW. 2002. Optical frequency metrology. Nature 416: 233237.
- UZAN JP. 2003. The fundamental constants and their variation: observational status and theoretical motivations. Rev Mod Phs 75: 403455.
- VANIER J AND AUDOIN C. 1989. The Quantum Physics of Atomic Frequency Standards. Adam Hilger imprint by IOP Publishing Ltd.
- VESSOT RFC AND LEVINE MW. 1979. A test of the equivalence principle using a space-borne clock. General relativity and gravitation 10: 181204.
- VESSOT RFC ET AL. 1980. Test of relativistic gravitation with space borne hydrogen maser. Phys Rev Lett 45: 20812084.
- WU A AND FEESS B. 2000. Development and evaluation of GPS space clocks for GPSIII and beyond. Proceeding of 32nd Annual systems and applications meeting, p. 389399.
- WYNANDS R AND WEYERS S. 2005. Atomic fountain clocks. Metrologia 42: S64S79.
Correspondence to:
Publication Dates
-
Publication in this collection
14 May 2008 -
Date of issue
June 2008
History
-
Accepted
18 Dec 2007 -
Received
07 July 2007























































