Abstracts
A rigorous microscale electrokinetic model for hydrogel-colloid composites is adopted to compute macroscale profiles of electrolyte concentration, electrostatic potential, and hydrostatic pressure across membranes that separate electrolytes with different concentrations. The membranes are uncharged polymeric hydrogels in which charged spherical colloidal particles are immobilized and randomly dispersed with a low solid volume fraction. Bulk membrane characteristics and performance are calculated from a continuum microscale electrokinetic model (Hill 2006b, c). The computations undertaken in this paper quantify the streaming and membrane potentials. For the membrane potential, increasing the volume fraction of negatively charged inclusions decreases the differential electrostatic potential across the membrane under conditions where there is zero convective flow and zero electrical current. With low electrolyte concentration and highly charged nanoparticles, the membrane potential is very sensitive to the particle volume fraction. Accordingly, the membrane potential - and changes brought about by the inclusion size, charge and concentration - could be a useful experimental diagnostic to complement more recent applications of the microscale electrokinetic model for electrical microrheology and electroacoustics (Hill and Ostoja-Starzewski 2008, Wang and Hill 2008).
electrodiffusion; electrokinetic phenomena; hydrogel-colloid composites; membrane potential; microhydrodynamics; soft composite materials; streaming potential
Um modelo eletrocinético rigoroso para compósitos formados por um hidrogel e um colóide é adotado para computar os perfis macroscópicos de concentração eletrolítica, potencial eletrostático e pressão hidrostática através de uma membrana que separa soluções com diferentes concentrações eletrolíticas. A membrana é composta por um hidrogel polimérico sem carga elétrica onde partículas esféricas são imobilizadas e dispersas aleatoriamente com baixa fração de volume do sólido. As características da membrana e a sua performance são calculadas a partir de um modelo eletrocinético de contínuo microscópico (Hill 2006b, c). As computações realizadas neste artigo quantificam os potenciais de corrente e de membrana. Para o potencial de membrana, aumentando a fração de volume das inclusões carregadas negativamente diminui o diferencial do potencial eletrostático através da membrana sob condições de fluxo convectivo e corrente elétrica nulos. Para concentrações eletrolíticas baixas o potencial de membrana torna-se muito sensível à fração de volume das partículas. De maneira similar, o potencial de membrana e as cargas elétricas trazidos pelo tamanho da inclusão, carga e concentração podem prover um diagnóstico experimental útil para complementar aplicações mais recentes do modelo eletrocinético microscópico em eletroacústica e eletro-micro-reologia (Hill and Ostoja-Starzewski 2008, Wang and Hill 2008).
eletrodifusão; fenômenos eletrocinéticos; Colóide-hidrogel compósitos; potencial de membrana; micro-hidrodinâmica; materiais compostos macios; potencial de corrente
CHEMICAL SCIENCES
Steady electrodiffusion in hydrogel-colloid composites: macroscale properties from microscale electrokinetics
Reghan J. Hill
Department of Chemical Engineering and McGill Institute for Advanced Materials McGill University, Montreal, Quebec, H3A 2B2, Canada
ABSTRACT
A rigorous microscale electrokinetic model for hydrogel-colloid composites is adopted to compute macroscale profiles of electrolyte concentration, electrostatic potential, and hydrostatic pressure across membranes that separate electrolytes with different concentrations. The membranes are uncharged polymeric hydrogels in which charged spherical colloidal particles are immobilized and randomly dispersed with a low solid volume fraction. Bulk membrane characteristics and performance are calculated from a continuum microscale electrokinetic model (Hill 2006b, c). The computations undertaken in this paper quantify the streaming and membrane potentials. For the membrane potential, increasing the volume fraction of negatively charged inclusions decreases the differential electrostatic potential across the membrane under conditions where there is zero convective flow and zero electrical current. With low electrolyte concentration and highly charged nanoparticles, the membrane potential is very sensitive to the particle volume fraction. Accordingly, the membrane potential and changes brought about by the inclusion size, charge and concentration could be a useful experimental diagnostic to complement more recent applications of the microscale electrokinetic model for electrical microrheology and electroacoustics (Hill and Ostoja-Starzewski 2008, Wang and Hill 2008).
Keywords: electrodiffusion, electrokinetic phenomena, hydrogel-colloid composites, membrane potential, microhydrodynamics, soft composite materials, streaming potential.
RESUMO
Um modelo eletrocinético rigoroso para compósitos formados por um hidrogel e um colóide é adotado para computar os perfis macroscópicos de concentração eletrolítica, potencial eletrostático e pressão hidrostática através de uma membrana que separa soluções com diferentes concentrações eletrolíticas. A membrana é composta por um hidrogel polimérico sem carga elétrica onde partículas esféricas são imobilizadas e dispersas aleatoriamente com baixa fração de volume do sólido. As características da membrana e a sua performance são calculadas a partir de um modelo eletrocinético de contínuo microscópico (Hill 2006b, c). As computações realizadas neste artigo quantificam os potenciais de corrente e de membrana. Para o potencial de membrana, aumentando a fração de volume das inclusões carregadas negativamente diminui o diferencial do potencial eletrostático através da membrana sob condições de fluxo convectivo e corrente elétrica nulos. Para concentrações eletrolíticas baixas o potencial de membrana torna-se muito sensível à fração de volume das partículas. De maneira similar, o potencial de membrana e as cargas elétricas trazidos pelo tamanho da inclusão, carga e concentração podem prover um diagnóstico experimental útil para complementar aplicações mais recentes do modelo eletrocinético microscópico em eletroacústica e eletro-micro-reologia (Hill and Ostoja-Starzewski 2008, Wang and Hill 2008).
Palavras-chave: eletrodifusão, fenômenos eletrocinéticos, Colóide-hidrogel compósitos, potencial de membrana, micro-hidrodinâmica, materiais compostos macios, potencial de corrente.
INTRODUCTION
Hydrogels are an important class of soft matter that have gained widespread application in drug delivery(Qiu and Park 2001, Lin and Netters 2006, Peppas et al. 2000), tissue engineering (Khademhosseini and Langer 2007, Barndl et al. 2007, Drury and Mooney 2003), advanced materials (Peppas et al. 2006,Eddington and Beebe 2004, Chaterji et al. 2007), and molecular separations (Wang et al. 1993, Kim and Park 1998). Novel characteristics can be achieved by immobilizing organic and inorganic colloidal particulates in the polymer skeleton. For example, embedding gold or gold-coated silica nanoparticles into a thermally responsive hydrogel induces light-wavelength-sensitive swelling to achieve optically active microfluidic flow control (Sershen et al. 2005). In biosensing, immobilizing silica nanoparticles in polyacrylamide hydrogels and applying an electric field increase the otherwise diffusion-limited flux of uncharged macromolecules across the composite membrane (Matos et al. 2006). Other applications include delivering growth factors for bone regeneration (Chung et al. 2007), improving the contrast of ultrasound imaging for early tumor detection (Liu et al. 2006, Dayton and Ferrara 2002), and absorbing infraredenergy for certain cancer treatment (Loo et al. 2005). Note also that polystyrene nanoparticles have been dispersed in neutral polyacrylamide hydrogels to increase the storage modulus and produce mechanoelectrical effects for artificial tactile perception and psycho-sensorial materials (Thévenot et al. 2007).
Hill (2006c, b) developed an electrokinetic transport model to quantify how imposed gradients of electrostatic potential, ion concentration, and pressure perturb an equilibrium state where each colloidal inclusion in the hydrogel-colloid composite is enveloped by a diffuse layer of counterions. Such an equilibrium is widely acknowledged to be reasonably well described by the non-linear Poisson-Boltzmann equation (Verwey and Overbeek 1948), which itself is a special case of a much more general electrokinetic transport (non-equilibrium) model (e.g., Overbeek 1943, Booth 1950). Similar methodologies have been adopted for ordered and random consolidated porous media with the immobile charge uniformly distributed on the solid matrix, often under conditions where the Debye length is smaller than the characteristic pore size (e.g., Gupta et al. 2007, Wang and Chen 2007).
Hill calculated perturbations to the equilibrium state of a single charged sphere immobilized in an uncharged porous medium (polymer hydrogel), and averaged the governing microscale equations to derive macroscale equations for dilute random dispersions, with transport coefficients derived from the microscale analysis of a single sphere. In principle, this theory could be advanced to handle higher particle concentrations by adopting cell models to account for particle interactions (e.g., Ahualli et al. 2006). Accordingly, the present macroscale equations are appropriate only when the inclusion volume fraction is sufficiently small, which, nevertheless, may often be the case. It should also be noted that the polymer skeleton is uncharged, so the immobile charge in the composite arises solely from the colloidal inclusions. Nevertheless, the calculations are valid for all practical values of the electrolyte concentration (Debye length), and particle size and surface charge density, which together determine the ζ -potential.
The hydrogel phase is modeled as a porous (Brinkman) medium with a very low volume fraction, so it hinders fluid flow due to hydrodynamic (Darcy) drag and viscous stresses, but does not hinder ion diffusion and electromigration. Predictions of the electroosmotic pumping capacity (termed the incremental pore mobility) and its relation to chemical and physical characteristics of the hydrogel and inclusions were recently found to compare well with experiments involving silica nanoparticles embedded in polyacrylamide (Hill 2007, Matos et al. 2006). Noteworthy is that the theoretical interpretation suggests that particle-particle and particle-polymer interactions (in the experiments) increase the effective hydrodynamic permeability of the hydrogel (Hill 2007).
The present model does not address elastic deformation, which is likely to be significant in situations where flow is driven by a sufficiently large applied pressure gradient (e.g., during streaming potential measurements), or the composite has to accommodate large gradients in the bulk concentration of electrolyte. However, recent advances of this model quantify how the electrolyte and inclusions couple (mechanically, electrically, and hydrodynamically) with the elastic polymer network (Hill 2006a, Hill and Ostoja-Starzewski 2008, Wang and Hill 2008), thereby facilitating calculations of the particle displacements and velocity when hydrogel-colloid composites are subjected to steady and oscillatory electric fields. Such experiments are relevant to the fields of microrheolgy (Cicuta and Donald 2007, Furst 2005, MacKintosh and Schmidt 1999) and electroacoustics (Hunter 1998, O'Brien 1990, 1988), which are widely used to probe the microstructure of complex fluids, including colloidal dispersions, polymer solutions and gels.
This paper establishes a systematic methodology for calculating macroscale transport properties of hydrogel-colloid composites based on earlier microscale analysis in the literature (Hill 2006c, b). These macroscale calculations are expected to complement experimental measurements of ion fluxes and membrane potentials. Accordingly, the paper begins by considering the continuum equations for a simple electrolyte in the absence of inclusions and hydrogel. This analysis of the well-known Poisson equation and ion-conservation equations is then used to rationalize an approximation (often referred to as an assumption) of bulk electroneutrality. The accompanying exact solution of this simple model provides a useful limiting case for interpreting subsequent numerical solutions of the non-linear coupled macroscale equations for hydrogel-colloid composite membranes: namely Hill's averaged ion-conservation equations, and fluid mass and momentum conservation equations. Several striking aspects of the results are physically interpreted using previous knowledge of the underlying microscale electrokinetic phenomena.
ELECTRODIFFUSION IN THE ABSENCE OF POLYMER AND INCLUSIONS
Here we consider electrodiffusion in an electrolyte without polymer or inclusions. Accordingly, the ions migrate by convection, diffusion and electromigration. If the fluid velocity is independently specified, then the equations required to determine the electrostatic potential ψ and N ion concentrations nj (zj is the valence and Dj the diffusion coefficient with j = 1 ... N) under steady conditions are the well-known Poisson and ion-conservation equations:
If the average fluid velocity u is specified, then this is a closed system of N +1 equations involving E = - ∇ψ and nj as unknowns ( o is the vacuum permittivity, kT is the thermal energy, and e is the fundamental charge). Note that electrical neutrality is not imposed explicitly, since it should emerge naturally from the boundary conditions.
o is the vacuum permittivity, kT is the thermal energy, and e is the fundamental charge). Note that electrical neutrality is not imposed explicitly, since it should emerge naturally from the boundary conditions.
For a one-dimensional problem (0 < x < L) with uniform dielectric constant  s, the equations above are
s, the equations above are
where subscripts x denote differentiation, and jj = const. is the flux of the jth species.
Note that the electrical current density is
so under conditions where i = 0 with a z-z electrolyte, j1 = j2 = j.
Alternatively, consider solving
If the average fluid velocity u is specified, then a closed system of N + 1 equations must be solved with ψ and nj as unknowns. However, while these equations could be solved with prescribed boundary conditions (at each end of the domain), the electrical current cannot be set to zero a priori. Rather, the electrostatic potential difference across the domain that yields zero electrical current must be established. Even so, a numerical solution may still be challenging because, as demonstrated below, the left-hand side of the Poisson equation above is extremely small compared to the right-hand side when the characteristic length scale is larger than the Debye length (typically between 1 and 100 nm).
ELECTRONEUTRALITY
Consider scaling the Poisson equation using a macroscopic length scale lc, with electrostatic potential scale ψc = kT/e and ion-concentration (charge density) scale nc. Accordingly, the left-hand side is O[(klc)-2] with respect to the right-hand side, with k-1 ~ [ o
o
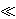 1. Therefore, in the 'outer' region where lc
1. Therefore, in the 'outer' region where lc  k-1 is indeed the appropriate length scale, the leading-order approximation of the Poisson equation becomes a statement of local electroneutrality, so the governing equations above become
k-1 is indeed the appropriate length scale, the leading-order approximation of the Poisson equation becomes a statement of local electroneutrality, so the governing equations above become
This important result was first established formally by MacGillivray (1968) using matched asymptotic expansions, and it is now widely adopted in standard texts. The following example establishes an explicit formula to be adopted in the following sections that address the much more difficult problem where charged colloidal inclusions are immobilized in an uncharged hydrogel skeleton.
For a z-z electrolyte, the bulk electroneutrality approximation requires n1 = n2 = n, so the ion-conservation equations are
or
Eliminating E gives
which is easily solved for n(x) given a constant value of u.
When the current density i = 0, j1 = j2 = j and
so
with
Note that with zero convective flux (u = 0),
and
where γ = D1/D2 and z1 = -z2. Moreover, the potential difference across the membrane (membrane potential) is
Let us examine the validity of the electroneutrality approximation by evaluating the left-hand side of the Poisson equation, which, recall, was neglected in reaching Eqn. (20):
This charge density is equivalent to a molar concentration of ions, each with charge z1e (NA is Avagadro's constant):
It is easily verified that this concentration is generally extremely small unless the characteristic length scale is O(nm). For example, for KNO3, γ = D+/D-≈ 73.5 / 71.46 ≈ 1.029. Therefore, with n(0) = 1 mmol l-1 and n(L) = 100 mmol l-1, Eqn. (22) gives a maximum at x = 0 of approximately 2 × 10-6 mmol l-1 when L = 1 mm. In general, therefore, and consistent with MacGillivray (1968), the electroneutrality approximation is reasonable when the characteristic length scale is greater than the Debye length.
ELECTRODIFFUSION IN HYDROGEL-COLLOID COMPOSITE MEMBRANES
The averaged equations derived by Hill (2006b) are written below for unidirectional transport of a z-z electrolyte in hydrogel composites. Note that the electroneutrality approximation requires ‹n1› = ‹n2› = ‹n› , and the fluid conservation (continuity) equation requires ‹u› = const., so the remaining ion conservation equations and momentum equation are
and
These are more compactly written
where
Note that the asymptotic coefficients: DE,  , CE; DB,
, CE; DB,  , CB; DU,
, CB; DU,  , CU are, in general, functions of the local scaled particle radius ka, scaled ζ-potential ζe/(kT), and scaled Brinkman screening length kℓ (or ℓ/a) for a given electrolyte [η is the fluid viscosity and ℓ2 is the hydrodynamic (Darcy) permeability of the polymer skeleton].
, CU are, in general, functions of the local scaled particle radius ka, scaled ζ-potential ζe/(kT), and scaled Brinkman screening length kℓ (or ℓ/a) for a given electrolyte [η is the fluid viscosity and ℓ2 is the hydrodynamic (Darcy) permeability of the polymer skeleton].
Again, with the local macroscale electroneutrality approximation, the bulk current density
provides an algebraic relationship between the two bulk ion fluxes. For the example below, however, there is zero electrical current, so ‹j1› = ‹j2› = ‹j› = const.
It is helpful to write the macroscale equations above in a form that explicitly relates the unknown gradients of ‹n› , ‹ψ› and ‹p› to the (co-linear) constants ‹j1› , ‹j2› and ‹u› , i.e.,
where
The components of matrix B depend on ‹n›(x), so this non-linear system of equations must be solved for y(x) = [‹n›(x), ‹ψ›(x), ‹p›(x)], given a constant b = (‹j1› , ‹j2› , ‹u›). This is easily achieved by numerically integrating1 1 This can be performed with any of the standard ordinary-differential-equation solvers in Matlab.
with 'initial condition' y(x = 0) = [‹n›(0), ‹ψ›(0), ‹p›(0)]. Because B(x) is independent of ‹ψ› and ‹p› , the solution provides Δy ≡ y(x = L) -y(x = 0) in the parameter space comprising b and y(x = 0). In practical terms, this means the flux j = |‹j›|, pressure differential Δ‹p›, and electrostatic potential differential Δ‹ψ› can be calculated (implicitly) as a function of the bulk convective flow u = |‹u›|, and bulk ion concentrations on each side of the composite membrane: e.g., with Δ‹n› = ‹n›(x = L) - ‹n›(x = 0) and ‹n›(x = 0) as two independent scalars.
In general, such a computation is rather intensive, since, in addition to the bulk ion concentration, the asymptotic coefficients vary with ka and ζe/(kT) (with fixed ℓ/a), both of which are non-linear functions of ‹n›(x). However, the asymptotic coefficients can be computed beforehand, and subsequently interpolated from sufficiently refined tables. Representative values (and several other quantities derived from them) are provided in Tables I, II and III for NaCl electrolyte with ℓ/a = 0.1 (a = 10 nm and ℓ = 1 nm). For the macroscale computations presented below, the asymptotic coefficients were available for many more values of ka and ζe/(kT). The reader is referred to Hill (2006a, c) for details of these microscale calculations and the physical significance of the other quantities provided2 2 The values of in Table II of Hill (2006c) are reported too small by factors of 10 -1 for ka = 10 and 10 -2 for ka = 100. All other values are correctly reported. . Note that it is straightforward to permit the inclusions to have a constant charge, in which case the ζ-potential varies with position according to the particle size and surface charge density, and the bulk electrolyte concentration (Verwey and Overbeek 1948, Russel et al. 1989).
The hydrogels for the calculations presented below have a Brinkman screening length ℓ = 1 nm, which is representative of polyacrylamide (Hill 2007). The inclusion radius a = 10 nm, and the electrolyte (NaCl) is moderately asymmetric with γ = D1/D2≈ 1.33/2.33. Note that the dimensionless parameter ℓ/a = 0.1, whereas previous microscale calculations reported in the literature for NaCl have ℓ/a ≈ 0.01 (a = 100 nm and ℓ ≈ 1 nm) (Hill 2006c, a). This difference affects all quantities derived from the microscale analysis that depend on convective flow3 3 This generally means the asymptotic coefficients denoted CX with X ∈ { E, B, U}, since these indicate the strength of the r -3 decaying microscale fluid velocity disturbance (Hill 2006a). .
STREAMING POTENTIAL
A fundamental characteristic of interest that has not been explicitly considered for hydrogel-colloid composites is the streaming potential. This is the differential potential Δ‹ψ› that prevails when Δ‹n› = i = 0 with u ≠ 0 and Δ‹p› ≠ 0. Accordingly, when 
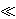 1, the streaming potential is
1, the streaming potential is
where, recall, γ = D1/D2. This equation is obtained by multiplying Eqn. (23) for each species by zje and setting their sum (electrical current) to zero. Note that terms involving the product  ‹∇ψ› are O(
‹∇ψ› are O( ) smaller than the electromigrative term for the pure electrolyte, and a consistent approximation of Eqn. (24) is u ≈ -(ℓ2/η)Δ‹p›/L, since
) smaller than the electromigrative term for the pure electrolyte, and a consistent approximation of Eqn. (24) is u ≈ -(ℓ2/η)Δ‹p›/L, since 
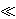 1.
1.
Writing Eqn. (39) in terms of the dimensionless asymptotic coefficients provided in Table 3 above gives
where  and
and  with u* =
with u* =  o
o
CONCENTRATION-GRADIENT DRIVEN FLUX WITH ZERO ELECTRICAL CURRENT AND FLOW
In the following example, the flux is specified as j = -De[‹n›(L) - ‹n›(0)] [Eqn (15)], with ‹n›(0) = 0.01 mmol-1, ‹n›(L) = 10 mmol-1 and L = 500 µm, so Δ ln ‹n› ≈ 6.9. Recall, this flux prevails in the absence charged inclusions when u = 0. The electrical current density i = 0, so j1 = j2. Note that the numerically exact solutions do not yield ‹n› (x = L) = 10 mmol-1, because the charged inclusions change the macroscale fluxes. Also, while the calculations could be performed with Δ‹p› = 0 and, hence, u ≠ 0, for simplicity the computations were undertaken with u = 0, so Δ‹p› ≠ 0. The asymptotic coefficients are determined by the local bulk electrolyte concentration. Accordingly, from the local values of ka and ζe/kT, asymptotic coefficients are obtained by interpolating refined versions of Tables I, II and III. Details of the microscale calculations, and a discussion of various quantities derived from them, are given by Hill (2006a, c).
When Δ ln ‹n› 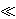 1, it is reasonable to approximate the asymptotic coefficients as constants based on an approximately constant bulk concentration ‹n›, so
1, it is reasonable to approximate the asymptotic coefficients as constants based on an approximately constant bulk concentration ‹n›, so
where, recall, γ = D1/D2, i = u = 0, and 
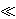 1. Again, this equation is obtained by multiplying Eqn. (23) for each species by zje and setting their sum (electrical current) to zero; note also that Δ‹n›/L ≈ (‹n›/L)Δ ln ‹n›. Writing Eqn. (41) in terms of the dimensionless asymptotic coefficients provided in Tables I and II gives
1. Again, this equation is obtained by multiplying Eqn. (23) for each species by zje and setting their sum (electrical current) to zero; note also that Δ‹n›/L ≈ (‹n›/L)Δ ln ‹n›. Writing Eqn. (41) in terms of the dimensionless asymptotic coefficients provided in Tables I and II gives
or
where  ≡ DB2Ie/(kTa3),
≡ DB2Ie/(kTa3),  ≡
≡  /a3,
/a3,  ≡ DE/a3 and
≡ DE/a3 and  ≡
≡  kT/(2Ia3e), with u* =
kT/(2Ia3e), with u* =  o
o
is the same as the more general expression of Hill (2006b). Furthermore, a careful inspection of Tables I and II reveals that the dimensionless asymptotic coefficients generally yield  ΔE ~ 1 only when ka < 1 and |ζ| > kT/e.
ΔE ~ 1 only when ka < 1 and |ζ| > kT/e.
Note that microscale theory does not account for particle interactions, so  * =
* =  [1 +(ka)-1]3 should be small. This is restrictive on the particle volume fraction
[1 +(ka)-1]3 should be small. This is restrictive on the particle volume fraction  = c(4/3)πa3 when ka
= c(4/3)πa3 when ka 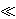 1 (c is the particle number density). For the specific example introduced above with Δ ln ‹n› ≈ 6.9, the macroscale calculations were undertaken with
1 (c is the particle number density). For the specific example introduced above with Δ ln ‹n› ≈ 6.9, the macroscale calculations were undertaken with  = 0.64(0, 0.1, 0.2, 0.4, 0.8) / [1 + (ka)-1]3, with ka < 1 evaluated at x = 0, which is generally the position where the ionic strength is lowest (with j > 0) and, hence, where ka is smallest. With ‹n› (0) = 0.01 mmol-1,
= 0.64(0, 0.1, 0.2, 0.4, 0.8) / [1 + (ka)-1]3, with ka < 1 evaluated at x = 0, which is generally the position where the ionic strength is lowest (with j > 0) and, hence, where ka is smallest. With ‹n› (0) = 0.01 mmol-1,  ≈ (0, 0.0534, 0.1069,0.2137, 0.4275) × 10-3. Note also that calculations were performed with a constant particle surface charge density σ = 1 µC cm-2, with the ζ-potential varying according to the (semi-empirical) formula (Russel et al. 1989)
≈ (0, 0.0534, 0.1069,0.2137, 0.4275) × 10-3. Note also that calculations were performed with a constant particle surface charge density σ = 1 µC cm-2, with the ζ-potential varying according to the (semi-empirical) formula (Russel et al. 1989)
When  = 0, the bulk concentration varies approximately linearly across the membrane, as given by Eqn. (15) when Pe → 0. As the inclusion volume fraction increases, the specified flux j is achieved with practically the same (almost uniform) electrolyte concentration gradient, even though the membrane is macroscopically inhomogeneous due to the varying ζ-potential. As seen in Figure 1, the high surface charge density and low bulk electrolyte concentration produce a high ζ-potential at x = 0. With higher electrolyte concentrations, the ζ-potentials are low (with fixed surface charge) and the diffuse double layers thin; accordingly, the inclusions behave as impenetrable uncharged spheres and the membrane potential tends to its value for pure electrolyte, and the effective diffusion coefficients tend to their Maxwell values (see below). These and other limiting cases were thoroughly discussed by Hill (2006b, c).
= 0, the bulk concentration varies approximately linearly across the membrane, as given by Eqn. (15) when Pe → 0. As the inclusion volume fraction increases, the specified flux j is achieved with practically the same (almost uniform) electrolyte concentration gradient, even though the membrane is macroscopically inhomogeneous due to the varying ζ-potential. As seen in Figure 1, the high surface charge density and low bulk electrolyte concentration produce a high ζ-potential at x = 0. With higher electrolyte concentrations, the ζ-potentials are low (with fixed surface charge) and the diffuse double layers thin; accordingly, the inclusions behave as impenetrable uncharged spheres and the membrane potential tends to its value for pure electrolyte, and the effective diffusion coefficients tend to their Maxwell values (see below). These and other limiting cases were thoroughly discussed by Hill (2006b, c).
As expected from the very small particle volume fractions ( ~ 10-4), the charge on the inclusions has a negligible influence on transport that occurs predominantly by gradient diffusion alone. However, as shown in the top panel of Figure 2, the inclusions have a significant impact on the electrostatic potential. Increasing the particle concentration decreases the membrane potential Δ‹ψ› = ‹ψ›(x = L). At the highest particle concentration of only
~ 10-4), the charge on the inclusions has a negligible influence on transport that occurs predominantly by gradient diffusion alone. However, as shown in the top panel of Figure 2, the inclusions have a significant impact on the electrostatic potential. Increasing the particle concentration decreases the membrane potential Δ‹ψ› = ‹ψ›(x = L). At the highest particle concentration of only  ≈ 4 ×10-4, Δ‹ψ› is about 20 mV lower than in the absence of inclusions. From Eqn. (20), Δ‹ψ› ≈ 24.6 mV. Therefore, the increment ΔE ≡ [‹ψ›(x = L;
≈ 4 ×10-4, Δ‹ψ› is about 20 mV lower than in the absence of inclusions. From Eqn. (20), Δ‹ψ› ≈ 24.6 mV. Therefore, the increment ΔE ≡ [‹ψ›(x = L;  = 0)/‹ψ›(x = L;
= 0)/‹ψ›(x = L;  ) - 1]/
) - 1]/ ~ -103, which is in good agreement with expectations for uniform membranes with small macroscale gradients (Hill 2006c, Fig. 7).
~ -103, which is in good agreement with expectations for uniform membranes with small macroscale gradients (Hill 2006c, Fig. 7).
As identified by Hill (2006c), the negatively charged inclusions here with Na+ counterion reduce the effective asymmetry of the electrolyte by increasing (decreasing) the effective diffusion coefficient of the otherwise less (more) mobile Na+ (Cl-) ion. This diminishes the accompanying electric field required to maintain equal bulk fluxes (zero electrical current). The bottom panel of Figure 2 shows the electrostatic potential for membranes with the same particle volume fractions and electrolyte, but with constant particle ζ-potential ( ζ = -4kT/e ≈ -100 mV) rather than constant surface charge. In both cases, the gradient of electrostatic potential is negative in a thin region at x = 0. In the absence of an accompanying pressure gradient, the large, positive electric field would drive electroosmotic flow in the direction of the bulk concentration gradient (from left to right). However, because these calculations have been performed with zero convective flow (u = 0), the pressure, which is plotted in Figure 3, varies in a very similar manner to the electrostatic potential.
A useful measure of the overall influence of the inclusions on transport is the bulk diffusion coefficient
This is plotted in Figure 4 scaled with the diffusion coefficient De given by Eqn. (17) for electrodiffusion in the absence of inclusions ( = 0). The fact that D* ≈ 1 when x ≈ L reflects the underlying (almost) linear bulk ion concentration profile. However, near x = 0, where ζe/(kT) is large and ka is small, D* is a complicated and rapidly changing function of position and particle concentration. Note that the effective diffusion coefficient of a tracer in a dilute random array of impenetrable spherical inclusions is (Maxwell 1873, Batchelor and O'Brien 1977)4
4
This is also evident from the microscale theory, which gives
→ -3/2 and
→ -3/2 as
ζ → 0 in
Table II (see also Hill 2006b).
= 0). The fact that D* ≈ 1 when x ≈ L reflects the underlying (almost) linear bulk ion concentration profile. However, near x = 0, where ζe/(kT) is large and ka is small, D* is a complicated and rapidly changing function of position and particle concentration. Note that the effective diffusion coefficient of a tracer in a dilute random array of impenetrable spherical inclusions is (Maxwell 1873, Batchelor and O'Brien 1977)4
4
This is also evident from the microscale theory, which gives
→ -3/2 and
→ -3/2 as
ζ → 0 in
Table II (see also Hill 2006b).
so with the largest value of  ≈ 0.000428, Eqn. (47) gives D*/D ≈ 0.9994. However, the top panel of Figure 4 indicates that D*/De ≈ 1.0030 when
≈ 0.000428, Eqn. (47) gives D*/D ≈ 0.9994. However, the top panel of Figure 4 indicates that D*/De ≈ 1.0030 when  = 0.000428, so, overall, the charge on the inclusions produces a higher effective diffusivity than expected from Eqn. (47).
= 0.000428, so, overall, the charge on the inclusions produces a higher effective diffusivity than expected from Eqn. (47).
The overall, but very slight, increase in the flux due to the inclusions is more pronounced in the bottom panel of Figure 4, because the particle ζ-potential ( ζ ≈ -100 mV) is relatively high and uniform throughout the membrane; for example, D*(L)/De ≈ 1.0055 when  ≈ 0.000428. Here the incremental quantity [D*(L)/De - 1]/
≈ 0.000428. Here the incremental quantity [D*(L)/De - 1]/ ~ 10. This is much greater than the value -3/2 from Eqn. (47), but consistent with expectations for uniform composites with small macroscale gradients (Hill 2006b). For example, the incremental contributions to the individual ion diffusion coefficients in Table II (
~ 10. This is much greater than the value -3/2 from Eqn. (47), but consistent with expectations for uniform composites with small macroscale gradients (Hill 2006b). For example, the incremental contributions to the individual ion diffusion coefficients in Table II (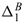 for Na+ and
for Na+ and 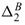 for Cl+) (see also Hill 2006b, Fig. 6) reveal that the inclusions increase (decrease) the effective diffusion coefficient of the otherwise less (more) mobile Na+ (Cl-) ion. Accordingly, the negatively charged inclusions decrease the asymmetry of the NaCl electrolyte, which explains the overall decrease in the membrane potential shown in Figure 1. It is also evident from Table II that when ζe/(kT) is large, the inclusions enhance the effective diffusivity of Na+ more than Cl-, i.e., |
for Cl+) (see also Hill 2006b, Fig. 6) reveal that the inclusions increase (decrease) the effective diffusion coefficient of the otherwise less (more) mobile Na+ (Cl-) ion. Accordingly, the negatively charged inclusions decrease the asymmetry of the NaCl electrolyte, which explains the overall decrease in the membrane potential shown in Figure 1. It is also evident from Table II that when ζe/(kT) is large, the inclusions enhance the effective diffusivity of Na+ more than Cl-, i.e., |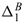 /
/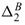 | > 1. This explains the overall tendency for D*(L)/De to be greater than one. Clearly, lower ζ-potentials will yield D*(L)/De less than one, as expected from Eqn. (47) when ζ → 0.
| > 1. This explains the overall tendency for D*(L)/De to be greater than one. Clearly, lower ζ-potentials will yield D*(L)/De less than one, as expected from Eqn. (47) when ζ → 0.
SUMMARY
Numerical solutions of the coupled macroscale ion conservation equations and fluid mass and momentum conservation equations for electrodiffusion across hydrogel-colloid composite membranes were presented for the first time. These computations were undertaken with the approximation of local macroscale electroneutrality, using bulk transport properties established in earlier work for microscale electrokinetic transport processes. The principal example presented was characterized by a low bulk electrolyte concentration on one side of the membrane, with a very low solid volume fraction of small, highly charged colloidal inclusions. The influence of these inclusions on the bulk fluxes was negligible in absolute terms, but the incremental contribution of the particles was significantly larger than expected from Maxwell's classical theory for impenetrable particles in a permeable continuum. Significant from a practical perspective was that very low concentrations of inclusions have a measurable impact on the membrane diffusion potential. Such changes reflect the size, charge, and concentration of the inclusions. Therefore, experimental measurements of the membrane potential may be promising for testing the microscale theory, which underlies several other interesting and technologically important microscale electrokinetic problems, including those of electrical microrheology and electroacoustics.
ACKNOWLEDGMENTS
RJH gratefully acknowledges support from the Natural Sciences and Engineering Research Council of Canada (NSERC) and the Canada Research Chairs program.
Manuscript received on June 2, 2008; accepted for publication on November 5, 2008
Selected paper presented at the IUTAM Symposium on Swelling and Shrinking of Porous Materials: From Colloid Science to Poromechanics - August 06-10 2007, LNCC/MCT.
E-mail: reghan.hill@mcgill.ca
- AHUALLI S, DELGADO AV, MIKLAVCIC SJ AND WHITE LR. 2006. Dynamic electrophoretic mobility of concentrated dispersions of spherical colloidal particle. On the consistent use of the cell model. Langmuir 22: 7041-7051.
- BARNDL F, SOMMER F AND GOEPFERICH A. 2007. Rational design of hydrogels for tissue engineering: impact of physical factors on cell behavior. Biomaterials 28: 134-146.
- BATCHELOR GK AND O'BRIEN RW. 1977. Thermal or electrical conduction through a granular material. Proc Royal Soc Lond A 355(1682): 313-333.
- BOOTH F. 1950. The cataphoresis of spherical, solid non-conducting particles in a symmetrical electrolyte. Proc Roy Soc Lond A 203: 514-533.
- CHATERJI S. KWON IK AND PARK K. 2007. Smart polymeric gels: Redening the limits of biomedical devices. Prog Polym Sci 32: 1083-1122.
- CHUNG Y-I, AHN K-M, JEON S-H, LEE S-Y, LEE J-H AND TAE G. 2007. Enhanced bone regeneration with BMP-2 loaded function nanoparticle- hydrogel complex. J Control Release 121: 91-99.
- CICUTA P AND DONALD AM. 2007. Microrheology: a review of the method and applications. Soft Matter 3: 1449-1455.
- DAYTON PA AND FERRARA KW. 2002. Targeted imaging using ultrasound. J Magn Reson Imaging 16: 362-377.
- DRURY JL AND MOONEY DJ. 2003. Hydrogels for tissue engineering: scaffold design variables and applications. Biomaterials 24: 4337-4351.
- EDDINGTON DT AND BEEBE DJ. 2004. Flow control with hydrogels. Adv Drug Deliv Rev 56: 199-210.
- FURST EM. 2005. Applications of laser tweezers in complex fuid rheology. Curr Opin Colloid Interface Sci 10: 79-86.
- GUPTA AK, COELHO D AND ADLER PM. 2007. Universal electro-osmosis formulae for porous media. J Colloid Interface Sci 319: 549-554.
- HILL RJ. 2006a. Electric-field-induced force exerted on a charged spherical colloid embedded in an electrolyte-saturated Brinkman medium. Phys Fluids 18: 043103.
- HILL RJ. 2006b. Transport in polymer-gel composites: Response to a bulk concentration gradient. J Chem Phys 124: 014901.
- HILL RJ. 2006c. Transport in polymer-gel composites: theoretical methodology and response to an electric field. J Fluid Mech 551: 405-433.
- HILL RJ. 2007. Electric-field-enhanced transport in polyacrylamide hydrogel nanocomposites. J Colloid Interface Sci 316: 635-644.
- HILL RJ AND OSTOJA-STARZEWSKI M. 2008. Electric-field-induced displacement of a charged spherical colloid embedded in an elastic Brinkman medium. Phys Rev E, Stat Phys, Plasmas, Fluids, Relat Interdiscip Top 77: 011404.
- HUNTER RJ. 1998. Recent developments in the electroacoustic characterisation of colloidal suspensions and emulsions. Colloids Surf A 141: 37-65.
- KHADEMHOSSEINI A AND LANGER R. 2007. Microengineered hydrogels for tissue engineering. Biomaterials 28: 5087-5092.
- KIM JJ AND PARK K. 1998. Smart hydrogels for bioseparation. Bioseparation 7: 177-184.
- LIN C-C AND NETTERS AT. 2006. Hydrogels in controlled release formulations: Network design and mathematical modeling. Adv Drug Deliv Rev 58: 1379-1408.
- LIU J, LEVINE AL, MATTOON JS, YAMAGUCHI M, LEE RJ, PAN XL AND ROSOL TJ. 2006. Nanoparticles as image enhancing agents for ultrasonography. Phys Med Biol 51: 2179-2189.
- LOO C. LOWERY A, HALAS N, WEST J AND DREZEK R. 2005. Immunotargeted nanoshells for integrated cancer imaging and therapy. J Am Chem Soc, Nano Lett 5: 709-711.
- MACGILLIVRAY AD. 1968. Nernst-planck equations and the electroneutrality and donnan equilibrium assumptions. J Chem Phys 48: 2903-2907.
- MACKINTOSH FC AND SCHMIDT CF. 1999. Microrheology. Curr Opin Colloid Interface Sci 4: 300-307.
- MATOS MA, WHITE LR AND TILTON RD. 2006. Electroosmotically enhanced mass transfer through polyacrylamide gels. J Colloid Interface Sci 300: 429-436.
- MAXWELL JC. 1873. Treatise on Electricity and Magnetism, vol. 1. Oxford University Press, London.
- O'BRIEN RW. 1988. Electro-acoustic effects in a dilute suspension of spherical particles. J Fluid Mech 190: 71-86.
- O'BRIEN RW. 1990. The electroacoustic equations for a colloidal suspension. J Fluid Mech 212: 81-93.
- OVERBEEK JTG. 1943. Theorie der elektrophorese. Kolloid-Beih 54: 287-364.
- PEPPAS NA, BURES P, LEOBANDUNG W AND ICHIKAWA H. 2000. Hydrogels in pharmaceutical formulations. Eur J Pharm Biopharm 50: 27-46.
- PEPPAS NA, HILT JZ, KHADEMHOSSEINI A AND LANGER R. 2006. Hydrogels in biology and medicine: from molecular principles to bionanotechnology. Adv Mater 18: 1345-1360.
- QIU Y AND PARK K. 2001. Environment-sensitive hydrogels for drug delivery. Adv Drug Deliv Rev 53: 321-339.
- RUSSEL W, SAVILLE DA AND SCHOWALTER WR. 1989. Colloidal Dispersions. Cambridge University Press, Cambridge, paperback edition 1991.
- SERSHEN SR, MENSING GA, NG M, HALAS NJ, BEEBE DJ AND WEST JL. 2005. Independent optical control of microfluidic valves formed from optomechanically responsive nanocomposite hydrogels. Adv Mater 17: 1366-1368.
- THÉVENOT C, KHOUKH A, REYNAUD S, DESBRIÈRES J AND GRASSL B. 2007. Kinetic aspects, rheological properties and mechanoelectrical effects of hydrogels composed of polyacrylamide and polystyrene nanoparticles. Soft Matter 3: 437-447.
- VERWEY EJW AND OVERBEEK JTG. 1948. Theory of Stability of Lyophobic Colloids. Elsevier, New York.
- WANG KL, BURBAN AND CUSSLER EL. 1993. Hydrogels as separation agents. Adv Polym Sci 110: 67-79.
- WANG M AND CHEN S. 2007. Electroosmosis in homogeneously charged micro- and nanoscale random porous media. J Colloid Interface Sci 314: 264-273.
- WANG M AND HILL RJ. 2008. Electric-field-induced displacement of charged spherical colloids in compressible hydrogels. Soft Matter 4: 1048-1058.
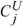 in
in 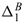 → -3/2 and
→ -3/2 and 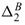 → -3/2 as
→ -3/2 as Publication Dates
-
Publication in this collection
25 Feb 2010 -
Date of issue
Mar 2010









































