Abstracts
A theoretical and numerical model is developed for the quantitative analysis of coupled processes taking place in active waste containment systems, such as electrokinetic barriers or fences, in which alow intensity DC current is circulated across the clay barrier to move polar and non-polar contaminants. A novel feature of the proposed approach is the allowance for the presence of air in the pore space. Under unsaturated conditions, all transport coefficients involved in the electrokinetic process are strongly dependent on the degree of saturation of pore liquid. In order to assess the predictive capability of the proposed theory and to appreciate the impact of gas production at the electrodes, a series of numerical simulations of simple onedimensional electrokinetic tests have been performed. The results of the simulations compare reasonably well with data obtained from laboratory experiments performed on an illitic clayey silt. The numerical results indicate that the impact of gas production at the electrodes can be significant, even in low-intensity and short-duration treatments.
electro-osmosis; experimental investigation; theoretical model; finite element analysis; unsaturated soils
Um modelo teórico e computacional é desenvolvido para a análise quantitativa de processos acoplados que tomam lugar em sistemas de contenção de lixo tais como barreiras ou grades eletrocinéticas no qual uma DC corrente de baixa intensidade é circulada através da barreira de argila para movimentar contaminantes polares e não polares. Uma nova característica da abordagem proposta é permitir a presença de ar nos poros. Sob condições não saturadas todos os coeficientes de transporte envolvidos nos processos eletrocinéticos são fortemente dependentes do grau de saturação do líquido. Com o objetivo de avaliar a capacidade do modelo proposto de predizer e de apreciar o impacto da produção de gás nos eletrodos uma série de simulações numéricas foi realizada em testes eletrocinéticos simples unidimensionais. Os resultados das simulações concordam razoavelmente bem com dados experimentais obtidos em experimentos de laboratório realizados em argilas. Os resultados numéricos indicam que o impacto da produção de gás nos eletrodos pode ser significativo mesmo em tratamentos de baixa intensidade e curta duração.
eletro-osmose; investigação experimental; modelo teórico; análise de elementos finitos; solos não saturados
EARTH SCIENCES
A model for coupled electro-hydro-mechanical processes in fine grained soils accounting for gas generation and transport
Claudio TamagniniI; Cristina JommiII; Fabio CattaneoI
IUniversità degli Studi di Perugia, Department of Civil and Environmental Engineering via G. Duranti 93, 06125 Perugia, Italy
IIPolitecnico di Milano, Department of Structural Engineering piazza Leonardo da Vinci 32, 20133 Milano, Italy
Correspondence to Correspondence to: Cristina Jommi E-mail: cristina.jommi@polimi.it
ABSTRACT
A theoretical and numerical model is developed for the quantitative analysis of coupled processes taking place in active waste containment systems, such as electrokinetic barriers or fences, in which alow intensity DC current is circulated across the clay barrier to move polar and non-polar contaminants. A novel feature of the proposed approach is the allowance for the presence of air in the pore space. Under unsaturated conditions, all transport coefficients involved in the electrokinetic process are strongly dependent on the degree of saturation of pore liquid. In order to assess the predictive capability of the proposed theory and to appreciate the impact of gas production at the electrodes, a series of numerical simulations of simple onedimensional electrokinetic tests have been performed. The results of the simulations compare reasonably well with data obtained from laboratory experiments performed on an illitic clayey silt. The numerical results indicate that the impact of gas production at the electrodes can be significant, even in low-intensity and short-duration treatments.
Key words: electro-osmosis, experimental investigation, theoretical model, finite element analysis, unsaturated soils.
RESUMO
Um modelo teórico e computacional é desenvolvido para a análise quantitativa de processos acoplados que tomam lugar em sistemas de contenção de lixo tais como barreiras ou grades eletrocinéticas no qual uma DC corrente de baixa intensidade é circulada através da barreira de argila para movimentar contaminantes polares e não polares. Uma nova característica da abordagem proposta é permitir a presença de ar nos poros. Sob condições não saturadas todos os coeficientes de transporte envolvidos nos processos eletrocinéticos são fortemente dependentes do grau de saturação do líquido. Com o objetivo de avaliar a capacidade do modelo proposto de predizer e de apreciar o impacto da produção de gás nos eletrodos uma série de simulações numéricas foi realizada em testes eletrocinéticos simples unidimensionais. Os resultados das simulações concordam razoavelmente bem com dados experimentais obtidos em experimentos de laboratório realizados em argilas. Os resultados numéricos indicam que o impacto da produção de gás nos eletrodos pode ser significativo mesmo em tratamentos de baixa intensidade e curta duração.
Palavras-chave: eletro-osmose, investigação experimental, modelo teórico, análise de elementos finitos, solos não saturados.
INTRODUCTION
In the last twenty years, the increased demand for innovative remediation technologies stimulated the development of electrokinetic treatments as a valuable tool for decontamination of clayey soils (Mitchell 1991, Yeung 1994, Alshawabkeh and Acar 1996).
To check the applicability of electrokinetic remediation, the various phenomena occurring in fine-grained soils upon application of a DC electric field, have been extensively studied (Acar et al. 1989, Acar and Alshawabkeh 1993, Virkutyte et al. 2002). Besides affecting pore water pressure regime by inducing in the soil mass a time-dependent coupled flow and deformation (consolidation) process, the application of an electric field to a fine-grained soil promotes complex electro-chemical phenomena, such as hydrolysis reactions at the electrodes, ion migration, changes in pore water pH, aqueous phase reactions, precipitation and dissolution, adsorption and desorption (Acar et al. 1990, Eykholt 1992, Eykholt and Daniel 1994, Acar and Alshawabkeh 1996, Alshawabkeh and Acar 1996, Yeung et al. 1997, Musso 2000, Alshawabkeh et al. 2004). These phenomena can, in turn, induce permanent modifications to the mechanical properties of the soil (Esrig and Gemeinhardt Jr. 1967, Gray 1970).
Besides electrokinetic remediation, the application of a DC electric field was proposed to realise active containment systems, such as electrokinetic barriers to enhance the performance of compacted clay liners, or electrokinetic fences for the manipulation and diversion of contaminant plumes in polluted sites (Mitchell 1991, Yeung et al. 1992, Yeung 1994). Electrokinetic barriers appear particularly promising in order to contrast the diffusive flow of contaminants through traditional liners for permanent containment. In this case, pollutants do not have to be removed from the soil mass, but simply prevented from migrating in the aquifer. Hence, a DC field is applied to counteract the migration of polluting species occurring because of diffusive and advective fluxes (see e.g., Yeung 1994).
Short-term duration of the treatment limits the effects of electrochemical reactions. The effects of the application of the DC field on the hydro-mechanical behaviour of the soil skeleton, if any, are expected to be mainly due to local desaturation following gas production during hydrolysis at the electrodes. In practical applications, the development of gas at the electrodes is not the only possible cause of loss of saturation. As a matter of fact, the soil used for the construction of clay liners is typically compacted in unsaturated conditions, while in polluted areas migration of contaminants often takes place in the unsaturated zone above the groundwater table. In any case, when the gas volume fraction in the pore space increases, the transport parameters involved in the electrokinetic process experience significant changes with the degree of saturation, and this might have a strong impact on the overall evolution of the electrokinetic treatment.
In spite of this observation, quantitative assessment of the impact of the degree of saturation on the evolution of electrokinetic processes does not appear to have been presented in the past, to the author's knowledge. A few pilot tests were performed in unsaturated soil layers with the aim of verifying the optimum electro-chemical conditions for polluted soil remediation (Mattson et al. 2002, Wieczorek et al. 2005, Chang et al. 2006). Mattson et al. (2002) suggested a model for electrokinetic ion transport through unsaturated sands in which a power law, calibrated on their experimental results, was assumed to describe the dependence of effective diffusion coefficient and effective ionic mobility on the degree of saturation. The relationship between electrical conductivity and degree of saturation has been the object of different investigations (see, e.g., Mualem and Friedman 1991), while the work of de Wet (1995) provides a few laboratory data for the characterization of the electro-osmotic permeability in unsaturated conditions.
The work presented in this paper is part of a larger research project, aimed at assessing the potential applicability of electrokinetic barriers or fences, including: i) the development of innovative experimental techniques for the measurement of the electrokinetic properties of both natural and compacted soils (Gabrieli et al. 2008b); ii) the performance of a limited number of pilot-scale laboratory tests for the experimental validation of the proposed models (Gabrieli et al. 2008a, Airoldi et al. 2009); iii) the development of theoretical models for the quantitative description of the coupled electro-chemo-hydro-mechanicalprocesses taking place within the soil during electrokinetic treatments; iv) their numerical implementation in FE codes for the solution of practical design problems.
In this paper, a four-field theoretical model is presented for the quantitative analysis of the coupled flow and deformation processes taking place in unsaturated fine-grained soils during electrokinetic treatment, and its FE numerical implementation is briefly discussed. The model is developed under the simplifying assumptions of negligible chemical reactions and negligible changes in pore water pH and ionic concentrations of dissolved species. Numerical simulations of one-dimensional electrokinetic filtration and consolidation tests are presented, and the numerical results are compared to experimental data obtained in a series of laboratory electrokinetic filtration tests and electrokinetic consolidation tests, performed with an electrokinetic oedometer designed by Tamagnini (1994). Both experimental data and numerical resultssuggest that, for electrokinetic treatments of limited duration, the gas generated by electrolysis at the electrodes has a definite impact on the time evolution of the process.
THEORY
In the development of the theoretical model proposed for fully coupled electro-hydro-mechanical processes, which occur in fine-grained soils during a typical short-term electrokinetic treatment, the following assumptions are introduced:
i) in order to account for gas generation and transport, the soil is considered as a three-phase porous medium, with a deformable solid skeleton the pores of which are occupied by water and, possibly, gas;
ii) the solid skeleton deformation is governed by a hypo-elastic constitutive equation, defined in terms of a Bishop's type effective stresses (Lewis and Schrefler 1998, Jommi 2000);
iii) the solid phase can be considered incompressible ( ρs = const.);
iv) fluxes of mass and electric charge are quasi-linear functions of relevant potential gradients (conduction coefficients may change due to modifications in porosity, degree of saturation, etc.);
v) electrophoresis and streaming currents are negligible;
vi) the coupled conduction processes occur under isothermal conditions;
vii) no significant chemical reactions (precipitation, dissolution, aqueous phase reactions and sorption) occur during the entire duration of the process, except electrolysis at the electrodes;
viii) no significant changes in ionic concentrations of dissolved species in the pore fluid and in pore water pH occur during the entire duration of the process.
Assumptions (i) and (ii) constitute a notable extension of currently available theories for the description of electrokinetic processes, typically developed for fully saturated soils with a rigid solid skeleton (see, e.g., Alshawabkeh and Acar 1996, Yeung and Mitchell 1993). In environmental geotechnical applications, assumption (iii) can be considered largely acceptable, while assumptions (iv) and (v) are widely supported by a large body of experimental evidence (see, e.g., Mitchell 1993). As for assumptions (vi) to (viii), it is well known that prolonged electrokinetic treatments can give rise to heating and to strong variations in both ionic concentrations of dissolved species and pore water pH. However, for short duration treatments, where low current densities are used and the duration of the process is relatively short, these assumptions can be considered a reasonable first-order approximation.
BALANCE EQUATIONS
The relevant balance equations for the three-phase porous continuum are derived following the approach of macroscale mixture theories of porous media (Panday and Corapcioglu 1989, Coussy 1995, de Boer 1995, Lewis and Schrefler 1998). Following the usual conventions in material mechanics, tractions and fluid pressures will be assumed positive. Boldface notation is adopted for vectors and tensors.
Balance of mass for the solid phase
In the absence of mass exchange between solid and liquid phases due to chemical reactions, the balance of mass equation for the solid phase reads:
where n = nw+ ng is the soil porosity, sum of the volume fractions of the liquid (nw) and gas (ng) phases; υs is the spatial velocity of the solid skeleton and
is the material time derivative following the motion of the solid skeleton.
Balance of mass for water
Let Sw : = nw/n be the degree of saturation of the pore space with respect to water, and
denote the seepage (Darcy) velocity of the liquid within the pores. The balance of mass equation for water reads:
where ρw is the intrinsic density of water.
Combining equations (4) and (1) to eliminate the material time derivative of the porosity, andneglecting the spatial water density gradient, the balance of mass equation for water, eq. (4), reduces to:
Balance of mass for gas species
Let Sg := ng/n = 1 - Sw be the degree of saturation of the pore space with respect to gas, and
denote the seepage (Darcy) velocity of the gas within the pores. The balance of mass equation forgas reads:
where ρg is the intrinsic density of the gas, and H is Henry's constant, accounting for gas solubility in water.
Combining equations (7) and (1) to eliminate the material time derivative of the porosity, and neglecting the spatial gas density gradient, the balance of mass equation for gas reduces to:
Finally, observing that, from eq. (5)
eq. (8) can be further simplified as follows:
Balance of linear momentum for the mixture
For quasi-static deformation and flow processes, the balance of linear momentum in local form for the three-phase mixture reads:
where σ is the total stress tensor, b is the gravity acceleration,
is the mass per unit volume of the mixture, and ρs is the intrinsic average density of the solid particles.
Balance of electric charge
In the presence of an external electric field, the balance of electric charge equation reads:
where j is the electric current density, and  e is the charge density per unit volume of the mixture. Neglecting the electric capacitance of the soil, the source term in eq. (13) vanishes and the balance equation reduces to:
e is the charge density per unit volume of the mixture. Neglecting the electric capacitance of the soil, the source term in eq. (13) vanishes and the balance equation reduces to:
CONSTITUTIVE EQUATIONS
Closure of the coupled multiphysics conduction and deformation problem requires the introduction of suitable constitutive equations for the stress tensor σ , the degree of saturation Sw, the densities ρw and ρg of the liquid and gas phases, and the fluxes ww, wg and j.
Solid skeleton
Under the assumption of linear kinematics, the constitutive equation of the solid skeleton is formulatedin the following incremental form:
after, e.g., Bolzon et al. (1996), Jommi (2000), Borja (2004). In eq. (15):
is a Bishop's type effective stress tensor, pw is the pore water pressure, pg is the pore gas pressure, s := pg - pw is the matric suction,  := sym∇us is the linearised deformation tensor, and D is thetangent stiffness of the solid skeleton, typically depending on the current effective stress state σ" and on a set of internal variables q, which quantify the effects of previous loading and hydraulic history. Following a standard practice in soil mechanics, stresses and fluid pressures, pw and pg are defined relative to the atmospheric pressure.
:= sym∇us is the linearised deformation tensor, and D is thetangent stiffness of the solid skeleton, typically depending on the current effective stress state σ" and on a set of internal variables q, which quantify the effects of previous loading and hydraulic history. Following a standard practice in soil mechanics, stresses and fluid pressures, pw and pg are defined relative to the atmospheric pressure.
To keep the formulation as simple as possible, in this work the solid skeleton has been assumed as an isotropic and hypoelastic material. Therefore, the tangent stiffness tensor assumes the following form:
in which:
are the bulk and the shear tangent moduli of the solid skeleton, respectively,
is the mean effective stress, n is Poisson ratio and λ* is a logarithmic compressibility coefficient.
Fluid phases
Assuming a barotropic behaviour for water and gas, their intrinsic densities variation read:
where Kw is the bulk modulus of the liquid, assumed constant, and Kg is the bulk modulus of the gas. Identifying eq. (20b) with the equation of state of a perfect gas under isothermal conditions, it follows that:
where patm is the atmospheric pressure.
Water retention properties of the solid skeleton
Available experimental evidence (see, e.g., Alonso et al. 1987, Romero et al. 1999) indicates that the degree of saturation of the soil with respect to the liquid phase, Sw, is a function of the suction s and of the hydraulic history of the soil. In this work, only monotonic desaturation processes are of interest. Hence, the simple reversible law proposed by van Genuchten (1980) is adopted:
in which αsw, nsw and msw are material constants.
Since Sw + Sg = (nw + ng)/n = 1, from (22) it follows that:
In the above equation, the non-negative storage coefficient:
represents the rate at which the volumetric fluid content decreases due to increasing suction.
Liquid phase flow
The constitutive equation for the liquid seepage velocity, ww, is provided by the generalised Darcy's law for the liquid:
where µw is the liquid viscosity, k and kw,rel are the absolute and relative hydraulic permeabilities of the soil, ke and ke,rel are the absolute and relative electro-osmotic permeabilities of the soil, and 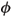 is the electric potential.
is the electric potential.
The first term on the right-hand side of eq. (25) accounts for the water flow induced by the hydraulic gradient. The second term represents the contribution to water flow due to electro-osmosis, which can be expressed as a linear function of the applied electric potential gradient via an electro-osmotic permeability tensor (see, e.g., the review paper by Mitchell 1991). The minus sign in front of this term is motivated by the available experimental evidence, which indicates that electro-osmotic flows occurs from the anode to the cathode, opposite to the electric gradient.
Following a standard practice in unsaturated soil mechanics, in eq. (25) both hydraulic and electro-osmotic permeabilities are defined as products of an intrinsic permeability tensor, depending on the microstructural properties of the porous medium, and a non-dimensional relative permeability coefficient, which accounts for the effects of partial saturation on soil conduction properties.
Relative permeabilities are increasing functions of the degree of saturation Sw. In the present work, based on available experimental data, the following simple power laws have been adopted for kw,rel and ke,rel:
where aw, bw, ae and be are material constants.
Gas phase flow
The constitutive equation for the gas seepage velocity, wg, is provided by the following generalisedDarcy's law for the gas phase:
where µg is the gas viscosity, and kg,rel is the relative permeability of the soil with respect to the gas flow. The second term on the right-hand side of eq. (27) accounts for the flow of gas dissolved in the liquidphase via Henry's constant H.
Relative permeability of gas is a decreasing function of the water saturation degree. Consistently with the the previous choice for water, a power law was adopted to describe its variation:
where ag, bg are material constants.
Electric flow
Neglecting the contribution of streaming currents produced by liquid flow - assumption (v) - the constitutive equation for the electric current density, j, is provided by the following generalised Ohm's law forthe porous medium:
where χ* is the effective electric conductivity of the porous medium in unsaturated conditions. The conductivity coefficient can be expressed as the sum of two terms (see, e.g., Mualem and Friedman 1991):
where χs is the apparent electric conductivity of the solid skeleton, χb is the apparent electric conductivity of bulk pore water under saturated conditions, and χrel(Sw) is the relative electric conductivity, accounting for the effects of partial saturation. The following power law, similar to eq. (26), has been assumed in this work (Mualem and Friedman 1991, Mattson et al. 2002):
where aχ and bχ are material constants.
GOVERNING EQUATIONS IN STRONG FORM
Taking into account the constitutive equations for the two fluids, eqs. (20), and the definitions of the constitutive stress (16) and of the storage coefficient (24), the balance equations (11), (5), (10) and (14) for the coupled flow and deformation problem can be recast as follows:
where:
and the flows σ", ww, wg and j are expressed as functions of the primary unknown fields u = us (solid displacement), pw (liquid pressure), pg (gas pressure), and 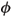 (electric potential) through the constitutive equations (17), (25), (27) and (29).
(electric potential) through the constitutive equations (17), (25), (27) and (29).
INITIAL AND BOUNDARY CONDITIONS
The primary unknown fields of the problem are the displacement vector, u(x,t), of the solid skeleton, the pore liquid pressure, pw(x,t), the pore gas pressure, pg(x,t), and the electric potential, 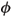 (x). Assuming initially saturated conditions, pg0 is set equal to pw0, which typically corresponds to a hydrostatic pore pressure distribution. The hypoelastic character of the constitutive equation (15) requires to specify the initial effective stress state:
(x). Assuming initially saturated conditions, pg0 is set equal to pw0, which typically corresponds to a hydrostatic pore pressure distribution. The hypoelastic character of the constitutive equation (15) requires to specify the initial effective stress state:
The initial electric field is assumed to be zero everywhere. Appropriate values for displacements, pore water pressure and electric field are conveniently imposed in terms of simple Dirichelet or Neumann conditions at the two boundaries. As for gas, a constant atmospheric pressure is imposed for the whole duration of the process at the cathode. At the anode, the production of oxygen arising from electrolysis of water is simulated by relating the inward gas flow to the instantaneous electric current density:
where  is the calculated gas inflow per unit area,
is the calculated gas inflow per unit area,  is the inward electric current density, R is theuniversal gas constant, T is the absolute temperature, and F is the Faraday's constant.
is the inward electric current density, R is theuniversal gas constant, T is the absolute temperature, and F is the Faraday's constant.
The efficiency parameter, η < 1, is introduced to account for possible losses at the electrode, due to non-controlled concomitant chemical reactions.
FE IMPLEMENTATION
Following standard arguments - see, e.g., Hughes (1987) - the weak form of the coupled flow and deformation problem is implemented. Introducing a suitable spatial discretisation of the domain into finite elements, a standard Galerkin FE approximations for the unknown fields u, pw, pg and 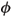 leads to the followingmatrix form of eqs. (32):
leads to the followingmatrix form of eqs. (32):
where d is the nodal displacement vector; pw is the nodal pore liquid pressure vector; pg is the nodal pore gas pressure vector; 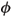 is the nodal electric potential vector. The definition of the matrices Pw, Pg, Hw, Hg, H
is the nodal electric potential vector. The definition of the matrices Pw, Pg, Hw, Hg, H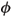 , Hgw, Cws, Csw, Cgs, Csg, Cw
, Hgw, Cws, Csw, Cgs, Csg, Cw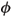 , Cg
, Cg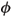 and of the vectors Fint, Fext,
and of the vectors Fint, Fext,  ,
,  , Jext is provided in the AppendixAppendix be the discrete gradient operators, such that: Let Nf be the interpolation functions adopted for the generic primary field f, and let Bu, Ep, Ef be the discrete gradient operators, such that: .
, Jext is provided in the AppendixAppendix be the discrete gradient operators, such that: Let Nf be the interpolation functions adopted for the generic primary field f, and let Bu, Ep, Ef be the discrete gradient operators, such that: .
Matrix equations (36) define a differential-algebraic problem, which was implemented in the FEplatform COMSOL Multiphysics v3.4. Quadratic elements have been adopted for the relevant primary fields, while time integration of the system has been performed using a built-in version of the large-scale DAE solver DASPK, using a fifth order, variable-step size, implicit backward differentiation formula(BDF). No stabilization techniques of the numerical procedure were adopted, in order to highlight instabilities of the physical process arising when gas production overcomes the amount of gas which can be transported in the same time interval. The choice is discussed by Jommi et al. (1997) and Jommi and Vaunat (1998).
EXPERIMENTAL PROGRAMME
An experimental programme, aimed at improving the current state of knowledge on the coupled deformation and hydraulic, ionic and electric flow processes taking place under electrokinetic treatments, was planned as part of the ongoing research project. In the following, the experimental apparatus used in short-term electrokinetic tests is briefly discussed, and a few basic results are presented to provide experimental support to the basic assumptions of the theory and to the constitutive equations presented in the previous sections.
EXPERIMENTAL EQUIPMENT
A number of short-duration electrokinetic tests have been performed in an electrokinetic oedometer originally designed by Tamagnini (1994). A perspex lateral ring (with internal diameter of 80 mm), sufficiently rigid to provide the necessary lateral constraint to lateral deformations while preventing lateral electric and hydraulic flows, contains the soil specimen. A cylindrical perspex piston, freely moving within the lateral ring, is connected to the external loading frame by a stainless steel piston, and transmits the vertical load. A fixed perspex top cap, with a bellofram seal in the center, allows the stainless steel piston to move freely in the vertical direction while keeping the interior of the cell hydraulically isolated from theexterior. Back-pressure can be imposed to the sample from an hydraulic connection at the base, and the amount of water entering the specimen through the bottom porous plate is measured by means of a standard volume gauge.
In order to minimise lateral friction between the piston and the lateral ring, a layer of silicon grease is placed on the interior surface of the ring. The hydraulic connection between the specimen and the external reservoirs is achieved by two porous plates, with a diameter of 70 mm, acting as electrodes in electrokinetic tests. The original porous plates, made of sintered bronze, were replaced with porous graphite plates, in the current version of the apparatus, in order to guarantee a better control of the electrochemical processes taking place at the electrodes. To perform electrokinetic filtration or consolidation tests, the two graphite porous plates are connected to a DC power supply. Tests can be performed either controlling the imposed difference of potential at the electrodes, or the applied current density.
MATERIAL TESTED, TESTING PROGRAMME AND CALIBRATION OF PARAMETERS
The experimental tests were performed on a clayey silt from the site of Viadana, in the Po river valley. The soil is characterised by specific gravity Gs = 2.74, liquid limit wL = 0.59, plasticity index PI = 0.30 and activity A = 0.9. The dry soil was mixed with distilled water at a water content of w0 = 0.280 and prepared by dynamic compaction to a target void ratio of e0 = 0.89, directly into the cell where the electro-hydro-mechanical tests were performed. The as-compacted degree of saturation of the soil samples was Sw0 = 0.85.
Some of the tests were run on specimens saturated under back-pressure prior to the application ofelectric field, while the remaining tests were performed on specimens starting from the as-compacted conditions. In the latter case, the measurement of water flow and vertical displacement allowed for tracking the degree of saturation throughout the tests.
A few tests were run alternating controlled load steps, increasing vertical stress at null electrical potential ( Δσυ > 0, 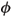 = 0), and electrokinetic filtration steps at constant vertical load ( Δσυ = 0, Δ
= 0), and electrokinetic filtration steps at constant vertical load ( Δσυ = 0, Δ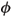 ≠ 0), imposing free drainage at both ends of the specimen. The test results are described in detail in Gabrieli et al. (2008a, b). Only the most relevant data will be recalled here, in the light of the following numerical simulations.
≠ 0), imposing free drainage at both ends of the specimen. The test results are described in detail in Gabrieli et al. (2008a, b). Only the most relevant data will be recalled here, in the light of the following numerical simulations.
In Figure 1 the results of one-dimensional compression performed after short-term electrokinetic treatments are compared to similar data for the natural, saturated soil.
The comparison highlights that the electrokinetic treatment induces an initial increment of the soil stiffness. This effect is quantitatively more pronounced at low stress levels, but it occurs systematically at all stress levels investigated. Nevertheless, when the treated sample is left under a constant load for a sufficient period of time - at least 24 hours - it recovers the same total strain as the untreated one, following an abrupt volume reduction taking place 5 to 10 hours after the application of the load increment. Systematic repeatability of the observation at increasing stress level suggests that reversible processes are taking place during short-term electrokinetic treatments.
The observed behaviour is thought to be a consequence of the gas production associated to electrolysis of water. The oxygen generated at the anode cannot escape easily from the sample, as it is entrapped by the water flowing into the sample. When the electric field is removed and a load increment is applied, the direction of the water flow is reversed and the entrapped air may eventually flow out from the sample with the aid of the load-induced water flow. If the sample, or at least a part of it, partially desaturates due to gas generation, capillary forces arise, which could be responsible for an increase in the soil stiffness. As the gas escapes, full saturation is recovered and the temporary increase in stiffness is lost.
In Figure 2 the evolution of the semi-logarithmic compliance, λ , of the treated sample with the duration of the electrokinetic treatment is shown.
The longer the duration of the treatment, the higher is the reduction in the degree of saturation that can be expected due to gas production. Such decrease in Sw is consistent with the observed reduction of soil compliance. These data allowed to calibrate the hypoelastic law (18), with λ * = 0.062 and ν = 0.3.
The time evolution of vertical displacements during a purely mechanical consolidation step applied to a saturated sample at null electric field was back-analysed to determine the hydraulic conductivity of the soil, as depicted in Figure 3.
The best agreement between measured and predicted consolidation curves is obtained assuming an absolute permeability k = 0.2×10-16 m2.
The relative hydraulic conductivity with respect to water, kw,rel, has been assumed to be given by eq. (26a), with aw = 1 and bw = 5, as suggested by the experimental data presented in Caruso and Jommi (2005). Consistently, in the relationship (28), describing the relative permeability with respect to gas, kg,rel, the constants ag = 1 and bg = 5 were assumed.
Electrokinetic filtration steps were performed at constant electric field, under constant vertical stress ranging from συ = 20 kPa up to συ = 500 kPa and constant back pressure, to determine the electro-osmotic permeability (Gabrieli et al. 2008a). The imposed electric field and duration of the tests were chosen to be comparable to those adopted in the in-situ electrokinetic fencing application reported by Narasimhan and Sri Ranjan (2000). The measured electro-osmotic permeability is ke = 0.9×10-9 m2/(Vs).At constant electric field, no significant dependence of the water volume outflow on the applied stress level was observed, indicating that, within the stress range investigated, the electro-osmotic permeability can be considered practically independent of the void ratio (in the range 0.8 < e < 0.9).
The dependence of the electro-osmotic permeability on the degree of saturation was investigated starting from the experimental results obtained by Gabrieli et al. (2008b) in electrokinetic filtration tests performed on unsaturated specimens in the as-compacted state. The experimental results obtained compare well with the results reported by de Wet (1995), as shown in Figure 4.
The two data sets suggest that the relative electro-osmotic permeability, ke,rel, can be given as a function of the degree of saturation by the power law of eq. (26b), with ae = 1 and be = 3.2.
From the measurements of electric current densities during the electrokinetic filtration tests, an effective saturated bulk electrical conductivity, χ* = 0.109 S/m, has been estimated. The apparent conductivity of the soil skeleton was assumed to be negligible. The relative electrical conductivity, χrel, was assumed to depend on the degree of saturation according to eq. (31), with aχ = 1 and bχ = 2, as suggested by literature experimental data (see e.g., Mualem and Friedman 1991, Mattson et al. 2002).
The characterisation of the hydraulic properties of Viadana silt is completed by the soil-water retention curve shown in Figure 5, derived from experimental results given by Caruso and Jommi (2005).
The experimental data are well interpolated by the curve described by (22), with asw = 0.00851 kPa-1, nsw = 1.31 and msw = 1-1/nsw.
NUMERICAL SIMULATIONS
To evaluate the influence of soil desaturation on the time evolution of the electrokinetic transport processes, two series of numerical simulations have been performed. In the first series, electrokinetic filtration tests were reproduced by imposing a constant electric field and computing the resulting water outflow at the anode. In the second series, electro-osmotic consolidation tests were reproduced by applying a constant electric field and assuming free drainage at the cathode and no hydraulic flow at the anode (impervious boundary).
ELECTROKINETIC FILTRATION TEST
The ideal scheme for a one-dimensional electrokinetic filtration test on a saturated soil specimen is represented in Figure 6.
By imposing a constant potential difference through the specimen, a uniform water flux is induced due to electro-osmosis. If the material is assumed to be fully saturated, the solution is characterised by constant pore water pressure, and uniform water flow is recovered. The water pressure remains constant and equal to the back-pressure imposed at the specimen draining boundaries.
In reality, water hydrolysis at the electrodes develops oxygen gas at the anode, and hydrogen gas at the cathode. While the latter does not enter into the specimen due to the outward water flux, the oxygen produced at the anode remains entrapped by the inward water flux and slowly penetrates into the sample. The amount of gas produced at the anode is calculated from eq. (35). A sensitivity analysis has been performed to evaluate the influence of the efficiency parameter η on the overall evolution of the water outflow at the cathode.
In Figure 7, the time evolution of the computed values of the vertical seepage velocity ww at the cathode, obtained with two different values of the efficiency parameter η , are compared with the experimental data from an electrokinetic filtration test performed on an initially saturated specimen underthe same electric potential difference.
The experimental data clearly show that the initial flow rate tends to decrease as the duration of the test increases. In the numerical simulations, the decrease of the flow rate is associated to the progressive desaturation at the anode due to gas production. The outflow rate clearly depends on the amount of gas produced, as shown by the comparison between the two different numerical simulations. By increasing the amount of gas produced at the anode, an unstable outflow rate can be observed both from the experimental data and the numerical results. The numerical instability could be reduced by introducing a convenient minimum threshold for the hydraulic permeability to gas. Nonetheless, as pointed out previously, herethe choice not to introduce numerical procedures to stabilise the simulation of an inherently unstablephysical process was followed (Jommi and Vaunat 1998).
The isochrones of water pressure and of degree of saturation, obtained in the two numerical simulations, are shown in Figures 8 to 11 .
The results indicate that, due to gas generation, the water pressure does not remain constant throughout the sample, although pore pressure variations remain relatively small. For the duration of the test considered, the advancing desaturation front only affects a small portion of the specimen close to the anode.
ELECTROKINETIC CONSOLIDATION TEST
The second simulation series is relative to an electrokinetic consolidation test, performed by imposing a constant electric field to a soil specimen with free drainage at the cathode and no drainage at the anode.
The ideal scheme for a one-dimensional electrokinetic consolidation test on a saturated soil specimen is represented in Figure 12.
If water drainage at the anode is prevented when the electric field is applied, a water pressure gradient must develop to counteract locally the electro-osmotic induced flow. Water can flow out from the sample at the draining cathodic boundary only if an equal amount of pore volume reduction is induced by soil skeleton deformation. As the drainage process is controlled by the volumetric deformation rate of the soil skeleton, which in turns depends on the changes in vertical effective stress, the specimen undergoes a time-dependent deformation process whose time evolution is ruled by soil hydraulic conductivity, soil stiffness and specimen size. Neglecting gravity effects, the final stationary conditions are expected to be characterised by a constant pore pressure gradient and null water flow, so that, in the vertical direction,
throughout the specimen.
Numerical simulations of an electrokinetic consolidation test were performed assuming either fully saturated conditions throughout the test (no gas production at the anode), or progressive desaturation at the anode induced by gas production at the electrode, assuming efficiencies η = 0.1 or η = 0.4.
Numerical results are compared to actual experimental data from an electrokinetic consolidation test performed on a sample of Viadana silt in Figure 13, which shows the time evolution of pore water pressure at the anode.
It is worth mentioning that the electrokinetic consolidation test was performed under an initial back pressure of 200 kPa. The initial back pressure was imposed to dissolve at least part of the gas generated at the anode, and to keep the sample as near as possible to fully saturated conditions. The water pressure at the bottom of sample (on the anodic side) and the vertical displacement at the top were measured during the whole duration of the test.
The comparison indicates that the decrease of pore water pressure at the anode is only slightly influenced by gas production. Nevertheless, the presence of gas affects the shape of the isochrones of pore water pressure in the sample, as shown in Figures 14 to 16 .
From the shape of the pore water pressure isochrones it can be observed that, while for the three simulations the computed pore water pressures at the anode are comparable, the computed values of pore water pressure within the sample tend to increase as gas production at the anode increases. This has a significant impact on the computed vertical effective stress field, and therefore on the computed vertical strain and displacement field. This is clearly shown in Figure 17, where the vertical displacement computed at the top surface of the specimen in the three simulations is plotted as a function of the elapsed time. In the figure, the vertical displacement recorded in the actual experiment is also reported.
The comparison between experimental data and numerical results indicates that, the higher the amount of gas produced at the electrode, the stiffer the system, consistently with the expected role played by suction on the mechanical behaviour of the coupled system.
In spite of the simple constitutive laws adopted, a fairly good match between numerical predictions and experimental results is obtained with an efficiency factor η = 0.4. Differences between measured and predicted pore water pressures may be ascribed to a slight underestimation of hydraulic conductivity at high saturation degrees.
CONCLUSIONS
A theoretical model was developed to perform a quantitative analysis of coupled deformation and flow processes, occurring during low-intensity and short-duration electrokinetic treatments characterising the design of electrokinetic barriers and fences for pollutant migration control. The model has been implemented numerically using the finite element method, and adopting a monolithic approach.
A novel feature of the model is the possibility to take into account the effects of partial saturation on the electric, water and gas flows within the porous medium, and on the mechanical response of the soil skeleton. A set of suitable constitutive laws was formulated in terms of suction and degree of saturation, based on the results of an ongoing experimental programme, in order to cope with the experimentally observed variation of the mechanical, electrical, hydraulic and electro-osmotic conduction properties of the soil.
In a series of numerical simulations of one-dimensional electrokinetic filtration and consolidation tests, the proposed model was used to assess the role played by gas generation at the electrodes by electrolysis and its effects on the transport processes through the soil. Numerical predictions are compared to experimental data obtained in laboratory electrokinetic filtration tests and electrokinetic consolidation tests. The formulation helps in the interpretation of the experimental tests, and it captures quite well the relevant features of the observed behaviour.
Experimental results suggest that, for electrokinetic treatments of limited duration, when chemical gradients are negligible, the development of pore water and gas pressure gradients within the soil mass can be induced by oxygen gas generation at the anode due to water hydrolysis. The gas generated has a definite impact on the time evolution of the process, affecting the hydraulic, electro-osmotic and electrical conduction properties, as well as on the soil skeleton stiffness.
The proposed model can be further used as an interpretative tool for ongoing experimental tests. Besides, it can be introduced as a design tool for the development of the electrokinetic barrier technology, to provide useful indications about the optimal design parameters, electrode geometry, applied voltage and time of treatment.
ACKNOWLEDGMENTS
The financial support of the Italian Ministry of University and Research, through the grant PRIN 2006080119-2006, Experimental and theoretical study of the applicability of electrokinetic processes for the control of contaminant propagation in fine grained soils, is gratefully acknowledged.
Manuscript received on July 5, 2008; accepted for publication on May 18, 2009
Selected paper presented at the IUTAM Symposium on Swelling and Shrinking of Porous Materials: From Colloid Science to Poromechanics - August 06-10 2007, LNCC/MCT.
with m being the second-order unit tensor in Voigt notation:
Then, the FE matrices appearing in eqs. (36) are given by:
and the FE vectors appearing in eqs. (36) are given by: ()
where  is the geometrical domain and ∂
is the geometrical domain and ∂ its boundary.
its boundary.
- ACAR YB AND ALSHAWABKEH AN. 1993. Principles of electrokinetic remediation. Environ Sci Technol 27(13): 26382647.
- ACAR YB AND ALSHAWABKEH AN. 1996. Electrokinetic remediation. I: Pilot-scale tests with lead-spiked kaolinite. J Geotech Engrg 122(3): 173185.
- ACAR YB, GALE RJ, PUTNAM GA AND HAMED J. 1989. Electrochemical processing of soils: its potential use in environmental geotechnology and significance of pH gradients. In: 2ND INT SYMP ON ENVIR GEOTECHNOLOGY. Envo Publishing 1, p. 2538.
- ACAR YB, GALE RJ, PUTNAM GA, HAMED J AND WONG RL.1990. Electrochemical processing of soils: Theory of pH gradient development by diffusion, migration, and linear convection. J Env Sci Health A25: 687714.
- AIROLDI F, JOMMI C, MUSSO G AND PAGLINO E. 2009. Influence of calcite on the electrokinetic treatment of a natural clay. J Appl Electrochem 39: 22272237.
- ALONSO EE, GENS A AND HIGHT DW. 1987. Special problem soils. General report. In: PROC IX ECSMFE, Dublin, Ireland. Balkema, Rotterdam, p. 10871146.
- ALSHAWABKEH AN AND ACAR YB. 1996. Electrokinetic remediation. II: Theoretical model. J Geotech Engng ASCE 122(3): 186196.
- ALSHAWABKEH AN, SHEAHAN TC AND WU X. 2004. Coupling of electrochemical and mechanical processes in soils under DC fields. Mech Mater 36(5-6): 453465.
- BOLZON G, SCHREFLER BA AND ZIENKIEWICZ OC. 1996. Elastoplastic soil constitutive laws generalized to partially saturated states. Géotechnique 46: 279289.
- BORJA R. 2004. Cam-clay plasticity. Part V: A mathematical framework for three-phase deformation and strain localization analyses of partially saturated porous media. Comp Meth Appl Mech Engng 193: 53015338.
- CARUSO M AND JOMMI C. 2005. An evaluation of indirect methods for the estimation of hydraulic properties of unsaturated soils. In: BILSEN H AND NALBANTOGLU Z (Eds), Problematic Soils. Eastern Mediterranean University Press 1, p. 183191.
- CHANG JH, QIANG Z AND HUANG CP.2006. Remediation and stimulation of selected chlorinated organic solvents in unsaturated soil by a specific enhanced electrokinetics. Colloid Surface A 287(1-3): 8693.
- COUSSY O. 1995. Mechanics of Porous Continua. J Wiley & Sons, NY, USA.
- DE BOER R. 1995. Theory of Porous Media. Springer, Berlin.
- DE WET M. 1995. Electro-kinetics, infiltration and unsaturated flow. In: ALONSO E AND DELAGE P (Eds), Unsaturated Soils. A.A. Balkema, Rotterdam 1, p. 283291.
- ESRIG M AND GEMEINHARDT JR J. 1967. Electrokinetic stabilisation of an illitic Clay. J Soil Mech Found Div ASCE 93(3): 109128.
- EYKOLT G. 1992. Driving and complicating features of the electrokinetic treatment of contaminated soil. Ph.D. Thesis, University of Texas at Austin, Texas.
- EYKHOLT GR AND DANIEL DE. 1994. Impact of system chemistry on electroosmosis in contaminated soil. J Geotech Engng, ASCE 120: 797815.
- GABRIELI L, JOMMI C, MUSSO G AND ROMERO E. 2008a. Influence of electroosmotic treatment on the hydromechanical behaviour of clayey silts: preliminary experimental results. J Appl Electrochem 38: 10431051.
- GABRIELI L, JOMMI C, MUSSO G AND ROMERO E. 2008b. Electrokinetic treatment of a natural silt in saturated and unsaturated conditions. In: SHAO JF AND BURLION N (Eds), Thermo-hydromechanical and Chemical Coupling in Geomaterials and Applications: Proceedings of the 3rd International Symposium GeoProc2008. Wiley, ISTE, p. 203210.
- GRAY DH. 1970. Electrochemical hardening of clay soils. Géotechnique 20: 8193.
- HUGHES TJR. 1987. The Finite Element Method. Prentice-Hall, Englewood Cliffs.
- JOMMI C. 2000. Remarks on constitutive modelling of unsaturated soils. In: TARANTINO A AND MANCUSO C (Eds), Experimental Evidence and Theoretical Approaches in Unsaturated Soils. Balkema, Rotterdam, p. 139153.
- JOMMI C AND VAUNAT J. 1998. A note on finite element modelling of unsaturated consolidation problems. In: CIVIDINI A (Ed), Application of Numerical Methods to Geotechnical Problems, NUMGE98. CISM, Udine, p. 315326.
- JOMMI D, VAUNAT J, GENS A, GAWIN D AND SCHREFLER BA. 1997. Multiphase flow in porous media: a numerical benchmark. In: Proceedings of NAFEMS World Congress 97, 2, p. 13381349.
- LEWIS RW AND SCHREFLER BA. 1998. The Finite Element Method in the Static and Dynamic Deformation and Consolidation of Porous Media. J Wiley & Sons, NY, USA.
- MATTSON ED, BOWMAN RS AND LINDGREN ER. 2002. Electrokinetic ion transport through unsaturated soil: 1. Theory, model development, and testing. J Contam Hydrol 54(1-2): 99120.
- MITCHELL JK 1991. Conduction phenomena: from theory to geotechnical practice. Géotechnique 41: 229340.
- MITCHELL JK. 1993. Fundamentals of Soil Behavior. 2nd ed., J Wiley & Sons, NY, USA.
- MUALEM Y AND FRIEDMAN S. 1991. Theoretical prediction of electrical conductivity in saturated andunsaturated soil. Water Resour Res 27(10): 27712777.
- MUSSO G. 2000. Electrokinetic phenomena in soils. Ph.D. Thesis, Politecnico di Torino.
- NARASIMHAN B AND SRI RANJAN R. 2000. Electrokinetic barrier to prevent subsurface contaminant migration: theoretical model development and validation. J Contam Hydrol 42(1): 117.
- PANDAY S AND CORAPCIOGLU MY. 1989. Reservoir transport by compositional approach. Transport Porous Med 4: 369393.
- ROMERO E, GENS A AND LLORET A. 1999. Water permeability, water retention and microstructure of unsaturated compacted boom Clay. Eng Geol 54: 117127.
- TAMAGNINI C.1994. Electrokinetic phenomena in clayey soils and electrokinetic consolidation theory: experimental investigation and numerical modelling (in italian). Ph.D. Thesis, Università degli Studi di Roma la Sapienza.
- VAN GENUCHTEN MT. 1980. A closed form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci Soc Am J 44: 892898.
- VIRKUTYTE J, SILLANPÄÄ M AND LATOSTENMAA P. 2002. Electrokinetic soil remediation critical overview. Sci Total Environ 298(1-3): 97121.
- WIECZOREK S, WEIGAND H, SCHMID M AND MARB C. 2005. Electrokinetic remediation of an electroplating site: design and scale-up for an in-situ application in the unsaturated zone. Eng Geol 77(3-4): 203215.
- YEUNG AT. 1994. Electrokinetic flow processes in porous media and their applications. In: CORAPCIOGLU MY (Ed), Advances in Porous Media 2: 309395.
- YEUNG AT AND MITCHELL JK. 1993. Coupled fluid, electrical and chemical flows in soil. Géotechnique 43: 121134.
- YEUNG AT, SADEK SM AND MITCHELL JK. 1992. A new apparatus for the evaluation of electrokinetic processes in hazardous waste management. Geotech Testing J 15: 207216.
- YEUNG AT, HSU CN AND MENON RM.1997. Physicochemical soil-contaminant interactions during electrokinetic extraction. J Hazard Mater 55(1-3): 221237.
Appendix
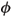 be the discrete gradient operators, such that:
be the discrete gradient operators, such that: Let Nf be the interpolation functions adopted for the generic primary field f, and let Bu, Ep, Ef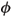 be the discrete gradient operators, such that:
be the discrete gradient operators, such that:
Correspondence to:
Publication Dates
-
Publication in this collection
03 Mar 2010 -
Date of issue
Mar 2010
History
-
Accepted
18 May 2009 -
Received
05 July 2008



























































