MATHEMATICAL SCIENCES

 

Injectivity of the Dirichlet-to-Neumann Functional and the Schwarzian Derivative

 

 

Fernando A.F.C. Silva^I; Pedro A.G. Venegas^II; Ramón O.M. Ahumada^I

^IUniversidade Federal de Pernambuco, CCEN – Departamento de Matemática, Av. Prof. Luiz Freire s/n Cidade Universitária, 50740-540 Recife, PE, Brasil
^IIUniversidade Federal da Paraíba, CCEN – Departamento de Matemática, Cidade Universitária 58059-970 João Pessoa, PB, Brasil

Correspondence to

 

 

---

ABSTRACT

In this article, we show the relation between the Schwartz kernels of the Dirichlet-to-Neumann operators associated to the metrics g₀ and h = F* (e^2φ g₀) on the circular annulus A_R, and the Schwarzian Derivative of the argument function f of the restriction of the diffeomorphism F to the boundary of A_R.

Key words: annulus, Dirichlet-to-Neumann Functional, Schwarzian Derivative.

---

RESUMO

Neste artigo mostramos a relação entre os núcleos de Schwartz dos operadores Dirichlet-to-Neumann associados à métrica g₀ e h = F* (e^2φ g₀), no anel circular A_R, e a Derivada Schwarziana da função argumento f, da restrição do difeomorfismo F à fronteira de A_R.

Palavras-chave: anel, Funcional Dirichlet-Neumann, Derivada Schwarziana.

---

 

 

INTRODUCTION

Let  denote the space of all Riemannian metrics on a compact manifold, with  boundary, and denote by  the space of continuous linear operators acting on C^∞(∂Ω).

The Dirichlet-to-Neumann functional  is a mapping from  into  such that, for each, , takes Dirichlet boundary values to Neumann boundary values. More precisely, if  is the unique solution of the Dirichlet problem  in Ω, , then, where  (resp. ) is the Laplace-Beltrami operator (resp. unit interior normal vector field) associated to the metric. The study of this functional goes back to the seminal paper of (Calderón 1980).

It is known (Lee and Uhlmann 1989) that  is in fact an elliptic self-adjoint pseudo-differential operator of order one, whose principal symbol is , , and .

Let  be the group of diffeomorphism of . The semi-direct product  (Polyakov 1987) of the groups  and  defined by

provides a natural right action on , given by

      

where  denotes the pull-back of F.

The main obstruction to injectivity, in the two-dimensional case, is the semidirect product of the groups of diffeomorphisms that restricts to the identity on the boundary, and the Abelian group of real-valued functions that equals zero on it. In fact, as formula (2.1) shows, the Dirichlet-to-Neumann Functional is constant on the orbits determined by ; this is a normal subgroup of .

With respect to the determination of the metric  from the Dirichlet-to-Neumann Operator, we recommend the papers (Lee and Uhlmann 1989), (Lassas and Uhlmann 2001) and (Lassas et al. 2003). In these papers, they solve, in a more general setting, the problem of recovering the manifold and the metric.

In the case of a fixed annulus, all metrics can be written as  for  coming from the pull-back of the euclidean metric in the annulus of radius  and . We prove, in this special case, that the equality of the Dirichlet-to-Neumann Operators associated to both metrics  and  gives us a relation involving the Schwarzian derivative of  ( the lifting to  of the restriction to the boundary of the diffeomorphism ).

Furthermore, we also show that the conformal factor restricted to the boundary of the annulus is determined by .

More precisely, we shall prove in Section 2 that, if  is the annulus

          

 is conformal to the euclidean metric, , where  and ; the equality of the Schwartz kernels of  and of  implies that the argument function , of the restriction of  to , satisfies the differential equation

and  denotes the Schwarzian Derivative of . It follows that, if , then,  and  equals zero on the boundary.

 

2 GEOMETRIC FORMULATION

Here on we will denote by  the Schwartz kernel of . We start with two lemmas.

LEMMA . Given a two-dimensional compact manifold  with  boundary and,, and, we have

         

Proof. See (Gómez and Mendoza 2006).

LEMMA . Let  be a two-dimensional compact manifold with  boundary,  where , ,  and  the unitary vector field to, with respect to the metric. Then,

   

where  denotes the real, valued function on  such that .

Proof. Let ,

 

changing variables  we get:

   

 

where  denotes the unique real, valued function defined on  such that

         

and  is the tangent unitary vector field on  such that  and . The above equation means at every point  the following:  and  belong to the same one-dimensional tangent space ; consequently, the first one is a real multiple of the second. In fact, this multiple is unique and it is equal to .

For the second equality,

  

finishing the proof.

The next Lemma establish, a relation between  and the Green function  of the Laplacian with Dirichlet condition on  (Guillarmou and Sá Barreto 2009).

LEMMA . The Schwartz kernel  of  is given for y, y' ∈ ∂Ω, y ≠ y', by

       

where, 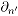 are, respectively, the inward pointing vector fields to the boundary in variable  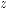and .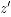

Proof. Let  be the distance function to the boundary in ; it is smooth in a neighborhood of  and the normal vector field to the boundary is the gradient  of . The flow  of  induces a diffeomorphism  defined by, and we have . This induces natural coordinates  near the boundary, these are normal geodesic coordinates. The function  is the unique solution of the Dirichlet problem  in, and  can be obtained by taking

   

where  is any smooth function on  such that . Now, using Green’s formula and , where  is the Dirac mass on the diagonal, we obtain for

        

   

We have Taylor expansion  near the boundary. Let  and take  supported near. Thus, pairing with  gives

     

Now taking  with support disjoint to the support of , thus , and differentiating (2.2) in x, we see, in view of the fact that Green’s function  is smooth outside the diagonal, that

which proves the claim.

Let  be a Riemannian manifold, and let us denote by  the geodesic distance between , and we denote . If

    

does not depend on x, we have the following result:

COROLLARY . If then for .

PROOF. Using the equalities of the Dirichlet-to- Neumann operators and Lemma 2.2 we have

On the other hand, since

then, taking the limit when  in (2.3), the demonstration follows.

REMARK 2.5. From LEMMA 2.2 and COROLLARY 2.4 we have the following equation,

The set of solutions of equation (2.4) is a group with multiplication law given by composition of functions, that is, if  and  are solutions of the equation (2.4), then,  is solution of (2.4). In fact,

In what follows, we use an explicit formula for the Green’s Function of  on the annulus  (Bârza and Guisa 1998). There,  is given in polar coordinates by:

 

and it is conformal to the euclidean metric, with conformal factor.

Then, the normal derivative of  with respect to  on, is , is:

Analogously, the normal derivative of, with respect to  on, is :

The Green’s function of  is given by

where , , , , , .

LEMA . The Schwartz kernel of Λ_g0,  being of the form, is

 

The equality above is in the distributions sense.

PROPOSITION 2.7 . Let p ,q Î ¶ A_r then,

 

where  denotes the geodesic distance between  and  with respect to the Euclidean metric in ∂ A_r.

Proof. In order to prove equation (2.8), we write

Then, the sequence  has the following property:  for all  where  is a constant that depends only on k and. In fact,. Hence, the series  represents a  function. On the other hand, using the Fourier series of the function, with, we have that

that is,

which implies:

the equality being in the distributions sense.

Then, multiplying (2.6) by  and taking the limit as , we get the following:

Analogously, we get (2.9).

REMARK . It follows from the proof of the Proposition (2.6) that the Schwartz kernel of  can be written as:

where  is a  function given by

TEOREMA . Let  be a metric as in,  where, ,  and. If, then,

        

where  denotes the Schwarzian Derivative of  (see  and the line right after it).

Proof. Using the equality of the Dirichlet-to-Neumann operators, it follows from Lemma 2.2 that

Writing,  and using (2.8), we have that

On the other hand, we have from Corollary 2.4 and (2.8) that  on the boundary. Hence,

We obtain, then,

Since the left hand side of the equation (2.12) is the  component of the Schwartz kernel, then if we take , we get

In what concerns the right hand side of the equation (2.12), we use Taylor expansion of order  of the expression in brackets, for  near ; we get, with ,

which can be written as follows,

        

Since the limit exists, when d ® 0, we obtain from (2.12) and (2.13) that

which implies:

or, more precisely:

Let us λ= λ (R) denote, the expression

Then, it, follows that

 

where

From equations (2.14) and (2.15) we have that

       

which implies:

            

The right-hand side of (2.18) is called the Schwarzian Derivative  of  (Navas 2007).

REMARK . The numerical study of  defined in (2.16) is done in Mendoza et al. 2009.

COROLLARY . The solution of the equation  for  is .

Proof. Making the change of variables: , the equation (2.18) becomes

   

Since,f(θ + 2π) =f (θ + 2π) we have that  and  are periodic of period 2π. Then, integrating (2.20) between  and 2π  we obtain

On the other hand,

  

that is,

          

which implies that . Because there is such that , we get . Therefore,.

It follows that restricted to the exterior boundary is a rotation and  equals zero there. The same conclusion holds for the restriction of  to the interior boundary.

The general solution of the equations (2.18) can be obtained using the formulas of Chuaqui et al. 2003, page 1.

 

ACKNOWLEDGMENTS

We thank Gustavo Tamm and Henrique Araújo for helping us to solve and to understand the non-linear ordinary differential equation (2.18).

 

REFERENCES

BÂRZA I AND GUISA D. 1998. Explicit Formulas for Green's Functions on the Annulus and on the Möbius Strip. Acta Appl Math 54: 289-302.         [ Links ]

CALDERÓN AP. 1980. On an inverse boundary value problem. Seminar on Numerical Analysis and its applications to continuum physics. Soc Bras Mat, Rio de Janeiro, RJ, Brasil, p. 65-73.         [ Links ]

CHUAQUI M, DUREN P AND OSGOOD B. 2003. The Schwarzian derivative for harmonic mappings. J d'Analyse Math 91(1): 329-351.         [ Links ]

GÓMEZ P AND MENDOZA R. 2006. Uniqueness for the Dirichlet-Neumann elliptic functional. Inverse Problem 22: 1575-1578.         [ Links ]

GUILLARMOU C AND SÁ BARRETO A. 2009. Inverse Problems for Einstein Manifolds. Inverse probl Imag 3:1-15.         [ Links ]

LASSAS M AND UHLMANN G. 2001. On Determining a Riemannian manifold from the Dirichlet-to-Neumann map. Ann Sci École Norm Sup 34(5): 771-787.         [ Links ]

LASSAS M, TAYLOR M AND UHLMANN G. 2003. The Dirichlet-Neumann map for complete Riemannian manifold with boundary. Comm Anal Geom 11: 207-221.         [ Links ]

LEE J AND UHLMANN G. 1989. Determining anisotropic real analytic condutivities by boundary measurements. Comm Pure Appl Math XLII: 1097-1112.         [ Links ]

MENDOZA R, ROJAS J, CAMPOS M AND BARRETO R. 2009. Injetividade do Funcional de Dirichlet-Neumann Elíptico via Matemática Intervalar. Temas, SBMAC 10: 31-40.         [ Links ]

NAVAS A. 2007. Grupos de difeomorfismos del círculo. Ensaios Matemáticos 13, SBM.         [ Links ]

POLYAKOV AM. 1987. Gauge Fields and Strings. Harwood Academic Publishers, Chur.         [ Links ]

 

 

Correspondence to:
Ramón Orestes Mendoza Ahumada
E-mail: ramon@dmat.ufpe.br

Manuscript received on October 1, 2008; accepted for publication on August 11, 2010