Abstracts
In this work we study the problem of modeling identification of a population employing a discrete dynamic model based on the Richards growth model. The population is subjected to interventions due to consumption, such as hunting or farming animals. The model identification allows us to estimate the probability or the average time for a population number to reach a certain level. The parameter inference for these models are obtained with the use of the likelihood profile technique as developed in this paper. The identification method here developed can be applied to evaluate the productivity of animal husbandry or to evaluate the risk of extinction of autochthon populations. It is applied to data of the Brazilian beef cattle herd population, and the the population number to reach a certain goal level is investigated.
Richards growth model; population risk; harvested populations; parametric estimate; likelihood profile function
Neste trabalho estudamos o problema de identificação do modelo de uma população utilizando um modelo dinâmico discreto baseado no modelo de crescimento de Richards. A população é submetida a intervenções devido ao consumo, como no caso de caça ou na criação de animais. A identificação do modelo permite-nos estimar a probabilidade ou o tempo médio de ocorrência para que se atinja um certo número populacional. A inferência paramétrica dos modelos é obtida através da técnica de perfil de máxima verossimilhança como desenvolvida neste trabalho. O método de identificação desenvolvido pode ser aplicado para avaliar a produtividade de criação animal ou o risco de extinção de uma população autóctone. Ele foi aplicado aos dados da população global de gado de corte bovino brasileiro, e é utilizado na investigação de a população atingir um certo número desejado de cabeças.
Modelo de crescimento de Richards; risco de populações; populações exploradas; estimação de parâmetros; função perfil de máxima verossimilhança
AGRARIAN SCIENCES
Richards growth model and viability indicators for populations subject to interventions
Selene LoibelI; Marinho G. AndradeII; João B.R. do ValIII; Alfredo R. de FreitasIV
IDepartamento de Estatística, Matemática Aplicada e Computação, Instituto de Geociências e Ciências Exatas, Universidade Estadual Paulista Julio de Mesquita Filho, Av.
24 A, 1515, 13000-900 Rio Claro, SP, Brasil
IIDepartamento de Matemática Aplicada e Estatística, Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo, Caixa Postal 668, 13560-970 São Carlos, SP, Brasil
IIIDepartamento de Telemática, Faculdade de Engenharia Elétrica e de Computação, Universidade de Campinas, Av. Albert Einstein, 400, Cidade Universitária Zeferino Vaz, 13083-852 Campinas, SP, Brasil
IVEMBRAPA Pecuária Sudeste, Caixa Postal 339, 13560-970 São Carlos, SP, Brasil
Correspondence to Correspondence to: João B.R. do Val E-mail: jbosco@dt.fee.unicamp.br
ABSTRACT
In this work we study the problem of modeling identification of a population employing a discrete dynamic model based on the Richards growth model. The population is subjected to interventions due to consumption, such as hunting or farming animals. The model identification allows us to estimate the probability or the average time for a population number to reach a certain level. The parameter inference for these models are obtained with the use of the likelihood profile technique as developed in this paper. The identification method here developed can be applied to evaluate the productivity of animal husbandry or to evaluate the risk of extinction of autochthon populations. It is applied to data of the Brazilian beef cattle herd population, and the the population number to reach a certain goal level is investigated.
Key words: Richards growth model, population risk, harvested populations, parametric estimate, likelihood profile function.
RESUMO
Neste trabalho estudamos o problema de identificação do modelo de uma população utilizando um modelo dinâmico discreto baseado no modelo de crescimento de Richards. A população é submetida a intervenções devido ao consumo, como no caso de caça ou na criação de animais. A identificação do modelo permite-nos estimar a probabilidade ou o tempo médio de ocorrência para que se atinja um certo número populacional. A inferência paramétrica dos modelos é obtida através da técnica de perfil de máxima verossimilhança como desenvolvida neste trabalho. O método de identificação desenvolvido pode ser aplicado para avaliar a produtividade de criação animal ou o risco de extinção de uma população autóctone. Ele foi aplicado aos dados da população global de gado de corte bovino brasileiro, e é utilizado na investigação de a população atingir um certo número desejado de cabeças.
Palavras-chave: Modelo de crescimento de Richards, risco de populações, populações exploradas, estimação de parâmetros, função perfil de máxima verossimilhança.
INTRODUCTION
There are multiple reasons for modeling the growth of a population of a certain species. A growth model of a population is an important tool for understanding how environmental uncertainties affect growth, and it provides the foundations to growth control policies, slaughter control, etc. These models help to forecast populational behavior and to evaluate the risk of extinction or, in the other extreme, population explosions. From the stochastic viewpoint, they allow calculations of the probability of extinction, explosion and to achieve a particular population goal or the expected time for the occurrence of these events. These populational characteristics are known as population viability indicators. The population viability analysis (PVA) is one of the central tools for conservation planning and evaluation of management options. Compared to other methods, PVA has several advantages (Boyce 1992, Omlin and Reichert 1999, Akçakaya and Sjögren-Gulve 2000). PVA provides a rigorous methodology that can use different types of data a way to incorporate uncertainties, natural variabilities and products or predictions that are relevant to conservation and management goals. The disadvantages of PVA include its single-species focus and requirements for data that may not be available for many species.
There are many works dealing with the population growth of a single population with growth rates depending on its size (see Ludwig 1996, 1999, Allen and Allen 2003, Matis and Kiffe 2004). In (Ludwig 1996, 1999), the Gompertz and the logistic model for single species are considered to calculate extinction probability. In (Matis and Kiffe 2004), a stochastic (Markovian) logistic population growth model with immigration and multiple births is derived, and the equilibrium distribution of the population is approximated to provide the extinction time of a species. The use of some of these models to evaluate the economic impact of population growth control can be found in (Yamauchi 2000). In (Matis et al. 2007), it was developed a generalization of the deterministic and stochastic population size model based on power-law kinetics for the black-margined pecan aphid. Deriso et al. (2008) present a framework for evaluating the cause of fishery declines by integrating covariates into a fisheries stock assessment model. In (Polansky et al. 2008), it was used simulated data to quantify the relative effects of sample size, population disturbances and environmental stochasticity on statistical inference. They focused on the key parameters that inform population dynamics predictions in a generalized Beverton-Holt model. In (Jiao et al. 2009), a hierarchical Bayesian approach for population dynamics modelling was developed to simulate variability in the population growth rates of three fish species.
In this paper, PVA is used to estimate the limiting probability of a population to reach a certain level, or the expected time for the occurrence of this event. It considers the population dynamics described by the Richards model, (Richards 1959), also known as generalized logistic model. As implied, it generalizes the logistic and also the Gompertz growth model (see Loibel et al. 2006). The Richards model was first used for the growth of animals (weight × age) and only later it was applied to model the populational growth (Fitzhugh 1974). A variation of this model, proposed by Gilpin and Ayala (1973), is known as theta-logistic, and it is used by Saether et al. (2000, 2002a, b) for the study of different populations.
Most of the works found in the literature relies on the logistic or the Gompertz models due to the difficulties to estimate the form parameter of the Richards model. The models with two parameters have a growth rate per capita that is symmetric near the inflexion point at mid level of the carrying capacity. However, this is not the case of populations of large mammals (see Fowler 1981). A three parameter model, such as Richards’, is able to fit better to an asymmetric growth rate per capita due to the extra form parameter (see Sibly et al. 2005). In addition to the usual Richards model, we introduce an extension to take into account exogenous interventions on the population. Modeling with interventions becomes very important when we need to identify the growth parameters of a population subjected to human intervention with economic and/or ecological motivations.
In this work, we present an analysis of the Brazilian beef cattle populational growth, here considered as a single gross population with growth rate depending on the population. Brazil currently occupies the second place in bovine herd size and in production of beef meat, only surpassed by the USA. The Brazilian bovine population has presented growth in recent years, having about 169 million head of cattle, and an increase of more than 10 million just in the last ten years (see ANUALPEC 2008).
The Brazilian cattle production in the last decades presented constant growth rates in production terms, export and consumption. Brazil has a potential domestic market for food consumption mainly for the beef meat. The domestic cattle production has always been characterized by an extensive system, since the cattle are mostly bred as unconfined herds, being relying on pastures. In recent years, with the incorporation of new technologies that aim at increasing productivity, the intensive systems of production increased in some regions, being called confined or semi-confined. However, the physical space and other production factors needed for further growth are bound to be scarce in the future, creating a saturation of the growth rate that are well described by the class of growth models here studied.
The development of cattle raising becomes even more attractive when the social-economic potential of the meat production chain is considered. The agro-industrial system of animal meat has the largest impact on the Gross National Product, and the segment denominated steer alone is responsible for more than US$ 30 million a year. According to Pineda (2002), a goal for Brazil to take advantage of its full potential and to definitely hold the position as one of the international main producers and exporters of bovine meat would be to keep a bovine population stable with more than 200 million animals.
Several factors contribute to the growth of bovine populations, which assign an stochastic behavior to the growth process. As a result, the use of methodologies that provide accurate estimates of bovine population growth in the country is important, as they contribute to the organization of this sector giving support to policies on internal consumption, exports and marketing, among others. In this work, we apply specifically the Richards model with exogenous interventions on the population to make estimates of the probability of the population beef cattle to achieve a particular goal. The model also allows the average time up to the occurrence of these events by taking into account the interventions on the population.
The identification problem of the Richards model without intervention and a detailed analysis of the inference of the model parameters were previously addressed in Loibel et al. (2006) by using bootstrap techniques. As in this case, the inference of the present model is treated with the use of the likelihood profile function technique that, roughly speaking, fix some parameters (the nuisance parameters) to estimate others see also (Seber and Wild 1989). Here the intervention is taken into account as part of the population that is removed, which may be brought about by fishing, hunting or slaughter in the case of animal husbandry. In these cases, we are interested in estimating the parameters of the model, not only the ones related to the free trajectory of the process, but also those associated with the intervention  modeled as a stochastic process.
modeled as a stochastic process.
This work is organized in the following way: in section 2, we present Richards’ populational growth model with intervention. In section 3, we present the procedure for identification of the parameters of this model employing the maximum likelihood profile function technique. In section 4, we present a Monte Carlo simulation approach to evaluate the indicators of the populational viability. In section 5, we present the results of this analysis for the data gathered over a period of 25 years (1983 to 2008) regarding the Brazilian bovine population. We calculate the probability of the Brazilian herd reaching the goal of 200 million head proposed by Pineda (2002), and the time expected for the Brazilian herd to reach this goal if an adequate slaughter policy is established. Apart from its own importance, this case study offers signposts for similar populational studies.
RICHARDS MODEL WITH INTERVENTION
We consider the size of the population as a stochastic process, where  is the set of non-negative integers. This population consists of adults and young, but only adults can be recruited to slaughter. Denoting the number of slaughtered individuals by, the number of individuals who remain in the population is, where
is the set of non-negative integers. This population consists of adults and young, but only adults can be recruited to slaughter. Denoting the number of slaughtered individuals by, the number of individuals who remain in the population is, where  represents the stock of animals available for slaughter in the next instant t + 1.
represents the stock of animals available for slaughter in the next instant t + 1.
To write a growth model with an intervention function (or slaughter), we consider the population size  and
and  in two consecutive instants t and t + 1, respectively, and the number of slaughtered individuals. The total number of individuals
in two consecutive instants t and t + 1, respectively, and the number of slaughtered individuals. The total number of individuals  can be written as a function of the population size in the instant t (we denote this function by
can be written as a function of the population size in the instant t (we denote this function by  ) subtracted from individuals who will be slaughtered in the instant t + 1. Then, the dynamic model can be written as Rt-1= N+1 - Ht+1 =ht(Rt)Rt .
) subtracted from individuals who will be slaughtered in the instant t + 1. Then, the dynamic model can be written as Rt-1= N+1 - Ht+1 =ht(Rt)Rt .
We model the interventions on this population as a function,  where
where  represents the fraction of
represents the fraction of  of a removed population in the instant t + 1. Then, the number of slaughtered individuals
of a removed population in the instant t + 1. Then, the number of slaughtered individuals  is given by
is given by  . Then, the dynamic model can be written as a cause-effect relation as
. Then, the dynamic model can be written as a cause-effect relation as
Supposing that the total population  and
and  are related by the Richards growth function, then we can write that
are related by the Richards growth function, then we can write that
where ∈t is an stochastic process in which each value is independent and identically distributed (i.i.d) with distribution  for
for  . It represents the random effects of environment on the growth rate of the Richards model. Parameters ρ is the intrinsic growth rate, K is the carrying capacity, and
. It represents the random effects of environment on the growth rate of the Richards model. Parameters ρ is the intrinsic growth rate, K is the carrying capacity, and  is a form parameter that changes the shape of the growth curve.
is a form parameter that changes the shape of the growth curve.
Replacing the equation (2) in (1), we can write the complete model in the presence of interventions as:
To elaborate the intervention function, note that it should depend on the available population, and an admissible model for  is a linear piecewise model given by:
is a linear piecewise model given by:
where  is the minimum viable population size, below which the population is considered extinct (call it realistic extinct).
is the minimum viable population size, below which the population is considered extinct (call it realistic extinct).  is certainly a possible choice because, with less than two individuals, there is no reproduction, but we can choose larger values for, if there are Allee effects. The rate, is the maximum intervention rate due to the technological and physical limitations for the intervention action. The equation (4) can be written as:
is certainly a possible choice because, with less than two individuals, there is no reproduction, but we can choose larger values for, if there are Allee effects. The rate, is the maximum intervention rate due to the technological and physical limitations for the intervention action. The equation (4) can be written as:
where  is a non-correlated i.i.d. stochastic process with distribution
is a non-correlated i.i.d. stochastic process with distribution  , with
, with  . We assume that ∈t and
. We assume that ∈t and  are independent processes; therefore, we have that
are independent processes; therefore, we have that  . In (5) we have,
. In (5) we have,  ,
,  or
or  and
and  . Considering the model in (5) for the rate of intervention
. Considering the model in (5) for the rate of intervention  as a function of the available population
as a function of the available population  , we have that the conditional distribution density
, we have that the conditional distribution density  is a Gaussian
is a Gaussian  .
.
The equation (3) can be written as:
We denote  and
and  , and also set
, and also set  and
and  . We can, then, rewrite the equation (6) as a linear relation:
. We can, then, rewrite the equation (6) as a linear relation:
with  and
and  .
.
From the fact that  is a i.i.d stochastic process with distribution
is a i.i.d stochastic process with distribution  , it follows that
, it follows that  is also i.i.d stochastic process with Gaussian density with zero mean and variance
is also i.i.d stochastic process with Gaussian density with zero mean and variance  . We, then, conclude from the equation (7) that the conditional density
. We, then, conclude from the equation (7) that the conditional density  is Gaussian, with mean
is Gaussian, with mean  and variance
and variance  We use this characterization to formulate the identification problem for the Richards model.
We use this characterization to formulate the identification problem for the Richards model.
MODEL FITTING
In order to formulate the problem of fitting the Richards model with intervention, by maximum likelihood method, it is necessary to know the joint distribution of the processes  . If we know the stochastic processes
. If we know the stochastic processes  and ht(Rt), we can recover the stochastic process
and ht(Rt), we can recover the stochastic process  using the relation
using the relation  . We begin the evaluations with the joint distribution of the processes
. We begin the evaluations with the joint distribution of the processes  ; we have, therefore:
; we have, therefore:
To write the joint density for the original processes,  , we should consider the Jacobian of the transformation
, we should consider the Jacobian of the transformation  given by:
given by:
The joint conditional density for  may be calculated, since
may be calculated, since  is a function only of Rt, by:
is a function only of Rt, by:
Considering the model in (5) and (7), we can write the joint conditional density (10) for  as:
as:
With (11) we can construct the likelihood function used to estimate the parameters of the model.
LIKELIHOOD FUNCTION
Adopting the matrix notation  ,
, ,
,  ,
,  ,
,  ,
,  , we conclude that the likelihood function for the Richards model with stochastic intervention is given by:
, we conclude that the likelihood function for the Richards model with stochastic intervention is given by:
and
In the equation (13), we are using the notation ,
,  and
and  ,
,  with
with  being a
being a  vector of ones. Due to the separability of
vector of ones. Due to the separability of  regarding the parameters
regarding the parameters  ,
,  and
and  , we can write the log-likelihood function as:
, we can write the log-likelihood function as:
where:
and
To make inference about model parameters it is necessary to calculate the Fisher information matrix. We adopted the matrix notation  and
and  . Then, for a fixed q, the Fisher information matrix for
. Then, for a fixed q, the Fisher information matrix for 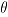 and
and  has the form:
has the form:
where if
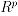 ,
, 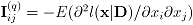 ,
, 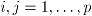 . The fact that
. The fact that 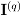 is a block diagonal matrix implies in the independence between the estimators
is a block diagonal matrix implies in the independence between the estimators 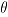 and γ.
and γ.
THE ESTIMATION OF THE PARAMETERS
We use the likelihood function for the Richards model (15), for a fixed value of the parameter q to calculate the maximum likelihood estimates (MLE) of the parameters  , conditioned to a particular value of q. We denote these estimators by
, conditioned to a particular value of q. We denote these estimators by  . Substituting these estimators in equation (15), we have the profiled likelihood function for parameter q given by
. Substituting these estimators in equation (15), we have the profiled likelihood function for parameter q given by
The equation (18) is a modified version of the profile likelihood function for the Richards model, Loibel et al. (2006), which includes the presence of the intervention in the vector  . We should find the maximum profile likelihood estimate (MPLE)
. We should find the maximum profile likelihood estimate (MPLE)  of the parameter
of the parameter  evaluating the function (18) for many values of the parameter
evaluating the function (18) for many values of the parameter  , and finding
, and finding  that maximizes the function (18).
that maximizes the function (18).
The maximum likelihood estimates (MLE) of the parameters θ(q) = (α(q),  , conditioned to
, conditioned to  are given by
are given by
The variance for these conditional maximum likelihood estimators is analogous to the one developed in Loibel et al. (2006). The variance for  can be calculated using the result of the asymptotic theory, Seber and Wild (1989),
can be calculated using the result of the asymptotic theory, Seber and Wild (1989),  . Consider the original vector of parameters
. Consider the original vector of parameters  conditioned on the parameter
conditioned on the parameter  and the vector of parameters
and the vector of parameters  given by parametrization
given by parametrization  ,
,  . The observed information matrix
. The observed information matrix  can be calculated with the observed information matrix
can be calculated with the observed information matrix  and the Jacobian of the transformations,
and the Jacobian of the transformations,  (to details, see Seber and Wild (1989)), given by
(to details, see Seber and Wild (1989)), given by
The Fisher information matrix for the original vector of parameters is given by
and we have the variance for the estimates of the original parameters  given by
given by  , and the variance for
, and the variance for  given by
given by 
ESTIMATION OF THE PARAMETER
The estimators of maximum likelihood for  and
and  are calculated by maximizing the function
are calculated by maximizing the function  given in (16). Therefore, we have:
given in (16). Therefore, we have:
The variance for  can be calculated straightforward by
can be calculated straightforward by  . The relation
. The relation  and
and  are used to estimate the parameters present in the slaughter function. The variance for the vector of original parameters
are used to estimate the parameters present in the slaughter function. The variance for the vector of original parameters  can be estimated with the observed information matrix
can be estimated with the observed information matrix  calculated with the observed information matrix
calculated with the observed information matrix  and the Jacobian of the transformations
and the Jacobian of the transformations  and
and  (to details, see Seber and Wild (1989)), given by
(to details, see Seber and Wild (1989)), given by
The Fisher information matrix for the original vector of parameters is given by
the variance for the estimates of the original parameters  is given by
is given by
and the variance for  is given by
is given by 
ESTIMATION OF THE PARAMETER
It is often of interest to test if the parameter  of the Richards model is equal to a known value
of the Richards model is equal to a known value  , that is,
, that is,  . In this way, we can easily obtain from the profile a likelihood ratio (LR) statistics
. In this way, we can easily obtain from the profile a likelihood ratio (LR) statistics  to test
to test  , which has an asymptotical Chi-square
, which has an asymptotical Chi-square  distribution with one degree of freedom, (Barndorff-Nielsen and Cox 1994). From this result, we can produce a large sample confidence interval for
distribution with one degree of freedom, (Barndorff-Nielsen and Cox 1994). From this result, we can produce a large sample confidence interval for  by inverting the LR test. An approximate confidence interval for
by inverting the LR test. An approximate confidence interval for  is, then, readily obtained from
is, then, readily obtained from  , and the accuracy of this approximation comes from the fact that
, and the accuracy of this approximation comes from the fact that  .
.
CALCULATION OF VIABILITY INDICATORS
In general, the growth models are adjusted to allow the calculation of viability indicators of a population, such as the probability of the population to reach a determined upper level defined by  ,
,  , or an upper level set
, or an upper level set  ,
,  . These intervals may be associated to a very low level, which indicates a state of near extinction, or an upper goal, which indicates a demographic explosion or an economically and/or ecologically desired objective.
. These intervals may be associated to a very low level, which indicates a state of near extinction, or an upper goal, which indicates a demographic explosion or an economically and/or ecologically desired objective.
MONTE CARLO SIMULATION APPROACH
We consider the populational growth model given by equations (3) and (5), remembering that  and
and  are independent processes, with ∈t, i.i.d.
are independent processes, with ∈t, i.i.d.  and
and  , i.i.d. N (0, η-1). With these models, we can simulate the behavior of a population over a long period of time and generate possible trajectories for the processes
, i.i.d. N (0, η-1). With these models, we can simulate the behavior of a population over a long period of time and generate possible trajectories for the processes  for values of time beginning with
for values of time beginning with  , for a certain initial instant
, for a certain initial instant  of interest. In this way, we estimate the risk or probability of the population reaching a goal by counting how many trajectories were necessary for this goal to be achieved among all of the
of interest. In this way, we estimate the risk or probability of the population reaching a goal by counting how many trajectories were necessary for this goal to be achieved among all of the  generated trajectories. We denote the time elapsed to achieve this goal by
generated trajectories. We denote the time elapsed to achieve this goal by  , with
, with  and the number associated to these occurrences by
and the number associated to these occurrences by  . Therefore, we have the probability estimate of the population reaching a certain goal by:
. Therefore, we have the probability estimate of the population reaching a certain goal by:
In some cases, we may be interested in calculating not only the probability of the population to reach a certain state, but also to evaluate the expected time for the population to reach a certain state. The time necessary for the population to reach a goal is a stop time  and its expected value can be estimated using the generated trajectories by simply evaluating the time to reach the level to each realization
and its expected value can be estimated using the generated trajectories by simply evaluating the time to reach the level to each realization  ,
,  . We, then, have the estimate:
. We, then, have the estimate:
We should adopt a very large number of J trajectories in view of the law of large numbers to assure the convergence of the estimators (28) and (29) for the true values. Another difficulty found in the practical application of this technique is that, depending on the intervention policy adopted {ht (Rt), t > T0}, the goal may become unreachable or perhaps reachable with a very low probability. It is necessary, therefore, to establish a limit for the maximum simulation time that will be associated with infinity. We denote the infinite time by T¥, that is, {Tk < ¥} ≡ {Tk < T∞}. Then, in the simulation process Nt, we have Nt < G for t < T¥ and we consider that the goal was not reached.
DETERMINISTIC INTERVENTION
There are situations in which we can consider the intervention  as a deterministic function. One of these situations occurs when we want to evaluate the impact of an intervention, for example, in an event where a government policy establishes that the removal of a population should be done in a certain period of the year. An estimate of the mean removal can be established, and we wish to evaluate the impact of this average removal on the population. Another situation occurs in long-term studies when we want to evaluate the impact on the population when a mean removal is carried out over a long period of time.
as a deterministic function. One of these situations occurs when we want to evaluate the impact of an intervention, for example, in an event where a government policy establishes that the removal of a population should be done in a certain period of the year. An estimate of the mean removal can be established, and we wish to evaluate the impact of this average removal on the population. Another situation occurs in long-term studies when we want to evaluate the impact on the population when a mean removal is carried out over a long period of time.
In these cases, the estimates of the parameters and the risk of extinction are obtained for a predetermined intervention policy. Assuming that {ht (Rt), t > 0} which means a deterministic function of  that represents the proportion of removed animals at time t +1, we can write the Richards model with interventions in the same way as in (3), and estimates of the parameters
that represents the proportion of removed animals at time t +1, we can write the Richards model with interventions in the same way as in (3), and estimates of the parameters 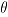 and
and  can be calculated as in the section for stochastic interventions.
can be calculated as in the section for stochastic interventions.
MARKOV CHAIN WITH DETERMINISTIC INTERVENTION
When the intervention  is deterministic, the recursive equation (2) can generally be written as
is deterministic, the recursive equation (2) can generally be written as
The subscript  indicates that, somehow, the function
indicates that, somehow, the function  depends on the action h. In the model proposed in this paper, the intervention h affects the maximum likelihood estimators of the parameters of the function, which are calculated using the equations (19)(21). The process
depends on the action h. In the model proposed in this paper, the intervention h affects the maximum likelihood estimators of the parameters of the function, which are calculated using the equations (19)(21). The process  is independent and identically distributed, with
is independent and identically distributed, with  and
and  if
if  and
and  .
.
We can adopt a discrete state space model for the problem of population growth whose continuous states space E can be decomposed into the disjoint union
The probability of the population to reach a certain state  at instant, given the records of the population
at instant, given the records of the population  and of the intervention, is written as follows:
and of the intervention, is written as follows:
where
From (30) we see that the random process  is function of the basic random process
is function of the basic random process  , which is independent of Ît. Hence,
, which is independent of Ît. Hence,  is also independent of
is also independent of  . Under these conditions, we can write that
. Under these conditions, we can write that
If  , for some
, for some  , we can adopt a Markov chain model for the problem of population growth with the probability of transition between states
, we can adopt a Markov chain model for the problem of population growth with the probability of transition between states  and Ij,
and Ij,  , given by:
, given by:
Let  be a square matrix with the elements
be a square matrix with the elements  , defined for all
, defined for all  . Then,
. Then,  is called Markov matrix over E if it satisfies the following properties:
is called Markov matrix over E if it satisfies the following properties:
We are interested in calculating the probability of the chain leaving a state  at instant
at instant  and reaching a state
and reaching a state  at instant t + s, s > 0. Therefore, we should calculate the transition probability matrix in s steps denoted by
at instant t + s, s > 0. Therefore, we should calculate the transition probability matrix in s steps denoted by  . For any
. For any  , the probability of the chain leaving the state
, the probability of the chain leaving the state  for state
for state  in
in  steps is
steps is  , for all
, for all  and
and  . To calculate this probability, we can use the Chapman-Kolmogorov equation.
. To calculate this probability, we can use the Chapman-Kolmogorov equation.
In many problems, we may be interested in calculating the probability of a population reaching any state above  . Thus, denoting
. Thus, denoting  , we have:
, we have:
In other words, the probability of reaching  is the sum of columns l, so that
is the sum of columns l, so that  on line
on line  of the matrix
of the matrix  s.
s.
For the calculation of the transition matrix using the Richards model with intervention, we denote  and rewrite the model (3) as:
and rewrite the model (3) as:
If  and
and  are any two states of space of states E, and assuming that
are any two states of space of states E, and assuming that  , then an interval
, then an interval  exists so that we can calculate the transition matrix in one step with elements
exists so that we can calculate the transition matrix in one step with elements  and rewrite the equation (34) by:
and rewrite the equation (34) by:
to find  . We can use the equation (37) to write:
. We can use the equation (37) to write:
Then, we can write that
With equations (38) and (39), we can write that
Assuming that  is a process with Gaussian distribution N(0, τ-1), we can calculate
is a process with Gaussian distribution N(0, τ-1), we can calculate  from the standard Gaussian accumulated distribution function with:
from the standard Gaussian accumulated distribution function with:
This form of calculating the matrix of transition probabilities is a discrete approximation, since we consider the probabilities of transition between the intervals  and
and  independent of the values that the population may assume within the intervals. The accuracy of this approach depends on the discretization refinement of the space of states.
independent of the values that the population may assume within the intervals. The accuracy of this approach depends on the discretization refinement of the space of states.
Given that  , we wish to calculate the expected value
, we wish to calculate the expected value  , so that
, so that  makes the first passage for the state Ij. In practice, there are many situations where the calculation of first-passage time is important. In the case of control of populations that grow explosively, we want to calculate the time expected for the population to reach a point that justifies intervention, such as controlled slaughter.
makes the first passage for the state Ij. In practice, there are many situations where the calculation of first-passage time is important. In the case of control of populations that grow explosively, we want to calculate the time expected for the population to reach a point that justifies intervention, such as controlled slaughter.
DEFINITION 1. First-passage time: Let  and
and  be two states of a Markov chain
be two states of a Markov chain  with space of states. If, for a given time
with space of states. If, for a given time  , the first-passage time of the state
, the first-passage time of the state  to state
to state  is defined as:
is defined as:
DEFINITION 2. For any, the probability function of  is defined by:
is defined by:
By convention, we adopt gij(0) = 0.
DEFINITION 3. Expected value of first-passage time:
PROPOSITION 1. For every pair of states  , we have:
, we have:
PROOF. Using Definition 2 for  , we have:
, we have:
Therefore,
Since  and considering all of the possible states
and considering all of the possible states  with
with  , we have:
, we have:
We, then, have:
PROPOSITION 2.  with
with  ; let
; let  and
and  e
e  be the expected times to reach state, starting from any
be the expected times to reach state, starting from any  state. We can calculate
state. We can calculate  by resolving the system of equations given by:
by resolving the system of equations given by:
where  is the matrix identity
is the matrix identity  ,
,  is a vector
is a vector  , and
, and  is the matrix
is the matrix  obtained by removing the line and the column
obtained by removing the line and the column  from the matrix
from the matrix  .
.
PROOF. We will consider that:
We can write that:
Replacing (54) in (55), we have:
Establishing a  and writing (57) for
and writing (57) for  e, we have the system of equations given by:
e, we have the system of equations given by:
The Markov chain modeling can only be used together with a constant slaughter rate, and it is more appropriate for evaluation of scenarios in long-term planning. On the other hand, the Monte Carlo simulation approach can handle more general slaughter functions but it also requires a larger computational effort. A comparison between these two approaches, for constant slaugher rates is presented in the Results section.
RESULTS
In this study, we propose an evaluation of the growth of meat production in Brazil based on data regarding the number of cattle and annual slaughter between 1983 and 2008 (ANUALPEC 2008). The population and slaughter data referring to this period are presented on the graphs shown in Figures 1 and 2 , in millions of heads, together with the adjusted values, according to the equations (3) and (5), respectively.
Table I presents the maximum likelihood estimates (MLE) and the standard deviation (SD) of the parameters of the Richards model adjusted to the population data in Figure 1, and of the parameters of the slaughter function adjusted to the data in Figure 2
, as well as the 95% confidence interval for  obtained from
obtained from  , with
, with  . The relation
. The relation  and
and  was used to estimate the parameters present in the slaughter function ht.
was used to estimate the parameters present in the slaughter function ht.
An important observation refers to the estimated values of  and
and  that represent the carrying capacity and maximum slaughtering allowed, respectively. Note that the carrying capacity estimate K = 217.5701 exceeded the maximum population level N26 = 176.1144 million head of cattle observed in 2004 (see Figure 1) and h0 = 0.3294 that represents an estimate of the maximum slaughter rate that is exceeding the maximum rate, which was about, observed in 2006 (see Figure 2
). K and
that represent the carrying capacity and maximum slaughtering allowed, respectively. Note that the carrying capacity estimate K = 217.5701 exceeded the maximum population level N26 = 176.1144 million head of cattle observed in 2004 (see Figure 1) and h0 = 0.3294 that represents an estimate of the maximum slaughter rate that is exceeding the maximum rate, which was about, observed in 2006 (see Figure 2
). K and  are the two main parameters that affect the population growth. In this work, we perform simulations of population growth for different values of K and
are the two main parameters that affect the population growth. In this work, we perform simulations of population growth for different values of K and  , close to estimates values, in order to estimate the probability and the expected time of the population to reach a given goal.
, close to estimates values, in order to estimate the probability and the expected time of the population to reach a given goal.
The graph in Figure 3 presents some of the 100 thousand simulations of trajectories of the process that were generated to calculate the probability of the population reaching the goal of 200 million heads.
In Table II, we present the probability  (Percent) and the expected time T (year) for this event to occur, considering scenarios with K increased from the estimated value to the value of 250 million heads, and
(Percent) and the expected time T (year) for this event to occur, considering scenarios with K increased from the estimated value to the value of 250 million heads, and  increased from the actual observed value 0.21 to the estimated value 0.3294 given in Table II.
increased from the actual observed value 0.21 to the estimated value 0.3294 given in Table II.
Note that the probability that the Brazilian herd will reach the goal of 200 million head proposed by Pineda (2002) when h0 = 0,3294 and K = 217 million heads is only p = 0.02%, and the time expected for this event to occur is  years. These results point out that an optimized slaughter policy is needed, together with investments in technology that improve the reproduction rates and carrying capacity of the Brazilian bovine herd and make possible to reach the population goal in a desirable time interval as
years. These results point out that an optimized slaughter policy is needed, together with investments in technology that improve the reproduction rates and carrying capacity of the Brazilian bovine herd and make possible to reach the population goal in a desirable time interval as  years with, which can be achieved with
years with, which can be achieved with  and
and  million head.
million head.
COMPARISON BETWEEN THE MARKOV CHAIN MODEL AND MONTE CARLO SIMULATION
In this study, two indices of viability were calculated: the probability of achieving a particular goal (200 million head) and the mean time for the occurrence of this event. To calculate these indices we used two methods: one based on Monte Carlo simulation, and another using a Markov chain model. To compare these two methods we presented, in Figure 4, both indices calculated with each of the methodologies presented, considering K = 230. Estimates made by the Monte Carlo simulation are in the third column of Table I. An analysis of the curves in Figure 4 shows a great similarity between the two approaches. However, being practical, the modeling by Markov chain requires some careful with the choice of size and the discretization of the space state. These results can be seen in Table III and on the graphs in Figure 4.
From the results of Table III we note that, with a maximum slaughter rate of 21%, we reach the population goal with the probability of 63% and a mean time period of 22 years for this event to occur. However, this is not a good policy because the production would be very small. On the other hand, with a maximum slaughter rate larger than 25%, the time intervals necessary to reach the goal become very long, and this slaughter policy is also not advisable with, but with K = 250 (see Table II).
CONCLUSIONS
In this work, we presented the adjustment of the Richards growth model for the bovine population in Brazil taking into consideration the populational losses due to the slaughter intervention. With the model adjustment that includes the stochastic intervention and posteriorly Monte Carlo simulations, we were able to estimate the indicators of the population viability. By considering deterministic intervention, we calculated the indicators, assuming that the population can be modeled by a Markov chain. We also employed Monte Carlo simulations to compare the results between these two methods. The Markov chain model would be the most natural manner of obtaining estimates of a population viability indicators, but it depends on the discretization of the space of states. On the other hand, the method using Monte Carlo simulation requires the establishment of an upper limit that, in this work, we call T¥. This limitation may impair the accurate calculation of the time expected to reach the population goal.
The analysis of the numerical results shows that a slaughter rate higher than 25% can make the growth of the population difficult and, in the future, lead to the reduction of bovine meat production in Brazil. To reach a higher goal, such as 200 million heads in a period less than 20 years, an optimized slaughter policy is fundamental in order to maximize a certain expected return within a finite horizon.
Considering the stochastic intervention, we simulated 10 scenarios changing the maximum slaughter rate and the carrying capacity, and concluded that the goal will be reached in 8 to 20 years (with K = 250). This leads us to believe that the use of a fixed intervention equal to 25% (slaughter in 2005) does not guarantee a sustainable production for K < 240. Given the present scenario, we can conclude that the Brazilian bovine herd will not reach the goal of 200 million heads in the expected time of 15 years.
ACKNOWLEDGMENTS
Research partially supported by Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), Grant 07/007612-0 and by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Grant number 300235/2005-5
Manuscript received on December 12, 2008; accepted for publication on August 16, 2010
- AKÇAKAYA HR AND SJÖGREN-GULVE P. 2000. POPULation viability analysis in conservation planning: an overview. Ecol Bull48: 8-21.
- ALLEN LJS AND ALLEN EJ. 2003. A coparison of three different stochastic population models with regard to persistence time, Theor Popul Biol 64: 439-449.
- ANUALPEC. 2008. Anuário da Pecuária Brasileira (Annual of Brazilian Cattle, in Portuguese), Publisher FNP, 359 p.
- BARNDORFF-NlELSEN OE AND Cox DR. 1994. Inference and Asymptotics, Chapman & Hall, 360 p.
- BOYCE MS. 1992. Population Viability Analysis. Annu Rev Ecol Syst 23(4): 481-506.
- DERISO RB, MAUNDER MN AND PEARSON WH. 2008. Incorporating covariates into fisheries stock assessment models with application to Pacific herring. Ecological applications: a publication of the Ecol Soc Am 18(5):1270-1286.
- FlTZHUGH Jr HA. 1974. Analysis of growth curves and strategies for altering their shapes. J Anim Sci 42(4): 1036-1051.
- FOWLER CW. 1981. Density Dependence as Related to Life History Strategy. Ecology 62: 602-610.
- GILPIN ME AND AYALA FJ. 1973. Global Model of Growth and Competition. Proc Nat Acad Sci 70(12): 35903593.
- JlAO Y, HAYES C AND CORTÉS E. 2009. Hierarchical Bayesian approach for population dynamics modelling of fish complexes without species-specific data. ICES J Mar Sci 66(2): 367-377.
- LOIBEL S, ANDRADE MG AND VAL TOR. 2006. Inference for the Richards Growth Model Using Box and Cox Transformation and Bootstrap Techniques. Ecol Model 191(3-4): 501-512.
- LUDWIG D. 1996. Uncertainty and the Assessment of Extinction Probabilities. Ecol Appl 6(4): 1067-1076.
- LUDWIG D. 1999. Is it meaningful to estimate a probability of extinction. Ecology 1(80): 298-310.
- MATIS JH AND KIFFE TR. 2004. On Stochastic Logistic Population Growth Models With Immigration and Multiple Births. Theor Popul Biol 65: 89-104.
- MATIS JH, KIFFE TR, MATIS TI AND STEVENSON DE. 2007. Stochastic modeling of aphid population growth with nonlinear, power-law dynamics. Math Biosci 208: 469-494.
- OMLIN M AND REICHERT P. 1999. A Comparison of Techniques for the Estimation of Models Prediction Uncertainty. Ecol Model 115: 45-59.
- PINEDA NR. 2002. Cenário da cadeia Produtiva de Carne Bovina no Brasil. Revista da Associação Brasileira dos Criadores de Zebuinos-ABCZ 2(10): 186-187.
- POLANSKY L, DE VALPINE P, LLOYD-SMITH JO AND GETZ WM. 2008. Parameter estimation in a generalized discrete-time model of density dependence. Theor Ecol 1: 221-229.
- RICHARDS JF. 1959. A flexible growth function for empirical use. J Exp Bot 1(10): 290-310.
- SAETHER BE, ENGEN S, LANDE R, ARCESE P AND SMITH JNM. 2000. Estimating the time extinction in an island population of song sparrow. Proc Roy Soc Lond 267(B): 621-626.
- SAETHER BE, ENGEN S, LANDE R, BOTH C AND VISSER M. 2002a. Density dependence and stochastic variation in newly established population of a small songbird. OIKO 99(B): 331-337.
- SAETHER BE, ENGEN S, FILL F, AANES R, SCHRODER W AND ANDERSEN R. 2002b. Stochastic population dynamics of an introduced swiss population of the Ibex. Ecology 83(12): 3457-3465.
- SEBER GAF AND WILD CJ. 1989. Nonlinear Regression. J Wiley & Sons, 774 p.
- SIBLY RM, BARKER D, DENHAM MC, HONE J AND PAGEL M. 2005. On the Regulation of Populations of Mammals, Birds, Fish, and Insects, SCIENCE. www.sciencemag.org 309(22): 607-610.
- YAMAUCHI A. 2000. Population Persistence Time Under Intermittent Control in Stochastic Environments. Theor Popul Biol 57: 391-398.
Publication Dates
-
Publication in this collection
28 Feb 2011 -
Date of issue
Dec 2010
History
-
Accepted
16 Aug 2010 -
Received
12 Dec 2008



































































