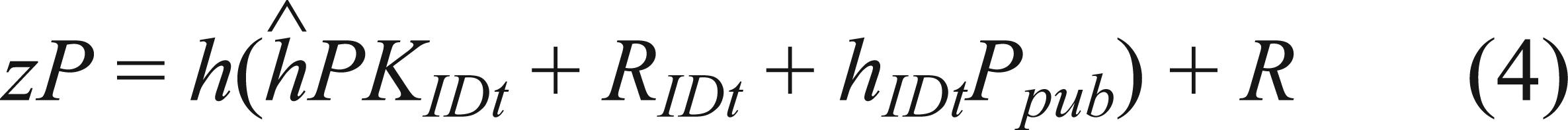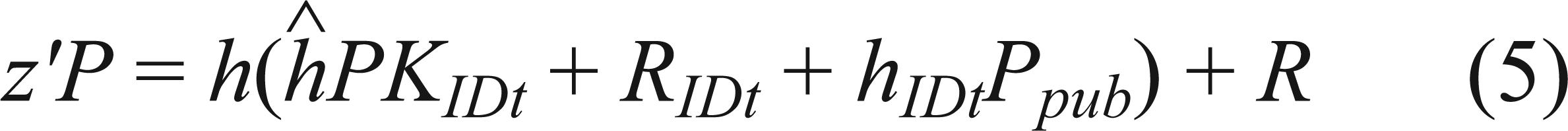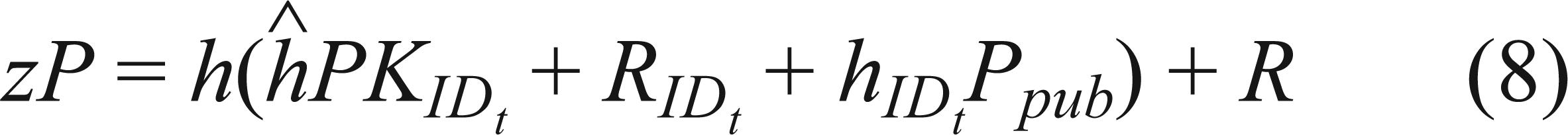Abstracts
Recently, the certificateless public key cryptography (CLPKC) has been studied widely since it could solve both of the certificate management problem in traditional public key cryptography (TPKC) and the key escrow problem in the identity-based public key cryptography (ID-based PKC). To satisfy requirements of different applications, many certificateless blind signature (CLBS) schemes using bilinear pairing for the CLPKC setting have been proposed. However, the bilinear pairing operation is very complicated. Therefore, the performance of those CLBS schemes is not very satisfactory. To solve the problem, we propose an efficient CLBS scheme without bilinear pairing. Performance analysis shows that the proposed scheme could reduce costs of computation and storage. Security analysis shows the proposed scheme is provably secure against both of two types of adversaries.
blind signature; certificateless cryptography; bilinear pairing; random oracle model
Recentemente, a criptografia de chave pública sem certificado (CLPKC) tem sido amplamente estudada, uma vez que poderia resolver o problema de gerenciamento de certificados na criptografia de chave pública tradicional (TPKC) e o problema chave de escrow da criptografia de chave pública baseada em identidade (ID-based PKC). Para atender aos requisitos de diferentes aplicações, têm sido propostos muitos sistemas de assinatura cega sem certificado (CLBs), sistemas que utilizam o emparelhamento bilinear para a configuração de CLPKC. No entanto, a operação de emparelhamento bilinear é muito complicada. Portanto, o desempenho desses regimes CLBs não é muito satisfatório. Para resolver o problema, propomos um esquema de CLBS eficiente sem emparelhamento bilinear. Uma análise de desempenho mostra que o esquema proposto poderia reduzir os custos de computação e armazenamento. Uma análise de segurança mostra que o esquema proposto é comprovadamente seguro contra dois tipos de adversários.
assinatura cega; criptologia sem certificado; emparelhamento bilinear; modelo de oráculo aleatório
INTRODUCTION
The blind signature (BS) scheme is a variation of digital signature scheme, which was first proposed by Chaum (1983)Chaum D. 1983. Blind signatures for untraceable payments. Proc CRYPTO 82,199 p.. In the BS scheme, a user could get a signature for any message but the signer does not know the content of the message. Due to such properties, BS schemes are widely used in electronic voting, electronic payment and electronic cash.
After Chaum's work, many BS schemes in the traditional public key cryptography (TPKC) were proposed for different applications. However, the TPKC faces with the certificate management problem since a certificate generated by a trusted third party is needed to bind the user's identity and his public key. To solve the problem, Shamir (1984)Shamir A. 1984. Identity-based cryptosystems and signature schemes. Proc CRYPTO 84, 47 p.introduced the concept of the identity-based public key cryptography (ID-based PKC). In the ID-based PKC, no certificate is required since the user's identity is his public key. However, the ID-based PKC faces with the key escrow problem since the user's private key is generated by the key generation centre (KGC) and the KGC knows all users' private keys. To solve the certificate management problem in the TPKC and the key escrow problem in ID-based PKC, Al-Riyami and Paterson (2003)Al-Riyami S and Paterson K. 2003. Certificateless public key cryptography. Proceedings of ASIACRYPT03, 452 p.proposed the concept of the certificateless public key cryptosystem (CLPKC). In the CLPKC, a user's private key consists of two parties, i.e. a partial secret key generated by the KGC and a secret value generated by the user.
Since groundbreaking work of Al-Riyami and Paterson (2003)Al-Riyami S and Paterson K. 2003. Certificateless public key cryptography. Proceedings of ASIACRYPT03, 452 p., many certificateless encryption (CLE) schemes (Sun and Zhang 2010Sun Y and Zhang F. 2010. Secure certificateless encryption with short ciphertext. Chinese J Electron 19: 313-318.) (Yang and Tan 2011Yang G and Tan C. 2011. Certificateless public key encryption: A new generic construction and two pairing-free schemes. Theor Comput Sci 412: 662-674.), certificateless signature (CLS) schemes (Tian and Huang 2012Tian M and Huang L. 2012. Cryptanalysis of a certificateless signature scheme without pairings. DOI: 10.1002/dac.2310.
https://doi.org/10.1002/dac.2310...
) (Tsai et al. 2012Tsai J, Lo N and Wu T. 2012. Weaknesses and improvements of an efficient certificateless signature scheme without using bilinear pairings. DOI: 10.1002/dac.2388.
https://doi.org/10.1002/dac.2388...
) (Gong and Li 2012Gong P and Li P. 2012. Li, Further improvement of a certificateless signature scheme without pairing. Int J Commun Syst. DOI: 10.1002/dac.2457.
https://doi.org/10.1002/dac.2457...
) (He et al. 2012cHe D, Chen J and Zhang R. 2012c. An efficient and provably-secure certificateless signature scheme without bilinear pairings. Int J Commun Syst 25: 1432-1442., 2013aHe D, Chen Y and Chen J. 2013a. A provably secure certificateless proxy signature scheme without pairings. Math Comput Model Dyn 57: 2510-2518., bHe D, Huang B and Chen J. 2013b. A new certificateless short signature scheme, IET Information Security 7: 113-117.) and certificateless key agreement schemes (HE et al. 2011cHe D, Chen Y, Chen J and Zhang R. 2011c. A new two-round certificateless authenticated key agreement protocol without bilinear pairings. Math Comp Model Dyn 54: 3143-3152., 2012aHe D, Chen J and Hu J. 2012a. A pairing-free certificateless authenticated key agreement protocol. Int J Commun Syst 25: 221-230., dHe D, Padhye S and Chen J. 2012d. An efficient certificateless two-party authenticated key agreement protocol. Comput Math Appl 64: 1432-1442.) have been proposed for applications in CLPKC setting. Several certificatless blind signature (CLBS) schemes (Zhang and Zhang 2008Zhang L and Zhang F. 2008. Certificateless signature and blind signature. J Electron 25: 629-635.) (Wang and Lu 2008Wang C and Lu R. 2008. A certificateless restrictive partially blind signature scheme. 2008 International Conference on Intelligent Information Hiding and Multimedia Signal Processing, 279 p.) (Yang et al. 2009Yang X, Liang Z and Wei P. 2009. A provably secure certificateless blind signature scheme. 5th International Conference on Information Assurance and Security, 643 p.) (Sun and Wen 2009Sun S and Wen Q. 2009. Novel efficient certificateless blind signature schemes. International Symposium on Computer Network and Multimedia Technology, 1 p.) (Zhang and Gao 2010) (Zhang et al. 2011Zhang L, Zhang F, Qin B and Liu S. 2011. Provably-secure electronic cash based on certificateless partially-blind signatures. Electron Commer R A 10: 545-552.) also were proposed. Zhang and Zhang (2008)Zhang L and Zhang F. 2008. Certificateless signature and blind signature. J Electron 25: 629-635. proposed the fist CLBS scheme using bilinear pairing. Then several other CLBS schemes (Wang and Lu 2008Wang C and Lu R. 2008. A certificateless restrictive partially blind signature scheme. 2008 International Conference on Intelligent Information Hiding and Multimedia Signal Processing, 279 p.) (Yang et al. 2009Yang X, Liang Z and Wei P. 2009. A provably secure certificateless blind signature scheme. 5th International Conference on Information Assurance and Security, 643 p.) (Sun and Wen 2009Sun S and Wen Q. 2009. Novel efficient certificateless blind signature schemes. International Symposium on Computer Network and Multimedia Technology, 1 p.) (Zhang and Gao 2010) (Zhang et al. 2011Zhang L, Zhang F, Qin B and Liu S. 2011. Provably-secure electronic cash based on certificateless partially-blind signatures. Electron Commer R A 10: 545-552.) using bilinear pairing were proposed to improve performance or security of Zhang et al.'s scheme. However, the bilinear pairing operation is very complicated. Theoretical analysis (Chen et al. 2007Chen L, Cheng Z and Smart N. 2007. Identity-based key agreement protocols from pairings. Int J Inf Secur 6: 213-241.) (Hankerson et al. 2004Hankerson D, Menezes A and Vanstone S. 2004. Guide to elliptic curve cryptography. New York: Springer-Verlag, 220 p.) and experimental results (Cao and Kou 2010Cao X and Kou W. 2010. A pairing-free identity-based authenticated key agreement scheme with minimal message exchanges. Inform Sciences 180: 2895-2903.) (He et al. 2011aHe D, Chen J and Hu J. 2011a. An ID-based proxy signature schemes without bilinear pairings. Ann Telecommun 66: 657-662., 2012bHe D, Chen J and Hu J. 2012b. n ID-based client authentication with key agreement protocol for mobile client-server environment on ECC with provable security, Inform Fusion 13: 223-230.) demonstrate that the computation cost of a bilinear pairing operation is similar to that of a dozen or so elliptic curve scalar multiplication operations. Therefore, the performance of those CLBS schemes is not very satisfactory and CLBS scheme without bilinear pairing is required for practical applications.
In this paper, we propose an efficient CLBS scheme without bilinear pairing operation and show it is secure against both of two kinds of various attacks. Section 2 gives some background about CLBS schemes. Section 3 proposes a new CLBS scheme without bilinear paring. Security analysis and performance analysis are proposed in Section 4 and Section 5 separately. Some conclusions are given in Section 6.
PRELIMINARIES
Notations
For convenience, some notations used in the paper are described as follows.
-
p, n: two large prime numbers;
-
Fp: a finite field;
-
E(Fp): an elliptic curve defined by the equation y2= x3 + ax + b over Fp, where a, b ∈ Fp and Δ = 4a3 + 27b2 ≠ 0 (Koblitz 1987Koblitz N. 1987. Elliptic curve cryptosystem. Math Comput 48: 203-209.);
-
G: the group with order n consisting of points on E(Fp) and the point at infinity O;
-
P: a generator of the group G;
-
DLP: the discrete logarithm problem (DLP), whose task is to compute x for given Q = xP;
CLBS Scheme
There are six polynomial time algorithms (Zhang et al. 2011Zhang L, Zhang F, Qin B and Liu S. 2011. Provably-secure electronic cash based on certificateless partially-blind signatures. Electron Commer R A 10: 545-552.) in a CLBS scheme, i.e. Setup, PartialPrivateKeyExtract, SetSecretValue, SetPublicKey, Sign and Verify.
Setup: Taking a security parameter k as input, this algorithm is executed by the KGC to generate the system parameters params and the master key mk.
PartialPrivateKeyExtract: Taking the system parameters params, the master key mk and a users identity ID as inputs, this algorithm is executed by the KGC to generate the users partial private key IDD.
SetSecretValue: Taking the system parameters params as input, this algorithm is executed by a user to generate his secret value xID.
SetPublicKey: Taking the system parameters params and a users secret value xID as inputs, this algorithm is executed by the user to generate his public key PKID.
Sign: Taking the system parameters params, the partial private key DID, the secret value xID and a message m as inputs, this algorithm is executed by the user to generate a signature. There are three sub-algorithms in the algorithm, i.e. Blind, BSign and Unblind.
-
Blind. Taking message m and a random string r as inputs, the sub-algorithm is executed by the user to generate a blinded message m′.
-
BSign. Taking a blind message m′, the signers private signing key
 and the system parameters params as inputs, the sub-algorithm is executed by the signer to generate a blind signature σ′.
and the system parameters params as inputs, the sub-algorithm is executed by the signer to generate a blind signature σ′. -
Unblind. Taking a blind signature σ′, the previously generated random string r and the system parameters params as inputs, the sub-algorithm is executed by the user to generate an unblinded signature σ.
Verify: Taking the system parameters params, a signer's identity ID, a signer's public key PKID, a message m and a signature σ as inputs, this algorithm is executed by the verifier to verify the legality of σ. If σ is legal, 1 will be outputted; otherwise, 0 will be outputted.
Security Model for CLBS Scheme
There are two kinds of adversaries in the CLBS scheme, i.e. the Type I adversary A1 and the Type II adversary A2.A1 could replace user's public keys with some value he chooses, but he cannot get the master key. A2 represents a malicious KGC, who cannot replace users' public keys but he could use the master key to generate users' partial private keys. The type adversaries in CLBS could be divided into normal adversary, strong adversary, and super adversary according to their attacks power (Huang et al. 2007Huang X, Mu Y, Susilo W, Wong D and Wu W. 2007. Certificateless signature revisited. 12th Australasian Conference Information Security and Privacy, 308 p.). In the security analysis of the proposed CLBS scheme, we just need to consider two strongest types of adversaries, i.e. the super Type I adversary and the super Type II adversary. The abilities of an adversary A ∈ {A1, A2} are formally modeled by queries issued by adversaries.
ExtractPartialPrivateKey(ID): The adversary A could get the partial private key DID through the query.
ExtractSecretValue(ID): The adversary A could get the secret value xID through the query.
RequestPublicKey(ID): The adversary A could get the public key PKID through the query. ReplacePublicKey(ID,  ): The adversary A could replace the public key PKID with a new public key
): The adversary A could replace the public key PKID with a new public key  through the query.
through the query.
SuperSign(ID, m): The adversary A could get a signature σ through the query such that 1 ← Verify (params, ID,  , m, σ), where
, m, σ), where  is the current public key and it may be replaced by A.
is the current public key and it may be replaced by A.
We consider the following games against the super Type I and the super Type II adversaries.
Game 1: The first game is performed between a challenger C and a super Type I adversary A1 for a CLBS scheme as follows.
Initialization. C runs Setup algorithm and generates a master secret key mk, public system parameters params. C keeps mk secret and then gives params to A1.
Queries. A1 can adaptively issue the ExtractPartialPrivateKey, ExtractSecretValue, RequestPublicKey, ReplacePublicKey, and SuperSign queries to C.
Output. Eventually, A1outputs (IDt, mt, σt). A1 wins the game if
-
ExtractPartialPrivateKey(IDt) and SuperSign (IDt, mt) queries have never been queried.
-
1 ← Verify(params, IDt,
 , m, σ), where
, m, σ), where  which may be replaced by A1 is the current public key of IDt
which may be replaced by A1 is the current public key of IDt
Game 2: The second game is performed between a challenger C and a super Type II adversary A2 for a CLBS scheme as follows:
Initialization. C runs Setup algorithm and generates a master secret key mk, public system parameters params. C gives mk and params to A2.
Queries. A2 can adaptively issue the ExtractPartialPrivateKey, ExtractSecretValue, RequestPublicKey, and SuperSign queries to C.
Output. Eventually, A2outputs (IDt, mt, σt). A1 wins the game if
-
ExtractSecretValue(IDt) and SuperSign (IDt, mt) queries have never been queried.
-
1 ← Verify(params, IDt,
 , m, σ), where
, m, σ), where  is the original public key of IDt
is the original public key of IDt
Definition 1 (Blindness) (Zhang et al. 2011Zhang L, Zhang F, Qin B and Liu S. 2011. Provably-secure electronic cash based on certificateless partially-blind signatures. Electron Commer R A 10: 545-552.). Suppose two honest users U0 and U1 engage in the blind signature issuing protocol with a probabilistic polynomial-time adversary A on two messages mb and m1−b, and output two signatures σ and σ′ respectively, where b ∈ {0; 1} is a random bit chosen uniformly. At last, (m0, m1, σb, σ1− b) are sent to A and then A outputs b′ ∈ {0, 1}. We call a signature scheme is blind if the inequation |Pr[b = b′] − 1/2| < n–c holds for all such adversaries A, any constant c, and sufficiently large n.
Definition 2. We say that a certicateless blind signature scheme is secure against the super Type I adversary if for any polynomially bounded super Type I adversary A1,  is negligible, where
is negligible, where  denote the success probability that A wins in Game 1.
denote the success probability that A wins in Game 1.
Definition 3. We say that a certicateless blind signature scheme is secure against the super Type II adversary if for any polynomially bounded super Type II adversary A2,  is negligible, where
is negligible, where  denote the success probability that A1 wins in the Game 2.
denote the success probability that A1 wins in the Game 2.
We say a certificateless blind signature scheme is secure if it is blind and secure against two types of adversaries.
THE PROPOSED CLBS SCHEME
Based on He et al. work (He et al. 2011aHe D, Chen J and Hu J. 2011a. An ID-based proxy signature schemes without bilinear pairings. Ann Telecommun 66: 657-662., bHe D, Chen Y, Chen J and Zhang R. 2011b. An efficient identity-based blind signature scheme without bilinear pairings. Comput Electr Eng 37: 444-450.), we propose a new CLBS scheme without bilinear pairing. The proposed scheme consists of six algorithms, i.e. Setup, PartialPrivateKeyExtract, SetSecretValue, SetPublicKey, Sign and Verify. The details of these algorithms are described as follows:
Setup: Given a security parameters k, KGC does the following steps to generate the system parameters and the mast key.
-
KGC chooses a k-bit prime p, generates an elliptic curve E(Fp) over finite feld Fp. KGC chooses a group G) with order n over E(Fp) and chooses a generator P) of the group G).
-
KGC chooses a random
 as the master mk and computes public key Ppub = sP.
as the master mk and computes public key Ppub = sP. -
KGC chooses three secure hash functions
 ,
,  and
and  .
. -
KGC publishes the system parameter params = {p, n, E(Fp), G, P, Ppub, H1, H2, H3} and keeps the master key s secretly.
PartialPrivateKeyExtract: Given the system parameter params, the master key mk, and a user's identity ID, KGC generates a random number  , computes RID = rIDP, hID = H1(ID, RID) and sID = rID + hIDs mod n. Then KGC returns the partial private key DID = (sID, RID) to the user.
, computes RID = rIDP, hID = H1(ID, RID) and sID = rID + hIDs mod n. Then KGC returns the partial private key DID = (sID, RID) to the user.
SetSecretValue: Given the system parameter params, the user with identity ID generates a random number  , computes PID = xIDP and sets xID as his secret value.
, computes PID = xIDP and sets xID as his secret value.
SetPublicKey: Given the system parameter params and the user's secret value xID, the user computes his public key PID = xIDP.
Sign: Given a message m, the following three sub-algorithms are executed to generate a legal signature. First of all, the signer generates a random number  , computes
, computes  and sends
and sends  and RID to the user.
and RID to the user.
-
Blind: Upon receiving the message
 and RID, the user generates three random numbers α, β,
and RID, the user generates three random numbers α, β,  , computes h = H2(m, R, ID, RID, PKID, Ppub), hID = H1(ID, RID),
, computes h = H2(m, R, ID, RID, PKID, Ppub), hID = H1(ID, RID),  ,
,  and
and  . At last, the user sends
. At last, the user sends  to the signer.
to the signer. -
BSign: Upon receiving the message
 , the signer computes
, the signer computes  and
and  . At last, the signer sends
. At last, the signer sends  to the user.
to the user. -
Unblind: Upon receiving the message
 , the user computes
, the user computes  and outputs the signature σ = (RID, R, z).
and outputs the signature σ = (RID, R, z).
Verify: To verify the legality of the signature σ = (RID, R, z) for message m and the signer with identity ID, the verifier computes h = H2(m, R, ID, RID, PKID, Ppub), hID = H1(ID, RID) and  . The verifier checks whether zP and
. The verifier checks whether zP and  are equal. If they are equal, 1 is returned; otherwise, 0 is returned.
are equal. If they are equal, 1 is returned; otherwise, 0 is returned.
SECURITY ANALYSIS
In this section, we will analyze the security of the proposed CLBS scheme. We will show the proposed scheme is provably secure in the random oracle model (Bellare and Rogaway 1993Bellare M and Rogaway P. 1993. Random oracles are practical: a paradigm for designing efficient protocols. ACM CCCS'93, 62 p.). The following theorems are proposed for the security.
Theorem 1. The proposed CLBS scheme is blind.
Proof. Let (RID, R, z) be one of the two signatures given to the adversary A. Let (RID,  ,
,  ,
,  ) be the message transmitted between the user and the signer. We just need to show that there are three random factors (α, β, γ) that could map (RID,
) be the message transmitted between the user and the signer. We just need to show that there are three random factors (α, β, γ) that could map (RID,  ,
,  ,
,  ) to (RID, R, z). From the description of the proposed CLBS scheme, we could get that
) to (RID, R, z). From the description of the proposed CLBS scheme, we could get that
Through equations (2) and (3), we could get that  and
and  . With the two above equations and equation (1), we could get that only a unique element
. With the two above equations and equation (1), we could get that only a unique element  exists. Then we could get β and γ also exist uniquely since
exists. Then we could get β and γ also exist uniquely since  and
and  .
.
Then, we could conclude that three random factors (α, β, γ) always exist between (RID, R, z) and (RID,  ,
,  ,
,  ). Therefore, A outputs a correct value b′ with probability exactly 1/2 and the proposed CLBS scheme is blind.
). Therefore, A outputs a correct value b′ with probability exactly 1/2 and the proposed CLBS scheme is blind.
Theorem 2. The proposed CLBS scheme is secure against the super Type I adversary in random oracle model if the DLP is hard.
Proof. Suppose there is a super Type I adversary A1 has non-negligible εadvantage in attacking the proposed CLBS scheme. We will show that an algorithm C could solve the DLP running A1 as a subroutine.
Given a DLP instance Q = αPfor randomly chosen  , C picks an identity ID* at random as the challenged ID, sets Ppub= Q, chooses three secure functions and gives system parameters to A1. C answers A1's queries as follows.
, C picks an identity ID* at random as the challenged ID, sets Ppub= Q, chooses three secure functions and gives system parameters to A1. C answers A1's queries as follows.
-
H1 query: A1 maintains a list
 of tuples < ID, RID, hID >. Upon receiving a query on a message ID, RID, C returns hID to A1 if
of tuples < ID, RID, hID >. Upon receiving a query on a message ID, RID, C returns hID to A1 if  contains a tuple < ID, RID, hID >, otherwise, C picks a random number hID ∈ Z*n, adds < ID, RID, hID > to
contains a tuple < ID, RID, hID >, otherwise, C picks a random number hID ∈ Z*n, adds < ID, RID, hID > to  and returns hID to A1.
and returns hID to A1. -
H2 query: A1 maintains a list
 of tuples < m, R, ID, RID, PKID, Ppub, h >. Upon receiving a query on a message < m, R, ID, RID, PKID, Ppub>, C returns h to A1 if
of tuples < m, R, ID, RID, PKID, Ppub, h >. Upon receiving a query on a message < m, R, ID, RID, PKID, Ppub>, C returns h to A1 if  contains a tuple < m, R, ID, RID, PKID, Ppub, h >; otherwise, C picks a random number
contains a tuple < m, R, ID, RID, PKID, Ppub, h >; otherwise, C picks a random number  , adds < m, R, ID, RID, PKID, Ppub, h > to
, adds < m, R, ID, RID, PKID, Ppub, h > to  and returns h to A1.
and returns h to A1. -
H3 query: A1 maintains a list
 of tuples < ID, RID, PKID, Ppub, h >. Upon receiving a query on a message < ID, RID, PKID, Ppub>, C returns h to A1 if
of tuples < ID, RID, PKID, Ppub, h >. Upon receiving a query on a message < ID, RID, PKID, Ppub>, C returns h to A1 if  contains a tuple < ID, RID, PKID, Ppub, h >, otherwise, C picks a random number h∈ Z*n, adds < ID, RID, PKID, Ppub, h >to
contains a tuple < ID, RID, PKID, Ppub, h >, otherwise, C picks a random number h∈ Z*n, adds < ID, RID, PKID, Ppub, h >to  and returns h to A1.
and returns h to A1. -
ExtractPartialPrivateKey(ID) query. Upon receiving a query with the user's identity ID, C answers the query as follows.
1)If ID ≠ ID*, C generates two random numbers aID,
 , sets RID ← aIDP − bIDPpub, hID = H1(ID, RID) bID and sID← aID. C adds < ID, RID, hID > and < ID, sID, RID to
, sets RID ← aIDP − bIDPpub, hID = H1(ID, RID) bID and sID← aID. C adds < ID, RID, hID > and < ID, sID, RID to  > and
> and  separately. C returns < sID, RID > to A1.
separately. C returns < sID, RID > to A1.2)Otherwise, C generates two random numbers aID,
 , sets RID ← aIDP, hID = H1(ID, RID) ← bID and sID← ⊥. C adds < ID, RID, hID> and < ID, sID, RID to
, sets RID ← aIDP, hID = H1(ID, RID) ← bID and sID← ⊥. C adds < ID, RID, hID> and < ID, sID, RID to  > and
> and  separately. C returns < sID, RID to A1.
separately. C returns < sID, RID to A1. -
RequestPublicKey(ID) query. Upon receiving a query with the user's identity ID, C returns PKID to A1.
-
ExtractSecretValue(ID) query. Upon receiving a query with the user's identity ID, C picks a random number
 , computes PKID = xIDP, adds < ID, xID, PKID> to
, computes PKID = xIDP, adds < ID, xID, PKID> to  and returns xID to A1.
and returns xID to A1. -
ReplacePublicKey(ID,
 ) query. Upon receiving a query with the message (ID;
) query. Upon receiving a query with the message (ID;  ), C sets
), C sets  , and
, and  if the list
if the list  contains < ID, xID, PKID >, otherwise, C makes a ExtractSecretV alue query with ID, sets
contains < ID, xID, PKID >, otherwise, C makes a ExtractSecretV alue query with ID, sets  , and
, and  .
. -
SuperSign(ID, m) query. Upon receiving a query with the message (ID, m), Clooks up
 and
and  for the tuples< ID, sID, RID > and < ID, xID, PKID > and performs as follows:
for the tuples< ID, sID, RID > and < ID, xID, PKID > and performs as follows:1)If xID ≠ ⊥, then C performs according to the description of the scheme, and returns the generated (RID, R, z) to A1.
2)Otherwise, C generates two random a;
 , sets z ← a, H2(m, R, ID, RID, PKID, Ppub) ← b,
, sets z ← a, H2(m, R, ID, RID, PKID, Ppub) ← b,  , where
, where  . C returns σ = (RID, R, s) to A1 and adds < m, R, PKID, RID, Ppub, b > to
. C returns σ = (RID, R, s) to A1 and adds < m, R, PKID, RID, Ppub, b > to  .
.
Eventually, A1 outputs a valid signature (ID, mt, σt), where  . If IDt ≠ ID*, C stops the simulation; otherwise, C finds < IDt,
. If IDt ≠ ID*, C stops the simulation; otherwise, C finds < IDt,  ,
,  > and < IDt,
> and < IDt,  ,
,  > in
> in  and
and  respectively. From the forgery lemma (David and Jacque 2000David P and Jacque S. 2000. Security arguments for digital signatures and blind signatures. J Cryptol 13: 361-396.), we know that A1 could output another legal signature
respectively. From the forgery lemma (David and Jacque 2000David P and Jacque S. 2000. Security arguments for digital signatures and blind signatures. J Cryptol 13: 361-396.), we know that A1 could output another legal signature  if the same random number replayed but with different choice of the random oracle H2.
if the same random number replayed but with different choice of the random oracle H2.
The following equation holds because the signature is valid
andLet l,  ,
,  and α denote discrete logarithms of R;
and α denote discrete logarithms of R;  ,
,  and Ppub respectively, i.e. R = lP,
and Ppub respectively, i.e. R = lP,  ,
,  and Ppub = P. Then we could get the following two equations.
and Ppub = P. Then we could get the following two equations.
Because only l and α are unknown to C in the above two equations, he could solve those equations and outputs α as the solution of the DLP. Since ID* is randomly chosen, then we have  , where
, where  is the number of H1 query A1 has made. C could solve the DLP with a non-negligible probability
is the number of H1 query A1 has made. C could solve the DLP with a non-negligible probability  . This contradicts the hardness of the DLP. Therefore, the proposed scheme is secure against the super Type I adversary.
. This contradicts the hardness of the DLP. Therefore, the proposed scheme is secure against the super Type I adversary.
Theorem 3. The proposed CLBS scheme is secure against the super Type II adversary in random oracle model if the DLP is hard.
Proof. Suppose there is a super Type II adversary A2 has non-negligible advantage ε in attacking the proposed CLBS scheme. We will show that there is an algorithm C could solve the DLP running A2 as a subroutine.
Given a DLP instance Q = αPfor randomly chosen  , C picks an identity ID* at random as the challenged ID, chooses a random number
, C picks an identity ID* at random as the challenged ID, chooses a random number  , sets Ppub = sP, and chooses three secure functions. C give the master key s and system parameters to A2. C answer H1 query, H2 query, H3 query, ExtractPartialPrivateKeyquery, ReplacePublicKey query and SuperSign(ID, m) query like he does in the above theorem. C simulates other oracle queries of A2 as follows:
, sets Ppub = sP, and chooses three secure functions. C give the master key s and system parameters to A2. C answer H1 query, H2 query, H3 query, ExtractPartialPrivateKeyquery, ReplacePublicKey query and SuperSign(ID, m) query like he does in the above theorem. C simulates other oracle queries of A2 as follows:
-
ExtractPartialPrivateKey(ID) query. Upon receiving a query with the user's identity ID, C generates a random number
 , computes RID = rIDP, hID = H1(ID, RID) and sID = rID+ hIDs mod n. C adds < ID, RID, hID> and < ID, sID, RID > to
, computes RID = rIDP, hID = H1(ID, RID) and sID = rID+ hIDs mod n. C adds < ID, RID, hID> and < ID, sID, RID > to  and
and  separately. Then, C returns < sID, RID > to A2.
separately. Then, C returns < sID, RID > to A2. -
ExtractSecretValue(ID) query. Upon receiving a query with the user's identity ID, C does as follows. If ID ≠ ID*, C picks a random number
 and computes PKID = xIDP, returns xID to A2 and adds < ID, xID, PKID > to
and computes PKID = xIDP, returns xID to A2 and adds < ID, xID, PKID > to  ; otherwise, C sets PKID = Q, adds < ID, ⊥, PKID > to
; otherwise, C sets PKID = Q, adds < ID, ⊥, PKID > to  .
.
Eventually, A2 outputs a valid signature (ID, mt, σt), where  . If IDt ≠ ID*, C stops the simulation; otherwise, C finds < IDt,
. If IDt ≠ ID*, C stops the simulation; otherwise, C finds < IDt,  ,
,  > and IDt,
> and IDt,  ,
,  in
in  and
and  respectively. The public key
respectively. The public key  is the original pub key is IDt. From the forgery lemma (David and Jacque 2000David P and Jacque S. 2000. Security arguments for digital signatures and blind signatures. J Cryptol 13: 361-396.), we know that A2 could output another legal signature
is the original pub key is IDt. From the forgery lemma (David and Jacque 2000David P and Jacque S. 2000. Security arguments for digital signatures and blind signatures. J Cryptol 13: 361-396.), we know that A2 could output another legal signature  if the same random number replayed but with different choice of the random oracle H2. The following equation holds because the signature is valid.
if the same random number replayed but with different choice of the random oracle H2. The following equation holds because the signature is valid.
Let l, α,  and s denote discrete logarithms of R,
and s denote discrete logarithms of R,  ,
,  and Ppub respectively, i.e. R = lP,
and Ppub respectively, i.e. R = lP,  ,
,  and Ppub = sP. Then we
and Ppub = sP. Then we
Because only l and α are unknown to C in the above two equations, he could solve those equations and outputs as the solution of the DLP. Since ID* is randomly chosen, then we have  , where
, where  is the number of H1 query A2 has made. C could solve the DLP with a non-negligible probability
is the number of H1 query A2 has made. C could solve the DLP with a non-negligible probability  . This contradicts the hardness of the DLP. Therefore, the proposed scheme is secure against the super Type II adversary.
. This contradicts the hardness of the DLP. Therefore, the proposed scheme is secure against the super Type II adversary.
PERFORMANCE ANALYSES
In this section, we will compare the efficiency of the proposed CLBS scheme with the three latest CLBS schemes, i.e. Sun et al.'s CLBS scheme (Sun and Wen 2009Sun S and Wen Q. 2009. Novel efficient certificateless blind signature schemes. International Symposium on Computer Network and Multimedia Technology, 1 p.), Zhang et al.'s scheme (Zhang and Gao 2009) and Zhang et al.'s CLBS scheme (Zhang et al. 2011Zhang L, Zhang F, Qin B and Liu S. 2011. Provably-secure electronic cash based on certificateless partially-blind signatures. Electron Commer R A 10: 545-552.).
To achieve the security level of 1024 bits RSA, bilinear pairing-based CLBS scheme and ECC-based CLBS scheme, we have to use the Tate pairing defined over a supersingular elliptic curve on a finite field Fq and a secure elliptic curve on a finite field Fp separately, where the length of q and p are 512 bits and 160 bits respectively. We also assume the output of the hash function is 160 bits. Some notations are defined as follows.
-
e: a bilinear pairing operation;
-
E: a modular exponentiation operation;
-
M: an ECC-based scale multiplication operation;
-
Mpair: a bilinear pairing-based scale multiplication operation;
It is well known that the computational cost of a hash function operation could be ignored when it is compared with that of a bilinear pairing operation, a modular exponentiation operation, a ECC-based scale multiplication operation or a bilinear pairing-based scale multiplication operation. Therefore, we just need to counter the bilinear pairing operation, the modular exponentiation operation, the ECC-based scale multiplication operation and the bilinear pairing-based scale multiplication operation in performance comparisons. The comparisons are listed in Table I.
Theoretical analyses (Chen et al. 2007Chen L, Cheng Z and Smart N. 2007. Identity-based key agreement protocols from pairings. Int J Inf Secur 6: 213-241.) and experimental results (Cao and Kou 2010Cao X and Kou W. 2010. A pairing-free identity-based authenticated key agreement scheme with minimal message exchanges. Inform Sciences 180: 2895-2903.) (He et al. 2011aHe D, Chen J and Hu J. 2011a. An ID-based proxy signature schemes without bilinear pairings. Ann Telecommun 66: 657-662., 2012bHe D, Chen J and Hu J. 2012b. n ID-based client authentication with key agreement protocol for mobile client-server environment on ECC with provable security, Inform Fusion 13: 223-230.) demonstrate that the computation costs of a bilinear pairing operation, a modular exponentiation operation and a bilinear pairing-based scale multiplication operation are about 19, 3 and 3 times of that of a ECC-based scale multiplication operation. Therefore, we could get that the computational cost of the Sign algorithm in the proposed scheme is 60%, 54.55% and 10.71% of that in Sun et al.'s CLBS scheme (Sun and Wen 2009Sun S and Wen Q. 2009. Novel efficient certificateless blind signature schemes. International Symposium on Computer Network and Multimedia Technology, 1 p.), Zhang et al.'s CLBS scheme (Zhang and Gao 2009) and Zhang et al.'s CLBS scheme (Zhang et al. 2011Zhang L, Zhang F, Qin B and Liu S. 2011. Provably-secure electronic cash based on certificateless partially-blind signatures. Electron Commer R A 10: 545-552.) separately. The computational cost of the Verify algorithm in the proposed scheme is 16%, 16%, 6.35% of that in Sun et al.'s CLBS scheme (Sun and Wen 2009Sun S and Wen Q. 2009. Novel efficient certificateless blind signature schemes. International Symposium on Computer Network and Multimedia Technology, 1 p.), Zhang et al.'s CLBS scheme (Zhang and Gao 2009) and Zhang et al.'s CLBS scheme (Zhang et al. 2011Zhang L, Zhang F, Qin B and Liu S. 2011. Provably-secure electronic cash based on certificateless partially-blind signatures. Electron Commer R A 10: 545-552.) separately. Besides, the signature size in the proposed scheme is 39.06%, 39.06% and 67.57% of that in Sun et al.'s CLBS scheme (Sun and Wen 2009Sun S and Wen Q. 2009. Novel efficient certificateless blind signature schemes. International Symposium on Computer Network and Multimedia Technology, 1 p.), Zhang and Gao's CLBS scheme (Zhang and Gao 2009) and Zhang et al.'s CLBS scheme (Zhang et al. 2011Zhang L, Zhang F, Qin B and Liu S. 2011. Provably-secure electronic cash based on certificateless partially-blind signatures. Electron Commer R A 10: 545-552.) separately. Therefore, the proposed CLBS scheme has better performance than those previous CLBS schemes.
CONCLUSIONS
Recently, the certicicateless public key cryptography without bilinear pairing operation attracted wide attention since such schemes have better performance than traditional ones. In this paper, we propose the first CLBS scheme without bilinear pairing operation. Performance analyses demonstrates that the proposed scheme has much better performance than previous CLBS schemes. We also show that the proposed scheme is provably secure against both of two types of adversaries in the random oracle. Therefore, the proposed scheme is more suitable for practical applications.
The authors thank Dr. Alexander Kellner and the anonymous reviewers for their valuable comments. This research was supported by the Application Foundation Research Project of Yunnan Science and Technology Department (No. 2011FZ168), the Key Scientific Research Projects of Yunnan Education Department (No. ZD201109) and the National Natural Science Foundation of China (Nos. 61202447 and 61201180).
REFERENCES
- Al-Riyami S and Paterson K. 2003. Certificateless public key cryptography. Proceedings of ASIACRYPT03, 452 p.
- Bellare M and Rogaway P. 1993. Random oracles are practical: a paradigm for designing efficient protocols. ACM CCCS'93, 62 p.
- Cao X and Kou W. 2010. A pairing-free identity-based authenticated key agreement scheme with minimal message exchanges. Inform Sciences 180: 2895-2903.
- Chaum D. 1983. Blind signatures for untraceable payments. Proc CRYPTO 82,199 p.
- Chen L, Cheng Z and Smart N. 2007. Identity-based key agreement protocols from pairings. Int J Inf Secur 6: 213-241.
- David P and Jacque S. 2000. Security arguments for digital signatures and blind signatures. J Cryptol 13: 361-396.
- Gong P and Li P. 2012. Li, Further improvement of a certificateless signature scheme without pairing. Int J Commun Syst. DOI: 10.1002/dac.2457.
» https://doi.org/10.1002/dac.2457 - Hankerson D, Menezes A and Vanstone S. 2004. Guide to elliptic curve cryptography. New York: Springer-Verlag, 220 p.
- He D, Chen J and Hu J. 2011a. An ID-based proxy signature schemes without bilinear pairings. Ann Telecommun 66: 657-662.
- He D, Chen J and Hu J. 2012a. A pairing-free certificateless authenticated key agreement protocol. Int J Commun Syst 25: 221-230.
- He D, Chen J and Hu J. 2012b. n ID-based client authentication with key agreement protocol for mobile client-server environment on ECC with provable security, Inform Fusion 13: 223-230.
- He D, Chen J and Zhang R. 2012c. An efficient and provably-secure certificateless signature scheme without bilinear pairings. Int J Commun Syst 25: 1432-1442.
- He D, Chen Y and Chen J. 2013a. A provably secure certificateless proxy signature scheme without pairings. Math Comput Model Dyn 57: 2510-2518.
- He D, Chen Y, Chen J and Zhang R. 2011b. An efficient identity-based blind signature scheme without bilinear pairings. Comput Electr Eng 37: 444-450.
- He D, Chen Y, Chen J and Zhang R. 2011c. A new two-round certificateless authenticated key agreement protocol without bilinear pairings. Math Comp Model Dyn 54: 3143-3152.
- He D, Padhye S and Chen J. 2012d. An efficient certificateless two-party authenticated key agreement protocol. Comput Math Appl 64: 1432-1442.
- He D, Huang B and Chen J. 2013b. A new certificateless short signature scheme, IET Information Security 7: 113-117.
- Huang X, Mu Y, Susilo W, Wong D and Wu W. 2007. Certificateless signature revisited. 12th Australasian Conference Information Security and Privacy, 308 p.
- Koblitz N. 1987. Elliptic curve cryptosystem. Math Comput 48: 203-209.
- Shamir A. 1984. Identity-based cryptosystems and signature schemes. Proc CRYPTO 84, 47 p.
- Sun S and Wen Q. 2009. Novel efficient certificateless blind signature schemes. International Symposium on Computer Network and Multimedia Technology, 1 p.
- Sun Y and Zhang F. 2010. Secure certificateless encryption with short ciphertext. Chinese J Electron 19: 313-318.
- Tian M and Huang L. 2012. Cryptanalysis of a certificateless signature scheme without pairings. DOI: 10.1002/dac.2310.
» https://doi.org/10.1002/dac.2310 - Tsai J, Lo N and Wu T. 2012. Weaknesses and improvements of an efficient certificateless signature scheme without using bilinear pairings. DOI: 10.1002/dac.2388.
» https://doi.org/10.1002/dac.2388 - Wang C and Lu R. 2008. A certificateless restrictive partially blind signature scheme. 2008 International Conference on Intelligent Information Hiding and Multimedia Signal Processing, 279 p.
- Yang G and Tan C. 2011. Certificateless public key encryption: A new generic construction and two pairing-free schemes. Theor Comput Sci 412: 662-674.
- Yang X, Liang Z and Wei P. 2009. A provably secure certificateless blind signature scheme. 5th International Conference on Information Assurance and Security, 643 p.
- Zhang and Gao S. 2009. Efficient provable certificateless blind signature scheme. International Conference on Networking, Sensing and Control, 292 p.
- Zhang L and Zhang F. 2008. Certificateless signature and blind signature. J Electron 25: 629-635.
- Zhang L, Zhang F, Qin B and Liu S. 2011. Provably-secure electronic cash based on certificateless partially-blind signatures. Electron Commer R A 10: 545-552.
Publication Dates
-
Publication in this collection
June 2014
History
-
Received
27 May 2013 -
Accepted
10 Dec 2013