ABSTRACT
We discuss two changes of paradigms that occurred in science along the XXth century: the end of the mechanist determinism, and the end of the apparent incompatibility between biology, where emergence of order is law, and physics, postulating a progressive loss of order in natural systems. We recognize today that three mechanisms play a major role in the building of order: the nonlinear nature of most evolution laws, along with distance to equilibrium, and with the new paradigm, that emerged in the last forty years, as we recognize that networks present collective order properties not found in the individual nodes. We also address the result presented by Blumenfeld (L.A. Blumenfeld, Problems of Biological Physics, Springer, Berlin, 1981) showing that entropy decreases resulting from building one of the most complex biological structures, the human being, are small and may be trivially compensated for compliance with thermodynamics. Life is made at the expense of very low thermodynamic cost, so thermodynamics does not pose major restrictions to the emergence of life. Besides, entropy does not capture our idea of order in biological systems. The above questions show that science is not free of confl icts and backlashes, often resulting from excessive extrapolations.
Key words:
chaos; dynamical systems; entropy; evolution of Science; pattern formation; theoretical biology
RESUMO
Este trabalho discute duas mudanças de paradigma ocorridas na ciência ao longo do século XX: fi m do determinismo mecanicista, e fi m da aparente incompatibilidade entre a biologia, onde a emergência de ordem é lei, e a física, postulando a progressiva desordenação dos sistemas naturais. Reconhecemos hoje que três mecanismos desempenham papel primordial na construção de ordem: a condição necessária de não linearidade, presente em muitas das leis de evolução, juntamente com distância do equilíbrio, e com o novo paradigma que emergiu nos últimos quarenta anos, de que redes apresentam propriedade coletivas de ordem não encontradas nos nós individuais. Discute-se também o resultado apresentado por Blumenfeld (L.A. Blumenfeld, Problems of Biological Physics, Springer, Berlin, 1981), mostrando que os decréscimos de entropia resultantes da formação de uma das mais complexas estruturas biológicas - o ser humano - são pequenos, podendo ser trivialmente compensados por processos químicos e físicos associados, de modo a satisfazer as leis da termodinâmica. A vida se faz ao preço de baixo custo termodinâmico, de modo que as leis da termodinâmica não representam, de fato, maior restrição à emergência de vida e de ordem em sistemas fora do equilíbrio. A entropia não captura a noção que temos de ordem nos sistemas biológicos. As questões acima mostram que a ciência não se está livre de confl itos e de recuos, muitas vezes resultantes de extrapolações excessivas.
Palavras-chave:
caos; sistemas dinâmicos; entropia; evolução da Ciência; formação de padrões; biologia teórica
1- INTRODUCTION
Among the advances and changes brought by science throughout the XXth century, two are, in our point of view, of particular importance and addressed in this work: on one hand, the end of the mechanist determinism, originated from the extrapolation of the achievements of the Newtonian mechanics at the XVIIth and XVIIIth centuries, and on the other, the end of the apparent incompatibility between biology, where the emergence of ordered structures is a law, and physics, postulating, since the XIXth century a progressive loss of order in natural systems, quantified by an irreversible increase of entropy.
We discuss how the diffusion of the determinism principles occurred in the Western civilization, how the extrapolation of these principles beyond the limits of the movement of bodies progressively took place, some confl icts and consequences of that extrapolation, and the new vision we currently have of evolution. We recognize today that the future can be changed and we understand that the onset of both order, with unpredictable features, namely,
the onset of the fully new and of the aperiodic behavior, unpredictable beyond a finite limit of time, with features of what we call today Chaos, are compatible with the laws governing the evolution of the natural systems; and we identify in the nonlinear nature of the evolution laws, a mechanism commonly found in the evolution laws of natural systems, as a major driving property that prompts for shaping the future, and stays on the basis of both the self-organization, and of the chaotic evolution of systems. Order and chaos share the same origin. In addition, a new paradigm has emerged in the last forty years as we recognize that non equilibrium networks not too far from the chaotic behavior, and consisting of nodes sparsely connected, are a major source of emerging structures, with properties not deriving from those of the individual nodes. We call these networks as Complex Systems.
We also recognize that the laws of thermodynamics do not pose major restrictions to the onset of order in biological systems. In this sense, we address the problem of quantifying order in living matter, and discuss todays well known result showing that the building of living matter is not made at the expense of signifi cant decreases of entropy (Blumenfeld 1981BLUMENFELD LA. 1981. Problems of Biological Physics. Springer, Berlin, 224 p.). Living matter does not present an "anti-entropic" tendency, what leads to the conclusion that entropy does not capture the intuitive idea of order we have in living beings; and we do not have an alternative variable available for that. But the result also shows that entropy decreases occurring at the ordering of living systems can be easily compensated with associated physical and chemical processes in order to fulfi ll the overall restriction posed by thermodynamics. Biological systems self organize at a very low thermodynamic cost.
The two questions point to principles originated in science that we recognize today as false: the mechanist determinism and the apparent incompatibility between physics and biology. We then discuss the question that science is not free of confl icts, lines of thinking and backlashes, often resulting from excessive extrapolations.
2- FROM RENASCENCE TO THE XVIIIth CENTURY
Though existing before Renascence, the ideas about determinism spread in the Western civilization from that period, and were boosted by the outstanding achievements of the Rational Mechanics of the XV th and XVIth centuries. Its principle postulates that given the state of a system at a certain time, the whole future is uniquely defi ned as the past uniquely defi nes the present. Both the entire future and the entire past are contained in the present. Extrapolation of the principle beyond the domain of mechanics led to the idea that the future, also including men's future, is fully defined at the present and therefore cannot be changed. The principle collides with the Western civilization traditions that postulate man's freedom, and his ability to create the new.
Renascence was characterized by the exhaustion of the model of life proposed to the Western man, developed throughout the Middle Age with strong influence of the Church, and to a return to the principles that guided men in the classical Greek-Roman period. In parallel, the discovery of the Earth's roundness, confi rmation that the Sun is at the center of the Solar System, the discovery of the laws governing the dynamics of the Universe, the wealth brought by the New World, and the diffusion of the knowledge through the recently invented press gave man an unprecedented autonomy. Among the advances experienced by science we may cite Galileo's studies of the fall of bodies in the slippery slope. Galileo showed that the velocity attained by a body depends only on the height of the device and not on its slope. Galileo also showed that, in the opposite sense, a single height can be associated to each given velocity, defi ning a one to one relationship between velocity and height (Stengers 1989STENGERS I. 1989. Les affaires Galilée. In: Serres M (Ed), Eléments d'Histoire des Sciences, volume 1, chapter 9, p. 223-249. Bordas, Paris, France. ). For some authors, this fi nding inaugurates Mathematical Physics, or Rational Mechanics. Later, Kepler identifi ed the laws governing the planets motion around the Sun, which were subsequently generalized by Newton.
The decline of the Church's infl uence on the principles that guided the Western man left a room to be fi lled. Vargas Llosa (1995) cites the replacement of the Church's saints by new symbols with similar status, like algebra, geometry, astronomy, anatomy, poetry and logics, among others. Monuments left by the Renascence testify to this fact. By saints we refer to symbols that express man's need and search for endurance and transcendence.
Not surprisingly, in consequence of the autonomy acquired by the understanding of the laws of the Universe, and with the affl uence brought by the wealth from the New World, the baroque emerged in the Western culture, a rich period committed to a new formalism. The baroque is not limited to art, but also encompasses science. Major advances in mechanics occurred at that period, like the development of calculus with several variables, and the discovery of the laws governing wave motion, among others. The rigorous and elegant mathematical formalism of the rational mechanics became well established, both refl ecting and contributing to shape the culture of the period. Modern science experienced a golden age at the XVIIIth century, with dominance of the mechanics. In a more general way, the outstanding achievements of science strongly infl uenced the development of the Enlightenment and Rationalism, which endorse the use of mathematics as an essential tool to explain the truth.
In economy, mathematical modeling was boosted with the development of the theory of probabilities and of actuarial science, with contributions by De Moivre, Daniel and Nicolas Bernoulli, among others. Irreversible advances of the Western civilization occurred at that period with the Declaration of Human Rights and the recognition as legitimate of the demands for equal representation of the social classes in the chambers of political decisions, made by Sieyès in the fi rst years of the French Revolution. Ideas about liberalism, socialism and of social democracy are also from this period. Among the important thinkers of the Enlightenment we may cite the names of Descartes, Voltaire, Spinoza, Leibiniz, Adam Smith, Jean Jacques Rousseau, Benjamin Franklin in the United States and Marquis of Pombal with the modernization undertaken in Portugal.
The works of Maupertuis (1698-1759) (cited by Moreira 1999MOREIRA IC. 1999. Maupertuis (1698-1759) e o princípio da mínima ação. Rev Bras Ensino de Física 21(1): 172-186. ) in the domain of mechanics and beyond exemplify the major influence exerted by science on the Western culture of the XVIIIth century. One of the first to introduce Newton's ideas in France, Maupertuis led a program that contributed to confi rm Newton's assertions about the oblate spheroid shape of the Earth, with an equatorial diameter bigger than the polar one. Maupertuis' position eventually proved to be true, on contrary to what was advocated by the French Cartesianism (Moreira 1999). Upon addressing the problem of light refraction, Maupertuis proposed a principle of minimum action, according to which light chooses a path where neither the length of the path nor the elapsed time taken to travel between two points located in different mediums is minimum. Rather, nature minimizes the "action" defined as the sum of the products of distances covered times the corresponding velocities.
Maupertuis subsequently extended the minimum action principle to the dynamics of particles in movement, stating that all changes in the universe proceed to minimize the sum of the product of the bodies (masses) times the length of the path covered and the associated velocity. Lack of precise specifi cation of the intervals to which the principle should be applied and the fact it holds only when energy is conserved, as found by Euler, prevented Maupertuis' action principle of leading to new signifi cant results in the framework of mechanics (Moreira 1999MOREIRA IC. 1999. Maupertuis (1698-1759) e o princípio da mínima ação. Rev Bras Ensino de Física 21(1): 172-186. ). However, his efforts to introduce an unifying minimization or maximization principle for the whole mechanics deserve mention. Proceeding with his extrapolations, Maupertuis proposed an arithmetic model for men's moral behavior and political action based on his minimum action principle where life pains and diffi culties are minimized and enjoyments are maximized. In the realm of biology, he proposed a theory of generation (i.e. reproduction) where living matter possessed a self-organizing "intelligence" that was analogous to the current concept of affi nity. By looking at the history of the scientifi c institutions and how relations between science and political power evolved we note that Maupertuis presents the vision of an ordered and hierarchical world that reassured the nobility (Moreira 1999).
At the end of the century, science attained political power, with Laplace being senator and minister of Napoleon. But, as Renascence pointed to the exhaustion of a model and to the end of an era, Enlightenment and Rationalism became exhausted at the end of the XVIIIth century. A symbol of this exhaustion are the French military defeats of the beginning of the XIXth century.
3- XIXth CENTURY AND BEGINNING OF THE XXth CENTURY
To the Enlightenment and the Rationalism raised in opposition the Romantic movement, born in Germany and England. At fi rst, Romanticism broke with the dominant formalism. In music, Beethoven gradually dropped the form so far used. Works like his sixth symphony praise nature, countryside life and simpleness, in contrast with the exuberance adopted by the baroque to portray the reality. But Beethoven's Romanticism is also characterized by the condemnation of the excesses of Rationalism, in particular of Napoleon's wars, as expressed in his ninth symphony. In Spain, Beethoven fi nds parallel in Goya, with his denounce of the horrors of the war, as portrayed for instance in the Massacre of the May 3rd, 1808 (see Fig. 1). His paintings also portray the impairment of the royalty to figure out the essential of the moment, praise Spanish countryside scenes and dive in the depths of the human soul as depicted in the black series. To our understanding, Romanticism played the important role of denouncing the excesses of the XVIIIth century, also including those of mechanics. The movement decayed through the XIXth century into alternative forms, and left room to the Modernism at the end of the century.
Francisco Goya (1746-1828): The Massacre of the May 3rd 1808 (Prado Museum, Madrid). The painting portrays the horrors of Napoleon's invasion of the Iberian Peninsula and denounces the excesses of the Rationalism, to which science was strongly committed.
In science, the century opened with the debacle of Napoleon's empire and with the decline of
Enlightenment and Rationalism was also the century of the decline of mechanics (Truesdell 1982aTRUESDELL C. 1982a. História da Mecânica Clássica - parte I, até 1800. J Braz Soc Mech Sci Eng 4(2): 3-17. , b). Right in 1806 Fourier enunciated the law governing heat conduction in solids, which does not derive from the laws of mechanics, breaking the dominance of the discipline and joining the Romantic movement in the criticism to principles established in the previous century. For some authors, this law inaugurates thermodynamics (Prigogine and Stengers 1979PRIGOGINE I AND STENGERS I. 1979. La Nouvelle Aliance. Gallimard, Paris, France. ).
The development of thermodynamics proceeded through the XIXth century, and at the second half of the century, electromagnetism prospered. However, thermodynamics brought along with the second law the notions of irreversibility, of the progressive disordering of an initial order and the concept of entropy, a new variable expected to quantify order. By doing so, thermodynamics introduced a new point of confl ict between science and evidences of the onset of order recurrently arising in nonequilibrium systems.
In the last years of the XIXth century and fi rst years of the XXth modern physics emerged with the discoveries of discontinuity of the matter and the formulation of the theories of relativity and quantum mechanics. Classical mechanics no longer applied to heat, to the too big, and to the too small. But it was up to Poincaré to further restrict the limits of the discipline by verifying, upon addressing the three-bodies problem in celestial mechanics, that orbits initially close follow intricate trajectories and eventually diverge. Poincaré then raised doubts about the ability of Newtonian mechanics to predict the future of systems whose evolution is governed by said laws. Indeed, Poincaré missed the computer - an essential instrument for our present understanding of nature - that would have allowed him to further investigate what he clearly devised, and that we call today by chaos.
Still in the XIXth century Liouville found the sufficient conditions for periodicity of the motion of Hamiltonian systems, by showing that if a constant of the entire system exists for the pair energy/momentum associated to each body, then periodicity is enforced (Nicolis 1995NICOLIS G. 1995. Introduction to Nonlinear Science. Cambridge, England. ). This is the case of the two-bodies problem, where we have a pair energy/momentum for each body and two constants of the whole system, namely its total energy and momentum. As no further constants exist for the motion of more than two bodies, periodicity is no longer enforced, though not forbidden. The reading of some authors suggests that the accomplishment of the theory was still in course (Truesdell 1982aTRUESDELL C. 1982a. História da Mecânica Clássica - parte I, até 1800. J Braz Soc Mech Sci Eng 4(2): 3-17. , b), and that periodicity would eventually be proved for all cases, what is actually not the case. Periodicity is not enforced for systems comprising more than two bodies, the most common situation found in celestial mechanics.
Reactions from thinkers against Rationalism and to the apparent incompatibility between physics and biology proceeded in the fi rst years of the XXth century. Bergson (1907BERGSON H. 1907. Evolution Créatrice. Presses Universitaires de France, Paris, France. , cited by Glansdorff and Prigogine 1971GLANSDORFF P AND PRIGOGINE I. 1971. Structure, Stabilité et Fluctuations. Masson, Paris, France.) postulated the impossibility of determinism by stating:
The more we devise the nature of time, the more we understand that duration means invention, creation of forms, building of what is absolutely new.
The ideas of the English philosopher H. Spencer are, in this aspect, similar to Bergson's ones. Spencer issues the fundamental principle of evolution in nature on grounds of the Instability of the Homogeneous (cited by Henderson 1917HENDERSON LJ. 1917. The Order of Nature. Harvard University Press, Cambridge, Massachussets, USA. and by Glansdorff and Prigogine 1971GLANSDORFF P AND PRIGOGINE I. 1971. Structure, Stabilité et Fluctuations. Masson, Paris, France.).
4- CHAOS
Objections to the ideas of the mechanist determinism progressively made room through the XXth century. The pioneer work of Poincaré on chaotic dynamics proceeded in the decade of 1920 with the works of Birkhoff (1927, cited by McMurann and Tattersall 1966), later with Cartwright and Littlewood (McMurann and Tattersall 1996) in the decades of 1940 and 1950, of Smale (1967SMALE S. 1967. Differentiable dynamical systems. Bull Amer Math Soc 73: 747. ) in the 1960's and with the Russian school of mathematicians, specially with Arnold (1963ARNOLD VI. 1963. Small denominators ii, proof of a theorem of A. N. Kolmogorov on the preservation of conditionallyperiodic motion under a small perturbation of the Hamiltonian. Russ Math Survey 18: 5. ), Kolmogorov and coworkers (MacKay and Meiss 1987, Ott 1993OTT E. 1993. Chaos in Dynamical Systems. Cambridge, England., Schuster 1995SCHUSTER HG. 1995. Deterministic Chaos. VCH, Weinheim. ). Landau (1944LANDAU EM. 1944. On the problem of turbulence. C R Acad Sci URSS 44: 311. ) assumed turbulence as a phenomena consisting of an infi nite number of oscillators, each one with undefi ned phase.
However, the existence of an infi nite number of oscillators (degrees of freedom) is not mandatory for the emergence of chaos. In 1963 Lorenz, addressed the evolution of a system with a three dimensional dynamics, known as the Lorenz model. The model was obtained upon simplifying the equations governing the evolution of the RayleighBénard system, which consists of a thin layer of fl uid heated by below. The rest state becomes unstable and is replaced by a structure of convection cells as the imposed temperature difference between the horizontal lower and upper boundaries exceeds a certain threshold. Lorenz noted that trajectories in the space of independent variables (phase space) present an aperiodic behavior, though converging to a limited subspace named attractor. In addition, trajectories initially close eventually divert away. Any error in identifying the initial condition prevents the evaluation of the system position in the phase space beyond a fi nite horizon of time. The aperiodic and deterministic character, but nevertheless unpredictable due to the sensitivity of the evolution to uncertainties in the initial condition, makes the Lorenz model chaotic (see Fig. 2).
About sixty years after the works of Poincaré, Kolmogorov (1954KOLMOGOROV AN. 1954. Preservation of conditionally periodic movments with small change in the Hamiltonian function. Dokl. Akad. Nauk SSSR, 98: 527. Reprinted in MacKay and Meiss, 1987, Hamiltonian Dynamical Systems: A Reprint Selection. Adam Hilger, Bristol. ), Arnold (1963ARNOLD VI. 1963. Small denominators ii, proof of a theorem of A. N. Kolmogorov on the preservation of conditionallyperiodic motion under a small perturbation of the Hamiltonian. Russ Math Survey 18: 5. ) and Moser (1967MOSER J. 1967. Convergent series expansions of quasiperiodic motions. Math Ann 169: 163. ) proved the result nowadays known as the KAM theorem, which shows that the motion in the phase space of systems governed by Hamiltonian mechanics is neither completely regular nor completely irregular, but that the type of trajectory is strongly affected by the chosen initial conditions. Thus, stable regular classical motion is the exception, on contrary to what was previously assumed (Schuster 1995SCHUSTER HG. 1995. Deterministic Chaos. VCH, Weinheim. ). It should be noted that the irregular motion described for instance by planets around a star results from the weak disturbance introduced by other celestial bodies, like natural satellites, or other planets in orbit with the same star. Irregularities in the orbit of a planet occur in long term time scales, often of order of a billion of years.
Chaotic Behavior of the Lorenz model: the fi gure shows the evolution of trajectories starting from two close initial conditions evolving to the system attractor (Lorenz butterfl y). The trajectories are aperiodic and diverge. Any uncertainty in the initial condition prevents predictions about the system state beyond a certain horizont.
In 1971 Ruelle and Takens justifi ed Lorenz' result by showing that the conjecture posed by Landau, requiring an infi nite number of degrees of freedom for the onset of chaos was actually
excessive and that systems with three degrees of freedom can already display chaos.
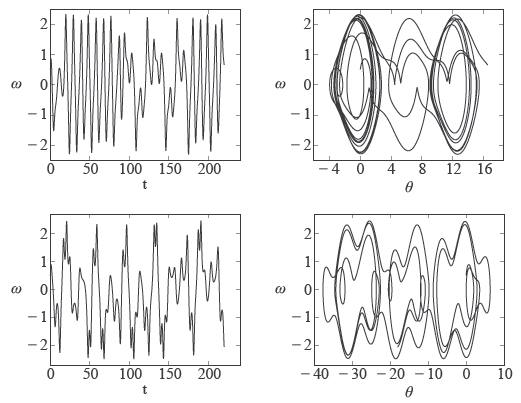
As another example of system showing aperiodic behavior with sensitivity to the initial conditions we may cite the pendulum. When left to oscillate freely the pendulum dynamics possesses two independent variables only, the angular displacement θ with respect to the vertical and the angular velocity θ=ω, not fulfi lling thus the necessary condition identifi ed by Ruelle and Takens, as above, for the existence of chaos. Introduction of an external perturbation adds the missing third dimension to the dynamics and the pendulum, driven suffi ciently away from equilibrium becomes chaotic. The motion of the damped pendulum driven by a periodic force is governed by the equation:
where the term  stands for the external forcing and the required third degree of freedom for the onset of chaotic behavior. It can be shown that the response of a nonlinear system to a forcing with a periodic frequency Ω progressively contains new harmonics, generated by nonlinearities, namely, by products of functions describing the system state. If the distance to equilibrium states is small values taken by these functions are also small and so are their products and the new harmonics added to the system state. Distance to equilibrium is thus a requirement for triggering nonlinear effects. The new harmonics strongly depend on the previous state, which ultimately depends on the initial condition. Small differences in the initial condition may result in quite different states after fi nite elapsed times; and the continuous addition of new harmonics may lead to aperiodic behavior. Sensitivity to the initial conditions along with aperiodic behavior are basic features of a chaotic evolution.
stands for the external forcing and the required third degree of freedom for the onset of chaotic behavior. It can be shown that the response of a nonlinear system to a forcing with a periodic frequency Ω progressively contains new harmonics, generated by nonlinearities, namely, by products of functions describing the system state. If the distance to equilibrium states is small values taken by these functions are also small and so are their products and the new harmonics added to the system state. Distance to equilibrium is thus a requirement for triggering nonlinear effects. The new harmonics strongly depend on the previous state, which ultimately depends on the initial condition. Small differences in the initial condition may result in quite different states after fi nite elapsed times; and the continuous addition of new harmonics may lead to aperiodic behavior. Sensitivity to the initial conditions along with aperiodic behavior are basic features of a chaotic evolution.
Fig. 3 shows the results of two simulations of the undamped pendulum in the chaotic regime, driven with different frequencies. Diagrams at the left show the evolution of the angular velocity ω as function of time and, at right, the evolution projected in the ω × θ plane of the phase space.
Chaotic motion of pendulum driven with two different frequencies. Left: diagrams θ × t. Right: trajectories projected in the ω × θ plane of the phase space.
The above examples show how evidences built up through the XXth century, that even systems governed by deterministic laws may present unpredictable behavior beyond a certain time limit. In this respect Lighthill (1986LIGHTHILL J. 1986. The recently recognized failure of predictability in newtonian dynamics. Proc R Soc Lond A 407: 37-50. ) writes:
We are deeply conscious today that the enthusiasm of our forebears for the marvelous achievements of Newtonian Mechanics led them to make generalizations in this area of predictability which, indeed, we may have generally tended to believe before 1960, but which we recognize were false.
5- TEMPORAL ORDER
Not only chaos was identifi ed in natural systems along the fi rst half of the XXth century, but also the onset of cooperative effects, rhythms and spatial order. Belousov (1958, cited by Murray 1989MURRAY JD. 1989. Mathematical Biology. Springer-Verlag, Berlin, Germany.) and Zhabotinsky (1967) (cited by Glansdorff and Prigogine 1971GLANSDORFF P AND PRIGOGINE I. 1971. Structure, Stabilité et Fluctuations. Masson, Paris, France.) addressed the chemical oscillations found in the oxidation of a solution of malonic acid in presence of cerium sulfate and potassium bromate. In addition to time oscillations the chemical system shows propagation of flat, curve and spiral waves, steady patterns and spatiotemporal chaos.
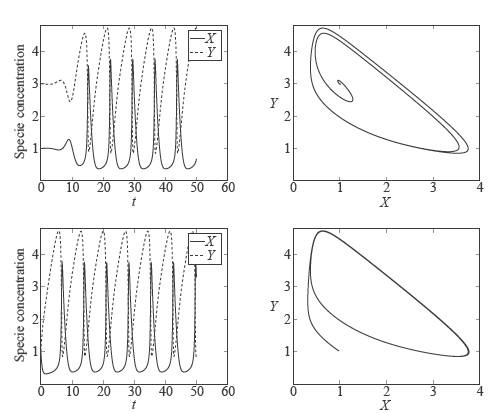
Since the decade of 1950 Prigogine (Prigogine 1967PRIGOGINE I. 1967. Introduction to Thermodynamics of Irreversible Processes. Wiley, New York, USA. , Glansdorff and Prigogine 1971GLANSDORFF P AND PRIGOGINE I. 1971. Structure, Stabilité et Fluctuations. Masson, Paris, France., Nicolis and Prigogine 1977NICOLIS G AND PRIGOGINE I. 1977. Self Organization in Nonequilibrium Systems. Wiley, New York, USA. , Prigogine and Stengers 1979, 1988) struggled against determinism and looked for scientifi c reasons justifying the onset of order. In 1970 Prigogine and Lefever (Glansdorff and Prigogine 1971) proposed an auto-catalytic model of chemical reactions later named as Brusselator.
The model is given by:
where A and B are reagents kept with constant concentrations. Application of the mass action law leads to the following two nonlinear equations:
where A, B, X and Y stand, in the above equations, for the concentration of the corresponding chemical species. The system presents a steady state (fixed point) X 0 = A, Y 0 = B / A. Linear stability analysis of the fi xed point shows that it becomes unstable when B > A 2 +1, giving raise to nonlinear limit cycle oscillations, with well defi ned amplitude and frequency, as shown in Fig. 4. The fi xed point locates inside the limit cycle and any trajectory originated in or outside evolves towards that curve. The Brusselator is thus an example of the onset of temporal order. Having a two dimensional dynamics the model, without spatial dependence, does not present chaotic behavior. As in the Belousov-Zhabotinsky reaction, introduction of spatial dependence provides the model with an infinite dimensional dynamics, which shows steady patterns of several types, waves and spatiotemporal chaos (Borckmans et al. 1993BORCKMANS P, DE WIT A AND DEWEL G. 1993. Chaotic Turing Hopf mixed mode. Phys Rev E 48: R4191-R4194. ).
6 - SPATIAL ORDER
As an example of spatial order in physical systems we may cite the buckling of a slender beam submitted to compressive loading along its neutral line. As the loading exceeds a critical threshold the straight neutral line looses stability and is replaced by a curve which depends on the applied loading and on the boundary conditions. The amplitude of the curve grows until saturation by the nonlinearities of the problem.
As a second example we cite the development of a boundary layer over a fl at plate. Close to the leading edge the boundary layer is laminar. Upon moving away from that point the laminar flow (base state) becomes unstable and fi rst time dependent perturbations appear. Being initially small the products of functions describing different perturbations are negligible in the evolution equations. Each perturbation evolves independently of others. Upon moving further away from the leading edge the amplitude of perturbations increase and the product of the functions describing different ones can no longer be neglected in the evolution equations. Perturbations start inter- acting, leading to cooperative effects, to the onset of more complex structures and eventually, to a progressive disordering of the structures and to turbulence. The non-dimensional distance to the leading edge is the Reynolds number, which is the bifurcation parameter that controls the stability of the base state (see Fig. 5).
Onset of temporal order: the figure shows the time behavior of the Brusselator, a model of auto catalytic chemical reactions, from an initial condition close to the unstable steady state, towards the limit cycle. First line: left diagram shows the evolution of X and Y as a function of time, from an initial condition internal to the limit cycle and close to the unstable steady state. The right diagram shows the evolution of the same initial condition in the phase space (space of the independent variables X and Y ). Second line: same, starting from an initial condition outside the limit cycle.
Onset of order and turbulence in a boundary layer developed by the fl ow over a fl at plate: At short distances from the leading edge the boundary layer is laminar. Beyond a critical distance to the leading edge the laminar flow becomes unstable and fi rst time dependent perturbations are amplifi ed. As the amplitude of the unstable perturbations increase interactions take place leading to the emergence of new unstable modes and eventually to the onset of turbulence where an explosion of more complex spatio-temporal structures of vortices occurs, as far as distance of equilibrium is maintained.
We may also cite the spatial structures theoretical found by Turing (Turing 1952TURING A. 1952. The chemical basis of morphogenesis. Phil Trans Royal Soc B 237(641): 37-72., Murray 1989MURRAY JD. 1989. Mathematical Biology. Springer-Verlag, Berlin, Germany.) by considering the stability of the space homogeneous solutions of a set of two nonlinear reactiondiffusion equations. Turing showed that, if the ratio between the diffusion coeffi cient of the two chemical species exceeds a critical value (bifurcation point) the spatial homogeneous solution, with the concentration of both chemical species independent of the position in the reactor is unstable to periodic perturbations, which grow developing a spatial pattern. The theoretical work of Turing was confi rmed experimentally in 1990 by de Kepper in Bordeaux, France (Castets et al. 1990CASTETS V, BOISSONADE J, DULOS E AND DE KEPPER P. 1990. Experimental evidence of a sustained Turing-type nonequilibrium chemical pattern. Phys Rev Lett 64(24): 2953-2956.), and by Swinney in Austin, Texas (Virgil et al. 1992). The ratio between the diffusion coeffi cients is thus the bifurcation parameter that controls the stability of the homogeneous state.
As another example, we cite the spatial patterns developed in the hydrodynamic fi eld developed between two coaxial counter-rotating disks. Rotation of the disks induces an outward fl ow close to the surface which is replaced by an infl ow at the center of the setup Fig. 6. Several stationary solutions exist, independent of the azimuthal angular coordinate θ. As in the problem of the boundary layer developed over a fl at plate, where the stability of the base state is controlled by a Reynolds number that is the non-dimensional distance to the leading edge, the stability of the fl ow between the counter rotating disks is controlled by non-dimensional distance to the rotation axis. The steady solutions loose stability beyond a certain distance and a spatial pattern emerges. An example of pattern formation in the setup is shown in Fig. 6 (Ferreira 2013FERREIRA DVA. 2013. Estudo do campo hidrodinâmico entre dois discos rotatórios. Master's thesis, Instituto Alberto Luiz Coimbra de Pós-Graduação em Engenharia COPPE - Universidade Federal do Rio de Janeiro. (Unpublished). ).
Scheme of the fl ow between counter-rotating disks (left) and spatial patterns developed in the hydrodynamic fi eld (right).
7- ORDER AND COMPLEXITY
Over the last three centuries science has followed the program of breaking complex systems into parts and parts into successive smaller parts hoping to understand the whole by understanding the behavior of the individual smaller ones. This program - reductionism - though spectacularly successful in the past, and certainly in the future, not always gives hints on how to use information gathered from the parts to understand the behavior of the whole. Here, the diffi culty lies in the fact that suffi ciently large systems may display emergent collective properties not existing in the parts (Kauffman 1987, 2008). In the last forty years we devise a new way to pursue, opposite to the prevailing reductionism, and consisting in understanding the behavior of complex systems, namely, of networks of connected nodes driven far from equilibrium, and displaying emerging self organizing properties not found in the dynamics of the individual nodes.
As an example we discuss some properties of suffi ciently large networks of boolean nodes studied by Kauffman (Kauffman 1995KAUFFMAN SA. 1995. At Home in the Universe: the Search of Laws for Self-Organization. Oxford, New York, USA. , 2008, Nussensweig 1999NUSSENSWEIG HM. 1999. Complexidade e Caos. Editora COPEA/UFRJ, Rio de Janeiro, RJ, Brasil. ). Nodes in these networks can be activated or not, depending on information received from a number of other nodes and on the control rules randomly assigned to the nodes. Networks so constructed show a variety of qualitatively different behaviors. Starting from an out of equilibrium initial conditions networks too loosely connected evolve to a steady state with part of the nodes activated and the remaining ones deactivated. If the state of a few number of nodes changes the original state is rapidly restored. The network is too rigid and does not propagate information. Networks too connected evolve towards a chaotic state with almost all nodes twinkling between the two states. Changing the state of a few number of nodes does not refl ect on the chaotic behavior of the network. These networks do not propagate information either. Kauffman observed that networks sparsely connected, and not too far from the chaotic behavior, often present a number of emerging properties not existing in the individual nodes, and that cannot be derived from the particular dynamics of each one. This is what we call complexity. These networks self organize in an ordered steady state with clusters of activated nodes, clusters of inactivated ones and clusters of nodes switching between the two states. Change of the state of a not too big number of nodes temporarily changes the state of part of the network but the original structure of steady and twinkling nodes is eventually restored. The network does propagate information. Larger perturbations may drive the network to a different steady state. However, attraction basins exist, with states in the neighborhood of a steady state eventually evolving to a tiny subspace of the space of possible states the system may attain. Kauffman found a number of attractors substantially smaller than the number of possible states of the network.
In addition, Kauffman observed networks at the edge of chaos, showing a compromise between stability and fl exibility to cope with an evolving environment. Stability comes from the fact that small changes in the environment, for instance, in the rules governing the input signals and the corresponding effect on the state of some nodes does not affect the steady state of the network. Flexibility is reflected in small changes in the steady state of the network, in response to changes in the environment.
Applying the results concerning the behavior of boolean networks to genetic regulation Kauffman interprets the attractors as different types of cell (Nussensweig 1999NUSSENSWEIG HM. 1999. Complexidade e Caos. Editora COPEA/UFRJ, Rio de Janeiro, RJ, Brasil. ).
8- ORDER AND ENTROPY
Most processes taking place inside living cells, also including those that lead to the onset of order, result in positive or negative changes of entropy, which is the variable we have available to quantify order. This section summarizes the results presented by Blumenfeld (1981BLUMENFELD LA. 1981. Problems of Biological Physics. Springer, Berlin, 224 p.), showing that entropy decreases associated to "biological ordering" are small and that onset of life is done at a very low thermodynamic cost. Blumenfeld evaluated the entropy decrease associated to the following processes:
-
Building, from individual cells, a multicellular living organism containing 1013 cells, which is the approximate number found in a human being. It was assumed that all cells are different and that positions of cells are not interchangeable. An entropy decrease ∆S = 10−9cal/K was found;
-
Building of 1013 cells from biopolymers like proteins, nucleic acids (DNA), phospholipids, etc., each cell having 108 biomolecules. It was assumed that all molecules are different and that the position of each molecule is unique. The entropy decrease found was ∆S = 6×10−2cal/K. This value comprises the decrease associated to the placement of each cell;
-
Formation of 7 kg of proteins and of 150 g of nucleic acid (DNA), which are the approximate amounts found in a human being, from the corresponding monomers. These amounts correspond to 3 × 1025 aminoacid residues and to 3 × 1023 nucleotide residues, respectively. The estimated entropy decreases are ∆S = 300cal/K and ∆S = 1,6cal/K, respectively. These fi gures take into account the decrease associated to the positioning of each residue in a cell and the placement of each cell in the multicellular being.
Building of a biological structure like a human being requires thus an approximate entropy decrease of 301,6 cal/K, the main contribution being due to the formation of proteins and of DNA from monomers. The entropy decrease associated to the formation of one the most complex biological structures - the human being - may thus be trivially compensated by associated physical or chemical processes. For instance, evaporation of 170 g water or oxidation of 900 g of glucose results in an entropy increase of 300 cal/K; and, according to thermodynamic criteria, 1013 different unicellular organisms are almost as organized as a human being. Formation of biological structures is made thus almost free of thermodynamic cost.
9- NONLINEARITY AND COMPLEXITY: ENGINES OF UNPREDICTABILITY AND OF THE ONSET OF ORDER
The facts and examples discussed in Secs. 4 - 7 show how ideas about determinism lost room and it became clear that the onset of chaos, but also, of temporal and spatial order is consistent with the natural laws. The new paradigm became indisputable from the decade of 1970. In 1970 Prigogine coined the expression Dissipative Structures to name the class of temporal and/or spatial structures developed in far from equilibrium systems. Haken (1983HAKEN H. 1983. Synergetics - An Introduction. SpringerVerlag, Berlin, Germany. , 1993) named as Sinergy the cooperative effects resulting from nonlinear effects and leading to the onset of order. The expression is widely used nowadays outside science.
The onset of order and of chaos relies on the nonlinear nature of the evolution laws, a mathematical property frequently found in evolution laws. As discussed in Sec. 4 nonlinearity provides a mechanism to continuously adding new harmonics to the functions describing the system behavior. Distance to equilibrium is a must to trigger nonlinear effects and a minimum of three degrees of freedom is required for the onset of chaos, a condition easily fulfi lled by natural systems. In the last forty years an additional paradigm emerges as we recognize that networks consisting of suffi ciently large number of sparsely connected nodes, and not too far from the chaotic behavior - Complex Systems - display new collective order properties not found in the nodes.
Life is made at the expense of very low thermodynamic cost so the thermodynamic laws do not pose, in fact, major restrictions to the onset of life.
10- A WORD ON THE POSITION OF CONTEMPORARY SCIENCE
As discussed in this work modern science evolved from a confl icting position with the Western culture, to a different view of nature. The confl ict resulted from the statement that all natural phenomena evolve deterministically, a postulate that collides with the principle that man is free and that the future can be shaped. In the words of Prigogine:
The collision between the Western civilization and modern science was unavoidable, since Western civilization is based on the JudaicChristian tradition, where time is the most important element, and time does not exist in modern science, where the whole past and the whole future are contained in the present.
An additional point of conflict arose from the principle that order can be destroyed but not created. Both principles were criticized by philosophers, by art and by science itself, along the XIXth century and fi rst years of the XXth century. It is clear today that the spontaneous emergence of new ordered structures, of rhythms, but also of chaos, is a rule in far from equilibrium systems and in large networks. At the same time, we realize that our ability to predict the future is limited. We cannot even predict the motion of three coupled pendula (Kauffman 1995KAUFFMAN SA. 1995. At Home in the Universe: the Search of Laws for Self-Organization. Oxford, New York, USA. ). But man has recovered the freedom and responsibilities lost with the development of Newtonian mechanics. The future can be shaped in absolutely new structures. Science gives us today a picture in constant evolution of nature, as evolves our understanding of the Universe from other points of view. We live in a period where science and other tools we dispose to describe and understand nature provide complimentary and, in many aspects, converging views.
ACKNOWLEDGMENTS
The author warmly acknowledges prof. Luiz Bevilacqua, from the Federal University of Rio de Janeiro, Brazil, for discussions that lead to this work. He also acknowledges the Free University of Brussels - ULB, in particular professor René Lefever; and he acknowledges Eduardo Vitral for Figs. 2, 3 and 4, Davi Vaz de Andrade Ferreira for Fig. 6, and the Brazilian agencies Conselho Nacional de Desenvolvimento Científi co e Tecnológico (CNPq) and Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ) for fi nancial support.
REFERENCES
- ARNOLD VI. 1963. Small denominators ii, proof of a theorem of A. N. Kolmogorov on the preservation of conditionallyperiodic motion under a small perturbation of the Hamiltonian. Russ Math Survey 18: 5.
- BERGSON H. 1907. Evolution Créatrice. Presses Universitaires de France, Paris, France.
- BLUMENFELD LA. 1981. Problems of Biological Physics. Springer, Berlin, 224 p.
- BORCKMANS P, DE WIT A AND DEWEL G. 1993. Chaotic Turing Hopf mixed mode. Phys Rev E 48: R4191-R4194.
- CASTETS V, BOISSONADE J, DULOS E AND DE KEPPER P. 1990. Experimental evidence of a sustained Turing-type nonequilibrium chemical pattern. Phys Rev Lett 64(24): 2953-2956.
- FERREIRA DVA. 2013. Estudo do campo hidrodinâmico entre dois discos rotatórios. Master's thesis, Instituto Alberto Luiz Coimbra de Pós-Graduação em Engenharia COPPE - Universidade Federal do Rio de Janeiro. (Unpublished).
- GLANSDORFF P AND PRIGOGINE I. 1971. Structure, Stabilité et Fluctuations. Masson, Paris, France.
- HAKEN H. 1983. Synergetics - An Introduction. SpringerVerlag, Berlin, Germany.
- HAKEN H. 1993. Advanced Synergetics. Springer-Verlag, Berlin, Germany.
- HENDERSON LJ. 1917. The Order of Nature. Harvard University Press, Cambridge, Massachussets, USA.
- KAUFFMAN SA. 1995. At Home in the Universe: the Search of Laws for Self-Organization. Oxford, New York, USA.
- KAUFFMAN SA. 2008. Reinventing the Sacred. Perseus Books Group, New York, USA.
- KOLMOGOROV AN. 1954. Preservation of conditionally periodic movments with small change in the Hamiltonian function. Dokl. Akad. Nauk SSSR, 98: 527. Reprinted in MacKay and Meiss, 1987, Hamiltonian Dynamical Systems: A Reprint Selection. Adam Hilger, Bristol.
- LANDAU EM. 1944. On the problem of turbulence. C R Acad Sci URSS 44: 311.
- LIGHTHILL J. 1986. The recently recognized failure of predictability in newtonian dynamics. Proc R Soc Lond A 407: 37-50.
- LORENZ EN. 1963. Deterministic nonperiodic flow. J Atm Sci 20: 130.
- MCMURANN SL AND TATTERSALL J. 1996. The mathematical collaboration of M. L. Cartwright AND J. T. Littlewood. The Am Math Monthly 103(10) 883-845.
- MOREIRA IC. 1999. Maupertuis (1698-1759) e o princípio da mínima ação. Rev Bras Ensino de Física 21(1): 172-186.
- MOSER J. 1967. Convergent series expansions of quasiperiodic motions. Math Ann 169: 163.
- MURRAY JD. 1989. Mathematical Biology. Springer-Verlag, Berlin, Germany.
- NICOLIS G. 1995. Introduction to Nonlinear Science. Cambridge, England.
- NICOLIS G AND PRIGOGINE I. 1977. Self Organization in Nonequilibrium Systems. Wiley, New York, USA.
- NUSSENSWEIG HM. 1999. Complexidade e Caos. Editora COPEA/UFRJ, Rio de Janeiro, RJ, Brasil.
- OTT E. 1993. Chaos in Dynamical Systems. Cambridge, England.
- PRIGOGINE I. 1967. Introduction to Thermodynamics of Irreversible Processes. Wiley, New York, USA.
- PRIGOGINE I AND STENGERS I. 1979. La Nouvelle Aliance. Gallimard, Paris, France.
- PRIGOGINE I AND STENGERS I. 1988. Entre le Temps et l'Eternité. Fayard, Paris, France.
- SCHUSTER HG. 1995. Deterministic Chaos. VCH, Weinheim.
- SMALE S. 1967. Differentiable dynamical systems. Bull Amer Math Soc 73: 747.
- STENGERS I. 1989. Les affaires Galilée. In: Serres M (Ed), Eléments d'Histoire des Sciences, volume 1, chapter 9, p. 223-249. Bordas, Paris, France.
- TRUESDELL C. 1982a. História da Mecânica Clássica - parte I, até 1800. J Braz Soc Mech Sci Eng 4(2): 3-17.
- T RUESDELL C. 1982b. História da Mecânica Clássica - parte II, os séculos XIX e XX. J Braz Soc Mech Sci Eng 4(3): 3-21.
- TURING A. 1952. The chemical basis of morphogenesis. Phil Trans Royal Soc B 237(641): 37-72.
- VIGIL RD, OYANG Q AND SWINNEY HL. 1992. Turing patterns in a simple gel reactor. Physica A 188(1): 17-25.
Publication Dates
-
Publication in this collection
Apr-Jun 2016
History
-
Received
2014 -
Accepted
2015