ABSTRACT
Population dynamics of aphids have been studied in sole and intercropping systems. These studies have required the use of more precise analytical tools in order to better understand patterns in quantitative data. Mathematical models are among the most important tools to explain the dynamics of insect populations. This study investigated the population dynamics of aphids Aphis gossypii and Aphis craccivora over time, using mathematical models composed of a set of differential equations as a helpful analytical tool to understand the population dynamics of aphids in arrangements of cotton and cowpea. The treatments were sole cotton, sole cowpea, and three arrangements of cotton intercropped with cowpea (t1, t2 and t3). The plants were infested with two aphid species and were evaluated at 7, 14, 28, 35, 42, and 49 days after the infestations. Mathematical models were used to fit the population dynamics of two aphid species. There were good fits for aphid dynamics by mathematical model over time. The highest population peak of both species A. gossypii and A. craccivora was found in the sole crops, and the lowest population peak was found in crop system t2. These results are important for integrated management programs of aphids in cotton and cowpea.
Key words:
aphids; cotton; cowpea; dynamics; mathematical models
INTRODUCTION
The aphids Aphis gossypii Glover (Ramalho et al. 2012RAMALHO FS, FERNANDES FS, NASCIMENTO ARB, NASCIMENTO JÚNIOR JL, MALAQUIAS JB AND SILVA CAD. 2012. Feeding damage from cotton aphids, Aphis gossypii Glover (Hemiptera: Heteroptera: Aphididae), in cotton with colored fiber intercropped with fennel. Ann Entomol Soc Am 105: 20-27.) and Aphis craccivora Koch (Hemiptera: Heteroptera: Aphididae) (Moraes and Ramalho 1980MORAES GJM AND RAMALHO FS. 1980. Alguns insetos associados a Vigna unguiculata Walp no Nordeste. Embrapa-CPATSA, Petrolina, 10 p.) are serious crop pests in Brazil. These insects directly damage the plants by sucking the phloem, and indirectly by virus transmission and excretion of excess carbohydrates from their diet of phloem sap (Bachmann et al. 2014BACHMANN AC, NAULT BA AND FLEISCHER SJ. 2014. Alate aphid (Hemiptera: Aphididae) species composition and richness in northeastern USA snap beans and an update to historical lists. Fla Entomol 97: 979-994.). The excretions can foster the occurrence of fungus that inhibits photosynthetic activity, resulting in chlorosis and consequent loss of yield (Bachmann et al. 2014, Kadam et al. 2014KADAM DB, KADAM DR AND LEKURWALE RS. 2014. Seasonal incidence of sucking pests of Bt cotton in different intercropping systems and their natural enemies. J Plant Pest Sci 1: 29-34.). Ramalho et al. (2012) found that A. gossypii reduced the yield of cotton seed (Gossypium hirsutum Linnaeus) by 37% in sole cotton plots compared with 10% loss of cotton-seed yield per plant in the intercropping systems. On the other hand, A. craccivora, is a vector of several viruses including broad bean mosaic virus, and it can reach high abundances in warm-temperate and tropical regions (Gutierrez et al. 1974GUTIERREZ AP, HAVENSTEIN DE, NIX HA AND MOORE PA. 1974. The ecology of Aphis craccivora Koch and subterranean clover stunt virus in south-east Australia. J Appl Ecol 11: 21-35.). Munyuli (2009MUNYULI T. 2009. Effects of native insect predators on population densities of Aphis craccivora and yields of Vigna unguiculata and Arachis hypogeae grown under various cropping systems in Kivu Province, Eastern Democratic Republic of Congo. Tunis J Plant Prot 4: 197-209.) reported that in comparison with control treatments, biological control of A. craccivora with predators increased yields by up to 66% for cowpea Vigna unguiculata (Linnaeus) Walp.
Aphid populations can show periodic fluctuations (Brabec et al. 2014BRABEC M, HONĚK A, PEKÁR S AND MARTINKOVÁ Z. 2014. Population dynamics of aphids on cereals: digging in the time-series data to reveal population regulation caused by temperature. PLoS ONE 9: 1-8.). The population dynamics of aphids can be affected by seasonal changes in weather conditions, physiological characteristics of the host plant, farming methods, and management practices (Sequeira and Dixon 1997SEQUEIRA R AND DIXON AFG. 1997. Population dynamics of tree-dwelling aphids: the importance of seasonality and time scale. Ecology 78: 2603-2610.). Also, some crops may deter while others may attract sucking insects, and local variation in resource quality profoundly influences the overall population dynamics (Kadam et al. 2014KADAM DB, KADAM DR AND LEKURWALE RS. 2014. Seasonal incidence of sucking pests of Bt cotton in different intercropping systems and their natural enemies. J Plant Pest Sci 1: 29-34., Riolo et al. 2015RIOLO MA, ROHANI P AND HUNTER MD. 2015. Local variation in plant quality influences large-scale population dynamics. Oikos 124: 1160-1170.).
Although many studies have analyzed the population dynamics of aphid species in sole crops (Sequeira and Dixon 1997SEQUEIRA R AND DIXON AFG. 1997. Population dynamics of tree-dwelling aphids: the importance of seasonality and time scale. Ecology 78: 2603-2610., Leite et al. 2007LEITE GLD, PICANÇO M, ZANUNCIO JC AND GUSMÃO MR. 2007. Factors affecting colonization and abundance of Aphis gossypii Glover (Hemiptera: Aphididae) on okra plantations. Ciênc Agrotec 31: 337-343., Rakhshani et al. 2009RAKHSHANI H, EBADI R AND MOHAMMADI AA. 2009. Population dynamics of alfalfa aphids and their natural enemies, Isfahan, Iran. J Agric Sci Technol 11: 505-520.), no information is available about the dynamics of A. gossypii and A. craccivora in different arrangements of cotton intercropped with cowpea. Different crop arrangements or diversification can be effective management strategies to control insect pests (Burgio et al. 2014BURGIO G, KRISTENSEN HL, CAMPANELLI G, BAVEC F, BAVEC M, FRAGSTEIN PVON, DEPALO L, LANZONI A AND CANALI S. 2014. Effect of living mulch on pest/beneficial interaction, In: Rahmann G and Aksoy U (Eds), Eff. Living Mulch Pest/beneficial Interact. Building Organic Bridges, Germany, p. 741-744.).
Intercropping has been studied to assess its effects on the incidence of various insect species: intercropping cotton x corn (Zea mays Linnaeus) x sorghum (Sorghum bicolor (L.) Moench) x beans (Vigna unguiculata (L.) Walpers) or sesame (Sesamum indicum Linnaeus) (Gonzaga et al. 1991GONZAGA JV, RAMALHO FS AND SANTOS JW. 1991. Ditribuição de Aphis gossypii no algodoeiro nos sistemas de plantio solteiro e consorciado. Pesq Agropec Brasil 26: 1839-1844., Lin et al. 2003); cotton x alfalfa (Medicago sativa Linnaeus) (Lin et al. 2003); cotton x corn (Fabião and Sousa 2007FABIÃO H AND SOUSA A. 2007. Effect of strip intercropping of cotton and maize on pest incidence and yield in Mornumbala District, Mozambique. Afr Crop Sci Confer Proceeds 8: 1053-1055.); cotton x wheat (Triticum aestivum Linnaeus) (Zhang et al. 2007ZHANG I, VAN DER WERF W, ZHANG S, LI B AND SPIERTZ JHJ. 2007. Growth, yield and quality of wheat and cotton in relay strip intercropping systems. F Crops Res 103: 178-188. ); cotton x wheat x alfalfa x sorghum (Phoofolo et al. 2010PHOOFOLO MW, GILES KL AND ELLIOTT NC. 2010. Effects of relay-intercropping sorghum with winter wheat, alfalfa, and cotton on lady beetle (Coleoptera: Coccinellidae) abundance and species composition. Environ Entomol 39: 763-774. ); and cotton x fennel (Foeniculum vulgare Miller) (Ramalho et al. 2012RAMALHO FS, FERNANDES FS, NASCIMENTO ARB, NASCIMENTO JÚNIOR JL, MALAQUIAS JB AND SILVA CAD. 2012. Feeding damage from cotton aphids, Aphis gossypii Glover (Hemiptera: Heteroptera: Aphididae), in cotton with colored fiber intercropped with fennel. Ann Entomol Soc Am 105: 20-27., Fernandes et al. 2013FERNANDES FS, RAMALHO FS, GODOY WAC, PACHU JKS, NASCIMENTO ARB, MALAQUIAS JB AND ZANUNCIO JC. 2013. Within plant distribution and dynamics of Hyadaphis foeniculi (Hemiptera: Aphididae) in field fennel intercropped with naturally coloured cotton. Fla Entomol 96: 92-103.).
A possible way to represent the different feeding preferences among aphids and their ecological relationships is by using mathematical models (Underwood 2009UNDERWOOD N. 2009. Effect of genetic variance in plant quality on the population dynamics of a herbivorous insect. J Anim Ecol 78: 839-847.). A mathematical model is an equation or a set of equations that represent the behavior of an insect in the system, and gives an approximation of the observed data (Thornley and France 2006THORNLEY JHM AND FRANCE J. 2006. Mathematical models in agriculture: Quantitative methods for the plant, animal and ecological sciences. CABI, Wallingford, UK, 608 p.). Mathematical models may provide useful and essential analytical tools to interpret important ecological patterns for a given agroecosystem, and may also allow predictions to be made about population outbreaks of insect pests. According to Tenhumberg et al. (2009TENHUMBERG B, TYRE AJ AND REBARBER R. 2009. Model complexity affects transient population dynamics following a dispersal event: a case study with pea aphids. Ecology 90: 1878-1890.) and Singh et al. (2014SINGH A, SINGH S, SHARMA RK, SINGH PK AND KUMAR A. 2014. A mathematical model for n-species competition for aphid population in limited resources. J Appl Sci Res 2: 119-123.), structured population models are useful to examine population dynamics of insects in crops, and they can be used to explain aphid species competition in situations of limited food resources.
Several investigators have developed models to describe aphid species dynamics. Plantegenest et al. (1996PLANTEGENEST M, PIERRE JS, CAILLAUD CM, SIMON JC, DEDRYVER C AND CLUZEAU S. 1996. A model to describe the reproductive rate in the aphid Sitobion avenae (Hemiptera: Aphididae): A case study. Eur J Entomol 93: 545-553.) used a mathematical approach to simulate changes in populations of the grain aphid Sitobion avenae (Fabricius) (Hemiptera: Heteroptera: Aphididae) on wheat, Triticum aestivum Linnaeus). Arbab et al. (2006ARBAB A, KONTODIMAS A AND SAHRAGARD DC. 2006. Estimating development of Aphis pomi (DeGeer) (Homoptera: Aphididae) using linear and nonlinear models. Environ Entomol 35: 1208-1215.) tested non-linear and linear models to estimate the development of Aphis pomi De Geer (Hemiptera: Aphididae). However, models have not been used to analyze the population dynamics of A. gossypii and A. craccivora feeding on sole crops or on cotton with naturally colored fiber intercropped with cowpea. Knowledge of patterns of distribution of insect pests within intercropping systems is essential to make decisions and to implement integrated pest-management programs in both cotton and cowpea crops. This study investigated the population dynamics of wingless and winged aphids (A. gossypii and A. craccivora) over time, taking into account different crop arrangements, using mathematical models composed of a set of differential equations as a helpful analytical tool to understand the population dynamics of A. gossypii and A. craccivora in different arrangements of cotton with cowpea.
MATERIALS AND METHODS
STUDY LOCATION AND COTTON AND COWPEA CULTIVARS
This study was carried out in greenhouse conditions at the Department of Entomology - ESALQ/USP, Piracicaba, São Paulo, Brazil. A naturally colored cotton cultivar (BRS Safira) and cowpea cultivar BRS Itaim were planted on the local red latosol.
APHID SPECIES
Two species of aphids (A. gossypii and A. craccivora) in both forms, wingless and winged, were used in the study. The specimens of A. gossypii were collected in a cotton field of the Department of Entomology, ESALQ/USP, Piracicaba, São Paulo State, Brazil. A. craccivora specimens were collected from cowpea plants in an experimental area of the Brazilian Agricultural Research Corporation (EMBRAPA), located at Lagoa Seca, Paraíba State, Brazil. Both species of aphids were identified and reared on plants of their hosts, cotton and cowpea, respectively. The plants were maintained in plastic cages at 25 ± 1 ºC, 70 ± 10% RH and LD 12:12 h. The aphids were observed daily in the cages, and when necessary, they were separated according to their life-cycle stage (nymphs and adults).
BIOASSAY
A randomized block design was used, with five treatments: t1) two cotton plants : two cowpea plants in the row, with each row starting and ending with two cotton plants; t2) two cowpea plants : two cotton plants in the row, with alternate rows starting and ending with two cowpea plants; t3) one row of cotton : one row of cowpea; t4) cotton; and t5) cowpea, with three replications.
The intercropping cotton-cowpea experimental units consisted of rows composed of two cotton plants alternating with two cowpea plants in each row, or a row of cotton alternately with a row of cowpea (Fig. 1). In both the sole and intercropped plots, the cotton and cowpea rows were spaced 0.40 m apart with 0.20 m between the plants in each row. The experimental units were spaced 1.00 m apart (Fig. 1). Each experimental unit was placed in a transparent plastic cage, which were protected with white voile.
Plan of experimental units in the cotton-cowpea intercropping system and cotton monoculture. Cotton with naturally colored fibers (closed circles) and cowpea (open circles).
Seeds of cotton and cowpea were sown in plastic pots (0.40 x 0.40 x 0.30 m) and the plants were watered on alternate days.
Twenty-eight days after the plants sprouted, 15 4th-instar nymphs of A. gossypii and 15 4th-instar nymphs of A. craccivora were placed in each plastic cage with sole cotton (t4) and sole cowpea (t5), respectively. Similarly, one cotton plant and one cowpea plant in each intercropped plot were infested with the same number of each species of aphid. In the intercropped plots, each experimental unit received 15 4th-instar nymphs of A. gossypii and 15 4th-instar nymphs of A. craccivora, which were placed on one cotton and one cowpea plant, respectively. The number of aphids per plant was recorded weekly between 35 and 77 days after the plants sprouted. The number of aphids was recorded on three plants (the infested plant and two previously uninfested plants) in the sole crop or intercropping systems, which were marked with nylon tape. The counts were made 7, 14, 28, 35, 42 and 49 days after the plants were first infested.
Aphid populations were then measured to determine growth as a function of the initial population density, in both the sole and intercropping systems. A mathematical model was used to compare the observed with the expected data sets.
MATHEMATICAL MODEL
The mathematical model used to estimate the population dynamics of wingless and winged aphids in the sole and intercropped plots was comprised of four differential equations, representing the population dynamics of wingless and winged aphids, and cotton and cowpea plants (eqs. 1 - 4).
Equations 1 to 4 describe the population dynamics of aphids (P1 and P2) and plants (P3 and P4). The expected fits were obtained using the equations of the package solve library from R software, including:
Each mathematical term is specified in Table I, and the scheme of the relationships among the variables of the model and parameters is shown in Fig. 2.
Schematization of the mathematical model. The parameters correspond to the rate at which the component at the arrow tail is consumed (“cowpea” and “cotton”) or another at the arrowhead (“winged aphids”, “wingless aphids” and “death”).
PARAMETER SENSITIVITY ANALYSIS
Sensitivity is an important issue in attempting to make predictions for qualitatively different attributes, such as types of dynamics (Perry et al. 1993PERRY JN, WOIWOD IP AND HANSKI I. 1993. Using response-surface methodology to detect chaos in ecological time series. Oikos 68: 329-339.). In order to determine the model parameter sensitivities, the values of all parameters were fixed, except one, which was varied, in order to analyze how the aphid model reacted to this variation.
COTTON APHID
In descending order, the output sensitivity of the output model for A. gossypii is shown in the form: δ > β > θ2 > α > γ > α2 > φ > ω2 > θ > γ2 > ω > ε > λ > λ2.
COWPEA APHID
In descending order, the output sensitivity of the output model for A. craccivora is presented in the form: ε > φ > θ2 > γ > α > δ > θ > ω > β > ω2 > γ2 > α2 > λ> λ2.
RESULTS AND DISCUSSION
The population dynamics of the two species behaved similarly, with an initial increase followed by a rapid decay (Figs. 3 and 4). This pattern probably reflects a synchrony between the aphid populations and the food availabilities. This behavior is typical of situations when food resources are limited (Pollard and Rothery 1994POLLARD E AND ROTHERY P. 1994. A simple stochastic model of resource-limited insect populations. Oikos 69: 287-294.), as was the case on the intercropping systems in our study. When the populations of A. gossypii and A. craccivora were small, they increased until the food resources were exhausted, which resulted in a negative growth rate. The decay was smoother for the aphids on cotton intercropped with cowpeas, compared to a sole crop, probably because the intercropping systems reduced the aphid pressure compared to the sole system.
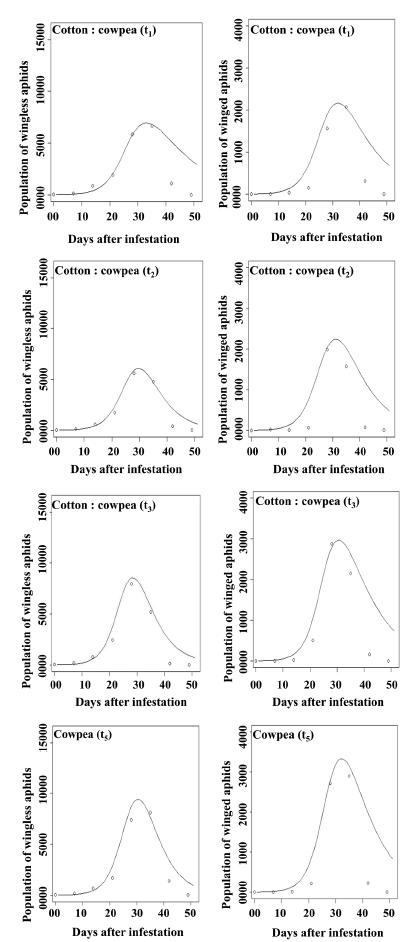
Observed data set (open circles) and model prediction (solid line) for the population dynamics of wingless (left) and winged (right) A. gossypii over time for each crop system. Each data point represents the total number of aphids (wingless or winged) on all leaves and reproductive structures of nine cotton plants.
Observed data set (open circles) and model prediction (solid line) for the population dynamics of wingless (left) and winged (right) A. craccivora over time for each crop system. Each data point represents the total number of aphids (wingless or winged) on all leaves and reproductive structures of nine cowpea plants.
As shown in Fig. 3, in sole cotton (t4) both wingless (13,377 aphids) and winged (3,599 aphids) cotton aphids reached a higher population peak than in crop system t1 (9,848 wingless aphids; 2,208 winged aphids), crop system t2 (8,299 wingless aphids; 1,756 winged aphids), and crop system t3 (13,158 wingless aphids; 2,298 winged aphids). The lowest peak for the cotton aphid population was found in crop system t2 (8,299 wingless aphids; 1,756 winged aphids). In the sole cotton (t4), t1 and t3 crop systems, wingless A. gossypii peaked at 42 days, while in crop system t2 the cotton aphid peaked at 35 days after the plant infestations. The winged A. gossypii peaked at 42 days in sole cotton (t4) and also in crop system t1, while in crop systems t2 and t3, the cotton aphid peaked 35 days after the plant infestations.
Both wingless and winged forms of A. craccivora showed the numerically highest population peaks in sole cowpea (t5) (8,150 and 2,900 aphids, respectively) and lowest peaks in the crop system t2 (4,774 and 1,576 aphids, respectively). The population peaks of wingless and winged A. craccivora in sole cowpea (t5) and in crop systems t1, t2 and t3 occurred at 35 days after the cowpea infestations. These results indicate that the sole cowpea crop hosted numerically more A. craccivora than the cowpea intercropped with cotton. The results obtained in this study concord with those reported by Mitiku et al. (2014MITIKU A, CHALA A AND BEYENE Y. 2014. Effect of intercropping on aphid vectors and yield of pepper (Capsicum annum L.) in southern part of Ethiopia. Int J Technol Enhanc Emerg Eng Res 2: 24-34.), who used intercropping of plants to reduce aphid pressure. Pahla et al. (2014PAHLA I, TUMBARE T, CHITAMBA J AND KAPENZI A. 2014. Evaluation of Allium sativum and Allium cepa intercrops on the control of Brevicoryne brassicae (Homoptera: Aphididae) in Brassica napus. Int J Farming Allied Sci 3: 1069-1074.) reported that intercropping of brassica crop plants confers advantages, such as greater leaf mass and less leaf damage caused by sucking insects. Fernandes et al. (2013FERNANDES FS, RAMALHO FS, GODOY WAC, PACHU JKS, NASCIMENTO ARB, MALAQUIAS JB AND ZANUNCIO JC. 2013. Within plant distribution and dynamics of Hyadaphis foeniculi (Hemiptera: Aphididae) in field fennel intercropped with naturally coloured cotton. Fla Entomol 96: 92-103.) reported that in a sole-cotton system, A. gossypii populations peaked between 74 and 95 days, whereas in a cotton-fennel intercropping system, populations of this aphid peaked between 74 and 102 days. Resende et al. (2004RESENDE ALS, PAIXÃO FHM, MENEZES EB, GUERRA JGM AND MENEZES ELA. 2004. Flutuação populacional de pulgões alados (Hemiptera: Aphididae) em cultivo de couve e sua relação com fatores climáticos e densidade de insetos predadores. Agronomia 38: 6-10.) also observed that populations of winged A. gossypii peaked on 77-day-old kale plants (Brassica oleraceae Linnaeus). These findings are consistent with those of Parajulee et al. (1997PARAJULEE MN, MONTANDON R AND SLOSSER JE. 1997. Relay intercropping to enhance abundance of insect predators of cotton aphid (Aphis gossypii Glover) in Texas cotton. Int J Pest Manag 43: 227-232.), who described similar aphid population peaks in an intercropping system containing cotton, wheat (Triticum aestivum Linnaeus), sorghum [Sorghum bicolor (Linnaeus) Moench], and rapeseed (Brassica napus Linnaeus). On the other hand, populations of A. gossypii may peak at different stages of plant growth and development (Afshari et al. 2009AFSHARI A, SOLEIMAN-NEGADIAN E AND SHISHEBOR P. 2009. Population density and spatial distribution of Aphis gossypii Glover (Homoptera: Aphididae) on cotton in Gorgan, Iran. J Agric Sci Technol 11: 27-38.). According to Celini and Vaillant (2004CELINI L AND VAILLANT J. 2004. A model of temporal distribution of Aphis gossypii Glover (Hemiptera: Aphididae) on cotton. J Appl Entomol 128: 133-139.), the population growth curves for A. gossypii on cotton plants at similar physiological ages behaved similarly. Resende et al. (2004) linked aphid population fluctuations to the action of predators, and showed that the presence of predators causes the aphid population to drop. However, Kindlmann and Dixon (1996KINDLMANN P AND DIXON AFG. 1996. Population dynamics of a tree-dwelling aphid: individuals to populations. Ecol Model 89: 23-30.) explained that aphid dynamics do not exhibit a definite pattern but vary throughout the year, and that these dynamics can be similar or different depending on the mechanisms used by the insects. Similar patterns for aphid population dynamics, with an exponential increase and decrease of a population were reported by Ullah et al. (2014ULLAH S, BIBI R, BASHIR MA, IBRAHIM M, SAEED S AND HUSSAIN MA. 2014. Population dynamics of aphid and its bio-control agents in wheat crop. Pakistan J Nutr 13: 146-150.). These authors also noted that aphid populations on crops can increase during the vegetative growth phase of the plants; however, a population may decline due to reduction of plant quality, mycoses, and senescence (Honek and Martinkova 2004HONEK A AND MARTINKOVA Z. 2004. Host plant age and population development of a cereal aphid, Metopolophium dirhodum (Hemiptera: Aphididae). Bull Entomol Res 94: 19-26.). This may explain our observation that many plants started the senescence stage at 42 days after the aphid infestation began. However, further studies will be necessary for better understanding of population dynamics of aphids, taking into account different crop systems.
The equation system was solved for each crop system (t1, t2, t3, t4 and t5) and species (A. gossypii and A. craccivora). The model proposed considered that the ecological interaction between aphid species (intra-specific competition) was almost null, and for this reason each species was treated individually. The fits of the population growth rates over time are shown in Fig. 3 (A. gossypii) and Fig. 4 (A. craccivora).
The corresponding values of each parameter used for each simulation are listed in Tables II and III. The values of each parameter were defined by using the interpolation method. Taking into account the biological differences between the two species, we assumed that A. gossypii could not show a higher feeding rate on cowpea than on cotton, and the reverse for A. craccivora.
Parameter values for each crop system to simulate the population dynamics of A. craccivora .
The model resulted in a good prediction for the population dynamics of A. gossypii and A. craccivora, and also for all crop systems (p > 0.90) (Fig. 5). The results, shown in Figs. 3 and 4, are consistent with the catastrophe theory models of Kot et al. (1996KOT M, LEWIS MA AND DRIESSCHE PV. 1996. Dispersal data and the spread of invading organisms. Ecology 77: 2027-2042.) and Piyaratne et al. (2014PIYARATNE MKDK, ZHAO H, HU Z, HU X, WANG Y AND WANG B. 2014. A model to analyze weather impact on aphid population dynamics: an application on swallowtail catastrophe model. Eur Sci J 10: 1857-7431.). The fit of the aphid growth rate, in all cases, followed an exponential pattern, with one peak and a subsequent decline in the aphid population. This may indicate that the time period was important, because after the aphid infestations, the occurrence of events was dependent on the time elapsed. Other factors that were not included in this study but that should be considered in future field research are abiotic factors, such as the mean and cumulative rainfall during the growing season. According to Watts and Worner (2007WATTS MJ AND WORNER SP. 2007. Further sensitivity analysis of simple evolving connectionist systems applied to the Lincoln aphid data set. Bio Prot Ecol Tech Rep New Zeal 3: 1-11.), rainfall can differ over time. Variations in rainfall may reduce the aphid population during the time of rain incidence. This argument was well explained by M. Navas, unpublished data, who found no aphid occurrences during the rainy period.
SENSITIVITY ANALYSIS FOR COTTON APHID AND COWPEA APHID
The sensitivity analysis for A. gossypii demonstrated that the main parameters that influenced the aphid populations were those related to cotton consumption (δ and β) (Table II). This showed that the availability of cotton plants and the consumption rate regulate the population dynamics of this aphid, and explains why the aphid population dropped rapidly when the values of δ and β were increased, i.e. increasing the consumption rate. Since cotton is the main host of A. gossypii, this result was expected.
The analysis also showed that the influence of parameters related to the consumption of cotton and cowpea by wingless aphids was stronger than the consumption by winged aphids. One possible explanation is that the initial release of only immature aphids on each plot favored the proliferation of larger numbers of wingless aphids; however, winged aphids were produced by their wingless parents in the cotton crop systems over time.
Likewise, just as with A. gossypii, the population dynamics of A. craccivora was regulated predominantly by the rates of consumption on its main host, in this case, the cowpea (ε and φ) (Table III). However, the sensitivity of A. craccivora for both parameters was higher than the sensitivity of A. gossypii for δ and β. Considering the biology of the two species, this result was expected since the consumption of A. craccivora on cowpea plants was higher than that of A. gossypii on cotton plants, consequently accelerating the nutritional depletion of cowpea plants.
As with A. gossypii, the population of wingless A. craccivora had more influence on the model than did the population of winged aphids. Malaquias et al. (2015MALAQUIAS JB, RAMALHO FS, LIRA ACS, OLIVEIRA FQ, FERNANDES FS, ZANUNCIO JC AND GODOY WAC. 2015. Estimating the development of the fennel aphid, Hyadaphis foeniculi (Passerini) (Hemiptera: Aphiididae), using non-linear models. Pest Manag Sci 71: 744-751.) presented information to predict aphid outbreaks, and stated that it is useful for developing phenological models based on relationships involving temperature and development rates, facilitating the prediction of outbreaks of Hyadaphis foeniculi (Passerini) (Hemiptera: Aphididae) in fennel (Foeniculum vulgare Miller). Adetiloye (1985ADETILOYE PO. 1985. A mathematical model for formulating intercrop proportions for intercropping systems’ design. Ecol Modell 25: 81-93.) used mathematical models comparing intercropping in different crop systems to elucidate the advantages of the mixture of plants, taking productivity into account; however, he did not study the relationship between insect pests on the plants. Aphids pose a significant challenge to food production (Bell et al. 2015BELL JR, ALDERSON L, IZERA D, KRUGER T, PARKER S, PICKUP J, SHORTALL CR, TAYLOR MS, VERRIER P AND HARRINGTON R. 2015. Long-term phenological trends, species accumulation rates, aphid traits and climate: five decades of change in migrating aphids. J Anim Ecol 84: 21-34.) and structured models are commonly used to examine their population dynamics (Tenhumberg et al. 2009TENHUMBERG B, TYRE AJ AND REBARBER R. 2009. Model complexity affects transient population dynamics following a dispersal event: a case study with pea aphids. Ecology 90: 1878-1890.). The present results found using mathematical models to describe aphid growth rates are important because they can help to understand the population dynamics of different aphid species in sole crops of cotton and cowpea, and in cotton intercropped with cowpea. Knowledge of insect pest dynamics is essential for the establishment of integrated pest management, and modeling of dynamics can predict crop damage (Jonsson et al. 2014JONSSON M, BOMMARCO R, EKBOM B, SMITH HG, BENGTSSON J, CABALLERO-LOPEZ B, WINQVIST C AND OLSSON O. 2014. Ecological production functions for biological control services in agricultural landscapes. Methods Ecol Evol 5: 243-252.). The fitted model can also help to predict the timing of aphid peaks in each crop system. Prediction of aphid peaks is an important tool for ecological studies, and can also be useful for field crops (Malaquias et al. 2015).
CONCLUSIONS
The results obtained in this study are helpful in understanding the population dynamics of A. gossypii and A. craccivora on this naturally colored cotton cultivar and cowpea, respectively, in sole and in cotton-cowpea intercropping systems. The insights gained may be useful in decision-making, implementing controls, and determining the timing of population peaks for these important cotton and cowpea pests. We believe that simulations using these models is a new approach for short-term prediction of cotton-aphid or cowpea-aphid population dynamics in sole crops and cotton intercropped with cowpea. However, the models developed in this study require field testing before they can reach their full potential for predicting the population dynamics of A. gossypii and A. craccivora in sole and in intercropping systems.
ACKNOWLEDGMENTS
Support for this research was provided by the Financiadora de Estudos e Projetos (FINEP), Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), and Fundação de Amparo a Pesquisa do Estado de São Paulo (FAPESP).
REFERENCES
- ADETILOYE PO. 1985. A mathematical model for formulating intercrop proportions for intercropping systems’ design. Ecol Modell 25: 81-93.
- AFSHARI A, SOLEIMAN-NEGADIAN E AND SHISHEBOR P. 2009. Population density and spatial distribution of Aphis gossypii Glover (Homoptera: Aphididae) on cotton in Gorgan, Iran. J Agric Sci Technol 11: 27-38.
- ARBAB A, KONTODIMAS A AND SAHRAGARD DC. 2006. Estimating development of Aphis pomi (DeGeer) (Homoptera: Aphididae) using linear and nonlinear models. Environ Entomol 35: 1208-1215.
- BACHMANN AC, NAULT BA AND FLEISCHER SJ. 2014. Alate aphid (Hemiptera: Aphididae) species composition and richness in northeastern USA snap beans and an update to historical lists. Fla Entomol 97: 979-994.
- BELL JR, ALDERSON L, IZERA D, KRUGER T, PARKER S, PICKUP J, SHORTALL CR, TAYLOR MS, VERRIER P AND HARRINGTON R. 2015. Long-term phenological trends, species accumulation rates, aphid traits and climate: five decades of change in migrating aphids. J Anim Ecol 84: 21-34.
- BRABEC M, HONĚK A, PEKÁR S AND MARTINKOVÁ Z. 2014. Population dynamics of aphids on cereals: digging in the time-series data to reveal population regulation caused by temperature. PLoS ONE 9: 1-8.
- BURGIO G, KRISTENSEN HL, CAMPANELLI G, BAVEC F, BAVEC M, FRAGSTEIN PVON, DEPALO L, LANZONI A AND CANALI S. 2014. Effect of living mulch on pest/beneficial interaction, In: Rahmann G and Aksoy U (Eds), Eff. Living Mulch Pest/beneficial Interact. Building Organic Bridges, Germany, p. 741-744.
- CELINI L AND VAILLANT J. 2004. A model of temporal distribution of Aphis gossypii Glover (Hemiptera: Aphididae) on cotton. J Appl Entomol 128: 133-139.
- FABIÃO H AND SOUSA A. 2007. Effect of strip intercropping of cotton and maize on pest incidence and yield in Mornumbala District, Mozambique. Afr Crop Sci Confer Proceeds 8: 1053-1055.
- FERNANDES FS, RAMALHO FS, GODOY WAC, PACHU JKS, NASCIMENTO ARB, MALAQUIAS JB AND ZANUNCIO JC. 2013. Within plant distribution and dynamics of Hyadaphis foeniculi (Hemiptera: Aphididae) in field fennel intercropped with naturally coloured cotton. Fla Entomol 96: 92-103.
- GONZAGA JV, RAMALHO FS AND SANTOS JW. 1991. Ditribuição de Aphis gossypii no algodoeiro nos sistemas de plantio solteiro e consorciado. Pesq Agropec Brasil 26: 1839-1844.
- GUTIERREZ AP, HAVENSTEIN DE, NIX HA AND MOORE PA. 1974. The ecology of Aphis craccivora Koch and subterranean clover stunt virus in south-east Australia. J Appl Ecol 11: 21-35.
- HONEK A AND MARTINKOVA Z. 2004. Host plant age and population development of a cereal aphid, Metopolophium dirhodum (Hemiptera: Aphididae). Bull Entomol Res 94: 19-26.
- JONSSON M, BOMMARCO R, EKBOM B, SMITH HG, BENGTSSON J, CABALLERO-LOPEZ B, WINQVIST C AND OLSSON O. 2014. Ecological production functions for biological control services in agricultural landscapes. Methods Ecol Evol 5: 243-252.
- KADAM DB, KADAM DR AND LEKURWALE RS. 2014. Seasonal incidence of sucking pests of Bt cotton in different intercropping systems and their natural enemies. J Plant Pest Sci 1: 29-34.
- KINDLMANN P AND DIXON AFG. 1996. Population dynamics of a tree-dwelling aphid: individuals to populations. Ecol Model 89: 23-30.
- KOT M, LEWIS MA AND DRIESSCHE PV. 1996. Dispersal data and the spread of invading organisms. Ecology 77: 2027-2042.
- LEITE GLD, PICANÇO M, ZANUNCIO JC AND GUSMÃO MR. 2007. Factors affecting colonization and abundance of Aphis gossypii Glover (Hemiptera: Aphididae) on okra plantations. Ciênc Agrotec 31: 337-343.
- LIN R, LIANG H, ZHANG R, TIAN C AND MA Y. 2003. Impact of alfalfa/cotton intercropping and management on some aphid predators in China. J Appl Entomol 127: 33-36.
- MALAQUIAS JB, RAMALHO FS, LIRA ACS, OLIVEIRA FQ, FERNANDES FS, ZANUNCIO JC AND GODOY WAC. 2015. Estimating the development of the fennel aphid, Hyadaphis foeniculi (Passerini) (Hemiptera: Aphiididae), using non-linear models. Pest Manag Sci 71: 744-751.
- MITIKU A, CHALA A AND BEYENE Y. 2014. Effect of intercropping on aphid vectors and yield of pepper (Capsicum annum L.) in southern part of Ethiopia. Int J Technol Enhanc Emerg Eng Res 2: 24-34.
- MORAES GJM AND RAMALHO FS. 1980. Alguns insetos associados a Vigna unguiculata Walp no Nordeste. Embrapa-CPATSA, Petrolina, 10 p.
- MUNYULI T. 2009. Effects of native insect predators on population densities of Aphis craccivora and yields of Vigna unguiculata and Arachis hypogeae grown under various cropping systems in Kivu Province, Eastern Democratic Republic of Congo. Tunis J Plant Prot 4: 197-209.
- PAHLA I, TUMBARE T, CHITAMBA J AND KAPENZI A. 2014. Evaluation of Allium sativum and Allium cepa intercrops on the control of Brevicoryne brassicae (Homoptera: Aphididae) in Brassica napus. Int J Farming Allied Sci 3: 1069-1074.
- PARAJULEE MN, MONTANDON R AND SLOSSER JE. 1997. Relay intercropping to enhance abundance of insect predators of cotton aphid (Aphis gossypii Glover) in Texas cotton. Int J Pest Manag 43: 227-232.
- PERRY JN, WOIWOD IP AND HANSKI I. 1993. Using response-surface methodology to detect chaos in ecological time series. Oikos 68: 329-339.
- PHOOFOLO MW, GILES KL AND ELLIOTT NC. 2010. Effects of relay-intercropping sorghum with winter wheat, alfalfa, and cotton on lady beetle (Coleoptera: Coccinellidae) abundance and species composition. Environ Entomol 39: 763-774.
- PIYARATNE MKDK, ZHAO H, HU Z, HU X, WANG Y AND WANG B. 2014. A model to analyze weather impact on aphid population dynamics: an application on swallowtail catastrophe model. Eur Sci J 10: 1857-7431.
- PLANTEGENEST M, PIERRE JS, CAILLAUD CM, SIMON JC, DEDRYVER C AND CLUZEAU S. 1996. A model to describe the reproductive rate in the aphid Sitobion avenae (Hemiptera: Aphididae): A case study. Eur J Entomol 93: 545-553.
- POLLARD E AND ROTHERY P. 1994. A simple stochastic model of resource-limited insect populations. Oikos 69: 287-294.
- RAKHSHANI H, EBADI R AND MOHAMMADI AA. 2009. Population dynamics of alfalfa aphids and their natural enemies, Isfahan, Iran. J Agric Sci Technol 11: 505-520.
- RAMALHO FS, FERNANDES FS, NASCIMENTO ARB, NASCIMENTO JÚNIOR JL, MALAQUIAS JB AND SILVA CAD. 2012. Feeding damage from cotton aphids, Aphis gossypii Glover (Hemiptera: Heteroptera: Aphididae), in cotton with colored fiber intercropped with fennel. Ann Entomol Soc Am 105: 20-27.
- RESENDE ALS, PAIXÃO FHM, MENEZES EB, GUERRA JGM AND MENEZES ELA. 2004. Flutuação populacional de pulgões alados (Hemiptera: Aphididae) em cultivo de couve e sua relação com fatores climáticos e densidade de insetos predadores. Agronomia 38: 6-10.
- RIOLO MA, ROHANI P AND HUNTER MD. 2015. Local variation in plant quality influences large-scale population dynamics. Oikos 124: 1160-1170.
- SEQUEIRA R AND DIXON AFG. 1997. Population dynamics of tree-dwelling aphids: the importance of seasonality and time scale. Ecology 78: 2603-2610.
- SINGH A, SINGH S, SHARMA RK, SINGH PK AND KUMAR A. 2014. A mathematical model for n-species competition for aphid population in limited resources. J Appl Sci Res 2: 119-123.
- TENHUMBERG B, TYRE AJ AND REBARBER R. 2009. Model complexity affects transient population dynamics following a dispersal event: a case study with pea aphids. Ecology 90: 1878-1890.
- THORNLEY JHM AND FRANCE J. 2006. Mathematical models in agriculture: Quantitative methods for the plant, animal and ecological sciences. CABI, Wallingford, UK, 608 p.
- ULLAH S, BIBI R, BASHIR MA, IBRAHIM M, SAEED S AND HUSSAIN MA. 2014. Population dynamics of aphid and its bio-control agents in wheat crop. Pakistan J Nutr 13: 146-150.
- UNDERWOOD N. 2009. Effect of genetic variance in plant quality on the population dynamics of a herbivorous insect. J Anim Ecol 78: 839-847.
- WATTS MJ AND WORNER SP. 2007. Further sensitivity analysis of simple evolving connectionist systems applied to the Lincoln aphid data set. Bio Prot Ecol Tech Rep New Zeal 3: 1-11.
- ZHANG I, VAN DER WERF W, ZHANG S, LI B AND SPIERTZ JHJ. 2007. Growth, yield and quality of wheat and cotton in relay strip intercropping systems. F Crops Res 103: 178-188.
Publication Dates
-
Publication in this collection
01 Feb 2018 -
Date of issue
Jan-Mar 2018
History
-
Received
23 July 2015 -
Accepted
04 May 2016