Abstract
We introduce a new three-parameter lifetime model called the Lindley Weibull distribution, which accommodates unimodal and bathtub, and a broad variety of monotone failure rates. We provide a comprehensive account of some of its mathematical properties including ordinary and incomplete moments, quantile and generating functions and order statistics. The new density function can be expressed as a linear combination of exponentiated Weibull densities. The maximum likelihood method is used to estimate the model parameters. We present simulation results to assess the performance of the maximum likelihood estimation. We prove empirically the importance and flexibility of the new distribution in modeling two data sets.
Key words
Lindley G-Family; maximum likelihood; moments; order statistics
1-INTRODUCTION
We propose a new generalization of the Weibull (W) distribution named the Lindley Weibull (LiW) model. The W distribution has been widely used in reliability analysis and in applications of several different fields; see, for example Lai et al. (200319 LAI CD, XIE M AND MURTHY DNP. 2003. A modified Weibull distribution. IEEE Trans Reliab 52: 33-37.). Although its common use, a negative point of the distribution is the limited shape of its hazard rate function (hrf) that can only be monotonically increasing or decreasing or constant.
Generally, practical problems require a wider range of possibilities in the medium risk, for example, when the lifetime data present a bathtub shaped hazard function such as human mortality and machine life cycles. Researchers in the last years developed various extensions and modified forms of the W distribution to obtain more flexible distributions. A state-of-the-art survey on the class of such distributions can be found in Lai et al. (200118 LAI CD, XIE M AND MURTHY DNP. 2001. Bathtub-shaped failure rate life distributions. Handbook of Statistics 20: 69-104.) and Nadarajah (200926 NADARAJAH S. 2009. Bathtub-shaped failure rate functions. Qual Quant 43: 855-863.).
Some extensions of the W distribution are available in the literature such as the exponentiated W (exp-W) (Mudholkar et al. 199322 MUDHOLKAR GS AND SRIVASTAVA DK. 1993. Exponentiated Weibull family for analyzing bathtub failure-real data. IEEE Trans Reliab 42: 299-302., 199523 MUDHOLKAR GS, SRIVASTAVA DK AND FREIMER M. 1995. The expnentiated Weibull family: a reanalysis of the bus-motorfailure data. Technometrics 37: 436-445., 199624 MUDHOLKAR GS, SRIVASTAVA DK AND KOLLIA GD. 1996. A generalization of the Weibull distribution with application to the analysis of survival data. J of the Ameri Stat Associa 91: 1575-1583.), additive W (Xie and Lai 199534 XIE M AND LAI CD. 1995. Reliability analysis using an additive Weibull model with bathtubshaped failure rate function. Reliab Eng Syst Saf 52: 87-93.), Marshall–Olkin extended W (Ghitany et al. 200515 GHITANY ME, AL-HUSSAINI EK AND AL-JARALLAH RA. 2005. Marshall-Olkin extended Weibull distribution and its application to censored data. J Appl Stat 32: 1025-1034.), modified W (Lai et al. 2003, Sarhan and Zaindin 200931 SARHAN AM AND ZAINDIN M. 2009. Modified Weibull distribution. Applied Sciences 11: 123-136.), extended W (Xie et al. 200235 XIE M, TANG Y AND GOH TN. 2002. A modified Weibull extension with bathtub failure rate function. Reliab Eng Syst Saf 76: 279-285.), beta-W (Lee et al. 200720 LEE C, FAMOYE F AND OLUMOLADE O. 2007. Beta-Weibull distribution: some properties and applications to censored data. J Mod Appl Stat Methods 6(1): 173-186.), beta modified W (Silva et al. 201033 SILVA GO, ORTEGA EMM AND CORDEIRO GM. 2010. The beta modified Weibull distribution. Lifetime Data Anal 16: 409-430.), Kumaraswamy W (Cordeiro et al. 201012 CORDEIRO GM, ORTEGA EMM AND NADARAJAH S. 2010. The Kumaraswamy Weibull distribution with application to failure data. J Franklin Inst 347: 1399-1429.), transmuted W (Aryal and Tsokos 20116 ARYAL GR AND TSOKOS CP. 2011. Transmuted Weibull distribution: a generalization of the Weibull probability distribution. Eur J Pure Appl Math 4: 89-102.), Kumaraswamy inverse W (Shahbaz et al. 201232 SHAHBAZ MG, SHAHBAZ S AND BUTT NM. 2012. The Kumaraswamy inverse Weibull distribution. Pak J Stat Oper 8: 479-489.), exponentiated generalized W (Cordeiro et al. 201311 CORDEIRO GM, ORTEGA EMM AND DA CUNHA DCC. 2013. The exponentiated generalized class of distributions. J Data Sc 11: 1-27.), McDonald modified W (Merovci and Elbatal 201321 MEROVCI F AND ELBATAL I. 2013. The McDonald modified Weibull distribution: properties and applications. arXiv preprint arXiv:13092961. (In Press).), beta inverse W (Hanook et al. 201316 HANOOK S, SHAHBAZ MQ, MOHSIN M AND KIBRIA G. 2013. A Note on Beta Inverse Weibull Distribution. Commun Stat Theory Methods 42: 320-335.), transmuted additive W (Elbatal and Aryal 201314 ELBATAL I AND ARYAL G. 2013. On the transmuted additive Weibull distribution. Austrian J Stat 42: 117-132.), McDonald W (Cordeiro et al. 2014a10 CORDEIRO GM, HASHIMOTO EM AND ORTEGA EMM. 2014a. The McDonald Weibull model. Stat J Theor Appl Stat 48: 256-278.), Kumaraswamy modified W (Cordeiro et al. 2014b13 CORDEIRO GM, ORTEGA EMM AND SILVA GO. 2014b. The Kumaraswamy modified Weibull distribution: theory and applications. J Stat Comput Simul 84: 1387-1411.), transmuted complementary W geometric (Afify et al. 20143 AFIFY AZ, NOFAL ZM AND BUTT NS. 2014. Transmuted complementary Weibull geometric distribution. Pak J Stat Oper Res 10: 435-454.), transmuted exponentiated generalized W (Yousof et al. 201536 YOUSOF HM, AFIFY AZ, ALIZADEH M, BUTT NS, HAMEDANI GG AND ALI MM. 2015. The transmuted exponentiated generalized-G family of distributions. Pak J Stat Oper 11: 441-464.), Marshall–Olkin additive W (Afify et al. 20182 AFIFY AZ, CORDEIRO GM, YOUSOF HM, ABDUS S AND ORTEGA EMM. 2018. The Marshall-Olkin additive Weibull distribution with variable shapes for the hazard rate. Hacettepe J Math Stat 47: 365-381.), Kumaraswamy transmuted exponentiated additive W (Nofal et al. 201629 NOFAL ZM, AFIFY AZ, YOUSOF HM, GRANZOTTO DCT AND LOUZADA F. 2016. Kumaraswamy transmuted exponentiated additive Weibull distribution. Int J Stat Probab 5: 78-99.), generalized transmuted W (Nofal et al. 201728 NOFAL ZM, AFIFY AZ, YOUSOF HM AND CORDEIRO GM. 2017. The generalized transmuted-G family of distributions. Commun Stat Theory Methods 46: 4119-4136.), Topp-Leone generated W (Aryal et al. 20175 ARYAL GR, ORTEGA EMM, HAMEDANI GG AND YOUSOF HM. 2017. The Topp-Leone generated Weibull distribution: regression model, characterizations and applications. Int J Stat Probab 6: 126-141.) and Kumaraswamy complementary W geometric (Afify et al. 20171 AFIFY AZ, CORDEIRO GM, BUTT NS, ORTEGA EMM AND SUZUKI AK. 2017. A new lifetime model with variable shapes for the hazard rate. Braz J Probab Stat 31: 516-541.) distributions. Among these models, the exp-W is certainly the most popular one.
Recently, Cakmakyapan and Ozel (20178 CAKMAKYAPAN S AND OZEL G. 2017. The Lindley family of distributions: properties and applications. Hacettepe J Math Stat 46: 1-27.) proposed a new class of distributions called the Lindley generator (Li-G) with one extra parameter. For an arbitrary baseline cumulative distribution function (cdf) , the Li-G family with one extra positive shape parameter has cdf and probability density function (pdf) (for ) given by
and
respectively, where , and is a positive shape parameter.
The cdf and pdf of the W distribution are given by
and
respectively, where is a scale parameter and is a shape parameter.
The main objectives of this paper is to obtain a more flexible model by inducting just one extra shape parameter to the W model and to improve goodness-of-fit to real data. The basic motivations for the LiW distribution in practice are: (i) to make the kurtosis more flexible as compared to the baseline model; (ii) to produce skewness for symmetrical distributions; (iii) to construct heavy-tailed distributions that are not longer-tailed for modeling real data; (iv) to generate distributions with symmetric, left-skewed, right-skewed and reversed-J shaped; (v) to provide consistently better fits than other generated models under the same underlying distribution.
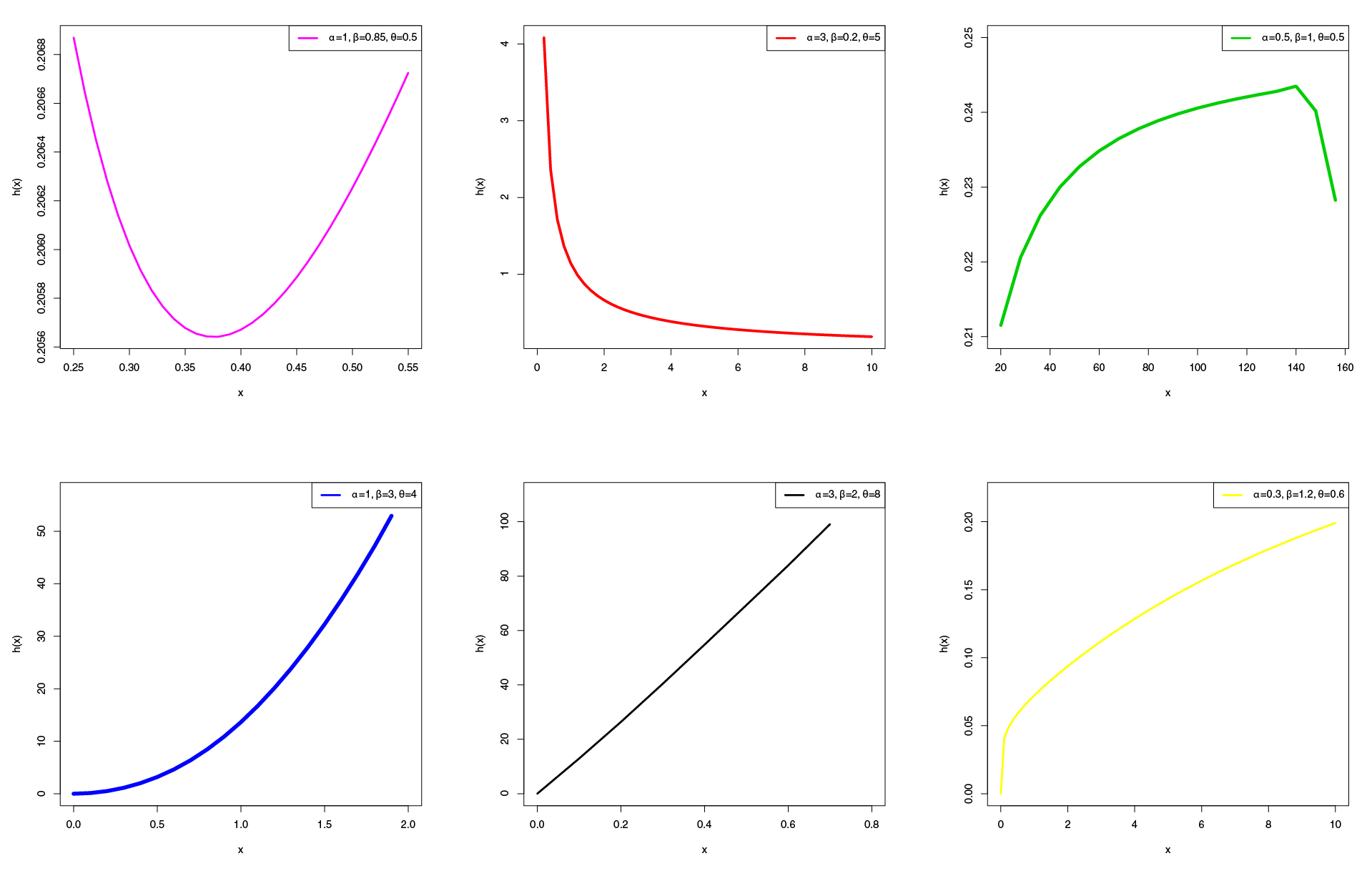
In fact, we prove empirically that the proposed distribution provides better fits to two real data sets than other six extended W distributions with three and four parameters (see Section 7). These examples really show that the new distribution is a good alternative for modeling survival data. Further, the LiW density can be symmetric, left-skewed, right-skewed or reversed J-shape (see Figure 1), whereas the LiW hrf can be bathtub, unimodal, reversed J-shape, monotonically increasing and decreasing shapes (see Figure 2). The skewness of the LiW distribution can range in the interval (-0.9, 6.5), whereas the skewness of the W distribution varies only in the interval (-0.63, 3.12) when the scale parameter is one and the shape parameter takes values from 0.75 to 10. Further, the spread for the LiW kurtosis is much larger ranging from 2.7 to 82, whereas the spread for the W kurtosis only varies from 2.85 to 18.98 with the above parameter values.
Based on the Li-G family, we construct the LiW distribution and provide a comprehensive description of some of its mathematical properties. The paper is outlined as follows. In Section 2, we define the LiW distribution. In Section 3, we derive useful representations for the pdf and cdf of the new distribution. Some mathematical properties including the ordinary and incomplete moments and other types of moments, quantile function (qf), moment generating function (mgf), order statistics and quantile spread order are investigated in Section 4. In Section 5, we obtain the maximum likelihood estimates (MLEs) of the model parameters. In Section 6, we verify the consistency of the estimates by means of some simulations. In Section 7, we prove empirically that the LiW distribution provides better fits than other seven lifetime models, each one having the same number of parameters, by means of two applications to real data sets. Finally, in Section 8, we provide some concluding remarks.
2-THE LIW DISTRIBUTION
In this section, we define the LiW model and provide some plots of its pdf and hrf. The LiW cdf is given by
The pdf corresponding to (5) is given by
The LiW model is very attractive to define special models with different types of hazard rates. Figure 1 displays some plots of the LiW density for different values of , and . These plots reveal that the LiW density can be symmetric, left-skewed, right-skewed or reversed J-shape. The hrf plots of the LiW distribution given in Figure 2 can be bathtub, unimodal, reversed J-shape, increasing and decreasing shapes.
3-LINEAR REPRESENTATION
In this section, we obtain a very useful linear representation for the LiW density. An expansion for (6) can be derived using the very popular exponentiated Weibull (exp-W) distribution, whose applications have been widespread in several areas. A random variable has the exp-W density with the baseline W given in (3) and power parameter , say exp-W , if its cdf and pdf (for ) are given by
and
respectively.
Using the generalized binomial expansion, the Li-G cdf in (1) can be expressed as
Consider the logarithmic power series given by
We can write
and then equation (7) becomes
Equivalently, we obtain
where and
By differentiating the last equation, the LiW pdf reduces to
where denotes the exp-W density with power parameters . Equation (8) reveals that the LiW density can be expressed as a linear combination of exp-W densities. Thus, several mathematical properties of the new model can be obtained from those properties of the exp-W distribution. This is the main result of this section. The hrf of the exp-W model allows for constant, monotonically increasing, monotonically decreasing, unimodal and bathtub shaped hazard rates. So, these forms also hold for the hrf of the new distribution (as shown in Figure 2).
4-SOME PROPERTIES
The formulas derived in this section are simple and manageable, and with the use of modern computer resources and their numerical capabilities, the LiW model may prove to be a useful addition to those distributions applied for modeling data in economics, medicine, reliability, engineering, among other areas.
4.1-ORDINARY AND INCOMPLETE MOMENTS
The several types of moments of a random variable are important especially in applied work. Some of the most important features and characteristics of a distribution can be studied through moments, e.g., tendency, dispersion, skewness and kurtosis, mean deviations, Bonferroni and Lorenz curves, etc.
First, we provide explicit formulas for the th ordinary and incomplete moments of the exp-G random variable (defined in the last section) given by
and
respectively, where , is the complete gamma function and is the lower incomplete gamma function.
Second, the th ordinary moment of , say , follows from (8) and the above results as
where .
The mean, variance, skewness and kurtosis of the LiW distribution are computed numerically for and some selected values of and using the R software. The numerical values displayed in Table I indicate that the skewness of the new distribution can range in the interval . The spread for its kurtosis is much larger ranging from to .
Mean, variance, skewness and kurtosis of the LiW distribution for and different values of and .
Third, the th incomplete moment of , say , can be expressed from (8) as
where .
The first incomplete moment given by (9) (with ) has some important applications. For example, the mean deviations about the mean and about the median of are given by and , respectively, where , Median is the median (see Section 4.2) and is easily calculated from (5).
The Bonferroni and Lorenz curves are defined (for a given probability ) by and , respectively, where is the qf of at .
Fourth, the th moment of the residual life of , say … and , uniquely determines , and it is given by
Using equation (8), we can write
where is the the falling factorial.
Fifth, the th moment of the reversed residual life of , denoted by for and , uniquely determines , and it is defined by
Then, reduces to
The mean residual life (MRL) and mean inactivity time (MIT) of follow simply by setting in and , respectively. The MRL of at age represents the expected additional life length for a unit which is alive at age , whereas the MIT of at age represents the waiting time elapsed since the failure of an item on condition that this failure had occurred in .
4.2-QUANTILE AND GENERATING FUNCTIONS
The qf of , say , is obtained by inverting the following equation
Let and . We have
and then
where denotes the negative branch of the Lambert W-function (also known as product log function in the Wolfram Language) which is the inverse function of . We can invert to obtain as
We have checked the above power series expansion for using the Mathematica software that gives as the principal solution for in .
The pdf of , , can be expanded using the power series
Then, the pdf of can be expressed as
where denotes a two-parameter W density with scale parameter and shape parameter . Equation (10) can be used to derive the mgf of the LiW distribution from that of a two-parameter W distribution.
Let be the complex parameter Wright generalized hypergeometric function with numerator and denominator parameters (Kilbas et al. 200617 KILBAS AA, SRIVASTAVA HM AND TRUJILLO JJ. 2006. Theory and Applications of Fractional Differential Equations Elsevier, 1st ed., Amsterdam, 540 p.) defined by the power series
Then, following similar algebraic developments of Nadarajah et al. (201327 NADARAJAH S, CORDEIRO GM AND ORTEGA EMM. 2013. The exponentiated Weibull distribution: A survey. Stat Pap 54: 839-877.), we can write the mgf of , say , as
where
Hence, the mgf of the Li-W model follows from (8) as
where
and
Equation (12) can be easily evaluated by scripts of the Maple, Matlab and Mathematica plataforms.
4.3-ORDER STATISTICS AND QUANTILE SPREAD ORDER
Order statistics make their appearance in many areas of statistical theory and practice. They enter in the problems of estimation and hypothesis tests in a variety of ways. We now discuss some properties of the order statistics for the LiW distribution. Let denote the th order statistic from a random sample from the LiW distribution. Then, the pdf of the th order statistic of is given by
The quantile spread (QS) of the random variable LiW having cdf (5) is given by
which implies
where and is the survival function. The QS of a distribution describes how the probability mass is placed symmetrically about its median and hence can be used to formalize concepts such as peakedness and tail weight traditionally associated with kurtosis. So, it allows us to separate concepts of kurtosis and peakedness for asymmetric models. Let and be two random variables following the LiW model with quantile spreads and , respectively. Then is called smaller than in quantile spread order, denoted as , if . The following properties of the QS order can be obtained:
The order islocation-free
The order is dilative
Let and be symmetric, then
The order implies ordering of the mean absolute deviation around the median, say MAD,
and
where
Finally
5-MAXIMUM LIKELIHOOD ESTIMATION
The MLEs enjoy desirable properties and can be used for confidence intervals and test statistics. The normal approximation for these estimators in large sample theory is easily handled either analytically or numerically. Here, we determine the MLEs of the parameters of the LiW model from complete samples only. Further works could be addressed using different methods to estimate the LiW parameters such as moments, least squares, weighted least squares, bootstrap, Jackknife, Cramér-von-Mises, Anderson-Darling, Bayesian analysis, among others, and compare the estimators based on these methods.
Let be a random sample from the LiW distribution with parameters and . Let () be the parameter vector. Then, the log-likelihood function for , say , is given by
Equation (13) can be maximized either directly by using the R ( optim function), SAS (PROC NLMIXED) or Ox program (sub-routine MaxBFGS) or by solving the nonlinear likelihood equations obtained by differentiating (13).
The score vector components, say , are available from the corresponding author.
Setting the nonlinear system of equations and solving them simultaneously yields the MLE of . These equations cannot be solved analytically but Newton-Raphson type algorithms can be used to solve them numerically.
For interval estimation of the model parameters, we require the observed information matrix which comes as output using the above maximization procedures. Under standard regularity conditions when , the distribution of can be approximated by a multivariate normal () distribution to construct approximate confidence intervals for the parameters. Here, is the total observed information matrix evaluated at . The method of the re-sampling bootstrap can be adopted for correcting the biases of the MLEs of the model parameters. Interval estimates may also be obtained using the bootstrap percentile method. Likelihood ratio tests can be performed for the proposed family of distributions in the usual way.
6-SIMULATION STUDY
We perform a Monte Carlo simulation study to verify the finite sample behavior of the MLEs of and . All simulation results are obtained from Monte Carlo replications carried out using the statistical software R. In each replication, a random sample of size is drawn from LiW and the conjugate gradient method has been used for maximizing the total log-likelihood function. The LiW random number generation is performed using the inversion method via the qf given in Section 4.2. Five different combinations of true parameter values in the first column of Tables II and III are adopted for the data generating process. Tables II and III list the mean values and mean square errors (MSEs) of the MLEs of the model parameters by taking sample sizes and . The figures in both tables indicate that the MSEs decrease when the sample size increases as expected under first-order asymptotic theory.
7-APPLICATIONS
We provide two applications of the LiW model to prove empirically its potentiality by comparing to the fits of other competitive models, namely: the Weibull Lindley (WLi) (Asgharzadeh et al. 20187 ASGHARZADEH A, NADARAJAH S AND SHARAFI F. 2018. Weibull Lindley distribution. Revstat 16: 87-113.), Weibull Fréchet (WFr) (Afify et al. 2016b4 AFIFY AZ, YOUSOF HM, CORDEIRO GM, ORTEGA EMM AND NOFAL ZM. 2016. The Weibull Frechet distribution and its applications. J Appl Stat 43: 2608-2626.), transmuted complementary Weibull geometric (TCWG) (Afify et al. 2014), Kumaraswamy Weibull (KwW) (Cordeiro et al. 2010), beta Weibull (BW) (Lee et al. 2007), gamma Weibull (GW) (Provost et al. 201130 PROVOST SB, SABOOR A AND AHMAD M. 2011. The gamma Weibull distribution. Pak J Stat 27: 111-131.) and W distributions, whose pdfs (for ) are given in Appendix A.
In order to compare the fits of the LiW model with other competing distributions, we consider the Anderson-Darling and Cramé r-von Mises () statistics. The two statistics are widely used to compare non-nested models and to determine how closely a specific cdf fits the empirical distribution of a given data set. These statistics are given by
and
respectively, where and the ’s values are the ordered observations.
Data Set I: Exceedances of Wheaton River Flood
The data represent the exceedances of flood peaks (in m/s) of the Wheaton River near Carcross in Yukon Territory, Canada. The data consist of 72 exceedances for the years 1958–1984, rounded to one decimal place (see Choulakian and Stephens 20019 CHOULAKIAN V AND STEPHENS MA. 2001. Goodness-of-fit for the generalized Pareto distribution. Technometrics 43: 478-484.).
Data Set II: Failure Times of 84 Aircraft Windshield
The second data set consists of 84 failure times for a particular windshield device. These failures do not result in damage to the aircraft but do result in replacement of the windshield (Murthy et al. 200425 MURTHY DNP, XIE M AND JIANG R. 2004. Weibull Models. Hoboken, NJ, 1st ed., J Wiley & Sons, 408 p.).
Tables IV and V list the values of the statistics and for eight fitted models to these two data sets. The MLEs and their corresponding standard errors (in parentheses) of the model parameters are also given in these tables. The figures in both tables reveal that the LiW distribution yields the lowest values of these statistics among the fitted models and then provides the best fit to both data sets. Hence, we prove empirically that the proposed distribution provides better fits in two applications than other six extended Weibull distributions with three and four parameters. There are too many models to fit and this fact really shows that the LiW distribution can be a good alternative for modeling survival data.
The figures in these tables are calculated using the MATHCAD program. In this program, we provide any initial values (in several cases from fits of special models) and then the program calculates the MLEs. After that, we update the initial estimates to obtain new values for the MLEs. This process continues up to obtain the final MLEs, which make the first derivatives of the log-likelihood function equal to zero.
More information is provided by a visual comparison of the histogram of the data with the fitted density functions. The plots of the fitted LiW, WLi, KwW, GW, BW, TCWG, WFr and W densities are displayed in Figures 3 and 4 for the two data sets, respectively.
The fitted densities for the: (a) LiW, WLi, KwW and GW models; (b) LiW, BW, TCWG, WFr and W models (data set I).
The fitted densities for the: (a) LiW, WLi, KwW and GW models; (b) LiW, BW, TCWG, WFr and W models (data set II).
CONCLUSIONS
In this paper, we propose a new three-parameter model, called the Lindley Weibull (LiW) distribution, which extends the Weibull (W) distribution. In fact, the LiW distribution is motivated by the wide use of the W distribution in many applied areas and also for the fact that the generalization provides more flexibility to analyze real data. The LiW density function can be expressed as a linear combination of the exponentiated-W (exp-W) densities. We derive explicit expressions for the ordinary and incomplete moments, moments of the (reversed) residual life, quantile and generating functions and order statistics. We discuss the maximum likelihood estimation of the model parameters. Two applications illustrate that the proposed model provides consistently better fit than other competitive models. We hope that the new distribution will attract wider applications in reliability, engineering and other areas of research. Estimation of the model parameters under the bayesian paradigm is currently underway and will be reported in a separate article elsewhere. However, we must make a note of the fact under the Bayesian setting, that a non informative prior approach is essentially maximum likelihood estimation under the classical approach. In the absence of an appropriate conjugate prior, the choice of prior will be a challenging in such a setting. As a future work we will consider bivariate and multivariate extension of the LiW distribution. In particular with the copula based construction method, trivariate reduction etc.
ACKNOWLEDGMENTS
The authors are thankful to the Editor and the reviewers for their constructive comments and suggestions which greatly improved the current version.
REFERENCES
-
1AFIFY AZ, CORDEIRO GM, BUTT NS, ORTEGA EMM AND SUZUKI AK. 2017. A new lifetime model with variable shapes for the hazard rate. Braz J Probab Stat 31: 516-541.
-
2AFIFY AZ, CORDEIRO GM, YOUSOF HM, ABDUS S AND ORTEGA EMM. 2018. The Marshall-Olkin additive Weibull distribution with variable shapes for the hazard rate. Hacettepe J Math Stat 47: 365-381.
-
3AFIFY AZ, NOFAL ZM AND BUTT NS. 2014. Transmuted complementary Weibull geometric distribution. Pak J Stat Oper Res 10: 435-454.
-
4AFIFY AZ, YOUSOF HM, CORDEIRO GM, ORTEGA EMM AND NOFAL ZM. 2016. The Weibull Frechet distribution and its applications. J Appl Stat 43: 2608-2626.
-
5ARYAL GR, ORTEGA EMM, HAMEDANI GG AND YOUSOF HM. 2017. The Topp-Leone generated Weibull distribution: regression model, characterizations and applications. Int J Stat Probab 6: 126-141.
-
6ARYAL GR AND TSOKOS CP. 2011. Transmuted Weibull distribution: a generalization of the Weibull probability distribution. Eur J Pure Appl Math 4: 89-102.
-
7ASGHARZADEH A, NADARAJAH S AND SHARAFI F. 2018. Weibull Lindley distribution. Revstat 16: 87-113.
-
8CAKMAKYAPAN S AND OZEL G. 2017. The Lindley family of distributions: properties and applications. Hacettepe J Math Stat 46: 1-27.
-
9CHOULAKIAN V AND STEPHENS MA. 2001. Goodness-of-fit for the generalized Pareto distribution. Technometrics 43: 478-484.
-
10CORDEIRO GM, HASHIMOTO EM AND ORTEGA EMM. 2014a. The McDonald Weibull model. Stat J Theor Appl Stat 48: 256-278.
-
11CORDEIRO GM, ORTEGA EMM AND DA CUNHA DCC. 2013. The exponentiated generalized class of distributions. J Data Sc 11: 1-27.
-
12CORDEIRO GM, ORTEGA EMM AND NADARAJAH S. 2010. The Kumaraswamy Weibull distribution with application to failure data. J Franklin Inst 347: 1399-1429.
-
13CORDEIRO GM, ORTEGA EMM AND SILVA GO. 2014b. The Kumaraswamy modified Weibull distribution: theory and applications. J Stat Comput Simul 84: 1387-1411.
-
14ELBATAL I AND ARYAL G. 2013. On the transmuted additive Weibull distribution. Austrian J Stat 42: 117-132.
-
15GHITANY ME, AL-HUSSAINI EK AND AL-JARALLAH RA. 2005. Marshall-Olkin extended Weibull distribution and its application to censored data. J Appl Stat 32: 1025-1034.
-
16HANOOK S, SHAHBAZ MQ, MOHSIN M AND KIBRIA G. 2013. A Note on Beta Inverse Weibull Distribution. Commun Stat Theory Methods 42: 320-335.
-
17KILBAS AA, SRIVASTAVA HM AND TRUJILLO JJ. 2006. Theory and Applications of Fractional Differential Equations Elsevier, 1st ed., Amsterdam, 540 p.
-
18LAI CD, XIE M AND MURTHY DNP. 2001. Bathtub-shaped failure rate life distributions. Handbook of Statistics 20: 69-104.
-
19LAI CD, XIE M AND MURTHY DNP. 2003. A modified Weibull distribution. IEEE Trans Reliab 52: 33-37.
-
20LEE C, FAMOYE F AND OLUMOLADE O. 2007. Beta-Weibull distribution: some properties and applications to censored data. J Mod Appl Stat Methods 6(1): 173-186.
-
21MEROVCI F AND ELBATAL I. 2013. The McDonald modified Weibull distribution: properties and applications. arXiv preprint arXiv:13092961. (In Press).
-
22MUDHOLKAR GS AND SRIVASTAVA DK. 1993. Exponentiated Weibull family for analyzing bathtub failure-real data. IEEE Trans Reliab 42: 299-302.
-
23MUDHOLKAR GS, SRIVASTAVA DK AND FREIMER M. 1995. The expnentiated Weibull family: a reanalysis of the bus-motorfailure data. Technometrics 37: 436-445.
-
24MUDHOLKAR GS, SRIVASTAVA DK AND KOLLIA GD. 1996. A generalization of the Weibull distribution with application to the analysis of survival data. J of the Ameri Stat Associa 91: 1575-1583.
-
25MURTHY DNP, XIE M AND JIANG R. 2004. Weibull Models. Hoboken, NJ, 1st ed., J Wiley & Sons, 408 p.
-
26NADARAJAH S. 2009. Bathtub-shaped failure rate functions. Qual Quant 43: 855-863.
-
27NADARAJAH S, CORDEIRO GM AND ORTEGA EMM. 2013. The exponentiated Weibull distribution: A survey. Stat Pap 54: 839-877.
-
28NOFAL ZM, AFIFY AZ, YOUSOF HM AND CORDEIRO GM. 2017. The generalized transmuted-G family of distributions. Commun Stat Theory Methods 46: 4119-4136.
-
29NOFAL ZM, AFIFY AZ, YOUSOF HM, GRANZOTTO DCT AND LOUZADA F. 2016. Kumaraswamy transmuted exponentiated additive Weibull distribution. Int J Stat Probab 5: 78-99.
-
30PROVOST SB, SABOOR A AND AHMAD M. 2011. The gamma Weibull distribution. Pak J Stat 27: 111-131.
-
31SARHAN AM AND ZAINDIN M. 2009. Modified Weibull distribution. Applied Sciences 11: 123-136.
-
32SHAHBAZ MG, SHAHBAZ S AND BUTT NM. 2012. The Kumaraswamy inverse Weibull distribution. Pak J Stat Oper 8: 479-489.
-
33SILVA GO, ORTEGA EMM AND CORDEIRO GM. 2010. The beta modified Weibull distribution. Lifetime Data Anal 16: 409-430.
-
34XIE M AND LAI CD. 1995. Reliability analysis using an additive Weibull model with bathtubshaped failure rate function. Reliab Eng Syst Saf 52: 87-93.
-
35XIE M, TANG Y AND GOH TN. 2002. A modified Weibull extension with bathtub failure rate function. Reliab Eng Syst Saf 76: 279-285.
-
36YOUSOF HM, AFIFY AZ, ALIZADEH M, BUTT NS, HAMEDANI GG AND ALI MM. 2015. The transmuted exponentiated generalized-G family of distributions. Pak J Stat Oper 11: 441-464.
Publication Dates
-
Publication in this collection
Jul-Sep 2018
History
-
Received
15 Aug 2017 -
Accepted
16 Nov 2017