Abstract
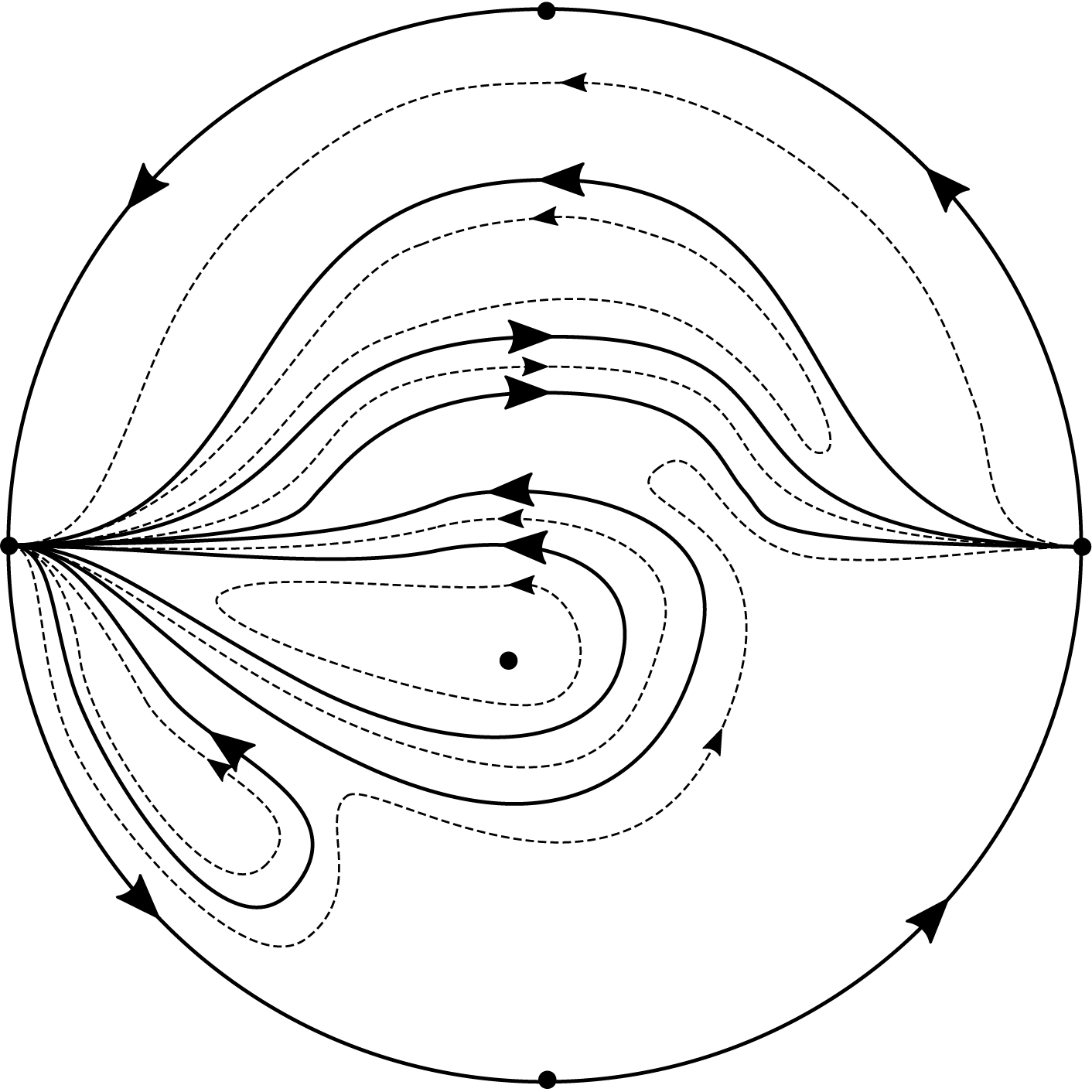
In this paper we describe the global phase portrait of the Hamiltonian system associated to a Pinchuk map in the Poincaré disc. In particular, we prove that this phase portrait has 15 separatrices, five of them singular points, and 7 canonical regions, six of them of type strip and one annular.
Key words
center; global injectivity; real Jacobian conjecture; Pinchuk map
Introduction
As far as we know, the simplest class of non-injective polynomial local diffeomorphisms of are the Pinchuk maps, constructed by Pinchuk (1994PINCHUK S. 1994. A counterexample to the strong real Jacobian conjecture. Math Z 217: 1-4.). The existence of these maps disproves the real Jacobian conjecture, that a polynomial local diffeomorphism of is globally injective. One open problem is to know what exactly fails in this conjecture.
One of the most known conditions for a local diffeomorphism to be a global one is that it is proper. The asymptotic variety of a map of is the set of points where the map is not proper (i.e., points that are limits of the map under sequences tending to infinity). In particular, a local diffeomorphism is a global diffeomorphism if and only if this set is empty. Gwoździewicz (2000GWOŹDZIEWICZ J. 2000. A geometry of Pinchuk’s map. Bull Polish Acad Sci Math 48: 69-75.) and Campbell (arXiv:math/9812032 in 1998, 2011CAMPBELL LA. 2011. The asymptotic variety of a Pinchuk map as a polynomial curve. Appl Math Lett 24: 62-65.) calculated the asymptotic variety of two Pinchuk maps in details. Our aim in this paper is to do a similar work, i.e., to describe a Pinchuk map, but now from a different point of view.
Let be an open connected set. Let be a local diffeomorphism. Let and consider the Hamiltonian system
where the dot denotes derivative with respect to the time . The singular points of system (1) are characterized by the following result, that we shall prove below.
Lemma 1.The singular points of system (1) are the zeros of , each of them is a center of system (1).
The following is a generalization of the characterization of global invertibility of polynomial maps given by Sabatini (1998SABATINI M. 1998. A connection between isochronous Hamiltonian centres and the Jacobian conjecture. Nonlinear Anal 34: 829-838.). This version is due to Braun and Llibre (arXiv:1706.02643 in 2017).
Theorem 2. Let such that . The center of system (1) is global if and only if (i) is globally injective and (ii) or is an open disc centered at the origin.
In the special case that is a polynomial map and , it follows that provided is injective (Białynicki-Birula and Rosenlicht 1962BIAŁYNICKI-BIRULA A AND ROSENLICHT M. 1962. Injective morphisms of real algebraic varieties. Proc Amer Math Soc 13: 200-203.). Hence, in this case, is a global center of (1) if and only if is globally injective. An application of this result was given by Braun et al. (2016BRAUN F, GINÉ J AND LLIBRE J. 2016. A sufficient condition in order that the real Jacobian conjecture in R2 holds. J Differential Equations 260: 5250-5258.).
Since the phase portrait on the Poincaré sphere of a Hamiltonian polynomial vector field having a global center is simple, i.e., at the infinite either it does not have singular points, or the infinite singular points are formed by two degenerate hyperbolic sectors (for Hamiltonian vector fields, the infinity contains only isolated singular points), it is interesting to know how complex can be the phase portrait of a non-global center of a Hamiltonian system (1).
In this paper we provide the qualitative global phase portrait of the Hamiltonian system (1) when is given by the Pinchuk map considered by Campbell (1998, 2011), after a translation in the target in order to have only a point such that . More precisely, we prove the following result.
Theorem 3. Let , where is the Pinchuk map considered by Campbell (1998, 2011) (see the definition below). Then the phase portrait of the Hamiltonian system (1) in the Poincaré disc is topologically equivalent to the phase portrait given in Fig. 1.
To prove Theorem 3, we first study the infinite singular points of system (1). These infinite singular points are very degenerate, and we apply homogeneous and quasi-homogeneous blow ups to study them. Then, we complete the proof of Theorem 3 by proving that the separatrix configuration of system (1) is qualitatively the one presented in Fig. 1.
We think that a good understanding of what fails in the real Jacobian conjecture could be interesting to investigate a related problem, the Jacobian conjecture in , that a polynomial local diffeomorphism whose Jacobian determinant is constant is globally injective. This conjecture remains unsolved until now. For the Jacobian conjecture we address the reader to the works of Bass et al. (1982BASS H, CONNEL EH AND WRIGHT D. 1982. The Jacobian conjecture: reduction of degree and formal expansion of the inverse. Bull Amer Math Soc 7: 287-330.) and Van Den Essen (2000VAN DEN ESSEN A. 2000. Polynomial automorphisms and the Jacobian conjecture. Progress in Mathematics, 190. Basel: Birkhäuser Verlag, 329 p.).
Injectivity, centers and a Pinchuk map
We begin with the proof of Lemma 1.
Proof of Lemma 1. Let be a singular point of the Hamiltonian system (1). We have
which is true if and only in because the Jacobian determinant of is nowhere zero.
The point is a center of the Hamiltonian system (1) because it is an isolated minimum of .
Now, we select the map that we are going to work in this paper. Let and . A Pinchuk map is a non-injective polynomial map with nowhere zero Jacobian determinant of the form such that and , where is chosen so that . The following is the Pinchuk map studied by Campbell (1998, 2011):
According to Campbell (2011), the points and have no inverse image under , all the other points of the curve
which is a parametrization of the asymptotic variety of , have exactly one inverse image under this map, and the points of have two inverse images. Hence, in particular, the point has precisely one inverse image under .
We consider the map given by the translation
Observe that is a Pinchuk map according to our above-definition. Moreover, now there exists exactly one point such that . From Lemma 1 the point is the only finite singular point of system (1), corresponding to a non-global center of this system according to Theorem 2. Further, the curve
, is the asymptotic variety of , whose points have exactly one inverse image over , but the points and , which have none.
From now on, we restrict our attention to the specific Pinchuk map (2).
We first calculate the coordinates of the point . Observe that is a factor of . If this factor annihilates, then and . The other factor of is
We observe that and do not annihilate at the same time, thus the first coordinate of the point is not . Moreover, since the leading coefficient of as a polynomial in is , it follows that the first coordinate of will be a point where the resultant in between and is zero. This resultant is the cubic multiplied by . The discriminant of is negative, so it has only one real root, which will be the first coordinate of the point .
Repeating a similar reasoning now looking and as polynomials in , we calculate their resultant and obtain that its zero is the only real root of the cubic , which will be the second coordinate of the point .
Hence approximately. Since is a center, the only finite singular point of system (1), near the phase portrait of this system is simple. Indeed, since is the minimum point of , it follows that the gradient of points outward of each closed orbit of the center, and so each closed orbit of the center rotates in counterclockwise around .
In the following section we shall investigate the infinite of system (1).
The infinite of system
In this section, we will use results and notations on the Poincaré compactification of polynomial vector fields of . In particular , are the canonical local charts of the Poincaré sphere .
For details on this technique we refer the reader to Chapter 5 of (Dumortier et al. 2006DUMORTIER F, LLIBRE J AND ARTÉS JC. 2006. Qualitative theory of planar differential systems. Universitext, Springer-Verlag, 298 p.) or to (González Velasco 1969GONZÁLEZ VELASCO EA. 1969. Generic properties of polynomial vector fields at infinity. Trans Amer Math Soc 143: 201-222.).
We call a singular point of a vector field linearly zero when the linear part of the vector field at this point is identically zero.
We begin by proving a general fact about the infinite singular points of Hamiltonian systems of the form (1). Writing , where is the homogeneous part of degree of the polynomial , it is simple to conclude that the infinite singular points of system (1) in the local charts and are the points satisfying and , respectively. Let be an infinite singular point of system (1) and assume it is in the chart . The linear part of the vector field at is
Assuming , we have and and . Since , it follows that , and hence . Therefore, is a linearly zero singular point. This proves the following result.
Lemma 4. The infinite singular points of the Hamiltonian system (1) are linearly zero.
Now, we return to the Pinchuk map defined by (2). Observe that the highest homogeneous part of is . Thus, the origins of the charts and are the infinite singular points of the Hamiltonian system (1), each of them linearly zero from Lemma 4.
We will use the quasi-homogeneous directional blow up technique to desingularize each of these infinite singular points. An exposition about blow-ups can be found in (Álvarez et al. 2011ÁLVAREZ MJ, FERRAGUT A AND JARQUE X. 2011. A survey on the blow up technique. Internat J Bifur Chaos Appl Sci Engrg 21: 3103-3118.), see also Chapter 3 of (Dumortier et al. 2006). We now recall the directional blow up transformations.
By the quasi-homogeneous blow up in the positive (resp. negative) -direction with weights and , or simply -blow up in the positive (resp. negative) -direction, we mean the transformation which carries the variables to the variables according to the formulas
respectively. Similarly, by the quasi-homogeneous blow up in the positive (resp. negative) -direction with weights and , or simply -blow up in the positive (resp. negative) -direction, we mean the transformations
respectively.
Clearly if (resp. ) is odd, then, the blow up in the positive -direction (respec. -direction) provides the information of the respectively negative blow ups. Also, if is odd, the -directional blow ups swap the second and third quadrants, while the -directional blow ups swap the third and the fourth quadrants if is odd. After the -blow up in the -direction, a system is transformed into
with and , in the positive and negative directions according to . Similarly, the -blow up in the -direction transforms into
with and , in the positive and in the negative directions according to .
After the blow up in the -direction (resp. -direction) we cancel a common appearing factor () for a suitable . So, if is odd, the direction of the orbits are reversed in ().
The weights and are chosen analyzing the Newton polygon of , see the construction in (Álvarez et al. 2011).
The application of -blow ups with usually reduces the number of blow ups necessary for studying the local phase portrait of a linearly zero singular point.
To make the exposition clearer, we shall apply the most part of the blow ups in the -direction. So, sometimes, we will first apply a -change, before making the blow-up.
In the next two subsections we will desingularize the origin of the charts and , respectively. We will denote the coordinates of the system in the step of the algorithm as the variables , so that after either a -change, a translation or a blow up, the new obtained system will be written in the variables . In each step, we will denote the system simply as .
Since the Hamiltonian system (1) with the polynomials and given by (2) has degree , it follows that for the calculations in each step of the algorithm we have to deal with polynomials of very high degree. So, we persuade these calculations with the algebraic manipulator Mathematica. We do not show in each step the whole expressions of the systems because this would be impractical.
The origin of the chart
We write the compactification of system (1) in the chart in the variables , as . From Lemma 4, the singular point is linearly zero.
We first apply a -change and write the new system in the variables as .
The Newton polygon of system has only one compact edge contained in the straight line . We apply -blow ups in the positive -direction and in the positive and negative -directions obtaining systems and , in the variables and , after canceling the common factors and , respectively. The first terms of these systems have the following expressions:
and
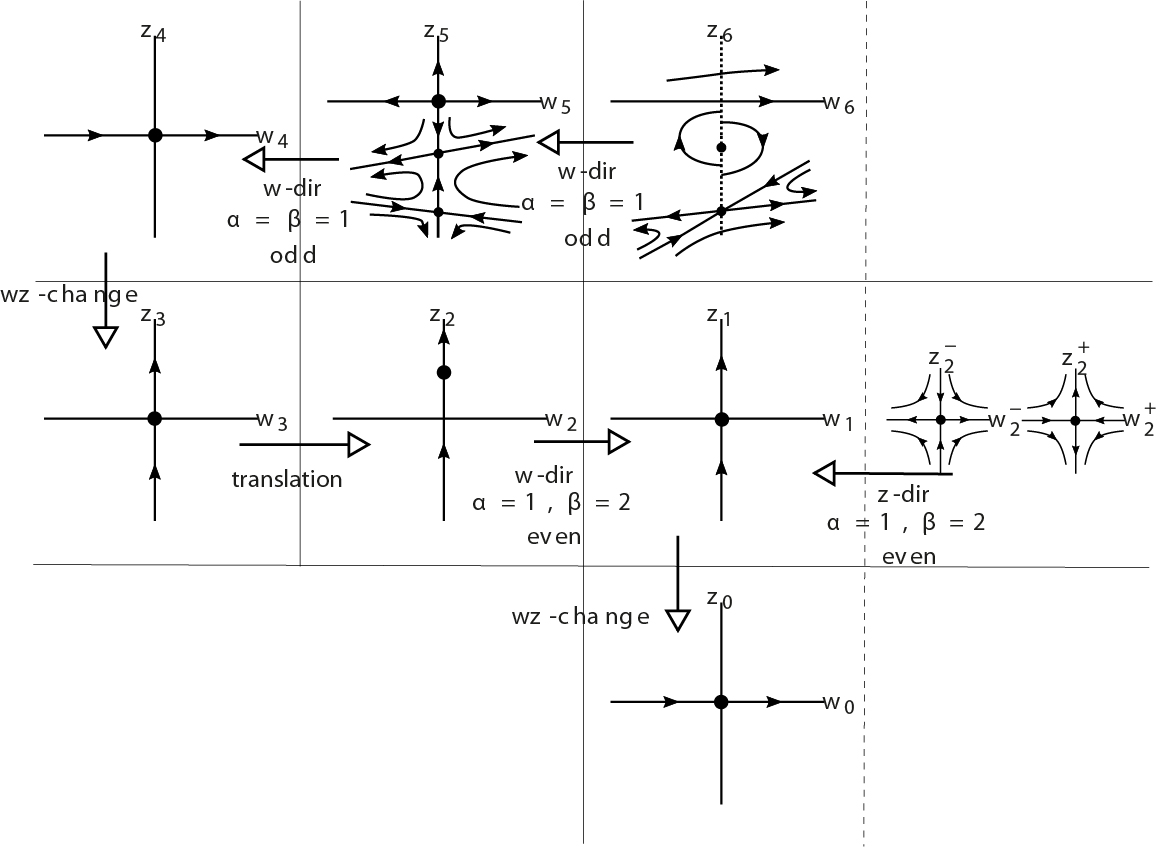
The only singular point of over the line is the linearly zero singular point . The origin of the systems are saddles as depicted in the planes and of Fig. 2.
The reader can follow a schema of each step of the calculations in Fig. 2. We just need to analyze the origin of the systems , because the other singularities over the lines will correspond to the singularity of .
We now analyze this linearly zero singularity. We first do a translation bringing this point to the origin, obtaining the new system in the variables . We also apply a -change obtaining the system in the variables . The Newton polygon of this system has two compact edges. We choose the one contained in the straight line . This compact edge has the point of negative abscissa , thus, concerning -blow ups, it follows from Proposition 3.2 of (Álvarez et al. 2011) that is not a characteristic direction, and so we only need to apply a -directional -blow up, obtaining the system in the variables , after canceling the common factor . The first terms of are:
Over the line , the singular points of are and two points of the form , with the two real solutions of
The discriminant of this quartic equation is negative, thus, it has two real solutions. Those are approximately and . The singular point is linearly zero and the other two singular points are saddles, as represented in the -plane of Fig. 2.
Now, we study the linearly zero point of . It is clear from (4) that the characteristic equation of is identically zero, so is a dicritical singular point. We apply -blow ups in both the - and -directions obtaining systems and in the variables and , after canceling the factors and , respectively. System does not have as a singular point, so we just need to consider system over the line . We have
By using Sturm’s theorem (see for instance (Isaacson and Keller 1994ISAACSON E AND KELLER HB. 1994. Analysis of numerical methods, Corrected reprint of the 1966 original Wiley. New York: Dover Publications, 541 p.); in the software Mathematica, the Sturm theorem is programed by the instruction CountRoots) we see that the polynomial of degree multiplying in has no real roots, so, the only singular points are and . The first one is a weak focus and the second one is a saddle, as depicted in the plane of Fig. 2. Since the origin of is dicritical, it follows that each orbit crossing the line will correspond to two orbits tending to in positive or negative directions.
We now begin the process of blowing down.
It is simple to conclude that the phase portrait of the system close to the origin is qualitatively the one depicted in (a) of Fig. 3.
Consequently, by considering also the information close to the other two singular points in the line (see the plane of Fig. 2), we can understand the behavior near the origin of system . We then apply a -change and conclude that the behavior of system near the origin is the one presented qualitatively in (b) of Fig. 3.
By translating to and by using the information provided by the saddles of planes , we make the blow downs with and , obtaining the origin of system . We then finally apply a -change and conclude that the origin of system is qualitatively as drawn in Fig. 4.
The origin of chart
As in the calculations made above, we write the compactified vector field in the chart as . The Newton polygon of has two compact edges: one of them contained in the straight line . We apply a -blow up in the -direction, obtaining the system after canceling the factor . The first terms of and are:
The polynomials and have degree .
It is clear that at we have a saddle. The other singular point of in the line is , and it is a linearly zero point. See the -plane of Fig. 5. The reader can follow the steps of the calculations in the schema shown in this figure. We just warn that, differently of Fig. 2, we already draw the final phase portrait of each step, including the behavior close to the linearly zero points (information that we will know only after persuading all the blow ups).
We also apply -blow ups in the positive and negative -directions, obtaining the systems , respectively, with linearly zero singular points at . The polynomials and have degree and is a factor of .
We do not need to analyze the other singular points over the lines , as the information provided by them is already contained in the -directional blow up. We desingularize these points applying -blow ups in the -direction. Here, we do not need to apply blow ups in the -directions because the characteristic equations of the systems are
and so are not characteristic directions. We obtain the systems after canceling a factor . The polynomials and have degree , and up to order they have the same expressions:
Thus, at the systems have a saddle, as depicted in the planes of Fig. 5. Moreover, any other singularity of the form must satisfy
By using Sturm’s theorem, we conclude that this equation has no real solution.
Now, we desingularize the point of system . First, we apply a translation to bring this point to the origin, obtaining the system in the variables . We also apply a -change obtaining the system in the variables . The Newton polygon of this system has only one compact edge contained in the line , and this edge has points of negative abscissa, so, concerning -blow ups we just need to apply them in the -direction, according to Proposition 3.2 of (Álvarez et al. 2011). Hence, we apply a -blow up in the positive -direction, obtaining the system in the variables , after canceling a factor of . These polynomials have degree , and their first terms are:
Clearly, is a singularity corresponding to a saddle. The other singular point in the line is , where is the only real root of the cubic
which is approximately . This cubic has only one real root because its discriminant is negative. A calculation shows that is linearly zero. See the plane in Fig. 5.
Now, we apply a translation to bring the point to the origin, obtaining system written in the variables . Since is not a rational number, we do this translation with a parameter , and thus and are polynomials in and . We simplify these polynomials substituting them by the remainder of the division of each of them by , obtaining so polynomials of degree in , and hence when we substitute by , we obtain the same expressions. We keep the notation .
The Newton polygon of this system has just one compact edge contained in the line . So, the blow ups here will be homogeneous ones. The characteristic equation of system is a multiple of
with . It would thus be enough to apply a -blow up in the -direction, and to study the singularities of the new system in (this could evidently also be concluded by observing that the compact edge of the Newton polygon of has a point of negative ordinate). We prefer though to apply -blow ups in the and -directions and to study the singularities of the new systems either in the line and in the origin, respectively. The reason why we do this is that the singularities other than the origin are linearly zero and we have to apply new blow ups after persuading a translation. The matter here is that the blow up in the -direction produces a vector field of degree , while the blow up in the -direction produces a vector field of degree . Thus, it is simpler to do a translation and after to apply the polynomial remainder in the vector field with smaller degree.
Then, after applying -blow ups in either the positive - and -directions, we obtain the systems and in the variables and , after canceling factors and , respectively. The first terms of these systems are:
with
and
with .
The origin of system is a saddle (see the plane in Fig. 5). On the other hand, the singularities of over the line are the points , with the real solutions of
with . The discriminant of this quadratic equation is a polynomial in whose division by has remainder equal to . This means that the only real solution of (5) is , where and are the coefficients of and in (5), respectively. Substituting by after applying the polynomial remainder again we have
The point is linearly zero, so, we translate it to the origin obtaining the system in the variables . We again persuade this translation considering as a polynomial of . Again and will be polynomials in and . As before we substitute these polynomials by the remainder of the division of them by , obtaining polynomials of degree in . We keep the notation and for them.
The Newton polygon of this system has only one compact edge contained in the straight line . The characteristic equation of this system has as a solution.
As above, we apply -blow ups in either the positive - and -directions, obtaining the systems and in the variables and , respectively. We then study the origin of and the singularities of over the line . The reason is again computational, as the degree of is and the degree of is . The first terms of these systems are:
with , and
with .
System has a saddle at the origin (see the plane in Fig. 5), while the singular points of over the line are the points , with the real roots of
with . The discriminant of this equation is a polynomial in whose division by has remainder . Thus, the only real solution is , where and are the coefficients of and of the equation, respectively. After applying the polynomial remainder, we substitute by obtaining
The point is linearly zero, so, we translate it to the origin obtaining the system in the variables . As before, we make this translation with the parameter , so that and are polynomials in . Keeping the notation we substitute these polynomials by the remainder of the division of them by .
As before the Newton polygon of this system has only one compact edge contained in the straight line . Moreover, the characteristic equation does not have as a solution. Here, we just apply a -blow up in the positive -direction, obtaining system in the variables , after canceling the factor (here we do not use the superscript as this is the only system in this step). The degree of this new system is , but as we are going to see, just the origin is a singular point in the line . The first terms of and are:
with .
Now, over the line , the singular points of are and the points , with the real roots of
with . The discriminant of this equation after applying the polynomial remainder is
It is simple to conclude that , thus, only is a singular point of in . This singular point is the saddle depicted in the plane of Fig. 5.
Since the behavior near each appearing singular points in each step above is very simple, the blow down of each step is also very simple: following the arrays in Fig. 5, it is easy to conclude that the origin of has a degenerate hyperbolic sector as shown in the -plane of Fig. 5.
The global phase portrait
We begin with a background on separatrices and canonical regions of the Poincaré compactification in the Poincaré disc of a polynomial system . Let be the flow of defined in . As usual we denote by the flow of on an invariant subset . Two flows and are said to be topologically equivalent if there exists a homeomorphism sending orbits of onto orbits of preserving or reversing the orientation of all the orbits.
Following Markus (1954MARKUS L. 1954. Global structure of ordinary differential equations in the plane. Trans Amer Math Soc 76: 127-148.), we say that the flow is parallel if it is topologically equivalent to one of the following flows: (i) the flow defined in by the system ; (ii) the flow defined in by the system in polar coordinates ; and (iii) the flow defined in by the system in polar coordinates . Parallel flows topologically equivalent to (i), (ii) and (iii) are called stripannular and spiral (or radial), respectively.
We denote by the orbit of passing through when with maximal interval , and the positive (resp. negative) orbit of by (resp. ). Then we set , here as usual denotes the closure of . Observe that differs from in the case of periodic orbits and singular points: indeed, and in this case (similarly for and ). An orbit of is called a separatrix of if it is not contained in an open neighborhood such that is parallel and such that both for all and consists of and exactly two orbits and such that .
If is a polynomial vector field it is known that the separatrices of are (i) the finite and infinite singular points of ; (ii) the orbits of contained in the boundary of ; (iii) the limit cycles of ; and (iv) the separatrices of the hyperbolic sectors of the finite and infinite singular points of . Moreover, if has finitely many finite and infinite singular points and finitely many limit cycles, then has finitely many separatrices. We call each connected component of the complement of the union of separatrices a canonical region of . Neumann (1975NEUMANN DA. 1975. Classification of continuous flows on 2-manifolds. Proc Amer Math Soc 48: 73-81.) proved that each canonical region of a vector field is parallel.
To the union of the separatrices of together with an orbit belonging to each canonical region of we call a separatrix configuration of . We say that the separatrix configurations and of and are topologically equivalent if there exists an orientation preserving homeomorphism from to which transforms orbits of onto orbits of . The following is the Markus-Neumann-Peixoto classification theorem (Markus 1954, Neumann 1975, Neumann and O’Brien 1976NEUMANN DA AND O’BRIEN T. 1976. Global structure of continuous flows on 2-manifolds. J Differ Equations 22: 89-110., Peixoto 1973PEIXOTO MM. 1973. On the classification of flows on 2-manifolds. Dynamical systems (Proc. Sympos., Univ. Bahia, Salvador, 1971). New York: Academic Press, p. 389-419., Dumortier et al. 2006) for the Poincaré compactification in the Poincaré disc of polynomial systems.
Theorem 5 (Markus-Neumann-Peixoto). Let and be the Poincaré compactification of two polynomial systems and , respectively. The flows of and on the Poincaré disc are topological equivalent if and only if the separatrix configurations of and are topological equivalent.
Hence, in order to qualitatively describe the phase portrait on the Poincaré disc of system (1) it is enough to qualitatively describe its separatrix configuration. This was done in Fig. 1, where we have drawn the separatrices other than singular points with bold lines. The other lines are orbits contained in its respective canonical regions. We observe from Fig. 1 that system (1) has separatrices, five of them singular points, and canonical regions, six of them of type strip and the one formed by the closed orbits surrounding , annular.
Below, we prove Theorem 3 by proving that Fig. 1 is a separatrix configuration of system (1).
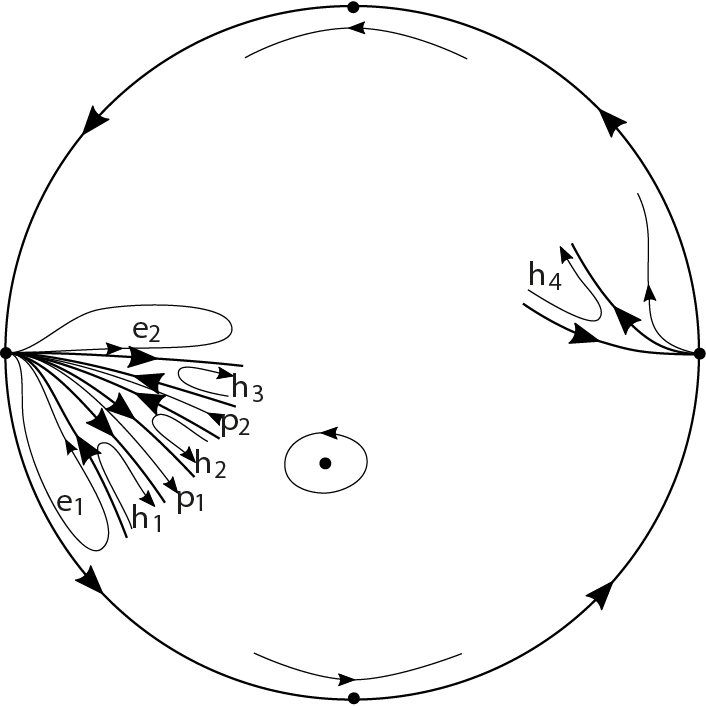
From the previous sections we conclude that close enough to the singular points, the phase portrait of system (1) is qualitatively the one presented in Fig. 6.
For further references we label the hyperbolic, parabolic and elliptic sectors presenting in the origins of the charts and in Fig. 6 as and , respectively.
From the definition of system (1), each of its orbits is a connected component of a level set of (because the only singular point of this system is the center ), which in turn is the inverse image under of circles surrounding the point . Since preserves orientation (because the Jacobian determinant of is positive), each orbit of (1) is carried onto a curve contained in a circle with counterclockwise orientation. As we have seen, the curve defined in (3) is the asymptotic variety of . Moreover, the points and of this curve have no inverse image under , all the other points of this curve have exactly one inverse image and the other points of have precisely two inverse images. Acting as Campbell (arXiv:math/9812032 1998), we delete from the curve the points and , obtaining three curves: and . According to Campbell (1998), the inverse image under of each is a curve that divides the plane into two connected components. We call the inverse image of . The set is called by Campbell (1998) the asymptotic flower of . It follows that is formed by connected components, each of them mapped twice onto each of the two connected components of . Each curve has a natural orientation, given by its parametrization (it is the opposite orientation used by Campbell (1998)). So, each curve also has a natural orientation (recall that preserves orientation). The graphics of and , are given in (a) and (b) of Fig. 7, respectively. As in (Campbell 1998, 2011) the axes in (a) have different scales. Following Campbell (1998), we label the regions as (right) and (left) of the curves and .
Since for each
and this polynomial of degree multiplying has no real zeros by Sturm’s theorem, it follows that the curves and are transversal to the circles centered at . As a consequence the curves and are transversal to the non-singular orbits of system (1). In particular, the image of a non-periodic orbit of system (1) has - and -limits contained in the curve . Below, we will say that the image of an orbit starts or finishes at meaning that its - or -limit is , respectively. Moreover, through each point in the intersection of with a circle, it crosses exactly one image of an orbit of system (1).
We call and the circles centered at and containing the points and , respectively.
The point , being the inverse image under of , is contained in the curve . The images under of the closed orbits surrounding are circles surrounding contained in the bounded region defined by . Thus the boundary of the period annulus of the center corresponds to the arc of circle contained in , starting and finishing at the point . This means that the boundary of the period annulus is an orbit that goes to infinity through the region labeled by in (b) of Fig. 7. In particular, in the Poincaré disc, this orbit tends to the origin of the chart . Then, analyzing the possibilities in Fig. 6, we see that this orbit contains the two separatrices of the hyperbolic sector . This period annulus is an annular canonical region.
Now we analyze the parabolic sectors and .
Close to the two points of cut by the orbit giving the boundary of the period annulus of the center (i.e., the orbit connecting the two separatrices of the hyperbolic sector ), and outside the period annulus, there must exist orbits cutting . Analyzing the images of these orbits, they are contained in circles surrounding the circle . So, there are two possibilities for the images of these orbits: either they are arcs starting and finishing at a point of the curve , or they are arcs starting at the curve and finishing at the curve or . At a first glance both of these possibilities are compatible with the parabolic sectors and in Fig. 6. We claim that the correct possibility is the first one. Indeed, we can increase the radii of these circles containing the images of the orbits of and until we achieve the circle . If we are in the second possibility, the orbit whose image is contained in and starts at a point of will contain the separatrice of the end of the parabolic sector . But, this orbit will not contain the separatrice of the end of the parabolic sector , because we can continue drawing arcs starting at with radii bigger than the radius of . Thus, the parabolic sector will not finish, a contradiction with the nature of the vector field at the origin of the chart , as shown in Fig. 6. This proves the claim.
So, the image of the orbits of the parabolic sectors and are arcs starting and finishing at a point of the curve . And since we can continue drawing these arcs until we arrive at circle , this means that the parabolic sectors and are connected, and the image of the orbit containing the separatrices that separate from and from is contained in the arc of starting and finishing at the point . The region connecting to is a strip canonical region, see Fig. 1.
Now, since the image of this last orbit cuts the curves and , there must exist orbits near it whose images cross and . The only possibility is that those images are arcs of circles starting at the curve , rotating a complete turn crossing and and continue up to finishing in the curve . We call these orbits the big orbits. A big orbit whose image is contained in a circle close enough to enters both the hyperbolic sectors and . We have to see where the big orbits start and finish.
The orbits whose images are arcs of the circles with radii smaller than the radius of , starting and finishing at and contained in the region correspond to an elliptic sector with boundary formed by an orbit having image contained in the arc of starting at an finishing at . Close to this boundary and out of the elliptic sector there must exist orbits whose images start at . These orbits are the big orbits. Hence, it follows that this elliptic sector is and that the big orbits start at the origin of , see Fig. 1.
The orbits whose images are arcs starting and finishing at and contained in the region form the elliptic sector . Clearly its boundary is formed by the two orbits containing the separatrices of the hyperbolic sector . The image of these orbits are the arcs starting at and finishing at and starting at and finishing at , respectively.
In particular, this means that the big orbits must finish at the origin of the chart , below the hyperbolic sector . Since their images are contained in the circles bigger than , there exist orbits whose images are arcs contained in the circles between and , starting at , crossing and finishing at . These orbits produce a parabolic sector between and , and give rise to a strip canonical region as presented in Fig. 1.
The big orbits also produce a strip canonical region.
The orbits of the strip canonical region placed above the hyperbolic sector have their images contained in arcs of circles with radii bigger than the radius of , starting at and finishing at .
The elliptic sectors and form another two strip canonical regions.
Hence we have canonical regions, six of them are strip and one is annular. Analyzing Fig. 1, we see there are finite orbits that are separatrices. The infinite has another orbits. Hence, since there are singular points, we have separatrices in the separatrix configuration of system (1) in the Poincaré disc.
Acknowledgments
The first and third authors are partially supported by the Ministerio de Economia y Competitividad (MINECO) grant number MTM2013-40998-P, the Agència de Gestió d’Ajuts Universitaris i de Recerca (AGAUR) grant number 2014SGR 568 and the grants from European Commission (FP7-PEOPLE-2012-IRSES) numbers 316338 and 318999. The second author is partially supported by Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), grant number 2014/ 26149-3. The second and third authors are also partially supported by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), grant 88881. 030454/ 2013-01 from the program CSF-PVE.
REFERENCES
- ÁLVAREZ MJ, FERRAGUT A AND JARQUE X. 2011. A survey on the blow up technique. Internat J Bifur Chaos Appl Sci Engrg 21: 3103-3118.
- BASS H, CONNEL EH AND WRIGHT D. 1982. The Jacobian conjecture: reduction of degree and formal expansion of the inverse. Bull Amer Math Soc 7: 287-330.
- BIAŁYNICKI-BIRULA A AND ROSENLICHT M. 1962. Injective morphisms of real algebraic varieties. Proc Amer Math Soc 13: 200-203.
- BRAUN F, GINÉ J AND LLIBRE J. 2016. A sufficient condition in order that the real Jacobian conjecture in holds. J Differential Equations 260: 5250-5258.
- CAMPBELL LA. 2011. The asymptotic variety of a Pinchuk map as a polynomial curve. Appl Math Lett 24: 62-65.
- DUMORTIER F, LLIBRE J AND ARTÉS JC. 2006. Qualitative theory of planar differential systems. Universitext, Springer-Verlag, 298 p.
- GONZÁLEZ VELASCO EA. 1969. Generic properties of polynomial vector fields at infinity. Trans Amer Math Soc 143: 201-222.
- GWOŹDZIEWICZ J. 2000. A geometry of Pinchuk’s map. Bull Polish Acad Sci Math 48: 69-75.
- ISAACSON E AND KELLER HB. 1994. Analysis of numerical methods, Corrected reprint of the 1966 original Wiley. New York: Dover Publications, 541 p.
- MARKUS L. 1954. Global structure of ordinary differential equations in the plane. Trans Amer Math Soc 76: 127-148.
- NEUMANN DA. 1975. Classification of continuous flows on 2-manifolds. Proc Amer Math Soc 48: 73-81.
- NEUMANN DA AND O’BRIEN T. 1976. Global structure of continuous flows on 2-manifolds. J Differ Equations 22: 89-110.
- PEIXOTO MM. 1973. On the classification of flows on 2-manifolds. Dynamical systems (Proc. Sympos., Univ. Bahia, Salvador, 1971). New York: Academic Press, p. 389-419.
- PINCHUK S. 1994. A counterexample to the strong real Jacobian conjecture. Math Z 217: 1-4.
- SABATINI M. 1998. A connection between isochronous Hamiltonian centres and the Jacobian conjecture. Nonlinear Anal 34: 829-838.
- VAN DEN ESSEN A. 2000. Polynomial automorphisms and the Jacobian conjecture. Progress in Mathematics, 190. Basel: Birkhäuser Verlag, 329 p.
Publication Dates
-
Publication in this collection
Jul-Sep 2018
History
-
Received
22 Oct 2017 -
Accepted
13 Dec 2017