Resumos
OBJETIVOS: Medir o gasto energético de repouso (GER, kcal/d), comparar as equações de predição disponíveis na literatura e associar a composição corporal. MÉTODOS: Vinte e oito sedentárias foram voluntárias [peso: 79 ± 12 kg; estatura: 164 ± 5 cm; idade: 36 ± 11 anos; índice de massa corporal (IMC): 29 ± 4 kg/m²]. A composição corporal foi estimada por antropometria, o GER foi medido por calorimetria indireta e estimado pelas principais equações da literatura. Foram desenvolvidas equações para estimativa do GER sendo a melhor a GER-Nosso. RESULTADOS: Diferentes tempos de coleta produziram resultados similares para o GER medido. O GER estimado pelas fórmulas de Harris & Benedict, FAO/WHO/UNO somente peso e peso mais altura, Schofield e GER-Nosso foram estatisticamente iguais ao GER medido. As equações do Siervo & Falconi, Schofield e Henry & Rees não foram correlacionadas ao GER medido. O melhor preditor isolado do GER foi a massa corporal e a melhor associação quando ajustado por unidade (kg) foi a massa magra. A equação desenvolvida no presente trabalho foi: GER(kcal/d)= 21837 - 14,448 * Peso(kg) + 54,963 * Massa Magra(kg) - 9,341 * Estatura(cm) - 4,349 * Idade(anos) - 19753 * Densidade Corporal(g/ml). CONCLUSÃO: As equações de predição do GER podem induzir a erros de predição e parecem ser população-específicas. O melhor resultado de predição foi para fórmula desenvolvida com os dados antropométricos das voluntárias (medido= 1617 ± 237 kcal/d; GER-Nosso= 1616 ± 167 kcal/d).
Calorimetria; Massa magra; Massa gorda; IMC; Antropometria
OBJECTIVES: To compare the resting energy expenditure (REE, kcal/d) measured to the disposable equation of literature and to associate this to body composition. METHODS: Twenty-eight sedentary women were volunteers [weight: 79 ± 12 kg; stature: 164 ± 5 cm; age: 36 ± 11 years; body mass index (BMI, kg/m²): 29 ± 4]. The body composition was estimated with anthropometry methods; REE was measured by indirect calorimetry and was estimated by the main equations of the literature. Equations were developed to estimate REE and the best of them was REE-Our. RESULTS: The different time of harvest produced a similar result to REE measured. The Harris & Benedict, FAO/WHO/UNO only weight, and weight plus height, Schofield and REE-Our equations results were statistically similar to REE measured. The Siervo & Falconi, Schofield and Henry & Rees equations did not have correlation with the measured calorimetry. The best-isolated predictor of the REE was the body mass and the best association when adjusted to unit (kg) was lean body mass. The equation developed in the present work was: REE(kcal/d)= 21837 - 14,448 * Weight(kg) + 54,963 * Lean Mass(kg) - 9,341 * Stature(cm) - 4,349 * Age(years) - 19753 * Body Density(g/ml). CONCLUSION: The REE prediction equations can prompt to errors and seem to be population specific. The best prediction result was with the equation developed with anthropometrics variables of the volunteers (measured= 1617 ± 237 kcal/d; REE-Our= 1616 ± 167 kcal/d).
Calorimetry; Lean body mass; Fat body mass; BMI; Anthropometry
ARTIGO ORIGINAL
Gasto energético de repouso medido vs. estimado e relação com a composição corporal de mulheres
Resting energy expenditure measured vs. estimated and this relationship with body composition in women
Carlos A. FettI; Waléria C.R. FettII; Julio S. MarchiniII
IFaculdade de Educação Física da Universidade Federal de Mato Grosso, Cuiabá, MT
IILaboratório de Espectrometria de Massa, Divisão de Nutrologia do Departamento de Clínica Médica da Escola de Medicina da Universidade de São Paulo, SP
Endereço para correspondência Endereço para correspondência: Carlos Alexandre Fett Faculdade de Educação Física Universidade Federal de Mato Grosso Avenida Fernando Correa da Costa s/nº Campus, Ginásio de Esportes, Secretaria 78060-900 Cuiabá, MT E-mail: cafett@hotmail.com
RESUMO
OBJETIVOS: Medir o gasto energético de repouso (GER, kcal/d), comparar as equações de predição disponíveis na literatura e associar a composição corporal.
MÉTODOS: Vinte e oito sedentárias foram voluntárias [peso: 79 ± 12 kg; estatura: 164 ± 5 cm; idade: 36 ± 11 anos; índice de massa corporal (IMC): 29 ± 4 kg/m2]. A composição corporal foi estimada por antropometria, o GER foi medido por calorimetria indireta e estimado pelas principais equações da literatura. Foram desenvolvidas equações para estimativa do GER sendo a melhor a GER-Nosso.
RESULTADOS: Diferentes tempos de coleta produziram resultados similares para o GER medido. O GER estimado pelas fórmulas de Harris & Benedict, FAO/WHO/UNO somente peso e peso mais altura, Schofield e GER-Nosso foram estatisticamente iguais ao GER medido. As equações do Siervo & Falconi, Schofield e Henry & Rees não foram correlacionadas ao GER medido. O melhor preditor isolado do GER foi a massa corporal e a melhor associação quando ajustado por unidade (kg) foi a massa magra. A equação desenvolvida no presente trabalho foi: GER(kcal/d)= 21837 14,448 * Peso(kg) + 54,963 * Massa Magra(kg) 9,341 * Estatura(cm) 4,349 * Idade(anos) 19753 * Densidade Corporal(g/ml).
CONCLUSÃO: As equações de predição do GER podem induzir a erros de predição e parecem ser população-específicas. O melhor resultado de predição foi para fórmula desenvolvida com os dados antropométricos das voluntárias (medido= 1617 ± 237 kcal/d; GER-Nosso= 1616 ± 167 kcal/d).
Descritores: Calorimetria; Massa magra; Massa gorda; IMC; Antropometria
ABSTRACT
OBJECTIVES: To compare the resting energy expenditure (REE, kcal/d) measured to the disposable equation of literature and to associate this to body composition.
METHODS: Twenty-eight sedentary women were volunteers [weight: 79 ± 12 kg; stature: 164 ± 5 cm; age: 36 ± 11 years; body mass index (BMI, kg/m2): 29 ± 4]. The body composition was estimated with anthropometry methods; REE was measured by indirect calorimetry and was estimated by the main equations of the literature. Equations were developed to estimate REE and the best of them was REE-Our.
RESULTS: The different time of harvest produced a similar result to REE measured. The Harris & Benedict, FAO/WHO/UNO only weight, and weight plus height, Schofield and REE-Our equations results were statistically similar to REE measured. The Siervo & Falconi, Schofield and Henry & Rees equations did not have correlation with the measured calorimetry. The best-isolated predictor of the REE was the body mass and the best association when adjusted to unit (kg) was lean body mass. The equation developed in the present work was: REE(kcal/d)= 21837 14,448 * Weight(kg) + 54,963 * Lean Mass(kg) 9,341 * Stature(cm) 4,349 * Age(years) 19753 * Body Density(g/ml).
CONCLUSION: The REE prediction equations can prompt to errors and seem to be population specific. The best prediction result was with the equation developed with anthropometrics variables of the volunteers (measured= 1617 ± 237 kcal/d; REE-Our= 1616 ± 167 kcal/d).
Keywords: Calorimetry; Lean body mass; Fat body mass; BMI; Anthropometry
A CALORIMETRIA TEVE SEU INÍCIO no final do século XIX para aplicação na termodinâmica da vida animal (1,2). Em 1893, Friedrich Müller relacionou o aumento do metabolismo do bócio exoftálmico à diminuição da excreção de nitrogênio, e Graham Lusk, em 1933, uniformizou e padronizou esta metodologia, relacionada ao estudo do metabolismo intermediário (3).
A estimativa do gasto energético é importante para ajustar a oferta nutricional de cada indivíduo (4). A adequação nutricional é necessária para orientar quanto à oferta energética adequada à demanda da atividade envolvida (5) e para economia em saúde pública, reduzindo o custo em pacientes hospitalizados (6).
O gasto energético (GE) pode ser estimado de forma direta ou indireta. A forma direta consiste na medida das trocas de calor entre o organismo e o meio ambiente, sendo necessária uma câmara de isolamento para sua realização, e tem custo elevado. Já a calorimetria indireta pode ser obtida a partir do consumo de oxigênio e produção de dióxido de carbono, reduzindo o custo comparado à medida direta, mas ainda é cara para a realidade da maioria dos locais (5).
Devido à dificuldade de se medir a calorimetria, vários autores tentaram estabelecer equações que pudessem predizer o GE, a partir de dados como sexo, idade, massa corporal e estatura (7). Estudos têm demonstrado que algumas equações correspondem aos resultados obtidos na calorimetria indireta, mas outras não (4,8). Ainda, algumas equações apresentam correspondência em determinado estudo, mas não em outro (4). Dados em pacientes obesos são ainda mais contraditórios (4).
Portanto, os principais objetivos deste estudo foram: 1) comparar diferentes tempos de coleta de dados e seleção de pontos da calorimetria indireta entre si; 2) comparar os resultados obtidos pela medição da calorimetria indireta ao resultante do uso de equações de estimativas utilizadas na literatura; 3) estabelecer por regressão linear equações de predição do gasto energético de repouso (GER) e comparar a melhor delas ao medido pela calorimetria indireta e pelas outras equações da literatura; 4) verificar a correlação entre as equações de estimativas ao medido pela calorimetria indireta, e 5) verificar quais variáveis antropométricas seriam melhor relacionadas ao GER.
MATERIAL E MÉTODOS
Vinte e oito mulheres sedentárias da normalidade à obesidade foram voluntárias para este estudo (tabela 1). Elas foram aleatoriamente engajadas através de divulgação no Campus de Ribeirão Preto da Universidade de São Paulo. O estudo foi previamente aprovado pelo Comitê de Ética em Pesquisa do Hospital das Clínicas da Faculdade de Medicina de Ribeirão Preto, Universidade de São Paulo (HCFMRP-USP), e todas assinaram termo de consentimento livre e esclarecido. Todas foram avaliadas clinicamente sempre pelo mesmo médico da equipe de Nutrologia do HCFMRP-USP.
A massa corporal (kg) foi obtida por meio de balança de plataforma da marca Filizola® Eletrônica ID 1500 (São Paulo, SP, Brasil), com precisão de 0,1 kg, e a estatura em uma barra metálica graduada com precisão de 0,5 cm (9). A partir da massa corporal e estatura foi calculado o índice de massa corporal (IMC= kg/m2).
Para medida da espessura das pregas cutâneas foi utilizado um adipômetro da marca Lange® (Beta Technology INC; Santa Cruz, CA, EUA), com pressão constante de 10 g/mm2 na superfície de contato, e precisão de 1 mm e escala de 065 mm. O valor anotado foi a média de três medidas consecutivas. As pregas cutâneas mensuradas foram: tríceps, bíceps, peito, abdômen, supra-ilíaca, sub-escapular, coxa e panturrilha. A densidade corporal foi estimada a partir das medidas das pregas cutâneas corrigidas pela idade (9). O percentual de gordura foi obtido pelo cálculo da densidade corporal, usando a fórmula de Siri (10).
Para medir o GER foi utilizado um aparelho móvel Vmáx. 29 Sensor Medics® (Yorba Linda: CA, EUA). O equipamento era calibrado antes de cada mensuração, utilizando-se uma mistura de gases a uma concentração-padrão conhecida (Calibração 1: 26% O2, 0% CO2; Calibração 2: 16% O2, 4% CO2). O fluxo era realizado com uma seringa padronizada de três L. Se a fração inspirada de O2 flutuasse mais que 3% e o quociente respiratório ficasse fora da faixa de 0,671,3, a coleta era considerada inválida. A variação entre fração inspirada e a expirada de O2 devia estar entre 24%, a temperatura entre 540ºC, a umidade entre 1595% (não condensado) e o aparelho era aquecido por 30 minutos nas condições STPD (standard temperature pressure dry), ou seja, ar seco, 0ºC e 760 mmHg.
As voluntárias chegavam ao laboratório em jejum de 12 horas, às 7:00 horas, sendo cada uma delas agendada a cada 30 minutos até as 9:00 horas. Repousavam, então, por 30 minutos sentadas e mais 30 minutos deitadas, onde era medida a calorimetria por mais 30 minutos. Uma vez que a máscara era colocada na voluntária, aguardava-se em torno de 10 minutos até atingir o estado estável para o VO2. As participantes deviam ficar em repouso absoluto, evitando inclusive conversar, mas não era permitido dormir. O GER diário foi calculado pela equação de Weir (11).
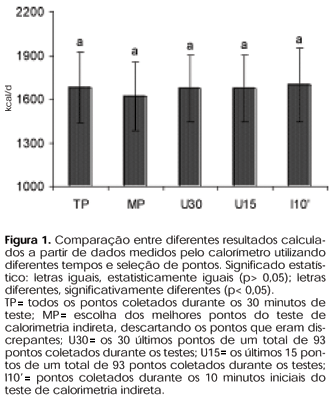
Todos os pontos das variáveis coletadas pelo equipamento ainda sem tratamento eram tabulados em uma planilha de cálculos. Então, eram estimados os seguintes GERs usando-se todos os pontos (TP) coletados durante os 30 minutos de teste; os melhores pontos (MP), onde eram descartados os valores discrepantes; os 10 minutos iniciais (I10) de coleta; os 30 últimos pontos (U30), e os últimos 15 pontos (U15), de um total de 93 pontos coletados durante os testes.
O GER também foi calculado por equações desenvolvidas para mulheres, descritas na tabela 2. Todas as equações são relacionadas ao GER como medido no presente estudo e não ao gasto energético basal. A equação de Harris & Benedict (12) é representada como gasto energético basal, mas, de fato, ela foi medida nas condições de repouso e não no basal (4). As referências das equações citadas ao longo do texto estão na tabela 2. Os percentuais de diferença entre os valores de GER estimados por cada uma das equações e o medido pela calorimetria indireta foram calculados pela fórmula: %Dif= [(GERestimado GERmedido)/GERmedido]/100.
Para comparação entre as diferentes medidas do que foi calculado e o que foi estimado para o gasto energético de repouso, foi utilizada one way ANOVA para medidas repetidas e seguida da comparação múltipla pós-teste de Tukey-Kramer. Para verificar a concordância entre estas medidas, foi feita uma matriz de correlação e, posteriormente, comparadas aos pares pela correlação linear de Pearson. A regressão linear múltipla foi utilizada para desenvolver fórmulas de estimativa do gasto energético de repouso a partir de variáveis antropométricas. A diferença foi considerada significante com p< 0,05 e intervalo de confiança de 95%. Os resultados foram apresentados como média ± DP.
RESULTADOS
Os diferentes tempos da coleta e seleção do número de pontos das variáveis da calorimetria indireta, utilizadas para cálculo do GER, não apresentaram diferença entre si (figura 1).
A equação GER-Nosso, usando variáveis antropométricas, foi estatisticamente igual aos resultados de todos os pontos, dos melhores pontos e dos 10 iniciais medidos pela calorimetria indireta. Os melhores pontos medidos pela calorimetria indireta, a equação de Harris & Benedict, a da FAO/WHO/ UNO, somente peso e a com peso e altura, a de Schofield e o GER-Nosso foram estatisticamente iguais entre si. As estimativas do GER pelas equações de Mifflin e cols., a de Harris & Benedict, a da FAO/WHO/UNO, somente peso e a com peso e altura, a de Schofield e a de Henry & Rees foram estatisticamente iguais entre si. As estimativas de Mifflin e cols., a de Siervo e cols. e a de Henry & Rees foram estatisticamente iguais entre si. A equação de Siervo e cols. foi estatisticamente igual à de Owen (figura 2).
O gasto energético total foi estimado multiplicando-se o GER por 1,56, considerando-se mulheres sedentárias (8). Uma vez que o gasto energético total era obtido por uma constante, os resultados estatísticos para comparação entre as diferentes medidas e estimativas foram idênticos às comparações feitas para o GER.
Somente os GERs estimados pelas fórmulas do Siervo e cols., Schofield e Henry & Rees não tiveram correlação significativa com todos os pontos, os melhores pontos e os 10 iniciais medidos pela calorimetria indireta (tabela 3).
Foram geradas oito fórmulas para estimativa do GER, a partir de variáveis antropométricas como variáveis independentes e o GER estimado pelos melhores pontos como variável dependente (tabela 4). O melhor preditor isolado do GER foi a massa corporal (kg), seguido pelo IMC. Das várias combinações, a que melhor predisse o GER foi a que utilizou a massa corporal, a estatura, a massa magra, a idade e a densidade corporal.
O GER medido foi significativamente correlacionado à massa corporal, à massa magra, ao IMC, à massa gorda e à densidade corporal, mas não à idade e à estatura (tabela 5).
As maiores diferenças observadas entre o cálculo da calorimetria de repouso, utilizando-se os melhores pontos e as equações de estimativa, foram para a de Owen e a Siervo e cols., subestimando em aproximadamente 16% e 12%, respectivamente, o GER dos melhores pontos medidos pela calorimetria. A equação de estimativa que menor diferença apresentou ao GER medido pelos melhores pontos foi a desenvolvida neste estudo (GER-Nosso), com aproximadamente 0% de diferença, seguida pelas equações da FAO/WHO/ UNO somente peso, com 3% de diferença, a de Harris & Benedict, a da FAO/WHO/UNO com peso e altura e a de Schofield, que subestimavam em torno de 4% comparadas à média obtida para o GER medido (figura 3).
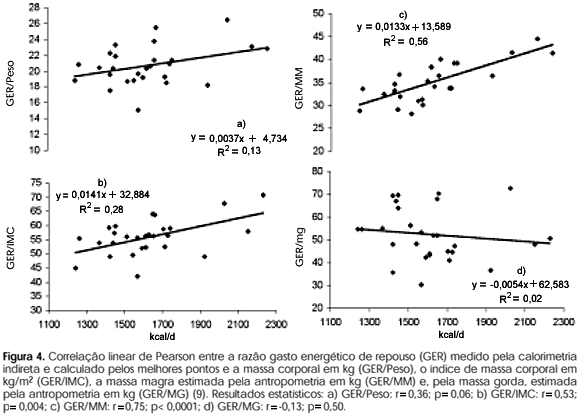
A razão entre os melhores pontos medidos pela calorimetria e índices antropométricos mostrou que o IMC e a massa magra tiveram significativas correlações com o gasto energético de repouso. Já a massa corporal tendeu (p= 0,06) e a massa gorda não apresentou esta relação (figura 4).
DISCUSSÃO
Foi observado que os diferentes tempos de coleta e a seleção de pontos dos dados da calorimetria indireta não diferiam entre si. A redução do tempo de medida da calorimetria sem perda da qualidade dos dados obtidos reduz os custos operacionais. Como aqui, já foi observado que um tempo menor de steady state, comparado aos protocolos de 30 minutos, pode produzir resultados equivalentes (6).
A equação desenvolvida no presente estudo foi a de menor diferença percentual comparada ao estimado pelo melhores pontos da calorimetria indireta, seguida pela FAO/WHO/UNO somente peso. O melhor dado para predição do GER em uma equação foi a massa corporal, e a melhor relação por unidade de kg foi a massa magra. Como a maioria dos serviços de saúde, atividade física e nutrição não dispõem de equipamentos para mensurar a calorimetria, é importante o desenvolvimento de equações confiáveis para suprir esta demanda.
Entretanto, os resultados da comparação da calorimetria medida à estimada são variados na literatura. Wahrlich & Anjos (18), estudando 60 mulheres de Porto Alegre, RS, observaram que as equações de Harris & Benedict, FAO/WHO/UNO somente peso, Schofield e Henry & Rees, não eram adequadas para estimar o GER, superestimando os resultados obtidos pela medida. Estas equações foram desenvolvidas com amostras, em sua maioria, das populações norte-americanas e européias, e sugere-se que superestimam os resultados das populações que vivem nos trópicos (18,19). Entretanto, outros estudos demonstraram que estas equações superestimam o GER não apenas nas populações dos trópicos, mas em várias outras etnias. A equação da FAO/WHO/UNO somente peso superestimava em 9,1% em uma amostra de homens americanos (20); a de Schofield superestimava em 8,2% em homens canadenses (21); a FAO/WHO/UNO somente peso superestimava em 12,1% em índios americanos (22); em uma população de índios mexicanos homens, a FAO/WHO/UNO somente peso superestimava em 9,8% em indivíduos com déficit de peso, em 9,6% nos de IMC normal, em 7,8% nos com sobrepeso e em 5,5% em obesos (19).
Já os resultados do presente estudo não corroboram estes achados. Ao contrário, todas as equações subestimaram o GER comparado ao GER medido pelos melhores pontos. Ainda, diferente dos outros estudos citados, as equações da FAO/WHO/UNO somente peso, a de Harris & Benedict, a da FAO/WHO/UNO peso mais altura e a de Schofield parecem também produzir resultados satisfatórios, uma vez que elas subestimavam o GER medido em 3 e 4%, respectivamente, e eram estatisticamente iguais entre si e ao medido pelos melhores pontos da calorimetria.
Um estudo de revisão, comparando a capacidade de predição das estimativas do GER ao medido pela calorimetria indireta, concluiu que a equação de Mifflin e cols. era a mais adequada para ser utilizada nas populações em geral, comparada às outras equações. Todavia, os autores observam que erros podem surgir ao ser aplicada individualmente e quando generalizada em certas populações como idosos ou determinados grupos étnicos (4). No presente estudo, a equação de Mifflin e cols. foi apenas a quinta melhor estimativa quanto à comparação das médias pelo ANOVA e a diferença percentual das médias entre o GER estimado e medido, sugerindo que esta diferença de resultados foi causada pela população estudada. Todavia, a correlação linear de Pearson com os melhores pontos medidos pela calorimetria mostrou que a equação de Mifflin e cols. teve melhor resultado que a FAO/WHO/UNO peso mais altura e que a de Schofield, sugerindo uma correspondência mais consistente.
Foi observado que a equação de Owen não é adequada para indivíduos obesos (4), concordando com o observado no presente estudo, onde a maioria era sobrepeso ou obesas. Por outro lado, foi demonstrado em um estudo, que a equação de Owen se ajustava melhor que as outras para pessoas com peso normal, a de Bernstein para pessoas com sobrepeso e a equação de Robertson & Reid era mais adequada para obesos em um comparativo de cinco equações ao GER medido por calorimetria indireta (7). No presente estudo, a equação de Robertson & Reid teve um resultado intermediário entre as piores e melhores predições (dados não apresentados).
A inclusão de dados da composição corporal deve ter favorecido a melhor predição do GER pela equação GER-Nosso, pois o resultado pode ser afetado por fatores como a heterogeneidade da composição corporal (8). As outras equações utilizam apenas o sexo, idade, massa corporal e estatura. A massa magra parece exercer efeito importante na predição do GER. O índice criado pela divisão do GER pela massa magra foi o melhor associado ao GER medido. O índice criado pelo IMC também correspondeu significativamente ao GER medido, mas não os criados pela massa corporal e pela massa gorda (figura 4). Vários estudos têm sugerido que a massa magra é o principal determinante do GER (18,23). Foi observado que o GER, quando expressado em unidades da massa corporal, tinha valores maiores para mulheres com percentual de gordura menor que 25%, comparado àquelas de percentual de gordura acima deste valor. Todavia, estes autores observaram que a diferença desaparecia quando o GER era apresentado em termos de massa magra (18).
Em indivíduos obesos, a acurácia de todas as equações de predição diminui comparada com indivíduos não obesos, e a faixa de erros individuais aumenta (4). Como já foi discutido, isso deve ser devido à massa magra ter maior relação com o GER que a massa gorda. Entretanto, em um estudo quando a massa magra era associada ao IMC, ou a massa gorda, a predição aumentava significantemente (19). Todavia, no presente estudo a variável individual que melhor predisse o GER nas equações foi a massa corporal. Mas, quando se acrescia a idade e a estatura à equação, a predição era melhor do que associando o IMC ou a massa magra (tabela 4). Uma possível explicação é que todas as variáveis da composição corporal correlacionaram-se significativamente ao GER. Portanto, como o aumento de qualquer componente da composição corporal aumenta a massa total, eles já eram contemplados mesmo que de forma indireta, o que não ocorria com a estatura e a idade.
Não existe uma explicação clara para a correlação negativa da densidade corporal e positiva da massa gorda com o GER, uma vez que a massa magra também era positivamente associada (tabela 5). Isto sugere que outros fatores metabólicos, como alterações hormonais e enzimáticas, não controladas neste estudo devem ter contribuindo para alterações do GER. Portanto, as variáveis antropométricas per se são limitadas para predizer o GER quanto às variabilidades populacionais e individuais.
As equações parecem ser população-específicas e sofrem influência da composição corporal, que melhoram a capacidade de predição. De todos os dados antropométricos, a massa corporal foi a que mais influenciou na predição do GER, e, quando ajustada para unidades de massa magra, esta foi a melhor associada. Para estas mulheres, a equação desenvolvida neste estudo prediz o GER de forma equivalente ao medido. Das equações encontradas na literatura, as que melhor predisseram o GER e de forma equivalente entre si foram a FAO/WHO/UNO somente peso e peso mais altura, a de Harris & Benedict e a de Schofield.
AGRADECIMENTOS
Agradecemos à Maria do Rosário Del Lama de Unamuno, Célia Marques Pereira Rosário e Sandra Regina Oyama, pelo suporte técnico e material.
Recebido em 31/01/06
Revisado em 11/05/06
Aceito em 10/07/06
- 1. Atwater WO, Rosa EB. US Department of Agriculture, 1899
- 2. Atwater WO, Benedict FG. Carnegie Institute of Washington, DC, 1905
- 3. Du Bois EF. Basal Metabolism in Health and Disease 3rd edition. Philadelphia: Lea & Febiger, 1936
- 4. Frankenfield D, Roth-Yousey L, Compher C. Comparison of predictive equations for resting metabolic rate in healthy nonobese and obese adults: A systematic review. J Am Diet Assoc 2005;105:775-89.
- 5. Marchini JS, Fett CA, Fett WCR, Suen VMM. Calorimetria: Aplicações práticas e considerações críticas. Fit Perform J 2005;4:90-6.
- 6. Joosten KF. Why indirect calorimetry in critically ill patients: What do we want to measure? Intensive Care Med 2001;27:1107-9.
- 7. Siervo M, Boschi V, Falconi C. Which REE prediction equation should we use in normal-weight, overweight and obese women? Clin Nutr 2003;22:193-204.
- 8. Alfonzo-Gonzalez G, Doucet E, Almeras N, Bouchard C, Tremblay A. Estimation of daily energy needs with the FAO/WHO/UNU 1985 procedures in adults: Comparison to whole-body indirect calorimetry measurements. Eur J Clin Nutr 2004;58:1125-31.
- 9. Pollock ML, Wilmore JH, Fox III SM. Exercícios na saúde e na doença Avaliação e prescrição para prevenção e reabilitação. Rio de Janeiro: Editora MEDSI, 1986
- 10. Siri WE. Body composition from fluid spaces and density. In: Brozek J, Henschel A, Editors. Techniques for measuring body composition Washington, DC: NAS, 1961 p. 223-44.
- 11. Weir JB. New methods for calculating metabolic rate with special reference to protein metabolism. J Physiol 1949;109:1-9.
- 12. Harris JA, Benedict FG. Biometric studies of basal metabolism in man Washington, DC: Carnegie Institute of Washington, 1919 (Publication Number 297).
- 13. Mifflin MD, St Jeor ST, Hill LA, Scott BJ, Daugherty SA, Koh Y. A new predictive equation for resting energy expenditure in healthy individuals. Am J Clin Nutr 1990;51:241-7.
- 14. Owen OE, Kavle E, Owen RS, Polansky M, Caprio S, Mozzoli MA, et al. A reappraisal of caloric requirements in healthy women. Am J Clin Nutr 1986;44:1-19.
-
15FAO/WHO/UNU. Energy and protein requirements. Report of a joint FAO/WHO/UNU expert consultation. World Health Organ Tech Rep Ser 1985;724:1-206.
- 16. Schofield WN. Predicting basal metabolic rate, new standards and review of previous work. Hum Nutr Clin Nutr 1985;39:5-41.
- 17. Henry CJ, Rees DG. New predictive equations for the estimation of basal metabolic rate in tropical peoples. Eur J Clin Nutr 1991;45:177-85.
- 18. Wahrlich V, Anjos LA Validação de equações de predição da taxa metabólica basal em mulheres residentes em Porto Alegre, RS, Brasil. Rev Saúde Pública 2001;35:39-45.
- 19. Valencia ME, Moya SY, McNeill G, Haggarty P. Basal metabolic rate and body fatness of adult men in Northern Mexico. Eur J Clin Nutr 1994:205-11.
- 20. Owen OE, Holup JL, Dalessio DA, Craig ES, Polansky M, Smalley KJ, et al. A reappraisal of the caloric requirements of men. Am J Clin Nutr 1991;54:613-4.
- 21. Clark HD, Hoffer LJ. Reappraisal of the resting metabolic rate of normal young men. Am J Clin Nutr 1991;53:21-6.
- 23. McNeill G, Rivers JP, Payne PR, De Britto JJ, Abel R. Basal metabolic rate of Indian men: No evidence of metabolic adaptation to a low plane of nutrition. Hum Nutr Clin Nutr 1987;41:473-83.
- 23. Melby C, Scholl C, Edwards G, Bullough R. Effect of acute resistance exercise on postexercise energy expenditure and resting metabolic rate. J Appl Physiol 1993;75:1847-53.
Endereço para correspondência:
Datas de Publicação
-
Publicação nesta coleção
08 Jan 2007 -
Data do Fascículo
Dez 2006
Histórico
-
Recebido
31 Jan 2006 -
Revisado
11 Maio 2006 -
Aceito
10 Jul 2006