Resumos
OBJETIVO: Compreender, por meio de figuras e funções matemáticas do cone, as lentes progressivas e mostrar que elas não são lentes multifocais porque, nelas, a refração da luz não obedece as leis da geometria euclidiana. MÉTODOS: Foi feito um estudo da geometria analítica do cone, com o programa de computador Auto-CAD 14, dando enfoque óptico às figuras geométricas obtidas com a sua secção. RESULTADOS: Pela análise das figuras obtidas da secção do cone, pudemos observar as superfícies que compõem as lentes progressivas. Estas superfícies são compostas de elipse, círculo, parábola e hipérbole. Diferente do que é dito na literatura, encontramos as elipses com diâmetro maior nas ordenadas e de mesmo sentido seguida por duas superfícies inferiores que são parábola e hipérbole e não o contrário. CONCLUSÕES: As lentes progressivas diferentemente das lentes multifocais apresentam prismas nos centros ópticos como decorrência da sua estrutura. No final, fizemos análise das suas formas mostrando o limite teórico da sua evolução.
Lentes oculares; Erros de refração; Refração ocular; Modelos teóricos; Córtex visual; Matemática
PURPOSE: To understand, by means of illustrations and mathematical functions of the cone, the progressive lenses and to show that they are not multifocus lenses because in these the light refraction does not obey the laws of the Euclidian geometry. METHODS: A study was carried out on the analytic geometry of the cone, with a computer program called Auto-CAD 14 focusing on the geometric illustrations obtained with its section. RESULTS: Through the analysis of the obtained illustrations of the cone section we could observe that: the surfaces that compose the progressive lenses are made of ellipse, circle, parabola and hyperbola. Differently from literature, we found the ellipses with a larger diameter and the same direction followed by parabola and posterior hyperbola and not the other way. CONCLUSIONS: Unlike the multifocus lenses, the progressive lenses present prisms in the optical centers as a consequence of their structure. We analyzed their forms showing the theoretical limit of these evolutions.
Ocular lens; refraction mistakes; ocular refraction; theoretical models; visual cortex; mathematics
ARTIGOS ORIGINAIS
Lentes progressivas x lentes multifocais - Um estudo baseado na geometria analítica do cone
Progressive lenses X multifocal lenses A study based on the analytic geometry of the cone
Marília Cavalcante AraújoI; Fernando Queiroz MonteII
Hospital Geral de Fortaleza, Rua Ávila Goulart, 900 Fortaleza (CE) CEP 60155-290
IResidente do segundo ano em Oftalmologia do Hospital Geral de Fortaleza - HGF
IICoordenador da Residência Médica em Oftalmologia do Hospital Geral de Fortaleza - HGF
Endereço para correspondência Endereço para correspondência Marília Cavalcante Araújo Rua Frei Caneca, 750/3161 São Paulo (SP) Cep 01307-000 E-mail: madsaraujo@bol.com.br
RESUMO
OBJETIVO: Compreender, por meio de figuras e funções matemáticas do cone, as lentes progressivas e mostrar que elas não são lentes multifocais porque, nelas, a refração da luz não obedece as leis da geometria euclidiana.
MÉTODOS: Foi feito um estudo da geometria analítica do cone, com o programa de computador Auto-CAD 14, dando enfoque óptico às figuras geométricas obtidas com a sua secção.
RESULTADOS: Pela análise das figuras obtidas da secção do cone, pudemos observar as superfícies que compõem as lentes progressivas. Estas superfícies são compostas de elipse, círculo, parábola e hipérbole. Diferente do que é dito na literatura, encontramos as elipses com diâmetro maior nas ordenadas e de mesmo sentido seguida por duas superfícies inferiores que são parábola e hipérbole e não o contrário.
CONCLUSÕES: As lentes progressivas diferentemente das lentes multifocais apresentam prismas nos centros ópticos como decorrência da sua estrutura. No final, fizemos análise das suas formas mostrando o limite teórico da sua evolução.
Descritores: Lentes oculares; Erros de refração/terapia; Refração ocular; Modelos teóricos; Córtex visual/fisiologia; Matemática
ABSTRACT
PURPOSE: To understand, by means of illustrations and mathematical functions of the cone, the progressive lenses and to show that they are not multifocus lenses because in these the light refraction does not obey the laws of the Euclidian geometry.
METHODS: A study was carried out on the analytic geometry of the cone, with a computer program called Auto-CAD 14 focusing on the geometric illustrations obtained with its section.
RESULTS: Through the analysis of the obtained illustrations of the cone section we could observe that: the surfaces that compose the progressive lenses are made of ellipse, circle, parabola and hyperbola. Differently from literature, we found the ellipses with a larger diameter and the same direction followed by parabola and posterior hyperbola and not the other way.
CONCLUSIONS: Unlike the multifocus lenses, the progressive lenses present prisms in the optical centers as a consequence of their structure. We analyzed their forms showing the theoretical limit of these evolutions.
Keywords: Ocular lens; refraction mistakes / therapy; ocular refraction; theoretical models; visual cortex / physiology; mathematics
INTRODUÇÃO
Historicamente, as lentes progressivas passaram por vários estágios de aperfeiçoamento até onde se encontram hoje.
Apresentada inicialmente por Orford, em 1910* * Orfod 1910 apud (1) ** Maitenaz 1950 apud (1) , como modelo de concavidade parabolóide, foi posteriormente aperfeiçoada por outros pesquisadores, na tentativa de fazê-la utilizável(1). O fracasso das diversas tentativas foi o de manter as pesquisas dentro do universo convencional (esfera e cilindro), isto é, mantendo a multifocalidade.
As lentes progressivas tiveram sua grande evolução técnica por um físico francês B. Maitenaz que em 1950** * Orfod 1910 apud (1) ** Maitenaz 1950 apud (1) desenvolveu uma lente com poder dióptrico progressivo e boa capacidade de utilização prática. Em 1965, o próprio B. Maitenaz aprimorou ainda mais sua criação dando um grande passo na evolução das lentes progressivas(1).
Erroneamente confundida com lentes multifocais, as lentes progressivas não seguem a geometria euclidiana (clássica), pois possuem superfícies mais complexas que são as responsáveis pela progressão dos valores dióptricos observados e que por serem complexas são dotadas de incontáveis focos; diferentemente das lentes multifocais que são trabalhadas com superfícies clássicas (esférica ou cilíndrica) e como tal podem ser denominadas de acordo com a quantidade de focos nelas existentes (bifocal, trifocal e quadrifocal).
Como são negadas, pelas indústrias ópticas, aos oftalmologistas informações técnicas sobre as lentes e o que recebemos são as recomendações que são passadas aos balconistas das ópticas decidimos tentar compreender as lentes atuais1.
Não pretendemos fazer como Pascal (1623-1662) que aos sete anos de idade redescobriu a geometria euclidiana.
O objetivo é de trabalharmos os achados das lentes progressivas e ordená-las dentro dos conhecimentos geométricos e explicar certas qualidades dessas lentes que são mal compreendidas.
MÉTODOS
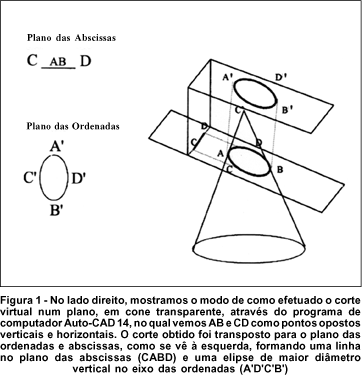
Foi feito um estudo da geometria analítica do cone, dando enfoque especial a cada figura geométrica obtida da secção do mesmo. O cone foi tomado como um corpo transparente e, portanto, capaz de refratar a luz, por querermos transportar para a óptica os achados geométricos. O estudo foi feito com cortes na figura sólida em diversas posições, sendo realizado uma construção tridimensional de um cone no Programa de Computador Auto-CAD 14, com cortes em varredura, sendo as imagens dos cortes transportadas para os planos das abscissas e ordenadas (Figura 1). Após realização dos cortes com imagens subseqüentes, foram tomados alguns planos e verificada a função óptica decorrente da transparência das superfícies obtidas.
RESULTADOS
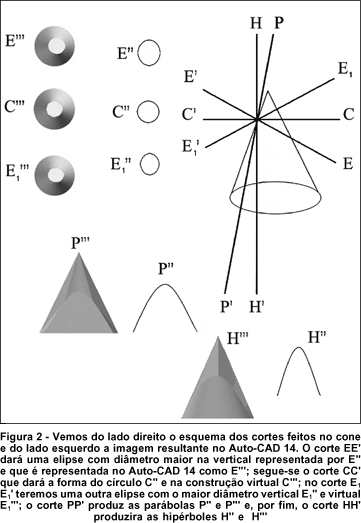
Recordando os cortes obtidos da secção do cone, encontramos nesta ordem: elipse de diâmetro maior na ordenada, seguida pelo círculo, o qual antecede a próxima elipse de diâmetro também maior nas ordenadas; seguem-se parábola e hipérbole (Figura 2). A elipse resulta da secção que corta completamente uma superfície do cone; o circulo é um caso especial da elipse, produzido por uma secção perpendicular ao eixo. A parábola é produzida por um corte no plano paralelo a uma linha geral. O plano que corta ambas as superfícies sem, no entanto, passar através da interseção das superfícies produz a hipérbole.
DISCUSSÃO
Ultrapassando a geometria euclidiana que trabalha com figuras geométricas em que o centro das figuras circulares encontra-se sobre um ponto que pode ser determinado, e a do cilindro em que as figuras circulares se dispõem em torno de uma linha, as lentes progressivas vão mais além e, baseada no estudo da figura geométrica do cone, possuem superfícies mais complexas, as quais são representadas como elipses, parábolas e hipérboles; ademais se associam às superfícies clássicas para oferecer correção para as ametropias e presbiopia.
Desta forma no gráfico de secção do cone encontramos a elipse, seguida da parábola e posteriormente a hipérbole, ou seja, a parábola é um caso limite entre a elipse e a hipérbole. Estas figuras geométricas transportadas para um corpo sólido transparente são as responsáveis pela progressão dos valores dióptricos nas lentes progressivas e por apresentarem infinitos focos entre seus focos principais, essas lentes não podem ser chamadas de lentes multifocais.
Chamamos a atenção para o que foi descrito em trabalhos anteriores, onde se afirmava que a zona de progressão seria composta de uma elipse de maior diâmetro vertical, uma esfera, uma elipse de maior diâmetro horizontal, seguido de uma hipérbole e de uma parábola(2). As nossas pesquisas discordam em dois pontos. A primeira discordância, relaciona-se às elipses. Os nossos achados mostram que as duas elipses têm o mesmo diâmetro predominante. A segunda é a de que no cone a parábola antecede a hipérbole e não o contrário. Podemos até propor uma simplificação: classificar o círculo como uma forma de elipse e a hipérbole uma forma de parábola. Certas variações de funções matemáticas fazem com que elas sejam tidas como independentes.
Diferentemente dos outros tipos de lentes que têm seus centros ópticos sobre um ponto ou uma linha (lente esférica e cilíndrica, respectivamente) e somente acima, abaixo ou lateralmente aos mesmos há um efeito prismático, nas lentes progressivas encontramos no local que fica o centro óptico necessariamente um prisma isto porque seja na elipse, parábola ou hipérbole o centro óptico dista desigualmente de qualquer ponto da sua superfície. Depreende-se daí, que o centro óptico para longe, perto e os múltiplos da zona de progressão têm prisma apesar do seu poder dióptrico ser dado por superfícies esféricas e cilíndricas.
Estes fatos são, por vezes, mal compreendidos como o freqüente equívoco de autores de grande autoridade na área, como o que chama as lentes progressivas de multifocais(3) e o que denomina de multifocais progressivos(4).
Tomando como base a formação de imagens numa lente convexa que forma imagem real e invertida e numa lente côncava que forma imagem virtual e de mesmo sentido e transportando para uma lente progressiva, teremos na lente convexa para longe uma imagem real e invertida acrescida de prisma de base inferior e para perto, imagem semelhante acrescida de prisma de base superior. O oposto acontece com as lentes côncavas. Esses fatos foram descritos ao examinar as lentes progressivas no lensômetro(5).
O valor prismático fora do centro óptico nas lentes esféricas e cônicas (essas dependentes da sua posição no espaço, ou quando associadas às esféricas) pode ser calculado baseando-se na regra de Prentice (P=Dxd), sendo a dioptria (D) representada pela lente esférica, cilíndrica ou esferocilíndrica as quais se encontram associadas às demais superfícies complexas da progressiva, sendo aplicável, talvez, apenas acima da zona de progressão. O talvez que imprime a nossa incerteza é porque admitimos que sendo o círculo uma forma de elipse, os cálculos para o círculo poderiam se reproduzir na elipse.
CONCLUSÕES
As lentes progressivas são constituídas de superfícies complexas, resultantes da secção da figura geométrica do cone e representada pela elipse, parábola e hipérbole, sendo estas as responsáveis tanto pela presença de prisma no centro óptico como pela progressão dos valores dióptricos observados nestas lentes. Resolvemos, à míngua de informações, determinar modelos para o seu estudo e a sua compreensão. No presente trabalho procuramos fazer uma análise usando, por inferência, a relação óptica refratométrica e geométrica do cone, procurando buscar através dos cortes virtuais do mesmo, a sua representação geométrica e expressão óptica oriundas de sua transformação num corpo sólido transparente que sofre desvios dos raios luminosos ao atravessar interfaces de diferentes índices de refração.
Recebido para publicação em 11.04.2003
Versão revisada recebida em 31.10.2003
Aprovação em 05.01.2004
- 1. Monte Q. Particularidades sobre a correção da presbiopia: lentes progressivas. Rev Bras Oftalmol 1980;39:241-50.
- 2. Arbens JP. Ein neues Mahrstarkglas. Ophthalmologica (Basel) 1975;170;370-9.
- 3. Zamboni FJ. Correção da presbiopia. In: Uras R. Óptica e refração ocular. Rio de Janeiro: Cultura Médica; 2000. p.109.
- 4. Alves AA. A nossa experiência pessoal com multifocais progressivos. In: Alves AA. Refração. 2Şed. Rio de Janeiro: Cultura Médica; 1994. p.258-69.
- 5. Monte FQ. Erros de confecção das lentes progressivas e as suas manifestações clínicas. Arq Bras Oftalmol 1984;47:51-6.
Datas de Publicação
-
Publicação nesta coleção
06 Jul 2004 -
Data do Fascículo
Jun 2004
Histórico
-
Aceito
05 Jan 2004 -
Revisado
31 Out 2003 -
Recebido
11 Abr 2003