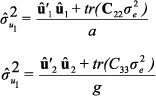Heredabilidad del contenido de proteína total en papa diploide Solanum tuberosum grupo Phureja

Herdabilidade do conteúdo de proteína total em batata diplóide Solanum tuberosum grupo Phureja

Heritability of total protein content in diploid potato Solanum tuberosum group Phureja

MEJORAMIENTO GENÉTICO VEGETAL

Heredabilidad del contenido de proteína total en papa diploide Solanum tuberosum grupo Phureja

Herdabilidade do conteúdo de proteína total em batata diplóide Solanum tuberosum grupo Phureja

Heritability of total protein content in diploid potato Solanum tuberosum group Phureja

Daniel Rodríguez CaicedoI, ^*; Carlos Eduardo Ñustez López^II; Jose Miguel Cotes Torres^III; Luis Ernesto Rodríguez Molano^II

^IUniversidad Militar Nueva Granada, Facultad de Ciencias, Programa de Biología Aplicada, Carrera 11 #101-80, Bogotá, Colombia

^IIUniversidad Nacional de Colombia, Facultad de Agronomía, Carrera 45 #26-85, Bogotá, Colombia

^IIIUniversidad Nacional de Colombia, Facultad de Ciencias Agropecuarias, Departamento de Agronomía, Carrera 59A #63-20, Medellín, Colombia

RESUMEN

En los últimos años se ha puesto de manifiesto la importancia de realizar estudios genéticos que permitan llevar a cabo el mejoramiento de la papa a nivel de su valor nutricional. Solanum tuberosum Grupo Phureja es una especie que además de tener un alto potencial para la exportación posee características nutricionales superiores a las de especies provenientes de los otros grupos. En el presente trabajo se realizó la estimación de heredabilidad del contenido de proteína en papa criolla mediante cuatro métodos: componentes de varianza mediante ANOVA de una vía, regresión padre-progenie, máxima verosimilitud restricta y estimación bayesiana. El contenido de proteína total fue evaluado en 103 familias de hermanos medios maternos. Para ello se determinó el nitrógeno total por el método de Kjeldahl y se empleó el factor de conversión a proteína. Para los cuatro métodos de estimación de heredabilidad se obtuvieron estimativos de 0.35, 0.28, 0.40 y 0.41 respectivamente. De acuerdo a las estimaciones de heredabilidad obtenidas, con una presión de selección moderada (20%) sería posible obtener incrementos en porcentaje de proteína entre 0.55% y 0.78% por ciclo de selección.

Palabras clave: papa criolla, estimación bayesiana, regresión padre-progenie, ganancia genética.

RESUMO

Nos últimos anos, pesquisas básicas de genética que ajudem no estabelecimento de programas de melhoramento de plantas visando à qualidade nutricional da batata têm tido muita importância. Solanum tuberosum Grupo Phureja é uma espécie que tem potencialidade para a exportação, além de características superiores quando comparadas com espécies de outros grupos. Nesta pesquisa, obteve-se a estimativa da herdabilidade do conteúdo de proteína em batatas nativas da Colômbia por quatro métodos: componentes da variância através do ANAVA, regressão pai-progênie, máxima verossimilhança restrita e estimação bayesiana. O teor de proteína total foi avaliado em 103 famílias de irmãos maternos. Para este fim, determinou-se o nitrogênio total pelo método Kjeldahl e foi utilizado o fator de conversão em proteína. Por meio destes métodos obtiveram-se estimativas de 0,35, 0,28, 0,40 e 0,41 respectivamente. Tendo em conta estas estimativas e uma pressão de seleção moderada (20%) é possível obter ganhos genéticos na porcentagem de proteína de batata entre 0,55% e 0,78% por ciclo de seleção.

Palavras-chave: batata nativa, inferência bayesiana, regressão pai-progênie, ganho genético.

ABSTRACT

In recent years, genetic studies that supports the plant breeding program for improve the nutritional value of potato tuber have been very important. Solanum tuberosum Group Phureja is a species with high potential for exportation and better nutritional characteristics than species from other groups. In this research we estimate de heritability by variance components based on analysis of variance, parent offspring regression, restricted maximum likelihood and bayesian estimation. The total protein content was assessed in 103 sib maternal families. For this purpose we determined the total nitrogen by the Kjeldahl method and the protein conversion factor was used. The estimates were 0.35, 0.28, 0.40 and 0.41 respectively. According to the heritability estimates and supposing a moderate selection pressure (20%), increments in protein content from0.55% to 0.78% could be obtained by each selection cycle.

Key words: yellow creole potato, Bayesian estimation, parent-offsping regression, genetic gain.

1. INTRODUCCION

Si bien la papa no es usualmente considerada una fuente importante de proteína, su calidad tiene propiedades deseables en un alimento. Posee un alto valor nutricional, incluso al ser comparada con la del huevo (DESBOROUGH y LAUER, 1977) y un perfil muy bien balanceado en cuanto a su composición de aminoácidos esenciales. De acuerdo con HORTON (1988) su valor nutricional es similar al de la proteína de la leche y es sobresaliente la forma como se complementa con otras proteínas como las de la soya, en la elaboración de suplementos alimenticios. En relación al peso seco se han reportado contenidos entre 7-10% es decir, comparable al contenido presente en el trigo y superior al que posen la mayoría de variedades de Maíz y Arroz (KAPOOR et al., 1975).

Existen diversas razones para incrementar el contenido de proteínas de la papa, una de ellas es el hecho de que mientras en la mayoría de los países desarrollados se cuenta con amplia variedad de fuentes de proteína, en muchos de los países en vías de desarrollo la dieta es insuficiente en proteínas (ORTÍZ y HUAMÁN, 1996). Además, durante el procesamiento de la papa para la producción de almidón se puede recuperar la proteína como un subproducto de amplio uso en la elaboración de suplementos alimenticios (KNORR, 1978).

La papa criolla Solanum tuberosum Grupo Phureja (HUAMÁN y SPOONER, 2002) representa uno de los recursos genéticos de mayor importancia en el país, teniendo en cuenta su alto valor alimenticio, su gran aceptación en el mercado, fácil preparación, precio asequible y alto potencial de exportación como producto procesado exótico con destino a países como Estados Unidos y Japón (PORRAS, 2000). Disponer de información acerca del control genético de la característica, como su heredabilidad es de gran importancia para orientar al mejorador acerca de la técnica a emplear, el tamaño de las poblaciones que debe manejar y el tiempo aproximado que requerirá para obtener los resultados deseados (ORTÍZ y HUAMÁN, 1996).

Se han propuesto diversos métodos para la estimación de la heredabilidad, aplicables a diferentes situaciones prácticas. Uno de ellos consiste en el análisis de varianza (ANAVA) de las familias de hermanos medios, donde se obtiene la heredabilidad en sentido estrecho, asumiendo que los efectos epistáticos son despreciables, por lo que en este método la varianza aditiva y la ganancia de selección esperada podrían ser sobreestimadas.

El método de regresión padre-progenie es uno de los más empleados para la estimación de heredabilidad en sentido estrecho, por varias razones. Una de ellas es que la estimación se hace por regresión lineal mediante mínimos cuadrados, cuyas propiedades estadísticas son bien conocidas, lo que permite obtener intervalos de confianza para los estimativos, y realizar las pruebas de hipótesis de interés. Ese método es muy utilizado en los programas de mejoramiento de alógamas principalmente, porque en esas especies se colectan semillas a partir de poblaciones naturales, donde solo se conoce el progenitor femenino. Otra alternativa para la estimación de la heredabilidad es el uso de los modelos mixtos, donde se considera a) el parentesco entre los individuos, b) tamaños diferentes de familias y c) apareamiento no aleatorio. La estimación de los parámetros de los modelos mixtos por el método de máxima verosimilitud restricta (REML por su abreviatura en inglés) es insesgada y el balanceo no es un aspecto relevante (SEARLE et al., 1992). Los modelos mixtos en genética cuantitativa son también estimados por el método Bayesiano, lo cual presenta la ventaja de la incorporación de la información a priori debida a la experiencia del investigador o a la información valiosa de experimentos anteriores (SORENSEN y GIANOLA, 2002). En años recientes el método bayesiano ha sido empleado en diversos estudios de herencia en cultivos semestrales y forestales (MORA et al., 2008a; 2008b; MORA y PERRET, 2007; MORA et al., 2007). Esta investigación tiene como objetivo estimar la heredabilidad del contenido de proteína total en la papa criolla mediante los métodos de análisis de varianza, regresión padre progenie, máxima verosimilitud restricta y estimación bayesiana, así como analizar las implicaciones de la heredabilidad estimada para fines de mejoramiento.

2. MATERIALES Y METODOS

El presente ensayo se realizó en el municipio de Soacha (Cundinamarca) a 2.900 m s.n.m. La siembra se llevó a cabo en bolsas plásticas de 6 kg. Se realizó fertilización con 3g de 12-34-12 por bolsa. Como sustrato se empleó suelo de la zona, sin uso previo, de tipo franco arcilloso, mezclado con arena de río en proporción 3:1. Se realizó fertilización foliar en tres ocasiones luego del primer mes.

Las progenies a evaluar se obtuvieron a partir de parentales de la colección de Solanum tuberosum Grupo Phureja de la Universidad Nacional de Colombia, que posee 144 accesiones colectadas principalmente en el departarmento de Nariño y el Norte de Ecuador, área donde esa especie presenta una diversidad importante. A partir de esa colección se obtuvieron 103 familias F1 de hermanos medios maternos. De estas, se sembraron 20 semillas en germinadores, sin embargo solamente 6 plántulas obtenidas fueron transplantadas a bolsas a libre exposición y algunas de ellas se perdieron en el desarrollo del experimento causando un desbalance en el número de individuos por familia. Así, fueron tomados un máximo de seis individuos por cada una de las familias para realizar el análisis de contenido de proteína total según la norma técnica ICONTEC NTC 1556 (1999). Los padres se sembraron en dos ambientes antes de la siembra de la F1 y para la evaluación de la proteína total se utilizaron tres plantas por cada parental.

Con el fin de comparar las estimativas de la heredabiliad se utilizaron cuatro diferentes métodos.

Análisis de varianza

Se realizó con las familias de hermanos medios maternos, y se estimó la heredabilidad con base en el coeficiente de correlación intraclase. Debido a que los tamaños de familias fueron diferentes, se empleó la aproximación donde es el tamaño total de la muestra. A partir de la esperanza de los cuadrados medios se obtuvieron las varianzas genética y fenotípica . El coeficiente de correlación intra-clase corresponde a y la heredabilidad se obtuvo como h² = 4σ (LYNCH y WALSH, 1998)

Regresión Padre progenie:

Esta se obtuvo con la modificación propuesta por KEMPHTORNE y TANDON (1953) para el caso de desigual número de individuos por familia. En este caso, el coeficiente de regresión se obtiene como:

donde:

que corresponden a las medias ponderadas de los padres y las progenies, respectivamente: z_pi = Fenotipo para el i-ésimo padre = Promedio fenotípico familiar del i-ésimo padre. Los w_i corresponden a las ponderaciones familiares:

Aquí n_i es el tamaño de la i-ésima familia y t corresponde al coeficiente de correlación intraclase, mientras que B es un estimativo inicial de la pendiente, obtenido mediante una regresión lineal simple sin considerar las ponderaciones.

Estimación REML

Se utilizo el siguiente modelo mixto:

Donde y es el vector de observaciones n × 1, 1_n y µ son un vector de unos de tamaño n y la media general, respectivamente, Z₁ y u₁ son la matriz de incidencia de tamaño n × 3 y el vector de efectos aleatorios correspondientes a los ambientes, Z₂ y u₂ son la matriz de incidencia de tamaño n × 688 y el vector de efectos aleatorios de los genotipos y e es un vector de residuales. Se asume que y . Siendo la matriz de covarianzas de ambientes y la matriz de covarianzas de los efectos de genotipos En este caso A es una matriz con elementos A_ij=2θ_ij y θ_ij es el coeficiente de coancestro de los individuos i y j (KEMPTHORNE, 1969) También se asume que .

En el presente trabajo, se dispone de progenitores y familias de hermanos medios maternos. Para el caso de padre-progenie se sabe que θ_ij=1/4 y para hermanos medios θ_ij=1/8. Puesto que los progenitores se asumen no correlacionados, el coancestro entre miembros de diferentes familias se ha tomado como cero. Las soluciones de los efectos fijos y aleatorios para la estimación por REML se obtienen de la siguiente forma (SEARLE, 1992):

Para obtener los componentes de varianza, se emplean los términos de la inversa de la matriz 3x3 en [2], denominada M:

Los componentes de varianza para ambientes, genotipos y el error respectivamente se estiman como:

Para obtener las estimaciones se emplea un algoritmo iterativo en el cual se asignan valores iniciales a los componentes de varianza, los cuales se emplean para estimar los efectos fijos y aleatorios presentados en [2].Con base en la estimación de estos efectos se actualiza el valor de los componentes de varianza, los cuales son para obtener una segunda estimación de los efectos fijos y aleatorios. Este procedimiento se repite hasta lograr convergencia.

Estimación bayesiana

Para el modelo mixto anterior [1] se utilizaron las siguientes distribuciones a priori:

µ~Cte

para los efectos de ambiente

para los efectos de genotipo

para la varianza del error

para la varianza de los ambientes

para la varianza de los genotipos

donde indica una distribución Chi cuadrado invertida escalada (GELMAN et al., 2004), en la que V_e y S_e son los grados de credibilidad y la varianza a priori para el efecto del error, Vu₁ y Su₁ son los grados de credibilidad y la varianza a priori para el efecto de los ambientes, y Vu₂ y Su₂ son los grados de credibilidad y la varianza a priori para el efecto de los genotipos.

La distribución posterior conjunta, posee una forma normal-gamma (WANG et al., 1994):

donde

G = Matriz de identidad I de orden 3 para el efecto de los ambientes (i=1) y la matriz A, es decir, dos veces el coeficiente de coancestro para el efecto de los genotipos (i=2).

v=Vector de grados de credibilidad a priori.

s=Vector de varianzas a priori.

A partir de la distribución de probabilidad conjunta se pueden obtener las distribuciones de probabilidad condicionales para los diferentes parámetros, las cuales son necesarias para el algoritmo de GIBBS y los estimadores de tales parámetros. Para obtener la condicional de un parámetro, todos los demás se asumen conocidos. A continuación se dan las condicionales y los estimadores respectivos.

Para los efectos aleatorios la distribución condicional es (WANG et al., 1993):

Y los estimadores de los efectos aleatorios son:

Para varianza del error la distribución de probabilidad es una chi-cuadrado invertida:

Los estimadores son v_e=n y

Para la varianza de los genotipos y los ambientes también se emplean distribuciones chi-cuadrado invertidas:

El estimador de la varianza del i-ésimo efecto aleatorio es

Muestreador de Gibbs

Se empleó el muestreador de Gibbs con el fin de obtener las distribuciones marginales a partir de las distribuciones conjuntas descritas en la sección anterior. El procedimiento empleado se describe a continuación:

1. Proponer valores iniciales arbitrarios para σ²_e, u_i y v. Generar un estima tivo de σ²_e con los valores arbitrarios de los otros parámetros y el estimador y actualizar

2. Generar estimativos de a partir del estimador y los otros valores arbitrarios de los demás parámetros y actualizar .

3. Estimar los efectos aleatorios de ambiente y genotipo mediante y los otros valores arbitrarios. Actualizar los valores de los efectos aleatorios.

4. Repetir los pasos 1-4 hasta tener un número grande de muestras que permita generar las distribuciones marginales (m veces). En el presente trabajo se empleó m=20.000.

Puesto que el objetivo en el contexto de este trabajo es estimar la heredabilidad, solo son de interés los componentes de varianza, y los ambientes han sido asumidos como efectos aleatorios al igual que los genotipos. Esto permite estimar la varianza fenotípica en términos de tres componentes:

Con las 20.000 muestras generadas con valores de σ_u1, σ_u2, y σ_e se realizan 20.000 estimaciones de la heredabilidad. Con estas estimaciones se debe construir la distribución marginal a posteriori. Esto se llevó a cabo mediante el procedimiento KDE del programa SAS (Versión 9.1). Este es un procedimiento no paramétrico, el cual realiza una estimación estadística de densidad. La estimación estadística de densidad aproxima una función de densidad de probabilidad a partir de los datos proporcionados (SAS INSTITUTE, 2004). En este caso, la distribución . Por ser una aproximación numérica esta distribución no se puede enunciar como una función. Sin embargo, es posible al realizar este procedimiento, obtener la gráfica de la función de densidad, el promedio, la varianza y los percentiles.

3. RESULTADOS

Estimación mediante análisis de varianza de las progenies:

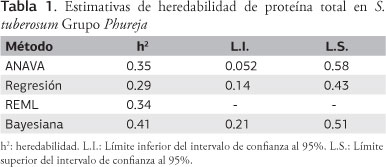
A partir de los cuadrados medios del análisis de varianza se obtuvieron los estimadores de σ²_s (0.057) y σ²_e (0.60). El estimativo de h²y su intervalo de confianza al 95% se presentan en la tabla 1. Puede interpretarse con base en estos valores que la característica presenta una heredabilidad intermedia (ALLARD, 1999).

Estimación mediante regresión padre-progenie:

A partir de la estimación del coeficiente de correlación intraclase se realizaron los cálculos iterativos hasta llegar a una estimación definitiva de la pendiente de regresión, obteniendo un valor de 0.14, con un error estándar de 0.018. La heredabilidad de la característica es dos veces el valor del , por tratarse de una regresión con familias de hermanos medios. Al calcular el error estándar de la heredabilidad en forma análoga, se obtienen los estimativos presentados en la tabla 1. Al igual que en el caso del método anterior, se puede decir que el contenido de proteína en papa criolla posee una heredabilidad intermedia.

Estimación por REML:

Este método arrojó un valor de heredabilidad de 0.341, que corresponde a una estimación puntual. Tal valor es superior a la estimación obtenida mediante regresión padre-progenie y similar a la estimación mediante análisis de varianza. Para la varianza ambiental se obtuvo una estimación de 0.4001 por este método. BURCH y IYER (1997) proponen un método exacto para la estimación del intervalo de confianza de la heredabilidad obtenida como cociente de dos componentes de varianza: que corresponde a la varianza aditiva y que corresponde a la varianza ambiental. En el presente caso sin embargo, el modelo planteado descompone la variación ambiental en una varianza de ambientes y la varianza del error , por lo que la heredabilidad no puede ser considerada como cociente de dos componentes de varianza. Puesto que para este último caso no existe una solución exacta reportada en la literatura, en el presente trabajo no se presenta intervalo de confianza para la heredabilidad estimada por REML.

Estimación Bayesiana:

Luego de obtener las 20.000 muestras con el muestreador de Gibbs, se construyó la función de densidad de probabilidad mediante el procedimiento KDE (Figura 1). Los percentiles 2.5 y 97.5 se pueden interpretar como los límites de un intervalo de confianza al 95% (Tabla 1). El estimativo obtenido por esta metodología es notablemente superior a los calculados mediante la regresión y los componentes de varianza, aunque nuevamente indica una heredabilidad intermedia. La estimación de la varianza ambiental por este método fue de 0.6021.

4. DISCUSIÓN

Tomando en cuenta los análisis realizados, la heredabilidad de la característica oscila entre 0.28-0.41. El estimativo resulta inferior al reportado por SINGH y ASNANI (1975) para el maíz (h²=0.66), aunque es igual al encontrado por DUDLEY et al. (1971) para el mismo cultivo (0.41). En trabajos previos no se han propuesto estimativos de heredabilidad para el contenido de proteína en papa, aunque si se han realizado algunos estudios acerca de la genética para esta característica (DESBOROUGH y WEISER, 1972; DESBOROUGH y LAUER, 1977; VEILLEUX et al., 1981). Al realizar cruzamientos entre parentales del grupo Phureja seleccionados por alto contenido de proteína (11-13%) y parentales del grupo Tuberosum, cuyo contenido de proteína estaba en torno al 6%, DESBOROUGH y LAUER (1977) obtuvieron un clon con un contenido de proteína estable durante tres ciclos de cultivo. En la localidad Crookston ese clon expresó un contenido de proteína de 9.2%, mientras que en las localidades Grand Rapids y Grand Forks se obtuvieron contenidos de 9.2% y 9.5% respectivamente, para este clon. De acuerdo con esto, resultaría viable esperar en una progenie F1 obtenida de cruzamientos entre padres de alto contenido de proteína y variedades comerciales, incrementos del orden de 3% en el contenido de proteína, lo cual resultaría ser una ganancia importante.

VEILLEUX et al. (1981) encuentran por el contrario, que si bien los progenitores del grupo Phureja expresan altos contenidos de proteína, estos son pobremente transmitidos a las progenies obtenidas de cruzamientos con el grupo Tuberosum.

A partir de los resultados obtenidos en el presente trabajo, es claro que la expresión de la característica es en una proporción determinada por el genotipo, y que es posible esperar transmitir en una proporción moderada el contenido de proteína de padres a progenies. De acuerdo con esto, se podría incrementar el contenido de proteína de los materiales cultivados, así como generar poblaciones de alto contenido de proteína, a través de procesos de mejoramiento que involucren a los genotipos del Grupo Phureja que han sido caracterizados como de alto contenido. Esta ganancia dependerá según plantea ALLARD (1999), de la heredabilidad, la intensidad de selección y la desviación estándar fenotípica (G_s=kσ_ph² ). En esta expresión k corresponde a un valor de z de la distribución normal estándar que depende de la intensidad de selección definida por el mejorador, h² es la heredabilidad y σ_p es la desviación estándar de los promedios de la población de genotipos de la población original. Si lo que se desea es generar una población de alto contenido de proteína a partir de la variabilidad genética disponible, se debe considerar que para una característica con una heredabilidad moderada y que seguramente es gobernada por un número grande de genes, resultaría recomendable no emplear una intensidad de selección demasiado alta (1-5%), pues esto podría agotar rápidamente la variabilidad genética de la población, al aumentar la probabilidad de excluir alelos favorables. En trabajos previos, como los ya citados para el caso del maíz, se han empleado intensidades de selección del 20%. Para esta intensidad se tiene que el valor de k corresponde a.1.4. La desviación estándar fenotípica se obtiene a partir de los promedios de los genotipos de la colección empleada para el presente trabajo y asume un valor de 1.3735; h² sería igual al 0.2875, según la estimación por el método de KEMPTHORNE y TANDON (1953), que corresponde a la más baja de las estimaciones.

Con los valores antes definidos tendríamos que la ganancia esperada sería G_s=(1.4)(1.3735)(0.2874)=0.55, de modo que se podría incrementar el promedio de la población en 0.55% de contenido de proteína en cada ciclo de selección. Si aplicamos los mismos cálculos con el estimativo bayesiano de 0.41 (el más alto), se obtiene G=(1.4)(1.3735)(0.41)=0.78, casi un 0.8% de incremento en el contenido de proteína.

Este resultado podría asociarse con un tipo de respuesta categorizada por ALLARD (1999) como "tipo 2", la cual es lenta, constante y continuada durante mucho tiempo, lo cual es consistente con caracteres regidos por sistemas complejos de genes, donde cada uno de ellos presenta un efecto pequeño. El cambio en frecuencia (Δq) de cualquier gen en particular es tan pequeño, que la fijación se alcanza muy lentamente, acorde con el llamado "modelo infinitesimal" (BARTON y KEIGHTLEY, 2002). Bajo estas circunstancias, se espera que la media de la población se incremente en forma lenta pero continuada y que gradualmente aparecerán genotipos superiores a todos los presentes en la población original, sin que se presente una disminución importante de la variabilidad genética. Este tipo de respuesta se encontró al realizar procesos para mejorar el contenido de proteína en el maíz en la Estación Experimental de Illinois, donde el contenido de proteína de la población original era de 11.97% y pudo llevarse, al cabo de 103 generaciones, a valores por encima de 30%, sin que se estabilizara en una meseta (MOOSE et al., 2004). Según los resultado obtenidos, al cabo de 10 ciclos de selección, el promedio de proteína en esta población del grupo Phureja bajo selección, se podría llevar de 5.52 hasta 10.47 asumiendo heredabilidad de 0.28 ó 12.54 si se asume h²=0.41 siempre que se trabaje bajo diseños experimentales apropiados, que permitan discriminar el efecto genético del ambiental e involucrando localidades. Es importante no perder de vista que para las estimaciones realizadas mediante los cuatro métodos antes descritos, se asume que no existen efectos ambientales comunes que puedan incrementar la correlación intrafamiliar. En el presente trabajo se emplearon familias de hermanos medios maternos, debido a las ventajas logísticas que esto planteaba. Si bien no puede descartarse con certeza la presencia de efectos maternos determinando la herencia del contenido de proteína, tampoco hay evidencia fuerte que permita suponer que están presentes. Mientras que en el trigo hay evidencias claras de que los efectos maternos tienen un papel importante en el contenido de proteína (MILLET et al., 1984; DHALIWAL, 1977), en otras especies como el fríjol, el efecto no significativo de la variación atribuida a los cruzamientos recíprocos en diseños dialélicos, sugiere que los efectos maternos no son importantes en la herencia del contenido de proteína total (MEBRAHTU y MOHAMED, 2003). En maíz, RUSKOVA (1974) encuentra efectos maternos débiles afectando el contenido de proteína, mientras que GARWOOD et al. (1970) plantean la ausencia de efectos maternos afectando dicho carácter. POLLMER et al. (1979) trabajando con 42 cruces de maíz y sus recíprocos, encuentran que la variación en contenido de proteína por efecto de la diferencia entre los cruces recíprocos no es significativa. En el maíz dulce, HAS y HAS (2009) encuentran que la varianza genética debida a efectos maternos no es significativa para el contenido de proteína. Estudios tan específicos en el caso del contenido de proteína en la papa no han sido realizados. Sin embargo, GOLMIRZAIE y ORTÍZ (2003) evaluaron la importancia que podrían tener los efectos maternos en la papa, encontrando que son importantes para características reproductivas como la cantidad de polen producido (lo cual no es extraño pues se sabe que la esterilidad masculina en papa, resulta de la interacción de material genético presente en el citoplasma con genes nucleares dominantes), pero no para otras características como por ejemplo el rendimiento, por lo que suponer que los efectos maternos no son tan importantes en el contenido de proteína, es una hipótesis plausible.

Finalmente, cabe resaltar que en el proceso de selección para mejorar el contenido de proteína en papa deberán tomarse en cuenta otras características, principalmente contenido de almidón, materia seca y rendimiento, pues el contenido alto de proteína esta correlacionado de manera inversa con el contenido de almidón (SNYDER y DESBOROUGH, 1978), el cual constituye el mayor porcentaje de la materia seca del tubérculo. En Illinois al realizar mejoramiento del contenido de proteína en el maíz, se encontró que el rendimiento tendía a disminuirse (ALLARD, 1999). La autoincompatibilidad genética existente a nivel de la especie (ESTRADA, 2000) y el incremento de la endogamia son también aspectos de gran importancia, que podrían afectar negativamente un proceso como el descrito anteriormente y deberán evaluarse en forma cuidadosa. Adicionalmente sería importante realizar el mejoramiento de poblaciones con el fin de obtener para el futuro progenitores con mayor contenido de proteína que los actuales, así como adelantar estudios para establecer a nivel de progenitores de interés, su habilidad combinatoria general y específica.

5. CONCLUSIÓN

Se estimó la heredabilidad por medio de diferentes métodos estadísticos encontrándose que esta oscila entre 28%-41%, lo cual corresponde a un valor moderado de la misma, que permitiría incrementar el contenido de proteína total entre 0.55% y 0.78% por cada ciclo de selección, empleando una intensidad de selección moderada, en torno a 20%.

Se pudo establecer que el contenido de proteína total es gobernado genéticamente, pero su expresión también es afectada por condiciones ambientales, como lo evidencia la heredabilidad moderada que se obtuvo. Por lo tanto el manejo apropiado del cultivo es un aspecto clave con miras a incrementar el contenido de proteína, además del mejoramiento genético.

Recibido: 4/mar./2011

Aceptado: 19/abr./2011.

(

• ALLARD, R.W. Principles of plant breding. 2.ed. London: John Wiley and Sons, 1999. 254p.
• BARTON, N.H.; KEIGHTLEY, P.D. Understanding quantitative genetic variation. Nature Reviews Genetics, v.3, p.1-21, 2002.
• BURCH, B.D.; IYER, H.K. Exact confidence intervals for a variance ratio (or heritability) in a mixed linear model. Biometrics, v.53, p.1318-1333, 1997.
• DESBOROUGH, S.; LAUER, F. Improvement of potato protein II. Selection for protein and yield. American Potato Journal, v.54, p.371-377, 1977.
• DESBOROUGH, S.; WEISER, C.J. Protein comparisions in selected phureja-haploid tuberosum families. American Potato Journal, v.49, p.227-233, 1972.
• DHALIWAL, H.S. Genetic control of seed proteins in wheat. Theoretical and Applied Genetics, v.50, p.235-239, 1977.
• DUDLEY, J.W.; LAMBERT, R.J.; ALEXANDER, D.E. Variability and relationships among characters in Zea mays L. synthetics and improved proteína quality. Crop Science, v.11, p.512-514, 1971.
• ESTRADA, R.N. La biodiversidad en el mejoramiento genético de la papa. La Paz: PROINPA, CID y CIP, 2000. 372p.
• GELMAN, A.; CARLIN, J.B.; STERN H. S.; RUBIN D.B. Bayesian data analysis. 2. ed. London: Chapman & Hall, 2004. 526p.
• GARWOOD, D.L.; WEBER, E.J.; LAMBERT, R.J.; ALEXANDER, D.E. Effect on different cytoplasms on oil, fatty acids, plant height, and ear height in maize (Zea mays L.). Crop Science, v.10, p.39-41, 1970.
• GOLMIRZAIE, A.; ORTIZ, M. Reciprocal effects in true potato seed breeding in short-day length environments. Plant Breeding, v.122, p.372-374, 2003.
• HAS, V.; HAS, I. Genetic inheritance of some important characters of sweet corn. Notulae Botanicae Horti Agrobotanici Cluj-Napoca, v.37, p.244-248, 2009.
• HORTON, D.E. Las papas en los países en desarrollo. Revista Latinoamericana de la Papa, v.1, p.9-17, 1988.
• HUAMÁN, Z.; SPOONER, D.M. Reclassification of landrace populations of cultivated potatoes (SOLANUM SECT. PETOTA). American Journal of Botany, v.89, p.947-965, 2002.
• ICONTEC - Instituto Colombiano de Normas Técnicas. Norma técnica NTC 1556. Carne y productos cárnicos: Método para determinar el contenido de nitrógeno (Método de referencia). Bogotá: ICONTEC, 1999. 20p.
• KAPOOR, A.C.; DESBOROUGH, S.; LI, P.H. Potato tuber proteins and their nutritional quality. Potato Research, v.18, p.469-478, 1975
• KEMPTHORNE, O. An introduction to genetics statistics. Ames: Iowa State University Press, 1969. 228p.
• KEMPTHORNE, O.; TANDON, O. The estimation of heritability by regression of offspring on parent. Biometrics, v.9, p.90-100, 1953.
• KNORR, D. Protein quality of the potato and potato protein concentrates. Lebensmittel-wissenschaft und technologie, v.11, p.109-115, 1978.
• LYNCH, M.; WALSH, B. Genetics and analysis of quantitative traits. Sunderland: Sinauer Associates, 1998. 803p.
• MEBRAHTU, T.; MOHAMED, A. A seven parental diallel analysis of nutritional composition of common beans. Plant Foods for Human Nutrition, v.58, p.1-11, 2003.
• MILLET, E.; LEVY, A.A.; AVIVI, L.; ZAMIR, R.; FELDMAN, M. Evidence for maternal effect in the inheritance of grain protein in crosses between cultivated and wild tetraploid wheats. Theoretical and Applied Genetics, v.67, p.521-524, 1984.
• MOOSE, S.; DUDLEY, J.W.; ROCHEFORT, T.R. Maize selection passes the century mark: a unique resource for 21^st century genomics. Trends in Plant Science, v.9, p.1360-1385, 2004.
• MORA, F.; PERRET, S. Aplicación de técnicas bayesianas en el análisis genético de árboles forestales. Bosque, v.28, p.198-206, 2007.
• MORA, F.; PERRET, S.; SCAPIM, C.A.; MARTINS, E.N.; MOLINA, M.P. Source-dependent blooming variability of Eucalyptus cladocalyx in the Region of Coquimbo, Chile. Ciencia e Investigación Agraria, v.34, p.99-106, 2007.
• MORA, F.; GONÇALVES-VIDIGAL, M.C.; SANTOS, A.I. Bayesian analysis of the genetic control of survival in F₃ families of common bean. Chilean Journal of Agricultural Research, v.68, p.334-331, 2008a.
• MORA, F.; TAPIA, F.; IBACACHE, A.; MARTINS, E.N.; SCAPIM, C.A. Evaluación genética de clones de olivo en el desierto de Atacama, Chile. Agrociencia, v.42, p.777-786, 2008b.
• ORTIZ, R.; HUAMAN, Z. Inheritance of morphological and tuber characteristics. En: Potato Genetics. BRADSHAW J.; MACKAY R. (Ed.). London: CAB International, 1996. p.285-319.
• POLLMER, W.G.; KLEIN D.; DHILLON B.S. Differences in reciprocal crosses of maize inbred lines diverse for protein content. Euphytica, v.28, p.325-328, 1979.
• PORRAS, P. Guía para papa criolla "Clon 1". En: Papas colombianas con el mejor entorno ambiental. Bogotá: Fedepapa, 2000. p.65-66.
• RUSKOVA, K. The effect of the direction of the cross on oil, protein and lisyne content in the grain of maize. Genetika i selektsiya, v.7, p.353-360, 1974.
• SAS INSTITUTE. The KDE procedure. En: SAS/STAT 9.1 User's Guide, Cary, New York, 2004. p.1993-2029.
• SEARLE, S.R.; CASELLA, G.; MCCULLOCH, C.E. Variance Components. New York: John Willey and Sons, 1992. 528p.
• SINGH, J.; ASNANI, V.L. Present status and future prospects of breeding for better protein quality in maize through opaque-2. In: MERTZ E.T. (Ed.). High Quality Protein Maize. Stroudsburg, Pennsylvania: Dowden, Hutchinson and Ross, 1975. p.86-101
• SNYDER, J.; DESBOROUGH, S. Protein, starch and non-protein nitrogen accumulation in high protein hybrids and low protein cultivars. American Potato Journal, v.55, p.453-459, 1978.
• SORENSEN, D.; GIANOLA, D. Likelihood, Bayesian and MCMC methods in genetics. New York: Springer-Verlag, 2002. 740p.
• VEILLEUX, R.E.; LAUER, F.I. ; DESBOROUGH, S. Breeding behavior for tuber protein in Solanum tuberosum and tuberosum-phureja hybrids. Euphytica, v.30, p.563-577, 1981.
• WANG, C.S.; RUTLEDGE, J.J.; GIANOLA, D. Marginal inferences about variance components in a mixed linear model using Gibbs sampling. Genetics, Selection and Evolution, v.25, p.41-62. 1993.

Fechas de Publicación

• Publicación en esta colección
  19 Ene 2012
• Fecha del número
  2011

Histórico

• Acepto
  19 Abr 2011
• Recibido
  04 Mar 2011