Abstracts
The isothermal deterministic model adherence was studied to evaluate the population dinamic of Synthesiomyia nudiseta (Diptera, Muscidae). The linear form of equation obtained for the experiments in the several phases, were for Egg: 1/D = -0.18 + 0.02 . T; Larva: 1/D = -0.028 + 0.01. T; Pupa: 1/D = -0.069 + 0.01 . T; and Adult: 1/D = -0.4178 + 0.02 . T. In function of temperature, S. nudiseta can present from 4.18 to 8.95 and from 4.91 to 8.99 generations per year, when calculated through the equations of development and through the simulations, respectively. And the higher the temperature the larger the generation number. Through variance analysis it was verified the significance for the regression equations in relation to the annual generation number (Ng/year) of S. nudiseta in function of the isothermals, for two studied situations. It was obtained a significance of 0,1%. The regression equations obtained for these situations were: Ng/year = 5.4 + 0.5 . T and Ng/year = 5.1 + 0.52 . T. The number of generations of S. nudiseta varies linearly with the isothermal. Besides that, the number of annual generations for each isothermal does not differ statistically when calculated through the development equations or through the simulations. Such conditions suggest the adaptation of the deterministic model adopted.
deterministic model; population dynamics; Synthesiomyia nudiseta; diptera
Estudou-se a aderência de um modelo determinístico de isotermas para avaliar a dinâmica populacional de Synthesiomyia nudiseta (Diptera, Muscidae). As formas lineares das equações obtidas para os experimentos nas diversas fases foram: para ovo: 1/D = -0,18 + 0,02 . T; larva: 1/D = - 0,028 + 0,01 . T; pupa: 1/D = -0,069 + 0,01 . T; e adulto: 1/D = -0,4178 + 0,02 . T. Em função da temperatura, S. nudiseta pode apresentar de 4,18 a 8,95 e de 4,91 a 8,99 gerações por ano, quando calculadas por meio das equações de desenvolvimento e pelas simulações, respectivamente. Sendo que, quanto mais alta a temperatura, maior o número de gerações. Por intermédio da análise de variância verificou-se a significância para as equações de regressão relativas ao número de gerações anuais (Ng/ano) de S. nudiseta em função das isotermas, para duas situações estudadas. Obteve-se uma significância de 0,1%. As equações de regressão obtidas para essas situações foram: Ng/ano = 5,4 + 0,5 . T e Ng/ano = 5,1 + 0,52 . T. O número de gerações de S. nudiseta varia linearmente com as isotermas. Além disso, o número de gerações anuais para cada isoterma não difere estatisticamente quando calculadas por meio das equações de desenvolvimento ou por meio das simulações. Tais condições sugerem a adequação do modelo determinístico adotado.
modelo determinístico; dinâmica de populações; Synthesiomyia nudiseta; diptera
APPLICATION OF DETERMINISTIC MODEL OF ISOTHERMALS FOR POPULATION DYNAMICS OF Synthesiomyia nudiseta (DIPTERA, MUSCIDAE)
ALMEIDA, J. R. de,1 OLIVEIRA, S. G. de,2 BORGES, I. L.3 and D'ALMEIDA, J. M.4
1Programa de Planejamento Energético, COPPE/UFRJ, C.P. 68565, CEP 21945-970, Cidade Universitária, Ilha do Fundão, Rio de Janeiro, RJ, Brazil
2, 3Setor de Ecologia, Departamento de Biologia Animal e Vegetal, UERJ, Rua São Francisco Xavier, 524, Pavilhão Haroldo Lisboa Cunha, 2o andar, sala 220, CEP 20550-050, Rio de Janeiro, RJ, Brazil
4 Departamento de Biologia, Instituto Oswaldo Cruz/FIOCRUZ, Av. Brasil, 4365, Manguinhos, CEP 21045-900, Rio de Janeiro, RJ, Brazil
Correspondence to: Simone Gomes de Oliveira, Setor de Ecologia, Departamento de Biologia Animal e Vegetal, UERJ, Rua São Francisco Xavier, 524, Pavilhão Haroldo Lisboa Cunha, 2o andar, sala 220, CEP 20550-050, Rio de Janeiro, RJ, Brazil
Received November 24, 1999 Accepted March 3, 2000 Distributed February 28, 2001
ABSTRACT
The isothermal deterministic model adherence was studied to evaluate the population dinamic of Synthesiomyia nudiseta (Diptera, Muscidae). The linear form of equation obtained for the experiments in the several phases, were for Egg: 1/D = 0.18 + 0.02 . T; Larva: 1/D = 0.028 + 0.01. T; Pupa: 1/D = 0.069 + 0.01 . T; and Adult: 1/D = 0.4178 + 0.02 . T. In function of temperature, S. nudiseta can present from 4.18 to 8.95 and from 4.91 to 8.99 generations per year, when calculated through the equations of development and through the simulations, respectively. And the higher the temperature the larger the generation number. Through variance analysis it was verified the significance for the regression equations in relation to the annual generation number (Ng/year) of S. nudiseta in function of the isothermals, for two studied situations. It was obtained a significance of 0,1%. The regression equations obtained for these situations were: Ng/year = 5.4 + 0.5 . T and Ng/year = 5.1 + 0.52 . T. The number of generations of S. nudiseta varies linearly with the isothermal. Besides that, the number of annual generations for each isothermal does not differ statistically when calculated through the development equations or through the simulations. Such conditions suggest the adaptation of the deterministic model adopted.
Key words: deterministic model, population dynamics, Synthesiomyia nudiseta, diptera.
RESUMO
Aplicação do modelo determinístico de isotermas à dinâmica populacional de Synthesiomyia nudiseta (Diptera, muscidae)
Estudou-se a aderência de um modelo determinístico de isotermas para avaliar a dinâmica populacional de Synthesiomyia nudiseta (Diptera, Muscidae). As formas lineares das equações obtidas para os experimentos nas diversas fases foram: para ovo: 1/D = 0,18 + 0,02 . T; larva: 1/D = 0,028 + 0,01 . T; pupa: 1/D = 0,069 + 0,01 . T; e adulto: 1/D = 0,4178 + 0,02 . T. Em função da temperatura, S. nudiseta pode apresentar de 4,18 a 8,95 e de 4,91 a 8,99 gerações por ano, quando calculadas por meio das equações de desenvolvimento e pelas simulações, respectivamente. Sendo que, quanto mais alta a temperatura, maior o número de gerações. Por intermédio da análise de variância verificou-se a significância para as equações de regressão relativas ao número de gerações anuais (Ng/ano) de S. nudiseta em função das isotermas, para duas situações estudadas. Obteve-se uma significância de 0,1%. As equações de regressão obtidas para essas situações foram: Ng/ano = 5,4 + 0,5 . T e Ng/ano = 5,1 + 0,52 . T. O número de gerações de S. nudiseta varia linearmente com as isotermas. Além disso, o número de gerações anuais para cada isoterma não difere estatisticamente quando calculadas por meio das equações de desenvolvimento ou por meio das simulações. Tais condições sugerem a adequação do modelo determinístico adotado.
Palavras-chave: modelo determinístico, dinâmica de populações, Synthesiomyia nudiseta, diptera.
INTRODUCTION
The thermal constant obey a rectangular hyperbole equation that relates temperature and time of biological development, where K = y (t a). Being K the expressed thermal constant in degrees day (dd); y the time required to complete the development (days); t the ambient temperature (oC); a the development thershold temperature (oC) and (t a) it is the effective temperature. The development speed can be calculated by its reciprocal (v = 1/y), being y = K/(t a). Thus 1/y = (t a)/ K; and thus being 1/K = b constant, remains: 1/y = bt ab = bt K. Then 1/y = bt + K, it represents a straight line equation. However the development speed is just a straight line in a narrow temperature strip around the great, because reaching the ends acquires a form sigmóide (Almeida & Carvalho, 1984; Almeida et al., 1985a, b; Xerez & Almeida,1986).
The logistic equation that is more realistic, allows a better comprehension of these phenomena. This equation is expressed by 1/y = K/(1 + e (a bt)) or 100/y = K/(1 + e (a bt)) when it places in the ordinates the development percentage average instead of the development duration. The development duration curve is given by y = (1 + e (a bt))/K. For studies of this nature, the techniques of systems analysis and mathematical modeling are particularly useful. Among the used models the most versatile and of better operationality in the mathematical treatment, are compartimental deterministic ones (Almeida et al., 1985a, b; D'Almeida & Almeida, 1996).
The saturation deficiency law establishes that when the insects die for desiccation of their tissues, their longevity is inversely proportional to the air saturation deficiency, and it establishes that water evaporation of an insect is proportional to the air saturation deficit that involves it. However this occurs in particular circumstances, not always a linear function implies proportionality (Schaeffer, 1974; Stearns, 1976; Sibly & Calow, 1984).
Thus, the weight loss of the insect body through evaporation (P) is a lineal function if the saturation deficit (d) thus: P = a + Kd; being a the development thershold temperature (oC) and K a corresponding constant at the rate of molecules diffusion, that is a straight line equation, and a particular case, when this straight line intercept the origin, a = 0, then P = K.d.
The main mistake of this equation is to consider that all weight loss is due to evaporation, what does not actually occur. Then, if it considers that a represents the weight loss through others ways (excretion, for example) and P evaporation, (P a) wil be the loss through evaporation. Then E = K.d, e.g., the evaporation is proportional to the saturation deficit, which occurs when there are no losses through other sources (a = 0). From this hypothesis, and, considering that the insect will have a shorter life the faster it loses water from its body, due to the critical level that needs to be kept in it, the longevity must be inversely proportional to the sum of lost water for time unit. Logically, that will also be inversely proportional to the saturation deficit for each temperature, which will be explained by a hyperbole, representative of straight line.
Considering that all insects die when they lose a great quantity of water from their bodies (K2) and that the relation between loss of water and the saturation deficit is given by the equation P = a + K1d, it states that the longevity (L) will be expressed by the equation L = K2 . 1/P \ L = K2 . 1/(a + K1d). If occurs only the loss by evaporation, it states L = K2 . 1/K1d and in this case, the relation between K2/K1 will also be a constant (K). then: L = K/d.
It considers also that the mortality ratio is proportional to the saturation deficit product per time of exhibition. Although this also applies for a lot of insects, we can't forget some mistake causes. The loss ratio of water is not determined only by the temperature independent saturation deficit. For any temperature, the loss ratio of water can be a function of saturation deficit but not necessarily proportional to it (Almeida & Mizuguchi, 1978, 1979a, b, 1982).
The relationship that exists between the loss of water and the saturation deficit is not the same that exists between the saturation deficit and the mortality ratio. If one is lineal and the other can be sigmoide, to apply that hypothesis it should be considered that for a group of insects of a species, sometimes, the loss of a certain amount of water can be fatal for some individuals but not for all them. In this work we studied the isothermal deterministic model adherence was studied to evaluate the population dinamic of Synthesiomyia nudiseta (Diptera, Muscidae).
MATERIAL AND METHODS
The flies were captured with a trap suited for diptera built with metal frame painted black, measuring 22 cm diameter for 40 cm height with two openings shutter kind of 3 cm width at the bottom, in order to allow the entrance of the flies. Inside the traps it was placed a nylon funnel with its base directed downwards, in order to address the diptera to the top of the trap. The traps were placed at a height of 1 meter from the soil, remaining 2 m away from each other. It was placed five traps, one for each bait, in each collection location. It was used this trap for it attended better to the purpose. It was used five different kinds of bait (100 g) in each collections location: mouse carcass, chicken viscera, fish viscera, onion and human feaces. The baits were exposed fresh and observed during their decomposition, evaluating their capacity of attracting the flies in different putrefaction degrees, in natural conditions.
After the emergency, the adult flies were immediately packed in cages. (30 × 30 cm), covered with nylon screen and fed with fresh raw liver, a refined sugar mixture with desiccated milk (proteins: 26.4 g; lactose: 38.6 g; fats: 26 g; mineral salts (gray): 5.8 g), vitamins and water ad libitum changed daily.
It was adopted the Forrester's diagram (1976) to schematize the model used in the population dynamics of S. nudiseta. In this case: X1, X2, X3, X4, correspond to the egg, larva, pupa and adult (female) compartments, respectively; S (i) the survival of each compartment; bt (i) the base temperature (oC) for each compartment; K (i) corresponded to the thermal constant (degrees days = dd) for each compartment; RS the species sexual reason (females number) . (female number + male number = 0.5); SF represented the species fecundity (eggs number/females); SFF the species fertility (percents of larva appearance).
As the parameters that regulate the increase and/or decrease of S. nudiseta population were introduced into the model, it was made pertinent simulations, to verify if the mathematical equations used represented correctly the studied situation.
For the daily temperatures calculation, it was used direct measures data. The base temperature (bt) and the thermal constant (K) values were determined from the duration data (D) of each phase in temperature function (T), once K = D . (T bt) where T bt is the insect effective temperature. Writing this equation in linear form 1/D = bt/K + 1/K.T.
For the concept of constant thermal, the product of the duration of the development for the effective temperature is constant, being measured in degrees days. Therefore that unit (degree day), it represents the sum of favorable temperatures to the insects development during this period, that is to say, the temperatures that are above the temperature of the development threshold or temperature base. Graphically the degree day is given by the area understood between the curve of the daily temperature and the temperature base. Its estimate is made with the data of maximum, minimum and base temperatures.
RESULTS AND DISCUSSION
The equations obtained for the various phases, in their linear form were for egg: 1/D = 0.18 + 0.02 . T; for larva: 1/D = 0.028 + 0.01 . T; for pupa: 1/D = 0.069 + 0.01 . T; and for adult: 1/D = 0.4178 + 0.02 . T. So that if it observed a new one generation, was considered just the period of pre-ovoposition of the obtained females. The S. nudiseta development equation was determined making use of life tables data, being the pre-ovoposition period 1/D = 0.042 + 0.008 T. From these equations it was determined the generation number per year of S. nudiseta, for the isothermals from 25oC to 31oC. Through the number of individuals in the last compartment (females in pre-oviposition), obtained through the simulations, in function of time and for each isothermal, it was estimated the number of annual generations conditioned to a system without won nor losses.
In function of the temperature, S. nudiseta can introduce from 4.18 to 8.95 and from 4.91 to 8.99 generations per year, when obtained through the development equations and through simulations respectively, and the higher the temperature the larger the generation number. The Table 1 indicates the generation number/year of S. nudiseta, for each isothermal, determined through the development equations and the simulations.
In the Table 1, number of generation per year, Ng (a), was calculated from the equations: egg: 1/D = 0.18 + 0.02 . T; larva:1/D = 0.028 + 0.01 . T; pupa: 1/D = 0.069 + 0.01 . T; and adult: 1/D = 0.418 + 0.02 . T; Ng (b) is the area under the curve of number of individuals of the last compartment (pre-ovipositional period) in function of time, obtained through simulations of a closed system.
Through variance analysis it was verified a significance (0.1%) for the regression equations concerning the annual generation number of S. nudiseta in function of the isothermal, for both studied situations (Table 1). The regression equations obtained for these situations were (a) Ng/year = 5.49 + 0.5 . T and (b) Ng/year = 5.19 + 0.52 . T.
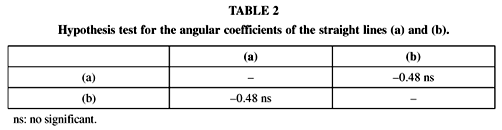
There is no significant difference between the angular coefficient of regression equations concerned to the annual generation number in function of the isothermal ("t" test), obtained from the simulations and through development equations (Table 2).
We can, therefore, affirm that the parameters used in the mathematical equations of the compartimental deterministic model are adjusted, portraying the population dynamics of S. nudiseta.
In the evaluation of the model, it was added a survival of 50% for each phase besides an average eggs fecundity/female. Due to great variability in the fertility data of S. nudiseta, this parameter was estimated in a way so we could obtain a mean increase of 5 times in the population of females in pre-oviposition period. Through the simulations, the value found for the fertility was 80%. In the Table 3, N(i) represents the complete generation of S. nudiseta (i = 1, 2, ... 5).
The generation number of S. nudiseta varies linearly with the isothermal and the number of annual generations for each isothermal, does not differ statistically when calculated through the development equations or through the simulations, indicating the adaptation to the model.
- ALMEIDA, J. R. & CARVALHO, C. J. B., 1984, Dípteros sinantrópicos de Curitiba e arredores (Paraná, Brasil) I: Muscidae. Revta. Bras. Ent., 13(2): 551-560.
- ALMEIDA, J. R., CARVALHO, C. J. B. & MALKOWSKI, S. R., 1985a, Dípteros sinantrópicos de Curitiba e arredores (Paraná, Brasil). II: Faniidae e Anthomyiidae. An. Soc. Entomol. Bras., 14(2): 277-288.
- ALMEIDA, J. R. & MIZUGUCHI, Y., 1978, Sistemas enzimáticos de Sitotroga cerealella (Lepidoptera, Gelechiidae) e considerações sobre a resistência a inseticidas. An. Soc. Entomol. Brasil., 7(2): 193-198.
- ALMEIDA, J. R. & MIZUGUCHI, Y., 1979a, Biologia populacional e caracterização enzimática do metabolismo alimentar de Oncopeltus fasciatus (Hemiptera, Lyeaeidae). Rev. Brasil. Biol., 39(3): 565-569.
- ALMEIDA, J. R. & MIZUGUCHI, Y., 1979b, Isoesterases em pragas de grãos armazenados Sitotroga cerealella, Sitophilus zeamais e Tribolium castaneum An. Soc. Entomol. Brasil., 8(2): 251-255.
- ALMEIDA, J. R. & MIZUGUCHI, Y., 1982, Volume de competição entre espécies de Dysdercus (Hemiptera, Pyrrhocoridae) por recursos alimentares. An. Soc. Entomol. Brasil., 1(2): 295-299.
- ALMEIDA, J. R., QUEIROZ, S. P. M. & DUDAS, L., 1985b, Bionomia de Sarconesia chlorogaster (Diptera, Caliphoridae) em Curitiba, Paraná. An. Soc. Entomol. Brasil., 14(1): 105-110.
- D'ALMEIDA, J. M. & ALMEIDA, J. R., 1996, Longevidade e curva de sobrevivência de dípteros caliptrados (Calliphoridae, Muscidae e Sarcophagidae) em condições de laboratório. Rev. Brasil. Biol., 56(3): 497-505.
- FORRESTER, J. W., 1976, Principles of systems Wright Allen Press. Inc., Cambridge, 320p.
- SCHAEFFER, W. M., 1974, Selection for optimal life histories: The effect of age structure. Ecology, 55: 291-303.
- SIBLY, R. & CALOW, P., 1984, Direct and abosortion costing in the evolution of life cycles. Journal of Theoretical Biology, 111: 463-473.
- STEARNS, S. C., 1976, Life history tactis: a review of the ideas. Quarterly Review of Biology, 51: 3-47.
- XEREZ, R. de & ALMEIDA, J. R., 1986, Bionomia de Dysdercus maurus (Hemiptera, Pyrrhocoridae). An. Soc. Entomol. Brasil., 15(1): 19-26.
Publication Dates
-
Publication in this collection
25 Apr 2001 -
Date of issue
Feb 2001
History
-
Accepted
03 Mar 2000 -
Received
24 Nov 1999