Abstracts
As an extension of Muinhos (1998), which found a negative relationship between capital inflows and inflation in Brazil, this paper attempts to obtain the intermediate variables that connect this relationship. Based on a three-good model of Agenor and Montiel (1996) it tests the real exchange rate and government debt as the intermediate using time series' tools, such as error correction VAR, impulse response function, and Granger causality, for the period that covers from 1975 to 1994. It concludes that in a context of capital inflows, there is an appreciation of the real exchange rate that causes a decrease in wages and inflation. Another possibility is that capital inflows decrease the government debt and that reduction affects negatively inflation.
capital inflow; inflation; time series; real exchange rate
Este artigo é uma extensão de Muinhos (1998), onde foi encontrada uma relação negativa entre entrada de capital e inflação. Aqui tenta-se obter quais as variáveis intermediárias que conectam esta relação. Com base em um modelo de três bens de Agenor e Montiel (1996), foram testadas a taxa real de câmbio e a dívida do governo, como os intermediários. As técnicas econométricas usadas no teste foram error correction VAR, resposta de impulso e causalidade de Granger para um período que cobre de 1975 a 1996. Conclui-se que, num contexto de entrada de capital, uma valorização da taxa de câmbio causa uma diminuição da inflação e dos salários. Outra possibilidade testada foi a de que a entrada de capital diminua a dívida do governo e esta redução afete negativamente a inflação.
From capital inflow to inflation: the role of exchange rate and government debt
Marcelo Kfoury Muinhos* * I would like to thank Tom Davis, Tim Vogelsang, Steve Kyle, Mark Tomajnovich, Jorge Restrepo, Wagner Guerra Jr., Renato Fragelli Cardoso, João Ricardo Faria, Danniel L. Machado, John Mcdermott, Pierre-Richard Agenor, João Victor Issler, one anonymous referee and all the participants in XX SBE. All mistakes are mine.
Cornell University and Central Bank of Brazil.
Correspondence Correspondence to Marcelo Kfoury Muinhos E-mail: mmuinhos@hotmail.com
Summary: 1. Introduction; 2. The model; 3. Empirical results; 4. Conclusion.
As an extension of Muinhos (1998), which found a negative relationship between capital inflows and inflation in Brazil, this paper attempts to obtain the intermediate variables that connect this relationship. Based on a three-good model of Agenor and Montiel (1996) it tests the real exchange rate and government debt as the intermediate using time series' tools, such as error correction VAR, impulse response function, and Granger causality, for the period that covers from 1975 to 1994. It concludes that in a context of capital inflows, there is an appreciation of the real exchange rate that causes a decrease in wages and inflation. Another possibility is that capital inflows decrease the government debt and that reduction affects negatively inflation.
Key words: capital inflow; inflation; time series; real exchange rate.
JEL Codes: E31, F32 and C32.
RESUMO
Este artigo é uma extensão de Muinhos (1998), onde foi encontrada uma relação negativa entre entrada de capital e inflação. Aqui tenta-se obter quais as variáveis intermediárias que conectam esta relação. Com base em um modelo de três bens de Agenor e Montiel (1996), foram testadas a taxa real de câmbio e a dívida do governo, como os intermediários. As técnicas econométricas usadas no teste foram error correction VAR, resposta de impulso e causalidade de Granger para um período que cobre de 1975 a 1996. Conclui-se que, num contexto de entrada de capital, uma valorização da taxa de câmbio causa uma diminuição da inflação e dos salários. Outra possibilidade testada foi a de que a entrada de capital diminua a dívida do governo e esta redução afete negativamente a inflação.
1. Introduction
In the recent Brazilian experience, capital inflows started three years before the Real Plan (1994). These were very important in building a comfortable level of foreign reserves and also helped to offset the current account deficits after the implementation of the plan. Capital inflow was even enough to increase the foreign reserves. The external funds were used to finance the capital account and even to fill the fiscal gap. But any disturbance in foreign capital market, as recently happened in the East Asia crises, increases the risk and forces the government to increase even more the real interest rate. The high levels of interest rates are very uncomfortable, hurting the government both politically (recession and unemployment) and economically (an increase in the debt service).
In a previous paper (Muinhos, 1998, ch. 2), we established the negative relationship between capital inflow and inflation in Brazil from 1975 until 1996. We considered a model where we could address the role of capital inflows. The theoretical results show necessary and sufficient conditions for a saddle path in the system. In the first comparative statics exercise, we show that conditions for a decrease in international interest rate reduce inflation. In the empirical part using cointegration, Granger causality and impulse response, we confirmed the direction of the causality. The capital inflows came first and they are an important predictor of the inflation, in the sense that an increase in foreign capital reduces inflation rates in Brazil for the broad period analyzed. In this paper, we would like to go further and explain why this relationship occurs and what are the intermediary steps going from capital inflow to inflation.
A benchmark for any open macroeconomic analysis is the Mundel-Fleming model. For our purpose, an interesting paper that is able to relate capital inflow, the exchange rate, government deficit, and inflation is Dornbusch (1988). In a static IS-LM diagram, in which equilibria in the goods market and in the balance of payments depend on the real exchange rate and budget deficit ratio, if the capital inflow is financing the trade deficit it is possible to obtain an appreciation of the exchange rate and an increase in the deficit ratio to clear the goods market as an outcome of the capital inflow. Considering inflation as a fiscal phenomenon, an increase in the deficit ratio will produce more inflation.
Three papers were important in the development of the theoretical model (two from Calvo and Vegh and one from Agenor and Montiel). Calvo and Vegh (1990a) try to explore the real differences between an exchange rate stabilization (Erbs) and a money based stabilization (MBS). The paper has four important features:
a) intertemporal consumption substitution;
b) liquidity-advance constraint;
c) price-staggering in the home goods sector;
d) currency substitution.
It concluded that Erbs causes expansion in the home goods sector, has little effect in inflation and reduces the real interest rates, while MBS brings recession, reduces inflation and increases the real interest rate. But the paper relies on the uncovered interest parity, so it does not allow a role for capital inflows.
Calvo and Vegh's (1994b) is similar to the previous paper, but the home sector price level is set based on a backward looking model of wage growth: ''the (future) rate of growth of nominal wages is adjusted according to the difference between inflation of home goods and the current rate of growth of nominal wages''.
One important conclusion of this paper is that the appreciation of the real exchange rate and expansion in the home goods demand depend on the intertemporal elasticity of substitution between traded and home goods.
The theoretical model of the Muinhos (1998) is very similar to that of Agenor and Montiel's (1996), with one good. In this paper we use the same modification of the previous one, but in the Agenor and Montiel (1996) model with three goods. We work with a risk parameter instead of a confiscation one, our tax scheme is simpler, there is no central bank and the comparative statics is different.
We have not seen any empirical work trying to relate inflation and capital inflow for Brazil. Morande (1988) used Granger causality to test two competing hypotheses about the relationship between capital inflow and the real exchange rate for Chile (1977-82). The first hypothesis states that an appreciation of the real exchange rate in the effort to decrease inflation generates a current account deficit, with capital inflow from abroad to finance this deficit. The alternative hypothesis considers the capital inflow as an exogenous variable and the cause of the appreciation of the real exchange rate. The author concluded in favor of the latter hypothesis, that capital inflow Granger causes exchange rate appreciation, even when he took into account the interest rate differential and the terms of trade.
Calvo, Leiderman and Reinhart (1993) stated that the decrease in the US interest rate was among the leading causes of the capital inflow in the first half of the 90's into Latin America, and the larger transfer from abroad has been associated with real exchange rate appreciation: ''the evidence from the impulse responses indicates that a decline in the US interest rate would, all else being equal, generate an accumulation of official reserves and an appreciation of the real exchange rate in most of the countries, although puzzling exceptions remain''.1 1 Pastore (1994) explained why Brazil was an exception to the real exchange rate appreciation after 1991.
Another interesting empirical reference is Moreira and Giambiagi (1997). They tried to estimate a pass-through coefficient from the exchange rate to inflation. Using a 3×3 VAR, with an exchange rate, inflation and unemployment, in that order, they found that a 10% devaluation in the real exchange rate, with no other contractionist policy, would generate inflation of 26% in six months.
This paper is mainly an empirical one, trying to estimate comparative statics based on the modified Agenor and Montiel (1996) model. In the first exercise we conclude, using an impulse response function based on an error correction VAR, that a decrease in the international interest rate may cause capital inflows, and capital inflows would cause exchange rate appreciation and a decrease in the wage and in inflation. Another exercise tries to incorporate the government debt into the context of reduction of inflation due to an increase in capital inflow.
The paper is organized as follows: section 2 presents the model; section 3 presents the empirical evidence; and section 4 concludes.
2. The Model
2.1 The consumer's problem
The consumer problem is divided into two different maximizations. In the first stage, the consumer chooses the total consumption and how to divide his savings among the three different assets, money, government debt and an international tradeable bond. This part is the same as in Muinhos (1998, ch. 2). In a second stage, the consumer divides his consumption between a home good and an imported one.
The representative agent, just like before, has the following utility function:
where ct denotes total consumption at time t, a is the discount rate and u(.) is assumed to have a logarithmic form.
Private agents can store their wealth in the form of: real stock of money (mt =  ), real stock of government bonds (bt =
), real stock of government bonds (bt =  ), or a real stock of the internationally tradeable asset (b*).
), or a real stock of the internationally tradeable asset (b*).
The output (yt) is the net factor income, the function v( ) characterizes transaction cost associated with the purchase of consumption goods (v¢
) characterizes transaction cost associated with the purchase of consumption goods (v¢  0 and v¢¢
0 and v¢¢ 0) and f (
0) and f ( ) is the risk parameter that depends negatively on the holdings of the tradeable assets. It is assumed, following McNelis and Schmidt-Herbel (1993) that:
) is the risk parameter that depends negatively on the holdings of the tradeable assets. It is assumed, following McNelis and Schmidt-Herbel (1993) that:
Government bonds pay a domestic interest rate i, and the international asset pays the international rate i*. et =  stands for the nominal rate of devaluation. Money, like in the previous paper, is important because it reduces the transaction costs of consumption. The term (mt + bt)[et + f (
stands for the nominal rate of devaluation. Money, like in the previous paper, is important because it reduces the transaction costs of consumption. The term (mt + bt)[et + f ( )] accounts for capital losses on the stock of money and domestic bonds resulting from changes in the exchange rate or breaks of contracts in the government's policy, meaning that if the consumer decreases his holdings of foreign assets he increases his risks.
)] accounts for capital losses on the stock of money and domestic bonds resulting from changes in the exchange rate or breaks of contracts in the government's policy, meaning that if the consumer decreases his holdings of foreign assets he increases his risks.  t is the real value of lump-sum taxes.
t is the real value of lump-sum taxes.
Using (2) in (3), the consumer budget constraint is:
where rt = it pt the real interest rate.
Therefore, maximizing equation (1) subject to the constraint (5), we get a path for cm, b*, b. The first order conditions of the Hamiltonian are:
where
t, the costate variable associated with the flow budget constraint, measures the marginal utility of wealth. The first conditions are similar up to now to those of the previous paper.Equation (7) can be written as:
And using equation (10), (7) can be written as:
Now the consumer has to decide how to allocate his total consumption. Following Agenor and Montiel (1996), let us define a subutility function v[cn(t),ci(t)], homogeneous of degree 1, and the budget constraint:
where PN(t) is the home good price, and  is the international price of the import good that is considered equal to 1. cN(t) is the consumption of the home good and cI(t) is the consumption of the imported good. By the FOC of this problem, the ratio of marginal utility is equal to the real exchange rate (zt = Et/Pn(t)), which represents the ratio of prices. According Agenor and Montiel (1996), if the subutility function has a Cobb-Douglas form, the definition of the domestic consumer price index, Pt, is
is the international price of the import good that is considered equal to 1. cN(t) is the consumption of the home good and cI(t) is the consumption of the imported good. By the FOC of this problem, the ratio of marginal utility is equal to the real exchange rate (zt = Et/Pn(t)), which represents the ratio of prices. According Agenor and Montiel (1996), if the subutility function has a Cobb-Douglas form, the definition of the domestic consumer price index, Pt, is
where d denotes the share of total spending falling on home goods. The solution to the second part of the maximization is:
where et is the rate of depreciation of the nominal exchange rate.
2.2 The supply side
Continuing as Agenor and Montiel (1996) and many others, we define the rule of the inflation of home goods:
where Qt is the mark-up over nominal wages, and  t denotes the rate of growth of nominal wages.
t denotes the rate of growth of nominal wages.
Output of the home goods are determined by the demand side of the market. The equilibrium condition for the home-goods markets, following equation (14), is:
Agenor and Montiel (1996), as usual in those kinds of models, ''considered that the mark-up rate varies procyclically over time and depends positively on the excess demand for home goods'':
where
N denotes capacity output.The supply equation of the export sector can be obtained by a simple profit maximization, where the production function has decreasing returns to scale and the international price of export goods equals 1. The output of exportable good is inversely related to the product wage:
where wt =  t /PX(t) is the real product wage in the export sector.
t /PX(t) is the real product wage in the export sector.
Wages are backward looking and depend only on past levels of prices. As usual in those models, the following equation describes the law of wage formation:
where s is a discount factor. The differentiation this of equation with respect to time yields:
The division of equation (21) by
t using the definition of real product wage yields:
2.3 The government problem
The government uses inflation tax revenue and its bond and money issues to finance real government transfers to the private sector, as well as required debt repayments. Its budget constraint is, then:
where g represents the primary (non-interest) deficit.
The real money supply is defined as:
where mt =  . But, in nominal terms, we can define:
. But, in nominal terms, we can define:
The money market equilibrium is, then:
To determine the interest rate equilibrium, instead of following the methodology of the last paper, when the closure rule was the government determining the nominal interest rate, now we are following Agenor and Montiel (1996), who set:
But we already know that ct = c( t,mt), so:
t,mt), so:
2.4 The external constraint
The balance of payments equilibrium is achieved by decreasing the international holdings of private agents or the foreign reserves. The combination of equation (3) and (23) yields the consolidated budget constraint of the economy:
The net effect of a real exchange rate depreciation is to reduce the consumption of imported goods, because their relative price increases.
2.5 Steady-state equilibrium
One important simplification to assure long-run solvency and eliminate Ponzi games, following Agenor and Montiel (1996), is that the government forgoes the issuance of bonds to finance its fiscal deficit  = 0. Also as a closure rule, the monetary policy is such that real credit stock remains constant so
= 0. Also as a closure rule, the monetary policy is such that real credit stock remains constant so  = 0. The government budget constraint is, thus:
= 0. The government budget constraint is, thus:
When we take the first derivative with respect to time of the real exchange rate, we get:
Combining equations (17), (19), (22) and (30),
According to Agenor and Montiel (1996), using the definition of the real product wage in the export sector,
So now the system is the equations (8), (9), (16), (28), (31), and (32). The steady-state equilibrium is characterized by:
By equation (8),
In the steady-state, the value of the real exchange rate can be:
Due to the
t = o, equation (9) tells us that:
Substituting equation (33) in (8b), we have:
By
t =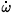 t = 0 and CN =
t = 0 and CN = 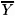 N, together with equations (31) and (32), we can get:
N, together with equations (31) and (32), we can get:
2.6 Comparative statics of steady state
Decrease in the international interest rate
Now consider a reduction in the international interest rate, from  to
to  . Let's suppose f¢(
. Let's suppose f¢( ) is linear, then the comparative statics in equation (34) yields:
) is linear, then the comparative statics in equation (34) yields:
We know that f¢( ) is negative, so if
) is negative, so if  > 0,2
2
That's in line with the findings of the second chapter of Muinhos (1998).
then
> 0,2
2
That's in line with the findings of the second chapter of Muinhos (1998).
then  is also positive. This means that if there is a decrease in the international interest rate, agents choose to decrease their international tradeable asset position leading to a decrease in the real exchange rate. The intuition behind the mathematics is also simple, because an increase in the supply of foreign currency decreases its price, that is, the nominal exchange rate.
is also positive. This means that if there is a decrease in the international interest rate, agents choose to decrease their international tradeable asset position leading to a decrease in the real exchange rate. The intuition behind the mathematics is also simple, because an increase in the supply of foreign currency decreases its price, that is, the nominal exchange rate.
In order to obtain the effect on inflation of an appreciation in the real exchange rate, we can differentiate equation (35) with respect to the real exchange rate:
Equation (37) is also positive if
In the steady state, we know that:
We can isolate wt in the following way:
Then we can analyze the sign of ¶wt / ¶zt:
We know that  is negative through the export sector production function, and also that
is negative through the export sector production function, and also that  is negative. By intuition we know
is negative. By intuition we know  is positive, because when the real exchange rate appreciates there is a tendency for a balance of payments crisis. By equation (34) we can see that
is positive, because when the real exchange rate appreciates there is a tendency for a balance of payments crisis. By equation (34) we can see that
then:
By f¢( ) being negative,
) being negative,  is positive. So the sign of ¶wt/¶zt is not trivial. Suppose the decrease in imports due to a depreciation in the exchange rate dominates and all terms inside the brackets in equation (40) are negative. Then ¶wt/¶zt is positive.
is positive. So the sign of ¶wt/¶zt is not trivial. Suppose the decrease in imports due to a depreciation in the exchange rate dominates and all terms inside the brackets in equation (40) are negative. Then ¶wt/¶zt is positive.
With that supposition, we can conclude our comparative statics. In our model an initial decrease in the international interest rate can bring capital inflow and exchange rate appreciation. That decrease in the real exchange rate affects negatively the wage and also the rate of inflation.
3. Empirical Results
In Muinhos (1998, ch. 2) we already showed a negative relationship between capital inflow and inflation. Now our goal is to support empirically the channels through which that previous relation appeared. In the theoretical part above, we suggested that the intermediaries in that relationship are the real exchange rate and the real product wage. So the first analysis is to find empirical evidence for equations (36) and (37). In order to check the sign of those equations, we construct impulse response functions. This procedure is valid to show the dynamics system just after a shock in one of the endogenous variables, not for a comparative analysis between two equilibria, which is what those equations represent.
The next task is to relax one of the assumptions of Agenor and Montiel (1996) to allow the government debt to play a role in the relationship and make estimates based on this modification. Lastly, we run a VAR with capital inflow, debt and inflation without any theoretical model behind it.
3.1 Data source
The source of the US real interest rate, capital inflows and inflation are already specified in the Muinhos (1998). The new variables for this part are the real exchange rate, real wage and government debt (quarterly).
The real exchange rate is the average nominal exchange rate for each month, multiplied by the US price index and divided by the Brazilian price index . Both indices use 1994 as the base. We compared that series with the one using a deflator for 15 countries and the results were very similar.
We used the real wage here instead of the real product wage. It is a series for industrial wages in São Paulo deflated by the Fipe (Fundação Instituto de Pesquisas Econômicas) price index.
Government debt comes from outstanding debt outside the Central Bank. It was updated for the year 1994.
Foreign reserves comes from international finance statistics published by the IMF. It consists of international liquidity in total reserves minus gold, and updated to dollars in 1994.
Real interest rates are the monthly rate from Over-Selic divided by the INPC from IBGE.
3.2 Unit root tests
We could not reject the unit root null hypothesis for the capital inflows (cap), inflation (resinf1), and real US interest rate (reusint) and these were showed in Muinhos (1998). Here we have to test the other new series: real exchange rate (exch), real wage (sal) and government debt.
The number of lags in the ADF tests were chosen by the following methodology: running a regression with k lags of the dependent variable, check the coefficient on the kth lag; if it is not significant, then reduce by 1 the number of lags; repeat the test, until either a statistically significant lag is found or k = 0.
We could not reject the null hypothesis of a unit root in any of these three variables, as can be seen in table 1. For the results for the real wage variable, we used the same methodology that was applied for inflation in the last paper. We included dummies for the heterodox plans (Cruzado, Collor and Real plans).
3.3 First exercise
In order to estimate the theoretical model of the comparative statics exercise done in section 2, we decided to work with two sets of VAR. Using a 5×5 VAR with the US interest rate, capital inflow, the real exchange rate, the real wage and inflation or even a 4×4 VAR (not including US interest rate) did not add any significant information, except for a negative relationship between capital inflow and inflation already found in Muinhos (1998). The relationship between capital inflow and the real exchange rate seems to be relevant if using many lags (six or eight), which is impossible in a very big system (VAR with four or five).
The two sets of VARs are also consistent with the comparative statics exercise in the theoretical part. The first one is for equation (36), where we work with the US interest rate, capital inflow and the real exchange rate. The other is for equation (37), which explores the relationship among the real exchange rate, the real wage and inflation. It is worth noting that we do not use the US interest rate as the parameter in the derivative (equation 37), because such rate is not significant for inflation or wages in Brazil. The real exchange rate is the key variable that connects both systems. With this setup, we can test if this negative relationship between capital inflow and inflation is due to the real exchange rate.
For each of the VARs, we test if there is cointegration among the variables. Some likelihood tests are also done to determine the appropriate lag length. After this, we conduct a Granger causality test to verify which variable is important to forecast some other variable. Finally, we present impulse response functions, where we obtain the direction of the relationship and determine if the results are consistent with the comparative statics exercise done in the theoretical part. It is not possible to present the confidence bounds in those impulse response functions, so we show the variance decomposition as a proxy. Some comments about the stability of the coefficients are also presented. All the tests and results start in 1975 and cover quarterly until the July 1994, because with the Real Plan there was a shift in regime that we are not considering in this paper.
US interest rate, capital inflows and the real exchange rate Cointegration test
Since we showed that the three series contain a unit root, we now test if they share a common stochastic trend. The Johansen method used here relies on the rank and eigenvalues of the matrix of the p coefficients. It is nothing more than a multivariate generalization of the Dickey-Fuller test. The basic equation is:
Table 2 shows the eigenvalues of p, and the likelihood test indicates that we can reject the null hypothesis of no-cointegration. The size of p in this test was 8. We also obtained cointegration with p equal to 1. In the next subsection we will test whether incorporating one or eight lags is more appropriate. Our results depend upon cointegration because any VAR in the first difference for those variables is completely useless.
Lag tests and Granger causality tests
In a VAR framework, an F test for each VAR is conducted in order to determine if the lag length is not appropriate. We performed a likelihood test. To compare which is more appropriate, eight or one lag we used the following test:
where T is the usable observations, c is the number of parameters in each equation of the unrestricted system and S is the variance/covariance matrix of the residuals. The test has a c2 distribution with the degrees of freedom equal to the number of restrictions. The calculated value for this specific test is 61.42. The c2 critical value for 63 restrictions at 5% is only slightly more than 61.42, which means that we would not reject the null hypothesis of only one lag. Even so we used eight lags, because this method seems to capture better the relationship between capital inflow and the real exchange rate.
Testing for Granger causality we can answer the following question: do past values of capital inflows help to predict current values of inflation? In general, if past values of y help to predict current values of x, then it is said that y Granger-causes x. It is a necessary but not sufficient condition for true causality.
To perform a Granger causality test, we again use the second step of the Engle-Granger methodology (the error correction term included in the first difference VAR). For example, to test if capital inflows Granger-cause the exchange rate, we ran a Wald-test in the D(cap) parameters and in the cointegration term of the D(exch) OLS equation.3 3 This methodology is discussed in more details in Muinhos (1998, ch. 2). The probability of those nine coefficients being zero is less than 1% (0.000171). Then we conclude that capital inflows indeed Granger-cause the real exchange rate. The causality is not true in the order direction, and the P-value for exchange rate causing capital inflow is 68%. This result is similar for Chile (1977-82), found by Morande (1998), and supports the idea that the real exchange rate was highly dependent on capital inflow.
The test to determine whether the US interest rate causes capital inflow for that period is similar, and the result is negative.4 4 See discussion of that relationship in the previous paper. But we could not find that the US interest rate Granger-causes the real exchange rate, with less than 5% chance of rejecting the true hypothesis when it is right.
Impulse response function
The identification criteria used in the impulse response is a Choleski decomposition, and the order is given by theoretical considerations: the US interest rate, a parameter that triggered the comparative statics in the theoretical part, comes in first place. Capital inflows come in second and finally the real exchange rate in third, as also indicated by the Granger causality test above. It is important to emphasize that those kind of VAR models may not be robust to different identification hypotheses.5 5 For a more detailed discussion, see Hamilton (1995, ch. 11).
As one can see in figure 1, the response of capital inflows to a shock in the US interest rate is negative. The response of the real exchange rate to capital inflows is also negative after eight periods. It is interesting to note how positive the response of the real exchange rate is to the US interest rate after five periods.
Figure 2 shows the variance decomposition for these three variables. The most relevant finding is how important the US interest rate is to predict the variance error in the real exchange rate in Brazil. The US interest rate counts for around 20% of the variance error of the capital inflow. The capital inflow explains only a small part of the variance in the real exchange rate, what might indicate that the confidence bounds of the impulse response for that case might contain zero.
The results cannot reject our theory that if there is a decrease in the US interest rate, capital inflow in Brazil is positively affected. This movement consequently brings about an appreciation of the real interest rate.
Those results are in line with equation (36). It seems to be true that  > 0. The empirical evidence shows a negative relation because of the definition of capital inflow. We also find that
> 0. The empirical evidence shows a negative relation because of the definition of capital inflow. We also find that  is positive as supposed in the theoretical exercise.
is positive as supposed in the theoretical exercise.
The coefficient stability
This set of VARs does not show any problems with coefficient's stability. We performance Chow tests and the recursive residual forecast tests. Both behaved properly. The F-test in the Chow procedure for a break-point in 1990 did not show any break. The recursive residual was estimated since 1984 and the series stayed within the confidence bounds. Even so, we divided the period in three parts, similar to Muinhos (1998). In the first one, from 1977 to 1984, the impulse response of the exchange rate to a shock in the capital inflow is similar to the one found for the broad period. However, for the two other periods (1984-89 and 1990-94), the similar impulse responses presents opposite directions.
The real exchange rate, wage, and inflation
With this second set, we can analyze the relations of equation (37). Now we test whether  and ¶wt/¶zt are indeed positive. As we have done for inflation, the wage variable is regressed against a constant, a time trend, and dummies for the Cruzado e Collor plans, and the residual is called Resal1. This is the relevant variable that is used in the VAR for real wage.
and ¶wt/¶zt are indeed positive. As we have done for inflation, the wage variable is regressed against a constant, a time trend, and dummies for the Cruzado e Collor plans, and the residual is called Resal1. This is the relevant variable that is used in the VAR for real wage.
Cointegration test
With these three variables we performed cointegration with three different lags. The test that we used has an intercept and a trend in the cointegration equation and no trend in the VAR. The results for one cointegration vector with two, six and eight lags are shown in table 3.
Lag test and Granger causality tests
In order to decide how long the lag should be, we perform the same test as before. First we test eight lags against six. The calculated value is 28.75 and the c2 critical value for 18 degrees of freedom is 28.27 at the 5% level. Thus, we can use only six lags. When we compare two and six, the calculated value is 62.23, the number of restrictions is 36, the c2 critical value for 5% is around 50.61. Thus we pick six lags because the restricted regression (two lags) is not binding.
The only unexpected result, as we can see in table 4, is the rejection of Granger causality from wage to inflation. The result is different in a 2×2 VAR with only inflation and real wage variables. But it is important to notice the relation between the real exchange rate and inflation. Exchange rate seems to be important for inflation because the first Granger-causes the second and the reversal is not true. The exchange rate can be considered exogenous in relation to inflation.
Impulse response function
It is very important to notice the positive relation between the exchange rate and the wage and also between the exchange rate and inflation, which is what we want to show (figure 3). The relation between wage and inflation is as expected. The positive response of the wage to inflation confirms the backward-looking theory. Also the positive response of inflation to wage, even if there is no Granger causality, is in the expected direction.
In the figure 4, we present the variance decomposition for the second set of the VAR. The picture in the left lower corner shows that real exchange rate is responsible for around 10% of the error in the variance of inflation after 10 periods. The impulse response of wages (to a shock in the real exchange rate) seems to be relevant in regard to the information of variance decompostion, but the positive response of inflation due to a shock in the real exchange rate might not be significantly different from zero.
Here is the second part of our supposition. With the appreciation of the exchange rate as explained above, we see a negative response in wages and in inflation. This is also consistent with a positive derivative in equation (37).
Coefficient's stability
In this set, the coefficients are not completely stable. The Chow forecast test shows a break between 1991 and 1994 and another one between 1985 and 1994. We also detected problems with the recursive residual test. It does not fit inside the bounds from 1990 and 1994. When we divided the period in three parts as before, the results were similar to the ones we found in the first set. The impulse responses only worked well in the first period.
3.4 Second exercise
When we try to obtain the direct relationship among capital inflows, government debt and inflation, the results are significant and go in the expected direction.
The Johansen test for cointegration shows, with less than 1% error, that there is one cointegration vector. In order to determine the lag length, we used equation (43) to choose two lags instead of one lag. If we were to use more than two, there would be no cointegration.
Table 5 shows the coefficients of the error correction VAR and the terms in parentheses confirm that the results are robust. Capital inflow Granger-causes debt and inflation, while debt also Granger-causes inflation. It is interesting to notice that coefficients for inflation in the debt equation are significant at the 1% level, assuring that inflation Granger-causes debt.
Impulse responses presented in figure 5 show that:
a) an increase in capital inflow decreases debt and inflation;
b) a decrease in the debt also negatively affects inflation;
c) a decrease in inflation decreases debt.
Figure 6 shows that capital inflow did not explain any significant part of the variance error of government debt. What means that if we could have drawn the confidence intervals in this impulse response it might have contained zero within this interval. In regard to the coefficient' stability, the coefficients did not behave very smoothly, because when we tested the recursive residual, it started to go out of bounds in 1986.
4. Conclusion
In the first exercise we tried to use the real exchange rate as the intermediary effect between capital inflows and inflation, with solid results. We could follow the comparative statics and draw conclusions consistent with the theory (equations 36 and 37) and our intuition. Capital inflow appreciates the real exchange rate because it increases the supply of the foreign exchange. The decrease in the price of foreign currency can decrease the real wage in the long run, thus reducing cost-push inflation. The positive relation between exchange rate and inflation is in the same direction found by Moreira and Giambiagi (1997). Last but not least, the positive relation between real wage and inflation agrees with the backward-looking theory for wage setting.
In the second exercise, the relevant variable relating capital inflows and inflation was government debt. The government debt could be connected to capital inflow and inflation, preserving the same direction of causality shown in Muinhos (1998, ch. 2). The negative relation between capital inflows and government debt contradicts Dornbusch (1988). The empirical evidence for Brazil demonstrates a negative relationship between capital inflow and government debt until 1991. After that year, both variables increase together, presumably reflecting the evolution of the capital market in Brazil. In the 70's, a large percentage of the capital inflow represented loans to the federal government denominated as foreign currency. In the 80's, the government was not able to obtain money from abroad (limited repatriation occurred) and started to finance itself by selling domestic currency, denominated as internal debt. This pattern helps to explain the negative relationship until 1991. After that date, the necessity of sterilization of the capital inflow (in order to maintain a high domestic interest rate and to accumulate external reserve) explains the positive relationship between capital inflow and government debt.
The positive relation between inflation and debt is also remarkable. An increase in the debt would require more inflation to generate sufficient inflationary tax revenue to cover it - consistent with equation (29).
Paper received in Oct. and approved in Dec. 1999.
- Agenor, Pierre & Mason, Paul R. Credibility, reputation and the Mexican crisis IMF, 1995.
- _______& Montiel, Robert. Development macroeconomics Princeton, Princeton University Press, 1996.
- Banco Central do Brasil. Evoluçăo da economia brasileira após o Plano Real. Boletim Separata, jun. 1996.
- _______. Boletim Mensal and Relatório Anual Several issues.
- Calvo, Guillermo & Vegh, Carlos. Credibility and the dynamics of stabilization policy: a basic framework 1990a. (IMF Working Papers, WP/90/110.
- _______& ______. Interest rate policy in a small open economy. IMF Staff Papers, 37, 1990b.
- _______& _______. Inflation stabilization and nominal anchor. Contemporary Economic Policy, 12:35-45, 1994a.
- _______&_______. Stabilization dynamics and back-looking contracts. Journal of Development Economics, 43, 1994b.
- _______; Reinhart, Carmen & Vegh, Carlos. Targeting the real exchange rate: theory and evidence. Journal of Development Economics, 47, 1993.
- Dornbusch, Rudiger. Inflation stabilization and capital mobility. In: Exchange rate and inflation MIT Press 1988. ch. 20.
- Enders, Walter. Applied econometric time series John Wiley & Sons, 1995.
- Hamilton, James. Time series analysis Princeton, Princeton University Press, 1995.
- McNelis, Paul & Schmidt-Herbel, Klaus. Financial liberalization and adjustment: the cases of Chile and New Zealand. Journal of International Money and Finance, 12(3):245-79, 1993.
- Morande, Felipe. Domestic currency appreciation and foreign capital inflows: what comes first? (Chile, 1977-82). Journal of International Money and Finance, 7, 1988.
- Moreira & Giambiagi. O impacto da taxa de câmbio sobre os preços. RBCE, (51), 1997.
- Muinhos, Marcelo. Capital inflow, inflation and exchange rate: theory and empirical evidence from Brazil (1975-1996). Cornell University, 1998. (Doctoral Dissertation.
- Pastore, Afonso C. Déficit público, a sustentabilidade do crescimento das dívidas externas e interna, senhoriagem em inflaçăo: uma análise do regime monetário brasileiro. Revista de Econometria (14), 1994.
- Perron, Pierre; Cati, Regina & Garcia, Márcio. Unit roots in the presence of abrupt governamental intervention with an application to Brazilian data. Journal of Applied Econometrics, s.d., forthcoming issue.
- Velasco, Andres. Real interest rates and government debt during stabilization. Journal of Money, Credit, and Banking, 25(2), 1993.
Publication Dates
-
Publication in this collection
20 Sept 2010 -
Date of issue
2000
History
-
Received
Oct 1999 -
Accepted
Dec 1999



























































