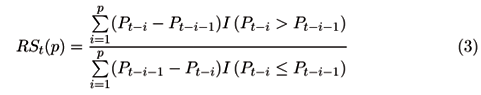Análise técnica: sorte ou realidade?

Análise técnica: sorte ou realidade?^*

Pedro A. C. Saffi

London Business School. E-mail: [e-mail]

RESUMO

Sumário: 1. Introdução; 2. Metodologia; 3. Resultados empíricos; 4. Conclusão.

Este trabalho busca testar a validade da hipótese de eficiência dos mercados no mercado futuro do índice Ibovespa através do uso das chamadas estratégias de análise técnica. São utilizados testes de habilidade preditiva para verificar a hipótese de superioridade destas regras de decisão como forma de investimento. Sua vantagem é considerar a possibilidade de data-snooping na escolha da melhor estratégia, permitindo identificar se a aparente capacidade preditiva destes modelos é realmente significativa ou mero produto do acaso. Os resultados indicam que as estratégias de análise técnica não são capazes de gerar retornos estatisticamente significativos quando os efeitos de data-snooping são levados em conta. Estes resultados estão de acordo com o previsto pela hipótese fraca de eficiência de mercado.

Palavras-chave: eficiência de mercado; comparação de modelos; bootstrap em blocos; teste de realidade de White.

Códigos JEL: C15; C52; G14.

ABSTRACT

The purpose of this paper is to test market efficiency by using the so-called ''technical analysis'' investment strategies. We apply predictive hability tests developed by White (2000) in order to measure whether these strategies are capable of producing excess returns relative to the buy-and-hold strategy. It considers the possibilty of data-snooping, allowing the detection of models whose seemingly good performance are in fact due only to chance. Our results indicate that technical analysis is not profitable and should not be used by investors, being in line with weak-form efficient market hypothesis predictions.

1 Introdução

A discussão sobre a eficiência dos mercados é um dos assuntos que mais controvérsia gerou (e ainda gera) entre os economistas, sendo até hoje alvo da atenção da comunidade acadêmica.

Dentre as diversas estratégias de investimento à disposição dos agentes, a análise técnica utiliza informações passadas sobre os preços para definir decisões de investimento. Este tipo de estratégia é utilizada por vários autores (Fama e Blume, 1966, Sweeney, 1988), em busca de evidências sobre sua performance superior na geração de retornos superiores à estratégia de referência ''comprar e esperar''.¹ Estas evidências por sua vez implicariam na rejeição da eficiência sob a forma fraca, resultados encontrados mesmo após considerarmos os custos de transação.

Uma das críticas feitas a estes trabalhos é que suas conclusões baseiam-se na aplicação das estratégias de análise técnica somente a uma realização do processo estocástico do preço do ativo: a série observada dos preços. Estaríamos portanto sujeitos aos problemas relacionados a data-snooping, já que é muito provável que, dentre milhares de estratégias diferentes, alguma (ou algumas) apresente performance superior (em termos de excesso de retorno). Isto poderia ter ocorrido simplesmente ao acaso e não devido à uma capacidade preditiva superior da estratégia.

Tentanto minimizar este problema, trabalhos posteriores (Brock et alii, 1992) utilizaram a técnica de bootstrap para simular realizações alternativas da série dos preços. Esta técnica permite, sob algumas condições, construir a distribuição empírica da performance de uma estratégia de análise técnica particular e assim, verificar se uma performance estatisticamente significativa é realmente devido à uma capacidade preditiva superior, ou um mero produto do acaso.

Este trabalho busca testar a validade da hipótese de eficiência dos mercados no mercado futuro do índice Ibovespa através do uso das chamadas estratégias de análise técnica. São utilizados testes de habilidade preditiva (White, 2000, Hansen, 2001) para verificar a hipótese de superioridade destas regras de decisão como forma de investimento. Os resultados indicam que nenhuma das 14.630 estratégias de análise técnica é capaz de gerar retornos estatisticamente significativos quando os efeitos de data-snooping são levados em conta. Estes resultados estão de acordo com o previsto pela hipótese fraca de eficiência de mercado.

2 Metodologia

2.1 Dados

O ativo escolhido para análise das estratégias no mercado brasileiro é o contrato futuro do índice Bovespa (Ibovespa) negociado na Bolsa de Mercadorias e Futuros (BM&F). Isto deve-se primordialmente à grande facilidade de execução de ordens de venda à descoberto, que são muito difíceis (quando não impossíveis) de serem efetuadas no mercado brasileiro de ações. Os contratos futuros possuem prazo de vencimento de três meses, sempre na quarta-feira mais próxima ao dia 15 do mês de vencimento, tendo como objeto de negociação o valor do Ibovespa na data de vencimento. A construção desta série é feita através da união dos preços dos contratos mais negociados em um dado momento. A fim de que os dados sejam consistentes, uma correção é feita através da multiplicação de toda a série antiga pelo percentual esperado de valorização/desvalorização expressa nos preços dos contratos futuros.² Isto é feito através da seguinte fórmula:

Este fator de ajuste nos dá o grau esperado de variação do Ibovespa pelos agentes. Quando multiplicado pela série antiga, ele faz com que os preços passados passem a fazer referência ao contrato mais líquido, garantindo a integridade dos dados após a união das séries. Estes dados ajustados nos permitem calcular retornos idênticos àqueles que seriam obtidos através da ''rolagem'' da posição de um contrato para outro.³ Os preços diários (máximo, mínimo, abertura e fechamento) utilizados compreendem o período entre 04/06/1992 e 08/01/2002, perfazendo um total de 2.369 observações.⁴

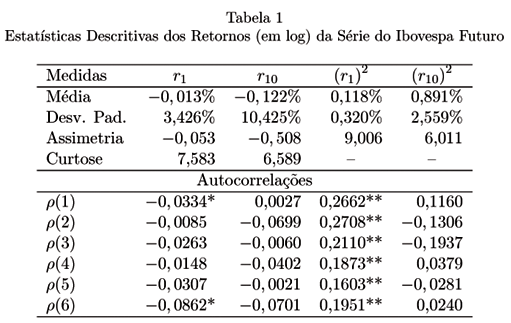
Os preços de fechamento exibem retornos logarítmicos negativos de -13,60% no período, sendo ligeiramente assimétricos à esquerda e leptocúrticos. A autocorrelação de primeira ordem, apesar de pequena, é estatisticamente significativa conforme mostra a tabela abaixo.⁵ Analisando o quadrado destes retornos, observamos grande autocorrelação, indicando a presença de um componente autoregressivo na variância condicional. Exibimos também os cálculos para os retornos não-justapostos no período de 10 dias. Neste caso, tanto r₁₀ quanto (r₁₀)² não exibem autocorrelações estatisticamente significativas, sugerindo que a hipótese de passeio aleatório pode ser aplicada neste caso.

2.2 Estratégias de análise técnica (Elder, 1993)

A análise técnica de investimentos baseia-se no uso da informação passada dos preços de um ativo para gerar sinais de compra e venda. Ela pode ser dividida em dois tipos básicos de estratégias: análise gráfica e análise computadorizada.

A análise gráfica teve início no começo do século XX e consiste na identificação de padrões recorrentes nos gráficos da série dos preços. Seu maior problema é a subjetividade da tomada de decisões e por isso tais estratégias não são consideradas neste trabalho, apesar de já terem sido alvo de estudos teóricos (Osler e Chang, 1995).

A análise computadorizada usa funções dos preços passados - os indicadores técnicos - na decisão de investimentos. Estes indicadores tentam expressar um suposto consenso de mercado para o preço do ativo no futuro, usando para isto informações correntes como volume e preços de fechamento, máximo ou mínimo. A facilidade com que estes indicadores podem ser calculados nos permite estabelecer objetivamente critérios de compra e venda de um ativo, tornando extremamente simples sua implementação computacional (Lo et alii, 2000).

São considerados cinco tipos básicos de estratégias: médias móveis, o índice de força relativa (Relative Strength Index - RSI), indicador William's %R, Estocástico e o indicador de Média Móvel Convergência-Divergência (Moving Average Convergence-Divergence - MACD). Este conjunto é escolhido por estas estratégias serem muito utilizadas pelos investidores nos mercados e possui a vantagem de ser mais complexo do que aqueles utilizados em trabalhos anteriores. Este espaço de estratégias considera não somente a série dos preços de fechamento, mas também as de máximo e mínimo, usando um conjunto de informações maior à disposição dos agentes. Isto também permite verificar se resultados anteriores, que indicam a rejeição da utilidade das estratégias de análise técnica, ocorrem devido ao tipo de estratégia utilizada.

2.3 Médias móveis

Esta estratégia consiste na compra do ativo quando a média móvel de curto prazo do preço de fechamento (P_t) for superior a uma média móvel de longo prazo, e na venda caso o inverso ocorra. O cálculo da média móvel com p defasagens de uma série é feito através da seguinte fórmula:

A explicação dada pelos analistas técnicos para o uso desta estratégia é que a média móvel nos permitem identificar uma opinião dos agentes a respeito dos preços. Suponha dois números c e l, onde c < l. Caso uma média móvel de curto prazo (P_t(c)) seja maior do que uma média móvel de longo prazo (P_t(l)), o mercado está mais otimista (''bullish'') e o ativo deve ser comprado.⁶

As diferentes estratégias são obtidas pela combinação de médias móveis com diferentes defasagens e também com a inclusão de filtros (1 + f), que alteram as decisões de investimento. Isto é feito para dificultar o início de uma operação sem impor restrições sobre seu término, diminuindo o número de ordens executadas e com isso, os custos de transação. A inclusão do filtro nos dá a seguinte regra de decisão:

Suponha um filtro de 5%, com P₁(2) = 100, P₁(20) = 95, P₁₀(2) = 95 e P₁₀(20) = 101. Como 100 = P₁(2) > (1 + f)P₁(20) = 99,75, compramos o ativo na data t = 1. Na data t = 10, 95 = P₁₀(2) < P₁₀(20) = 101 e por isso encerramos a operação e vendemos o ativo à descoberto somente se (1 + f)P₁₀(2) < P₁₀(20).

2.4 Índice de força relativa (RSI)

Este indicador técnico busca utilizar os preços de fechamento para identificar o potencial de incremento de um dado ativo. Seu cálculo é feito através de:

onde:

e I(.) denota a função indicadora.

Logo, RS_t(p) equivale à razão entre a média de crescimento dos preços nos dias em que o preço do ativo subiu e a média de decréscimo nos dias em que o preço do ativo caiu, implicando em RSI Î [0,100). A decisão de investimento baseia-se na seguinte regra:

A intuição por trás deste indicador é que quanto maior for o seu valor, menor é o potencial de crescimento do ativo. Caso o indicador fique menor do que o limite inferior (assumindo f = 0), o ativo tem maior potencial de valorização do que desvalorização e portanto deve ser comprado. Os valores Sup e Inf indicam os pontos à partir dos quais considera-se o ativo subavaliado ou sobreavaliado. Essas duas variáveis são escolhidas pelo agente de forma ad-hoc e constituem mais dois parâmetros de escolha.

2.5 Indicador William's %R

Este indicador calcula em que ponto está o último preço de fechamento em relação a amplitude dos preços em um período de p dias.

onde H_p = Max {P_t, ..., P_t–p}, L_p = Min {P_t, ..., P_t–p}.

O indicador vale zero quando o preço de fechamento (P_t) é igual ao preço máximo observado no período de p dias (H_t), e vale 100 quando P_t é igual ao preço mínimo (L_t) neste período. A estratégia para ele é dada por:

2.6 Estocástico

Neste caso as decisões de compra e venda baseiam-se em duas séries para identificar os pontos de entrada ou saída do mercado: o Estocástico rápido (%K) e o Estocástico lento (%D). Este indicador utiliza médias móveis que calculam em que ponto está o último preço de fechamento em relação à amplitude dos preços em um período de p dias.

O indicador lento busca filtrar o ruído de mercado e com isso diminuir o número de sinais falsos dado pelo William's %R. A estratégias também utilizam valores ad-hoc para definir os pontos de sobreavaliação (Sup) e subavaliação (Inf) do ativo. A decisão baseia-se na seguinte regra:

Valores altos de %K indicam que os ''comprados'' estão dominando o mercado, já que conseguem que o preço de fechamento esteja sempre próximo ao preço máximo observado no período. Esta maior influência dos ''comprados'' nos sugere comprar o ativo.

2.7 Indicador MACD

O último tipo de estratégia usa o indicador MACD. Este indicador é uma extensão das estratégias baseadas em médias móveis, utilizando suavizações das mesmas para reduzir a quantidade de falsos sinais de compra e venda. As decisões de investimento são tomadas através da comparação de médias de curto e longo prazo: quando a média de curto prazo cruza a média de longo prazo, é sinal que o ativo está se valorizando no curto prazo e portanto sugere sua compra. O cálculo do MACD é feito da seguinte forma: primeiro calculam-se duas médias móveis exponenciais (EWMA), de k e s períodos, do preço de fechamento. Com estas médias calcula-se MACD Rápido (k, s) = EWMA(k) – EWMA(s) e, por último, MACD Lento (k, s, d) = EWMA(d) de MACD Rápido.

A variável MACD Rápido retrata o consenso de mercado no curto prazo enquanto MACD Lento, por ser a média de MACD Rápido, denota um consenso de prazo mais longo. Se MACD Rápido < MACD Lento temos indicação que o preço do ativo deve cair e assim vendemos o ativo. A regra geral é dada por:

2.8 Técnica bootstrap

O próximo passo é a construção de realizações alternativas do processo estocástico dos preços do contrato futuro do índice Bovespa. Essas realizações são necessárias para calcular os retornos das estratégias de análise técnica e aplicar os testes de habilidade preditiva. Isto é feito através da técnica bootstrap, que consiste na reamostragem dos dados para estimação da distribuição de um estimador ou estatística de teste.

A dificuldade em encontrar analiticamente a distribuição dos retornos (ou o índice de Sharpe) das estratégias de investimento, torna necessário o uso de técnicas de reamostragem para estimá-la. O procedimento consiste em extrair aleatoriamente diversas amostras dos retornos, calculando em cada extraçã a estatística de teste desejada. Usamos estas estatísticas para encontrar a probabilidade empírica do evento desejado, possibilitando a realização dos testes de hipótese.

A existência de dependência nos dados faz com que esta reamostragem precise ser feita de forma a capturar adequadamente esta característica do processo gerador dos dados (PGD). Para evitar a especificação paramétrica do PGD, utilizamos o bootstrap em blocos (Künsch, 1989).

2.9 Bootstrap em blocos

A técnica não-paramétrica do bootstrap em blocos sobrepostos procura reproduzir a dependência através de blocos consecutivos de observações de tamanho q. A idéia é construir blocos que sejam independentes mas preservem a dependência dos dados dentro de um bloco, permitindo a aplicação da reamostragem dos dados. Para estimação de funções de distribuição simétricas (ex: P(T_n < t)), trabalhos anteriores (Hall et alii, 1995) mostram que q ~ . Conseqüentemente, com n = 2.369 temos blocos de tamanho q = 5. A estimação da técnica é feita através do seguinte procedimento:

Seja {X_i : i = 1, ..., n} um vetor contendo as k séries utilizadas, q o tamanho do bloco e B o número de séries construídas. Inicia-se com a formação de blocos de tamanho n, onde o m-ésimo é formado pelas observações {X_m, ..., X_m+q}. Depois, extraem-se blocos aleatoriamente com reposição, colando-os na ordem extraída. Por fim, repete-se o processo B vezes, denotando as séries construídas por: .

O procedimento nos permite calcular B realizações alternativas do processo gerador dos dados. Aplicando a estatística de teste a cada série criada, podemos construir a função de densidade empírica do teste.

2.10 Testes de habilidade preditiva

Os testes de habilidade preditiva têm como objetivo comparar a eficiência relativa de modelos estatísticos sob uma determinada medida de performance. Um exemplo seria o erro quadrático médio de uma previsão ou o excesso de retorno de uma estratégia. As hipóteses nulas destes testes envolvem o cálculo da distribuição do máximo de variáveis aleatórias, complicando a derivação da distribuição das estatísticas de teste. A aplicação de técnicas de reamostragem permitem estimar consistentemente a distribuição da estatística de teste via métodos numéricos.

Considere uma situação onde existam l + 1 modelos diferentes e desejamos testar se o modelo de referência 0 é inferior a qualquer um dos modelos k = 1, ..., l, onde l é o tamanho do espaço de modelos considerado. Seja m o vetor l-dimensional do desempenho de cada modelo alternativo em relação ao modelo de referência. Nossa hipótese nula é definida por H₀ : m < 0, equivalente a testar se m_maxº maxm_k < 0. Já a fronteira de H₀ é dada por: .

2.11 Teste de realidade (White, 2000)

A superioridade de uma estratégia na série original do Ibovespa futuro pode ocorrer simplesmente por acaso e não devido à superioridade da regra de decisão. Ao testar milhares de estratégias diferentes é muito provável que pelo menos uma apresente retornos significativos, sem nos dar algum tipo de informação à respeito de sua capacidade preditiva. O teste de realidade de White tem por objetivo justamente considerar esta possibilidade na avaliação das performances dos modelos.

A utilização indiscriminada da técnica bootstrap não é capaz de levar em conta os problemas causados por data-snooping. Anteriormente, comparávamos a melhor média de retorno na série original do Ibovespa futuro com os retornos obtidos por esta mesma regra em todas as reamostragens construídas. Os testes de habilidade preditiva comparam a melhor estratégia na série original com a melhor estratégia observada em cada uma das séries reamostradas. Esta estratégias podem ser (e geralmente são) diferentes da melhor estratégia encontrada na série original. Os resultados principais do teste criado por White (2000) são apresentados abaixo:

Seja n o tamanho da série utilizada. A hipótese é testada em um vetor E(f^*) de tamanho l × 1, onde f^*º f (Z, b^*) é um vetor l × 1 com elementos º f_k (Z, b^*) para o vetor aleatório Z e parâmetros b^*º plim. O vetor Z consiste em vetores de variáveis dependentes Y e regressores X.

O teste é baseado na estatística l × 1 denotada por . A hipótese nula que exprime o teste de ausência de superioridade preditiva em relação ao modelo de referência é dada por:

Para testar a hipótese de uma determinada estratégia produzir retornos superiores a uma estratégia de referência usamos = ln[1 + y_t+1S₁ (X_1,t+1,)] – ln[1 + y_t+1S₀ (X_0,t+1,)], onde y_t+1 representa o retorno diário e S₀ e S₁ representam funções que convertem os indicadores de análise técnica (X_0,t+1 e X_1,t+1) e os parâmetros ( e ) em posições de mercado. As funções podem assumir três valores: –1 (vendido a descoberto), 0 (fora do mercado) e 1 (comprado). Nesse caso, os parâmetros ( e ) são estabelecidos a priori e não precisam ser estimados (exemplo: o nº de defasagens utilizadas na estratégia de média móvel). Se a estratégia ''comprar e esperar'' for o modelo de referência, teremos S₀(X_0,t+1,) = 1 para todo t.

A hipótese nula que testa o modelo com melhor performance é dada por:

A hipótese múltipla, representada por (12), é uma interseção das hipóteses individuais da equação (10) para cada um dos l modelos.

2.12 Distribuição assintótica

A proposição 2.1 de White (2000) mostra que, se algum modelo supera aquele usado como referência, isto acaba sendo revelado por uma estimativa positiva da performance em relação ao modelo de referência na série original.

A proposição seguinte permite a construção de um teste para seleção do melhor modelo, utilizando o extremo de um vetor de variáveis normalmente distribuídas:

Suponha que com W positiva semi-definida. Então, para T ® ¥, temos:

onde H é um vetor l ×1 com componentes H_k ~ N (0, W).

Desta forma, estabelecida a distribuição assintótica, a conclusão do teste é a mesma independente da validade da hipótese nula. O teste da nula é reforçado utilizando o valor de E () menos favorável à alternativa: E() = 0, "k. Assim, o comportamento do critério de seleção do modelo que maximiza a estatística é conhecido, permitindo a construção de p-valores assintóticos.

Qualquer método que permita encontrar estimativas consistentes para os p-valores do teste H₀ = E () < 0 é chamado de ''teste de realidade''. O desafio em sua implementação é que a distribuição da estatística de teste (o máximo de um vetor de variáveis normalmente distribuídas e correlacionadas) é desconhecida, sendo necessário a implementação de métodos numéricos para estimá-la.

Isto é feito através da técnica bootstrap descrita anteriormente. Com repetidas extrações de ( - E () ) podemos encontrar uma estimativa da distribuição N (0, W). Os p-valores do teste de realidade podem ser obtidos pela comparação de , com os percentis de . Estes valores são obtidos através da aplicação desta estatística em cada série artificial gerada pela técnica bootstrap.

3 Resultados Empíricos

3.1 Testes iniciais

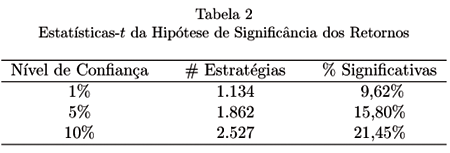
A primeira forma utilizada para testar a eficácia da análise técnica é através da estatística-t. Neste caso, testamos se a média do excesso de retorno de uma dada estratégia em relação à estratégia de ''comprar e esperar'' é estatisticamente significativa. Dentre as 11.780 estratégias consideradas, a que gera melhor resultado, tanto em termos de excesso de retorno quanto índice de Sharpe, é a Média Móvel(25, 30, Filtro = 0). Ela tem um retorno diário médio de 0,14% e desvio-padrão 4,71%. A estatística-t correspondente (1,47) não rejeita a hipótese nula de ineficácia da análise técnica (e conseqüentemente a EMH). Porém, como mostra a tabela abaixo, existe um grande número de estratégias cujos retornos são estatisticamente diferentes de zero.

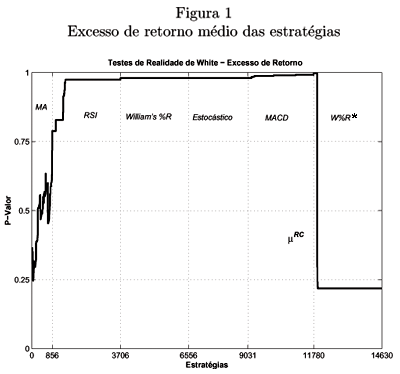
A figura 1 mostra o excesso de retorno de cada estratégia na série real do Ibovespa futuro. Apesar das estratégias do tipo RSI e Estocástico apresentarem baixa performance em termos de excesso de retorno, várias do tipo MACD obtêm retornos positivos na série real do Ibovespa futuro.

O uso de estratégias que utilizem não somente o preço de fechamento, mas também a informação contida nos preços de máximo e mínimo, parece adicionar ganhos de performance. No entanto esta afirmação precisa ser melhor avaliada, já que retornos superiores das estratégias Média Móvel e MACD podem ter ocorrido por acaso. Por isso, testaremos os retornos obtidos por esta estratégia na série real do Ibovespa futuro versus os retornos observados nas séries reamostradas.

3.2 P-valores nominais

O uso da estatística-t para avaliar a significância de uma estratégia utiliza apenas uma observação, isto é, sua aplicação na série real, para inferência sobre sua significância. Para resolver este problema, seguimos os passos de Brock et alii (1992), comparando agora o excesso de retorno de cada estratégia com sua distribuição empírica, gerada pela aplicação desta estratégia nas 500 séries reamostradas. O p-valor nominal encontrado nos mostra se a performance obtida na série real do Ibovespa futuro é um indicador confiável para o valor populacional, resolvendo o problema mencionado acima.⁷ Caso a performance na série real seja significativa, podemos rejeitar a hipótese que o resultado obtido ocorre somente devido à variabilidade amostral, indicando que a estratégia possui capacidade preditiva superior à do modelo de referência.

No espaço de 11.780 estratégias, 560 (5026) obtêm retornos (índice de Sharpe) significativos a 5% de confiança, correspondendo a 4,75% (42,66%) do total. A tabela abaixo resume os resultados:

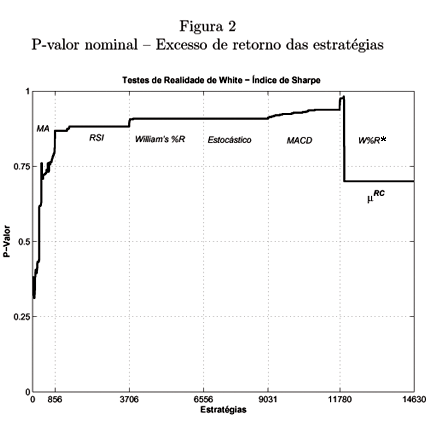
A figura 2 mostra o p-valor nominal para cada estratégia de investimento.

Como a decisão de compra de um ativo é feita de forma completamente ad-hoc, podemos nos perguntar o que aconteceria caso invertêssemos as decisões de investimento em cada estratégia. Ou seja, onde anteriormente comprávamos passamos a vender, e onde vendíamos, passamos a comprar o ativo.

A estratégia onde esta inversão aparenta ser mais útil é a William's %R (denotadas por W%R^*). O melhor resultado obtido com esta reversão é através da regra W%R^*(2, Sup = 30, Inf = 70, Filtro = 0), com excesso de retorno médio de 1,99% e desvio-padrão 4,27%.

Por questões de factibilidade computacional, os cálculos com regras de decisão invertidas serão refeitos utilizando somente as 2.850 combinações deste tipo de estratégia, aumentando o tamanho do espaço de modelos para 14.630 estratégias.

A figura 3 exibe os retornos do novo espaço de estratégias, onde percebemos que a reversão dos sinais de compra/venda das estratégias é capaz de produzir retornos significativos na série real do Ibovespa futuro.⁸

3.3 Teste de realidade de White

Neste ponto é pertinente a crítica feita por Sullivan et alii (1999) de que a distribuição empírica utilizada acima, considera somente a performance de uma estratégia aplicada às séries reamostradas. Este resultado pode ocorrer devido ao acaso (através de data-snooping) e não por uma maior capacidade preditiva da estratégia. O métodos que se propõem a corrigir este problema é o teste de realidade de White (White, 2000).

Assim, o excesso de retorno obtido na série real deve ser comparado ao maior retorno observado em cada série reamostrada pela aplicação das 14.630 estratégias. Caso a estratégia que obtenha o maior retorno na série real tenha significância rejeitada, temos indicação que nenhuma estratégia é significativa e assim não rejeitamos a EMH. A tabela 4 mostra os resultados obtidos.

Isto indica que nenhuma estratégia no espaço considerado possui performance estatisticamente superior à estratégia ''comprar e esperar'', tanto usando-se o excesso de retorno quanto o índice de Sharpe. A importância do uso de testes que considerem os efeitos de data-snooping é explicitado pelo resultado acima. Vimos que, dentre as 14.630 estratégias utilizadas, 5.985 (40,9%) possuem índice de Sharpe estatisticamente significativo. Ao utilizar conjuntamente a informação dada pelas estratégias, vemos que esta performance ocorre na verdade devido ao acaso.

Nas figuras 4 e 5, mostramos os comportamentos sequenciais do p-valor do teste ao adicionar uma estratégia ao espaço considerado para cada medida de performance. Se a estratégia adicionada não tem performance superior às utilizadas até então, o p-valor da hipótese nula irá subir, ou no extremo, permanecer estável. Por outro lado, caso o ganho de performance seja grande o suficiente o p-valor irá cair, indicando uma maior chance da performance deste modelo ser significativa.

Como a ordem das estratégias é arbitrária, o p-valor relevante é o situado mais à direita do gráfico. Porém, é interessante observar os ganhos ocorridos quando um modelo com capacidade preditiva superior àquelas utilizadas até então, é adicionado. Tomando o espaço inicial (11.780 estratégias), podemos observar que a ausência de uma estratégia com performance superior faz com que o p-valor vá subindo lentamente na direção da não-rejeição da nula. Ao incluir o novo conjunto de estratégias, vemos na figura 4 que quando a estratégia de maior excesso de retorno é adicionada (11.956), o p-valor cai abruptamente de 99% para aproximadamente 22%. Mesmo assim, não podemos rejeitar a hipótese nula de superioridade da estratégia ''comprar e esperar''.

Quando a estratégia com maior índice de Sharpe é adicionada (idêntica à de maior excesso de retorno), observamos na figura 5, que o p-valor do teste de realidade (RC) varia de aproximadamente 99% para 73%. Após a inclusão desta estratégia no espaço de amostras, nenhuma outra é capaz de gerar excesso de retorno superior e, por isto, o p-valor segue estável até o final.

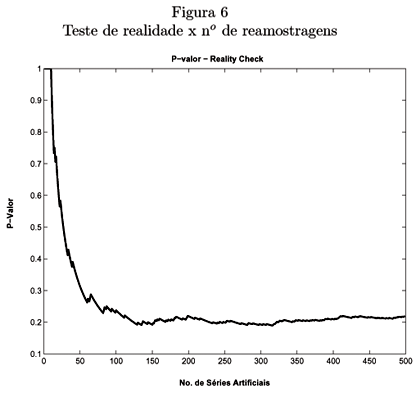
A figura 6 mostra o p-valor do teste para o índice de retorno em função do número de séries reamostradas. Podemos observar que um aumento do número de reamostragens não parece ser necessário.

Os resultados nos mostram que, ex-post, sempre podemos encontrar estratégias significativas. Porém, elas só podem ser consideradas úteis, caso esta performance significativa seja observada em diversas realizações do processo estocástico do ativo. Apesar de simples, estes tipos de estratégias são muito utilizados pelos investidores e a implicação dos resultados é que estas estratégias não devem ser utilizadas, já que o investidor médio corre sério risco de incorrer em prejuízos significativos.

Além dos resultados exibidos acima, aplicamos os testes de habilidade preditiva para o excesso de retorno das estratégias, também à sub-amostras dos dados, buscando incrementar a robustez dos resultados encontrados em favor da eficência de mercado. A diminuição do número de reamostragens para 100, reduzindo consideravelmente o tempo computacional necessário, permite o teste das estratégias em três sub-períodos. O primeiro é o período anterior ao início do plano Real. O segundo compreende o período imediatamente posterior. Por último, utilizamos o período após a desvalorização cambial em janeiro de 1999.

Os resultados abaixo vão ao encontro dos obtidos na amostra completa, onde a eficácia da análise técnica é rejeitada em todos os sub-períodos, reforçando a ineficácia destas estratégias em gerar retornos significativos.

4 Conclusão

Após a realização dos testes, concluimos que as estratégias de análise técnica não devem ser utilizadas para auxiliar as decisões de investimento. Não somos capazes então de rejeitar a hipótese de eficiência de mercado, já que as estratégias não remuneram adequadamente o investidor. Apesar de sua construção ser bastante simples (ou por causa dela), estas estratégias são utilizadas em larga escala por pequenos investidores no mercado financeiro brasileiro. Como mostram os resultados acima, a performance destas estratégias é fruto do acaso e seu uso leva o investidor médio a fracassar na tentativa de obter ganhos em relação aos da estrategia ''comprar-e-esperar''.

Outro ponto importante é a relevância de considerarmos todo o espaço de estratégias disponíveis ao investidor. As conclusões extraídas quando isto não é feito nos levam à rejeição da EMH. Porém, o uso conjunto das informações do espaço de estratégias,nos mostra na verdade, que elas não são capazes de gerar retornos significativos.

Em relação aos trabalhos feitos anteriormente no país, esperamos ter agregado valor à literatura dos testes de eficiência de mercado. O trabalho é o primeiro a chamar atenção para os problemas causados pelo uso de um mesmo conjunto de dados para comparação da capacidade preditiva de modelos na área de finanças. O teste de realidade é uma ferramenta poderosa que permite ao economista validar de forma mais precisa suas afirmações e teorias.

Os resultados são similares aos encontrados nos mercados internacionais, contribuindo para o conjunto de evidências que mostram aos investidores que as estratégias de análise técnica (pelo menos nas formas simples como as utilizadas neste artigo) não são úteis como investimento.

Artigo recebido em ago. 2002 e aprovado em jan. 2003.

Anexo

Abaixo seguem os parâmetros utilizados para construção das estratégias de análise técnica.

• Média Móvel

  c = [1 2 3 5 8 10 13 15 20 21 25 30 40 50 75 100 150 200 250]

  l = [2 3 5 8 10 13 15 20 21 25 30 40 50 75 100 150 200 250]

  f = [0 0.001 0.005 0.01 0.05]

• RSI, William's %R$ e W%R^*

  p = [1 2 3 5 8 10 13 15 20 21 25 30 40 50 75 100 150 200 250]

  f = [0 0.001 0.005 0.01 0.05]

  Inf = [5 10 15 20 25 30] , Sup = [70 75 80 85 90]

• Estocástico

  p = [3 5 8 13 21 50 75 100 150 200 250]

  d = [5 8 13 21 50 75 100 150 200 250]

  f = [0 0.001 0.005 0.01 0.05]

  Inf = [10 20 30] , Sup = [70 80 90]

• MACD

  k = [3 5 8 13 21 50 75 100 150 200 250]

  s = [5 8 13 21 50 75 100 150 200 250]

  d = [5 8 13 21 50 75 100 150 200 250]

  f = [0 0.001 0.005 0.01 0.05]

• Brock, W., Lakonishok, J., & LeBaron, B. (1992). Simple technical trading rules and the stochastic properties of stock returns. Journal of Finance, 49:153181.
• Elder, A. (1993). Trading for a Living: Psychology, Trading Tactics, Money Management
• Fama, E. & Blume, M. (1966). Filter rules and stock market trading profits. Journal of Business, 39:226241.
• Hall, P., Horowitz, J., & Jing, B. (1995). On blocking rules for the bootstrap with dependent data. Biometrika, 82:561574.
• Hansen, P. R. (2001). An unbiased and powerful test for superior predictive ability. Brown University Wroking Paper.
• Horowitz, J. (2001). The bootstrap. Handbook of Econometrics, 5.
• Künsch, H. (1989). The jackknife and the bootstrap for general stationary observations. Annals of Statistics, 17:12171241.
• Lo, A., Mamaysky, H., & Wang, J. (2000). Foundations of technical analysis: Computational algorithms, statistical inference, and empirical implementation. Journal of Finance, 55:17051765.
• Osler, C. L. & Chang, P. H. K. (1995). Head and shoulders: Not just a flaky pattern. Federal Reserve Bank of New York Staff Report 4.
• Sullivan, R., Timmermann, A., & White, H. (1999). Data-snooping, technical trading rules and the bootstrap. Journal of Finance, 54:16471692.
• Sweeney, R. (1988). Some new filter rule tests: Methods and results. Journal of Financial and Quantitative Analysis, 23:285300.
• White, H. (2000). A reality check for data snooping. Econometrica, 68:10971126.

*

Este trabalho apresenta os resultados da tese de mestrado defendida na EPGE/FGV-RJ. Agradeço aos comentários de Marcelo Fernandes, Marco Bonomo, Ricardo Brito e ao parecerista anônimo, além do apoio financeiro dado pelo banco BBM e a CAPES.

1

Todos os cálculos do retorno das estratégias estão em termos de excesso de rentabilidade em relação ao modelo de referência.

2

A série antiga refere-se à série de preços calculada até o momento.

3

Não considerados custos de transação. Esta hipótese não altera os resultados obtidos. Além disso, para grandes investidores (fundos de investimento, etc...) os custos são muito próximos a zero.

4

As séries foram obtidas através do programa Economática.

5

O termo

r_i representa o retorno no período de

i dias. r(

k) representa a autocorrelação de ordem

k. O símbolo *(**) denota confiança a 95% (99%).

6

As estratégias técnicas abaixo consideram tanto estratégias de ''momento'' quanto estratégias que buscam captar uma reversão à média dos preços.

7

Identifica-se na literatura como

p-valor nominal, o

p-valor do teste de significância através do uso da distribuição empírica da estratégia.

8

Os resultados das estratégias

W%

R

^* estão localizados nos pontos mais à direita nos gráficos

Datas de Publicação

• Publicação nesta coleção
  14 Jun 2004
• Data do Fascículo
  Dez 2003

Histórico

• Aceito
  Jan 2003
• Recebido
  Ago 2002