Abstracts
In this study we calculate optimal commodity taxes for Brazil. Simulations are based on the Almost Ideal Demand System , estimated using Brazilian household data. The trade off between equity and efficiency is taken into account by introducing a government aversion to inequality parameter into a social welfare function, which is maximized subject to a balanced government budget requirement. Our results show that the optimal commodity tax structure is characterized by selective tax rates when the only tax policy instrument available is commodity taxation. We extend the analysis by allowing for a uniform poll payment to be made by the government. In this case tax rates are regressive and poll transfer levels are unreasonably high. When we cap transfers with a binding ceiling the former pattern is restored. Comparing with Siqueira (1998), we have also observed a relative robustness of optimal tax rates to household preferences forms.
optimal commodity taxation; social welfare function; efficiency; equity; almost ideal demand system
O presente estudo tem como objetivo calcular a estrutura ótima da tributação sobre o consumo no Brasil. As simulações baseiam-se no sistema de demanda Almost Ideal Demand System estimados com dados da POF/IBGE. O trade off entre eqüidade e eficiência é incorporado no modelo com a introdução de um coeficiente de aversão à desigualdade social na função de bem-estar social, sujeita à restrição de receita do governo. Além da hipótese de que o único instrumento de política tributária disponível seja a tributação sobre o consumo, nosso modelo também admite a concessão de uma transferência uniforme lump sum de renda per capita do governo para todos os agentes econômicos. Os resultados mostram que a estrutura tributária sobre o consumo caracteriza-se pela seletividade das alíquotas, que se torna mais significativa para valores altos do parâmetro de aversão à desigualdade. Este resultado é revertido para uma estrutura tributária regressiva com a introdução de uma transferência uniforme lump sum de renda do governo para todos os agentes no modelo. Quando tetos bastante restritivos são impostos aos valores das transferências, o primeiro resultado é restabelecido. Com relação à forma escolhida da preferência do consumidor, nossos resultados também mostram relativa robustez com os obtidos em Siqueira (1998).
Optimal commodity taxes for Brazil based on AIDS preferences* * We wish to thank two referees for useful suggestions. Responsibility for any remaining errors is solely ours.
Seki AsanoI; Ana Luiza N. H. BarbosaII; Eduardo P. S. FiuzaIII
IDepartment of Economics, Tokyo Metropolitan University. E-mail: asano-seki@c.metro-u.ac.jp
IIDiretoria de Estudos Macroeconomicos, Instituto de Pesquisa Economica Aplicada. E-mail: aluiza@ipea.gov.br
IIIDiretoria de Estudos Macroeconomicos, Instituto de Pesquisa Economica Aplicada. E-mail: fiuza@ipea.gov.br
ABSTRACT
Summary: 1. Introduction; 2. The model; 3. Data; 4. Results; 5. Conclusion.
In this study we calculate optimal commodity taxes for Brazil. Simulations are based on the Almost Ideal Demand System , estimated using Brazilian household data. The trade off between equity and efficiency is taken into account by introducing a government aversion to inequality parameter into a social welfare function, which is maximized subject to a balanced government budget requirement.
Our results show that the optimal commodity tax structure is characterized by selective tax rates when the only tax policy instrument available is commodity taxation. We extend the analysis by allowing for a uniform poll payment to be made by the government. In this case tax rates are regressive and poll transfer levels are unreasonably high. When we cap transfers with a binding ceiling the former pattern is restored. Comparing with Siqueira (1998), we have also observed a relative robustness of optimal tax rates to household preferences forms.
Keywords: optimal commodity taxation; social welfare function; efficiency; equity; almost ideal demand system.
JEL codes: H21; D12; D31; D63; H31; C33.
RESUMO
O presente estudo tem como objetivo calcular a estrutura ótima da tributação sobre o consumo no Brasil. As simulações baseiam-se no sistema de demanda Almost Ideal Demand System estimados com dados da POF/IBGE. O trade off entre eqüidade e eficiência é incorporado no modelo com a introdução de um coeficiente de aversão à desigualdade social na função de bem-estar social, sujeita à restrição de receita do governo. Além da hipótese de que o único instrumento de política tributária disponível seja a tributação sobre o consumo, nosso modelo também admite a concessão de uma transferência uniforme lump sum de renda per capita do governo para todos os agentes econômicos.
Os resultados mostram que a estrutura tributária sobre o consumo caracteriza-se pela seletividade das alíquotas, que se torna mais significativa para valores altos do parâmetro de aversão à desigualdade. Este resultado é revertido para uma estrutura tributária regressiva com a introdução de uma transferência uniforme lump sum de renda do governo para todos os agentes no modelo. Quando tetos bastante restritivos são impostos aos valores das transferências, o primeiro resultado é restabelecido. Com relação à forma escolhida da preferência do consumidor, nossos resultados também mostram relativa robustez com os obtidos em Siqueira (1998).
1 Introduction
The trade-off between equity and efficiency is a major concern of optimal commodity taxation: how can the government collect a given tax revenue level and achieve distributive goals at the lowest cost in terms of efficiency?1 1 Ramsey's (1927) significant contribution on this subject is very well known, and so is its extension to the many-person case by Diamond and Mirrlees (1971).
The purpose of this paper is to calculate the optimal commodity tax structure for Brazil. The heavy reliance of tax revenue on this tax base (around 60% of the total) renders it a very important policy subject and one of the main tools available to the government for attaining distributive goals.
To the best of our knowledge, one pioneer study alone has studied the optimal commodity tax design in the Brazilian case thus far. Siqueira (1998) calculated the optimal commodity taxes based on a Linear Expenditure System (LES). The model was solved under alternative assumptions regarding the government's concern with inequality; the household preferences; the minimum government revenue level required and the constraints on the government's ability to tax. Households were distinguished between urban and rural population. It was acknowledged that due to the possibility of arbitrage between the urban and rural sectors, the government might be constrained to tax certain goods in both sectors at the same rate.
In this setup, in order to obtain meaningful implications for the optimal tax structure, a flexible utility function is needed, allowing for non-linear Engel curves. It is well known that the optimal tax structure is uniform if the demand system is LES, for which the Engel curves are linear. Thus, ordinarily the very assumption of LES functional form decides the optimal tax structure, and econometric analyses of consumer behavior have nothing to do with policy recommendation.2 2 This point is stressed by Atkinson (1980:434-435), and by Deaton (1997:281-282). Also, Deaton (1986) showed that linearity of Engel curves leads to the optimality of uniform tax, if Engel curves are parallel across households. The result holds when leisure is separable from consumption goods, and it carries over to the case in which intercepts vary across consumers, due to household characteristics.
Siqueira's exercise was based on one of the few estimations available at the time, by Rossi and Neves (1987). Those authors had used a logit specification, but Siqueira used the elasticities they found as inputs to calibrate an LES. As they had run nine separate regressions, one for each income stratum, the resulting Engel curves were only piecewise linear, with nine segments, thus attenuating the problems caused by a unique LES estimation.
This solution, however, is far from complete, as some severe limitations remain. First, consumers belonging to different strata will have different minimum requirements. So, as the total expenditure increases, the shape of the utility function changes, and the value of the cardinal utility will have jumps when we go across class borders. In fact, with the parameter values thus obtained and the data that they utilized we observed that at some of the class borders the value of utility decreases as total expenditure increases. Secondly, it is not clear how Siqueira dealt with cases where a transfer or the taxation itself moved a household from a stratum to the other, since this would generate "jumps", i.e., changes of classification would generate changes of preferences.
Following Siqueira's steps, we derive the optimal tax structure from a standard Diamond and Mirrlees (1971) many person model. However, unlike her, who allowed for a differential tax structure for urban and rural areas, we focus on a tax structure for a population in which consumers face the same commodity price vector. Our extensions, as compared to her model, are twofold:
-
our household preferences are based on a more flexible demand system, and
-
we update the data used for tax simulations.
In fact, our simulations are based on a more recent estimation, made available by Asano and Fiuza (2001). The model used in their estimation is the Almost Ideal Demand System (AIDS), proposed by Deaton and Muellbauer (1980), which allows for a flexible approximation to a general preference structure, thus avoiding the problems just pointed out. The preference parameters estimates are remarkably consistent with microeconomic demand theory (negativity, homogeneity and symmetry are supported by the data), thus giving us a strong confidence on the performance of the optimal commodity tax simulation. The paper is organized as follows. In the next section we introduce our model. Section 3 presents the data, and numerical results are discussed in section 4. Concluding remarks are in section 5.
2 The Model
The government chooses taxes ti(i = 1,...,n) so as to maximize the social welfare determined by a Bergson - Samuelson social welfare function, W (v1,...,vH). This function is based on the utilities of the H individuals, given their demand  (p, Yh), where p is the price vector (p1, p2,...pn) and Yh is individual h¢s total income (see below).
(p, Yh), where p is the price vector (p1, p2,...pn) and Yh is individual h¢s total income (see below).
The supply side of the economy is kept quite simple and we take the producer prices, qi as given. As the consumer price is pi = qi + ti, the effect of commodity taxes on consumer welfare comes entirely from changes in consumer prices. Labor is the numeraire and without loss of generality it is assumed to be untaxed.3 3 The untaxed labor supply does not cause any loss of generality since the simultaneous imposition of proportionate income tax at rate t and commodity tax at rates ( ti) is equivalent to the situation with no income tax and commodity tax at rate . Another assumption in the model is that, in addition to their labor income, consumers may also receive uniform payments from the government.
2.1 The Consumer
We assume that there are H individuals, denoted by a superscript h. Each consumer is assumed to choose consumption goods (xi) in order to maximize a well behaved utility function defined over n commodities given by uh = uh( ,¼,
,¼, ), where
), where  (i = 1,...,n) is the consumption of commodity i and
(i = 1,...,n) is the consumption of commodity i and  is net the consumption of leisure. Maximization of uh is subject to the following budget constraint:
is net the consumption of leisure. Maximization of uh is subject to the following budget constraint:
where
i is index over consumption goods;
pi is consumer price of good i;
 is consumption of good i by consumer h;
is consumption of good i by consumer h;
Yh is the household per capita income, including both the fixed labor income yh and I is a uniform lump-sum transfer received by each consumer from the government.
The solution of the consumer problem leads to the Marshallian demand function,  (p, Yh). Consumer prices (pi) and lump sum transfers (I) are variables subject to government control, while labor income, yh, is fixed. By substituting
(p, Yh). Consumer prices (pi) and lump sum transfers (I) are variables subject to government control, while labor income, yh, is fixed. By substituting  (p,Yh) into uh we obtain the indirect utility function of the hth individual, vh(p,Yh).
(p,Yh) into uh we obtain the indirect utility function of the hth individual, vh(p,Yh).
We assume that each consumer takes income as exogenous and that there are no savings, so that income and total consumption are interchangeable. Hence, it implies that labor supply is inelastic.
2.2 Aids demand system and its indirect utility function
Our results on optimal tax calculation are based on an Almost Ideal Demand System - AIDS, which specifies individuals' expenditure function, from which flexible share equations are derived.4 4 Share equations and details of AIDS model can be seen in a Deaton and Muellbauer (1980). AIDS is chosen because it provides usually desirable properties in the conventional demand system and permits a flexible approximation for the consumer preference structure. The AIDS expenditure function is:
where U is the utility index and
The linear homogeneity of the expenditure function with respect to the price vector requires the following constraints:
The parameter a0 in (2.3) can be interpreted as the subsistence expenditure when all prices are normalized to one.
Inverting the expenditure function, we obtain the AIDS indirect utility function:
Regarding the econometric specification, the AIDS parameters, used in our indirect utility function, are estimated by Asano and Fiuza (2001) with data from the two waves of POF (1987/88 and 1995/96). The model is augmented with demographic variables, so that the AIDS share equations are ultimately of the following form:
where  is the expenditure share of good i for individual h; pj is the price of good j(j = 1,..,n); Yh is total expenditure,
is the expenditure share of good i for individual h; pj is the price of good j(j = 1,..,n); Yh is total expenditure,  s (k = 1,.., K) are demographic variables (family size, age and education of the head of household, and a regional dummy). The price index is represented by a nonlinear function of prices, P and log P = log a(p). Underlying to this extension is an adaptation of the subsistence level to incorporate demographic factors:
s (k = 1,.., K) are demographic variables (family size, age and education of the head of household, and a regional dummy). The price index is represented by a nonlinear function of prices, P and log P = log a(p). Underlying to this extension is an adaptation of the subsistence level to incorporate demographic factors:
The estimation results display consistency with demand theory, and elasticity estimates are close to economic common sense. Elasticities are highly nonlinear in parameters, and depend on the values of prices and total expenditure at which they are evaluated. Total expenditure elasticities (a proxy for income elasticities) indicate that food and housing are the only necessities in Brazilian utility functions, whereas furnishings, clothing, transportation, health and personal expenses are found to be luxuries.5 5 The expenditure elasticities for AIDS are given by: h i = 1 + . It follows that if b i is negative the ith group is a necessity, and if b i is positive it is a luxury. In the estimation of Asano and Fiuza (2001), the coefficientis negative for food and housing and positive for all the other categories. All the own-price elasticities are significantly negative. Among them, those for food, housing and furnishings are significantly less than one (own-price inelastic), while clothing, transportation and communication, health care and personal expenses display own-price elasticities around one.6 6 See Asano and Fiuza (2001) for a concise description of the methodology adopted in the estimation of the parameters and an analysis about price and income elasticities.
2.3 Social welfare and government budget constraint
The social welfare function is based on individual welfare levels vh, and its functional form, as suggested by Atkinson (1970), is:
when vh is the consumer indirect utility expressed as an explicit function of pi and Yh is total income of individual h (including transfers received), and e is a non-negative parameter that measures the degree of social aversion to inequality. It varies from e = 0 (Utilitarianism) to e = ¥ (Rawlsian Maximin).
The government tax revenue is written as:
where
ti is the value of the tax on good i;
 is the consumption of good i by individual h and;
is the consumption of good i by individual h and;
I is the lump sum transfer. Following most of the optimal tax literature, we take the revenue requirement as given by a pre-specified ratio of expenditure in the economy and we assume that it is not spent on anything that can affect the consumer behavior.
The optimal choice of the consumption tax rates (ti) and of the lump sum transfers (I) is obtained by maximizing the welfare social function subject to the budget constraint. Optimal tax rate structure is derived under alternative assumptions on degrees of inequality aversion (e). The first-order conditions for ti and I are the following:
where L is the Lagrangian. The optimal tax rates and lump sum transfer are calculated by solving the many person Ramsey equations (2.10) and (2.11).
3 Data
The model was estimated from household-level monthly expenditures on seven consumption categories and their corresponding price indexes: 1. Food, 2. Housing (including rent), 3. Furnishings, 4. Clothing, 5. Transportation and communication, 6. Health and personal care, 7. Personal expenses, education and reading.
The data sources for expenditures are two waves of the Household Expenditure Survey conducted in 1987/88 and 1995/96, and the sources for price indexes are the monthly price collections for the national consumer price indexes. A new set of price indexes was constructed to allow a comparison of prices both across periods and regions.7 7 The regions surveyed are the metropolitan areas of São Paulo, Rio de Janeiro, Porto Alegre, Belo Horizonte, Recife, Belém, Fortaleza, Salvador and Curitiba, besides the cities of Brasilia-DF and Goiânia. A Regional Price Difference Index was constructed based on regional nominal prices, obtained upon request from IBGE (the Federal statistical bureau in charge of the surveys and of the national consumer price index calculation). It compares prices of a national average consumption bundle (based on the 1995/96 survey) both across periods and regions. See more details in Asano and Fiuza (2001).
We assume that the tax structure is common for all individuals. As prices differ across metropolitan areas, we also restrict our initial analysis to São Paulo's households. The optimal commodity tax rates are calculated for the seven groups of commodities described above.
4 Results
4. Optimal commodity tax rates
Table 1 presents the optimal tax rates (ti) derived from the estimates of AIDS demand system for different levels of inequality aversion (e). The government revenue requirement corresponds to 10% of the consumers' total expenditure. The results can be summarized as follows. At all levels of inequality aversion, except when e = 0.25, food should be subsidized. Regarding housing expenses, we note that a positive tax is replaced by a subsidy as inequality aversion increases (from e = 1.00 to 1.25). All the other commodity categories have positive tax rates and their values increase when e is higher.
For low levels of inequality aversion (e = 0.25), tax structure shows a movement towards uniformity. When e is near zero, there is no concern for inequality. In this situation, a uniform rate of tax on all goods is equivalent to a tax on labor alone. This corresponds to the conventional prescription that if there is a completely inelastic factor, this should bear all the tax . Therefore, as we are assuming that labor supply is completely inelastic, optimal tax rates are uniform.
As the parameter e increases, commodity tax structure presents non-uniformity in its optimal tax rates: the rate of subsidy increases for food and housing while tax rates also increase for the taxed items. In particular, tax rates on transportation and personal expenses increase substantially as the degree of inequality aversion becomes higher. This result reflects the fact that, according to the Household Expenditure Surveys and to the household expenditure aggregation made by Asano and Fiuza (2001),8 8 The aggregation followed IBGE's documentation that ruled the calculation of the price index weighting structure at group level. food and housing together correspond to more than 60% of the expenditure of the poorest household group and falls to nearly 24% for the richer household strata. The shares of all the other categories increase with income. The share of transportation, for instance, increases from 7% to 27% while personal expenses, which includes education, recreation and tobacco, increases from 8% to nearly 20% in the household budget. Also, these last categories are the ones that present the highest expenditure elasticities. As a whole, the results show that in order to achieve distributive goals a higher degree of selectivity in commodity tax rates structure is required.
Comparing our results with Siqueira's one is not an easy task, as the demand specifications (LES and AIDS are non-nested), samples and expenditure classifications differ in each study. Nevertheless, regarding the sensitivity of the results to the form of demand systems we note some similarities in the optimal tax rate structures based on AIDS and LES. Table 4 presents the optimal tax rates of Siqueira's simulations, which were based on LES. This demand system has not a flexible functional form, in the sense that its estimated elasticities are not independent of one another - see Deaton (1986) for further details. Moreover, certain restrictions are placed on consumer preferences by the linear structure. In particular, LES does not allow neither for inferior goods nor for complementarity within any pair of goods. LES also implies linear Engel curves, so that marginal expenditure shares are independent of total expenditure. AIDS, in contrast, places no restrictions on elasticities, which are highly nonlinear in parameters.9 9 It is important to stress that our optimal taxes were computed for different values of e(from 0.1 to 5) from Siqueira's ones. But this different range of value judgments does not prevent the comparisons.
For low levels of e, we note a movement towards uniformity in both models (see table 1 and table 4). As e increases items which lower income households spend most are subsidized. Also, in both models tax rates are higher for commodities with high income elasticities, what shows that the distributive role is targeting the higher income households, whose shares are greater in these commodities than the poor consumers.
Note, however, that in Siqueira's model, the magnitude of commodity tax rates is much higher than ours for all levels of parameter e. When e = 1.0, our highest tax rate is nearly 27% for personal expenses, while in Siqueira's case, the highest tax rate is 57% for durables, which in her classification includes furnishings and motor vehicles. This result can be explained by differences in commodity classification between the models. In our model commodity groups are classified into seven categories, while in Siqueira's they are classified into nine categories. This suggests that in our model commodity groups are broader than in Siqueira's and may include more diverse items. For instance, our food category includes all beverages, while tobacco is included in our personal expenditure group. On the whole, the differences in sample designs, categorization and in consumption patterns between the rich and the poor across broad categories of goods seem to account heavily for the difference of tax rates.
4.2 Optimal (unconstrained) uniform lump sum subsidy
Table 2 reports the results for the case in which the government sets an optimal uniform lump-sum subsidy to all individuals. The government revenue requirement is assumed to be 10% of consumers' total expenditure. The odd results for this case are the strikingly high levels both of commodity tax rates and of the optimal lump sum subsidies at all levels of inequality aversion. The lump sum subsidy estimated varies from R$ 1,760.00 to nearly R$ 3,530.00. This last figure corresponds to almost 2.5 of the yearly minimum wage in fore in September 1996. As e increases both the commodity tax rates and the lump sum subsidies increase.
The commodity tax structure is characterized by high levels on items that are price inelastic for low levels of e. One important feature to stress in this result is that this commodity tax structure remains similar as parameter e increases. Therefore, we conclude that in our model, when an optimal lump sum subsidy is introduced, there is no room for redistribution through commodity tax rates.
Siqueira considers the case in which government can grant uniform lump-sum subsidies to all households. In this case, when e was close to zero, there was still a movement towards uniformity. However, for high values of parameter e, tax rates' selectiveness was remarkably reduced in comparison to the case with no transfers (see table 4). As Siqueira points out, this is because lump sum subsidies are more efficient instruments (as they are by definition non-distortionary) to achieve redistribution than are differential commodity taxes.10 10 A large part of the literature on optimal commodity taxes has been concerned with the derivation of sufficient conditions for optimal tax rates to be uniform. These conditions are in particular associated with the preferences structure and with the tax instruments available. See more details in Fukushima (1991).
Unlike in the last section, our present results are quite different from Siqueira's. In our simulations, lump sum subsidies are playing entirely the distributive role for lower income households as commodity tax structure remains regressive when inequality aversion increases. In both models (LES and AIDS), if on the one hand preference specifications adopted differ, on the other hand the budget expenditure share structures present the same pattern, in that lower income households spend most in price-inelastic items and higher income households spend most in price-elastic items. Nevertheless, if we compare the derivative of demand with respect to price, 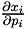 , and to income,
, and to income, 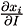 , in both models, we note significant differences on its values.11
11
Based upon AIDS and LES parameters and on the databases used in each model, we calculated all the terms of (2.10) and (2.11) equations in order to have a clear-cut comparison between the models. Both derivatives,
and
, are important elements for solving the first order conditions (equations 2.10 and 2.11) of the problem.
Regarding the
, in both models, we note significant differences on its values.11
11
Based upon AIDS and LES parameters and on the databases used in each model, we calculated all the terms of (2.10) and (2.11) equations in order to have a clear-cut comparison between the models. Both derivatives,
and
, are important elements for solving the first order conditions (equations 2.10 and 2.11) of the problem.
Regarding the 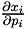 derivative, we find in our model lower values for food and housing categories than in Siqueira's model, while for the other categories our derivatives are higher than Siqueira's ones. For
derivative, we find in our model lower values for food and housing categories than in Siqueira's model, while for the other categories our derivatives are higher than Siqueira's ones. For 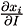 , we find almost the same structure in the results: lower values for food and housing and higher values for the other categories in our model in comparison to Siqueira's model.12
12
As mentioned above, it is worth noting that categories classifications are different between AIDS and LES simulations but this does not harm a general comparison as we do here.
The discussion of these derivatives is extremely important in the sense that they are the basis for the optimal tax rule. For instance, the term
, we find almost the same structure in the results: lower values for food and housing and higher values for the other categories in our model in comparison to Siqueira's model.12
12
As mentioned above, it is worth noting that categories classifications are different between AIDS and LES simulations but this does not harm a general comparison as we do here.
The discussion of these derivatives is extremely important in the sense that they are the basis for the optimal tax rule. For instance, the term 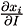 relates to an efficiency criterion in that, the more income goes down due to tax payment, the lower should be the tax rate imposed, so that the welfare loss is minimized, given a revenue target. And this is exactly what happens in the AIDS case for the categories other than food and housing, and vice versa for these two categories.
relates to an efficiency criterion in that, the more income goes down due to tax payment, the lower should be the tax rate imposed, so that the welfare loss is minimized, given a revenue target. And this is exactly what happens in the AIDS case for the categories other than food and housing, and vice versa for these two categories.
It is hard to disentangle the differences of the derivatives due to differences in relative prices (as the estimations were run on two different datasets), in parameters and in the formulas of the derivatives. What is clear is that in our optimal tax simulations based on AIDS, the income effects of the optimal lump sum transfers are much higher for the lower income households than are the income effects of the commodity taxation. As AIDS preference is less restrictive than LES, the former shares vary much more across households than the latter. In comparison to Siqueira's model, this fact can also explain why that commodity tax rates in AIDS simulations vary more significantly in magnitude from the situation with no lump sum transfer to the one with lump sum transfer. Moreover, we conclude that in optimal tax simulations based on a more flexible demand system, such as AIDS, the income effects of the optimal lump sum transfer are much higher than the commodity tax rates to the lower income households.
As the optimal lump sum subsidies are remarkably high in values, we chose to constrain the size of the lump sum subsidy in order to obtain more politically realistic results.
4.3 Constrained lump sum subsidy
The optimal lump sum subsidy's constraint is equal to 50% of the minimum observed income and we call it "bonus rate". The government revenue requirement is assumed to be 10% of individuals' total expenditure.
Table 3 shows that the lump sum subsidy is around R$ 127.00 yearly, an amount slightly above the minimum wage at that time (R$ 121.00 on September, 1996). We also have substantially higher tax rates (and lower subsidies) than the results presented in table 1 (the case with no lump sum transfers). The payment of an optimal uniform subsidy to all individuals, which is a more efficient tool to achieve redistribution, implies in the increase of commodity tax rates in order to finance it. However, as compared to the case of unconstrained optimal lump sum (last section), the present result shows that the introduction of a constrained lump sum makes some room for commodity taxation playing a distributive role, just like is Siqueira's model. As the inequality aversion increases, taxes for food and housing are substantially reduced. In particular, for inequality aversion equal to or above 1.25 food is subsidized. The higher commodity tax rates from the case with no transfers are also to finance food subsidy.
However, different from Siqueira's results in the case where she assumes a lump sum grant from the government to all households, ours do not show a movement towards uniformity in commodity tax rates when the degree of inequality aversion increases. Again, the differences in results can be explained by the different preference specifications (LES and AIDS) and its relation to income effect of the optimal income transfers adopted in each study.
5 Conclusion
This paper investigates the structure of optimal commodity taxes in Brazil. Unlike a number of empirical studies on commodity taxation based on very restrictive consumer preferences, our micro-simulations were based on a demand system estimated with a flexible functional form.
Our results showed that commodities in which the lower income classes spend most, should be subsidized. We have also extended our analysis by allowing for a uniform per capita lump sum payment to be made by the government to all households. The optimal lump sum transfer reverses the results previously such that the distributive role of taxes is canceled out and poll transfer levels are unreasonably high. However, when we constrain the lump sum transfer, tax structures follow similar patterns to the first case.
Regarding the sensitivity of results to the form of household's preferences we conclude that there is a relative robustness for the case where the only instrument available to the government is commodity taxation. This robustness does not occur when there is an inclusion of the unconstrained lump sum transfer.
Some final remarks should be stressed. Separability of labor supply and commodity demand has been assumed throughout the discussion. Although this is a useful assumption regarding consumer demand systems, the empirical evidence shows that when joint decision of leisure and commodity choice is taken into account along with flexible functional forms, separability is decisively rejected (Blundell and Walker, 1982) and Browning and Meghir (1991). We believe that an estimation based on an extended demand system with flexible form including labor supply could generate different results regarding optimal commodity taxation. This exercise for Brazil requires a richer data set, as our data source does not provide such information. Solutions on combining from the expenditure survey with labor survey are to be pursued as possible extensions. This study hasn't considered administrative costs and it also ignores a range of relevant institutional features. However, we believe that our empirical findings provide a valuable contribution for the current tax policy debate in Brazil.
This paper was received in Mar. 2002 and approved in Apr. 2003.
- Asano, S. (1997). Joint allocation of leisure and consumption commodities: A japanese extended consumer demand system 1979-90. Japanese Economic Review, 48(1):6580.
- Asano, S. & Fiuza, E. P. S. (2001). Estimation of the Brazilian consumer demand system. Texto para Discussão IPEA, Rio de Janeiro, n. 793.
- Atkinson, A. (1970). On the measurement of inequality. Journal of Economic Theory, 2:244263.
- Atkinson, A. & Stiglitz, J. E. (1972). The structure of indirect taxation and economic efficiency. Journal of Public Economics, 1:97119.
- Atkinson, A. & Stiglitz, J. E. (1980). Lectures on Public Economics McGraw-Hill, New York.
- Blundell, R. & Walker, I. (1982). Modeling the joint determination of household labor supplies and commodity demands. Economic Journal, 92:35164.
- Browning, M. & Meghir, C. (1991). The effects of male and female labor supply on commodity demands. Econometrica, 59:92551.
- Deaton, A. (1986). Consumers' expenditure. Discussion Paper n. 126. Research Program in Development Studies, Princeton University.
- Deaton, A. (1997). The Analysis of Household Survey The Jonns Hopkins University Press, Baltimore.
- Deaton, A. & Muellbauer, J. (1980). An almost ideal demand system. American Economic Review, 70(3):312326.
- Deaton, A. & Stern, N. (1986). Optimally uniform commodity taxes, taste diffrences and lumpsum transfer. Economics Letters, 20:263266.
- Diamond, P. A. & Mirrlees, J. A. (1971). Optimal taxation and public production: I / II. American Economic Review, 61:827 / 26178.
- Fukushima, T. (1991). Uniformity versus selectivity in tax structure: A simulation approach. Osaka Economic Papers, 40:34.
- King, M. A. (1983). Welfare analysis of tax reforms using household data. Journal of Public Economics, 21:183214.
- Ramsey, F. (1927). A contribution to the theory of taxation. Economic Journal, 37:4761.
- Rossi, J. W. & Neves, C. (1987). Elasticidades de Engel no Brasil usando um sistema de equações com especificações Logit. Revista Brasileira de Economia, 41:42534.
- Siqueira, R. B. (1998). Optimal indirect taxes for brazil: Combining equity and efficiency. Revista Brasileira de Economia, 52(1):3952.
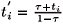 .
. 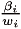 . It follows that if b
. It follows that if b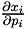 and
and 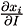 , are important elements for solving the first order conditions (equations 2.10 and 2.11) of the problem.
, are important elements for solving the first order conditions (equations 2.10 and 2.11) of the problem. Publication Dates
-
Publication in this collection
02 Sept 2004 -
Date of issue
Mar 2004
History
-
Accepted
Apr 2003 -
Received
Mar 2002















