Abstracts
In this paper we set up a model of regional banking competition based on Bresnahan (1982), Lau (1982) and Nakane (2002). The structural model is estimated using data from eight Brazilian states and a dynamic panel. The results show that on average the level of competition in the Brazilian banking system is high, even tough the null of perfect competition can be rejected at the usual significance levels. This result also prevails at the state level: Rio Grande do Sul, São Paulo, Rio de Janeiro, Pernambuco and Minas Gerais have high degree of competition.
Microeconomics; Industrial Organization; Banking Competition; Dynamic Panel Models
O presente artigo propõe um modelo regional de competição bancária baseado nas contribuições de Bresnahan (1982), Lau (1982) e Nakane (2002). O modelo estrutural formuladoé estimado utilizando as informações para oito estados brasileiros e um painel dinâmico. Os resultados mostram que, na média, o nível de competição no sistema bancário brasileiro é alto, embora a hipótese nula de competição perfeita possa ser rejeitada aos níveis usuais de significância. De uma forma geral, este padrão também prevalece nos estados: Rio Grande do Sul, São Paulo, Rio de Janeiro, Pernambuco e Minas Gerais têm elevado grau de competição.
Estimating a theoretical model of state banking competition using a dynamic panel: the Brazilian case* * We would like to thank Márcio Issao Nakane, Fabiana Rocha, Rodrigo Sekkel and an anonymous referee for helpful comments. Needless to say, remaining errors and omissions are of our responsibility.
Fábio A. Miessi SanchesI; Bruno de Paula RochaII; José Carlos Domingos da SilvaIII
IPhD Student at London School of Economics. E-mail: fmiessi@gmail.com
IITendências Consultoria Integrada and IBMEC São Paulo. E-mail: brunor@usp.br
IIIMsc in Economics at IPE/USP and FECAP São Paulo. E-mail: jcds@usp.br
ABSTRACT
In this paper we set up a model of regional banking competition based on Bresnahan (1982), Lau (1982) and Nakane (2002). The structural model is estimated using data from eight Brazilian states and a dynamic panel. The results show that on average the level of competition in the Brazilian banking system is high, even tough the null of perfect competition can be rejected at the usual significance levels. This result also prevails at the state level: Rio Grande do Sul, São Paulo, Rio de Janeiro, Pernambuco and Minas Gerais have high degree of competition.
Keywords: Microeconomics; Industrial Organization; Banking Competition; Dynamic Panel Models.
JEL Code: L10; C33; G21.
RESUMO
O presente artigo propõe um modelo regional de competição bancária baseado nas contribuições de Bresnahan (1982), Lau (1982) e Nakane (2002). O modelo estrutural formuladoé estimado utilizando as informações para oito estados brasileiros e um painel dinâmico. Os resultados mostram que, na média, o nível de competição no sistema bancário brasileiro é alto, embora a hipótese nula de competição perfeita possa ser rejeitada aos níveis usuais de significância. De uma forma geral, este padrão também prevalece nos estados: Rio Grande do Sul, São Paulo, Rio de Janeiro, Pernambuco e Minas Gerais têm elevado grau de competição.
1. INTRODUCTION
The overwhelming majority of the NEIO - New Empirical Industrial Organization - papers on banking conduct is basically focused on aggregate data and on national markets and, therefore, these papers implicitly neglects the existence of regional differences in the markets of banking services. Shaffer (1989, 1993), for example, employs the Bresnahan (1982) and Lau (1982) model - thereafter called the BL model - to test the conduct of American and Canadian banks using aggregated data from these countries. Bikker and Haaf (2002) use the BL model to infer the conduct of the banks in a variety of European countries.
An important issue behind this approach is that a broad definition of the relevant market can impose some kind of bias in the conduct parameter. In other words, the (average based) procedure used to aggregate the data at the firm level is notably less accurate when the aggregation embraces heterogeneous firms (markets). To be more explicit, we use the fact that the mean index is not a good indicator when the population is relatively more heterogeneous. Alternatively, a narrower definition for the relevant market helps us to sort out or, at least, to minimize this problem.
This point of view, on the other hand, deserves relatively more attention in countries where the regional segmentation of the banking market is stronger due to either legal restrictions or geographic determinants (or both). Particularly, in the U.S. case the former argument seems to have expressive appeal: in these circumstances the differences in the banking conduct across regions becomes an important parameter for the design of more accurate policies. As mentioned in the paragraph above, the aggregation of the data from states with different market structure will not produce a good measure of conduct.
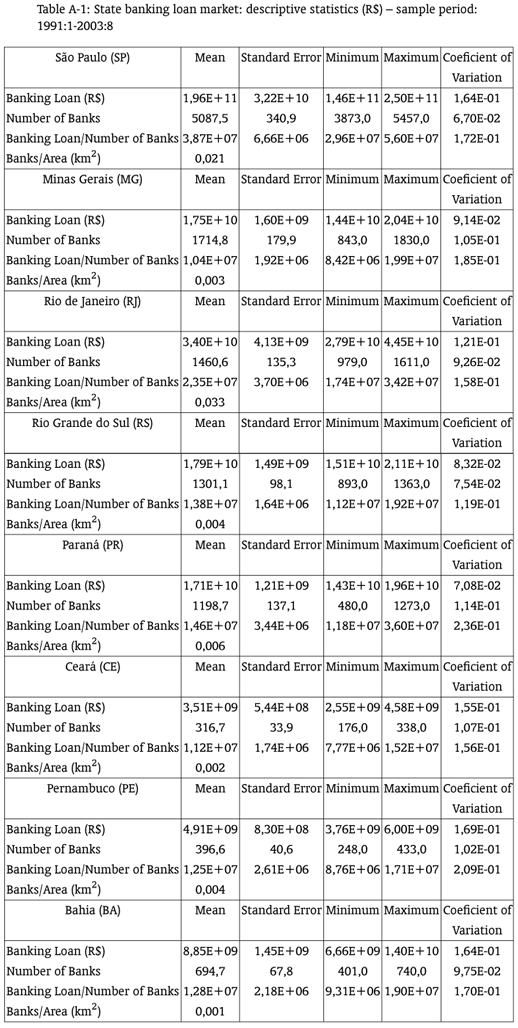
In the Brazilian case the enormous regional disparity seems to express itself in markets of credit with distinct characteristics. In the appendixappendix, the tables 6 and 7 present some descriptive statistics of the Brazilian credit market at the state level. Some comments on these data are illustrative.
Firstly, there are significant differences in the size of the state markets. For instance, São Paulo has a volume of banking loans about 50 times bigger than the observed in other states, such as Bahia and Ceará. Beyond the magnitude, the difference in the degree of stability of the markets is also impressive. We observed, in this case, the coefficient of variation is very distinct across the sample, indicating that in some states the market is relatively more stable. Additionally, the states of São Paulo and Rio de Janeiro have about 10 times more agencies that the other states.
Finally we observe the correlation between the markets. Again, São Paulo seems to differentiate itself, presenting a higher degree of independence, what is coherent with its condition of Brazilian's financial capital. Likewise, it is possible that these huge dissimilarities between the states can imply different degrees of competition.
Bearing these considerations in mind, we set up a model of banking competition following Nakane (2002), which in turn is based on Bresnahan (1982) and Lau (1982). Following this tradition, the model produces a measure of competition that can be (roughly) understood as the sensibility of the market equilibrium quantities to marginal alterations in the (optimum) supply decision of a single agent. The structural model is then estimated using a dynamic panel - see Arellano and Bond (1991) - and the relevant conduct parameter is obtained. When we exploit the panel structure of the data, we get more accurate parameters - relatively to the traditional studies on banking competition, which use only (aggregate) cross-sectional or time variation - and we also control for a regional specific effect. Apart from that, the estimation procedure easily overcomes the endogeneity problem by including lags of the variables as instruments. Finally, an interaction between a regional dummy and the relevant variable allows us to capture the differences of banking conduct across regions and the inclusion of time dummies in the model also allows us to capture the variations of the conduct parameters across the time.
The remaining of this paper is organized as follows: in section two we derive the model, in section three we briefly explain the estimation procedure and show the results and in the last section we sum up our main conclusions.
2. THE THEORETICAL MODEL
The theoretical model to be estimated here follows Nakane (2002) - which in turn is based on Bresnahan (1982) and Lau (1982) works. Shaffer (1989, 1993) also has a model of banking competition for Canada and U.S. and Bikker and Haaf (2002) have estimates of the banking conduct parameter for various European countries.
The foregoing model supposes a regional configuration to the demand for banking loans that has the following standard pattern:
In this equation i and j are the indexes for banks and states respectively, the variable aj is a specific effect for the state j, Lj =  lij is the aggregate demand for banking loans in state j,
lij is the aggregate demand for banking loans in state j,  is the interest rate1
1
The interest rate charged on banking loans is assumed equal for all banks located in state
j, although an individual bank with sufficient market power is able to affect it through his equilibrium allocation - see equation 5 below.
on loans in state j and Yj is an index of economic activity in state j. All these variables are stated in real terms. The importance of the parameter α3 multiplying the demand shifter (
is the interest rate1
1
The interest rate charged on banking loans is assumed equal for all banks located in state
j, although an individual bank with sufficient market power is able to affect it through his equilibrium allocation - see equation 5 below.
on loans in state j and Yj is an index of economic activity in state j. All these variables are stated in real terms. The importance of the parameter α3 multiplying the demand shifter ( ln Yj) is crucial for the identification of the market power parameter - as pointed out by Bresnahan (1982), Lau (1982) and Shaffer (1993).
ln Yj) is crucial for the identification of the market power parameter - as pointed out by Bresnahan (1982), Lau (1982) and Shaffer (1993).
On the other hand, the supply relation to be derived below assumes that bank i works with a (simplified) balance sheet given by:
The Expression 2 shows the balance sheet of the bank i in all the N states. In this case, Li =  lij, Di =
lij, Di =  dij is the total amount of deposits raised by the bank, Bi is the volume of public bonds in the bank's portfolio and µ is the reserve tax required by the Central Bank. In other words, this constraint only says that the overall amount of deposits raised by the bank will be allocated in (i) reserves, (ii) loans and (iii) public bonds.2
2
This balance sheet was originally proposed by Nakane (2002). As a matter of simplicity - these elements comprise the most relevant picture of the banking assets - and in order to make our results directly comparable to those presented by this author, we kept this same structure.
Again, it is worthwhile to assert that these variables are in real terms.
dij is the total amount of deposits raised by the bank, Bi is the volume of public bonds in the bank's portfolio and µ is the reserve tax required by the Central Bank. In other words, this constraint only says that the overall amount of deposits raised by the bank will be allocated in (i) reserves, (ii) loans and (iii) public bonds.2
2
This balance sheet was originally proposed by Nakane (2002). As a matter of simplicity - these elements comprise the most relevant picture of the banking assets - and in order to make our results directly comparable to those presented by this author, we kept this same structure.
Again, it is worthwhile to assert that these variables are in real terms.
Given this restriction, bank i maximizes the following profit function:
where: rB is the real interest rate paid by public bonds, and;  is the real interest rate paid by the bank in region j. The cost function cij (lij ,dij) has an additive-separable form and depends only on loans granted and on deposits raised.
is the real interest rate paid by the bank in region j. The cost function cij (lij ,dij) has an additive-separable form and depends only on loans granted and on deposits raised.
Assuming that rB is determined by the government and that bank i takes it as given, the first order condition for the firm in the region j is given bellow:
Additionally, from equations (1) and (4) we can find the following relation:
We can aggregate this equation summing and taking the averages across the nj banks acting in the state j to get an estimate of the average banking conduct in the state j. Likewise, from Equation 5, by the means of the procedure described above, we obtain:
where: 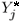 = (α1 + α3 ln Yj)-1; λj =
= (α1 + α3 ln Yj)-1; λj =  , and; cmgj =
, and; cmgj =  .
.
In this equation the parameter λj is our relevant measure of banking competition in each state j. It measures the (average) sensibility of the state j market supply of loans to a marginal increase in the loan supply of each agent. When this parameter tends to zero - meaning that, on average, the decision of a single agent has no effect on the total supply - the market is characterized by perfect competition. Analogously, if this parameter tends to one, we have a monopoly or a perfect cartel. If the parameter is located in the interval between zero and one the market can be represented by some oligopolistic structure (Steen and Salvanes, 1999).
Finally, we assume that the marginal cost depends on the total loans, labor, capital and a specific factor of cost for each region:3 3 This marginal cost function is also similar to that proposed by Nakane (2002). Particularly, the lack of deposits in the specification can be justified if we consider that the costs of loans are marginally higher than the costs to raise and manage deposits. With regard to this point, Fonseca (2005) explains that informational problems behind the loans are very significant and are not present in the management of deposits.
3. ESTIMATION PROCEDURE AND MAIN RESULTS
In this section we estimate the Equations 1 and 6 at the state level using panel data techniques. First we estimate the parameters of Equation 1 in order to calculate the variable 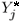 . As already mentioned, the parameter associated to
. As already mentioned, the parameter associated to 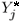 in (6) is our measure of conduct in the banking system in the state j.
in (6) is our measure of conduct in the banking system in the state j.
The dynamic specifications assumed in equations (1) and (6) include lags of the dependent variable among the explicative variables. Besides, the other explicative variables may be correlated with the regression residuals.4 4 In particular, production and state interest rate in the demand equation and state loans and the variable in the supply equation may be considered as endogenous. To overcome these problems we use the procedure suggested by Arellano and Bond (1991), with the equations written in first differences to eliminate the specific factor of regional cost.
Following Holtz-Eakin et al. (1988), Arellano (1989) and Arellano and Bond (1991), we use as instruments two lags of the level of each variable in the model. The identification hypothesis turns to be:
E[Φis uit] = 0,∀s < t - 1
where: Φis is the set of endogenous variables, and; uit is the idiosyncratic error term associated to the estimation equation.
Furthermore, lags of the dependent variable were included in the models to avoid second order autocorrelation in residuals. This strategy considers the more parsimonious model with the last lagged dependent variable statistically significant.
The sample consists of regional monthly data between January/1999 and August/2003. The states considered are: São Paulo, Minas Gerais, Rio de Janeiro, Rio Grande do Sul, Paraná, Ceará, Pernambuco and Bahia. It is worthwhile mentioning that these states are responsible for approximately 80% of the Brazilian GDP.
For the state production it was used the state industrial production real index calculated by the Geography and Statistics Brazilian Institute - IBGE. The total loan is a real index of the total amount of banking credit seasonally adjusted, calculated with the data from the Brazilian Central Bank. For public bonds interest rates, which is unique in all state markets, it was used the monthly (and inflation adjusted) overnight SELIC interest rate. Both the banking credit indicator and the public bonds interest rate has been adjusted at regional level by the consumption price index (IPCA), measured by IBGE in the metropolitan regions from the respective states.
The interest rate on state loans is not observed at regional (state) level even though it is assumed in the theoretical model. In order to construct a state proxy to that variable, we used the fact that the relevant interest rate is not the nominal but the real one. This interest rate would be the one that prevails after the adjustment by the state price index. Likewise, the interest rate used in the estimations consists of monthly average rate on freely allocated loans adjusted by the IPCA of the corresponding state.5 5 More specifically, the real interest rate on loans of each state is the national (average) nominal interest rate on freely allocated loans - which, in turn, is equal between states - corrected by the state price index (IPCA).
For state marginal cost function we have used the number of processed banking agencies in each state as a proxy to the banking capital stock. As a proxy to costs with labor factor, we have used a measure of the state minimum wage - which is the national minimum wage deflated by the state IPCA.
The results for demand equation can be seen in Table 1. First, it should be emphasized the statistical significance for the interaction term to the industrial production and interest rate. This fact shows that the variable 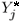 to be used at second stage is not a constant.
to be used at second stage is not a constant.
From Equation 1, we see that the interest rate elasticity of the loan demand is given by  (α1 + α3 ln Yj). Using the average of
(α1 + α3 ln Yj). Using the average of  and ln Yj for the Brazilian data and the values of α1 and α3 presented in the Table 1, we get elasticity equal to -0.0596. Nakane (2002), for example, found an elasticity of -0.128 using Brazilian aggregate time series data. Therefore, GMM estimates using state level data shows that the demand for loans is relatively more inelastic. We can also obtain the values of interest rates elasticity of loan demand for Brazilian states through their mean values of interest rates and income.
and ln Yj for the Brazilian data and the values of α1 and α3 presented in the Table 1, we get elasticity equal to -0.0596. Nakane (2002), for example, found an elasticity of -0.128 using Brazilian aggregate time series data. Therefore, GMM estimates using state level data shows that the demand for loans is relatively more inelastic. We can also obtain the values of interest rates elasticity of loan demand for Brazilian states through their mean values of interest rates and income.
The largest elasticities are observed in the markets of Rio de Janeiro, São Paulo and Paraná, with values equals to -0.11, -0.094 and -0.097, respectively. The analysis of the Table 2 shows that the lower elasticity for the Brazilian aggregated data is explained by the values of some states, more markedly the Ceará. This state has a positive estimate of the interest rate elasticity of the loan banking demand.
Following the procedure, we firstly estimated the supply Equation 6 in an aggregated way in order to analyze the average behavior of banking system in Brazil. Briefly, this equation considers the variable 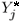 (estimated with the parameters of the first stage), three lags of the dependent variable (in order to avoid second order autocorrelation in residuals) and the variables in the cost function. The results are in Table 3.
(estimated with the parameters of the first stage), three lags of the dependent variable (in order to avoid second order autocorrelation in residuals) and the variables in the cost function. The results are in Table 3.
All variables included in the function of marginal cost are statistically significant and present the expected effect on the bank spread. As regards to the conduct parameter, the results point out a value statistically different from zero and therefore we can reject the hypothesis of perfect competition. The parameter also does not support the hypothesis of monopoly in the banking system - the null hypothesis, which states that this parameter is equal to one, can be rejected at 1%.
The magnitude of the parameter seems to confirm the evidence found by Nakane (2002) with Brazilian aggregate time series. Although the null hypothesis of perfect competition may be rejected, a high degree of competition in Brazilian banking system prevails.
Afterwards we estimated a model with interactions between the 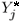 component and time dummies to capture time variations in the banking conduct. More specifically, we considered interactions between
component and time dummies to capture time variations in the banking conduct. More specifically, we considered interactions between 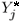 and a dummy for the first six months of 1999,
and a dummy for the first six months of 1999, 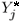 and a time dummy for the second semester of 1999 and so on, up to the first semester of 2003. Table 4 below summarizes the main results.
and a time dummy for the second semester of 1999 and so on, up to the first semester of 2003. Table 4 below summarizes the main results.
The results show that the conduct parameter is not significant in the years of 2000 and 2001 indicating a competitive behavior in these years. The evolution of the indicator during this period is shown in the figure above.
The gray bars show the periods when the conduct parameter is not significant. The highest value for the parameter is found in 2002 however this value continues to be far from 1. The last column of the figure shows the time-invariant parameter that was calculated above (Table 3). These results are also correlated with the findings of Jorge Neto et al. (2005). These authors show that the Brazilian banks operated in monopolistic competition during the 1995-2004 period - the same result is found in Belaisch (2003).
Now we proceed with the estimation of Equation 6 in order to make possible the analysis at the state level. The equation to be estimated considers one interaction between a dummy variable for each state and the variable 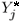 . The results are shown in the table 5.
. The results are shown in the table 5.
The results show that, on the whole, the Brazilian loans market is competitive even when we consider a regionally segmented market. It is also possible to classify the states through the level of competition: in Ceará, for example, we cannot reject the null of perfect competition. In Rio Grande do Sul, São Paulo, Rio de Janeiro, Pernambuco and Minas Gerais the coefficients are significant, but they are also close to zero. On the other hand, the coefficients estimated to Paraná and Bahia are negative. This finding indicates that the market for loans in these states is "super competitive". Shaffer (1993) argues that this pattern can be found in markets where the convergence process to the equilibrium is not complete.
4. CONCLUSIONS
In this paper we derived a model of regional banking competition based on Bresnahan (1982), Lau (1982) and Nakane (2002). More specifically, we generalized the model in Nakane (2002) in order to capture the regional differences in the markets for banking loans. This approach can be very useful in countries where the segmentation of the banking market is stronger due to either legal restrictions or geographic determinants (or both). Particularly in the U.S. case the former argument seems to have expressive appeal: in these circumstances the differences in the banking conduct across regions becomes an important parameter for the design of more accurate policies.
We estimated the structural model using data from eight Brazilian states and a dynamic panel model - see Arellano and Bond (1991). The results show that on average the level of competition in the Brazilian banking system is high, even tough the null of perfect competition can be rejected at the usual significance levels. This finding is similar to that presented by Nakane (2002). We also showed that the Brazilian market for loans were competitive during the years of 2000 and 2001. On the other hand, the value of the conduct parameter increased sharply in 2003.
Finally, these results also prevail at the state level: Rio Grande do Sul, São Paulo, Rio de Janeiro, Pernambuco and Minas Gerais have high degree of competition. In Ceará, the null hypothesis of perfect competition cannot be rejected. Notwithstanding, we should point out that Paraná and Bahia have negative and significant coefficients, what can be due some temporary disequilibrium in this markets (Shaffer, 1993).
BIBLIOGRAPHY
- Arellano, M. (1989). Anote on the Anderson-Hsiao estimator for panel data. Economic Letters, 31:337341.
- Arellano, M. & Bond, S. (1991). Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations. Review of Economic Studies, 58:277297.
- Belaisch, A. (2003). Do Brazilian banks compete? Technical Report 03/113, IMF.
- Bikker, J. & Haaf, K. (2002). Competition, concentration an their relationship: An empirical analysis of the banking industry. Journal of Banking and Finance, 26:21912214.
- Bresnahan, T.R. (1982). The oligopoly solutionis identified. Economic Letters, 10:8792.
- Fonseca, C.F. (2005). Estrutura, Concorrência e Performance Do Setor Bancário Em Um Mercado Heterogêneo PhD thesis, IPE/FEA/USP, São Paulo, Brasil.
- Holtz-Eakin, D., Newey, W., & Rosen, H. S. (1988). Estimating vector autoregressions with panel data. Econometrica, 56(6):13711395.
- Jorge Neto, P. M., Araújo, L. A., & Ponce, D. A. S. (2005). Competição e concentração entre bancos brasileiros. In ANPEC, XXXIII Encontro Nacional de Economia. Anais
- Lau, L.J. (1982). On identifying the degree of competitiveness from industry price and output data. Economic Letters, 10:9399.
- Nakane, M. I. (2002). A test of competition in Brazilian banking. Estudos Econômicos, 32.
- Shaffer, S. (1989). Competition in the U.S. banking industry. Economic Letters, 29:321323.
- Shaffer, S. (1993). A test of competition in Canadian banking. Journal of Money, Credit and Banking, 25:4961.
- Steen, F. & Salvanes, K.G. (1999). Testing for market power using a dynamic oligopoly model. International Journal of Industrial Organization, 17:147177.
appendix
 in the supply equation may be considered as endogenous.
in the supply equation may be considered as endogenous. Publication Dates
-
Publication in this collection
04 Oct 2011 -
Date of issue
Mar 2009















