Abstracts
We investigate the role of financial dollarization and systemic risks in the determination of real interest rates in Brazil. In a simple currency-choice portfolio model, we show that a strategy of reducing dollarization, if it fails to address fundamental macroeconomic risks, leads to higher domestic real interest rates. We confirm this prediction in an empirical panel-based model, involving systemic risk variables, but find that the effect is small after controlling for the risks of dilution and default. We apply our empirical estimates to the case of Brazil - a natural case study given its low degree of financial dollarization and very high real interest rates. The estimated model is unable to explain the high interest rate levels in the aftermath of Brazil's 1994 inflation stabilization. However, since the adoption in 1999 of inflation targeting and floating exchange rates, Brazil's real interest rates are found to be gradually converging to the model's predicted values. The estimation also shows that further reductions in Brazil's real interest rates could be achieved through sound fundamentals that led to investment-grade status rather than financial dollarization.
Financial Dollarization; Interest Rates; Brazil; Emerging Markets; Panel Data
Analisamos o papel da dolarização financeira e do risco sistêmico na determinação da taxa real de juros no Brasil. Em um modelo simples de portfólio, nós mostramos que a estratégia de reduzir a dolarização da economia, se ainda persistirem riscos macroeconômicos, leva a uma maior taxa real de juros doméstica. Nós confirmamos essa assertiva a partir de um modelo em painel, envolvendo variáveis de risco sistêmico; contudo, os efeitos são pequenos quando controlados por riscos de inflação e de default. Em seguida, aplicamos nossas estimações para o caso do Brasil - um caso natural dado seu baixo nível de dolarização financeira e altas taxas reais de juros. O modelo estimado é incapaz de explicar os elevados níveis de taxas de juros no Brasil após a estabilização da inflação, em 1994. Contudo, desde a adoção do regime de metas de inflação e de taxas de câmbio flutuantes, a taxa real de juros no Brasil tem convergido gradualmente para valores previstos pelo modelo empírico. Nossas estimações também mostram que reduções adicionais nas taxas de juros podem ser obtidas com melhorias naqueles fundamentos que levaram o Brasil para o status de grau de investimento muito mais do que por meios de dolarização financeira.
A panel-data analysis of interest rates and dollarization in Brazil* * With more than the usual caveats, we are indebted for suggestions to Persio Arida, William Cline, André Lara-Resende, Eduardo Levy-Yeyati, Marc Nerlove, Veronica Orellano, Felipe Salles, Andrei Spacov, Fernando Veloso, John Williamson, and Thomas Wu. Opinions herein are our own and do not represent those of the institutions to which we are associated.
Edmar L. BachaI; Márcio HollandII; Fernando M. GonçalvesIII
ISenior Fellow at IEPE/Casa das Garças. E-mail: edmarbacha@iepecdg.com
IISão Paulo School of Economics, FGV-EESP and CNPq researcher. Corresponding Author. Phone 55 11 3281 3372. Fax 55 11 3281 3357. E-mail: marcio.holland@fgv.br
IIIEconomist at JGP Asset Management. E-mail: fmg215@gmail.com
ABSTRACT
We investigate the role of financial dollarization and systemic risks in the determination of real interest rates in Brazil. In a simple currency-choice portfolio model, we show that a strategy of reducing dollarization, if it fails to address fundamental macroeconomic risks, leads to higher domestic real interest rates. We confirm this prediction in an empirical panel-based model, involving systemic risk variables, but find that the effect is small after controlling for the risks of dilution and default. We apply our empirical estimates to the case of Brazil - a natural case study given its low degree of financial dollarization and very high real interest rates. The estimated model is unable to explain the high interest rate levels in the aftermath of Brazil's 1994 inflation stabilization. However, since the adoption in 1999 of inflation targeting and floating exchange rates, Brazil's real interest rates are found to be gradually converging to the model's predicted values. The estimation also shows that further reductions in Brazil's real interest rates could be achieved through sound fundamentals that led to investment-grade status rather than financial dollarization.
Keywords: Financial Dollarization, Interest Rates, Brazil, Emerging Markets, Panel Data.
JEL Code: E43, F31, O16, O23, O54.
RESUMO
Analisamos o papel da dolarização financeira e do risco sistêmico na determinação da taxa real de juros no Brasil. Em um modelo simples de portfólio, nós mostramos que a estratégia de reduzir a dolarização da economia, se ainda persistirem riscos macroeconômicos, leva a uma maior taxa real de juros doméstica. Nós confirmamos essa assertiva a partir de um modelo em painel, envolvendo variáveis de risco sistêmico; contudo, os efeitos são pequenos quando controlados por riscos de inflação e de default. Em seguida, aplicamos nossas estimações para o caso do Brasil - um caso natural dado seu baixo nível de dolarização financeira e altas taxas reais de juros. O modelo estimado é incapaz de explicar os elevados níveis de taxas de juros no Brasil após a estabilização da inflação, em 1994. Contudo, desde a adoção do regime de metas de inflação e de taxas de câmbio flutuantes, a taxa real de juros no Brasil tem convergido gradualmente para valores previstos pelo modelo empírico. Nossas estimações também mostram que reduções adicionais nas taxas de juros podem ser obtidas com melhorias naqueles fundamentos que levaram o Brasil para o status de grau de investimento muito mais do que por meios de dolarização financeira.
1. INTRODUCTION
The persistently high level of real interest rates in Brazil has provoked much debate in the last two decades; yet, empirical-based analyses have been sparse. Recent interpretations that have received considerable attention stress the weakness of institutions. A conjecture about the relationship between the high level of real interest rates and the quality of institutions, proxied by jurisdictional uncertainty and currency inconvertibility, is developed in Arida et al. (2005). However, the results presented in Gonçalves et al. (2007), using panel data analysis, were by and large unfavorable to the hypotheses posed in that paper.
This paper empirically reconsiders the debate, stressing the role of systemic risk and dollarization on the determination of real interest rates in emerging market economies. More specifically, we expand the scope of the financial dollarization literature (particularly, Ize and Levy-Yeyati (2003); De La Torre and Schmukler (2004); and Levy-Yeyati (2006))1 1 See also Armas et al. (2006); Barajas and Morales (2003); De Nicoló et al. (2003); Galindo and Leiderman (2005); IADB (2005); Rennhack and Nozaki (2006); and Reinhart et al. (2003). We use indifferently the terms 'dollarization', 'financial dollarization', and 'deposit dollarization' to express the same empirical concept, namely, the ratio of foreign currency deposits to total banking deposits in a given country. Our use of the term 'dollarization' should not be associated with the earlier literature on currency substitution, as it in fact refers to the phenomenon of asset substitution. to analyze the effects of systemic risks and deposit dollarization on the real interest rate in emerging markets in general and Brazil in particular.
We follow De La Torre and Schmukler (2004) in emphasizing systemic risks as the main culprit for currency mismatches. However, these authors explicitly assume that investors are not compensated through the return on a home-currency financial contract for risks that are diversifiable by the use of foreign-currency contracts. In contrast, we also consider the potential role played by interest rate differentials as a way of compensating investors holding domestic-currency-denominated assets for systemic risks present in emerging economies.
For this endeavor, we first develop a simplified portfolio-choice model between local-currency and dollar-denominated assets, and in the following make use of the most recent cross-country multi-year data sets developed by international agencies and other researchers to develop our point empirically. Our panel-based results, obtained by use of instrumental-variable and panel-data econometric techniques, confirm the presumption that systemic risks such as price-dilution and debt-default risks increase the real interest rate. They also verify the existence of a trade-off between real interest rates and deposit dollarization - for given systemic risks, an increase in the relative supply of local dollar assets reduces the real returns that investors require on home currency assets.
Our main objective, however, is to apply this model to throw some light on the factors behind the mystery of very high real interest rates in Brazil.2 2 Besides Arida et al. (2005) and Gonçalves et al. (2007); see Barcelos-Neto and Portugal (2006); Fraga (2005); Miranda and Muinhos (2003); Muinhos and Nakane (2006); and Salles (2007). In particular, we want to determine the joint influence of systemic risks and restrictions to dollarization in the explanation of Brazil's continually high real interest rates even after the adoption of floating exchange rates and inflation targeting in early 1999.
The paper is organized as follows. The following section outlines a simple analytical model that demonstrates how macroeconomic risks and the degree of dollarization can affect the level of real local-currency interest rates. Section 3 presents and discusses the econometric results. Section 4 analyzes the Brazilian case. Section 5 concludes. Details on data sources, description of our panel-based data, empirical methods of estimation, and procedures are in Appendixes IAppendixes I and II.
2. ANALYTICAL MODEL
This section illustrates in a very simple model the price-quantity trade-offs involved in the choice between dollar and local-currency (peso) denominated assets. Suppose that a representative domestic agent can choose from two types of securities: peso assets, which yield a nominal interest rate of iP in pesos; and dollar assets, which pay a return of iD in dollars. Dollar inflation is assumed to be zero and the interest rate iD to be exogenous. The domestic agent values wealth in terms of peso's purchasing power, meaning that he converts any financial resources generated abroad or at home into its real value in pesos to infer the implied utility. Let W0 be the domestic agent's initial wealth in real pesos. One period later, his wealth will be given by
where π is the inflation rate and q is the rate of real exchange rate depreciation between periods 0 and 1; and θP and θD are, respectively, the shares of peso and dollar assets in domestic agent's portfolio (where, of course, θP + θD = 1).
We assume that the inflation rate and the real exchange rate depreciation rate are normally distributed random variables. Furthermore, the representative domestic agent has a utility function with constant absolute risk aversion, U(W)= - exp {-γ W }, where γ > 0 is the coefficient of absolute risk aversion. The domestic agent's problem is to choose a portfolio (i.e., the value of the share θP or, equivalently, of the share θD) to maximize utility given the constraint (1). If wealth W1 is normally distributed (which is the case given our assumptions about π and q), maximizing the expected value of U(W1)= - exp {-γW1} is equivalent to maximizing E(W1) -  V ar(W1), where E(.) and V ar(.) are the expectation and variance operators given the information available as of period 0. Using the fact that θP + θD =1, this maximization problem yields the following expression:
V ar(W1), where E(.) and V ar(.) are the expectation and variance operators given the information available as of period 0. Using the fact that θP + θD =1, this maximization problem yields the following expression:
To relate the issues addressed in this paper to the "minimum portfolio variance" explanation of financial dollarization, we rearrange equation (2), placing V ar(π)+ V ar(q)+2Cov(π,q) in evidence, which yields:
Ize and Levy-Yeyati (2003) demonstrate that the "minimum variance portfolio" share of dollar deposits (which we will denominate as MVP) is given by:
Moreover, given the assumption that foreign inflation is zero,
where V ar(e) is the variance of the nominal exchange rate.
Introducing (4) and (5) in (3), we obtain the following simplified relation:
Equation (6) shows that uncovered interest parity does not hold in our model provided that actual dollarization (θD) differs from the minimum variance portfolio dollarization (MV P). Instead, there is a risk premium between the ex ante real returns of peso (iP - E(π)) and dollar (iD + E(q)) assets, which is positively related to the minimum variance portfolio dollarization (MV P) and negatively related to actual dollarization (θD). Therefore, the less dollarized the economy is (vis-à-vis "optimum" dollarization given by MV P), the higher will be the equilibrium real peso interest rate (vis-à-vis the interest parity rate).
Equation (6) represents a demand for assets. Ize and Levy-Yeyati (2003) close their model by postulating a supply side that is the mirror image of the demand side for assets. Instead, we treat the currency composition of asset supply as a predetermined variable, cognizant of local governments' importance in its determination, through both rules and regulations and public debt composition. Thus, we leave the supply side unspecified, and merely try to determine how the real peso interest rate required by depositors is affected when the available shares of peso and dollar assets change.
The main message of our simple model can be summarized as follows: if there is no alteration in underlying macroeconomic risks (as captured in the model by the variances of inflation and exchange rate), any change in the composition of assets (quantities) will have effects on real interest rates (prices). In particular, a strategy of forcing a reduction of the dollarization, if it fails to properly address the fundamental macroeconomic risks of the economy, may only transform one problem (vulnerability to exchange rate shifts) into another (high local-currency real interest rates).
Our simple portfolio-choice model includes only locally available dollar and peso deposits, and risks that relate to yield volatility and not to default probability. However, in emerging markets, sovereign default risks are present and these, as illustrated by the 2001 Argentine's currency collapse, can affect both dollar and peso deposits. In this context, an appropriate modeling of systemic risks facing depositors in emerging countries should include the probability of sovereign default, protection against which would require, inter allia, higher real returns on local deposits, irrespectively of these being in dollars or pesos. For this reason, this section's model should only be used as a departing point for an empirical analysis on the determination of real domestic interest rates in emerging market economies. In the following section, we also contemplate indicators of sovereign-default risk as well as other policy-related variables, as suggested by the dollarization literature and by the debate on Brazil's high real interest rates.
3. EMPIRICAL FINDINGS
This estimation is also reported in Bacha et al. (2007). We use equation (6) as a departure point for the analysis of the determination of the real domestic interest rate in Brazil. Besides deposit dollarization, the interest rate is assumed to be a function of risk-and policy-related variables that are suggested in the financial dollarization literature and in the debate on interest rates in Brazil.
The data-set3 3 See the Appendix I for sources and construction details of each variable and also Appendix II for the estimation methods. spans the 1996-2004 period across 66 countries4 4 The countries in the sample are as follows: (1) Speculative grade: Argentina, Bolivia, Brazil, Bulgaria, Colombia, El Salvador, Grenada, Guatemala, India, Indonesia, Morocco, Mozambique, Pakistan, Paraguay, Philippines, Romania, Russia, Sri Lanka, Turkey, Ukraine, Uruguay, Venezuela; and (2) Investment grade: Australia, Austria, Bahrain, Belgium, Canada, Chile, China, Hong Kong, Croatia, Cyprus, Denmark, Estonia, Finland, France, Germany, Greece, Hungary, Iceland, Ireland, Israel, Italy, Japan, Korea, Kuwait, Latvia, Lithuania, Malaysia, Mexico, Netherlands, New Zealand, Norway, Poland, Portugal, Singapore, Slovak Republic, Slovenia, South Africa, Spain, Sweden, Switzerland, Thailand, Tunisia, United Kingdom, United States. from different parts of the world, including emerging market and OECD economies, and therefore we have relatively few time-series observations in an unbalanced panel.5 5 Table 1 presents basic statistics for the variables in the model, indicating their mean, median, maximum and minimum values, and standard deviations.
We proceed in two steps.6 6 We are indebted to Fernando Velloso for suggesting this two-step procedure. In step I we use policy-environment variables to generate an instrument for the deposit dollarization ratio, which subsequently enters the equation determining the real interest rate together with the systemic risk regressors (step II). The two-step procedure is necessary because the real interest rate and the dollarization ratio are jointly determined variables in a supply-and-demand model for local currency and dollar assets, of which equation (6) is merely a simple expression of the demand side. Thus, the dollarization ratio is positively correlated to the error term of the interest rate equation, and, if not properly instrumented, its coefficient will be biased toward a positive value. The correction of this bias requires an appropriate choice of instruments for the dollarization ratio - i.e., exogenous variables that are simultaneously not correlated with the error term of the interest rate equation and strongly correlated with the dollarization ratio. Fortunately, these instruments are at hand in our regressor set, as the three policy-environment variables - restrictions to dollarization, degree of capital account liberalization, and rule-of-law index - seem to fit these requirements. Previous research (Levy-Yeyati (2006), for example) showed the fundamental importance of the restrictions-todollarization variable in the determination of actual dollarization, and our own initial estimates (not reported) indicated that dollarization restrictions do not belong to the interest rate equation. The results in Table 2 indicate the relevance of capital account controls and rule of law for the degree of dollarization. Furthermore, previous research (Gonçalves et al. (2007); and Salles (2007)) found that capital controls and rule of law do not belong to the real interest rate equation.
Statistical results are reported in Tables 2 and 3. Consider initially the results of the instrumental regression for the dollarization ratio in Table 2. All coefficients are significant at 5 percent and the coefficient of determination (R2) is equal to 0.33 for the complete model (column 3 of Table 2). Local restrictions to dollar holdings have by far the strongest impact on dollarization: as they go from a minimum of zero to a maximum of 5, dollarization declines by 36.25 percentage points, a figure similar in magnitude, but opposite in sign, to the equation's constant term (which means that, abstracting from other effects, as restrictions reach a maximum, dollarization is practically equal to zero). Jurisdictional uncertainty as captured by the complement to the World Bank 0-to-100 rule-of-law index is also relevant: as it rises from zero to 100, dollarization increases by 25 percentage points. In addition, the 0-to-100 capital liberalization index has a significant impact: as capital controls are reduced from a maximum of 100 to a minimum of zero, the dollarization ratio declines by 9.5 percentage points.7 7 As in equation (7) in Appendix II we also included a vector of covariates used in the second stage of the two stage estimation. Their coefficients are not reported here for convenience. They are available upon to request.
The instrumented dollarization ratio has a significant negative impact on the real interest rate, as indicated in regression 5 of Table 3, which includes all variables specified in equation (8) in Appendix II. The coefficient of D* is -0.011, which means that, as dollarization rises from zero to 100, the interest rate declines by 1.1 percentage points on impact, and by 2.3 percentage points in the long run (this last figure is obtained by dividing 100 times the impact coefficient by 1 minus .510, where the latter value is the coefficient of the one-year lagged interest rate). Interestingly enough, when we substitute actual for instrumented dollarization in the regression (not shown), the coefficient of this variable becomes positive (although not significant). This is not surprising given that the supply of dollar assets, which is not our focus, would induce a positive correlation between the peso interest rate and actual dollarization. The policy-environment variables used as instruments are able to reverse the "wrong" positive sign of the dollarization ratio coefficient. Thus, by using the instrumental procedure, we managed to overcome the simultaneous equation problem and correctly estimate a negative coefficient for the dollarization ratio, as anticipated in the analytical model.
We tested whether our policy-environment variables - restrictions to dollarization, rule of law, and capital account liberalization - had some direct explanatory power on the real interest rate and the results were negative. This confirms and expands a result by Gonçalves et al. (2007) that - contrary to a presumption in Arida et al. (2005) - also found that jurisdictional uncertainty (measured by rule of law as here) and capital account controls (measured by a different index from ours) were not significant explanatory variables for the real interest rate.
Consider now the effect of price-dilution risk variables on the interest rate. Firstly, the real interest rate is positively associated to MVP, defined in equation (4) of the previous section. As the latter increases from 0 to 1, the real interest rate increases by 0.3 percentage points on impact and by 0.6 percentage points in the long run. The coefficient of the inflation-acceleration variable (delta-inflation) indicates that as yearly inflation increases by, say, 10 percentage points (approximately one standard deviation of this variable in our sample), the real interest rate increases by 0.1 percentage points on impact and by 0.2 percentage points in the long run. The median real interest rate in our sample is 3.1 percent (Table 1), hence these price-dilution effects do not seem very large.
Our proxies for sovereign-default risk work very well, indicating that they probably capture different aspects of such risk. We consider particularly significant the results obtained for IGRADE - i.e., the dummy variable indicating whether a country is investment grade or not according to Standard & Poor's. Investment grade status reduces the real interest rate by a full 2 percentage points on impact and by 4 percentage points in the long run. Per capita income (measured in units of 1,000 dollars) has also a very strong impact - an increase in per capita income of $1,000 reduces the real interest rate by 0.8 percentage points on impact and by 1.6 percentage points in the long run.8 8 This effect could be highly nonlinear, fading away for the largest per-capita income figures, but we were not able to capture this nonlinearity either by using the inverse of per capita income or its squared value. ,9 9 In preliminary estimations we also included public-debt ratio to GDP as a regressor and found disappointingly small estimated coefficients. This might be a consequence of the fact that domestic debt is not properly accounted for (which is important in many countries - e.g. Brazil, where it represents more than 80 percent of all debt). It may also be the case that debt-to-GDP ratios do not capture important fiscal characteristics of each country, such as the degree of flexibility of revenue, expenditure pressures, and contingent liabilities. While fiscal positions are likely important determinants of interest rates, we believe their effects are better summarized by our sovereign default rating dummy, as described in Beers and Cavanaugh (2006). Therefore, we do not include the debt-to-GDP ratio directly in our regressions.
In summary, we have shown that, appropriately instrumented, financial dollarization has a significant negative impact on the real interest rate, but the magnitude of the impact is economically small. We found the real interest rate variable to be significantly autoregressive, indicating the importance of using a dynamic model. We also established the negative effect on the real interest rate of price-dilution risks measured by inflation volatility and inflation acceleration. Investment-grade status and per-capita income were shown to have large negative effects on the real interest rate. We did not find any direct effects on the real interest rate of rule of law, capital controls, and dollarization restrictions. But these variables were shown to have a significant role to play as instruments for the dollarization ratio that enters the real interest rate equation.
4. THE MISTERY OF HIGH INTEREST RATES IN BRAZIL
Brazil offers an interesting case study for our findings. A "serial defaulter" in the terminology of Reinhart and Rogoff (2004b), and second country in their list in terms of the magnitude of currency depreciation in the 1970-2001 period (Reinhart and Rogoff, 2004a), it nonetheless managed to avoid financial dollarization and developed a large and sophisticated financial market based entirely on its own domestic currency. Short-duration is pervasive, but what most calls attention is the country's very high real interest rate. It may be the case that these are interrelated phenomena: for a given degree of systemic risks, high real interest rates would be the price to pay to escape dollarization.
As shown in Figure 1, Brazil is "underdollarized" when compared to its peers. The picture depicts deposit dollarization ratios, both domestic and off-shore, for Latin American countries in 2001. With a 10 percent ratio of (fully off-shore) dollar deposits to total onshore and off-shore bank deposits, Brazil is by far the country with the lowest dollarization ratio in the region. Furthermore, the level of Brazil's real interest rates is very high in comparison to other countries. This is shown in Figure 2, in which Brazil's real interest rates over time are compared to the mean of the overall and the sub-investment grade countries, and to the sums of such means with one standard deviation. From 1996 to 1999, Brazil's rates are higher than the means-plus-one-standard-deviation limits. Since then, they have hovered around this level (except for the electoral transition years of 2002 and 2003), meaning they have been always much higher than the sample means.
However, stating that interest rates in Brazil are higher than average by comparing them to a simple cross-country average is not very informative. Macroeconomic fundamentals and risks may explain much of the differences in interest rate levels across countries, implying that a more informative comparison is that between Brazil's interest rate and an average rate conditional on those fundamentals and risks, which can be obtained directly from the fitted values for Brazil of our estimated panel regression equation.10 10 As in any regression, the fitted value is the expected value of the dependent variable r conditional on the set of independent variables X. Therefore, we use our estimated model to compare r to E( r| X) instead of comparing r to E(r).
The model seems suitable to capture many of Brazil's experience: past high inflation volatility, sub-investment grade status, and lack of dollarization. Furthermore, Brazil's capital controls and jurisdiction quality (as captured by World Bank's rule-of-law index) are also present in our analysis. How far then are we able to unveil the mystery of Brazil's high interest rates with our model?
To answer this question, we constructed Table 4 on Brazil's interest and inflation rates.11 11 Expected inflation is the median expectation for consumer price inflation of year t at December of year t - 1, taken from the Central Bank monthly survey of market expectations (Central Bank of Brazil, 2008), available from January 2000. Real interest rate forecasts are based on regression (5) of Table 3. Note that we used this regression, which was estimated for the 1996-2004 period, to forecast 2005 and 2006 as well. The column items are self-explanatory, except for the central bank's "implied real interest rate", defined as the minimum between actual and expected real interest rate, where the latter is obtained from the deflation of the nominal interest rate by expected inflation. The usefulness of this concept is described below.
Figure 3 summarizes the evolution of actual, predicted, and implied real interest rates. Consider first predicted real interest rates in the 1996-2004 period. Except for two extreme values in the neighborhood of 10 percent during Brazil's 1998-1999 balance of payment crisis, these rates are surprisingly stable, remaining within the interval of 5.5 percent to 7.5 percent. The overall (geometric) average is 7.2 percent but, excluding the crisis years of 1998 and 1999, the average is 6.7 percent. In the 2000-2004 period, when the exchange rate was floating and inflation targeting was in place, the geometric average of predicted real interest rates is 6.6 percent.
Comparing predicted to actual real interest rates shows clearly that our empirical model is unable to replicate the extremely high real interest rates in 1996-1999. In this period actual real interest rates were on average twice as high as predicted real interest rates. In the aftermath of the sharp 1994 inflation stabilization, an overvalued exchange rate peg prevailed, while international financial crises were frequent. In 1996-98, interest rates were maintained at high levels, in an attempt at simultaneously keeping inflation under control and counteracting successive foreign capital sudden stops. In 1999, after the exchange rate peg collapsed in January, monetary policy was held tight to prevent an inflation surge. The empirical model fails to capture all the idiosyncrasies of this early inflation-stabilization period.12 12 On Brazil's 1994 stabilization program, see Bacha (2003); on the country's subsequent crises and economic policy making, see Giavazzi et al. (2005).
The model's predictions are closer to actual interest rate levels for the 2000-2006 period, during which an inflation-targeting framework was in force and the exchange rate was allowed to float. But even then, with the exception of the electoral year of 2002, actual real interest rates are higher than predicted real interest rates. More specifically, in 2000-2004 the geometric average of actual real interest rates is 9.3 percent which compares with a predicted real interest rate of 6.6 percent in the same period.
Is it possible to say that there is a trend toward the convergence of actual to predicted real interest rates in Brazil? To answer this question we use regression 5 in Table 3 to forecast real interest rates for 2005 and 2006, as shown in the last two lines in column 7 of Table 4, and the answer is that we cannot, as the ratios of actual to forecast real interest rates in this latter period are even higher than in 2000-2004. An important caveat is however in order, and here we use the concept of central bank's implied real interest rates. The central bank board members most directly responsible for monetary policy in 2003-2006 have argued in Bevilaqua et al. (2007) that a fundamental challenge for monetary policy in this period was to establish central bank's inflation fighting reputation in a context of adverse expectations and above-the-target inflation rates. Indeed, inflation expectations were always higher than actual inflation in the 2003-2006 period, as shown in Table 4 (which also displays the 2003 inflation surge that was subsequently contained despite adverse inflationary expectations).
In order to take into account the central bank's reaction to adverse expectations and obtain a better measure of central bank's implied real interest rate, we conceive the following scheme:
This essentially says that if the central bank observes an expected inflation rate higher than the actual rate then, in order to bring inflationary expectations down, it fixes the nominal interest rate according to expected inflation (this occurred in 2000 and 2003-2006). If however it anticipates that inflation will be higher than market expectations, it fixes the nominal interest rate according to actual inflation (this occurred in 2001 and 2002, as seen in Table 4). Inverting the terms of the above equation, we constructed a series for implied real interest rates simply by dividing the nominal interest rate by the higher of actual and expected inflation. The conclusion is that Brazil's high real interest rate mystery diminishes but is still there, except for 2002 (see Figure 3). Furthermore, we do not observe a trend for this difference to subside through time.
Nonetheless, observe in Figure 3 that the remaining discrepancy between actual and predicted real interest rates is due to two jumps in implied real interest rate, in 2003 and 2005. The former was the initial year of Lula's presidency, and it would be natural that central bank's recently-appointed board would wish to leave no doubt in market-participants' minds of their commitment to fight an inflation rate that reached 12 percent in the previous year - hence a high implied real interest rate for 2003 is explainable. Observers have argued that in 2005 the central bank may have overreacted to a temporary surge in inflation in mid-2004, as suggested by the below-the-target inflation rate in 2006.13 13 Target for inflation was 4.5% ± 2%, while actual inflation was 3.1%. 14 More specifically, suppose that the extrapolation of inflation by investors imply that expected inflation is a weighted average of current and future inflation rates: , where α is the weight. Thus the real interest rate is , where NIR is the nominal interest rate. We approximate the real interest rate by subtracting the current inflation rate from nominal interest rate and estimate α by including the term ( π t+1 - π t) as a dependent variable. 15 S&P's specific country-ratings converted into a numerical sequence were also tested with poorer results, which we do not report. 16 Other World Bank institutional quality indicators were tested, with poorer results. 17 See Alonso-Borrego and Arellano (1999); and Blundell and Bond (1998). 18 Several types of panel unit root tests were run, but they are not reported here for convenience. In general, they strongly fail to accept the null hypothesis of presence of unit roots. They are available upon request. 19 We use the two-step version of the GMM system estimator to obtain the Sargan test statistics, as the one-step version of the Sargan test over-rejects the validity of the set of instruments in presence of heteroskedasticity. However, it is well known that the Sargan test may have low power in finite samples. To have some indication of the power of the test, we estimated the real interest rate equations with its endogenous lagged one year value as an additional (but invalid) instrument in the transformed equations. This test overwhelmingly rejects the null hypothesis of instrument validity. 20 Arellano and Bond's (1991) test of serial correlation suggests that the error terms are white noise. However, from late-2005 the central bank has started an easing cycle that is still on course.
Data for 2007 and expectations for 2008 and 2009 indicate that real interest rates are finally converging to levels that are compatible with our empirical model. Thus, CPI inflation was 4.4 percent in 2007, while the average Selic rate was 11.9 - this results in a real interest rate of 7.2 percent. Market participants in the February 8, 2008 Central Bank survey (Central Bank of Brazil, 2008) anticipate an accumulated overnight rate of 11.25 percent for 2008. They also expect an inflation rate of 4.45 percent for this year, thus implying a real interest rate of 6.5 percent. For 2009, market-participants expect an accumulated overnight rate of 10.25 percent and inflation of 4.2 percent, implying an expected real interest rate of 5.8 percent. This implies that Brazil is finally converging toward a real interest rate that, according to our empirical model, is compatible with a small set of variables that capture its fundamentals and policy idiosyncrasies - it is still high, but there is no longer a mystery about it.
5. CONCLUSIONS
One purpose of this paper was to expand the scope of the financial dollarization literature to analyze the systemic risk determinants of the real interest rate in Brazil. We were particularly interested in investigating the negative relation between deposit dollarization and local-currency real interest rates for a given set of fundamentals, as anticipated in our simple analytical model. Our findings, obtained with a panel of 66 countries in the 1996-2004 period, indicated that, appropriately instrumented, deposit dollarization has a negative impact on the real interest rate, but the magnitude of this effect is small.
We used a dynamic specification to account for the fact that real interest rate changes are typically smooth (thus, it is in general a strongly autoregressive variable). We also established the negative effects on the real interest rate of price-dilution risks measured by inflation volatility and inflation acceleration. Investment-grade status was shown to have large negative effects on the real interest rate: obtaining an investment grade rating would reduce the real interest rate by 2 percentage points on impact and by a 4 percentage points in the long run. We did not find any direct effects on the real interest rate of rule of law, capital controls, and dollarization restrictions. These policy-environment variables were however shown to have a critical role to play as instruments for the dollarization ratio entering the determination of real interest rates.
Brazil is an interesting case study for our findings, because despite past high systemic risks it managed to avoid financial dollarization and developed a large local-currency-based financial market. Short-duration is pervasive, but what most calls attention are the country's very high real interest rates. We investigated whether these phenomena were interrelated: for given systemic risks, high real interest rates are the price to pay to avoid dollarization. However, fitted values of our model proved to be largely off mark for Brazil, particularly in the 1996-98 period, when an exchange rate peg prevailed and monetary policy was mostly driven by adverse balance of payments considerations.
Even in the period 2000-2006, during which a regular inflation-targeting framework was in force and the exchange rate was allowed to float, we found actual real interest rates to be higher than predicted (2002 excepted). Allowing for the fact that in 2003-2006 the central bank under Lula wished to establish its reputation as an inflation hawk, we devised an exercise incorporating adverse expectations and central bank prudence in our estimates, thus being able to reduce Brazil's high real interest rate mystery to less than we initially estimated. Although we did not discern a clear trend for the remaining disparity to diminish after 1999, we noted that this lack of convergence was due to two specific years, 2003 and 2005. Making use of data for 2007 and of market-based expectations for 2008 and 2009, we observed that Brazil's real interest rates are indeed in the process of converging to our model's estimated real interest rates for the country, which range from 5.5 to 7.5 percent.
In conclusion, to bring real interest rates further down, the model indicates that Brazil should implement policies aimed at furthering investment grade status, and not allow deposit dollarization. From our estimations we conclude that the quantitative real interest rate gains of the policy of allowing Brazilians to hold dollar deposits domestically (0.011 percentage points on impact and 0.023 percentage points in the long run for a 1 percentage point increase in deposit dollarization) would not seem to justify the costs associated to this move. In fact, the dollarization literature (Armas et al. (2006), for example) provides many reasons associated to financial stability on why de-dollarization of the type achieved by Brazil is an object of desire for many emerging market countries. What our model shows is that much better for Brazil would be, for example, moving towards a strong fiscal consolidation as a means of speeding up its access to investment-grade status and thus being able to achieve real interest rate reductions of 2 percentage points or more according to our estimates.
A weak spot in our analysis is that our sample is short in the time dimension and includes a limited number of emerging markets. Future research with an expanded sample should thus endeavor to uncover dynamic relations not contemplated by our results. Furthermore, in our model we only considered two of the possible financial consequences of systemic risk, i.e., domestic financial dollarization and high real local-currency interest rates. Future research could attempt to incorporate financial shallowness, offshore dollarization, short-termism and indexation, as alternative systemic-risk-coping mechanisms in emerging economies.
BIBLIOGRAPHY
DATA SOURCES AND DESCRIPTIONS
Real Interest Rate (RIR) - Ratio of one plus the average of the annualized end-of-month money-market interest rate in IFS (line 60B, ZF) to one plus the average of the annualized monthly consumer price index variation (IFS, line CPI), minus one, in percentage terms.
Dollarization Ratio (DOLLAR) - Ratio of Dollar (or Euro) deposits over total bank deposits. Source is Levy-Yeyati (2006). Original sources: IMF Staff Reports, Central Bank bulletins, Bolino et al. (1999), De Nicoló et al. (2003), and Arteta (2003).
Delta-inflation (Δπ) - Difference between this year's and last year's inflation, both calculated as the average of the annualized monthly consumer price index variation (IFS, line CPI), in percentage terms.
Investment Grade (IGRADE) - Equal to 1 for a sovereign investment-grade rating and zero for a speculative-grade rating. This variable was maintained constant for each country on the basis of its status in 2004. Source: Standard & Poor's.
Jurisdictional Uncertainty (JU) - Equal to 100 minus the World Bank rule-of-law index ranging from 0 to 100. As we had values for this variable only for even years, odd-years values were interpolated. Source: World Bank, Governance Indicators.
Capital Account Liberalization Index (CAPLIB) - Index described in Edwards' (2005), gently provided to us by the author. It is a scale from zero to 100 in which higher values indicate increasing degrees of capital account liberalization.
Per Capita GDP (Y) - In constant 2000 US$. Source: World Bank, World Development Indicators (on line).
Restrictions (R) - Index of restrictions on holdings of foreign currency deposits by residents, ranging from zero (no restrictions) to 5 (maximum restrictions). Source: Levy-Yeyati (2006). Original sources: IMF's Annual Report on Exchange Arrangements and Exchange Restrictions (EAER), revised and expanded by Levy-Yeyati from De Nicoló et al. (2003) using the same methodology.
Minimum Variance Portfolio (MVP) - This is derived from a portfolio choice model, in which risk-averse local investors opt between a local-currency-denominated and a dollar-denominated asset. As shown in Ize and Levy-Yeyati (2003), if the uncovered interest-parity condition holds, the dollar share of the optimal investment portfolio, which replicates the minimum variance portfolio, is equal to:
where π is the inflation rate in local currency and q is the real exchange rate. To estimate a country's MVP for a given year, we used monthly data on inflation (CPI) and exchange rate changes for that country in that year. Source: IMF's International Financial Statistics.
7. APPENDIX II
REGRESSORS AND ESTIMATORS METHODS
The regressors we considered can be grouped into three types:
(i) price-dilution risks, captured by the minimum variance portfolio variable (MVP) discussed in the text, and by a delta-inflation variable (this year's inflation minus last years' inflation). The latter captures a possible inadequacy of our measured real local-currency interest rate, which subtracts on-going inflation from the nominal interest rate. Suppose investors are concerned with next-period wealth and extrapolate current inflation trends. Then, when inflation accelerates, as a protection mechanism investors would demand a higher real rate and a higher dollar deposit share;
(ii) sovereign default risks, captured by a dummy variable indicating whether the country is investment grade or not according to Standard & Poor's;(iii) policy-environment variables, captured by a 0-to-5 scale measuring the degree of legal restrictions on onshore dollar deposits; by a 0-to-100 index of capital account liberalization constructed by Edwards (2005); and by the complement of the World Bank 0-to-100 "rule-of-law" index
Further to these variables, preliminary analysis of the data indicated that the real local-currency interest rate was a strongly autoregressive variable, thus, its lag was included as a further regressor in the equation.
Thus, in a first step we generate an instrument for deposit dollarization, which is the fitted value of the auxiliary regression:
where
t indexes years and i indexes countries;
dollar is the share of bank deposits in dollars;
R is the index of restrictions on holdings of foreign currency deposits by residents (computed by De Nicoló et al. (2003), and also used by Levy-Yeyati (2006));
JU or jurisdictional uncertainty, is the complement to the World Bank rule-of-law 0-to-100 index;
CAPLIB is the 0-to-100 capital account liberalization index constructed by Edwards (2005);
Xit is a vector of covariates used in the second stage of the two stage estimation; and
η is the error term.
This equation was estimated according to a random effect model to generate the instrumental variable for the dollarization ratio (D*) subsequently used in the second-step regression for the interest rate equation.
The general equation for the second-step estimation of the real interest rate (r) is as follows:
where
γtand ωi are respectively the time and country specific effects;
D* is the instrument for the dollarization ratio;
MV P is the minimum variance portfolio;
Δπ is the change in CPI inflation rate;
IGRADE is sovereign risk measured by the Standard & Poor's ratings as captured by a dummy variable for the investment grade category;
y is per capita income; and
ε is the error term.
Further details on each of these variables are provided in the Appendix.
In the case of dynamic panel data models, the ordinary least square estimator is known to be biased and inconsistent. In dynamic panel data models where the autoregressive parameter is moderately large and the number of time series observations is moderately small, exactly as in our dataset, Blundell and Bond (1998) find the widely used linear Generalized Method of Moments (GMM) estimator obtained from the first differences of the sample variables to have large finite sample biases and poor precision in simulation studies. Lagged levels of the series provide weak instruments for first differences in this case.
Thus, to estimate the real interest rate equation with its one-year lagged value as one of the regressors, we adopted a two-step GMM system estimation (level and difference combined, GMM-SYS) proposed by Blundell and Bond (1998), based on Arellano and Bond (1991) and Arellano and Bover (1995). In this procedure, the one-lagged real interest rate is treated as an endogenous variable and the two-lagged real interest rate is an additional instrument.
- Alonso-Borrego, C. & Arellano, M. (1999). Symmetrically normalized instrumental variable estimation using panel data. Journal of Business and Economic Statistics, 17:36-49.
- Arellano, M. & Bond, S. R. (1991). Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations. Review of Economic Studies, 58:277-97.
- Arellano, M. & Bover, S. R. (1995). Another look at the instrumental-variable estimation of errocomponents models. Journal of Econometrics, 68:29-52.
- Arida, P., Bacha, E., & Lara-Resende, A. (2005). Credit, interest and jurisdictional uncertainty: Conjectures on the case of Brazil. In Giavazzi, F., Goldfajn, I., & Herrera, S., editors, Inflation Targeting, Debt and the Brazilian Experience, 1999 to 2003, pages 265-93. MIT Press.
- Armas, A., Ize, A., & Levy-Yeyati, E. (2006). Financial Dollarization: The Policy Agenda Palgrave Macmillan, New York.
- Arteta, C. O. (2003). Are financially dollarized countries more prone to costly crises? International Finance Discussion Papers 763, Board of Governors of the Federal Reserve System.
- Bacha, E. L. (2003). Brazil's Plano Real: A view from the inside. In Dutt, A. K. & Ros, J., editors, Development Economics and Structuralist Macroeconomics: Essays in Honor of Lance Taylor Edward Elgar, Cheltenham.
- Bacha, E. L., Holland, M., & Gonçalves, F. (2007). Is Brazil different? Risk, dollarization and interest rate in emerging market. IMF Working Paper 07/294.
- Barajas, A. & Morales, R. (2003). Dollarization of liabilities: Beyond the usual suspects. IMF Working Paper 03/11.
- Barcelos-Neto, P. & Portugal, M. (2006). The natural rate of interest in Brazil between 1999 and 2005. In Annals of the XXXIV National Economic Meetings, Salvador, BA. ANPEC. Available at www.anpec.org.br/encontro_2006.htm#trabalhos
- Beers, D. & Cavanaugh, M. (2006). Sovereign Credit Ratings: A Primer. Standard & Poor's Ratings Direct McGraw Hill, New York.
- Bevilaqua, A., Mesquista, M., & Minella, A. (2007). Brazil: Taming inflationary expectations. Central Bank of Brazil, Discussion Paper 129. Brasília.
- Blundell, R. & Bond, S. (1998). Initial conditions and moment restrictions in dynamic panel data models. Journal of Econometrics, 87:115-43.
- Bolino, T., Bennett, A., & Borensztein, E. (1999). Monetary policy in dollarized economies. IMF Occasional Paper 171. Washington, DC.
- Central Bank of Brazil (2008). Central Bank survey.
- De La Torre, A. & Schmukler, S. (2004). Coping with risks through mismatches: Domestic and international financial contracts for emerging economies. International Finance, 7(3):349-390.
- De Nicoló, G., Honohan, P., & Ize, A. (2003). Dollarization of the banking system: Good or bad? IMF Working Paper WP 03/146.
- Edwards, S. (2005). Capital controls, sudden stops and current account reversals. NBER Working Paper 11170. Cambridge, MA.
- Fraga, A. (2005). Comments. In Giavazzi, F., Herrera, S., & Goldfajn, I., editors, Inflation Targeting, Debt and the Brazilian Experience, 1999 to 2003 MIT Press.
- Galindo, A. & Leiderman, L. (2005). Living with dollarization and the route to dedollarization. IADB Research Department, Working Paper 526.
- Giavazzi, F., Herrera, S., & Goldfajn, I. (2005). Inflation Targeting, Debt and the Brazilian Experience, 1999 to 2003 MIT Press.
- Gonçalves, F. M., Holland, M., & Spacov, A. D. (2007). Can jurisdictional uncertainty and capital controls explain the high level of real interest rates in Brazil? Evidence from panel data. Revista Brasileira de Economia, 61(1):49-75.
- IADB (2005). Financial dollarization. Ch. 4 of Unlocking Credit: The Quest for Deep and Stable Bank Lending, Elsevier.
- IMF (2007). International financial statistics online. International Monetary Fund.
- Ize, A. & Levy-Yeyati, E. (2003). Financial dollarization. Journal of International Economics, 59:323-347.
- Levy-Yeyati, E. (2006). Financial dollarization: Evaluating the consequences. Economic Policy, 21(45):61-118.
- Miranda, P. & Muinhos, M. (2003). A taxa de juros de equilíbrio: Uma abordagem múltipla. Banco Central do Brasil, Discussion Paper 66.
- Muinhos, M. & Nakane, M. (2006). Comparing equilibrium real interest rates: Different approaches to measure Brazilian rates. Banco Central do Brasil, Discussion Paper 101.
- Reinhart, C. & Rogoff, K. (2004a). The modern history of exchange rate arrangements: A reinterpretarion. Quarterly Journal of Economics, 119(1):1-48.
- Reinhart, C. & Rogoff, K. (2004b). Serial default and the 'paradox' of rich to poor capital flows. American Economic Review, 94(2):52-8.
- Reinhart, C., Rogoff, K., & Savastano, M. (2003). Addicted to dollars. NBER Working Paper 10015.
- Rennhack, R. & Nozaki, M. (2006). Financial dollarization in Latin America. IMF Working Paper WP/06/07. Washington, DC.
- Salles, F. (2007). Liquidity, Jurisdictional Uncertainty and High Interest Rates in Brazil London School of Economics, London.
- Standard & Poor's (2005). Standard & Poor's data set. www.standardpoors.com
- Windmeijer, F. (2005). A finite sample correction for the variance of linear efficient two-step GMM estimators. Journal of Econometrics, 126:667-678.
- World Bank (2007a). Governance indicators. www.worldbank.org
- World Bank (2007b). World development indicators online. www.worldbank.org
Appendixes I
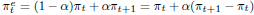 , where
, where 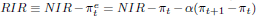 , where
, where Publication Dates
-
Publication in this collection
04 Dec 2009 -
Date of issue
Dec 2009


















