Abstracts
We extended the Cole and Kehoe model (1996) by adding trade and debt denominated in national currency. We then evaluated some external debt defaults and steep national currency devaluations occurred during last decades. Although default is unlikely, steep devaluation has been repeatedly triggered during financial distresses. It helps to overcome financial crisis as it improves trade balance and reduces national debt level. On the other hand, expected devaluation hurts welfare through both higher national debt cost and reductions in the investment level. We modeled such trade-offs and showed that trade openness, by and large, improves the expected welfare as it allows for a better devaluation-response technology. We ran model simulations based on past 48 crises occurred in 32 middle-income countries, reasonably fitting devaluation and default responses observed as from 1971.
Trade-openness; speculative attacks; debt crisis
Com base em uma versão estendida do modelo Cole and Kehoe (1996), avaliamos eventos de default e de desvalorizações cambiais. Historicamente, as desvalorizações têm ajudado na superação de crises financeiras ao estimular a balança comercial e ao reduzir o valor real da divida publica denominada em moeda nacional. Por outro lado, a expectativa de uma possível desvalorização produz efeitos negativos sobre o bem-estar: aumento do custo da divida e redução do nível de investimento privado. Modelamos esses trade-offs e mostramos que a abertura comercial melhora o bem-estar ao potencializar o efeito da desvalorização de câmbio sobre a balança comercial. Computamos simulações numéricas baseadas em 48 crises ocorridas em 32 países, e obtivemos resultados alinhados com as desvalorizações e os defaults observados desde 1971.
Speculative attacks, openness and crises* * We are grateful to Affonso Pastore, Arilton Teixeira, Carlos Hamilton Araujo, Helio Mori, Ilan Goldfajn, Luis Braido, Maria Cristina Terra, Peter B. Kenen, Renato Fragelli, Ricardo Cavalcanti, Roberto Ellery, Rubens Cysne and Timothy Kehoe for their comments. The views expressed here are those of the authors and do not necessarily reflect those of Banco Central do Brasil or its members.
Aloisio AraujoI; Marcia LeonII; Rafael SantosIII
IEscola de Pós-Graduação em Economia (Fundação Getulio Vargas) and Instituto de Matemática Pura e Aplicada. E-mail: aloisio.araujo@fgv.br
IIResearch Department, Banco Central do Brasil. E-mail: marcia.leon@bcb.gov.br
IIICorresponding author. Banco Central do Brasil E-mail: rafael.santos@bcb.gov.br
ABSTRACT
We extended the Cole and Kehoe model (1996) by adding trade and debt denominated in national currency. We then evaluated some external debt defaults and steep national currency devaluations occurred during last decades. Although default is unlikely, steep devaluation has been repeatedly triggered during financial distresses. It helps to overcome financial crisis as it improves trade balance and reduces national debt level. On the other hand, expected devaluation hurts welfare through both higher national debt cost and reductions in the investment level. We modeled such trade-offs and showed that trade openness, by and large, improves the expected welfare as it allows for a better devaluation-response technology. We ran model simulations based on past 48 crises occurred in 32 middle-income countries, reasonably fitting devaluation and default responses observed as from 1971.
Keywords: Trade-openness, speculative attacks, and debt crisis.
JEL Code: F34, F41, H63.
RESUMO
Com base em uma versão estendida do modelo Cole and Kehoe (1996), avaliamos eventos de default e de desvalorizações cambiais. Historicamente, as desvalorizações têm ajudado na superação de crises financeiras ao estimular a balança comercial e ao reduzir o valor real da divida publica denominada em moeda nacional. Por outro lado, a expectativa de uma possível desvalorização produz efeitos negativos sobre o bem-estar: aumento do custo da divida e redução do nível de investimento privado. Modelamos esses trade-offs e mostramos que a abertura comercial melhora o bem-estar ao potencializar o efeito da desvalorização de câmbio sobre a balança comercial. Computamos simulações numéricas baseadas em 48 crises ocorridas em 32 países, e obtivemos resultados alinhados com as desvalorizações e os defaults observados desde 1971.
1. INTRODUCTION
In the last decades, the academic debate on the best economic policies for economies that are dependent on international lending has been fed by recurrent steep currency devaluation episodes and by external-debt crises. Cole and Kehoe (Cole and Kehoe, 1996, 1998, 2000) developed a model where an indebted country was vulnerable to the willingness of the external creditors to keep its debt rolling, and applied it to the Mexican crisis. Calvo, Isquierdo and Talvi (Calvo et al., 2003), based on the Argentina crisis, linked the sudden stop events to current account adjustments, currency devaluation and default. They also suggest that the damage associated with the sudden stop may vary between countries, depending on the degree of dollarization1 1 To be "dollarized" means to be exposed to the exchange rate movements, which can increase obligations in foreign currency assumed previously. and openness.
Dollarization mechanisms were large used by emerging economies, specially as from the end of the 80's. The supply of international capital available and the low credibility of the emerging market currencies favored the adoption of price stabilization policies, based on fixed exchange rates, as the currency board in Argentina and the Real-Dollar pegged in Brazil. Some economists have pointed out that emerging economies should sustain a really fixed exchange rate regime because their difficulty in conducting appropriate monetary policy (Calvo, 2000, Dornbush, 2000, Hausmann, 1999). Other have argued that fixed exchange rates do not improve fundamentals and so, it may be just a delay mechanism for intense crises (Chang and Velasco, 2000, Mishkin, 1998, Sachs and Larrain, 1999). Finally, there are studies suggesting that different monetary policies can be adequate to different realities and that each country must find its own solution according to its peculiarities (Araujo and Leon, 2002, Araujo et al., 2006, Frankel, 1999, Mussa et al., 2000).
Although there was some disagreement about the best exchange rate regime for emerging countries in the past, now there is an agreement on the fact that the more indebted and dollarized the economy is, the greater is its vulnerability to sudden reversals in the capital inflows. Such reversals induce balance of payments crisis that may be combated through national currency devaluation, as it improves net exports. On the other hand, depending on the intensity of the crisis, external debt default can be desired to overcome the external constraint.
This paper aims at evaluating these issues considering 48 crises, occurred in 32 middle-income countries, as from 1971. We follow Reinhart, Rogoff and Savastano (Reinhart et al. (2003), tables 3 and 13) to select 31 middle income countries which with Singapore complete our sample.2 2 See Table 3. Iran, Lebanon, Panama, Peru and Poland are not considered in our sample because some of their information was not available. Selected economies had a significant portion of their external debt denominated in foreign currency when they found themselves in trouble because their inability to obtain new credit in the international market. Steep currency devaluation was present in almost all of the episodes if we consider "steep" a two-digits monthly exchange rate devaluation. Moreover, the high risk premium observed in the financial transactions involving foreign currency indexed bonds, and placed before devaluations, suggests that markets were aware that default could be occasionally used.
To study steep devaluations episodes including issues as the risk of devaluation and the degree of openness, we extend the self-fulfilling debt crisis model of Cole and Kehoe (Cole and Kehoe, 1996). Our model takes into account the effect of a real devaluation on the trade balance of goods. We suppose that, during times of intensive borrowing in the international financial markets, the indebted country imports heavily and, at times of scarce international credit, it makes adjustments to its trade balance to pay for previous indebtedness. Additionally, we consider that a real devaluation reduces the real public debt denominated in national currency through inflation, increasing the government ability to deal with external crises. The devaluation effectiveness depends on the degree of openness and on the pass-through. The openness affects the response of the trade sector to a change in the relative prices, and the pass-through affects the national debt reduction through inflation rate. Finally, we also consider the welfare cost of inflation, captured by a reduction in private investments and by a higher nominal interest rate over the public debt denominated in national currency.
To estimate the effect of the openness and debt levels over the exchange rate adjustment during financial distresses, we present in Figure 1 the currency depreciation3 3 We present details of these calculations and plot in the numerical exercise section and in the Table 3. Note that only devaluations bigger than 30% are selected. observed versus the degree of openness4 4 The degree of openness is defined as (Imports+Exports)/(GDP). and versus the external debt related taxes for the selected crisis sample. We also present the best linear proxies for both relations. Looking to the Figure 1, one can guess that in most open countries the devaluation required tends to be lesser, even without considering many other important variables in such analysis. It also tends to be lesser under lower external debt to tax ratio.
Figure 2 summarizes uncertainty and we describe it further (uncertainty sub-session). Figures 3 to 14 present results of the model simulation which are detailed in the section 3. They are divided in two blocks. In the first one we use Brazil as a benchmark economy to evaluate some qualitative results from the model, like the optimal fiscal policy function; the crisis zone; how the degree of openness can affect this zone and the devaluation-response; how much degree of openness is required to compensate the negative welfare effect of more vulnerability (more risk premium and/or more external debt); what should be the shock required for the default to be better than the devaluation; and how the degree of openness affects this requirement. In the second, we show aggregate results for all countries, verifying that our model can indicate, in a stylized way, the preferences for default-devaluation options and the magnitude of the currency depreciation required to overcome external crisis.
On a more methodological ground, the possibility that default can be welfare enhancing is in accordance with the current bankruptcy literature, which says that it is optimal to have some bankruptcy in equilibrium, contrary to conventional wisdom (see Geanakoplos, Dubey and Shubik (2005), for penalties on the utility function, and Araujo, Páscoa and Torres-Martínez et al. (2002), for infinite horizon economies). Although, the risk of default should be kept under control. Accordingly, the introduction of national currency and trade rises the possibility of a better bankruptcy technology through devaluation of the national currency, rather than repudiation of the external debt.
In the next section we describe the model and an equilibrium. Section 3 presents the numerical exercises and section 4 concludes.
2. THE MODEL WITH NATIONAL CURRENCY AND TRADE
We extended the Cole and Kehoe model (Cole and Kehoe, 1996) by including debt denominated in national currency and trade. There is only one good in the economy produced with capital, k, inelastic labor supply and price normalized to one; three participants national consumers, international bankers and the government; public external debt denominated in dollars or indexed to this currency, B*, and public internal debt denominated in national currency, B. The external public debt is only acquired by international bankers, and there is a positive probability of no rollover whenever its level is in the crisis zone. We consider that any suspension in its payment is permanent and total, as in the original model. On the other hand, public debt B is only taken up by national consumers, which are always prone to rolling it over, charging the price associated with the positive probability of partial repayment due to currency devaluation.
2.1. Uncertainty
To characterize uncertainty, we suppose that sunspot variables give a representation of real shocks and not just psychological ones. The model contains two sunspots: one representing the local investors' confidence, ζ, and another portraying external investors' confidence in the government, ζ*, which has uniform distribution on [0;1]. Even though these shocks are not explicitly modeled, the fear of a sudden fall in a commodity price that represents a big share of exports, of changing in the government preferences about public expenditure, or a political turmoil which contributes to the reversal of international capital flows are examples of shocks that the sunspot variables ζ* and ζ aim at representing. To generate extra revenues in response to a reversal of capital inflows the government can default on the dollar debt or else, it might devalue the national currency. Therefore, the realization ζ* indicates the confidence that international investors have that the government will not default on the dollar debt. Likewise, the sunspot ζ describes the national investors' confidence that the government will not devalue the national currency.
We consider that the sunspot ζ realization is conditional on ζ* realization. The probability that the international bankers' confidence is below a critical value π* is given by P(ζ* ≤ π*) = π*. If ζ* ≤ π*, ζ is supposed to be distributed with uniform [0;1], but if ζ* > π*, ζ is supposed to be one. The probability that the consumers' confidence is below the critical value π given that international bankers are not willing to renew their loans is π, i.e. P[ζ ≤ π | ζ* ≤ π*] = π. Then, in the model with debt in national currency, the probability of a self-fulfilling external debt crisis occurring is π*(1 π), which is equal to [P( ζ* ≤ π*)] · [P( ζ > π | ζ* ≤ π*)] . In this case, there is a suspension of foreign credits and the price that the international bankers are willing to pay for the new dollar debt, q*, is zero. The fear of default is self-fulfilling. With probability π*π there is an external crisis, q* = 0, but the government devalues its currency in order to avoid the default. In this case both national and foreign creditors have very low confidence that the government will honor its debt obligations. Figure 2 sums up the three possible states in the crisis zone.
To avoid unnecessary technicalities, we rule out from the model the possibility that both default and devaluation can be used together. Instead, we consider that during a crisis each one of them can be used with some positive probability, given by sunspot, ζ. These probabilities can be inferred from the spreads of the interest rates on national currency public debt and on dollar currency public debt over the free risk rate. We also assume that the commitment to no-devaluation (no-inflation) is enforceable when there is no external crisis (q* > 0). The results presented in the numerical solution (Figure 7) show that for low levels of the external debt, devaluation is the best response in the crisis zone and, for high levels, default is preferable.
2.2. Crises responses and trade openness
The decision to default on the dollar debt is characterized by the government's decision variable, z*, being equal to zero from default decision on, or being otherwise equal to one. We assume that default causes a permanent fall in national productivity, a, from 1 to α, with αε(0,1) . Meanwhile, the decision whether or not to devalue the national currency is described by the government decision variable, z, with zε(0,1]. On one hand, when international creditors do not renew their loans and the government chooses to default, the national-currency bond pays one good, z = 1, and the dollar bond pays nothing, z* = 0. The productivity of the economy falls to α. On the other hand, if the government decides for devaluation, then national-currency bond delivers ϕ goods, z = ϕ, there is no default on the dollar debt, z* = 1, and the productivity turns to be αϕ. The cost of devaluation is described by a permanent fall in productivity, a, from 1 to αϕ, with αϕε(0,1] for all ϕ. Note that ϕ corresponds to the best inflation response against the crisis and conditional on z* = 1.5 5 We consider that this best-response is also permanent, i.e. if zt = ϕ < 1 then zt+i = ϕ ∀ i ≥ 0. Then, there is a permanent and constant inflation rate equal to after devaluation. Real effects over local public debt return and real exchange rate is present in the first period after devaluation. From the second period on, inflation is predictable and affects only nominal variables. Therefore, devaluation of the national-currency also brings a cost in terms of lower productivity and a benefit of extra revenue that helps to avoid an external default. Finally, provided that there has not been either a default or an inflation tax, previously or at present, then a is equal to one and the government decision variables are z* = 1 and z = 1. Figure 2 shows the three possible government decisions and implied productivity, depending on the realization of the sunspots and considering external debt in the crisis zone. The crisis zone is defined as the interval of the external debt for which the government prefers to default if (q* = 0), and not to default if (q* > 0). Both equilibria are possible and the selected one is given by the sunspot variables.
-
Real devaluation
We do not model exchange rate transactions explicitly. Instead, we directly model the consequences of an exchange rate devaluation. Accordingly, it reduces the international value of a bond denominated in the devalued currency and it improves the trade balance. We also keep our framework based on a single good as in the original model. We assumed that the indebted country produces goods locally, and such goods have its price normalized to unity. When such good is exchanged abroad, its price changes. Therefore, there is only one good but with different prices depending on the place it is traded. This trade could be thought of as occurring through an exchange rate market. The government budget constraint in each period (t) , in units of the domestic goods, is given by:
with g being the public expenditure, θ being the tax rate, f(.)6 6 Continuous, concave, differentiable and strictly increasing; f(0) = 0; f '(∞) = 0; f '(0) = ∞. being the production function, K is the capital stock of the economy, R is the price of the domestic good when it is exchanged abroad, δ is the depreciation factor, TBt is the trade balance and q, q* are the prices of the national currency-denominated bond in unit of domestic goods and the dollar-denominated bond in units of domestic goods traded abroad, respectively.
We suppose that every country's international transaction occurs through the government budget constraint (1). This way, the imbalances in the current account, (TBt) , plus the imbalances in the nonreserve capital account,(Rt1zt*Bt* Rtqt*B*t+1) , are compensated by official reserve transactions, which cause a reduction in the public expenditure (g). We also assume that the nominal exchange rate is fixed or pegged to another currency, but might suffer a significant devaluation after the realization of an external shock. National governments may choose to devalue the national-currency in order to make local goods cheaper, impacting the trade balance, TBt, and the return of its debts. As long as the pass-through coefficient from nominal exchange rate to prices, τ, is less than one, the devaluation is followed by a rise in the real exchange rate, R, and a rise in the domestic inflation, which implies that z is less than one, i.e. z = ϕ(τ). In this case, the government pays ϕB to local investors, reducing the real return on the national-currency debt. Furthermore, the real devaluation increases the volume of exports and decreases the demand for both imports and new dollar debt. We consider that it does not increase the price to be paid for the old external debt as the government can pay it before changing R.
Then, the advantages of the devaluation-response embrace avoiding an external default, reducing the national-currency debt to GDP ratio; since ϕB, instead of B, is settled from the moment of the devaluation on; and improving the trade balance. All these gains should be weighed up in terms of welfare. On the other hand, there are costs related to the inflation tax and to the rise in the value of the foreign obligations.
To compute such effects in the trade balance, we consider that its value, TB(R), depends on the real exchange rate. At times of no external crisis, R is equal to one and the trade balance enters as a constant term in the government budget constraint. We are only interested in the revenue that the government obtains from an improvement in the trade balance after a real devaluation, D(R).7 7 TB( R > 1) TB(1). This revenue depends on the intensity of the real devaluation, the trade volumes, and the real-exchange-rate elasticities of exports and imports, η and η*, respectively,8 8 η > 0 and η* < 0. as developed in the AppendixAppendix. We set D(R) as
D(R) = (R 1)(ση + η*R 1)Imp(1)
where (R 1) is the rate of devaluation, σ is the export-import ratio and Imp(1) is the initial level of imports when R = 1. Then, a devaluation produces a positive change in the trade balance as long as (ση + η*R) is greater than one, which means that the trade account is improved when the response of export-import ratio to a change of the real exchange rate is preponderant. In this case, the more price-elastic the trade volumes are, the greater the improvement will be. Note that the devaluation also may worsen the trade account because of the negative wealth effect on the import volumes ordered before the change in the real exchange rate.
2.3. Market participants
At any time t, the representative consumer maximizes the expected utility
subject to the budget constraint, given by
ct + kt+1 kt + qtbt+1≤ [at . f(kt) δkt](1 θ) + bt bt(1 zt)
given k0 > 0 and b0 > 0. At time t, the consumer chooses how many goods to save for the next period, kt+1, to consume at present, ct, and the amount of new national-currency debt to buy, bt+1, which consists of zero-coupon bonds maturing in one period. The utility has two parts: a linear function of private consumption, ct, and a logarithmic function of government spending, v(gt) ≡ ln(gt). The right-hand side of the budget constraint corresponds to the sum of consumer's income from production, after taxes and capital depreciation, plus the return on the national-currency debt acquired in the previous period. If there is no devaluation, zt equals to one and this return equals to bt domestic goods.
Analogously, at any time t, the problem of the representative international banker is
subject to the budget constraint
given b0* > 0. At time t, the bankers choose how many goods to consume, xt, and the amount of new government bonds denominated in dollar to buy, b*t+1. The expenditure on new government debt is Rtqt*b*t+1, where qt* is the price of the zero-coupon bond that pays one unit of good at the maturity (t + 1) if the government does not default. The right-hand side includes the revenue received from the bonds purchased in the previous period, Rt-1zt*bt*, and the fixed endowment flow,  . The decision variable z* indicates whether the government defaults (z* = 0) or not (z* = 1). If it defaults, then the bankers receive nothing.
. The decision variable z* indicates whether the government defaults (z* = 0) or not (z* = 1). If it defaults, then the bankers receive nothing.
The government is assumed to be benevolent in the sense that it maximizes the welfare of national consumers, with no commitment to honor its obligations. Its budget constraint is given by (1), where the left-hand-side is the government's consumption and the right-hand-side includes the following terms: the income tax, the trade balance and the interest paid both on the dollar debt and on the national-currency debt.
In order to obtain the real exchange rate as a function of the government inflation decision, we define the real exchange rate devaluation as:
Assuming that the foreign price level P* is constant, we obtain the local-inflation rate ϰ:
with the pass-through from nominal exchange rate change to local prices, τ, being equal to  . The value of z, which corresponds to the units of domestic goods that a national-currency bond actual pays at maturity, is defined as
. The value of z, which corresponds to the units of domestic goods that a national-currency bond actual pays at maturity, is defined as
Because we consider only the devaluation possibility, i.e. Rt+1≥ Rt, we have zε(0,1]. Accordingly, we arrive at an expression that relates z to the change in the real exchange rate:
where the devaluation rate is given by (R 1), since R0 = 1.
The government is assumed to behave strategically as it can foresee the optimal decisions of all market participants; including its own, zt*, zt and gt; given the initial aggregate state of the economy and its choices of B*t+1 and Bt+1. To match aggregate and individual variables it is assumed that, in the initial period, the supply of dollar debt B0* is equal to the demand for this debt, b0*; the supply of national currency debt B0 is equal to its demand, b0; and the aggregate capital stock per worker, K0, is equal to the individual capital stock, k0. The population of both consumers and bankers is continuous and normalized to unit.
2.4. A recursive equilibrium
The definition of a recursive equilibrium follows the same procedure developed by Cole and Kehoe (Cole and Kehoe, 1996). The actions of the participants are taken backwards according to the timing in each period.
Timing of actions within a period
-
the sunspot variables ζ* and ζ are realized and the aggregate state of the economy is s ≡ (K, B*, B, a-1, ζ*, ζ);
-
the government, taking the dollar-bond price schedule q* = q*(s, B*',B') as given, chooses the new dollar debt, B*';
-
the government, taking the national-currency bond price schedule, q = q(s, B*',B') as given, chooses the new national-currency debt, B';
-
international bankers, taking q* and z* as given, choose whether to purchase B*';
-
local investors, considering q*, q and z as given, decide whether to acquire B';
-
the government decides whether or not to default on dollar debt, z*;
-
the government decides whether or not to devalue the national currency, z, and chooses its current consumption, g;
-
consumers, taking a(s,z*,z) as given, choose c and k'.
Given this timing of actions, we can work backward in each period to define the value functions and the states variables for each market participant, starting with consumers who move last. For simplicity, from now on, we refer to consumers and government decisions as C and G, respectively.9 9 C = ( c,k',b') , G = ( z,z*,g,B',B*').
Each consumer knows the stock of capital saved, k, the stock of national-currency debt purchased, b, the aggregate state of the economy s, and the new dollar and national-currency debts offered by the government, B*' and B'. Given s and B*', consumers take as given the price that international bankers are willing to pay for the new dollar debt, q*(s,B*',B'), and the price that turns them indifferent to accepting or not the new national-currency debt, q(s,B*',B'). They are also able to anticipate the government's decisions for the coming period, G(s'). Therefore, when consumers choose the amount of new national-currency debt, b', their state is sc ≡ (k,b,s,G(s)) . The value function for the representative consumer is given by:
Each international banker decides how much public debt b*' to buy, knowing the amount of dollar debt purchased in the previous period, b*, the aggregate state, s, and the government's decision G(s). They also take prices as given, q(s,B*',B') and q*(s,B*',B') , and the government decisions for the coming period G(s'). Accordingly, their state is sb ≡ (b*,s,G(s)) and their value function is defined by:
The subscript (-1) indicates that when q* = 0 and the government choose to devalue, it can pay the old debt first.
Finally, the government makes decisions twice within a period. When it chooses its new debt levels, it knows the state s. Moreover, it takes price schedules q*(s,B*',B') and q(s,B*',B') as given, as well as its optimal choices induced by the new debts, G(s'|B',B*'). Likewise, the government also recognizes that it can affect the optimal choices of consumers, C(sc), the price schedules q*(s,B*',B') and q(s,B*',B'), and the productivity a(s,z*,z) of the economy.
Then, in the beginning of each period, the government chooses B*' and B', and its value function is defined by
where the last three restrictions indicate that the government chooses the best actions given its previous choices about the debt level. sg is defined as the state of the government, (s,B*',B'). Therefore, after national and international investors decide about buying new debt, the government decides whether or not to default and whether or not to devalue the national currency. By comparing welfare levels according to repayments decisions, and taking all debt levels as given, the policy functions z*(sg), z(sg) and g(sg), are solutions for:
subject to,
where the last restriction indicates that default and devaluation cannot be implemented at the same time. We defined z and z* as function of s because when to default is better than not to default (z* = 0  g z* = 1|z = 1), then the actual government response to the crisis, namely devaluation or default, depends on the sunspot-ζ realization. We also consider that when devaluation is used to avoid the default, z is chosen to maximize the welfare conditional to z* = 1.
g z* = 1|z = 1), then the actual government response to the crisis, namely devaluation or default, depends on the sunspot-ζ realization. We also consider that when devaluation is used to avoid the default, z is chosen to maximize the welfare conditional to z* = 1.
Definition of an equilibrium
An equilibrium is defined as a list of value functions Vc for the representative consumer, Vb for the representative international banker, and Vg for the government; policy functions C for the consumer, b*', for the international banker, and G for the government; price functions for the dollar debt, q*, and for the national-currency debt, q; and an equation for the aggregate capital motion, K', as follows:
(i) given G,q,q*; Vc is the value function for the solution to the problem of the consumers (3), and C are their optimal choices;
(ii) given G,q,q*; Vb is the value function for the solution to the problem of the international bankers (4), and b*' is their optimal choice;
(iii) given C,q,q*; Vg is the value function for the solution to the problem of the government (5 and 6) and G are its optimal choices;
(iv) B*'(s) ∈ b*'(sb);
(vi) B'(s) ∈ b'(sc);
(vii) K'(s,G(s)) = k'(sc).
2.5. Equilibrium Analysis
The behavior of consumers and bankers depends on their expectations regarding whether or not the government will default on the dollar debt or create inflation tax on the national-currency debt through devaluation. On the other hand, the government actions also depend on these expectations which have real effects through the debt prices and investment levels.
When making their decisions about capital accumulation, consumers compute the expected productivity for the economy according to their beliefs about the possibility of a crisis occurring in the next period, and to the possibility that this crisis results in a default or a currency devaluation. Then, the optimal capital accumulation, kt+1, depends on the consumers' expectations about productivity, Et[at+1] , as follows:
Furthermore, consumers act competitively and are risk neutral, so they may purchase new public debt denominated in national-currency if its price equals the expected return to 1/β:
The more closed the economy is the greater is the devaluation (inflation) required during the crisis and the smaller is the expected value for zt+1. So, interpreting  as being the interest factor over the national currency debt we can say that the interest rate is decreasing in the degree of openness.
as being the interest factor over the national currency debt we can say that the interest rate is decreasing in the degree of openness.
Analogously, international bankers act competitively and are risk neutral, so they may purchase new public debt denominated in dollar-currency if its price equals the expected return to 1/β:
During a crisis ( * < π*) they are convinced about default on the next period and so they set qt* = 0.
* < π*) they are convinced about default on the next period and so they set qt* = 0.
Finally, to complete the equilibrium analysis we must find which are the government actions. Letting Vg(s|z,z*,q*) denote the payoff to the government conditional on its decisions, z and z*, and conditional on the price q*, and also considering that the public debt level denominated in the national currency cannot change over time (Bt = Bo∀t),10 10 From now on we consider that this assumption holds. Otherwise, there would be no external crisis since the absence of new external credit could be compensated by greater local currency debt level. An alternative would be to define a local debt crisis event to avoid such substitution effect. it is possible to construct an equilibrium with the crisis zone defined by the external debt level as in the Cole Kehoe model (Cole and Kehoe, 1996).
Next, we define the participation condition which ensures that the government will want to honor the current external debt given it is able to sell new one:
Analogously, we define the no-lending condition which ensures that the government will want to default during a crisis:
The crisis zone is defined as the interval for the current external debt level, (b,B], where b is the greatest external debt level so as equation (8) does not hold with (b,kn) εs, and B is the greatest external debt level so as equation (7) holds for (B,kπ*π)εs. When the economy is out of the crisis zone, i.e. B* ≤ b, there is always external credit available. Since the bankers know that the government would not to default even if the price were zero, they do not refuse to rollover new bonds. In the crisis zone the bankers are aware of the possibility of default, and may refuse to sell new bonds (q* = 0) . In this case, default is desirable, but with probability π the government devalues to avoid the default.
Although we do not compare the payoffs of devaluation versus default to characterize the crisis zone (we maintain the possibility of both responses occur), we compute in the numerical exercises, presented in the next section, the level of external debt,  , for which government would be indifferent between default and devaluation. We also verify that
, for which government would be indifferent between default and devaluation. We also verify that  ε(b,B) and that devaluation is the best response in the crisis zone if B* <
ε(b,B) and that devaluation is the best response in the crisis zone if B* <  . If B* >
. If B* >  , default is the best response in the crisis zone.
, default is the best response in the crisis zone.
Table 1 presents the four possible equilibrium capital accumulation and prices, according to the expectations. In the first line of the table we consider that the external debt is out of the crisis zone. In the second one we consider that the external debt level is in the crisis zone and the two last present the values for the after-crisis economy. Each one of the three last lines corresponds to the three states characterized in Figure 2.
3. NUMERICAL EXERCISES
In this section, we first present numerical exercises for the Brazilian economy to show some qualitative results from the model. Secondly, we present aggregate results for 58 currency crises and attempt to outline some of the factors that make countries adopt different crisis responses, with more or less devaluation, and choosing default or not.
3.1. Qualitative results
The parameters used in the simulations have been chosen to portray the Brazilian economy during 1998, period that precedes the Brazilian currency devaluation, starting in January 99. The definition of period length is based on the Brazilian government debt whose average length was varied from 7 to 10 months between 98-99. The government discount factor, β, is approximated by the yearly yield on government bond issued by the US, whose values were about 5 percent. Based on these figures, we interpret a period length as being one year and a yearly yield on risk free bonds, r, as being 0.05, which implies a discount factor β of 0.95( = (1 + r)1). The choice of the functional forms for v(.) and f(.) were the same used by Cole and Kehoe (1996), that is, v(g) = ln(g) and f(k) = Akλ where capital share λ is established at 0.4 and the scale factor at 10. The parameter α equals 0.95, assuming that default causes a permanent drop in productivity of 0.05. For z = ϕ, the correspondent inflation rate is (1 ϕ)/ϕ, which implies the welfare cost of inflation, αϕ, estimated according to Simonsen and Cysne11 11 In the estimation of welfare cost of inflation we use Bailey's approximation and the money demand specified as , where r is the logarithmic annual inflation (see Cysne and Simonsen, 1994). We set and equals to 0.07 and 0.6, respectively. . The probability of default, π*(1 π) , and the probability of inflation, π*(π) , are calculated on the basis of the risk premium practiced in the financial market according to the following expression:
where  and
and  are yearly yields on Brazilian public debt denominated, respectively, in dollar and in national currency (discounting the expected inflation of Brazilian currency), and ϕ is given by the unexpected yearly inflation associated with devaluation.
are yearly yields on Brazilian public debt denominated, respectively, in dollar and in national currency (discounting the expected inflation of Brazilian currency), and ϕ is given by the unexpected yearly inflation associated with devaluation.
Data for  are available for the period of analysis, while
are available for the period of analysis, while  only since January 2002, when its value was about 0.12.12
12
Yearly yield on LTN minus expected inflation.
Therefore, considering the values for ϕ,
only since January 2002, when its value was about 0.12.12
12
Yearly yield on LTN minus expected inflation.
Therefore, considering the values for ϕ,  , and
, and  equals to 0.5, 0.14, and 0.12, respectively, we can compute (π*,π) as being equal to (0.2,0.61). In Table 2 we present the values of parameters and variables used in the simulations for the Brazilian economy, whose results are described next.
equals to 0.5, 0.14, and 0.12, respectively, we can compute (π*,π) as being equal to (0.2,0.61). In Table 2 we present the values of parameters and variables used in the simulations for the Brazilian economy, whose results are described next.
Figure 3 shows that when the external public debt is in the crisis zone the optimal policy is to move out from it. But it may be difficult to reduce public expenditure and Figure 4 shows that an alternative policy could be lengthening the maturity.13 13 We follow Cole and Kehoe approach for "lengthening the maturity structure". Henceforth, lengthening the maturity structure means converting an initial quantity B* of one-period (one year) bonds into equal quantities Bn* of bonds of maturity n (1,2,..., N). Then, the government redeems Bn* bonds every period and sells Bn* n-period bonds, where Bn*(1 qn*) = B*(1 q*), and qn* = β n( E*tzt+n). These conclusions remain the same as in the original model. Figures 5, 6, and 7 present the effects of the degree of openness over the economy. As shown in Figure 5, if the economy has its imports and exports enlarged without changing the trade balance, i.e. the gains in the volume of exports (Dexp) equal the gains in the volume of imports (Dimp), then only the cap of the crisis zone becomes greater. But if the economy can improve its trade technology and enlarge exports faster than imports, then the international capital inflow becomes greater and both the floor and the cap increases. In figure 6 it is possible to see that, according to the model, the devaluation required to overcome a crisis is increasing in the external debt level and decreasing in the degree of openness. Figure 7 also shows that the "devaluation-better-than-default" region is increasing in the degree of openness. Finally, figures 8, 9, and 10 correspond to welfare analyses. They show how much debt must be paid to compensate the welfare loss related to an increase in the external risk, and how much improvement in the trade is required to compensate the welfare loss related to an increase in both the external risk and the external debt. Note that in Figure 10 both expected welfare and welfare after crisis are considered.
3.2. Cross country results
The parameters used in the simulations for the other countries are presented in Table 3. To compare results across countries we change only a few parameters which we consider more relevant to explain differences between economies and their responses to crisis. The variables that are not presented in Table 3 are the same for all countries including Brazil (Table 2).
Figure 11 shows that, according to the assumptions of our model, the "countries on the left side" were more prone to choosing default than the "ones on the right". Results match 85% of the crises with "reality" in predicting that default is the best response whenever it actually occurs and it is not the best response whenever it does not occur. Triangule marks show where the model failed.
Figure 12 presents the estimated devaluations for different pass-through values. Note that the results are quite similar to a wide range of this parameter. Devaluation rates change significantly only when considering that pass-through is very close to one.
Figure 13 compares actual devaluations and those predicted by the model. In the first plot the elasticities (η*,η) of 0.6 were considered, and in the second plot we double this value. Note that for greater elasticity less devaluation is required to overcome the external crisis as expected. Accordingly, most devaluations predicted are overestimated, but not too far from reality. Moreover, we do not consider that our numerical exercise is a good predictor for actual devaluation, since we have made simplifications to compute after-crisis payoffs as considering ( z*t+i = 0,zt+i = ϕ) for all i > 0, respectively, in default and devaluation responses. Our aim is to outline the different crisis responses adopted by countries considering factors as the degree of openness, debt levels in both currencies, taxes, and risk-premiums. In this sense, we are more interested in comparing the shape of predicted versus actual devaluations plots.
Figure 14 replicates Figure 13 excluding the devaluations lesser than 30% and separating countries that experienced default from the others.
Finally, it is also important to note that there are many ways to compute the actual devaluations of the currencies across countries. We use the exchange rate series published by IMF-Statistics, considering the bilateral price of the dollar related to the national currency, and the mean value for each month. Sudden and significant devaluations indicate the beginning of the crisis period, whose length is defined as six months for all crises. The new level of the exchange rate is considered as the mean of the exchange rate for this crisis period and the actual devaluation for each country is computed as from the exchange rate level immediately before the crisis period.
4. REMARKS
As Cole and Kehoe already pointed out, this type of model differs from most of the literature on debt crises by using a dynamic stochastic general equilibrium framework with an altruistic government rather than using a deterministic model or a model with a reduced form for the government. We extended their original debt crisis model by adding trade and local debt, without losing neither the dynamic stochastic general equilibrium framework nor the altruistic government. Original qualitative results remain in our extended version, i.e. the policy recommendation in almost all cases is to leave the crisis zone through both fiscal adjustments and through lengthening the maturity of the external debt. As a novelty, we present the positive welfare effect from trade openness and how it shifts the crisis zone up. Finally, we predicted, in a stylized way, the relative magnitude of the national currency depreciation required to overcome external crises and the preferences for default-devaluation options.
BIBLIOGRAPHY
5. FIGURES AND TABLES
A.1. Effect of Real Devaluation on the Trade Balance
Defining Exp as exports measured in domestic output units, Imp as imports denominated in units of good traded abroad, R1 as the initial real exchange rate, and R2 as its new level after devaluation, we can compute the trade balance change D(.) as:
Where η =  and η* =
and η* =  . Defining σ as the exports-imports ratio, R1≡ 1, and R2≡ R, we obtain
. Defining σ as the exports-imports ratio, R1≡ 1, and R2≡ R, we obtain
ΔTB = (R 1)[ησ + η*R 1]Imp(1)
- Araujo, A. & Leon, M. (2002). Ataques especulativos sobre dívidas e dolarização. Revista Brasileira de Economia, 56(1):746.
- Araujo, A., Leon, M., & Santos, R. (2006). Monetary arrangements for emerging economies.
- Araujo, A., Páscoa, M., & Torres-Martínez, J. P. (2002). Collateral avoids Ponzi schemes in incomplete markets. Econometrica, 70(4):16131638.
- Calvo, G. (2000). The case for Hard Pegs. Mimeographed, University of Maryland.
- Calvo, G., Izquierdo, A., & Talvi, E. (2003). Sudden stops, the real exchange rate, and fiscal sustainability: Argentina's lessons. Working Paper No. 9828 July 2003.
- Chang, R. & Velasco, A. (2000). Exchange rate policies for developing countries. American Association Papers and Proceedings, 90:7175.
- Cole, H. & Kehoe, T. (1996). A self-fulfilling model of Mexico's 1994-1995 debt crises. Journal of International Economics, 41:309330.
- Cole, H. & Kehoe, T. (1998). Self-fulfilling debt crises. Staff Report.
- Cole, H. & Kehoe, T. (2000). Self-fulfilling debt crises.
- Cysne, R. & Simonsen, M. (1994). Welfare costs of inflation: The case for interest-bearing money and empirical estimates for Brazil. Ensaios Econômicos, 245.
- Dornbush, R. (2000). Millenium resolution: No more funny money. January.
- Dubey, P.; Geanakoplos, J. & Shubik, M. (2005). Default and punishment in general equilibrium. Econometrica, 73(1).
- Frankel, J. (1999). No single currency regime is right for all countries or at all times. Cambridge, Mass 7338, National Bureau of Exonomic Research. W.P.
- Hausmann, R. (1999). Should there be five currencies or one hundred and five? Foreign Policy, (116):6579.
- Mishkin, F. (1998). The dangers of exchange rate pegging in emerging market countries. International Finance, 1(81):101.
- Mussa, M., Masson, P., A., S., Jadresic, E., & Mauro, P.; Berg, A. (2000). Exchange rate regimes in an increasingly integrated world economy. Washington,D.C.
- Paiva, C. (2003). Trade elasticities and market expectations in Brazil. WP/03/140, Jul. 2003.
- Reinhart, C. K., Rogoff, K., & Savastano, M. (2003). Debt intolerance. August 2003.
- Sachs, J. & Larrain, F. (1999). Why dollarization is more straitjacket than salvation. Foreign Policy, 116:8092.
Appendix
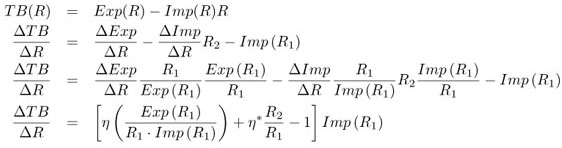
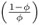 after devaluation. Real effects over local public debt return and real exchange rate is present in the first period after devaluation. From the second period on, inflation is predictable and affects only nominal variables.
after devaluation. Real effects over local public debt return and real exchange rate is present in the first period after devaluation. From the second period on, inflation is predictable and affects only nominal variables. 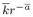 , where
, where 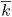 and
and 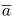 equals to 0.07 and 0.6, respectively.
equals to 0.07 and 0.6, respectively. Publication Dates
-
Publication in this collection
22 June 2012 -
Date of issue
June 2012





































