Opposite policy implications in the theory of money and banking

^ISchool of Economics, Business Administration and Accounting, FEARP-USP - E-mail: [e-mail]

^IIFGV/EPGE - Escola Brasileira de Economia e Finanças - E-mail: [e-mail]

ABSTRACT

The recent financial crisis creates a demand for welfare-based models of financial regulation and liquidity shortages. In this paper, we review policy implications from two cornerstone models and show that they imply different responses in terms of intertemporal returns of financial liabilities. In the first case, a version of the Cavalcanti and Wallace (1999), random-matching model, monitored agents are led to promote inflation in bank-issued money. In the second case, a sequential-service version of the Diamond and Dybvig (1983) model of bank runs with insolvency, increases in long-run returns can prevent bank runs by reducing the provision of liquidity.

Keywords: Inside Money, Inflation, Financial Fragility, Insolvency.

JEL Code: E4, E5.

RESUMO

A recente crise cria uma demanda por modelos de regulação e restrições de liquidez que sejam explícitos sobre efeitos de bem-estar. Neste artigo, nós revisamos as recomendações de política originárias em dois modelos canônicos, mostrando suas diferentes prescrições para taxas de intertem-porais de retorno financeiro. No primeiro, uma versão do modelo de en-contros aleatórios de Cavalcanti e Wallace (1999), agentes monitorados são levados a promover uma emissão inflacionária de moeda bancária. No segundo, uma versão sequencial do modelo de Diamond e Dybvig (1983) com insolvencia, aumentos nos retornos de longo prazo podem prevenir corridas bancárias através da contenção da liquidez.

1. INTRODUCTION

In his Nobel lecture at FGV in May 2013, Christopher Sims, when motivating ongoing research on a purely statistical, vector auto-regression model of financial variables, avoided using an out-of-the-shelf structural model. He claims that, in the universe of quantitative macroeconomics, existing theories of financial frictions are just "story-telling" devices. They would suffer from a serious limitation that he also believes is intrinsic to new-keynesian structures broadly used for guiding short-run monetary policy: he would not pursue welfare analysis in existing sticky-price models.

Attendants of Sims's lecture may wonder what a structural model of financial frictions must contain so that counterfactual exercises provide meaningful welfare comparisons. And of course, as he recognizes, there is a high degree of subjectivity on what researchers call "micro foundations". While most modern macroeconomists would agree that looking for welfare effects in, say, IS-LM models, makes no sense, the debate is more subtle when choosing from models in which agents are people endowed with utility functions and making choices under rational expectations. What could be wrong? The details on how money and banking work in the model?

Small but illustrative variations of liquidity-provision models, like one with insolvency, are considered in this paper. Our main point, however, is to notice that even mainstream, welfare-based analysis can offer different prescriptions depending on alternative notions of implementability used. To make this point, we focus on the issue of whether liquidity should be restrained or expanded, without worrying about quantitative effects. We work with two workhorses of modern money-and-banking theory that compete with new-keynesian models, namely the Kiyotaki and Wright (1989) model of money as a medium of exchange, and the Diamond and Dybvig (1983) model of financial fragility. Our objective is to highlight the fact that these two models can be extended to produce implications about liquidity-shortage episodes. In particular, using mechanism design, one can study inside money (banks) in the former, and insolvency in the latter. But despite the effort of constructing extensions in a way that maintains the validity of welfare analysis, these exercises can lead to somewhat opposite conclusions about how society should respond to liquidity shortages. In other words, alternative notions of liquidity and implementability lead to fairly different guidelines for central banking.

Our review is inspired by a recent paper of Wallace ("An alternative to new-keynesian models for the study of optimal (monetary) policy", 2013). He proposes using mechanism design — in random matching models with imperfect monitoring — as a foundation for central-bank interventions involving credit. In particular, he discusses policy implications of the Cavalcanti and Wallace (1999) model. That model blends monitored and anonymous agents in a mechanism-design version of the Kiyotaki and Wright (1989) model of money as a medium of exchange. Wallace finds that central-bank interventions, geared at 'improving' the distribution of money, have to resort to inflation-inducing money creation in order to achieve optimal allocations. And, moreover, that optimal policies are implemented through the monitored population, which can also be interpreted as regulated, private banks that create liquidity.

That inflation can be welfare improving should not be taken as a marginal detail in the models discussed by Wallace (2013). He argues that welfare gains associated with improvements in liquidity provision are robust and also appear in versions of random-matching models with seasons. As a matter of fact, Cavalcanti and Nosal (2009) have shown, in a simple environment with seasonal changes in utilities, that optimal allocations require interventions in the money supply because trades in a low-marginal-utility season can lead to a distribution of money that is unsuitable for the next season.

Wallace (2013) is certainly describing models that he can trust for welfare analysis. Since the same can be said about his proposal for a revision of the Diamond-Dybvig model of banking (see Wallace (1988)), it becomes therefore an interesting question what financial fragility means in banking models, and how policy recommendations addressing the issue compares, in terms of interest rates (or, more fundamentally, intertemporal rates of substitution) with optimal policies in monetary models.

Although the comparison is abstract, it can enrich the debate about welfare analysis in monetary theory. In what follows, we show that there is a simple extension of the Diamond-Dybvig model that can satisfy requirements of mechanism design and that can produce insolvency as an equilibrium outcome, a feature desirable to have in face of the recent financial crisis. We then show that a policy of increasing interest rates, defined as the return offered to patient individuals, can actually prevent bank runs and insolvency. As we explain below, it is important to take into account that our welfare analysis in the Diamond-Dybvig model, contrary to that in the Kiyotaki-Wright model of money, is guided by strong implementation, that is, when one is concerned about multiplicity of equilibria. Much of the differences in policy recommendations in the two models depends whether liquidity shortages are in fact related to multiplicity.

In the rest of the paper, Section 2 presents a review of results concerning the optimality of inflation in models of inside money. Section 3 reviews a basic version of the Diamond-Dybvig model with sequential service. Section 4 amends the latter so that insolvency becomes a possible outcome, and explains how an increase in planned rates of return can prevent bank runs. Section 5 concludes summarizing lessons about liquidity concepts and their implications. The appendix contains all proofs and an algorithm for numerical work.

2. A MECHANISM-DESIGN MODEL OF MONEY AND INFLATION

The bank sector is an important source of liquidity provision in that it is able to create money. In order to study such phenomenon, Cavalcanti and Wallace (1999) extend Kiyotaki and Wright (1989) monetary model by making society able to perfectly monitor actions taken by a proportion of the population, which we interpret as the bank sector. Without a monitoring technology, as in Kiyotaki and Wright (1989), society deals with scarce opportunities of exchange in the presence of individual's anonymity. This situation gives an essential role to an otherwise useless, durable object called money. It is used as a proof of past production by people who expect to be compensated by future consumption, thus working as a medium of exchange. By contrast, a monitoring ability, when combined with availability of printing presses, creates a sector that does need to hold money as a proof of past production, but that can credibly promise to redeem money they issue, enriching trade, and this new form of media of exchange is called inside money.

Exchange frictions are preserved by limiting the number of people each individual meets to only one person per period and by making such pairing involuntary and random. In addition, pairing can have no coincidence of interests: (i) there are K types of non-durable goods each period, and (ii) type-i individual is able to produce good i, but can only consume good i + 1, modulo K. As a consequence, people in a meeting can have no coincidence of interests or single coincidence of interests, but never double coincidence. For single-coincidence meetings, level of production/consumption y provides utility u(y) for the consumer and or the producer. Future payoffs are discounted according to intertemporal discount factor (0,1), time is discrete and horizon is infinite. There is a continuum of individuals in the economy and who live forever and are no able to commit to any future action.

If all people in the population is monitored then one obtains a credit-only economy: there is no need to issue and redeem money. In order to have credit coexisting with money one can just assume that only a fraction of the population can be monitored. This way, the non-monitored people demands money to be used among themselves and possibly in trades with the monitored people. Outside money is known to be essential (its use improves social welfare) in such random-matching economies if no monitoring technology is available. Cavalcanti and Wallace (1999) show that this is also the case if a fraction (0,1) of individuals can be permanently monitored. Because, in their setup, money holdings are restricted to be indivisible and at most one, there are then four basic types of people to be considered, according to the monitoring status and the money holding, {m1,m0,n1,n0}. Here m stands for monitored people (or "banks"), n stands for non-monitored people, 1 stands for holdings of one unit of money, and 0 stands for holdings of zero units of money. Restricting now attention to steady states, we can denote the distribution of people in S by The following table presents the potentially productive, pairwise meetings along with their frequency.

Meetings where the producer is n1 cannot have trade, since there is no incentive to incur the production cost (since the producer is at the upper bound, he or she cannot hold more money). When the consumer is n0, no money can be paid in exchange for production. Therefore, n-people are not willing to produce to him. Credit arrangements can however sustain exchange between m-people. And, a meeting (n0,m0) is productive under m-people access to printing presses. Otherwise, there is nothing to offer to the producer and the meeting is unproductive. The symbol *, used as a superscript, is a tag to remember that observation. Money creation and destruction can take place when m-people meets a n-people.

Deviatov and Wallace (2012) has studied optimality of inflation in this setup, a complementary analysis to the study of inflation in economies without monitoring technology. As they recognize, "there are, by now, several models of outside money in which some inflation produced by lump-sum transfers is optimal [see Levine (1991), Kehoe et al. (1992), Molico (2006), Green and Zhou (2005), Deviatov (2006)]. In those models, the transfers have a beneficial effect on extensive margins by altering the money holdings of those who trade in a way that more than offsets their harmful effect on intensive margins implied by the decrease in the return on money." They study a stochastic policy of destructing money. In particular, it is assumed that after created and issued money can disappear with a small probability that is chosen by society, î. This mechanism resembles the effects of inflation in the sense that it decreases expected return of money, since money holders face a positive probability of losing it. This pattern of probabilistic destruction mimics the proportional tax on money holdings used to represent inflation in models with divisible money. And here, each rate of money creation by banks requires a proportional rate of destruction (inflation) in order to keep the distribution of money stationary.

An obvious result is that it is optimal to allow monitored individuals to issue money whenever necessary. This simplifies the problem of finding the allocation that maximizes average welfare in the set of stationary, incentive-compatible ones, since one can set in advance, with the understanding that monitored individual without money (m0) issue money when necessary. It follows that money holdings is not used as a state variable for monitored people. Creation of money hence happens in meeting (n0,m0) and destruction in meeting (m0,n1). The other variables describing exchanges in the model must be found numerically, an exercise giving rise to the following table.¹

Output is reported as a proportion to the first-best level. The symbol *, used as a superscript, is used to remark that the participation constraint of the producer is active, which occurs when the producer is indifferent between trading and not trading.² We notice that output is higher when the producer is a monitored individual. This follows because society can observe a deviation of such individuals from the allocation recommended by the planner, and that the associated punishment is an exclusion from the set of monitored people, forcing the person to live as a non-monitored person afterwords. As a result, expected welfare of a monitored individual is higher than that of a non-monitored person. Production to non-monitored people, such as that in meeting (m0,n0), can be seen as a taxation of the monitored people. The level of output .296, below the maximal incentive-compatible one, .717, indicates that it is not optimal to tax too much in this meeting, since in this case there is no redemption of money, implying that such output is given out for free, which tends to reduce the return of money and, therefore, to tighten participation constraints in other meetings.

Using Table 1 and money-transfer information in Table 2, it can be seen that difference between inflows and outflows of money, with respect to the set of monitored people, is

Zero inflation in this economy would imply As discussed by Bertolaiet al. (2012), this distribution is not attractive because the quantity of productive meetings (extensive margin) are low. In effect, they show that the quantity of productive meetings is strictly decreasing in Intuitively, rich n-people are not willing to produce in exchange for money (just to consume), while poor n-people always wants to produce and can consume only when they meet m-people (banks). By deteriorating individual wealth, some inflation can increase the number of productive meetings.

As Bertolai et al. (2012) observe, the extensive margin could also be improved by reducing the injection of money, but this would make non-monitored producers less willing to produce in meeting (n0,m0). Inflation is a superior (cheaper) arrangement because the cost of destruction of money can be shared among all individuals with money. By contrast, the cost of reducing the injection of money is borne only by producers in meeting (n0,m0). As a conclusion, steady-state inflation is optimal since it allows society to keep money scarce and, consequently, to improve the extensive margin at a low cost in the intensive margin. In the particular case reported in the table, inflation implied by the destruction probability, , is able to sustain a steady-state distribution given by

More generally, inflation effects on extensive margin are identified by Wallace (2012) as the fundamental reason for his conjecture on the optimality of inflation in a general class of economies, denominated pure currency economies. An economy where people's histories are private and who, therefore, cannot be punished individually in the future for current actions.

Wallace (2013) advocates such class of monetary models as an alternative to New-Keynesian models when studying optimal monetary policy. He presents two variations of Cavalcanti and Wallace (1999) model intended to study optimality of inflation without inside creation of liquidity and to study seasonal monetary policy. In common, these variations have = 1/4 and the assumption that the planner, like a central bank, is able to make separate transfers to monitored and non-monitored people in a second stage for each period.

For the first objective, he discusses an example presented by Deviatov and Wallace (2010) where positive inflation is shown to be a feature of the optimal steady-state allocation, even if monitored people cannot print money³. That is, because the planner can give transfers directly to the monitored period after trade takes place, it is optimal to have the mass of such individuals without money to be zero. That is, = 0 since otherwise some m-people would not be able to consume. The following table summarizes the results:⁴

An insurance arrangement taking place in the second stage helps m-individuals to start everyperiod with money. Those spending money in the first stage and those losing their money under inflationary policy receive the money from those producing in the first stage. Remaining imbalances are covered by planner's transfers. As a consequence, the difference between inflows and outflows becomes

Again, the same reasoning discussed in Bertolai et al. (2012) applies and inflation must be positive to sustain a stationary quantity of money.

For the seasonal policy, Wallace (2013) discusses an example presented in Deviatov and Wallace (2009). Disutility of production is two-date periodic: at odd dates (winter) it is higher than at even dates (summer)⁵. That way, the first-best allocation assigns more production in summer than in winter. Tables 4 and 5 present the main numerical findings.

Again, m-people start every period with money. A novel feature is that more money are made available in the system during the winter. The next table helps to understand why.

Notice that the net inflow of money among n-people implied by optimal trade during the winter is negative, (.750 — .312)(.505) — .312(.813). The opposite net inflow is implied by trade during the summer, so that a two-date period allocation without inflation is sustained. This pattern of trade implies more money going to m-people at the end of the winter than they need to start the summer with one unit of money each. Also, m-people are receiving at the end of the summer less money than they need to start the winter with money. Then, as pointed by Wallace (2013), the intervention can be viewed as the planner extending zero-interest loans at the beginning of the winter with repayment made at the beginning of the summer.

3. A MECHANISM-DESIGN MODEL OF BANK DEPOSITS

The economy is now one with two dates and one consumption good per state of nature that must be properly stored and divided among a finite number, N, of individuals. We shall introduce a benchmark version first, and the discuss an extension featuring a richer set of types. We start assuming that people have random preferences that can assume two different forms. There is also the realization of the order (positions in a queue) in which they contact the bank (the planner) to inform the realization of their types and to obtain the adequate transfer of consumption goods planned for that contingency. Hence, in the benchmark case, it is understood that the economy is hit by a shock with support The parameter N stands for the number of positions, and is also the size of the population, composed by ex-ante identical depositors that live for two dates and derive utility from pairs (c₁ ,c₂) of consumption. These bundles must be supplied by a the bank (the benevolent social planner). The bank controls the aggregate endowment Y and make sequential transfers according to positions and announcements about preferences. An important aspect of the environment is that preferences are private information. While for now an individual can be of two types, 0 or 1, in the next section of the paper we add a third type in order to discuss insolvency.

Person i is called impatient if and called patient otherwise. The utility in the former case is Au(c₁) and in the latter is u(c₁ + c₂), where A > 1 and u(c) = and > 1. Thus, only patient individuals can substitute consumption across dates. The resources not consumed in date 1 are reinvested at gross rate-of-return R > 1. These preferences have been used by Green and Lin (2003), with A = 1, and Peck and Shell (2003), with A = 10.

Feasible transfers must be incentive-compatible and satisfy the sequential-service constraint. This constraint prevents date-1 consumption transferred to a person at position i to depend on information provided by someone at position n for n > i.

In the standard model, each individual draws a unique position i in {1,...,N} with probability and, as a result, the realization , without knowing the other coordinates of . As in Peck and Shell (2003), we shall assume that the individual is not informed of his position i. But we consider only the case where shocks are independent among individuals. In comparative-statics exercises with variations in population sizes, we shall keep the per capita endowment constant as the population size, N, varies.

A compact description of candidates for optimal allocations follows from additional notation. Let us denote by the vector , and by the profile that results from substituting the i-th coordinate of by k. Given that R > 1 we can restrict attention to transfers that assigns, to someone at position units of date-1 consumption, if that person is impatient, or units of date-2 consumption, otherwise. A typical transfer plan is a pair of vectors (x;y), each one being a function of .

It is useful to keep in mind the following conventions for understanding the nature of the planner's problem, and how its solution defines a game for depositors. There is a sequence of events with nature choosing , a vector with N entries. The planner must make a contingent plan for each possible realization of without knowing entirely. In particular, the planner starts with total reserves Y and makes a plan of transferring resources at position 1 depending on , which is informed by "person 1". A transfer takes place if the announcement is (when person 1 reports to be impatient), and is calculated using the implied distribution of . After such (positive or zero) transfer is made at position 1, the second person arrives and announces , and the process is repeated. After the last position, and after all impatient people have been paid, the planner finally learns the true state (assuming that everyone has reported truthfully). At this point there is no uncertainty to be dealt with: the planner uses the remaining reserves, augmented by output growth (at gross rate R), to finance consumption of patient individuals in the second date. It is for these reasons that consumption at date 1 has the form , being a function of , while consumption for date 2, is a function of the whole list .

The reader can by now anticipate that a person may be inclined to falsify his or her type, depending on details of the plan (x;y). There are two instances where this issue is important. First at the planning stage, we restrict the planner to choose (x;y) so as to satisfy a truth-telling constraint, according to which person i cannot gain by reporting to be type 0 if he or she is in fact type 1 and if all others are telling the truth. But this, an application of the revelation principle, does not imply that a type 1 person will report truthfully if all other patient people are lying (in what we call a bank run). We shall address this possibility numerically. Before getting to details we shall first be more explicit about how (x;y) is optimaly chosen.

The sequential-service requirement has thus shaped the domains of xi and yi. We notice that (x;y) is feasible if

and incentive-compatible if

that is, when patient individuals that are not informed of their positions agree with revelation.⁶

The planner's problem is that of maximizing the representative-agent utility, before types and positions are assigned,

subject to (1) and (2).

A realization is interpreted as the type-composition of a queue for being served by the bank. We assume that the probability distribution on types for someone in position i does not depend on the realized type for the person any other position. Therefore, if p (0;1) is a parameter, we assume that history has probability

where is the number of type-i individuals in history ,since and otherwise.

4. AN EXTENSION WITH INSOLVENCY

A fundamental feature of the economy presented in the previous section is that depositors, relative to what happens in monetary economies of the previous sections, are easily monitored. We now consider an extension in which the bank is not able to recognize people's identities during the whole first date. We also assume that it is possible for some patient people to make two successive contacts with the bank (as if they can secure two consecutive positions), and that this ability is granted to an individual with probability q > 0. These are the potential 'insiders' that can cause large losses to the financial system in case of a bank run. We also assume that, at the second date, the actions taken at date 1 are matched to the people claiming transfers at date 2. Hence the identities are recognized and matched to actions at the second date, but this may happen too late to make a difference in case of a run. In summary, the record of actions become updated with a lag, as in Kocherlakota and Wallace (1998). We shall see that the bank has to become more conservative. It has to keep a high level of reserves because some insiders may appear with a positive probability, and in order to keep these insiders away from embezzlement options the bank must increase interest rates with regards to the consumption of this subgroup.

The main purpose of this investigation is to show another side of weak implementation, meaning that stability programs should be taken seriously, using the basic ideas for calculating stability costs outlined in Bertolai and Cavalcanti (2012). For simplicity we focus below on some basic properties for this economy under weak implementation and independent shocks. We believe that, at least for small q, the main results about population increases apply. In what follows, we want to show how imperfect monitoring affects the level of insurance that can be provided, and the corresponding distortions. With this small change in the model, patient people will not be treated equally.⁷ And, we should keep in mind, that if runs are possible now, then it is demonstrated that a reasonably small change in the Diamond-Dybvig, following the contributions of Peck and Shell (2003) and Ennis and Keister (2009), can produce cases of insolvency in the sense that a group of people consume zero in equilibrium, thus facing in a very low utility in this scenario.

In the standard model, when actions are fully monitored, this double access assumed here would have no effect on optimal allocations: once date-1 consumption is first transferred to someone, and this person is identified at the second access, the optimum arrangement would trivially give no consumption at the second access. But the situation changes with the imperfect monitoring that we are assuming now. It is true that, under truth-telling, patient people will be led to consume at date 2, even those with the special abilities. But it is now important to convince the ones with double access to reveal their status freely. Under the current monitoring assumption, the bank is not able to detect this second access and, therefore, must distort allocations if it wants this information revealed.

The economy can be seen as populated by three types of agents. Type 0 individuals are impatient and have only one access to the bank. A person draws this type with probability p₀ = p. Patient agents with single access are designed by type 1. This is drawn with probability p₁ = (1 - p)(1 - q). Finally, double-access patient people are called type 2. This type occurs with probability p₂ = (1 - q)q. Since we are interested in computing optimal allocation under truth-telling beliefs, the second access can viewed as just a way for type-2 people to separate themselves from type 1. We shall see that we can leave the issue of double access confined to the introduction of a new truth-telling constraint, which allows us to keep the same structure with N access to the bank as before for much of the accounting that is needed. Accordingly, we set the aggregate state as , which occurs with probability

A mechanism is (x,y,z), where in addition to impatient date-1 consumption x and date-2 consumption y for type 1, it is introduced a date-2 consumption z for type 2. It is also useful to keep in mind that all type-2 individuals are, by assumption, necessarily patient. In a run they may want to withdraw resources that otherwise would be given to two impatient people. The list (x,y,z) is feasible if

where otherwise. It is incentive-compatible if

and

where The planner's problem is that of maximizing U(x,y,z), defined as

subject to (4), (5) and (6).

A computational method similar to that de scribed by Bertolai and Cavalcanti (2012) for the environment without insolvency can be designed for this economy. The main difference between the two cases is that the deviation payoff for type-2 individuals are not separable among positions [there are two transfers x_i and x_i+1 inside the utility function on the right-hand side of (6)]. In this situation the recursive formulation remains valid, but we are not able to get a closed solution for the optimal transfers at each position anymore. We propose to guess growth rates between xH and x_i+1, so that (6) becomes separable in positions. After computing optimal allocation using Bertolai and Cavalcanti (2012)' algorithm, we then iterate on growth rates guesses in order to achieve a numerical convergence to the true rates. The procedure is outlined in the ^{appendix A}.

4.1. Numerical findings

We first study how bank behavior under weak implementation is affected by the imperfect monitoring and double-access possibility. The following figure presents for some combinations (N,q) the expected interest rate type-2 individuals face when deciding to withdraw early or late. Specifically, if type-2 depositor is in position i he can consume x in date 1 in date 2. The ratio

is the relevant interest for him. Taking expectation in

_-i. and then in position i, we get the return measure presented in the figure. In these examples we consider symmetric utilities, so that marginal utility parameter for impatient type is A = 1. Remaining parameters are taken from Peck and Shell (2003) example: R = 1.05, p₀ = .5,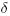 = 2, and y = 3.

It can be seen that the computed interest rate is decreasing in q. The figure also suggests that the interest rate is increasing in the population size N. The initial decreasing path follows from the fact that when N is very low, double access to the bank is not so effective. It is useful only on N - 1 of the N positions in the queue. For sufficiently high N, increasing interest rate holds.

Previous results can be interpreted in light of the analysis in Bertolai and Cavalcanti (2012). They show that increasing long term interest rate is the cheapest way to promote financial stability in the Diamond-Dybvig model. Here, society uses such instrument to avoid bank insolvency, by convincing type-2 individuals to not resort to their special ability. Zero consumption for some depositors is so damaging to society that it chooses to pay type-2 individuals to wait.

Next, we study the existence of pure-strategy run equilibria under the imperfect-monitoring assumption. In the next figure, parameters are the same used in the previous figure, except that now we keep N = 4 fixed and make A = 10, as in Peck and Shell (2003). The following figure presents, for some values of q and for each type of patient depositor, the difference of to the expected payoff in telling the truth (deviation from the run) to the expected payoff in lying (participating in the run) when patient depositor believes all other patient individuals are running. Because a run equilibrium exists when such measure is negative for both patient types, figure shows that there is a run equilibrium where type-1 and type-2 individuals withdraw early.

As previously discussed, patient behavior in this equilibrium makes insolvent the bank as long as there is a type-2 depositor. It is worth emphasizing the relevance of such result. Previous bank run models study illiquid banks subject to a mismatch between consumption needs and consumption allocation. In their run, the bank is always solvent. Our result provides a simple extension of the DD model in which insolvency is possible during a run equilibrium.

Our result also shows that previous results in the literature hold under imperfect monitoring. From the last figure and the next one, it is possible to conclude that our results on existence of run equilibria for low N depends on the assumed high A, as was the case in Peck and Shell (2003). The following figure presents again expected payoff in deviating from a run and keeps fixed q = .01 and A = 1.

It can be seen that type-1 individuals no more consider attractive to run, whereas a type-2 does. Then a run where all patient depositors lie is not an equilibrium. Nevertheless, population effects established by Bertolai et al. (2012) for the perfect monitoring case take place here. As N increases, type-1 individuals consider a deviation more and more attractive. A conjecture is that for sufficiently high N, the result of run existence holds again. Although not pursued here, verifying such conjecture is worth exploring, since the effect over type-2 depositors operate in the opposite direction and makes the result non-trivial.

The following table summarizes the basic results. It presents patient's expected payoff in telling the truth (net of the expected payoff in lying) when he or she believes that all other patient agents (type 1 and type 2) are lying. Parameterization is N = 5, = 2, p₀ = 1/2, y = 3, and R = 1.05. The table shows the effects of changes in q, the average fraction of insiders among patient individuals, and in A.

There are eight examples in the table, one for each pair (A,q). Accordingly, first rows (after labels row) refers to an economy in which A = 1, and first column (after column type) corresponds to an iid economy with perfect monitoring (PM) studied in Bertolai et al. (2012). It can be seen that there exists a complete (all patient runs) pure-strategy run only when A = 10. Such result is consistent with the PM iid case: there is not insurance enough to sustain a run equilibrium since A, ä, and N are low. This suggests that run equilibria is as easy to find in IM case as in the PM case. However, the fact that run strategy is always much more attractive for type-2 people is evidence that partial runs (in which only type 2 runs) can exist in economies where perfect monitoring would eliminate it. In this sense, a new source of instability emerges. Bertolai and Cavalcanti (2012) have shown that insurance level is the essence of run existence in the PM case. Now, a run would exist in economies with not so high insurance level, but with weaker monitoring capacity.

Increasing q from zero to 2% always decreases willingness to run since the relative payoff in telling the truth increases in all rows when changing columns from the left to the right. The reason is that the more likely type 2 is, more distortion is necessary to provide incentives to double-access people to tell the truth. Such distortions reduce insurance level and, therefore, the incentive to run.

5. FINAL REMARKS

In our introduction, we have motivated the need in macroeconomics of providing guidance to policies of liquidity provision. There is now a strong demand for understanding how money and banking frictions create difficulties for the provision of liquidity, and to what extent these frictions are important in a financial crisis like the recent one. We have quoted Sims as saying that this task will be challenging: not only crisis data are, by definition, scarce, but also popular models used by central banks can be described as story-telling devices that are not suitable for welfare analysis.

We then turned attention to recent work on the theory of money and banking seeking to capture financial frictions in ways consistent with welfare analysis. That consistency is assured by using the mechanism-design approach. Despite their attractive foundations, responses to liquidity shortages in these models can vary considerably. While work on inside money can recommend a reduction on the return of money, using inflation as a way to mitigate trade frictions, we have showed that, in banking models, liquidity provision should be cut in order to avoid insolvency. The obvious conclusion is that there is no clear principle to guide central-banking policies common to both models. In other words, even within the restricted subset of models compatible with welfare analysis, the debate about optimal responses to liquidity shortages is quite open.

We shall conclude this paper with few comments about the usefulness of the two models studied, and on the role of multiplicity of equilibria in shaping their conclusions. The first issue is whether we should use models with limited monitoring to study liquidity shortages. We have seen that the Diamond-Dybvig model of banking can be easily amended to include some form of imperfect monitoring. And that a particular form of imperfect monitoring can produce a bank-run outcome with zero consumption for a fraction of the population. We think that this kind of extension is valuable because every financial crisis displays episodes of bank insolvency or "default". Doing nothing about bank regulation can therefore have large welfare consequences in the extended model.

Also, imperfect monitoring is a cornerstone assumption for monetary theory. It is precisely because monitoring is limited in the random-matching model reviewed above that optimal allocations feature the actual use of fiat objects, instead of just forms of credit. This kind of models are also nice because they also allow for inside money, that is, they also allow for some form of credit to coexist with fiat objects since a subset of the population is perfectly monitored. And this coexistence justifies using some inside-money inflation for reasons related to the fact that imperfect monitoring always generate some heterogeneity. Given a heterogeneous distribution of promises, there is thus a possibility that interventions improve trade by improving that distribution.

Imperfect monitoring is a reasonable assumption in the field of money and banking. The two classes of models studied above, however, disagree about optimal interventions on intertemporal rates of return because they emphasize different notions of implementability. Initially the analysis of the optimal contract in both models was guided by weak implementation. In this case, one asks what kind of rules are incentive compatible, and from this set one looks of the ones that reach the highest expected utility on average. We have seen that for some parameters it is desirable to improve the purchasing power of the consumer (in the money model), or of the impatient depositor (in the banking model). For that, the planner taxes people with above-average money holdings (using lotteries if necessary) or the patient depositor; these are the people effectively providing liquidity insurance in both models. But differently from the money model, however, the banking model includes a second question: is the (weakly) optimal allocation subject to multiplicity? It is the answer of this second question, in the affirmative, that implies a reduction in the provision of liquidity in the banking model.

A reasonable surmise is that theory should try to introduce not only imperfect monitoring in models of money and banking, but also consider issues of multiplicity with regards to both money and banking arrangements. With that kind of development, the discussion of interventions in response to a financial crisis should improve our confidence on welfare analysis in macroeconomics.

BIBLIOGRAPHY

Bertolai, J. D. P. & Cavalcanti, R. O. (2012). High interest rates: the golden rule for bank stability in the Diamond-Dybvig model. In Jefferson D. P. Bertolai. PhD Thesis: Essays on Monetary and Banking Theory, pages 26-50.

Bertolai, J. D. P., Cavalcanti, R. O., & Monteiro, P. K. (2012). Transitions when money distribution matters. In Jefferson D. P. Bertolai. PhD Thesis: Essays on Monetary and Banking Theory, pages 14-25.

Cavalcanti, R. & Nosal, E. (2009). Some benefits of cyclical monetary policy. Economic Theory, 39(2):195-216.

Cavalcanti, R. O. & Wallace, N. (1999). Inside and Outside Money as Alternative Media of Exchange. Journal of Money, Credit and Banking, 31(3):443-57.

Deviatov, A. (2006). Money Creation in a Random Matching Model. The B.E. Journal of Macroeconomics, Topics.6(3):5.

Deviatov, A. & Wallace, N. (2009). A model in which monetary policy is about money. Journal of Monetary Economics, 56(3):283-288.

Deviatov, A. & Wallace, N. (2010). Interest on Cash with Endogenous Fiscal Policy. Working Papers 2010-012, Becker Friedman Institute for Research In Economics.

Deviatov, A. & Wallace, N. (2012). Optimal Inflation in a Model of Inside Money. Unpublished manuscript.

Ennis, H. M. & Keister, T. (2009). Run equilibria in the Green-Lin model of financial intermediation. Journal of Economic Theory, 144(5):1996-2020.

Green, E. J. & Lin, P. (2003). Implementing efficient allocations in a model of financial intermediation. Journal of Economic Theory, 109(1):1 - 23.

Green, E. J. & Zhou, R. (2005). Money As A Mechanism In A Bewley Economy. International Economic Review, 46(2):351-371.

Kehoe, T. J., Levine, D. K., & Woodford, M. (1992). The Optimum Quantity of Money Revisited. In Dasgupta, P., Gale, D., Hart, O., & Maskin, E., editors, Economic analysis ofmarkets and games: Essays in honor of Frank Hahn, pages 501-526. MIT Press.

Kiyotaki, N. & Wright, R. (1989). On Money as a Medium of Exchange. Journal of Political Economy, 97(4):927-54.

Kocherlakota, N. & Wallace, N. (1998). Incomplete Record-Keeping and Optimal Payment Arrangements. Journal of Economic Theory, 81(2):272-289.

Levine, D. K. (1991). Asset trading mechanisms and expansionary policy. Journal of Economic Theory, 54(1):148-164.

Molico, M. (2006). The Distribution Of Money And Prices In Search Equilibrium. International Economic Review, 47(3):701-722.

Peck, J. & Shell, K. (2003). Equilibrium Bank Runs. Journal of Political Economy, 111(1):103-123.

Wallace, N. (1988). Another attempt to explain an illiquid banking system: the Diamond and Dybvig model with sequential service taken seriously. Quarterly Review, 1(Fall):3-16.

Wallace, N. (2012). The Optimality of inflation in 'Pure Currency' Economies: A Conjecture. Unpublished manuscript.

Wallace, N. (2013). An alternative to New-Keynesian models for the study of optimal (monetary) policy. Unpublished manuscript.

for type-1 individuals, and

for type-2 individuals. Let be the growth rate of withdrawals between positions i and i + 1 when previous history of announcements is w^i-1. Therefore, we have p(w) = 0 and

follows that

Analogous algebra shows that

Therefore, the lagrangian for the imperfect monitoring case can be written as

where and If p is known for every possible w^i-1, then Bertolai and Cavalcanti (2012)'s algorithm can be applied to calculate optimal allocation. This follows from lagrangian linearity in individuals utilities. The innovation here resides on computing a fixed point for p.

Proposition A.l. Suppose that and p are known. Then the optimum value for the lagrangian is

where /'s are calculated using

and by the initial condition

Proof. Collecting terms for date-2 consumptions in history w, and using equal treatment among type 1 and among type 2, we have that planner must choose how to allocate an amount a(w)R between patient types in date 2

The solution is easily seen to be which produces optimal value

Consider planner choice before the last position and after partial history If a denotes the amount in the bank at this moment, then

Optimal solution is a(w,0)

Now, plugging these solutions in the objective function we have optimal value

Similar algebra can be used to get the result.

Previous result shows that if p is known, we are able to compute optimal solution relative to A by iterating object f_n. However, we generally do not know such growth rates. What we do is to is to guess this function. After computing a solution relative to this guess, we verify if the rates defined by the current solution and this function agree. If not, we use this new set of rates as a guess for the next step. This procedure is repeated until convergence. After convergence, we evaluate violation in truth-telling constraints and update multipliers ifnecessary.

Last step discussed above, requires computing truth-telling constraints under candidate optimal solution. The following lemma establishes a recursive way to compute it.

Lemma A.2. Let (x*,y*,z*) be the candidate optimal solution. Then

where g_N+₁can be computed using initial condition and recursive relation

where w = w^i-1 ;

(ii) type-1 truth-telling slackness equals

where hN+1 can be computed using initial condition and recursive relation

where w = w^i-1.

Proof. This can be established by just plugging optimal solution in w_t, from the end of the queue to its beginning. Remember that w₂(x,z) equals

Date-2 utility for a given history w is

It follows that

Integrating in w_N, and denoting and a = a(w), we have

Similar algebra can be used to get the result for type-2 individual. The proof for type-1 individuals is analogous and is omitted. □

After computing optimal allocation, it can be of interest to study the existence of run equilibria. In what follows we present accountability for complete run equilibrium, where all patient individuals lie. If a patient lies in this situation he consumes in the first date, as in the standard version of DD model. But now, double accesses during a run increase probability of withdrawing late in the queue. Specifically, the i-th individual to contact the bank is not able to withdraw payment designed to positions before position Therefore, expected payoff in lying during a run for type-1 individual is

where Xj = 0 for j > N. For type-2 patient depositor, we have

where p(-)'s account for double accesses.

When telling the truth, individual consumes in date 2. But again, the i-th individual in the queue access the bank only in position Therefore, expected payoff in telling the truth during a run for type-1 individual is

where yj = 0 for j > N. Analogously, we have for type-2 patient depositor

where yj =0 for j > N. That way, a run equilibrium exists if (A—1) is greater than (A—3) and (A—2) is greater than (A — 4). Although zero consumption is possible, making expected utility unbounded under CRRA specification, for the matter of run-existence accountability this does not imply difficulties. This is so because decision to participate or or not in the run does not affect zero consumption possibilities. It is previous double accesses that fully determine them.

A. APÊNDICE  A. THE IMPERFECT-MONITORING ALGORITHM

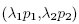for constraints (5) and (6) are known. In what follows, we present how recursive computation of optimal allocations deals with the difficulties implied by non-separability of date-1 consumption for type-2 individuals. First, remember that truth-telling slackness is

Opposite policy implications in the theory of money and banking

Jefferson D. P. Bertolai^I; Ricardo de O. Cavalcanti^II

1

The following specification is used: utility function

u(y) = 1 - e ^10y, cost in producing c(y) = y, and number of goods K = 3. Intertemporal discount factor is

â = .59 and first-best output is y* = ln(10)/10 a .23.

2

In general, when lotteries and planner's monetary transfers are not used, incentive constraint for n-type producer with i units of money is

where y is the production level, and

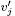is the indirect utility in holding j units of money at the beginning of the next period. Incentive constraint for n-type consumer with i units of money is

3

Deviatov and Wallace (2010) study desirability of interest on cash and the use of taxing on monitored people (fiscal policy) to increase the return of money to non-monitored people.

4

The specification is the same one used in Table 2's example.

5

In addition, inflation is omitted.

6

The expectations in (2) are taken with respect to the distribution of w_

_i on {0,1}

^N-1, given that

í¿h

= 1.

⁷

Bertolai and Cavalcanti (2012) also find unequal treatment of patient people under weak implementation for the conventional Peck-Shell economy when there is persistence in depositor type through the queue and

p = 2, for the Green-Lin economy with independence and active constraints, and under strong implementation for Peck-Shell economies with persistence.

8

Again, expectations are conditional on w¿ =

k for

k = 1 in (5) and

k = 2 in (6).

Publication Dates

• Publication in this collection
  26 Nov 2013
• Date of issue
  Dec 2013