Resumos
A utilização de técnicas não-destrutivas (NDT) pode incrementar o nível de informação tecnológica sobre espécies de madeira conhecidas, bem como daquelas ainda não estudadas. A principal vantagem das técnicas NDT é que são rápidas e várias medidas podem ser feitas, melhorando assim o nível de confiança dos resultados. Nesse contexto, o trabalho objetivou avaliar a viabilidade de utilização da técnica de ondas de tensão na estimativa de propriedades de flexão de seis espécies de madeiras amazônicas. As espécies foram escolhidas com base na sua densidade: Balfourodendron riedelianum, Cedrela fissilis, Cordia goeldiana, Bowdichia virgilioides, Dipteryx odorata and Tabebuia sp. Foram obtidas vinte amostras por espécie nas dimensões segundo ASTM D143-94 para a determinação das propriedades de flexão, totalizando assim 120 amostras. Antes do ensaio destrutivo em flexão estática, as amostras foram avaliadas não-destrutivamente por meio da técnica de ondas de tensão para a determinação do módulo de elasticidade dinâmico e a velocidade de propagação das ondas tensão. De acordo com os resultados, os modelos de regressão foram altamente significativos para a predição das propriedades de flexão do conjunto de espécies. Dessa forma, pode-se concluir que o método é adequado para predizer as propriedades de flexão onde há variação, por exemplo, entre espécies. No entanto, quando a variabilidade é baixa, como dentro da espécie, os modelos apresentaram baixa previsibilidade.
avaliação não-destrutiva; propriedades de flexão; madeiras tropiciais
The utilization of non-destructive testing (NDT) can augment the technological information about well-known wood species, as well as those which have not yet been investigated. The main advantage is that NDT methods are fast, and many measures can be undertaken to improve the confidence level of the evaluation. In this context, the paper aims to study the feasibility of the stress wave method to estimate flexural properties of six Brazilian tropical woods. The species were chosen according to density: Balfourodendron riedelianum, Cedrela fissilis, Cordia goeldiana, Bowdichia virgilioides, Dipteryx odorata and Tabebuia sp. Twenty samples from each species were cut and tested according to ASTM D143-94 (2000) to determine flexural properties, totaling 120 samples. Before mechanical testing, the samples were non-destructively tested by using the stress wave method, and their dynamic modulus of elasticity (Ed) and wave velocity (w v) were determined. Stepwise multiple linear regression analysis was run to select the best variables for estimating the flexural properties. According to the results, the models generated had higher values of R². Thus, it can be concluded that the stress wave method is suitable for predicting flexural properties where there is wood variability, for instance among species. On the other hand, when the variability is low, for instance within wood species, the models generated had low predictability.
nondestructive evaluation; tropical hardwoods; flexural properties
CIÊNCIAS FLORESTAIS
Estimativa das propriedades de flexão estática de seis espécies de madeiras amazônicas por meio da técnica não-destrutiva de ondas de tensão
Predicting flexural properties of six Amazonian hardwoods using stress wave nondestructive method
Cláudio Henrique Soares DEL MENEZZII, Rafael Rocha SILVEIRAII, Mário Rabelo de SOUZAIII
IUniversidade de Brasília - UNB, E-mail: cmenezzi@unb.br
IIUniversidade de Brasília - UNB, E-mail: rafaelrsilveira@gmail.com
IIIServiço Florestal Brasileiro - SFB, Email: mario.souza@florestal.gov.br
RESUMO
A utilização de técnicas não-destrutivas (NDT) pode incrementar o nível de informação tecnológica sobre espécies de madeira conhecidas, bem como daquelas ainda não estudadas. A principal vantagem das técnicas NDT é que são rápidas e várias medidas podem ser feitas, melhorando assim o nível de confiança dos resultados. Nesse contexto, o trabalho objetivou avaliar a viabilidade de utilização da técnica de ondas de tensão na estimativa de propriedades de flexão de seis espécies de madeiras amazônicas. As espécies foram escolhidas com base na sua densidade: Balfourodendron riedelianum, Cedrela fissilis, Cordia goeldiana, Bowdichia virgilioides, Dipteryx odorata and Tabebuia sp. Foram obtidas vinte amostras por espécie nas dimensões segundo ASTM D143-94 para a determinação das propriedades de flexão, totalizando assim 120 amostras. Antes do ensaio destrutivo em flexão estática, as amostras foram avaliadas não-destrutivamente por meio da técnica de ondas de tensão para a determinação do módulo de elasticidade dinâmico e a velocidade de propagação das ondas tensão. De acordo com os resultados, os modelos de regressão foram altamente significativos para a predição das propriedades de flexão do conjunto de espécies. Dessa forma, pode-se concluir que o método é adequado para predizer as propriedades de flexão onde há variação, por exemplo, entre espécies. No entanto, quando a variabilidade é baixa, como dentro da espécie, os modelos apresentaram baixa previsibilidade.
PALAVRAS-CHAVE: avaliação não-destrutiva, propriedades de flexão, madeiras tropiciais.
ABSTRACT
The utilization of non-destructive testing (NDT) can augment the technological information about well-known wood species, as well as those which have not yet been investigated. The main advantage is that NDT methods are fast, and many measures can be undertaken to improve the confidence level of the evaluation. In this context, the paper aims to study the feasibility of the stress wave method to estimate flexural properties of six Brazilian tropical woods. The species were chosen according to density: Balfourodendron riedelianum, Cedrela fissilis, Cordia goeldiana, Bowdichia virgilioides, Dipteryx odorata and Tabebuia sp. Twenty samples from each species were cut and tested according to ASTM D143-94 (2000) to determine flexural properties, totaling 120 samples. Before mechanical testing, the samples were non-destructively tested by using the stress wave method, and their dynamic modulus of elasticity (Ed) and wave velocity (wv) were determined. Stepwise multiple linear regression analysis was run to select the best variables for estimating the flexural properties. According to the results, the models generated had higher values of R2. Thus, it can be concluded that the stress wave method is suitable for predicting flexural properties where there is wood variability, for instance among species. On the other hand, when the variability is low, for instance within wood species, the models generated had low predictability.
KEYWORDS: nondestructive evaluation, tropical hardwoods, flexural properties.
INTRODUÇÃO
A utilização de técnicas não-destrutivas (NDT) para o estudo da madeira e de seus subprodutos é bastante difundida, e remonta desde a década de 1960. A técnica NDT pode ser definida como sendo aquela que identifica propriedades físicas e mecânicas de materiais sem alterar sua capacidade de uso final, para em seguida usar essa informação na tomada de decisão com relação a uma aplicação apropriada (Pellerin & Ross, 2002). O grande diferencial da NDT em relação à caracterização destrutiva é a rapidez na obtenção da informação com um menor volume de trabalho. Segundo Pellerin & Ross (2002) as principais técnicas NDT utilizadas para madeira são: colorimetria, resistência elétrica, propriedades dielétricas, propriedades vibracionais, ondas acústicas, raio-x e propagação de ondas. Na atualidade técnicas NDT são empregadas adequadamente na avaliação da integridade estrutural de edificações e de obras em madeira, como bem apresentam Ross et al. (2004) e Valle et al. (2004). No entanto, entre as técnicas mais empregadas estão aquelas baseadas nas características acústicas da madeira, tais como: propagação de ondas de tensão, ondas de ultrassom e vibração transversal.
O ultrassom é uma técnica que se baseia no princípio de aplicação de ondas inaudíveis pelo homem, em madeiras para a determinação de suas constantes elásticas. Assim, a onda ultra-sonora é emitida em determinada direção e ao encontrar um obstáculo à sua livre propagação, é refletida por ele, voltando ao aparelho emissor. Conhecendo-se a velocidade e propagação e a densidade do material é possível calcular sua constante elástica. No Brasil Vários trabalhos têm sido desenvolvidos empregando-se essa técnica: Oliveira et al. (2005), Miná et al. (2004), Nogueira & Ballarin (2002), Oliveira et al. (2002) e Gonçalez et al. (2001). Já a técnica de vibração transversal, parte do princípio que os materiais possuem uma freqüência natural à qual vibram. Um significante desvio desta vibração teórica natural é um indicador de um possível dano ou defeito neste material. Para a madeira, essa técnica tem sido usada para a determinação do módulo de elasticidade. Podem-se citar alguns trabalhos desenvolvidos no Brasil: Teles (2009), Targa et al. (2005), Calil Jr. JR & Miná (2003), e Zangiácomo (2003).
Por outro lado, no método de ondas de tensão a velocidade de propagação de uma onda de tensão induzida e sua atenuação no material são os principais parâmetros analisados nessa técnica. Baseia-se na teoria de propagação de ondas unidirecionais em uma barra homogênea e elástica. A aplicação de um impacto em umas das extremidades da barra gera uma onda que imediatamente movimenta-se ao longo do comprimento da barra. A onda percorre toda a extensão da barra a uma velocidade constante sendo captada na outra extremindade (Gorniak & Matos, 2000). Em nível de Brasil podem-se citar os seguintes trabalhos desenvolvidos a partir dessa técnica: Ferraz et al. (2009), Del Menezzi et al. (2007), Cruz (2006), Gabriel & Ballarin (2001) e Matos & Keinert (1998). Este método pode ser empregado para diversas finalidades, entre estas: estimativa de propriedades mecânicas, avaliação do grau de ataque biológico, classificação de lâminas e de madeira, etc. Ross e Pellerin (1994) usaram o método de ondas de tensão para determinar a velocidade da transmissão da onda, detectando indiretamente a presença de organismos xilófagos na madeira. Para alguns tipos de madeira, obtiveram resultados de até 93% de detecção de bactérias presentes na mesma. Ross et al. (1999) apresentaram a possibilidade de inspeção de pontes de madeira por meio da medição do tempo de propagação da onda de tensão.
Evidencia-se assim que um dos usos mais consagrados das técnicas NDT é na determinação da rigidez de peças de madeira sólida e de produtos compostos visando sua classificação. Entretanto, o estudo de madeiras tropicais é relativamente escasso, podendo-se citar Ravenshort et al. (2008) que empregaram ondas de tensão, enquanto Gonçalves & Costa (2008), Karlanasari et al. (2008), Oliveira et al. (2005), Oliveira et al. (2002) e Gonçalez et al. (2001) utilizaram ultrassom e Teles (2009) e Ilic (2003) vibração transversal.
Nesse contexto, o objetivo do trabalho foi de avaliar a viabilidade da estimativa das propriedades de flexão de seis espécies amazônicas por meio da técnica de ondas de tensão.
MATERIAIS E MÉTODOS
Material Lenhoso
Foram escolhidas seis espécies de madeira tropicais, da região amazônica, disponíveis no mercado madeireiro do Distrito Federal, observando-se as variações de densidade aparente. As espécies escolhidas foram: pau-marfim (Balfourodendron riedelianum (Engl)), cedro (Cedrela fissilis Veli.), freijó (Cordia goeldiana Huber), cumaru (Dipteryx odorata (Aubl.) Wild), sucupira (Bowdichia virgilioides H.B.K.) e ipê (Tabebuia sp.). Inicialmente, as pranchas foram identificadas macroscopicamente comparando-se com o material disponível na Xiloteca (Index Xilarium FPBw) do Setor de Anatomia da Madeira, do Laboratório de Produtos Florestais do Serviço Florestal Brasileiro (LPF/SFB). Em seguida as pranchas foram desdobradas para obtenção de 20 corpos-de-prova (CP) por espécie nas dimensões de 25 x 25 x 410 mm3 (l x e x c), segundo a norma ASTMD143-94 (2000) (Figura 1a). O desdobro foi orientado de forma a produzir CPs com seção transversal no esquadro e com duas faces radiais e duas faces tangenciais opostas entre si. Em seguida, os CPs foram acondicionados em câmara climática (65% UR; 20ºC) até atingirem peso constante.
Avaliação Não-destrutiva e Propriedades de Flexão
Os CPs foram avaliados não-destrutivamente por meio da técnica de ondas de tensão empregando-se o equipamento Stress Wave Timer 239A (Metriguard Inc.), que mede o tempo de propagação de uma onda de tensão pelo CP. A onda de tensão é induzida por um martelo, que na condição de laboratório, é representado por um pendulo fixado no conjunto de braçadeiras. O acelerômetro (Figura 1B-1), que está na condição de início, percebe o pulso da onda e o transforma em um sinal elétrico, que é enviado para console (Figura 1B-3), que por sua vez inicia a contagem do tempo. A onda percorre todo o corpo-de-prova até atingir o outro acelerômetro (Figura 1B-2) que então envia um sinal elétrico para a console que interrompe a contagem. O tempo decorrido é mostrado em tela de cristal líquido, no formato de microssegundos.
Desta forma, conhecendo-se o tempo, a densidade da madeira e a distância percorrida, foi determinado a velocidade de propagação da onda (vo) e o módulo de elasticidade dinâmico (Ed) no sentido longitudinal do corpo-de-prova (// às fibras) segundo as equações 1 e 2.
Onde:
vo = velocidade de propagação da onda, m/s;
Ed = módulo de elasticidade dinâmico, N/mm2;
L = distância percorrida pela onda, m;
T = tempo de trânsito da onda; μs
D = densidade da madeira; kg/m³;
g = aceleração da gravidade, 9,804 m/s²;
A distancia pré-determinada foi igual ao vão (L=14e) de ensaio indicado pela norma ASTM D143-94 (2000), para o ensaio de flexão estática. Em cada CP foram feitas três leituras do tempo de propagação da onda. O valor usado para o cálculo da velocidade correspondeu à média aritmética dos tempos. Após essa avaliação não-destrutiva, os CPs foram ensaiados em flexão estática até a ruptura segundo os procedimentos da norma ASTM D143-94 (2000) determinando-se assim módulo de elasticidade (EM), módulo de ruptura (fM), carga máxima (Pmáx), tensão no limite proporcional (Tlim) e carga no limite proporcional (Plim).
Análise estatítica
Inicialmente os dados obtidos foram analisados estatisticamente por meio de análise de variância (ANOVA), seguida de teste de Tukey a 5% para verificar a existência de diferenças significativas entre as espécies de madeira. Em seguida, foi feita análise de correlação de Pearson (r) entre todas as propriedades para se avaliar a adequação do modelo linear de regressão. Posteriormente os dados de Ed, vo, EM, fM, Pmáx, Plim, Tlim foram utilizados para gerar um modelo de regressão linear simples (y = a +bx). Nesta análise foi utilizado o método stepwise, onde Ed e Vo foram as variáveis independentes (x) enquanto Plim, Pmáx, Tlim, EM e fM, as variáveis dependentes (y). Essa análise de regressão foi feita para cada espécie individualmente (N=20) e também entre as seis espécies de madeira (N=120).
RESULTADOS E DISCUSSÃO
Propriedades das Madeiras
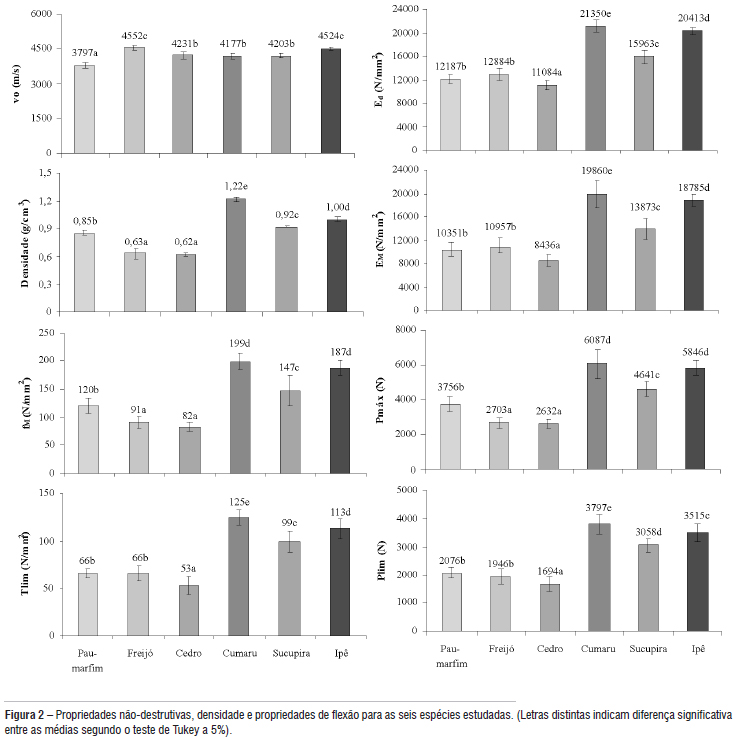
Na Figura 2 estão apresentados os resultados das propriedades não-destrutivas, densidade e propriedades de flexão das seis espécies estudadas. Como era de se esperar o teste de Tukey apontou diferenças significativas entre as espécies para todas as propriedades estudadas. Embora o cedro e o freijó tenham a mesma densidade, a velocidade de propagação da onda (vo) e o módulo de elasticidade dinâmico (Ed) foram diferentes.
Neste caso deve-se observar a vo, pois no cálculo de Ed ela também exerce influência. Contudo isto não explica como o pau-marfim e o freijó tendo vo e densidades diferentes resultaram em um mesmo Ed. Para este caso a igualdade de Ed provavelmente valeu-se de uma compensação entre a densidade e vo, isto é a maior vo do freijó compensou sua menor densidade, ao passo que a maior densidade do pau-marfim compensou sua menor vo. Sucupira, ipê e cumaru se comportaram de maneira semelhante, sendo representada para a maioria das características com as letras C, D e E respectivamente. As diferenças observadas entre os valores de Ed e vo para as espécies são provavelmente oriundas das diferenças anatômicas entre as mesmas, e será discutido mais a frente. Para verificar o nível de relacionamento das variáveis entre si e seu comportamento linear foi calculado o coeficiente de correlação de Pearson, cujos resultados estão apresentados na Tabela 1.
Pode-se destacar da Tabela 1 as fortes correlações entre a variável densidade com as variáveis, Ed, EM e fM. A correlação entre o módulo de elasticidade dinâmico (Ed) e o módulo de elasticidade estático (EM) apresentou valor de correlação igual a 0,954 ao nível α=0,01. Evidencia-se também que não houve relação entre a velocidade de propagação da onda de tensão e a densidade da madeira. Era de se esperar que, maior densidade, maior continuidade do material, e consequentemente maior velocidade da onda. Entretanto, de fato, essa relação direta não tem sido observada por outros autores. Oliveira et al. (2002) estudando espécies densas por meio da técnica de ultrasom obteve velocidade de onda de 4514 m/s para cupiúba (Goupia glabra, 0,83 g/cm3) and 4279 m/s para jatobá (Hymenaea sp., 1,15 g/cm3). Ilic (2003) avaliou o módulo de elasticidade dinâmico de 55 espécies madeireiras, compreendendo nove espécies de folhosas da América do Sul e da África. Para este grupo de espécie, embora a densidade tenha apresentado um grande variação (0,097 g/cm3 a 0,855 g/cm3), a velocidade da onda apresentou apenas uma pequena variação: 4210 m/s a 5540 m/s. Segundo o autor, o ângulo microfibrilar (AMF) da camada S2 da parede secundária teve uma clara influência sobre a velocidade de propagação das ondas de tensão. Desta forma, quanto menor o AMF, maior a velocidade de propagação da onda, o que segundo o autor explica porque a espécie Ochroma lagopus (0,097 g/cm3) apresentou velocidade próxima àquela observada em espécies mais densas, mas cujo AMF era maior.
Segundo Feeney et al. (1998) quando se descreve a propagação de ondas acústicas em materiais anisotrópicos como a madeira, considera-se que o material é homogêneo em cada um de seus eixos estruturais. Entretanto, é bem sabido que a madeira é naturalmente um material não-homogêneo, anisotrópico e, portanto a dissipação das ondas acústicas é maior que aquela observada em materiais homogêneos. Nesse contexto, depreende-se que os caracteres anatômicos macroscópicos e a microestrutura da madeira são a fonte da anisotropia da madeira, e, portanto da dissipação das ondas acústicas, como afirmam Bucur & Declerq (2006).
Estimativas das Propriedades de Flexão
A estimativa das propriedades de flexão foi feita em duas partes: primeiro foram analisadas as variáveis de forma agrupada, ou seja, reunindo todas as espécies em um único grupo com 120 observações. Em seguida foi analisada separadamente por espécie.
Análise agrupada
A análise de todas as espécies em um único conjunto de 120 observações mostrou ótimos resultados na estimativa das propriedades de flexão, quando o módulo de elasticidade dinâmico foi utilizado como estimador das propriedades de flexão (Figura 3). Na estimativa do módulo de elasticidade estático (EM), o Ed explicou a 91,1% da variação dos dados observados.
O modulo de ruptura (fM) teve 86,3% de sua variação explicada, enquanto a carga máxima (Pmáx), carga no limite proporcional (Plim) e a tensão no limite proporcional (Tlim) tiveram R2 superiores a 80%. Para todas as propriedades avaliadas, os modelos que utilizaram o Ed como estimador foram significativos ao nível de α=0,01. Deve-se destacar que a utilização de apenas vo na estimativa das propriedades de flexão no conjunto das espécies foi adequada apenas para EM.
Análise por Espécie
A Tabela 2 apresenta os modelos obtidos para a estimativa das propriedades de flexão das espécies individualmente, ou seja, dentre as espécies. Observa-se que das seis espécies estudadas, apenas para pau-marfim foi possível gerar modelos estatisticamente significativos para todas as propriedades de flexão avaliadas, para sucupira para quatro propriedades, enquanto que para cumaru e freijó apenas dois modelos significativos foram gerados.
Por outro lado, para o ipê nenhum modelo foi estatisticamente significativo. Observa-se que fM e Pmáx foram as propriedades de flexão que apresentaram o maior número de modelos estatisticamente significativos (4), enquanto as demais apenas 2 modelos. Deve-se salientar, que se fossem gerados modelos para todas as seis espécies para a cinco propriedades de flexão estudadas, ter-se-ia 30 modelos. No entanto, de acordo com os resultados da Tabela 2, apenas 14 modelos estatisticamente significativos puderam ser gerados, ou seja, menos da metade. Os coeficientes de determinação desses modelos podem se considerados baixos, frequentemente menores que 0,5. Exceção foi observada para a estimativa de EM do pau-marfim e do fm para o freijó (Figura 4). Dessa forma, as variáveis de dinâmicas vo e Ed explicam apenas parte da variação das propriedades de flexão dessas espécies, e outras variáveis, não avaliadas nesse estudo podem estar influenciando.
Oliveira et al. (2002) obtiveram R2 variando de 0,36 a 0,63 para a relação entre propriedades de flexão e coeficiente ultra-sônico (CLL) para Goupia glabra e Hymenea sp.. Ravenshorst et al. (2008) estudaram nove madeiras tropicais oriundas da América do Sul e África por meio da técnica de ondas de tensão. Os resultados apontaram para um R2=0,63 para a estimativa da rigidez. Argumentam que segundo os resultados não foi possível obter modelos precisos para as espécies individualmente, contrariamente do que pode ser obtido, por exemplo, para coníferas.
A explicação para os resultados obtidos na análise dentro de espécies talvez possa ser a baixa variabilidade observada para as propriedades de cada uma das espécies, como pode ser inferido pelas linhas de desvio padrão da Figura 2. Dessa forma, o método de ondas de tensão é mais preciso quando se tem variação mais acentuada das propriedades, como ocorrido quando se fez a análise entre as espécies, cujos R2 foram bastante significativos. Teles (2009) empregou três métodos não-destrutivos para avaliar a rigidez em tábuas da espécie louro-vermelho (Sextonia rubra), cujas densidades variavam de 0,53 a 0,85 g/cm3. Observou R2 superior a 0,83 para o método de ondas de tensão.
CONCLUSÕES
De maneira geral o módulo de elasticidade dinâmico Ed é um ótimo estimador das propriedades de flexão de madeiras tropicais, quando há variabilidade entre as espécies;
Por outro lado, quando a variabilidade é pequena, como dentro de uma mesma espécie, os modelos para estimativa das propriedades de flexão apresentaram baixa previsibilidade;
A análise por espécie feita neste trabalho demonstrou a necessidade de uma maior quantidade de amostras e que estas sejam originadas de árvores diferentes, para que assim a amostragem fique mais representativa para espécie estudada.
BIBLIOGRAFIA CITADA
Recebido em 05/02/2009
Aceito em 08/09/2009
- ASTM. 2000. Standard Test Methods for small clear specimens of timber. West Conshohocken. D143.
- Bucur, V.; Declerq, N. F. 2006. The anisotropy of biological composites studied with ultrasonic technique. Ultrasonics, 44: 829-831.
- Calil Jr. C.; Miná, A. J. S. 2003. Transverse vibration: An efficient method for structural timber classification. Revista Brasileira de Engenharia Agrícola e Ambiental, 7: 333-338. 2003. (in Portuguese, with abstract in English)
- Cruz, C.R. 2006. Utilization of stress waves for estimating the moisture content of the eucalytus wood. Tese de Doutorado, Universidade Federal do Paraná, Curitiba, 72 pp. (in Portuguese).
- Del Menezzi, C.H.S.; Tomaselli, I.; Souza, M.R. 2007. Non-destructive evaluation of thermally modified OSB: part 1 - effect of the thermal treatment on the stress wave velocity. Scientia Forestalis, 76: 67-75. (in Portuguese, with abstract in English)
- Feeney, F. E.; Chivers, R. C.; Evertsen, J. A.; Keating, J. (1998). The influence of inhomogeneity on the propagation of ultrasound in wood. Ultrasonics, 36: 449-453.
- Ferraz, J.M.; Del Menezzi, C.H.S.; Teixeira, D.E.; Okino, E.Y.A.; Souza, F.; Bravim, A.G. 2009. Properties of laminated strands panels used as an alternative to solid wood. Cerne, 19: 67-74. (in Portuguese, with abstract in English)
- Gabriel, M.S.C.; Ballarin, A.W. 2001. Mechanical characterization of Pinus taeda wet wood by stress wave non-destructive method. Energia na Agricultura, 16: 8-16. (in Portuguese, with abstract in English)
- Gonçalez, J.C.; Vale, A.T.; Costa, A.F. 2001. The use of ultrasonic method for estimating wood elastic constants. Cerne, 7: 81-92. (in Portuguese, with abstract in English)
- Ilic, J. 2003. Dynamic MOE of 55 species using small wood beams. Holz als Roh- und Werkstoff, 61: 167-172.
- Karlinasari, L.; Wabyuna, M.E.; and Nugroho, N. 2008. Non-destructive ultrasonic testing method for determining bending strength properties of Gmelina wood (Gmelina arborea). Journal of Tropical Forest Science 20: 99-104.
- Matos, J.L.M.; Keinert Jr, S. Utilization of wave acoustic emission for veneer grading and laminated veneer lumber production. In: ENCONTRO BRASILEIRO EM MADEIRAS E ESTRUTURAS DE MADEIRA, VI, Florianópolis, 1998. Anais. Florianópolis, IBRAMEM/UFSC. v.4, p.331-341.
- Miná, A.J.S.; Oliveira, F.G.R.; Calil Jr., C.; Dias, A.A.; Sales, A. 2004. Nondestructive evaluation of logs using ultrasonic technique. Scientia Forestalis, 65: 188-196. (in Portuguese, with abstract in English)
- Nogueira, M.; Ballarin, A.W. 2002. Relationship between static modulus of elasticity (bending) and dynamic (ultrasonic) for some eucalypts species. Floresta, 33: 19-25. (in Portuguese, with abstract in English)
- Oliveira, F.G.R; Candian, M.; F.F.Lucchette, J.L. Salgon, A. Sales. 2005. A technical note on the relationship between ultrasonic velocity and moisture content of Brazilian hardwood (Goupia glabra). Building and Environment 40: 297-300.
- Oliveira, F.G.R; Campos, J.A.O.; Sales, A.. 2002. Ultrasonic measurements in Brazilian hardwood. Materials Research 5: 51-55.
- Pellerin, R.F.; Ross, J.R. 2002. Nondestructive evaluation of wood. FPS. Madison. p.210.
Datas de Publicação
-
Publicação nesta coleção
19 Ago 2010 -
Data do Fascículo
2010
Histórico
-
Aceito
08 Set 2009 -
Recebido
05 Fev 2009