ABSTRACT
The spatial distribution of forest biomass in the Amazon is heterogeneous with a temporal and spatial variation, especially in relation to the different vegetation types of this biome. Biomass estimated in this region varies significantly depending on the applied approach and the data set used for modeling it. In this context, this study aimed to evaluate three different geostatistical techniques to estimate the spatial distribution of aboveground biomass (AGB). The selected techniques were: 1) ordinary least-squares regression (OLS), 2) geographically weighted regression (GWR) and, 3) geographically weighted regression - kriging (GWR-K). These techniques were applied to the same field dataset, using the same environmental variables derived from cartographic information and high-resolution remote sensing data (RapidEye). This study was developed in the Amazon rainforest from Sucumbíos - Ecuador. The results of this study showed that the GWR-K, a hybrid technique, provided statistically satisfactory estimates with the lowest prediction error compared to the other two techniques. Furthermore, we observed that 75% of the AGB was explained by the combination of remote sensing data and environmental variables, where the forest types are the most important variable for estimating AGB. It should be noted that while the use of high-resolution images significantly improves the estimation of the spatial distribution of AGB, the processing of this information requires high computational demand.
Keywords:
Geographically Weighted Regression; Geographically Weighted Regression-Kriging; RedEdge; Carbon emissions; Ecuadorian Amazon
RESUMO
A distribuição espacial da biomassa na Amazônia é heterogênea, variando temporalmente e espacialmente em relação aos diferentes tipos de formações vegetais abrangidas por este bioma. Estimativas de biomassa nesta região variam significativamente dependendo da abordagem aplicada e do conjunto de dados utilizados para sua modelagem. Assim, este estudo teve como objetivo avaliar três diferentes técnicas geoestatísticas na estimativa da distribuição espacial da biomassa acima do solo (BAS). As técnicas escolhidas foram: 1) regressão por mínimos quadrados ordinários (OLS), 2) regressão geograficamente ponderada (RGP) e, 3) regressão geograficamente ponderada - krigagem (RGP-K). Estas técnicas foram aplicadas sobre um mesmo conjunto de dados de campo, utilizando as mesmas variáveis ambientais decorrentes de dados cartográficos e de sensoriamento remoto de alta resolução espacial (RapidEye). Este trabalho foi desenvolvido na floresta amazônica da província de Sucumbíos no Equador. Os resultados deste estudo mostraram que a RGP-K, sendo uma técnica híbrida, forneceu estimativas estatisticamente satisfatórias com menor erro de predição em comparação com as outras duas técnicas. Além disso, observou-se que 75% da BAS foi explicada pela combinação de dados de sensoriamento remoto e variáveis ambientais, sendo os tipos de formações vegetais a variável de maior importância para estimar BAS. Cabe ressaltar que, embora o uso de imagens de alta resolução espacial melhora significativamente a estimativa da distribuição espacial da BAS, o processamento desta informação requer alta demanda computacional.
Palavras-chave:
Regressão Geograficamente Ponderada; Regressão Geograficamente Ponderada-Krigagem; RedEdge; emissões de carbono; Amazônia equatoriana
INTRODUCTION
The Amazon turns into annually greater amount of atmospheric carbon in vegetation biomass that any other terrestrial biome on the Planet, emphasizing its importance for the understanding and management of the global carbon cycle (Houghton et al. 2009Houghton, R.A.; Hall, F.; Goetz, S.J. 2009. Importance of biomass in the global carbon cycle. Journal of Geophysical Research, 114: G00E03.; Marvin et al. 2014Marvin, D.C.; Asner, G.P.; Knapp, D.E.; Anderson, C.B.; Martin, R.E.; Sinca, F.; et al. 2014. Amazonian landscapes and the bias in field studies of forest structure and biomass. Proceedings of the National Academy of Sciences, 111: E5224-E5232.), despite having been detected a decrease in the carbon accumulation trend in the last few years (Brienen et al. 2015Brienen, R.J.W.; Gloor, E.; Zuidema, P.A. 2015. Long-term decline of the Amazon carbon sink. Nature, 519: 344-348.).
The biomass varies temporally as a result of anthropogenic disturbance and secondary forest regeneration. In addition, its density varies spatially and considerably, in relation to the different types of vegetation (Houghton et al. 2009Houghton, R.A.; Hall, F.; Goetz, S.J. 2009. Importance of biomass in the global carbon cycle. Journal of Geophysical Research, 114: G00E03.).
Modelling the spatial distribution of biomass with greater accuracy at local and regional scales is significant to reduce the uncertainties on carbon emissions and sequestration estimates, understanding their roles in influencing the atmospheric temperature and water composition, availability and seasonality, and understanding the carbon budget role in environmental process and sustainability of terrestrial ecosystems (Foody 2003Foody, G.M. 2003. Remote sensing of tropical forest environments: Towards the monitoring of environmental resources for sustainable development. International Journal of Remote Sensing, 24: 4035-4046.).
It is estimated that about 120 ± 30 Pg C are stored in the Amazon rainforest biomass and that the aboveground biomass is the largest contributor of the net primary productivity (70%-89% of total) (Malhi et al. 2009Malhi, Y.; Aragão, L.E.O.C; Metcalfe, D.B.; Paiva, R.; Quesada, C.A.; Almeida, S.; et al. 2009. Comprehensive assessment of carbon productivity, allocation and storage in three Amazonian forests. Global Change Biology, 15: 1255-1274.) in this biome. The existing aboveground biomass (AGB) estimates are derived from national and regional forest inventories, which provide accurate information at a local level. However, this information will lose accuracy over broader spatial scales (Bacciniet al. 2008Baccini, A.; Laporte, N.; Goetz, S.J.; Sun, M.; Huang, D. 2008. A first map of tropical Africa's above-ground biomass derived from satellite imagery. Environmental Research Letters, 3: 1-9.).
The tools and models development based on remote sensing data has allowed "scale-up" or extrapolate the field data collected for larger scales (Saatchi et al. 2011Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; et al. 2011. Benchmark map of forest carbon stocks in tropical regions across three continents. Proceedings of the National Academy of Sciences, 108: 9899-9904.;Baccini et al. 2012Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; et al. 2012. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nature Climate Change, 2: 182-185.). However, the biomass mapping in the Amazon based on remote sensing present several challenges, mainly due to the spectral vegetation indices saturation in dense forests areas, and due to the high frequency of clouds that reduce significantly the availability of satellite images. In addition, when low spatial resolution satellite imagery with high temporal availability (most likely to have free-cloud images) is used to estimate biomass, there is a huge difference between the field-measurement data with the pixel size in the image (Lu 2006Lu, D. 2006. The potential and challenge of remote sensing based biomass estimation. International Journal of Remote Sensing 27: 1297-1328.), resulting in mixed pixels difficult the integration of both information.
Faced with this reality, in recent years, the remote sensing data has frequently been used in combination with other additional information for quantifying and modelling aboveground biomass (Liang et al.2012Liang, S.; Li, X.; Wang, J. 2012. Above-ground biomass. In: Liang, S.; Li, X.; Wang, J. (Ed.). Advance Remote Sensing: terrestrial information extraction and applications. Elsevier, Amsterdam, p.467-500.; French et al.2013French, N.H.F; Bourgeau-Chavez, L.; Falkowski, M.J.; Goetz, S.J.; Jenkins, L.K.; Camill III, P.; et al. 2013. Remote Sensing for Mapping and Modeling of Land-Based Carbon Flux and Storage. In: Brown, D.G.; Robinson, D.T.; French, N.H.F.; Reed, B.C. (Ed.). Land use and the carbon cycle: advances in integrated science, management, and policy. Cambridge University Press, New York, p. 95-143.) through several geostatistical techniques.
Recently, the Geographically Weighted Regression (GWR) has been shown as a powerful tool in exploring spatial heterogeneity, which estimates parameters for each sample location of the dataset. This technique takes into account the spatial non-stationarity and provides a detailed understanding of spatial variation in the data (Fotheringham et al.2002Fotheringham, A.S.; Brunsdon, C.; Charlton, M. 2002. Geographically Weighted Regression: the Analysis of Spatially Varying Relationships. Wiley, Chichester, 284p.), becoming a very attractive technique for modelling biomass through remote sensing (Propastin 2012Propastin, P. 2012. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data. International Journal of Applied Earth Observation and Geoinformation, 18: 82-90.). However, several studies have indicated that geostatistical hybrid techniques can improve than any pure approach (Harris et al. 2010Harris, P.; Fotheringham, A.S.; Crespo, R.; Charlton, M. 2010. The use of geographically weighted regression for spatial prediction: An evaluation of models using simulated data sets. Mathematical Geosciences, 42: 657-680.; Kumar et al. 2012Kumar, S.; Lal, R.; Lui, D. 2012. A geographically weighted regression kriging approach for mapping soil organic carbon stock. Geoderma, 189-190: 627-634.; Liu et al. 2015Liu, Y.; Guo, L.; Jiang, Q.; Zhang, H.; Chen, Y. 2015. Comparing geospatial techniques to predict SOC stocks. Soil and Tillage Research, 148: 46-58.); therefore, the GWR and Ordinary Kriging (OK) integration should makes possible to minimize the prediction error and thus improve de AGB estimates.
In this context, this study aimed to evaluate three different geostatistical techniques to estimate the spatial distribution of aboveground biomass (AGB). The selected techniques were: 1) ordinary least-squares regression (OLS), 2) geographically weighted regression (GWR) and, 3) geographically weighted regression - kriging (GWR-K). These techniques were applied to the same field dataset, using the same environmental variables derived from cartographic information and high-resolution remote sensing data (RapidEye, 5 m.).
Thus, this study becomes relevant for generating a methodological basis that makes possible to model the spatial distribution of aboveground biomass fitted to the Ecuadorian Amazon rainforest local conditions. This quantification is important for the implementation of mitigation policies related to the reducing emissions from deforestation and forest degradation (REDD).
MATERIALS AND METHODS
Study Area
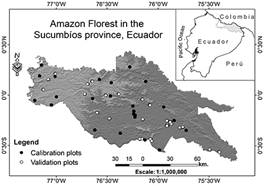
The analysis area included about 1.4 million ha of Amazon rainforest, located in the Sucumbíos province in northeast Ecuador with geographical coordinates 0°40' S to 0°29' N latitude and 77°20' to 75°15' W longitude as shown in Figure 1. The average annual precipitation varies from 3000 to 5000 mm, where April, May and June are the months with higher rainfall and, January, February and September are the months with the lowest precipitation. The temperature is relatively uniform with an annual mean of 25° C. This region is characterized by a no marked seasonality because even in the dry season the average monthly precipitation is greater than 200 mm.
Geographic location of the study area and spatial distribution of calibration (n=122) and validation (n=30) sampling plots in the Amazon forest in Sucumbíos province, Ecuador.
Four major forest types are present in the study area: "Tierra Firme" forest, floodplain forest, flooded forest (known locally as "Moretales"), and black-water riparian and lacustrine forest. Areas with high anthropogenic disturbance, rivers, urban area and bare ground have been ignored in this study.
Field Data
In 2011, the Ministry of Environment of Ecuador (MAE) through the "Evaluación Nacional Forestal" project distributed 484 georeferenced plots over different forests strata in the Ecuadorian Amazon, where several forest structural parameters have been measurement in order to estimate biomass forest. The MAE provided aboveground biomass information already quantified for the development of this study.
In the study area are located 152 plots, each plot with an area of 0.36 ha (60m x 60m). Thus, in order to validate the performance of AGB distribution models were randomly selected 80% of the occurrence plots as a calibration dataset (n=122) and the remaining 20% as a validation dataset (n=30). The Figure 1 shows the geographical location of the calibration and validation datasets.
Cartographic Data
Environmental variables used in this study to estimate aboveground biomass were: vegetation and soil types. The Ministry of Environment (MAE) provided this cartographic information at scales 1:100000 and 1:200000, respectively (PRONAREG-ORSTOM 1982PRONAREG-ORSTOM. Programa nacional de regionalización agraria - institut français de recherche scientifique pour le développement en coopération. 1982. Mapas morfopedológicos. Quito-Equador. Mapa Temático. Escala: 1:200.000.; MAE 2013MAE. Ministerio del Ambiente del Ecuador. 2013. Sistema de Clasificación de los Ecosistemas del Ecuador Continental. Subsecretaría de Patrimonio Natural, Quito, 232p.).
Within the study area can be identified 8 vegetation types: Floodplain forest of the rivers of Amazonian origin, Floodplain forest of the rivers of Andean and Amazon mountain range, Amazon wetland forest and black-water riparian and lacustrine vegetation, Wetland forest of the Amazon floodplain, Flooded Palm forest of the Amazon floodplain, Aguarico-Putumayo-Caquetálowland evergreen forest, Napo-Curaray lowland evergreen forest and, Riparian and lacustrine flooded herbaceous plants of the Amazon floodplain. Beside natural vegetation, five soil types were identified, that correspond to the Tropept, Fluvent, Fibrist, Aquept and Andept suborders according with the soil taxonomy classification (USDA 1999USDA. United States Department of Agriculture. 1999. Soil Taxonomy: A Basic System of Soil Classification for Making and Interpreting Soil Surveys. 2da ed. USDA, Washington, EEUU, 871p.).
Remote Sensing Data
RapidEye imagery was used for the development of this work, which were provided, in the same way, by the MAE. The RapidEye satellite sensor acquires image data in five different spectral band, each one with a pixel size (orthorectified) of 5 m. The principal feature that distinguished RapidEye´s satellite from other multispectral satellites is the presence of the RedEdge band (690-730 nm), located between the Red and Infra-red bands. The RedEdge band is able to provide additional information about variation in the vegetation in order to identify and characterize species and monitoring the health status of the vegetation.
We compiled a total of 45 images to cover the study area. The year 2011 was taking as a reference to estimate and modelling aboveground biomass, year in which the field data was collected in the Ecuadorian Amazon. However, due to the difficulty in acquiring all the images in the same reference date in this region because of its large area and frequent cloud cover, was established an acquisition interval time of ± 1 year. Hence, 13% of the images were acquired in 2010, 83% in 2011, and only 4% in 2012. In relation to the months of acquisition, all the images were acquired in the less rainy season (January, August, September and October). The entire image set presents radiometric, sensor and geometrically correction (level 3A ortho standard products).
Cartographic Data Processing
The vegetation map was reclassified into nine categories (eight classes of natural vegetation and a class that includes both disturbed area and water bodies). The soil map was reclassified into six categories, one of them corresponding to water bodies and the other corresponding to soil classes. Finally, this thematic information were converted from vector to raster format with a spatial resolution of 5 meter (matching the RapidEye images).
Normalized Difference Vegetation Index modified (NDVI_r)
The spectral vegetation index NDVI_r was used in this study in order to better the spatial correlation between spectral data and AGB data. Several procedures were applied to RapidEye images prior to NDVI_r calculation. These procedures aim to convert the digital numbers (DNs) of each image to surface reflectance values. These procedures were: (i) the masking of artefacts (cloud and cloud shadow) that can introduce error in future procedures, (ii) the conversion of DN into values of top-of-atmosphere reflectance (TOA) and, (iii) the elimination of the atmospheric interference over the reflectance values. For this last process was used the Quick Atmospheric Correction (QUAC) algorithm, which is based on empirical models that use only the information contained within the scene, not requiring auxiliary information (e.g. metadata). In addition, this approach improves the atmospheric correction at approximately 15% compared with physics-based models (Bernstein et al. 2012Bernstein, L.S.; Jin, X.; Gregor, B.; Adler-Golden, S.M. 2012. Quick atmospheric correction code: algorithm description and recent upgrades. Optical Engineering, 51: 1-11.).
The NDVI_r was calculated by replacing the near infrared band with the RedEdge band within the NDVI general equation proposed by Rouse et al. (1973Rouse, J.W.; Hass, R.H.; Schell, J.A.; Deering, D.W. 1973. Monitoring vegetation systems in the Great Plains with ERTS. In: Freden, S.C., Mercanti, E.P., Becker, M. (Ed.). Third Earth Resources Technology Satellite-1 Symposium Technical presentations, section A 1. Goddard Space Flight Center, National Aeronautics and Space Administration, Washington, DC, p. 309-317.). This modification used by Bindel et al.(2011Bindel, M.; Hese, S.; Berger, C.; Schmullius, C. 2011. Evaluation of red-edge spectral information for biotope mapping using RapidEye. Proceedings of SPIE of Remote Sensing for Agriculture, Ecosystems, And Hydrology XIII, Praga, 8174: 81740X 1-9.) and Sousa et al. (2012Sousa, C.H.R.; Souza, C.G.; Zanella, L.; de Carvalho, L.M.T. 2012. Analysis of rapideye's red edge band for image segmentation and classification. IV GEOBIA, Rio de Janeiro, 4: 518-523.) to validate the RedEdge band in the vegetation mapping, was adopted in this study for being the vegetation index that exhibited better spatial correlation with the AGB in Ramirez et al. (2014Ramírez, F.L.B.; Anderson, L.O.; Formaggio, A.R.; Santos, C.P.F. 2014. Regressão geograficamente ponderada aplicada a estimativa de biomassa acima do solo na Amazônia utilizando sensoriamento remoto de alta resolução. XI Seminário de atualização em sensoriamento remoto e sistemas de informações geográficas aplicados à engenharia florestal (SENGEF), Curitiba, 11: 637-645.) research. The equation that describes that modified index is detailed below.

After calculating the NDVI_r index in each RapidEye image, all the scenes were mosaicked into a single composite image that cover the study area. Consecutive scenes acquired along the same orbital path were combined seamlessly because these were acquired as one observation by the sensor. However, caution was taken to combine imagery from different orbital path to ensure seamlessness in a final mosaic. Thus, a reference swath image was selected, and each orbital path image was added one by one to be adjusted with the reference. In addition, to blend the seams along the edges of the overlapping areas, a histogram matching and an edge feathering were applied in the mosaicked image aimed their homogeneity. After some tests, 20 pixels (100 meters) was the specified distance in the blending edge. The generated mosaic were re-projected to the zone 17 south, keeping your WGS 84 UTM projection. To perform all these processes, the ENVI 5.1 software was used (Exelisvis 2009Exelisvis, 2009. ENVI EX User's Guide, 275p. ( (http://www.exelisvis.com/portals/0/pdfs/enviex/ENVI_EX_User_Guide.pdf
). Accessed on 15/03/2015.
http://www.exelisvis.com/portals/0/pdfs/...
).
Aboveground Biomass Spatial Distribution
Three independent or explanatory variables were selected for the AGB (dependent variable) spatial distribution modelling in the study area. These variables were: vegetation types (categorical variable), soil types (categorical variable), and NDVI_r vegetation index (continuous variable).
The NDVI_r for each sampling plot was extracted from the pre-processed satellite data before generating the mosaicked image. The mean NDVI_r derived from a 13 x 13 pixel window (65 m x 65 m) centred on the central position of each plot was extracted and used in the analysis. The window size is a compromise of the spatial resolution of the satellite data with the plot size, guaranteeing that the plot will be located within the selected window and the NDVI_r value represent the entire plot. In relation with the categorical variables (vegetation and soil types), the value assigned to each sampling plot was the one related with the class where the plot are located.
Then, three different geostatistical approaches were used to estimate and spatialize aboveground biomass in the study area. These approaches were the ordinary least-squares regression (OLS), the geographically weighted regression (GWR) and, the geographically weighted regression - kriging (GWR-K). For the performance and analysis of the three models was used the RStudio software. A brief description of each approach is detailed below.
Ordinary Least-Squares Regression (OLS)
The OLS regression is the most commonly statistical technique used for estimating forest structural parameters, where the depended variable is estimated by producing unbiased minimum sum of squared residuals in regards to the independent variables (Montgomery et al. 2001Montgomery, D.C.; Peck, E.A.; Vining, G.G. 2001. Introduction to Linear Regression Analysis. 3rd ed. John Wiley & Sons, Inc, New York, 672p.), in order to improve the model fit to all observed data. The equation used to perform OLS is given below:

where  is the dependent variable (in this case represents the AGB estimated),X1 toXnX1 toXn are the independent or explanatory variables,
is the dependent variable (in this case represents the AGB estimated),X1 toXnX1 toXn are the independent or explanatory variables, is the intercept parameter,
is the intercept parameter,  to
to 
 to
to are the regression coefficients, and
are the regression coefficients, and  are the regression residuals.
are the regression residuals.
Geographically Weighted Regression (GWR)
The GWR is a recent and powerful approach for modeling spatially heterogeneous processes (Kumar et al.2012Kumar, S.; Lal, R.; Lui, D. 2012. A geographically weighted regression kriging approach for mapping soil organic carbon stock. Geoderma, 189-190: 627-634.), which estimates individual parameters for each estimation location, and thus, do not assume that a single regression model can be fitted to the whole study area. The GWR model is considered by the following equation (Fotheringham et al.2002Fotheringham, A.S.; Brunsdon, C.; Charlton, M. 2002. Geographically Weighted Regression: the Analysis of Spatially Varying Relationships. Wiley, Chichester, 284p.):

where  is the dependent variable (in this case represents the AGB estimated),X1 toXnX1 toXn are the independent or explanatory variables,
is the dependent variable (in this case represents the AGB estimated),X1 toXnX1 toXn are the independent or explanatory variables, is the intercept parameter,
is the intercept parameter,  to
to 
 to
to are the regression coefficients,
are the regression coefficients,  are the regression residuals, x and y represent the coordinates of the plots in space.
are the regression residuals, x and y represent the coordinates of the plots in space.
The basic idea of this technique is to explore how the relationship between dependent and independent variables can vary across the geographic space. For this purpose, a search window is moving from one sampling plot in a data set to the next, working through them all in sequence. When the search window rests on a sampling plot, all other plots that are within and around the search window area identified. Thus, the regression model is fitted to that subset of sampling plots, giving most weight to the plots that are closest to the central plot (Kernel function).
The regression model calibration is based on the choice of a spatial kernel method, which depends on the spatial arrangement of data across the space to be analyzed: if the sampling plot configuration is regular, the kernel with a fixed distance (GWRF) is appropriate. If the sampling plot configuration is irregular, is better use the adaptive spatial kernel method (GWRA), where the bandwidth distance will change according to the spatial sample density, becoming a function of the number of nearest neighbors such that each local estimation is based on the same number of neighbors. In this study, both the fixed and adaptive spatial kernel methods were used.
The accuracy of the model prediction strongly depend on weighting function and bandwidth selected (Propastin 2012Propastin, P. 2012. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data. International Journal of Applied Earth Observation and Geoinformation, 18: 82-90.). This selection can be done by using the cross- validation or minimizing the Akaike Information Criterion (AIC). In this study, a Gaussian function Kernel (Propastin 2012Propastin, P. 2012. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data. International Journal of Applied Earth Observation and Geoinformation, 18: 82-90.) was used to fit the GWR model and the AIC to calibrate the model with respect to bandwidth.
Geographically Weighted Regression - Kriging (GWR-K)
The GWR-K is a hybrid prediction model where the residuals from the geographically weighted regression are interpolated with an Ordinary Kriging (OK). The Figure 2 show the flowchart of the GWR-K, where both approaches that composed this technique are modeled separately to finally carry out the spatial overlay between the trend item of regression prediction and the residual value of ordinary kriging to obtain the predicted value of the dependent variable. The equation used to perform GWR-K is given below:

where,  is the AGB estimated at location
is the AGB estimated at location  ,
,  is the drift fitted AGB using GWR at the same location, and
is the drift fitted AGB using GWR at the same location, and  are the residual values interpolated with OK.
are the residual values interpolated with OK.
Flowchart of Geographically Weighted Regression Kriging (GWR-K) in this study. GWR=geographically weighted regression; OK=ordinary kriging.
Methods evaluation
A total of 30 sampling plots (validation dataset) were reserved for evaluating the performance of the different approaches used in the AGB estimates. The estimate AGB was compared with the observed AGB by the root mean squared error (RMSE) and mean absolute estimation error (MAEE) as described in the equations below:


where,  is the estimated AGB using GWR-K at location
is the estimated AGB using GWR-K at location  ,
,  is the observed AGB at the same location, n is the total number of sample observations.
is the observed AGB at the same location, n is the total number of sample observations.
Low MAEE values often indicates a model with few error, while low RMSE values indicates a good fit between the model developed and the sampling plot and hence more accurate prediction. Thus, the model with the lowest RMSE and MAEE values will be considered as the most appropriate approach to AGB spatial distribution modeling.
RESULTS
Descriptive Statistics
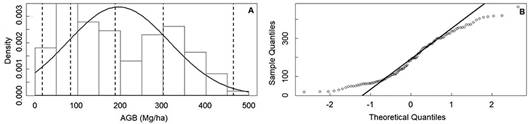
The aboveground biomass in the study area ranged from 17.48 Mg ha-1 e 464.90 Mg ha-1, with mean and standard deviation of 195.80 Mg ha-1 e 118.96 Mg ha-1, respectively. A moderate coefficient of variation (CV = %) of AGB reflects a significant spatial variability, showing the heterogeneity of AGB within the study area. A normality assumption on the distribution of the AGB dataset was evaluated by examining the histogram and the quantile-quantile (Q-Q) plot, where an approximately normal distribution was observed in the AGB dataset. It can be checked in Figure 3A, where the generate histogram show bell-shape curve (normal distribution pattern), and in Figure 3B, where the data, in general, are grouped around the 45-degree reference line generated in the Q-Q plot. The coefficient of kurtosis of AGB was 1.85 Mg ha-1, indicating that the distribution is less concentrated around the mean.
Spatial Structural of the GWR residuals
The geographically weighted regression residuals (GWR) area defined as the difference between the observed AGB values and these estimate by the GWR.
The experimental variogram of the GWR residuals is showed in Figure 4, also shows the quantitative description of its spatial variation. The best-fit variogram model used in this study is the spherical model and its associated parameters values are presented in Figure 4 along with the experimental variogram model. In addition, variogram model shows that the spatial correlation for the sampling plots is presents in an approximated distance of 49 kilometers. The model accuracy in the spatial distribution of the GWR residuals, interpolates with OK, was evaluated from root mean squared error (RMSE) and the mean error. The model produced RMSE value of 1.03 Mg ha-1, while the mean error was de -0.16 Mg ha-1. RMSE values close to 1 and mean error values close to 0 indicate a model that provides accurate predictions.
Experimental variogram model for geographically weighted regression (GWR) residuals. Co=Nugget Effect, C=Partial Sill, Co+C=Sill.
The spatial distribution of the GWR residuals, interpolates with OK, is presented in Figure 5. A strong spatial heterogeneity in the data distribution can be observed. The negative values were distributed in the east and southwest regions of the study area, which indicated that the estimated values were higher than those observed. The positive values where primarily observed in the center region of the study area being distributed from north to south, this indicates that the AGB estimates are lower than those observed.
Spatial distribution of geographically weighted regression (GWR) residuals interpolated by ordinary kriging (OK). This figure is in color in the electronic version.
Aboveground Biomass Estimates
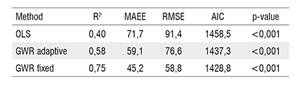
The descriptive statistics of the ordinary least-squared regression (OLS) and geographically weighted regression (GWR) models are reported in Table 1, where can be observed that the GWR has the potential to improve the AGB estimates in comparison with the OLS model. Thus, although the result of OLS model is statistically significant (p-value<0.001), it can only explain 40% of the spatial variation of biomass, whereas the GWR can explain between 58% and 75% of the biomass local variation in the study area.
Statistics indices for validation aboveground biomass using ordinary least-square regression (OLS), and geographically weighted regression (GWR) adaptive and fixed. MAEE: mean absolute estimation error, RMSE: root mean squared error, AIC: Akaike information criterion.
With respect to fixed and adaptive spatial kernel methods in the GWR approach, this study showed that the fixed method presents the lower MAEE, RMSE and Akaike Information Criterion (AIC) values, providing a better fit to the model. With these initial results, the GWR-K was developed using the fixed GWR results. InTable 2 are presented the maximum, minimum, median, mean, and standard deviation values of the parameters used in the GWRF model for predicting AGB. The variability in the model parameters suggests that the relationship between AGB and the explanatory variables is non-stationary in the study area.
Descriptive statistics of the coefficients used in the geographically weighted regression fixed (GWRF) model.
The GWR-K was used with in order to improve the accuracy of the AGB estimates, minimizing the GWRF residuals, which in turn minimizes the OLS residuals, as shown in Figure 6.
Residuals of three geostatistic approaches tested in this study: (A). Ordinary least-square regression (OLS); (B). Geographically weighted regression fixed (GWRF); and (C). Geographically weighted regression kriging (GWR-K). This figure is in color in the electronic version.
Models validation
Validation results of the three regression models are showed in Table 3, where the GWR-K approach improve biomass estimates performance compared with the other two approaches considered in this study. The GWR-K estimates showed lower RMSE and MAEE values (80.27 Mg ha-1 e 64.63 Mg ha-1; respectively), and higher correlation coefficient (R2 = 0.43). The RMSE for the GWR-K ((80.27 Mg ha-1) was 23% lower when compared to the OLS results (104.61 Mg ha-1), and only 3% lower when compared to the GWR results (82.99 Mg ha-1).
Comparison of the three approaches performance by root mean squared error (RMSE), mean absolute estimation error (MAEE) and the correlation coefficient R2.
Aboveground Biomass Spatial Distribution
The three models tested in this study, showed similar spatial distribution of AGB in terms of the spatial structure and variation trend in the study area, as showed in Figure 7. However, the two models developed from geographically weighted regression had significant differences in local details when compared with the OLS model. This can be attributed to the fact that the GWR and GWR-K take into account the spatial heterogeneity of the explanatory variables.
Estimated spatial distribution of AGB in the study area by three geostatistic approaches tested: (A). Ordinary least-square regression (OLS); (B). Geographically weighted regression fixed (GWRF); and (C). Geographically weighted regression kriging (GWR-K). This figure is in color in the electronic version.
Thus, in the northeast region of the study area is stored the higher AGB stocks (300 to 400 Mg ha-1), this area correspond to the "Tierra firme" forest. In contrast, the flooded forests in the study area stored lower biomass pool (75 to 150 Mg ha-1).
In the study area the total aboveground biomass estimated, ranges from 0.24 Pg to 0.31 Pg, depending upon the approach adopted as showed in Table 4.
Total estimated aboveground biomass for the tropical Amazon in the study area. Units are in Pg of biomass (1 Pg = 1015g).
DISCUSSION
Take into account the spatial heterogeneity of the forest structure components, new techniques are been explored to model this spatial variability and quantify the forest biomass at regional scale. Recently, several methodological approaches developed for modeling the AGB spatial distribution are found in the literature. Some of them are based in simple procedures, where a single value of biomass, estimated from field measurements, is assigned to each forest or vegetal types (Salimon et al. 2011Salimon, C.I.; Putz, F.E.; Menezes-Filho, L.; Anderson, A.; Silveira, M.; Brown, I.F; et al. 2011. Estimating state-wide biomass carbon stocks for a REDD plan in Acre, Brazil. Forest Ecology and Management, 262: 555-560.). However, other approaches use more sophisticated methods that integrate different data sources, requiring much more technologically demanding (Saatchi et al. 2011Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; et al. 2011. Benchmark map of forest carbon stocks in tropical regions across three continents. Proceedings of the National Academy of Sciences, 108: 9899-9904.; Baccini et al. 2012Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; et al. 2012. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nature Climate Change, 2: 182-185.).
Regression analyses have been the most widely used approach for modeling environment variables across the geographic space, being the ordinary least-square regression (OLS) the technique with greater demand. However, recent studies have shown that the geographically weighted regression (GWR) significantly improves the aboveground biomass estimates in the tropical rainforest (Propastin 2012Propastin, P. 2012. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data. International Journal of Applied Earth Observation and Geoinformation, 18: 82-90.), and that hybrid techniques such as geographically weighted regression kriging (GWR-K), help to minimize the prediction error variance, giving better results than pure techniques. This last approach has been showed satisfactory results in the soil carbon predictions (Kumar et al. 2012Kumar, S.; Lal, R.; Lui, D. 2012. A geographically weighted regression kriging approach for mapping soil organic carbon stock. Geoderma, 189-190: 627-634.; Kumar 2015Kumar, S. 2015. Estimating spatial distribution of soil organic carbon for the Midwestern United States using historical database. Chemosphere, 127: 49-57.; Liu et al.2015Liu, Y.; Guo, L.; Jiang, Q.; Zhang, H.; Chen, Y. 2015. Comparing geospatial techniques to predict SOC stocks. Soil and Tillage Research, 148: 46-58.), becomes interesting in the aboveground biomass estimates.
Thus, the results of this study show that the geographically weighted regression kriging (GWR-K) was the best technique to estimate the AGB spatial distribution, by the fact that this approach take into account the AGB spatial heterogeneity and remove the spatial dependency, and also to perform a spatial weighting of the AGB explanatory variables.
On the other hand, the use of high spatial resolution imagery allows getting detailed information of the vegetation types in a specific area. This information becomes very important in the AGB estimates due to high statistic correlation that exists between these two variables. However, working with high spatial resolution images over large areas (e.g. the Amazon) require better computational resources that allow processing and storing large volumes of data with high-speed and greater performance. The memory capacity of the computer is the most important resource for the processing of these images as it substantially streamlines the processing.
CONCLUSIONS
The success of a methodology for estimating AGB with higher accuracy depends mainly on the correct selection of the explanatory variables that will be used in the model. The same number or set of variables is not always needed to estimate AGB, depending of the locality, landscape variability and scale study. The results of this study indicate that the geographically weighted regression kriging method was more accurate in representing the heterogeneity of AGB, providing a high R2 of 44%. However, the availability of a sufficiently robust field dataset with a representative sampling plot on each land use/cover type can greatly reduce the uncertainties and improve the AGB estimates. In addition, the integration of another variables that area correlated with biomass (e.g. leaf area index) and the use of remote sensing information capable of capturing the spatial variability in forest structure (e.g. RADAR, LiDAR) is recommended to reduce the uncertainties in the spatial distribution of the aboveground biomass.
ACKNOWLEDGMENTS
This study was supported by the National Institute for Space Research - INPE, the CNPq, and the Environment Ministry of Ecuador - MAE, who provide the RapidEye images to Ecuadorian Amazon investigations. L.O.A acknowledges the support of Amazônica project (http://www.geog.leeds.ac.uk/projects/amazonica NERC- UK NE/F005806/1) and CNPq process 458022/2013-6.
- Baccini, A.; Laporte, N.; Goetz, S.J.; Sun, M.; Huang, D. 2008. A first map of tropical Africa's above-ground biomass derived from satellite imagery. Environmental Research Letters, 3: 1-9.
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; et al. 2012. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nature Climate Change, 2: 182-185.
- Bernstein, L.S.; Jin, X.; Gregor, B.; Adler-Golden, S.M. 2012. Quick atmospheric correction code: algorithm description and recent upgrades. Optical Engineering, 51: 1-11.
- Bindel, M.; Hese, S.; Berger, C.; Schmullius, C. 2011. Evaluation of red-edge spectral information for biotope mapping using RapidEye. Proceedings of SPIE of Remote Sensing for Agriculture, Ecosystems, And Hydrology XIII, Praga, 8174: 81740X 1-9.
- Brienen, R.J.W.; Gloor, E.; Zuidema, P.A. 2015. Long-term decline of the Amazon carbon sink. Nature, 519: 344-348.
- Exelisvis, 2009. ENVI EX User's Guide, 275p. ( (http://www.exelisvis.com/portals/0/pdfs/enviex/ENVI_EX_User_Guide.pdf ). Accessed on 15/03/2015.
» http://www.exelisvis.com/portals/0/pdfs/enviex/ENVI_EX_User_Guide.pdf - Foody, G.M. 2003. Remote sensing of tropical forest environments: Towards the monitoring of environmental resources for sustainable development. International Journal of Remote Sensing, 24: 4035-4046.
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. 2002. Geographically Weighted Regression: the Analysis of Spatially Varying Relationships. Wiley, Chichester, 284p.
- French, N.H.F; Bourgeau-Chavez, L.; Falkowski, M.J.; Goetz, S.J.; Jenkins, L.K.; Camill III, P.; et al. 2013. Remote Sensing for Mapping and Modeling of Land-Based Carbon Flux and Storage. In: Brown, D.G.; Robinson, D.T.; French, N.H.F.; Reed, B.C. (Ed.). Land use and the carbon cycle: advances in integrated science, management, and policy. Cambridge University Press, New York, p. 95-143.
- Harris, P.; Fotheringham, A.S.; Crespo, R.; Charlton, M. 2010. The use of geographically weighted regression for spatial prediction: An evaluation of models using simulated data sets. Mathematical Geosciences, 42: 657-680.
- Houghton, R.A.; Hall, F.; Goetz, S.J. 2009. Importance of biomass in the global carbon cycle. Journal of Geophysical Research, 114: G00E03.
- Kumar, S.; Lal, R.; Lui, D. 2012. A geographically weighted regression kriging approach for mapping soil organic carbon stock. Geoderma, 189-190: 627-634.
- Kumar, S. 2015. Estimating spatial distribution of soil organic carbon for the Midwestern United States using historical database. Chemosphere, 127: 49-57.
- Liang, S.; Li, X.; Wang, J. 2012. Above-ground biomass. In: Liang, S.; Li, X.; Wang, J. (Ed.). Advance Remote Sensing: terrestrial information extraction and applications. Elsevier, Amsterdam, p.467-500.
- Liu, Y.; Guo, L.; Jiang, Q.; Zhang, H.; Chen, Y. 2015. Comparing geospatial techniques to predict SOC stocks. Soil and Tillage Research, 148: 46-58.
- Lu, D. 2006. The potential and challenge of remote sensing based biomass estimation. International Journal of Remote Sensing 27: 1297-1328.
- MAE. Ministerio del Ambiente del Ecuador. 2013. Sistema de Clasificación de los Ecosistemas del Ecuador Continental. Subsecretaría de Patrimonio Natural, Quito, 232p.
- Malhi, Y.; Aragão, L.E.O.C; Metcalfe, D.B.; Paiva, R.; Quesada, C.A.; Almeida, S.; et al. 2009. Comprehensive assessment of carbon productivity, allocation and storage in three Amazonian forests. Global Change Biology, 15: 1255-1274.
- Marvin, D.C.; Asner, G.P.; Knapp, D.E.; Anderson, C.B.; Martin, R.E.; Sinca, F.; et al. 2014. Amazonian landscapes and the bias in field studies of forest structure and biomass. Proceedings of the National Academy of Sciences, 111: E5224-E5232.
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. 2001. Introduction to Linear Regression Analysis. 3rd ed. John Wiley & Sons, Inc, New York, 672p.
- PRONAREG-ORSTOM. Programa nacional de regionalización agraria - institut français de recherche scientifique pour le développement en coopération. 1982. Mapas morfopedológicos. Quito-Equador. Mapa Temático. Escala: 1:200.000.
- Propastin, P. 2012. Modifying geographically weighted regression for estimating aboveground biomass in tropical rainforests by multispectral remote sensing data. International Journal of Applied Earth Observation and Geoinformation, 18: 82-90.
- Ramírez, F.L.B.; Anderson, L.O.; Formaggio, A.R.; Santos, C.P.F. 2014. Regressão geograficamente ponderada aplicada a estimativa de biomassa acima do solo na Amazônia utilizando sensoriamento remoto de alta resolução. XI Seminário de atualização em sensoriamento remoto e sistemas de informações geográficas aplicados à engenharia florestal (SENGEF), Curitiba, 11: 637-645.
- Rouse, J.W.; Hass, R.H.; Schell, J.A.; Deering, D.W. 1973. Monitoring vegetation systems in the Great Plains with ERTS. In: Freden, S.C., Mercanti, E.P., Becker, M. (Ed.). Third Earth Resources Technology Satellite-1 Symposium Technical presentations, section A 1. Goddard Space Flight Center, National Aeronautics and Space Administration, Washington, DC, p. 309-317.
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; et al. 2011. Benchmark map of forest carbon stocks in tropical regions across three continents. Proceedings of the National Academy of Sciences, 108: 9899-9904.
- Salimon, C.I.; Putz, F.E.; Menezes-Filho, L.; Anderson, A.; Silveira, M.; Brown, I.F; et al. 2011. Estimating state-wide biomass carbon stocks for a REDD plan in Acre, Brazil. Forest Ecology and Management, 262: 555-560.
- Sousa, C.H.R.; Souza, C.G.; Zanella, L.; de Carvalho, L.M.T. 2012. Analysis of rapideye's red edge band for image segmentation and classification. IV GEOBIA, Rio de Janeiro, 4: 518-523.
- USDA. United States Department of Agriculture. 1999. Soil Taxonomy: A Basic System of Soil Classification for Making and Interpreting Soil Surveys. 2da ed. USDA, Washington, EEUU, 871p.
Publication Dates
-
Publication in this collection
Apr-Jun 2016
History
-
Received
08 Apr 2015 -
Accepted
08 Sept 2015