ABSTRACT
The Amazon forest comprises many different forest types, amongst them are campinas and campinaranas, which occur on Amazonian sandy soils, representing 2.65% of Amazonian territory. An understanding of the ecology and quantification of the environmental goods and services of campinaranas is key to their conservation. Based on a direct method to estimate biomass and carbon content of campinarana, we harvested and weighted 89 trees and other forest components in ten randomly allocated plots of 100 m2 (10 x 10 m) and 11 additional trees outside the plots. The data allowed us to describe how biomass is distributed amongst campinarana vegetation and amongst tree compartments. We developed allometric equations to estimate the total, above- and below-ground biomass and carbon stock of this forest type. We used a Weibull function to test if the diameter distribution of the individual trees sampled was consistent with the diameter distribution of the forest type. We also tested if terra-firme forest biomass equations could be used to estimate campinarana biomass, and whether a correction factor based on dominant height would reduce the error from these estimates. Allometric equations are considered to be the most reliable and rapid method for calculating forest biomass, and are used in forest management and climate change studies. These are the first total biomass equations developed for central Amazonian campinaranas. The best fitted allometric equation for total fresh biomass was: ln (Total Biomass) = -1.373 + 2.546 * ln DBH (R ² = 0.98, Sxy% = 4.19%).
KEYWORDS:
modelling; forests on sand; climate change
RESUMO
Entre as diversas fitofisionomias da Floresta Amazônica estão as campinas e campinaranas, que ocorrem sobre solos arenosos, ocupando 2,65% de seu território. Baseando-se no método direto, com a finalidade de estimar carbono e biomassa de uma campinarana na Amazônia Central, derrubamos, medimos e pesamos 89 árvores e outros componentes florestais em dez parcelas de 100 m² (10 x 10m) alocadas aleatoriamente, e mais 11 árvores fora das parcelas. A partir dos dados coletados, desenvolvemos equações alométricas para estimar a biomassa total, aérea e de raízes e o estoque de carbono para esse tipo florestal. A função Weibull foi utilizada para comprovar que a distribuição diamétrica das árvores coletadas é análoga a esse tipo florestal. Verificamos, ainda, qual o erro gerado ao se estimar a biomassa da campinarana utilizando equações desenvolvidas para florestas densas de terra-firme, e se o uso de um fator de correção baseado na altura dominante reduziria esse erro. O uso de equações alométricas é considerado o método mais preciso e rápido na obtenção da biomassa florestal, e é utilizado em questões ligadas, entre outras, às áreas de manejo florestal e de clima. Essas são as primeiras equações de biomassa total desenvolvidas para campinaranas nesta região da Amazônia. A melhor equação ajustada para estimar a biomassa total foi: ln(PFtotal) = -1,373 + 2,546 * ln(DAP) (R²=0,98; Sxy%= 4,19).
PALAVRAS-CHAVE:
modelagem; florestas sobre areia; mudanças climáticas
INTRODUCTION
Knowledge of plant biomass is important in many areas of forest management and research, including silviculture, climate change and forest ecology. In the Amazon, estimation of carbon stock and its cycling, assessed through studies of forest biomass, has become an important input for the current intense debate about climate change.
Plant biomass estimates can be obtained either directly or indirectly. The direct method consists of cutting and weighing the vegetation within fixed-area plots during a forest inventory. The indirect method consists of applying allometric equations to forest inventory data, which can provide faster and more accurate estimates of forest biomass than the direct method (Brown et al. 1989Brown, S; Gillespie, A. J.; Lugo, A. 1989. Biomass estimation methods for tropical forest with applications to inventory data. Forest Science, 35: 881-902.).
Allometric equations can be developed using analytical or empirical methods. Analytical equations are derived using allometric relations, which are based on scale proportions that are alike in nature. This method has the potential to replace the destructive (empirical) approach, however, it still needs further refinement from empirical data. Biomass studies by Zianis and Mecunccini (2004Zianis, D.; Mencuccini, M. 2004. On simplifying allometric analyses of forest biomass. Forest Ecology and Management , 187: 311-332.) and Chambers et al. (2004Chambers, J.; Higuchi, N. Teixeira, L.M; Santos, J.; Laurance, S.; Trumbore, S. 2004. Response of tree biomass and Wood litter to disturbance in a central Amazon forest. Oecologia, 141: 596-614.) showed that analytical equations introduce greater errors than those of empirical equations. In the empirical method, coefficients are obtained by fitting the equations to field data.
The development of specific equations for different forest types and site indexes, and the use of a network of long-term plots, are essential for obtaining reliable estimates of biomass and carbon stock and flux at larger scales. Biomass equations for dense and open rainforest have been developed by many authors (Uhl et al. 1988Uhl, C.; Buschbacher, R.; Serrão, E.A.S. 1988. Abandoned pastures in eastern Amazonia. I. Patterns of plant succession. Journal of Ecology, 76: 663-681.; Santos 1996Santos, J. 1996. Análise de modelos de regressão para estimar a fitomassa da floresta tropical úmida de terra-firme da Amazônia brasileira. Doctoral thesis, Universidade Federal de Viçosa, Viçosa, Brazil. 120p.; Higuchi 1998Higuchi, N.; Santos, J.; Ribeiro, R.J.; Minette, L.;Biot, Y. 1998. Biomassa da parte aérea da vegetação da floresta tropical úmida de terra-firme da Amazônia brasileira. Acta Amazonica , 28:153-166.; Araújo 1999Araújo, T. M., Higuchi, N., Carvalho Jr, J.A. 1999. Comparison of formulae for biomass content determination in a tropical rain Forest site in the state of Pará, Brazil. Forest Ecology and Management, 117: 43-52.; Nelson et al.1999Nelson, B. W.; Mesquita, R.C.; Pereira, J.L.G.; Souza, S.; Batista, G.T.; Couto, L.B. 1999. Allometric regressions for improved estimate of secondary forest biomass in the central amazon. Forest Ecology and Management , 117:149-167.; Chambers et al. 2001Chambers, J. Q.; Higuchi, N.; Tribuzy, E. S.; Trumbore, S. E. 2001. Carbon sink for a century. Nature, 410: 429.; Chave et al. 2005Chave, J.; Andalo, C.; Brown, S.; Cairns, M.; Chambers, J.C.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T; et al. 2005. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia , 145: 87-99; Silva 2007Silva, R.P. 2007. Alometria, Estoque e Dinâmica da Biomassa de Florestas Primárias e Secundárias na região de Manaus (AM). Doctoral thesis, Instituto Nacional de Pesquisas da Amazônia-INPA. Manaus, Brazil. 152p.), but there are still significant gaps to be filled, especially where different forest types, site indexes, below-ground biomass and forest components other than adult trees are concerned.
Campinarana forest is the taller part of the campina ecosystem, which consists of heath forests growing on Amazonian sandy soils. Despite the great richness of endemic species (Anderson et al. 1975Anderson, A. B.; Prance G. T.; Albuquerque B. W. 1975. Estudos sobre a vegetação das Campinas Amazônicas III. A vegetação lenhosa da Campina da Reserva Biológica INPA SUFRAMA (Manaus-Caracarai, Km 62). Acta Amazonica, 5: 225-246.) and the unknown ecological importance and economic potential of campinaranas, many are threatened by deforestation (Oliveira et al. 2001Oliveira, A.A.; Daly, D.C.; Vicentini, A.; Cohn-Haft, M. 2001. Florestas sobre areia: campinaranas e igapós. In: Oliveira, A.A.; Daly, D. Florestas do Rio Negro. Companhia das Letras: São Paulo, Brazil, p.181-219.). Understanding the ecology and quantifying the environmental goods and services of campinaranas is vital for their conservation. The present study is the first to present total biomass equations for campinaranas in the central Amazon.
The objectives of this study were to (a) obtain biomass content of a campinarana in central Amazonia, (b) develop allometric equations to estimate total, above- and below-ground biomass and carbon stock, and (c) test whether equations from terra-firme dense forest can be used to estimate campinarana biomass and if a correction factor based on dominant height would diminish the error from these estimates.
MATERIAL AND METHODS
Study site
The study was carried out in 20 hectares of campinarana in the Tropical Forestry Experimental Area of the Instituto Nacional de Pesquisas da Amazônia (EEST-INPA) in the central Amazon, located 90 kilometres from Manaus. The EEST-INPA comprises 21,000 ha and is located between 02º37’ and 02º38’S and 60º09’ and 60º11’W (Teixeira et al.2007Teixeira, L. M; Chambers, J.Q.; Silva, A. R.; Lima, A.; Carneiro, V.M; Santos, J.; Higuchi, N. 2007. Projeção da dinâmica da floresta natural de Terra-firme, região de Manaus-AM, com o uso da cadeia de transição probabilística de Markov. Acta Amazonica 37: 377-384.; Pinto 2008Pinto, F. R. 2008. Estimativa dos estoques de biomassa e nutrientes em florestas secundárias na Amazônia Central. Master’s dissertation, Instituto Nacional de Pesquisas da Amazônia - INPA, Manaus, Brazil. 162p.).
The local climate is classified as Amw by Köppen (hot and humid), and the annual temperature averages 26.7 ºC (Pinto et al. 2003Pinto, A. C. M., Higuchi, N., Iida, S., Santos, J, Ribeiro, R.J., Rocha, R.M., Silva, R.P. 2003. Padrão de distribuição espacial de espécies florestais que ocorrem na região de Manaus-AM. In: Santos, J. dos; Sampaio, P.; Marenco, R.A.; Ferraz, J.; Salles, P.C.; Saito, M.; Matsuomoto, S.; Higuchi, N. Projeto Jacarandá Fase II. Pesquisas Florestais na Amazônia Central. Instituto Nacional de Pesquisas da Amazônia - CPST/INPA: Manaus, p.1-20.). The average annual precipitation is 2610 mm. In 2000, the precipitation reached 3450 mm (Silva et al. 2002Silva, R.P.; Santos, J.; Tribuzy, E.S.; Chambers, J.Q.; Nakamura, S.; Higuchi, N. 2002. Diameter increment and growth patterns for individual trees in Central Amazon, Brazil. Forest Ecology and Management , 116: 295-301.; Chambers et al. 2004Chambers, J.; Higuchi, N. Teixeira, L.M; Santos, J.; Laurance, S.; Trumbore, S. 2004. Response of tree biomass and Wood litter to disturbance in a central Amazon forest. Oecologia, 141: 596-614.). The EEST-INPA soils vary mainly according to topography. On plateaus, the soil is more clayey, whereas in valleys (low-lying drainage areas with or without superficial water) the soil tends to be more sandy (Ferraz et al. 1998Ferraz, J.; Ohta, S.; Sales, P.C. 1998. Distribuição dos solos ao longo de dois transectos em floresta primária ao norte de Manaus (AM). In: Higuchi, N.; Campos, M.A.A.; Sampaio, P.T.B.; Santos, J. dos (Ed.). Pesquisas florestais para a conservação da floresta e reabilitação de áreas degradadas da Amazônia. INPA. Manaus, Amazonas, p.111-114.; Magalhães et al. 1998Magalhães, L.M.S; Blum, W.E.H.; Higuchi, N.; Santos, J. 1998. Relações entre o solo e a floresta no estabelecimento de unidades de paisagens florestais na Amazônia. Floresta e Ambiente, 5: 89-103.). The EEST-INPA campinarana soil is classified as Red-Yellow Podzolic with dense thin roots laying over the mineral soil (Nardoto 2005Nardoto, G. 2005. Abundância natural de 15N na Amazônia e Cerrado - implicações para a ciclagem de nitrogênio. Doctoral thesis, ESALQ/USP, Piracicaba, São Paulo, Brazil.100p.).
Data collection
In order to understand how aboveground biomass is allocated amongst different types of plants and litter in campinaranas, we utilized the direct method at ten randomly allocated plots of 100 m² (10 x 10 m). All above-ground biomass within each plot including seedlings, trees (DBH > 5 cm), palm trees, and lianas, were cut down and weighed separately (fresh biomass weight). In addition, litter was collected and weighed from five randomly allocated sub-plots of 1 m² within each plot.
Firstly, trees were cut down and measured for DBH, merchantable height (i.e., stem length from the base to the first branch) and total height, and then weighed separately by compartments. The above-ground portion of the trees was sub-divided into large branches (base diameter ≥10 cm), small branches (diameter < 10 cm) and leaves.
Roots from individual tress with DBH > 5 cm were dug out and weighed after cutting all aboveground biomass of the plots. Only coarse roots were considered below-ground; these were subdivided into two classes: 2 mm < base diameter < 5 cm and base diameter ≥ 5 cm. Thinner roots (< 2 mm) were not included because they are not distinguishable from litter (IPCC 2006IPCC, 2006. IPCC Guidelines for National Greenhouse Inventories ( IPCC Guidelines for National Greenhouse Inventories (http://www.ipcc.ch
). Accessed on 01/12/2009.
http://www.ipcc.ch...
).
Data from above- and below-ground biomass of the sampled trees within each plots, and of 11 additional trees selected randomly outside the plots were used to develop campinarana forest biomass equations. Thereby, a total of one hundred trees with DBH > 5 cm were harvested, dug out and weighed.
To test sample sufficiency, a trial regression was fitted after fifty trees were weighed. Sampling continued until a confidence interval inferior to 10% of the mean was reached, that´s was the main reason why we collected data from 11 trees outside the plots. This level of precision was based on the accepted limit value for forest inventories and other biomass studies (Silva 2007Silva, R.P. 2007. Alometria, Estoque e Dinâmica da Biomassa de Florestas Primárias e Secundárias na região de Manaus (AM). Doctoral thesis, Instituto Nacional de Pesquisas da Amazônia-INPA. Manaus, Brazil. 152p.). In addition, to confirm sample adequacy, a Weibull function was used to test if the diameter distribution from the individual felled trees was consistent with the diameter distribution of the forest. The Weibull probability density function is the most utilised due to its flexibility (Campos and Leite 2006) and has produced reliable results for the central Amazon (Higuchi 2007Higuchi, F.G. 2007. A influência do tamanho da parcela na precisão da função de distribuição de diâmetro de Weibull da floresta primária da Amazônia Central Master’s dissertation, Universidade Federal do Paraná. Curitiba, Brazil. 50p.).
Data analysis
To understand how biomass is distributed within campinarana forest, components (seedlings, trees, palm trees, lianas and litter) the confidence interval (CI 95%) and the uncertainty were calculated separately for each category. Uncertainty is the measure of dispersion currently used in climate change studies and adopted by the Intergovernmental Panel on Climate Change (IPCC). Uncertainty is estimated by dividing the confidence interval (z or t value multiplied by the standard error of the mean) by the mean of the desired variable (Silva 2007Silva, R.P. 2007. Alometria, Estoque e Dinâmica da Biomassa de Florestas Primárias e Secundárias na região de Manaus (AM). Doctoral thesis, Instituto Nacional de Pesquisas da Amazônia-INPA. Manaus, Brazil. 152p.). In accordance with common practice in forest inventories and forestry assessments, uncertainties below 10% were considered acceptable.
To develop biomass equations, regression coefficients (β0, β1 and β2) were estimated by inserting individual tree fresh biomass weights as dependent variables into seven different models (Table 1). These models were obtained from the allometric studies of Santos (1996Santos, J. 1996. Análise de modelos de regressão para estimar a fitomassa da floresta tropical úmida de terra-firme da Amazônia brasileira. Doctoral thesis, Universidade Federal de Viçosa, Viçosa, Brazil. 120p.) and Silva (2007Silva, R.P. 2007. Alometria, Estoque e Dinâmica da Biomassa de Florestas Primárias e Secundárias na região de Manaus (AM). Doctoral thesis, Instituto Nacional de Pesquisas da Amazônia-INPA. Manaus, Brazil. 152p.), and use DBH, total height and merchantable height as independent variables.
Logarithmic and exponential biomass allometric models proposed by Santos (1996Santos, J. 1996. Análise de modelos de regressão para estimar a fitomassa da floresta tropical úmida de terra-firme da Amazônia brasileira. Doctoral thesis, Universidade Federal de Viçosa, Viçosa, Brazil. 120p.) and Silva (2007Silva, R.P. 2007. Alometria, Estoque e Dinâmica da Biomassa de Florestas Primárias e Secundárias na região de Manaus (AM). Doctoral thesis, Instituto Nacional de Pesquisas da Amazônia-INPA. Manaus, Brazil. 152p.) used to adjust the biomass equations for campinarana forest.
These seven models were tested using the total biomass (i.e., above-ground plus coarse root biomass) as the dependent variable. Regressions were fitted using all of the tree data (n=100) divided into two diameter classes: saplings with DBH between 5 and 10 cm (n = 53) and adult trees with DBH ≥ 10 cm (n = 47). The model significance was ascertained with an Analysis of Variance for regression.
The performance of different equations was compared through the coefficient of determination (R²), which indicates how much of the dependent variable is explained by the independent variables in the equation, the standard deviation of the mean as a percentage (Sxy%), and the distribution of the residuals. The latter two measures indicate the equation’s precision. The standard errors of logarithmic models were recalculated because the original error generated by the regression refers to the natural logarithm of the biomass (lnB) and not to the biomass itself. This recalculation allowed the logarithmic and exponential equations to be compared.
Although campinarana forests are not as tall as primary dense forests, their structure is not dissimilar. To test whether biomass equations developed for dense forests can be used for campinaranas, equations developed for primary dense forest in the central Amazon (Silva 2007Silva, R.P. 2007. Alometria, Estoque e Dinâmica da Biomassa de Florestas Primárias e Secundárias na região de Manaus (AM). Doctoral thesis, Instituto Nacional de Pesquisas da Amazônia-INPA. Manaus, Brazil. 152p.) were fitted to the data collected in this study, and the error between estimated and true values was calculated. Also, we tested if this error may be reduced by incorporating a correction factor of campinarana dominant height divided by dense forest dominant height.
The dominant height of the campinarana was calculated as the mean height of the 20% largest felled trees (Loetsch et al. 1973Loetsch, F.; Zöhrer, F.; Haller, K. E. 1973. Forest Inventory. 2nd ed. BVL Verlagsgesellschaft: Munich, Germany, 469p.). For the primary dense forest, we used a dominant height of 28,6 m, as calculated by Lima (2010Lima, A.J.N. 2010. Avaliação de um sistema de inventário florestal contínuo em áreas manejadas e não manejadas do Estado do Amazonas (AM). Doctoral thesis, Instituto Nacional de Pesquisas da Amazônia - INPA, Manaus, Brazil. 183p.) using a dataset of 494 trees measured in the central Amazon, in the same region as the campinarana studied in here. The significance of this correction factor was tested.
RESULTS
Biomass
The above-ground fresh biomass of five fixed-area plots averaged 4,528 ± 1,530 kg (95% CI) and litter averaged 276,80 ± 155 kg (95% CI) per 100 m². Tree biomass represented 94% ± 2.7 (IC 95%) of the total fresh above-ground weight, whilst palm trees, lianas and seedlings represented altogether 6% ± 53 (IC 95%) of it (Table 2).
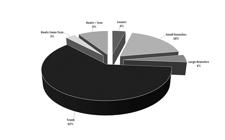
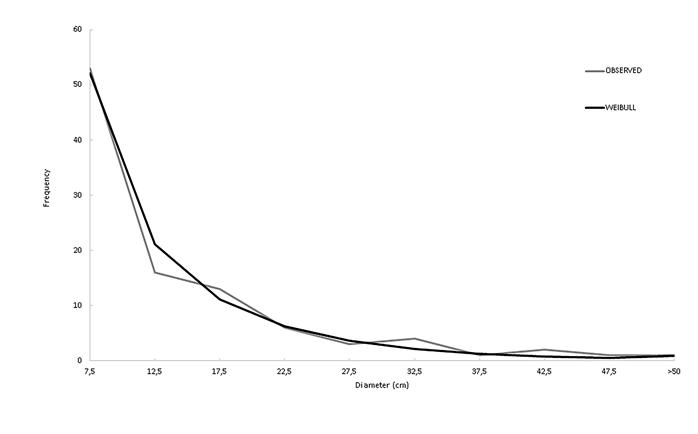
The above-ground biomass of individual trees averaged 389 ± 165 kg (CI 95%) and the below-ground biomass averaged 47 ± 21 kg (CI 95%), the trunk represented 62% of individual trees weight (Figure 1). The mean DBH of sampled trees was 13.4 ± 1.9 cm (95% CI), and the mean total height was 15.9 ± 1.1 m (95% CI). According to the Weibull function performed by chi-squared test, there was a weak evidence (p = 0.79) that the observed DBHs of sampled trees were different from the expected DBH distribution (Figure 2).
Campinarana tree above- and below-ground fresh biomass distribution of compartments of trees sampled in a campinarana forest in central Amazonia.
Distribution of measured DBH of trees sampled in a campinarana forest in central Amazonia compared to the estimated DBH distribution using a Weibull function.
Allometric equations
The regression using fresh weight data of trees fitted to the allometric models previously selected generated 54 different biomass equations. Our analysis of the allometric equations developed for campinaranas showed that all tested models were highly significant (p<0.001). In all nine tested categories, there was more than one equation that fulfilled the conditions of an error (Sxy%) inferior to 10%, a high coefficient of determination (R²) and a symmetrical residual distribution. The models performed better when all of the tree data were used together instead of divided into diameter classes. Hence, it is more efficient to use one equation for the whole tree population than to use separate equations for each diameter class. Except for the sapling equations, the exponential models had skewed residual distributions, indicating that they were inappropriate for estimating biomass over all diameter classes.
Although saplings were more numerous than adult trees, their coefficients of determination were lower and their errors were higher than those of adult trees. The two best fitted equations for each diameter category were selected (Table 3).
Use of primary dense forest equations
The fitting of campinarana data to primary dense forest equations to estimate above-ground, below-ground and total biomass suggested that, in the absence of a campinarana equation, the dense forest equation could be used, as campinarana has a similar structure to dense forest (Table 4). Multiplying the equations by the dominant height ratio was not effective in diminishing the error associated with the above-ground and total biomass equations. In all cases, contrary of what we predicted, the correction factor did not substantially change the error (Table 5). Dominant height calculated for campinarana was 24.6 m, and the correction factor in relation to the dominant height of an adjacent dense primary forest (28.6 m) was 0.86.
DISCUSSION
Biomass and carbon appraisals for tropical forests vary a lot in terms of values and methodologies. Houghton et al. (2000Houghton, R.A.; Skole, D.L; Nobre, C.A.; Hackler, J.L.; Lawrance, K.T; Chomentowsku, W.H. 2000. Annual fluxes of carbon from deforestation and regrowth in the Brazilian Amazon. Nature . 403: 301-304.) concluded that 60% of uncertainties related to Amazon forest carbon flux calculations are due to divergences in methods. Usually biomass is estimate using either direct or indirect methods. Higuchi and Carvalho Jr. (1994Higuchi, N.; Carvalho Jr., J.A. 1994. Fitomassa e conteúdo de carbono de espécies arbóreas da Amazônia. In: Seminário Emissão x Seqüestro de CO2: uma nova oportunidade de negócios para o Brasil. Anais... Companhia Vale do Rio Doce, Rio de Janeiro, Brazil. p. 125-153.) stressed that the direct method should perform better for homogeneous forest areas, but in general most studies include areas with large trees, resulting in overestimates. Gibbs et al. (2007Gibbs, H.; Brown, S.; Niles, J.; Foley, J.A. 2007. Monitoring and estimating tropical forest carbon stocks: making REDD a reality. Environment Research Letters, 2:045023.) discuss that the direct method is accurate to estimate specific local biomass, however, it is cost and labor demanding and prohibitive to use in large scale analysis. Our campinarana biomass estimates using the destructive method in fixed-area plots generated high uncertainties related to the calculated means, confirming that the direct method is unreliable because it is based on only a few small plots as stated by Brown et al. (1989Brown, S; Gillespie, A. J.; Lugo, A. 1989. Biomass estimation methods for tropical forest with applications to inventory data. Forest Science, 35: 881-902.).
While our estimate of campinarana above-ground fresh biomass, including seedlings, trees, lianas and palm trees, was 452.8 ± 153 t.ha-1, estimates of above-ground dry biomass of campinarana in Venezuela using the direct method ranged from 178.64 t.ha-1 (Bongers et al. 1985, apudBarbosa and Ferreira 2004Barbosa, R. I.; Ferreira, C.A.C. 2004. Biomassa acima do solo de um ecossistema de “campina” em Roraima, norte da Amazônia Brasileira. Acta Amazonica , 34: 577-586. ) to 237 t.ha-1 (Klinge and Herrera 1983Klinge, H.; Herrera, R. 1983. Phytomass structure of natural plant communities on spodosols in Southern Venezuela: The Tall Amazon Caatinga Forest. Vegetatio 53: 65-84). None of the latter studies reported the uncertainties around the means, therefore it was not possible to compare them statistically with the present study.
The use of the direct method in this study showed that approximately 94% of the campinarana biomass consisted of trees (DBH ≥ 5 cm) and that the uncertainty related to the mean of tree biomass was only 2.7%, corroborating that it is appropriate to develop allometric equations to estimate campinarana biomass indirectly using only the tree weight data.
Indirect methods to estimate forest biomass are based either on volume and wood density or on allometric relations of trees. The use of volumetric methods to estimate biomass is controversial among researches as many studies of Amazon forest biomass used volume data collected during Projeto RADAM, between 1960 and 1970. RADAM inventories were carried out with the purpose of forest management and harvesting, therefore the reported volumes referred only to merchantable height and could not be used to calculate total or above-ground biomass of Amazon forests. Another controversial point to volumetric methods is the use of wood density, since wood density can vary among tree species, among individuals of the same species, among different parts of the same individual, and also from the core to the bark in one part of an individual tree (Higuchi et al. 2004Higuchi, M. I. G; Higuchi, N. 2004. A Floresta amazônica e suas múltiplas dimensões: uma proposta de educação ambiental. 1st ed. INPA: CNPq, Brazil, 146p. ).
Some authors also multiplied a taper factor to adjust the volumetric equation, which can cause a distortion of biomass estimates. Taper factors are usually based on few species (Somogyi et al. 2006Somogyi, Z.; Cienciala, E.; Mäkipää, R., Muukkonen, P.; Lehtonen, A.; Weiss, P. 2006. Indirect methods of large forest biomass estimation. Europe Journal Forest Research., 126:197-207.) and there are also interspecific and inter-site variations (Higuchi et al. 2004Higuchi, M. I. G; Higuchi, N. 2004. A Floresta amazônica e suas múltiplas dimensões: uma proposta de educação ambiental. 1st ed. INPA: CNPq, Brazil, 146p. ).
The use of allometric equations is an alternative to the volumetric method. Allometry is the study of the growth of an organism part in relation to the growth of the whole organism or to geometric similarity (Niklas 1994Niklas, K.J. 1994. Plant allometry: the scaling of form and process. 1st ed. The University of Chicago Press: Chicago, United States. 395 p.). Allometric relations can be observed empirically or analytically, and is, essentially, based on regression analysis (Niklas 1994). The empirical approach is labor intensive, time consuming and inefficient for nationwide estimates (Zianis and Mecunccini 2004Zianis, D.; Mencuccini, M. 2004. On simplifying allometric analyses of forest biomass. Forest Ecology and Management , 187: 311-332.). However, this approach has generated highly accurate estimates of dense forest biomass and of carbon stocks in the Amazon on a regional scale (Silva 2007Silva, R.P. 2007. Alometria, Estoque e Dinâmica da Biomassa de Florestas Primárias e Secundárias na região de Manaus (AM). Doctoral thesis, Instituto Nacional de Pesquisas da Amazônia-INPA. Manaus, Brazil. 152p.), and was validated by Araújo et al. (1999Araújo, T. M., Higuchi, N., Carvalho Jr, J.A. 1999. Comparison of formulae for biomass content determination in a tropical rain Forest site in the state of Pará, Brazil. Forest Ecology and Management, 117: 43-52.) in Tomé-Açu, Pará state.
The lower coefficients of determination indicate that saplings do not yet have an established pattern of growth and that variables other than DBH and height might be more appropriate for lower diametric classes. A test of similar allometric models showed that, for seedlings and saplings (higher than 30 cm and below 5 cm DBH), the use of diameter at ground basis is more adequate than DBH (Ribeiro et al. 2014Ribeiro, G.H.P.M., Suwa, R., Marra, D. M., Lima, A.J.N., Kajimoto, T., Ishizuka, M., Higuchi, N. 2014. Allometry for juvenile trees in an Amazonian Forest after wind disturbance. Japan Agricultural Research Quarterly, 8: 213-219.).
In addition to evaluating the three parameters used to compare the allometric equations in this study, variables such as time to collect data and costs should also be considered before using the equations to estimate tropical forest biomass in future studies. Models using only DBH as the independent variable would be more cost and time efficient, considering the difficulty in measuring tree height in the Amazon moist forest, and that height estimates can cause high levels of non-sampling errors.
Although it is generally accepted that in the Amazon forest below-ground biomass is equivalent to 20% of the above-ground biomass (Gibbs et al. 2007Gibbs, H.; Brown, S.; Niles, J.; Foley, J.A. 2007. Monitoring and estimating tropical forest carbon stocks: making REDD a reality. Environment Research Letters, 2:045023.), our results showed the below-ground biomass in central Amazon campinarana to correspond only to 12% of the above-ground biomass. Also, the dominant height of campinaranas was 14% lower than the dominant height of the adjacent dense forest (Silva 2007Silva, R.P. 2007. Alometria, Estoque e Dinâmica da Biomassa de Florestas Primárias e Secundárias na região de Manaus (AM). Doctoral thesis, Instituto Nacional de Pesquisas da Amazônia-INPA. Manaus, Brazil. 152p.).
Both forest types occur in the same area and share the same temperature and precipitation conditions, supporting the assumption that the most limiting factor for campinaranas is related to edaphic conditions (Prance 1975Prance, G.T. 1975. Estudos sobre a vegetação das Campinaranas - I. Introdução a uma série de publicações sobre a vegetação das Campinas Amazônicas. Acta Amazonica , 5: 211-223.; Klinge et al. 1977Klinge, H., Medina, E., Herrera, R. 1977. Studies on the Ecology of Amazon Caatinga Forest in southern Venezuela. Acta Cientifica Venezolana, 28: 270-276.; Luizão 2007Luizão, F. J.; Luizão, E.R.; Proctor, J. 2007. Soil acidity and nutrient deficiency in central Amazonian heath forest soils. Plant Ecology, 192: 209-224.). Nardoto (2005Nardoto, G. 2005. Abundância natural de 15N na Amazônia e Cerrado - implicações para a ciclagem de nitrogênio. Doctoral thesis, ESALQ/USP, Piracicaba, São Paulo, Brazil.100p.) compared campinarana and dense forest soil properties in the same area of the present study and found that campinarana Red-Yellow Podzolic consisted of 15% of clay and the dense forest oxisol consisted of 75% of clay. Campinarana carbon-to-nitrogen ratio (C:N) was 16.1, whilst the dense forest was 13,9. Higher C:N ratios indicate presence of more carbon in relation to nitrogen, what can hind organic matter decomposition and cause nitrogen immobilization by microbial cells, affecting negatively plants nutrition.
CONCLUSIONS
This study confirms that calculating forest biomass in the Amazon using the direct method with fixed-area plots can be highly inefficient. Preferably, biomass should be estimated using allometric equations developed for specific sites and forest types. The fixed-area plots used in this study revealed that approximately 94% of a campinarana forest total above-ground biomass in the central Amazon is composed of trees, indicating the suitability of using only tree data in developing biomass equations. In all three biomass categories used to develop allometric equations, there were at least two equations with high coefficients of determination (R²) and errors (Sxy%) below 10%. In the absence of a specific campinarana biomass equation, a dense forest biomass equation could be used to estimate biomass and carbon stock for campinaranas. A correction factor based on dominant height showed to be inefficient in diminishing the error associated with estimates for campinarana using dense forest equations.
ACKNOWLEDGMENTS
The authors thank Andrew Gordon, Ruth Gordon and Helen Nathan for English review of the manuscript and comments, and Henrique Nascimento for help with the data analysis. The entire ZF-2 field team is acknowledged for working hard during the data collection. The authors are grateful to Instituto Nacional de Pesquisas da Amazônia - INPA and Conselho Nacional de Desenvolvimento Científico e Tecnológico - CNPq for intellectual, infra-structure and financial support.
- Anderson, A. B.; Prance G. T.; Albuquerque B. W. 1975. Estudos sobre a vegetação das Campinas Amazônicas III. A vegetação lenhosa da Campina da Reserva Biológica INPA SUFRAMA (Manaus-Caracarai, Km 62). Acta Amazonica, 5: 225-246.
- Araújo, T. M., Higuchi, N., Carvalho Jr, J.A. 1999. Comparison of formulae for biomass content determination in a tropical rain Forest site in the state of Pará, Brazil. Forest Ecology and Management, 117: 43-52.
- Barbosa, R. I.; Ferreira, C.A.C. 2004. Biomassa acima do solo de um ecossistema de “campina” em Roraima, norte da Amazônia Brasileira. Acta Amazonica , 34: 577-586.
- Brown, S; Gillespie, A. J.; Lugo, A. 1989. Biomass estimation methods for tropical forest with applications to inventory data. Forest Science, 35: 881-902.
- Chambers, J.; Higuchi, N. Teixeira, L.M; Santos, J.; Laurance, S.; Trumbore, S. 2004. Response of tree biomass and Wood litter to disturbance in a central Amazon forest. Oecologia, 141: 596-614.
- Chambers, J. Q.; Higuchi, N.; Tribuzy, E. S.; Trumbore, S. E. 2001. Carbon sink for a century. Nature, 410: 429.
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.; Chambers, J.C.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T; et al 2005. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia , 145: 87-99
- Ferraz, J.; Ohta, S.; Sales, P.C. 1998. Distribuição dos solos ao longo de dois transectos em floresta primária ao norte de Manaus (AM). In: Higuchi, N.; Campos, M.A.A.; Sampaio, P.T.B.; Santos, J. dos (Ed.). Pesquisas florestais para a conservação da floresta e reabilitação de áreas degradadas da Amazônia INPA Manaus, Amazonas, p.111-114.
- Gibbs, H.; Brown, S.; Niles, J.; Foley, J.A. 2007. Monitoring and estimating tropical forest carbon stocks: making REDD a reality. Environment Research Letters, 2:045023.
- Higuchi, F.G. 2007. A influência do tamanho da parcela na precisão da função de distribuição de diâmetro de Weibull da floresta primária da Amazônia Central Master’s dissertation, Universidade Federal do Paraná. Curitiba, Brazil. 50p.
- Higuchi, N.; Santos, J.; Ribeiro, R.J.; Minette, L.;Biot, Y. 1998. Biomassa da parte aérea da vegetação da floresta tropical úmida de terra-firme da Amazônia brasileira. Acta Amazonica , 28:153-166.
- Higuchi, M. I. G; Higuchi, N. 2004. A Floresta amazônica e suas múltiplas dimensões: uma proposta de educação ambiental 1st ed. INPA: CNPq, Brazil, 146p.
- Higuchi, N.; Carvalho Jr., J.A. 1994. Fitomassa e conteúdo de carbono de espécies arbóreas da Amazônia. In: Seminário Emissão x Seqüestro de CO2: uma nova oportunidade de negócios para o Brasil. Anais... Companhia Vale do Rio Doce, Rio de Janeiro, Brazil. p. 125-153.
- Houghton, R.A.; Skole, D.L; Nobre, C.A.; Hackler, J.L.; Lawrance, K.T; Chomentowsku, W.H. 2000. Annual fluxes of carbon from deforestation and regrowth in the Brazilian Amazon. Nature . 403: 301-304.
- Klinge, H., Medina, E., Herrera, R. 1977. Studies on the Ecology of Amazon Caatinga Forest in southern Venezuela. Acta Cientifica Venezolana, 28: 270-276.
- Klinge, H.; Herrera, R. 1983. Phytomass structure of natural plant communities on spodosols in Southern Venezuela: The Tall Amazon Caatinga Forest. Vegetatio 53: 65-84
- IPCC, 2006. IPCC Guidelines for National Greenhouse Inventories ( IPCC Guidelines for National Greenhouse Inventories (http://www.ipcc.ch ). Accessed on 01/12/2009.
» http://www.ipcc.ch - Lima, A.J.N. 2010. Avaliação de um sistema de inventário florestal contínuo em áreas manejadas e não manejadas do Estado do Amazonas (AM). Doctoral thesis, Instituto Nacional de Pesquisas da Amazônia - INPA, Manaus, Brazil. 183p.
- Loetsch, F.; Zöhrer, F.; Haller, K. E. 1973. Forest Inventory 2nd ed. BVL Verlagsgesellschaft: Munich, Germany, 469p.
- Luizão, F. J.; Luizão, E.R.; Proctor, J. 2007. Soil acidity and nutrient deficiency in central Amazonian heath forest soils. Plant Ecology, 192: 209-224.
- Magalhães, L.M.S; Blum, W.E.H.; Higuchi, N.; Santos, J. 1998. Relações entre o solo e a floresta no estabelecimento de unidades de paisagens florestais na Amazônia. Floresta e Ambiente, 5: 89-103.
- Nardoto, G. 2005. Abundância natural de 15N na Amazônia e Cerrado - implicações para a ciclagem de nitrogênio Doctoral thesis, ESALQ/USP, Piracicaba, São Paulo, Brazil.100p.
- Nelson, B. W.; Mesquita, R.C.; Pereira, J.L.G.; Souza, S.; Batista, G.T.; Couto, L.B. 1999. Allometric regressions for improved estimate of secondary forest biomass in the central amazon. Forest Ecology and Management , 117:149-167.
- Niklas, K.J. 1994. Plant allometry: the scaling of form and process 1st ed. The University of Chicago Press: Chicago, United States. 395 p.
- Oliveira, A.A.; Daly, D.C.; Vicentini, A.; Cohn-Haft, M. 2001. Florestas sobre areia: campinaranas e igapós. In: Oliveira, A.A.; Daly, D. Florestas do Rio Negro Companhia das Letras: São Paulo, Brazil, p.181-219.
- Pinto, A. C. M., Higuchi, N., Iida, S., Santos, J, Ribeiro, R.J., Rocha, R.M., Silva, R.P. 2003. Padrão de distribuição espacial de espécies florestais que ocorrem na região de Manaus-AM. In: Santos, J. dos; Sampaio, P.; Marenco, R.A.; Ferraz, J.; Salles, P.C.; Saito, M.; Matsuomoto, S.; Higuchi, N. Projeto Jacarandá Fase II. Pesquisas Florestais na Amazônia Central Instituto Nacional de Pesquisas da Amazônia - CPST/INPA: Manaus, p.1-20.
- Pinto, F. R. 2008. Estimativa dos estoques de biomassa e nutrientes em florestas secundárias na Amazônia Central. Master’s dissertation, Instituto Nacional de Pesquisas da Amazônia - INPA, Manaus, Brazil. 162p.
- Prance, G.T. 1975. Estudos sobre a vegetação das Campinaranas - I. Introdução a uma série de publicações sobre a vegetação das Campinas Amazônicas. Acta Amazonica , 5: 211-223.
- Ribeiro, G.H.P.M., Suwa, R., Marra, D. M., Lima, A.J.N., Kajimoto, T., Ishizuka, M., Higuchi, N. 2014. Allometry for juvenile trees in an Amazonian Forest after wind disturbance. Japan Agricultural Research Quarterly, 8: 213-219.
- Santos, J. 1996. Análise de modelos de regressão para estimar a fitomassa da floresta tropical úmida de terra-firme da Amazônia brasileira Doctoral thesis, Universidade Federal de Viçosa, Viçosa, Brazil. 120p.
- Silva, R.P.; Santos, J.; Tribuzy, E.S.; Chambers, J.Q.; Nakamura, S.; Higuchi, N. 2002. Diameter increment and growth patterns for individual trees in Central Amazon, Brazil. Forest Ecology and Management , 116: 295-301.
- Silva, R.P. 2007. Alometria, Estoque e Dinâmica da Biomassa de Florestas Primárias e Secundárias na região de Manaus (AM) Doctoral thesis, Instituto Nacional de Pesquisas da Amazônia-INPA. Manaus, Brazil. 152p.
- Somogyi, Z.; Cienciala, E.; Mäkipää, R., Muukkonen, P.; Lehtonen, A.; Weiss, P. 2006. Indirect methods of large forest biomass estimation. Europe Journal Forest Research, 126:197-207.
- Teixeira, L. M; Chambers, J.Q.; Silva, A. R.; Lima, A.; Carneiro, V.M; Santos, J.; Higuchi, N. 2007. Projeção da dinâmica da floresta natural de Terra-firme, região de Manaus-AM, com o uso da cadeia de transição probabilística de Markov. Acta Amazonica 37: 377-384.
- Uhl, C.; Buschbacher, R.; Serrão, E.A.S. 1988. Abandoned pastures in eastern Amazonia. I. Patterns of plant succession. Journal of Ecology, 76: 663-681.
- Zianis, D.; Mencuccini, M. 2004. On simplifying allometric analyses of forest biomass. Forest Ecology and Management , 187: 311-332.
-
ASSOCIATE EDITOR:
Oscar Valverde -
CITE AS:
Woortmann, C.P.I.B.; Higuchi, N.; dos Santos, J.; da Silva, R.P. 2018. Allometric equations for total, above- and below-ground biomass and carbon of the Amazonian forest type known as campinarana. Acta Amazonica 48: 85-92.
Publication Dates
-
Publication in this collection
Apr-Jun 2018
History
-
Received
13 Mar 2017 -
Accepted
15 Dec 2017