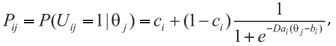Resumos
A preocupação com medidas de traços psicológicos é antiga, sendo que muitos estudos e propostas de métodos foram desenvolvidos no sentido de alcançar este objetivo. Entre os trabalhos propostos, destaca-se a Teoria da Resposta ao Item (TRI) que, a princípio, veio completar limitações da Teoria Clássica de Medidas, empregada em larga escala até hoje na medida de traços psicológicos. O ponto principal da TRI é que ela leva em consideração o item particularmente, sem relevar os escores totais; portanto, as conclusões não dependem apenas do teste ou questionário, mas de cada item que o compõe. Este artigo propõe-se a apresentar esta Teoria que revolucionou a teoria de medidas.
Medidas; métodos e teorias; Psicometria; Testes psicológicos; Questionários
La preocupación con las medidas de los rasgos psicológicos es antigua y muchos estudios y propuestas de métodos fueron desarrollados para lograr este objetivo. Entre estas propuestas de trabajo se incluye la Teoría de la Respuesta al Ítem (TRI) que, en principio, vino a completar las limitaciones de la Teoría Clásica de los Tests, ampliamente utilizada hasta hoy en la medida de los rasgos psicológicos. El punto principal de la TRI es que se tiene en cuenta el punto concreto, sin relevar las puntuaciones totales; por lo tanto, los resultados no sólo dependen de la prueba o cuestionario, sino que de cada ítem que lo compone. En este artículo se propone presentar la Teoría que revolucionó la teoría de medidas.
Mediciones; métodos y teorías; Psicometría.; Pruebas psicológica; Cuestionario
The concern with measures of psychological traits is old and many studies and proposals of methods were developed to achieve this goal. Among these proposed methods highlights the Item Response Theory (IRT) that, in principle, came to complete limitations of the Classical Test Theory, which is widely used until nowadays in the measurement of psychological traits. The main point of IRT is that it takes into account the item in particular, not relieving the total scores; therefore, the findings do not only depend on the test or questionnaire, but on each item that composes it. This article proposes to present this Theory that revolutionized the theory of measures.
Measurements; methods and theories; Psychometrics; Psychological tests; Questionnaires
ARTIGO ORIGINAL
Teoria da Resposta ao Item
Teoria de la respuesta al item
Eutalia Aparecida Candido de AraujoI; Dalton Francisco de AndradeII; Silvana Ligia Vincenzi BortolottiIII
IDoutora em Saúde Pública pela Faculdade de Saúde Publica da Universidade de São Paulo. Bolsista PRODOC/CAPES - Programa de Pós-Graduação em Enfermagem na Saúde do Adulto (PROESA) da Escola de Enfermagem da Universidade de São Paulo. São Paulo, SP, Brasil. eutalia@usp.br
IIProfessor Titular do Departamento de Informática e Estatística da Universidade Federal de Santa Catarina. Campus Universitário. Florianópolis, Santa Catarina, Brasil. dandrade@inf.ufsc.br
IIIMestre e Doutoranda em Engenharia de Produção pela Universidade Federal de Santa Catarina. Medianeira, Paraná, Brasil. sligie@globo.com
Correspondência Correspondência: Dalton Francisco de Andrade Campus Universitário Trindade - Cx Postal 476 CEP 88040-900 - Florianópolis, SC, Brasil
RESUMO
A preocupação com medidas de traços psicológicos é antiga, sendo que muitos estudos e propostas de métodos foram desenvolvidos no sentido de alcançar este objetivo. Entre os trabalhos propostos, destaca-se a Teoria da Resposta ao Item (TRI) que, a princípio, veio completar limitações da Teoria Clássica de Medidas, empregada em larga escala até hoje na medida de traços psicológicos. O ponto principal da TRI é que ela leva em consideração o item particularmente, sem relevar os escores totais; portanto, as conclusões não dependem apenas do teste ou questionário, mas de cada item que o compõe. Este artigo propõe-se a apresentar esta Teoria que revolucionou a teoria de medidas.
Descritores: Medidas, métodos e teorias. Psicometria. Testes psicológicos. Questionários.
RESUMEN
La preocupación con las medidas de los rasgos psicológicos es antigua y muchos estudios y propuestas de métodos fueron desarrollados para lograr este objetivo. Entre estas propuestas de trabajo se incluye la Teoría de la Respuesta al Ítem (TRI) que, en principio, vino a completar las limitaciones de la Teoría Clásica de los Tests, ampliamente utilizada hasta hoy en la medida de los rasgos psicológicos. El punto principal de la TRI es que se tiene en cuenta el punto concreto, sin relevar las puntuaciones totales; por lo tanto, los resultados no sólo dependen de la prueba o cuestionario, sino que de cada ítem que lo compone. En este artículo se propone presentar la Teoría que revolucionó la teoría de medidas.
Descriptores: Mediciones, métodos y teorías. Psicometría. Pruebas psicológicas. Cuestionario.
INTRODUÇÃO À TEORIA MODERNA DA MENSURAÇÃO
A procura por informações de medida de propriedades psicológicas de indivíduos levou muitos pesquisadores a desenvolver modelos que pudessem estimar estas propriedades (propriedades psicológicas, também referidas por traço latente, que são características individuais que não podem ser observadas diretamente, tais como: proficiência em determinado conteúdo na avaliação educacional, atitude em relação à mudança organizacional, nível de estresse, nível de depressão, qualidade de vida etc.).
Essa busca teve início no final do século 19 e continua até os dias de hoje e vários foram os trabalhos desenvolvidos com o intuito de propor uma modelagem estatística para o traço latente. Este artigo tem como objetivo apresentar a Teoria da Resposta ao Item - TRI - que trouxe muitos benefícios à Psicometria.
Inicialmente, faz-se um relato breve sobre a trajetória da teoria de medidas e TRI e em seguida, apresentam-se a TRI, os seus fundamentos e pressupostos e alguns de seus modelos.
UMA BREVE HISTÓRIA DA TEORIA DE MEDIDAS E DA TRI
Um dos primeiros estudos de interesse em medida remonta ainda ao século 19 com trabalhos de psiquiatras franceses e alemães, que verificaram a influência da doença mental em habilidades motoras, sensoriais e cognitivo-comportamentais, e de pesquisadores ingleses na área de genética, que destacaram a importância de medidas de diferenças individuais ao utilizar uma metodologia bem definida(1).
Posteriormente, no início do século 20, veio a contribuição de Charles Spearman(2) que desenvolveu uma metodologia e conceitos que, em seguida, seria conhecida como a Teoria Clássica de Medidas e Análise Fatorial.
Ainda no início desse século, os trabalhos de Thurstone(3-4) proporcionaram uma grande contribuição na construção de medidas de traço latentes e, em especial, na medida de atitude. Em seu trabalho, o autor(3-4) desenvolveu um método de medida estatístico denominado Lei dos Julgamentos Comparativos que pode ser visto como o mais importante precursor probabilístico da Teoria da Resposta ao Item(1). No desenvolvimento deste método, Thurstone introduziu dois mecanismos de respostas ou princípios para construção de escalas psicológicas que hoje são conhecidos como mecanismos acumulativo e de desdobramento(5).
Os primeiros modelos para variáveis latentes foram apresentados nos estudos de Lawley(6), Guttman(7) e Lazarsfeld(8), marcando, assim, o início da TRI.
Mas foi com as publicações de Frederic Lord(9) que, nos anos 1950, a TRI ganhou força, pois, com seu trabalho, ele deu início ao desenvolvimento formal da Teoria da Resposta ao Item. Além disso, contribuiu para o desenvolvimento de programas para computadores, imprescindíveis para colocar esta teoria em prática. Mais tarde, Lord elaborou com Novick(10) um livro clássico no qual estabeleceram várias teorias estatísticas de escores de teste mental e ainda escreveu aplicações desta teoria(11).
Paralelamente ao trabalho de Lord, Georg Rasch, que trabalhava desde os anos 1940 com medidas de traço latente, começou a desenvolver seu trabalho para modelos dicotômicos e criou o modelo conhecido como Modelo de Rasch(12).
Lord(9) foi o primeiro a desenvolver o modelo unidimensional de 2 parâmetros de natureza acumulativa para respostas dicotômicas (certo ou errado), baseado na distribuição normal (ogiva normal). Entretanto, o próprio Lord sentiu a necessidade da incorporação de um parâmetro que tratasse do problema do acerto casual, desenvolvendo o modelo de 3 parâmetros. Alguns anos mais tarde, Birnbaum(13)forneceu uma contribuição muito importante a estes modelos, ao sugerir a substituição, em ambos os modelos, da função ogiva normal pela função logística, matematicamente mais conveniente(14).
A necessidade de introduzir, nos testes psicométricos, respostas que não fossem consideradas exclusivamente dicotômicas proporcionou o desenvolvimento de modelos da TRI de natureza acumulativa para respostas politômicas, nominais ou graduadas, como o Modelo de Resposta Nominal de Bock(15), o Modelo de Resposta Graduada de Samejina(16), o Modelo de Crédito Parcial proposto por Masters(17), entre outros.
Durante as últimas décadas, os modelos da TRI de natureza acumulativa se desenvolveram consideravelmente e tiveram um notável avanço em várias aplicações, enquanto que os modelos da TRI de natureza de desdobramento não alcançaram tanto progresso e a razão disso se deve principalmente à compreensão do seu mecanismo de resposta e a falta de programas computacionais para estimar parâmetros deste tipo de modelo. O primeiro modelo de desdobramento desenvolvido, de natureza determinística, foi proposto por Coombs(18) para medidas de preferências, o qual foi quem formalizou o termo desdobramento. Anos mais tarde, veio a contribuição de Davison(19), apresentando uma aplicação do modelo de desdobramento em dados de desenvolvimento de personalidade. Nas décadas de 80 e 90, começaram aparecer os primeiros modelos probabilísticos de natureza de desdobramento com Andrich(20-21), Hoijtink(22-23), Andrich e Luo(24), entre outros.
A TRI foi desenvolvida principalmente para suprir limitações que a Teoria Clássica de Medidas apresentava. Embora a Teoria Clássica tenha sido muito útil, alguns autores(25) citam várias limitações, dentre as quais se destaca que o instrumento de medida é dependente das características dos examinados que se submetem ao teste ou ao questionário.
A TRI surgiu como uma forma de considerar cada item particularmente, sem relevar os escores totais; portanto, as conclusões não dependem exclusivamente do teste ou questionário, mas de cada item que o compõe.
Deste modo, a TRI não entra em conflito com os princípios que fundamentam a Teoria Clássica de Medidas e possibilita uma nova proposta de análise estatística, centrada em cada item, que transcende limitações impostas pela Teoria Clássica, na qual o modelo para construção da escala baseia-se diretamente no resultado obtido do instrumento como um todo.
FUNDAMENTOS DA TEORIA DA RESPOSTA AO ITEM
A TRI fornece modelos matemáticos para os traços latentes, propondo formas de representar a relação entre a probabilidade de um indivíduo dar uma certa resposta a um item, seu traço latente e características (parâmetros) dos itens, na área de conhecimento em estudo(14).
A partir de um conjunto de respostas apresentadas por um grupo de respondentes a um conjunto de itens, a TRI permite a estimação dos parâmetros dos itens e dos indivíduos em uma escala de medida. Por exemplo, considere o construto nível de qualidade de vida. Uma análise feita através da TRI pode estimar o nível de qualidade de vida do respondente (isto é, um parâmetro do indivíduo) e também os parâmetros dos itens, de modo a criar uma escala de medida de nível de qualidade de vida.
Dentre as grandes vantagens da Teoria de Resposta ao Item sobre a Teoria Clássica de Medidas estão: ela possibilita fazer comparações entre traço latente de indivíduos de populações diferentes quando são submetidos a testes ou questionários que tenham alguns itens comuns e permite, ainda, a comparação de indivíduos da mesma população submetidos a testes totalmente diferentes; isto é possível porque a TRI tem como elementos centrais os itens e não o teste ou questionário como um todo(14); possibilita uma melhor análise de cada item que forma o instrumento de medida, pois leva em consideração suas características específicas de construção de escalas; os itens e os indivíduos estão na mesma escala, assim o nível de uma característica que um indivíduo possui pode ser comparado ao nível da característica exigida pelo item; isso facilita a interpretação da escala gerada e permite também conhecer quais itens estão produzindo informação ao longo da escala(26); ela permite um tratamento para um conjunto de dados faltantes, utilizando para isso somente os dados respondidos, o que não pode acontecer na Teoria Clássica de Medidas. Outro benefício da TRI é o princípio da invariância, isto é, os parâmetros dos itens não dependem do traço latente do respondente e os parâmetros dos indivíduos não dependem dos itens apresentados(25).
Os diversos modelos de respostas ao item existentes se distinguem na forma matemática da função característica do item e/ou no número de parâmetros especificados no modelo. Todos os modelos podem conter um ou mais parâmetros relacionados aos itens e ao indivíduo(27). A distinção principal entre modelos da TRI refere-se à suposição sobre o relacionamento entre a seleção de opções de uma resposta e o nível do traço latente. Existem dois tipos de processo de resposta: o acumulativo e o de desdobramento . Foram desenvolvidos modelos de natureza acumulativa e de natureza de desdobramento para dados dicotômicos ou binários e politômicos, nominal ou graduados, modelos paramétricos e não paramétricos e modelos unidimensionais e multidimensionais.
PRESSUPOSTOS DA TRI
Os modelos utilizados na TRI requerem dois pressupostos relevantes(26): a curva característica do item - CCI, pois há uma forma específica para cada mecanismo do processo de resposta utilizado, e a independência local ou dimensionalidade.
A forma de uma curva característica do item descreve como a mudança do traço latente relaciona-se com a mudança na probabilidade de uma resposta especifica(26).
A independência local é obtida quando, controlados pelo nível do traço latente, os itens do teste são independentes, assim a probabilidade de responder um item é precisamente determinada pelo nível do traço latente do respondente e não por suas respostas a outros itens do conjunto(14,26). A independência local é vista como conseqüência da correta determinação da dimensionalidade dos dados(11). Dimensionalidade consiste no número de fatores responsáveis para expressar o traço latente. A dimensionalidade pode ser verificada através de uma Análise Fatorial apropriada para dados categorizados(14,26).
A seguir apresentam-se os principais modelos unidimensionais da TRI.
MODELOS DA TRI
Os modelos da TRI dependem do tipo de item e do tipo de processo de resposta. Eles podem ser acumulativos ou não acumulativos.
Modelos Acumulativos
Os modelos acumulativos surgiram para suprir deficiências da teoria clássica, principalmente em medidas de avaliação educacional, razão pela qual a maioria dos livros e artigos publicados da TRI definem estes modelos tomando sempre como exemplo de traço latente habilidade ou proficiência. Desta forma, se considerarmos então este traço latente, pode-se dizer que os modelos acumulativos da TRI são modelos em que a probabilidade de um indivíduo dar ou escolher uma resposta correta ao item aumenta com o aumento do seu traço latente, isto é, níveis maiores de traço latente conduzem a valores mais altos de probabilidade de resposta correta, apresentando um comportamento monotônico na CCI.
Modelos para Itens Dicotômicos
Dentre os modelos para itens com resposta dicotômica ou itens de múltipla escolha (corrigido como certo/errado) acumulativos destacam-se: o Modelo Logístico de 1 parâmetro, o Modelo Logístico de 2 parâmetros e o Modelo Logístico de 3 parâmetros.
O Modelo Logístico de 3 parâmetros adequado para respostas dicotômicas é dado por:
onde,
i = 1, 2, ...., I (representa os I itens propostos para avaliar o traço latente considerado) e j = 1, 2, ...., n (representa os n elementos que compõem a amostra, que podem ser indivíduos, empresas etc.);
Uijé uma variável dicotômica que assume os valores 1, quando o respondente j responde corretamente, concorda ou satisfaz as condições do item i, ou 0 caso contrário;
θj pode representar o traço latente do respondente j;
P(Uij=1|θj) é a probabilidade de o respondente j, condicionado no seu traço latente θj, responder corretamente, ou concordar ou satisfazer as condições do item i e é denominada de Função de Resposta do Item FRI;
bi é o parâmetro de dificuldade (ou de posição) do item i, medido na mesma escala do traço latente;
ai é o parâmetro de discriminação (ou de inclinação) do item i, com valor proporcional à inclinação da curva característica do item no ponto bi. Itens com maiores valores de ai fornecem melhores discriminações;
ci é o parâmetro do acerto casual;
D é uma constante de escala igual a 1, mas se utiliza o valor 1,7, quando se quer que os valores da função logística se aproximem da função ogiva normal.
Na interpretação do modelo logístico de 3 parâmetros, a P(Uij=1|θj) é considerada como a proporção de respostas corretas ou proporção de respostas concordo ou proporção de respostas que satisfazem o item i dentre todos os indivíduos da população com um traço latente.
Na Figura 1 temos um exemplo de uma CCI de um item com parâmetros a=1,4, b=1,2 e c=0,2, representados na escala (0,1) que será discutida mais adiante.
Na Figura 1, pode-se observar que se trata de um modelo não linear e, quanto maior a habilidade maior a probabilidade de responder o item corretamente. Esta relação tem o formato de uma curva em S com inclinação e deslocamento na escala do traço latente, definidos pelos parâmetros dos itens.
O parâmetro bi está na mesma unidade do traço latente. Este parâmetro representa o nível do traço latente necessário para que a probabilidade de uma resposta correta ou concordo ou satisfazer as condições do item seja de (1+c)/2(14). Desta forma, para um valor de bi alto, é necessário um traço latente alto para responder corretamente ou concordar ou satisfazer as condições do item.
O parâmetro ci é mencionado como a probabilidade de acerto casual. Se o traço latente é uma habilidade, então, o parâmetro ci corresponde à probabilidade de um aluno com baixa habilidade responder corretamente o item. Os modelos que não admitem o acerto casual atribuem c=0 e são conhecidos como Modelos Logísticos de 2 parâmetros.
Não são esperados valores negativos para o parâmetro ai, uma vez que valores negativos de ai indicariam que a probabilidade de responder corretamente, concordar ou satisfazer as condições do item diminui com o aumento do traço latente, o que contrairia a natureza do traço latente. Este parâmetro possibilita investigar a qualidade dos itens(14) Itens que apresentam um valor alto do parâmetro de discriminação são itens com CCI com maior inclinação e que discriminam melhor os indivíduos ou empresas. O Modelo Logístico de 1 parâmetro é aquele que, além de não admitir acerto casual, também pressupõe que os parâmetros ai têm todos o mesmo valor.
Os Modelos Logísticos de 1, 2 e 3 parâmetros são os mais utilizados, principalmente no campo de testes, como por exemplo, na análise dos dados do Sistema Nacional de Ensino Básico SAEB e em avaliações estaduais, como a do Sistema de Avaliação de Rendimento Escolar do Estado de São Paulo SARESP.
Modelos para Itens Politômicos
Os modelos para itens politômicos dependem da natureza das categorias de resposta. Em testes de múltipla escolha em que as categorias não são ordenadas, o modelo é denominado Modelo Nominal e, nos casos em que as categorias são ordenadas, o modelo é denominado Modelo Ordinal, por exemplo, quando as categorias dos itens são dadas conforme uma escala de Likert.
Além dos modelos politômicos já citados tem-se também o Modelo de Escala Gradual desenvolvido por Andrich(28) e o Modelo de Crédito Parcial Generalizado formulado por Muraki(29). Na Figura 2, apresenta-se a CCI do Modelo de Resposta Gradual de Samejima(16) de um item com quatro categorias de resposta.
Observa-se na Figura 2, que os respondentes com traço latente até 2,0 têm maior probabilidade de responder a categoria 0. Já os respondentes com traço latente entre -2,0 e 0,0 têm mais chance de alcançarem a categoria 1. Para os respondentes com o traço latente entre 0,0 e 2,0, a maior probabilidade é que respondam à categoria 2, enquanto que os respondentes com habilidade acima de 2,0 devem responder à categoria maior, isto é, a categoria 3(14).
Modelos de Desdobramentos unfolding model
Os modelos de desdobramento da TRI são baseados em processos de resposta de pontos ideais não-monotônicos que foram descritos por Coombs(18,30) e por Thurstone(4,31). A lógica por detrás destes modelos é que os indivíduos selecionam a opção da resposta que é a mais próxima da sua posição do traço latente.
Os modelos de desdobramentos se distinguem dos modelos acumulativos por serem modelos de proximidade, onde categorias de resposta mais altas são mais prováveis (indicativo de níveis mais fortes de concordância) quando a distância entre os parâmetros do indivíduo e o de posição do item na escala diminui. Ou seja, a probabilidade de um indivíduo dar uma resposta a um item está em função da distância entre os parâmetros do indivíduo e o de posição do item na escala, e não como função do parâmetro do indivíduo, como nos modelos acumulativos(27).
Embora os modelos de desdobramentos tenham sido projetados inicialmente para dados de medidas de atitude, estes modelos têm tido sucesso também para dados relacionados com comportamentos e etapas de desenvolvimento, como sugerido primeiramente por Coombs e Smith(32). Por exemplo, no estudo de Volet e Chalmers(33), sobre objetivos de aprendizagem de estudantes, e no trabalho de Davison, Robbins e Swanson(34), a respeito de uma re-análise da teoria do desenvolvimento moral de Kohlberg(35).
Nesses modelos, considera-se que há um ponto ideal para cada indivíduo na escala de um traço latente e a opção da resposta escolhida será a que estiver mais próxima do ponto ideal do indivíduo. Logo, os indivíduos com um nível do traço latente que é o mais próximo ao nível expressado no item terão maior probabilidade de concordar com o item.
Considere, por exemplo, o seguinte item, extraído de Richard(36), utilizado para medir atitude para a distância interpessoal a indivíduos homossexuais: Eu falaria com um homossexual na rua ou num ambiente social, mas eu não seria amigo de um, com as seguintes categorias de respostas: discordo, concordo.
Neste item, os indivíduos que têm uma baixa atitude com relação à distância interpessoal a indivíduos homossexuais, escolheriam a categoria de resposta discordo porque não concordariam com a parte do item. Eu falaria com um homossexual na rua ou num ambiente social. Indivíduos que têm atitude média com relação a este traço latente tenderiam a concordar com este item, isto é escolheriam a categoria concordo. Entretanto, indivíduos que têm uma alta atitude para a distância interpessoal a indivíduos homossexuais tenderiam a discordar porque elas não concordariam com a parte do item mas eu não seria amigo de um. Note que neste item, níveis altos do construto atitude para a distância interpessoal a indivíduos homossexuais não implica em categorias de respostas mais altas, como ocorre com os modelos acumulativos. Neste caso, o modelo acumulativo não seria adequado para a estimação do traço latente.
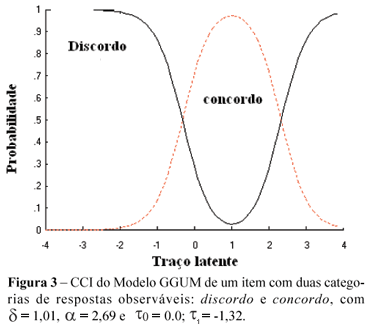
No modelo de desdobramento da TRI, a probabilidade de concordância com um item é maior quando há pouca distância entre o traço latente do respondente e a posição do item na escala. Deste modo, neste caso, uma curva em forma de sino com um único pico descreve a CCI do modelo de desdobramento, ao contrário da função monótona crescente dos modelos acumulativos. A representação gráfica apropriada para as categorias de resposta concordo e discordo do exemplo citado seria dada conforme a Figura 3.
Vários modelos de desdobramentos de resposta ao item unidimensional foram desenvolvidos para medida de atitude; alguns são adequados para respostas binárias, enquanto que outros são apropriados para respostas graduadas. Modelos para dados binários podem ser encontrados nos estudos(5,22-24,37-38) e modelos para dados graduados em outros(39-40). Dos modelos desenvolvidos, destacam-se: o Modelo Parella(22-23), GGUM (Generalized Graded Unfolding Model)(40) e o Modelo Cosseno Hiperbólico (HCM)(24).
Dentre os modelos citados, apresenta-se o GGUM por ser um modelo de desdobramento mais geral e adequado, tanto para respostas dicotômicas ou binárias, como também para respostas politômicas ordinais.
O GGUM foi desenvolvido a partir de quatro suposições básicas sobre o processo de resposta. Vale comentar duas delas. A primeira salienta que, quando um indivíduo é solicitado para expressar a sua opinião de aceitação em um item de atitude, o indivíduo tende a concordar com o item à medida que ele (o item) é localizado próximo de sua posição pessoal em uma escala do traço latente. Por exemplo, se δi denotar a posição do item i nesta escala e θj denotar a posição do indivíduo j na mesma escala, então o indivíduo é mais tendente a concordar com o item à medida que a distância entre θj e δi se aproxima de zero. A segunda proposição do modelo destaca que um indivíduo pode responder a uma determinada categoria de resposta, por exemplo, a resposta discordo, por duas razões: discorda acima ou discorda abaixo da posição do item. Estas possibilidades de resposta da categoria discordo, isto é, discordo acima ou discordo abaixo são denominadas de categorias de respostas subjetivas que o indivíduo pode usar. No exemplo citado sobre atitude para a distância interpessoal a indivíduos homossexuais, o indivíduo pode discordar por dois motivos: ou por que tinha uma baixa atitude ou uma alta atitude em relação ao relacionamento com homossexual.
O modelo GGUM é dado por(40):
onde,
Z i é uma resposta observável a um item de atitude i;
z = 0, 1, 2, 3,...H; z = 0 corresponde ao nível de discordância mais forte e z = H corresponde ao nível de concordância mais forte;
H é o número de categorias de respostas observáveis menos 1. M = 2H +1;
θj é o parâmetro de locação do indivíduo j na escala do traço latente;
δi é o parâmetro de locação do item i na escala do traço latente;
αi é o parâmetro de discriminação do item i;
τik é o parâmetro de posição do limiar de categoria de resposta subjetiva k na escala do traço latente relativa à posição do item i; corresponde ao valor da distância entre θj e δi que determina o ponto em que a k-ésima categoria de resposta subjetiva passa a ter probabilidade de resposta sobre (k-1)-ésima categoria de resposta subjetiva para o indivíduo j no item i e τi0 é, por definição, igual a zero;
M é o número das categorias de respostas subjetivas menos 1.
ESTIMAÇÃO E CONSTRUÇÃO DA ESCALA
Uma das etapas mais importantes da TRI consiste na estimação dos parâmetros dos itens e dos traços latentes. Existem vários métodos de estimação. Os mais empregados são o Método da Máxima Verossimilhança e Métodos Bayesianos. Na estimação dos parâmetros dos itens, que é comumente chamada de calibração, é usual a aplicação da Máxima Verossimilhança Marginal e na estimação dos traços latentes a aplicação do Método Bayesiano EAP(14).
A aplicação destes métodos de estimação requer a utilização de ferramentas matemáticas bastante complexas que necessitam de recursos computacionais. Dentre os programas computacionais existentes, destacam-se: BILOG(41), BILOG MG(42), PARSCALE(43), MULTILOG (44), para os modelos acumulativos e RUMMFOLD(45), MUDFOLD(46) e GGUM2004(47), para os modelos de desdobramentos.
Pode-se verificar nos modelos da TRI propostos, um problema denominado falta de identificabilidade do modelo. Esta não-identificabilidade ocorre porque mais de um conjunto de parâmetros produz o mesmo valor na probabilidade dada pelos modelos. Essa não-identificabilidade pode ser eliminada, por exemplo, fixando alguns valores para o traço latente.
Salienta-se que esta não-identificabilidade está fortemente relacionada com as características da população em estudo(14). Para resolver este problema, basta especificar uma medida de posição (média, por exemplo) e outra de dispersão (desvio-padrão, por exemplo) para o traço latente. Deste modo, ao definir uma métrica (unidade de medida) para o traço latente e naturalmente para os parâmetros dos itens, elimina-se o problema da não-identificabilidade. É usual definir esta métrica na forma (µ, σ) com µ = 0 e σ = 1(14).
Esta métrica (0,1) é utilizada pelos programas computacionais para as estimativas dos parâmetros. Embora a utilização desta métrica seja freqüente, podem-se fazer transformações lineares de modo a apresentar os resultados em outra métrica qualquer. Por exemplo, o SAEB/PROVA BRASIL usa a métrica (250, 50), que pode ser obtida através de uma transformação de escala. Assim, na escala (0,1) um indivíduo com traço latente 1,5 está a 1,5 desvios-padrões acima do traço latente médio na escala (0,1); este mesmo indivíduo teria um traço latente de 325, valor 1,5 desvios-padrões acima do traço latente médio na escala do SAEB/PROVA BRASIL. As mesmas relações existentes entre os parâmetros se mantêm nas duas métricas(14).
Uma vez especificada a escala, ela precisa ser interpretada à luz do tema, ou seja, dentro do problema que está sendo estudado. Por exemplo, se um traço latente representa a proficiência em matemática, qual o conhecimento de um aluno que obteve a estimativa do traço latente 1, numa escala (0,1). O que este aluno sabe e o que ele não sabe de matemática? A TRI permite essa interpretação, que é obtida a partir do posicionamento dos itens na escala. Um exemplo de uma escala interpretada é a denominada Escala Nacional de Proficiência do SAEB/PROVA BRASIL, disponível em: http://prova brasil.inep.gov.br/index.php?option=com_wrapper&Itemid=148. Maiores detalhes sobre construção e interpretação de escalas podem ser encontradas em Valle(48).
EQUALIZAÇÃO
Equalizar significa equiparar, tornar comparável, colocar os parâmetros dos itens provenientes de testes diferentes e traços latentes de respondentes de diferentes grupos na mesma métrica, tornando os itens e os respondentes comparáveis(14). Existem dois tipos de equalização: equalização via população, quando um único grupo de respondentes é submetido aos testes; via itens, quando grupos diferentes respondem testes diferentes com itens comuns entre eles. O segundo tipo de equalização pode ser realizado de dois modos: a posteriori e simultâneamente, através da utilização de modelos de grupos múltiplos(14).
CONSIDERAÇÕES FINAIS
A TRI, sem dúvida, revolucionou a Psicometria ao propor modelos para traços latentes, pois oferece muitas vantagens sobre a Teoria Clássica de Medidas, principalmente quanto à sua suposição de invariância. Assim, se um pesquisador deseja obter a medida de um determinado traço latente, ele deve caracterizar a natureza do traço latente a ser medido, construir os itens que devem cobrir todo o traço latente, observar o tipo de resposta que é dado ao item para verificar se os itens têm natureza acumulativa ou de desdobramento e, a partir daí, escolher o modelo da TRI mais adequado que se ajuste ao seus dados. Em seguida, estimar os parâmetros dos itens e dos respondentes e construir e interpretar a escala do traço latente.
Os modelos apresentados neste trabalho são modelos paramétricos e unidimensionais. Na TRI também existem modelos não paramétricos e multidimensionais.
Recebido: 17/07/2009
Aprovado: 24/08/2009
- 1. Junker W, Sijtsma K. Item Response Theory: past performance present, developments, and future expectations. Behaviormetrika. 2006;33(1):75-102.
- 2. Spearman C. "General Intelligence", objectively determined and measured. Am J Psychol. 1904;15(2):201-93.
- 3. Thurstone LL. A Law of comparative judgment. Psychol Rev. 1927;34(2):273-86.
- 4. Thurstone LL. Attitudes can be measured. Am J Sociol. 1928;26(2):249-69.
- 5. Andrich D. The application of an unfolding model of the PIRT type for the measurement of attitude. Appl Psychol Meas. 1988;12(1):33-51.
- 6. Lawley DN. On problems connected with item selection and test construction. Proceedings Royal Society Edinburgh, Series A. 1943;61(2):273-87.
- 7. Guttman L. The basis for scalogram analysis. In: Stouffer SA, Guttman L, Suchman EA, Lazarsfeld PF, Star SA, Clausen JA, editors. Measurement and prediction. Princeton, NY: Princeton University Press; 1950. v. 4, p. 60-90.
- 8. Lazarsfeld PF. The logical and mathematical foundation of latent structure analysis. In: Stauffer SA, Guttman L, Suchman EA, Lazarsfeld PF, Star SA, Clausen JA, editors. Measurement and prediction. Princeton, NJ: Princeton University Press; 1950. v. 4, p. 362-412.
- 9. Lord FM. A theory of test scores. Psychometric Monograph. 1952;(7).
- 10. Lord FM, Novick MR. Statistical theories of mental test scores. Reading, MA: Addison-Wesley; 1968.
- 11. Lord FM. Applications of item response theory to practical testing problems. Hillsdale, NJ: Lawrence Erlbaum; 1980.
- 12. Van der Linden WJ, Hambleton RK. Handbook of modern Item Response Theory. New York: Spring-Verlag; 1997.
- 13. Birnbaum A. Some latent trait models and their use in inferring and examinee's ability. In: Lord FM, Novick MR. Statistical theories of mental test scores. Reading, MA: Addison -Wesley; 1968.
- 14. Andrade DF, Tavares HR, Valle RC. Teoria de Resposta ao Item: conceitos e aplicações. São Paulo: Associação Brasileira de Estatística; 2000.
- 15. Bock RD. Estimating item parameters and latent ability when responses are scored in two or more nominal categories. Psychometrika. 1972;37(1):29-51.
- 16. Samejima FA. Estimation of latent ability using a response pattern of graded scores. Psychometric Monograph. 1969;(17).
- 17. Masters GN. A Rasch model for partial credit scoring. Psychometrika. 1982;47(1):149-74.
- 18. Coombs CH. A theory of data. New York: Wiley; 1964.
- 19. Davison ML. On a metric, unidimensional unfolding model for attitudinal and developmental data. Psychometrika. 1977;42(4):523-48.
- 20. Andrich D. A probabilistic IRT model for unfolding preference data. Appl Psychol Meas.1989;13(2):193-216.
- 21. Andrich D. Hyperbolic cosine latent trait models for unfolding direct responses and pairwise preferences. Appl Psychol Meas. 1995;19(2):269-90.
- 22. Hoijtink H. A latent trait model for dichotomous choice data. Psychometrika. 1990;55(5):641-56.
- 23. Hoijtink H. The measurement of latent traits by proximity items. Appl Psychol Meas. 1991;15(1): 153-69.
- 24. Andrich D, Luo G. A hyperbolic cosine latent trait model for unfolding dichotomous single-stimulus responses. Appl Psychol Meas. 1993;17(2):253-76.
- 25. Hambleton RK, Swaminathan H, Rogers HJ. Fundamentals of item response theory. Newbury Park, CA: Sage; 1991.
- 26. Embretson S, Reise SP. Item Response Theory for Psychologists. New Jersey: Lawrence Erlbaum Associates; 2000.
- 27. Andrade DF, Bortolotti SLV. Aplicação de um Modelo de Desdobramento Graduado Generalizado-GGUM da Teoria da Resposta ao Item. Estudos Avaliação Educ. 2007;18(37):157-87.
- 28. Andrich D. A rating formulation for ordered response categories. Psychometrika. 1978;43(4):561-73.
- 29. Muraki E. A generalized partial credit model: application of an EM algorithm. Appl Psychol Meas. 1992; 16(1):159-76.
- 30. Coombs CH. Psychological scaling without a unit of measurement. Psychol Rev. 1950;57(1):145-58.
- 31. Thurstone LL. The measurement of social attitudes. Abnormal Soc Psychol. 1931;26(2):249-69.
- 32. Coombs CH, Smith JEK. On the detection of structures in attitudes and developmental processes. Psychol Rev. 1973;80(3):337-51.
- 33. Volet SE, Chalmers D. Investigation of qualitative differences in university students' learning goals, based on an unfolding model of stage development. Br J Educ Psychol. 1992;62(1):17-34.
- 34. Davison M, Robbins A, Swanson D. Stage structure in objective moral judgments. Develop Psychol. 1978; 14 (1):137-46.
- 35. Kohlberg L. Stage and sequence: the cognitive-developmental approach to socialization. In: Goslin BA, editor. Handbook of socialization theory and research. San Francisco: Rand McNally; 1969. p. 347-80.
- 36. Richards B. Unidimensional unfolding theory and quantitative differences between attitudes. Unpublished empirical thesis submitted in partial fulfillment of the requirements for the BSc (Honours) degree in Psychology. Sydney: School of Psychology, University of Sydney; 2002.
- 37. Desarbo WS, Hoffman DL. Constructing MDS joint spaces from binary choice data: a multidimensional unfolding threshold model for marketing research. J Mark Res. 1987;24(1):40-54.
- 38. Verhelst ND, Verstralen HHFM. A stochastic unfolding model derived from the partial credit model. Kwantitative Methoden. 1993;42(1):73-92.
- 39. Andrich D. A general hyperbolic cosine latent trait model for unfolding polytomous responses: Reconciling Thurstone and Likert methodologies. Br J Mathem Statist Psychol. 1996;49(3):347-65.
- 40. Roberts JS, Donoghue JR, Laughlin JE. A general model for unfolding unidimensional polytomous responses using item response theory. Appl Psychol Meas. 2000;24(1):3-32.
- 41. Mislevy RJ, Bock RD. BILOG 3: Item Analysis and Test Scoring with Binary Logistic Models. Chicago : Scientific Software; 1990.
- 42. Zimowski MF, Muraki E, Mislevy RJ, Bock RD. BILOG-MG: Multiple-Group IRT Analysis and Test Maintenance for Binary Items. Chicago: Scientific Software; 1996.
- 43. Muraki E, Bock RD. PARSCALE : IRT Based Test Scoring and Item Analysis for Graded Open-Ended Exercises and Performance Tasks. Chicago: Scientific Software; 1997.
- 44. Thissen D. MULTILOG user's guide: Multiple categorical item analysis and test scoring using item response theory. Chicago: Scientific Software; 1991.
- 45. Andrich D, Luo G. RUMMFOLDTM for WindowsTM: A program for unfolding pairwise preferences [computer program]. Murdoch, Western Australia: Social Measurement Laboratory, Murdoch University; 1998.
- 46. Van Schuur WH, Post WJ. MUDFOLD. A program for multiple unidimensional unfolding [software manual]. Verson 4.0. Groningen: ProGAMMA; 1998.
- 47. Roberts JS, Fang H, Cui W, Wang Y. GGUM2004: a Windows-based Program to Estimate Parameters of the Generalized Graded Unfolding Model. Appl Psychol Meas. 2006;30(1):64-5.
- 48. Valle RC. Construção e interpretação de escalas de conhecimento: um estudo de caso. Estudos Avaliação Educ. 2001;23(1):71-92.
Datas de Publicação
-
Publicação nesta coleção
16 Dez 2009 -
Data do Fascículo
Dez 2009
Histórico
-
Aceito
24 Ago 2009 -
Recebido
17 Jul 2009