Resumos
Apresenta-se o papel desempenhado pelo Instituto de Matemática Pura e Aplicada, criado em 1952 pelo Conselho Nacional de Desenvolvimento Científico e Tecnológico, na formação de pesquisadores matemáticos no país. Mostra-se como este instituto, bem como a matemática ali produzida, serviram para a formação do campo científico de matemáticos no Brasil. Os principais resultados apontam para: a consolidação de linhas de pesquisa em Sistemas Dinâmicos, Álgebra, Análise Matemática, Geometria Diferencial e Estatística Matemática; a preocupação de formar pesquisadores para atender as demandas de quadros docentes das universidades brasileiras, produzir matemática e recrutar alunos "talentosos" visando garantir a formação de pesquisadores e a produção de matemática de qualidade. A rede de influências estabelecida pelos pesquisadores do instituto extrapolou seus limites, uma vez que os líderes ocupavam posições importantes nos órgãos de fomento e em outras instituições e sociedades intelectuais. O discurso dos pesquisadores revela a hierarquia acadêmica e o corporativismo reinante na instituição assim como seu prestígio na comunidade científica.
INSTITUIÇÕES DE PESQUISA; MATEMÁTICA; PESQUISADORES; FORMAÇÃO PROFISSIONAL
This article presents the role played by the Institute of Pure and Applied Mathematics - Impa -, created in 1952 by the National Council for Scientific and Technological Development, in the education of researchers in mathematics in Brazil. It shows how this Institute, as well as the knowledge of mathematics it produced, contributed to build the scientific field of mathematicians in the country. Its main results indicate the consolidation of lines of research such as Dynamic Systems, Algebra, Mathematical Analysis, Differential Geometry, and Mathematical Statistics, as well as a concern about the education of researchers to meet the demands of the teaching staff of Brazilian universities, to produce mathematics and recruit "talented" students to ensure the education of researchers and high quality mathematical production. The network of influences established by the Institute's researchers surpassed its limits, as its leaders had important positions in funding agencies and other scientific Institutions and societies. The discourse of these researchers reveals the academic hierarchy and the corporatism in force in the institution, as well as its prestige in the scientific community.
RESEARCH INSTITUTES; MATHEMATICS; RESEARCHERS; VOCATIONAL TRAINING
OUTROS TEMAS
O Impa e a comunidade de matemáticos no Brasil
The Impa and the community of mathematicians in Brazil
Circe Mary Silva da Silva
Professora do Programa de Pós-Graduação em Educação da Universidade Federal do Espírito Santo cmdynnikov@gmail.com
RESUMO
Apresenta-se o papel desempenhado pelo Instituto de Matemática Pura e Aplicada, criado em 1952 pelo Conselho Nacional de Desenvolvimento Científico e Tecnológico, na formação de pesquisadores matemáticos no país. Mostra-se como este instituto, bem como a matemática ali produzida, serviram para a formação do campo científico de matemáticos no Brasil. Os principais resultados apontam para: a consolidação de linhas de pesquisa em Sistemas Dinâmicos, Álgebra, Análise Matemática, Geometria Diferencial e Estatística Matemática; a preocupação de formar pesquisadores para atender as demandas de quadros docentes das universidades brasileiras, produzir matemática e recrutar alunos "talentosos" visando garantir a formação de pesquisadores e a produção de matemática de qualidade. A rede de influências estabelecida pelos pesquisadores do instituto extrapolou seus limites, uma vez que os líderes ocupavam posições importantes nos órgãos de fomento e em outras instituições e sociedades intelectuais. O discurso dos pesquisadores revela a hierarquia acadêmica e o corporativismo reinante na instituição assim como seu prestígio na comunidade científica.
INSTITUIÇÕES DE PESQUISA - MATEMÁTICA - PESQUISADORES - FORMAÇÃO PROFISSIONAL
ABSTRACT
This article presents the role played by the Institute of Pure and Applied Mathematics - Impa -, created in 1952 by the National Council for Scientific and Technological Development, in the education of researchers in mathematics in Brazil. It shows how this Institute, as well as the knowledge of mathematics it produced, contributed to build the scientific field of mathematicians in the country. Its main results indicate the consolidation of lines of research such as Dynamic Systems, Algebra, Mathematical Analysis, Differential Geometry, and Mathematical Statistics, as well as a concern about the education of researchers to meet the demands of the teaching staff of Brazilian universities, to produce mathematics and recruit "talented" students to ensure the education of researchers and high quality mathematical production. The network of influences established by the Institute's researchers surpassed its limits, as its leaders had important positions in funding agencies and other scientific Institutions and societies. The discourse of these researchers reveals the academic hierarchy and the corporatism in force in the institution, as well as its prestige in the scientific community.
RESEARCH INSTITUTES - MATHEMATICS - RESEARCHERS - VOCATIONAL TRAINING
Sem deixar de lado o papel importante que desempenharam alguns pioneiros professores de matemática das escolas politécnicas brasileiras desde o século XIX, pode-se dizer que a formação de uma comunidade de matemáticos no Brasil iniciou-se com a criação, em 1934, da Faculdade de Filosofia, Ciências e Letras, da Universidade de São Paulo - USP -, primeira faculdade do Brasil, no gênero, que se tornou o maior e mais antigo núcleo de formação de pessoal matemático habilitado no país. Fora da universidade, na década de 50, despontou o Instituto de Matemática Pura e Aplicada - Impa -, voltado para a pesquisa e formação de pesquisadores e sobre o qual dedicaremos uma análise mais pontual. Apresentaremos considerações sobre a sua criação, as atividades que desenvolveu, os pesquisadores que nele atuaram até o final da década de 1970 e as suas linhas de pesquisa.
Dialogando com teóricos da História Cultural, em especial com Pierre Bourdieu, de quem emprestamos o conceito de campo científico, e utilizando a análise de documentos (relatório de atividades, atas, entrevistas, depoimentos, cartas), pertencentes aos acervos de arquivos e bibliotecas do Impa, do Museu de Astronomia e Ciências Afins - Mast - e do Centro de Memória do Conselho Nacional de Desenvolvimento Científico e Tecnológico - CNPq -, identificamos o início da formação desse campo e da institucionalização da matemática brasileira.
A fim de entender melhor a formação do campo científico de matemáticos, procuramos analisar o discurso de alguns pesquisadores do Impa, reveladores das relações de poder e da hierarquia acadêmica. A questão do prestígio está presente na comunidade científica, bem como na relação com os cientistas de outras áreas do conhecimento e deixa entrever, além disso, que a matemática ali produzida apresenta padrão de qualidade equivalente àquele desenvolvido em outros países e por isso ela deve ser estimulada e fomentada. A inserção internacional de seus membros tem garantido status ao instituto tanto nacional quanto internacionalmente.
Como todas as práticas científicas estão orientadas para a aquisição de autoridade científica, o interesse por uma atividade científica tem sempre uma face dupla. Bourdieu (1989) alerta para o fato de que os segmentos dominantes, detentores de um maior capital científico, dedicam-se a atividades de manutenção da situação vigente, consagrando-se às estratégias de conservação que visam à perpetuação da ordem científica que vigora, com a qual concordam e não desejam que seja alterada. Ordem essa que engloba, inclusive, as instituições que estão encarregadas da produção e circulação dos bens científicos. Aqui se inclui, principalmente, o sistema de ensino que é o responsável por assegurar a permanência e a consagração da ciência oficial. É com esse olhar que procuraremos entender o papel que o Impa desempenhou na construção desse campo.
CRIAÇÃO DOS INSTITUTOS DE PESQUISA NO MUNDO E O IMPA
Os institutos voltados diretamente para a pesquisa matemática só surgiram no século XX (Silva, 2005a). Entre os pioneiros, costuma-se mencionar: Instituto Steklov (1919, São Petersburgo), Institute for Advanced Study (Princeton, 1930), Instituto de Matemática Pura e Aplicada (Rio de Janeiro, 1952); Institut des Hautes Études Scientifiques - Ihés (Bures-sur-Yvette, França, 1958) e também o Max-Planck-Institut für Mathematik (Bonn, 1981). Iniciativas anteriores como foi o caso, na Suécia, do Mittag-Leffler Institute, fundado em 1916 por Gösta Mittag-Leffler e sua esposa Signe, e incorporado à Real Academia Sueca de Ciências em 1919, não tiveram muito sucesso. As dificuldades financeiras e a morte de Mittag-Lefller, em 1927, levaram à sua quase desativação, funcionando por vinte anos praticamente em razão de sua biblioteca. Somente em 1969, Lennart Carleson conseguiu concretizar o sonho de Mittag-Leffler.
No Brasil, nos anos 50, os professores e pesquisadores estavam conscientes de que os empresários tinham pouco interesse pela produção de conhecimento científico, pouca atenção prestavam à ciência. Assim, a possibilidade de se promover a ciência e a tecnologia estava restrita à ação do Estado. A criação do CNPq, em 1951, ligado diretamente à Presidência da República, foi uma iniciativa governamental e constitui-se num divisor de águas. É possível falar da ciência no país antes e depois dele.
Nas reuniões do Conselho Deliberativo do CNPq, iniciaram-se, nesse período, as discussões sobre a criação de um instituto de matemática. Ao conselheiro Cândido Lima da Silva Dias (1913-1998), professor de matemática da Universidade de São Paulo, foi delegada a missão de elaborar um anteprojeto do instituto (CNPq, 1952).
Nem todos os conselheiros do CNPq estavam convictos da necessidade de se criar um instituto fora da universidade. Havia os que questionavam a criação de um instituto diretamente subordinado ao CNPq e fora da universidade. O motivo alegado por Cândido da Silva Dias era que as universidades tinham um número muito limitado de professores e que seria difícil a contratação de docentes que se dedicassem à pesquisa. Conforme consta da Ata da Seção 112 do Conselho Deliberativo (CNPq, 1952), ele afirmava:
Aliás, aqui no Rio, há uma parte dos pesquisadores que não está na faculdade. O problema, no Rio, é o seguinte: quem não está centralizado na Faculdade, em que é natural a pesquisa, por exemplo, na Faculdade de Filosofia, há um grupo ao qual o Conselho já tem auxiliado, forma um grupo tão numeroso, talvez maior, que está fora e é, justamente, a esse grupo, que está em parte no Centro de Pesquisas Físicas (CBPF) que o Instituto tem como objetivo principal exatamente dar uma forma estável de auxílio. (p.19)
Todavia, no dia da votação do projeto de criação do Impa, segundo o depoimento de Dias, não houve grande oposição. Mesmo em São Paulo, a ideia foi bem recebida (Dias, 1998, p.701).
Assim, diretamente ligado ao CNPq, surgiu o Impa. Sua criação, em 15 de outubro de 1952, tinha finalidade bem definida: "o ensino e a investigação científica no campo da Matemática pura e aplicada, assim como a difusão e elevação da cultura matemática no país" (CNPq, Arquivo t.6.3.002). Todavia, a criação só foi homologada em 1956. O instituto seria presidido por um diretor, nomeado em comissão pelo presidente do CNPq, e contava também com um Conselho Orientador1 1 . Posteriormente foi denominado Conselho Técnico e Científico - CTC - e, a partir de 1975, Comissão Técnica e Científica. , composto de seis membros, com a função de orientar científica, técnica e administrativamente o órgão. As atividades do Impa começaram em 1953, sem instalações próprias, funcionando no prédio do Centro Brasileiro de Pesquisas Físicas - CBPF -, no Rio de Janeiro.
Atividades do Impa
Para atender à finalidade com que foi criado, o instituto centrou suas ações, inicialmente, no desenvolvimento de pesquisas e na oferta de cursos de pós-graduação para a comunidade de professores de matemática do Brasil e países da América do Sul.
As atividades desenvolvidas pelo instituto foram:
Organização e execução de pesquisas por seus membros e por pessoal transitoriamente vinculado ao instituto.
Elaboração de currículos e realização de cursos de pós-graduação bem como cursos avançados extracurriculares.
Promoção de conferências e reuniões científicas de âmbito regional, nacional e internacional.
Intercâmbio de pessoal científico por meio de estudo e missões científicas no país e exterior.
Organização e manutenção de uma biblioteca especializada.
Publicação de apostilas, revistas, livros e outros trabalhos pertinentes às suas finalidades. (Impa, 1979)
O Conselho Técnico e Científico tinha a tarefa de orientar e planejar as atividades de ensino e pesquisa do instituto. Era formado pelo presidente, que, ao mesmo tempo, ocupava a direção do Impa, pelo vice-presidente, por quatro membros do corpo científico permanente do instituto e por membros escolhidos entre matemáticos ou pesquisadores de institutos congêneres no país. Os membros do CTC eram designados pelo CNPq. Claramente o CTC detinha o poder no instituto. Em 1970, o CTC era formado por sete membros e em 1975 passou a ter dez.
Os cursos de pós-graduação ministrados no Impa só foram reconhecidos pelo Conselho Federal de Educação em 1971, mas isso não impediu que o instituto titulasse mestres e doutores antes dessa data. Foram nove os doutoramentos concedidos no período de 1964 a 1971. Já na década de 1970, o número de doutoramentos chegou a quarenta.
Embora seu estatuto tenha previsto o desenvolvimento de pesquisas tanto na área da matemática pura quanto na aplicada, nos primeiros vinte anos, praticamente só sobressaíram as linhas de pesquisas em matemática pura. Até 1959, as duas principais correntes de estudo em matemática pura no Impa eram: Geometria Algébrica e a Teoria dos Números; Variedades Analíticas e Topologia Algébrica. Na década de 1960, as linhas de pesquisa estavam assim divididas: Análise Funcional, Equações Diferenciais, Topologia Diferencial. A partir de 1972, nos relatórios de atividades do instituto, encontramos explicitamente uma relação das linhas de pesquisa nele desenvolvidas. De 1972 a 1978, havia cinco grandes grupos de pesquisas: Sistemas Dinâmicos e Folheações, Geometria Diferencial, Álgebra, Análise e Estatística Matemática. Em 1979, encontra-se pela primeira vez referência à Matemática Aplicada, subdividida em três linhas de pesquisa: Estatística Matemática, Pesquisa Operacional e Economia Matemática.
A preocupação com a área de Matemática Aplicada tinha uma justificativa: o instituto estava procurando encaminhar-se para áreas consideradas importantes para o desenvolvimento do país e que não eram ainda suficientemente pesquisadas aqui, entre elas, a Economia Matemática. Em 1978, são introduzidas entre as disciplinas para mestrado e doutorado a Microeconomia (ao encargo de Aloísio Araújo), a Economia Dinâmica e a Teoria das Redes (ao encargo de José Scheinkman), a Teoria da Confiabilidade (ao encargo de Sandro Berenger).
Em 1971, começou a funcionar o mestrado em Estatística Matemática. O currículo foi elaborado por Pedro Fernandez, que fez seu doutorado na Universidade de Berkeley, e Allan Stuart, estatístico inglês da London School of Economics. A partir de 1973 o instituto contou com a participação de dois novos professores na área: Djalma Galvão Pessoa, com doutorado em Berkeley, e Sérgio Luiz de Bragança, doutor pelo Massachusetts Institut of Technology - MIT. Em 1975, o programa sofreu alteração, voltando-se mais para aplicações e fazendo uso do computador. Nesse início de utilização da moderna tecnologia, o Impa recebeu auxílio do Centro de Computação do CBPF. As principais linhas de pesquisa, nessa época, foram: Métodos Robustos, Análise Multivariada, Suficiência Estatística e Planejamento de Experimentos.
Todavia, desde essa época, Sistemas Dinâmicos despontavam com um número significativo de trabalhos investigativos. A maioria das teses de doutoramento eram nessa área (Silva, 2005).
Em 1971, foi realizado um simpósio internacional em Salvador sobre Sistemas Dinâmicos, com a participação de sessenta matemáticos nacionais e quarenta estrangeiros. Os dois ganhadores de Medalha Fields, René Thom e Stephan Smale, foram palestrantes destacados. Os temas do simpósio envolveram a Estabilidade e Propriedades Genéricas dos Sistemas Dinâmicos, Mecânica, Singularidades de Aplicações, Teoria das Catástrofes e Aplicações.
Trinta anos após esse evento, a área de Sistemas Dinâmicos ampliou-se, mas continua a ser centralizadora de atividades de investigação no instituto. As linhas de pesquisa guardam pouca relação com as desenvolvidas na década de 70 e são denominadas Sistemas Dinâmicos e Teoria Ergódica: atratores estranhos, medidas físicas, estabilidade estocástica; bifurcações homoclínicas e dimensões fractais; dinâmica simplética; dinâmica unidimensional; expoentes de Lyapunov e hiperbolicidade não-uniforme; hiperbolicidade parcial, decomposição dominada, robustez dinâmica.
OS PESQUISADORES
O Impa começou suas atividades com um diretor, Lélio Gama, dois pesquisadores titulares: Maurício Peixoto e Leopoldo Nachbin, e dois pesquisadores assistentes: Paulo Ribenboim e Carlos Benjamin Lyra2 2 . Carlos Lyra era professor da USP, em São Paulo. . As duas primeiras décadas constituíram uma tentativa de fortalecimento institucional, com um número reduzido de pesquisadores, conforme mostra o quadro 1. A década de 70 foi decisiva para a definição das linhas de pesquisas e fortaleceu-se muito devido aos fortes investimentos financeiros que recebeu.
Nomear todos os pesquisadores que atuaram no Impa, quer como visitantes por períodos curtos ou mais longos, quer como permanentes, formaria uma lista muito extensa e talvez pouco interessante3 3 . Uma relação detalhada dos pesquisadores visitantes no período de 1952 a 1969 encontra-se em Silva (2004); outra, do período de 1970 a 1979, está em Silva (2005). . Entre eles encontram-se alguns que continuam a atuar como pesquisadores titulares até o presente.
A formação de matemáticos de alto nível era uma "batalha" que o Impa havia se proposto a vencer. Elon Lages Lima (1989, p.41) afirma: "garantir a formação de matemáticos de alto nível, evitando os grupos de nível variado ou até medíocre que se formam em torno de pesquisadores bem qualificados nas universidades brasileiras". Esse foi o diferencial pelo qual o Impa optou - ser um instituto elitizado com espaço somente para os matemáticos talentosos.
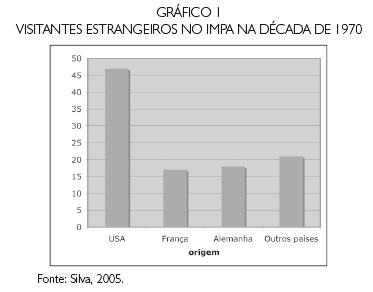
O instituto contou sempre com um numeroso grupo de pesquisadores visitantes nacionais e internacionais. Entre os estrangeiros, o maior número foi de pesquisadores americanos. No período de 1960 a 1969, estiveram no Impa 55 pesquisadores visitantes. Desses, 42% eram norte-americanos, 31%, europeus, 25%, da América Latina, 1% da Ásia e 1%, da África (Silva, 2004).
Na década de 70 essa cooperação ampliou-se. Foram 103 visitantes, com um elevado percentual de origem americana, conforme pode ser visto no gráfico 1:
As visitas de cooperação de pesquisadores de outras instituições ao Impa proporcionaram o desenvolvimento de muitas pesquisas em colaboração. Assim, artigos importantes4 4 . Consideramos artigos importantes as publicações selecionadas pelos próprios pesquisadores e indicadas na página de cada acadêmico na home-page da Academia Brasileira de Ciências ( http://www.abc.org.br/org/). surgiram envolvendo dois ou mais autores, em revistas especializadas e reconhecidas na área como: American Journal of Mathematics, Journal of Álgebra, Communications in Mathematical Physics, Acta Mathematica, Annals of Mathematics, Ergodic Theory and Dynamical Systems entre outros.
Na atualidade, o corpo permanente do Impa conta com 34 pesquisadores. Entre eles, encontram-se os pesquisadores eméritos: Elon Lages Lima, Mauricio Matos Peixoto e Manfredo Perdigão do Carmo. Os atuais cursos de mestrado e doutorado são programas de formação: o mestrado visa a fornecer uma "cultura básica que lhe permitirá ensinar disciplinas matemáticas em nível de graduação ou exercer atividades profissionais que requerem aplicações da Matemática a problemas técnicos ou científicos", e o doutorado visa à formação de pesquisadores. A expansão dos cursos de pós-graduação foi realmente significativa. Atualmente o estudante pode optar por cinco diferentes cursos de mestrado: Matemática, Computação Gráfica, Economia Matemática, Matemática Computacional e Modelagem, Métodos Matemáticos em Finanças.
A renovação do corpo de pesquisadores é essencial para a manutenção da comunidade de pesquisadores. Na visão de José Scheinckman, "A idéia de uma instituição como o Impa é sempre de reprodução; os professores querem discípulos que dêem continuidade à instituição" (Palis, Camacho, Lima, 2003, p.169).
O campo científico de matemáticos
Para Bourdieu (1983), o que está em jogo na luta dentro do campo científico é o monopólio da autoridade científica, ou seja, o monopólio da competência científica, que, para ele, é entendida como a capacidade de falar e agir legitimamente, isto é, de maneira autorizada e com autoridade.
O Impa, juntamente com as universidades, desempenhou um papel fundamental na constituição do campo científico de matemáticos brasileiros.
Como primeiro instituto voltado unicamente para as pesquisas em matemática, ele teve um papel de liderança no país. Moreira (Palis, Camacho, Lima, 2003, p.49) aponta essa função exemplar do instituto dentro da sociedade brasileira afirmando: "ele mostra que é possível fazer ciência de primeiro nível num país de terceiro mundo como o Brasil, e que é possível exercer liderança (no caso, científica) de forma generosa, solidária e construtiva".
Para melhor compreensão da formação desse campo, nos apoiamos novamente em Bourdieu que define o campo científico da seguinte maneira:
O campo científico é sempre o lugar de uma luta mais ou menos desigual, entre agentes desigualmente dotados de capital específico [...]. Em todo o campo [...] os dominantes, ocupando as posições mais altas na estrutura de distribuição de capital científico, e os dominados, isto é, os novatos, que possuem um capital científico tanto mais importante quanto maior a importância dos recursos científicos acumulados no campo. (1983, p.136-137)
Poderemos ver, no próprio discurso dos pesquisadores do Impa, como a instituição se estruturou e os valores defendidos por seus membros. Percebe-se claramente a presença de dominantes que segundo Bourdieu (1983, p.137) são aqueles que se consagram "às estratégias de conservação, visando assegurar a perpetuação da ordem científica estabelecida com a qual compactuam".
Além disso, Bourdieu demonstra que o capital cultural (diplomas, conhecimentos, códigos culturais, características linguísticas, bons modos), o capital social (relacionamentos e redes sociais) e o capital simbólico (reconhecimento) são recursos tão úteis quanto o capital econômico (bens financeiros, patrimônio) na determinação e na reprodução das posições sociais. No caso dos matemáticos, o capital cultural e capital simbólico revestem-se de grande importância e são almejados fortemente.
Os pesquisadores do Impa ocupavam posições importantes nos órgãos de fomento. Por exemplo: Elon Lages Lima fez parte de comissões em diferentes órgãos: Comissão Fullbrigt, Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Capes - e CNPq. Como membro do Conselho Deliberativo do CNPq, o poder de decisão era muito grande, conforme o próprio depoimento de Lima (apud Palis, Camacho, Lima, 2003, p.104): "o CNPq tinha uma comissão de pós-graduação, à qual eu pertencia, que avaliava os cursos de pós-graduação em várias áreas. E só ganhariam cotas de bolsas do conselho para seus alunos aqueles cursos aprovados por essa comissão". Os pesquisadores líderes do instituto tinham ao seu encargo decisões que implicavam o futuro acadêmico das pessoas, uma vez que eles decidiam sobre a aprovação de bolsas dos candidatos para realizar pós-graduação fora do país.
O depoimento de Manfredo do Carmo é bastante elucidativo:
Como o instituto foi criado como órgão do CNPq, [...] eram as mesmas pessoas nos dois lugares, praticamente. Maurício Peixoto e Leopoldo Nachbin eram diretores do CNPq e decidiam que pessoas iriam para o exterior ou receberiam bolsas no país; quando fui para os Estados Unidos fazer doutorado com bolsa do CNPq, foi exatamente por recomendação dos dois, que foram fundamentais para isso. (apud Palis, Camacho, Lima, 2003, p.211)
Esse depoimento é confirmado por Maurício Peixoto na mesma obra. Presidente do CNPq entre 1971 e 1973, Peixoto aproveitou essa posição para beneficiar o órgão.
A luta para assegurar espaços na política acadêmica nunca deixou de existir. Camacho (apud Palis, Camacho, Lima, 2003, p.62) afirma ter retornado à coordenação do comitê assessor do CNPq, recentemente, por imposição de alguns de seus colegas: "Não queria fazer novamente a mesma coisa! Mas estamos percebendo que a matemática está perdendo espaço para outras áreas; a física e a química estão crescendo muito, e esse fenômeno não está claro para nós".
Nesse período o Impa procurou sempre atrair diversos matemáticos estrangeiros, principalmente os americanos com quem mantinha um relacionamento mais intenso. Segundo Lima (Palis, Camacho, Lima, 2003, p.103), eles eram atraídos pela "qualidade dos trabalhos que começavam a ser feitos, em áreas novas. E também - por que não dizer? Pelo fato de que havia um grande crescimento econômico e o Impa dispunha de condições financeiras para trazer professores". Assim, a presença de recursos financeiros liberados pelos órgãos de fomento foi decisiva na década de 1970 para atrair e custear os gastos necessários para a construção de pesquisas em áreas de ponta. Essa relação entre recursos e pesquisa está claramente posta por Bourdieu:
...é preciso supor que os investimentos se organizam com referência a uma antecipação - consciente ou inconsciente - das chances médias de lucro em função do capital acumulado. Assim, a tendência dos pesquisadores a se concentrar nos problemas considerados como os mais importantes se explica pelo fato de que uma contribuição ou descoberta concernente a essas questões traz um lucro simbólico mais importante. (1983, p.125)
A fim de dar mais visibilidade ao instituto na sociedade e exercer mais poder político, seus membros, principalmente a partir da década de 1980, começaram a ocupar mais lugares de representação e participação em instituições, como CNPq, Capes e Academia Brasileira de Ciências. O depoimento de César Camacho é esclarecedor:
O Impa passou a se mostrar mais visível no meio político, a interagir mais com outras áreas da ciência, a participar mais do Conselho Deliberativo do CNPq, da Academia Brasileira de Ciências. Pesquisadores do instituto começaram a participar de conselhos externos multidisciplinares, atividade que era muito reduzida até a década de 70 [...]. Já na década de 80, o Impa passou a ter outras presenças e a se mostrar mais ao mundo externo. (apud Palis, Camacho, Lima, 2003, p.58-59)
O corporativismo é também visível em várias situações que ocorreram na história do instituto. Para Pyenson e Sheets-Pyenson (1999), as instituições científicas operam com base em estruturas corporativas e de conveniência privada e exibem uma solidariedade terrena e orgânica. Isso pode ser visto exemplarmente no caso do Impa. A seleção dos membros do corpo de pesquisadores quase sempre foi feita pelo critério da recomendação por membros externos à instituição e com reputação internacional, ou seja, com reconhecimento entre os seus pares. Em 1968, foram contratados como pesquisadores associados, Jacob Palis Jr. e Djairo Guedes Figueiredo. O primeiro recebeu carta de recomendações de E. C. Zeeman, R. F. Williams e Rene Thom. Com carta de indicação de Otto Endler, foi também contratado Jürgen Symann.
A promoção de pesquisadores no Impa baseava-se na produção científica. Segundo Simis: "promoção era, tradicionalmente, produto do exame de seu currículo, da sua produção científica e de cartas de recomendação. Normalmente ninguém solicitava a própria promoção; o normal era uma indicação de membros mais seniores da instituição" (apud, Palis, Camacho, Lima, 2003, p.25). Para Bourdieu,
Os julgamentos sobre a capacidade científica de um estudante ou de um pesquisador estão sempre contaminados, no transcurso de sua carreira, pelo conhecimento da posição que ele ocupa nas hierarquias instituídas (as grandes escolas na França ou as universidades nos EUA. (1983, p.124)
No Brasil, no campo da matemática, por institutos de pesquisa como o Impa.
A fim de manter a instituição no padrão de qualidade imaginado pelos seus líderes, ninguém escapava de punição, nem mesmo um pesquisador experiente, como foi o caso de Leopoldo Nachbin, primeiro matemático brasileiro com reconhecimento internacional. Segundo Maurício Peixoto, Nachbin como membro do CTC do Impa,
...insistia em colocar no Impa pessoas que, na opinião dos outros pesquisadores, não estavam no nível do instituto [...]. O instituto já tinha um certo tamanho, era importante. Para o pessoal da casa, esse negócio de nomes, adequados ou não, é fundamental, pois é uma instituição pequena, e qualquer problema se reflete na carreira de todos. A excelência é considerada essencial. (apud Palis, Camacho, Lima, 2003, p.246)
De acordo com a mesma fonte, para resolver o impasse e evitar a indicação feita por Leopoldo Nachbin, foi proposta mudança em dois membros do CTC: Cândido Lima da Silva Dias e Maurício Peixoto, com a concordância do presidente do CNPq, na época, Antônio Moreira Couceiro. Isso permitiria que o número de votos favoráveis à proposta de Nachbin ficasse reduzida, conforme depoimento de Elon Lages Lima: "Assim, o Couceiro nomeou como novos membros do CTC Ubirajara Alves e Alberto Azevedo. Com isso, a situação ficou meio a meio, e o voto decisivo seria do Lélio Gama" (p.103). Como no dia da votação houve um empate, Lélio Gama votou contra a indicação de Nachbin e isso significou o enfraquecimento de Nachbin e o seu afastamento. Para Lima "O voto do Lélio Gama decidiu o futuro do instituto. Na verdade, Lélio Gama salvou o Impa" (p.103). Para Peixoto a disputa trouxe perda para o Impa: "Foi um momento difícil [...] sobretudo porque o instituto tinha sido criado praticamente por causa dele. Mas ele acabou saindo. Foi uma grande perda" (p.246). Nesse episódio, vê-se, exemplarmente, a fidelidade dos membros à corrente de comando nas instituições. As ações dos membros não são apenas motivadas por escolha e inspiração, mas também por meio da convenção e autoridade.
Outra característica presente na comunidade científica é a luta pelo prestígio ou, na terminologia de Bourdieu, a luta pelo capital simbólico.
Aron Simis, em seu discurso, revela a luta para a manutenção do prestígio da área de matemática:
Não só eu, mas várias pessoas tinham essa consciência de que estávamos perdendo prestígio - e não só prestígio, estávamos perdendo terreno! Quando fui membro do Comitê Assessor da Matemática no CNPq, no início de 82 [...] lembro que éramos equiparados à química e muito acima da geologia e da geofísica. Hoje, a química tem três vezes mais em termos de auxílio financeiro... (apud Palis, Camacho, Lima, 2003, p.30)
Para Simis (p.35), ainda conforme essa fonte, assim como para a maioria dos pesquisadores, o instituto é uma instituição de excelência e "teve tradicionalmente esse papel de apontar a direção, de dar o exemplo para outras instituições de matemática no Brasil". Pesquisadores, como Arnaldo Garcia manifestam abertamente a satisfação que sentem em atuar em uma instituição de prestígio: "Uma das maiores satisfações em ser membro do corpo docente desta instituição vem do fato dela dar prioridade absoluta à pesquisa matemática de alto nível e ter em seu corpo discente estudantes altamente capacitados e motivados" (p.261).
Para o atual diretor do instituto, Jacob Palis Jr., a presença de jovens talentosos e brilhantes é muito relevante: "A renovação que tem sido feita é fundamental para a excelência de uma instituição em bases robustas: o perfil típico é o de jovens brilhantes" (p.135-136). Ressaltamos o acentuado valor atribuído aos jovens talentosos. É esse o perfil desejado para os candidatos ao ingresso no seleto instituto, o que revela claramente um elitismo na seleção dos alunos, os quais farão parte da comunidade de matemáticos brasileiros.
Nessa comunidade, percebe-se uma hierarquia dos membros. Paul Ernest (1991) propôs uma metáfora interessante para a comunidade matemática. Ele a vê como um "conjunto Fuzzy" de pessoas, que são os matemáticos, e que está parcialmente ordenado pelas relações de poder e status. Vê-se, no discurso de Carmo, como ele se refere à estrutura da comunidade:
Hoje deve haver umas cem mil pessoas no mundo fazendo matemática, divididas em núcleos pequenos, mas só um número limitado realmente conta; os líderes formam um conjunto pequeno. É uma estrutura vertical e quase eclesiástica: cardeal, arcebispo, bispo... Cada um conhece seu próprio lugar; as regras de acesso não são escritas, mas são conhecidas. (apud Palis, Camacho, Lima, 2003, p.204)
A pertinência das pessoas no conjunto dos matemáticos é como a pertinência num conjunto Fuzzy, que varia entre 0 a 1. Quanto mais próximo de 1, maior será a intensidade de pertinência da pessoa ao conjunto, e quanto mais próximo a 0 estiver, mais distante estará de pertencer à comunidade de matemáticos. Assim, constata-se a existência de membros fortes (institucionalmente poderosos ou pesquisadores matemáticos ativos), e membros fracos (professores de matemática).
A pertinência dos membros ao conjunto tem características que estão ligadas também à questão de identificação com a instituição. Segundo Aloisio Araújo (apud Palis, Camacho, Lima, 2003, p.16), "O Impa consegue se manter, porque possui um grupo bastante forte e coeso, de alta identificação institucional".
Na visão de Carmo (p.210), a "matemática é um negócio vertical quase eclesiástico: todo matemático foi aluno de um matemático". Enquanto a matemática tem para ele essa questão de hierarquia, a instituição também tem "vida", e assim ele se manifesta: "Estou convencido de que as instituições também cumprem um ciclo vital: nascem, crescem e morrem. A única maneira de uma instituição evitar o envelhecimento é absorver jovens talentosos" (p.222).
Para pertencer a essa comunidade, é necessário possuir produção científica reconhecida internacionalmente. A divulgação da produção é feita basicamente por artigos publicados em revistas especializadas.
Os veículos utilizados para a divulgação dos resultados das pesquisas do Impa, nessa época, não se limitaram aos nacionais, mas foram principalmente os internacionais de ampla circulação.
Que características devem ter os textos científicos? Para Simis (p.22), "tem que ser uma coisa mais curta, forte, mais bem escrita e objetiva". Carlos Gustavo Tamm de Araújo Moreira (p.44) reforça a ideia de que os textos matemáticos devem ser curtos: "Pode-se fazer coisas bastante importantes com menos de dez páginas. Tanto minha dissertação de mestrado quanto minha tese de doutorado não ocupam mais de 40 páginas".
Os textos científicos dos matemáticos desse orgão foram publicados tanto individualmente quanto em colaboração. Analisando os artigos mais destacados dos pesquisadores, percebe-se que houve trabalhos em colaboração tanto com os colegas de instituição quanto com pesquisadores externos a ela.
O Brasil conta atualmente com 31 programas de pós-graduação em matemática, mas, até a década de 1980, o número de programas não era muito expressivo, assim o Impa ocupava um lugar privilegiado porque contribuía de maneira significativa na formação da comunidade de matemáticos. Segundo Carmo
...num período curto formamos uns 400 mestres, que se espalharam pelo Brasil. Mudaram completamente a face da matemática brasileira porque trouxeram para a universidade a concepção de pesquisa, de renovação, de cursos novos, de ter que pensar, de atualização com a bibliografia. (apud Palis, Camacho, Lima, 2003, p.211)
Todavia, o próprio matemático ressalta que é preciso tomar cuidado com a hegemonia do Impa. Não deve "secar" as universidades, porque, se o fizer, ele também morrerá: "O Impa não pode viver sozinho; é uma instituição que só se justifica pela contribuição social que oferece, pelo fato de ter criado professores para as universidades, de ser o centro onde os professores podem fazer o seu pós-doutorado" (p.216).
AS ASSOCIAÇÕES, ACADEMIAS E PREMIAÇÕES
No Brasil, os matemáticos participam de várias academias e sociedades: Academia Brasileira de Ciências, fundada em 1916; Sociedade Brasileira de Matemática, fundada em 1969; Sociedade Brasileira de Matemática Aplicada e Computacional, fundada em 1978, entre outras.
A participação de pesquisadores do Impa, como membros da Academia Brasileira de Ciências, garante-lhes um status privilegiado na comunidade de matemáticos, assegurando-lhes um capital simbólico.
Godfrey Hardy, matemático inglês do século XX, deixa transparecer, com muita clareza, os fatores que motivam a prática científica de um matemático: "Imortalidade pode ser uma palavra tola, mas provavelmente são os matemáticos que têm a maior probabilidade de alcançá-la, seja ela o que for". Não importa o que digam os cientistas de outras áreas do conhecimento sobre os seus motivos para construir conhecimento, mas, para Hardy, havia três motivos respeitáveis:
O primeiro (sem o qual os demais nada valem) é a curiosidade intelectual, o desejo de conhecer a verdade. Depois, o orgulho profissional, a ânsia de ficar satisfeito com o próprio desempenho [...] Por fim, a ambição, o desejo de reputação, de alcançar uma boa posição social e até mesmo o poder ou o dinheiro a ela associados. (2000, p.75-76)
Vimos, em vários discursos da comunidade matemática brasileira, ligada ao Impa, o desejo de reputação social, a necessidade de manter e exercer o poder. Segundo essa visão, o instituto não poderia permitir a entrada de membros que não fossem detentores de qualidades intelectuais superiores: "jovens talentosos", "jovens brilhantes", "matemáticos de alto nível".
Um dos primeiros visitantes estrangeiros que o Impa contratou foi o jovem matemático Alexander Grothendieck (Silva, 2004). Os cursos que ministrou foram importantes para a formação dos primeiros professores e pesquisadores do instituto. Em 1966, recebeu a mais alta premiação em matemática - a Medalha Fields. Em testemunho autobiográfico, ele revela uma forte concordância com as ideias de Hardy, sobre ambição e vaidade dos cientistas. Ele afirma:
A verdade é que nas motivações do "cientista", que às vezes o empurram para trabalhar sem medida, a ambição e a vaidade jogam um papel tão importante e quase tão universal como em qualquer outra profissão. Isto toma forma mais ou menos grosseira, mais ou menos sutil, segundo o interessado. De modo algum pretendo ser uma exceção. A leitura de meu testemunho não deixará, espero, nenhuma dúvida a respeito. (Grothendieck, 2006, s/p. tradução nossa)
5 5 . Texto originalmente publicado, em 1985, no Centre National de Recherche Scientifique (Récoltes et semailles), posteriormente traduzido para o espanhol e disponibilizado na internet.
CONCLUSÕES
Em 1972, o instituto tinha como meta:
...cooperar para a formação, no Brasil, de uma equipe de matemáticos capazes de dar ao país o funcionamento adequado dos departamentos de Matemática de suas universidades e o exercício da pesquisa matemática como atividade permanente, que constituirá a base teórica do desenvolvimento científico e tecnológico da nação. (Impa, 1972, p.1)
Considerando o número expressivo de mestres e doutores que o instituto titulou ao longo de cinquenta anos de atividades: 228 doutores e 442 mestres até 2000 (Castelluber, 2003), pode-se concluir que ele cumpriu a meta proposta na década de 70, uma vez que, atualmente, já existe uma comunidade de matemáticos ativos no país integrada por muitos egressos do Impa.
Claramente, como afirmou Carmo, o Impa não pode viver sozinho e, ao longo sua história, ele necessitou da forte cooperação de outras instituições nacionais de pesquisa e ensino superior como: Universidade Federal do Rio de Janeiro, Instituto Tecnológico da Aeronáutica, Universidade de São Paulo, Centro Brasileiro de Pesquisas Físicas, Escola de Engenharia de São Carlos, Pontifícia Universidade Católica do Rio de Janeiro, Universidade de Brasília etc. Também recebeu visitantes de instituições estrangeiras, como: Universidade de Chicago, Universidade da Califórnia (Berkeley), Instituto Tecnológico de Massachussets, Universidade de Princeton, Universidade de Rochester, Institut des Hautes Études Scientifiques, Universidade de Dijon, Universidade de Bonn, Universidade de Konstanz, Universidade de Warwick, Universidade de Gronigen, Universidade de Toronto etc.
A hierarquia dentro da comunidade matemática é formada pelos membros "fortes" e pelos membros "fracos". Os membros fortes, que são os pesquisadores ativos, com muitas publicações internacionais, possuem status e prestígio dentro do grupo, com premiações e distinções. Além disso, exercem liderança pelos cargos que ocupam nas sociedades, academia e instituições de fomento à pesquisa.
Na seleção de estudantes para a pós-graduação e membros do Impa, percebe-se que a capacidade científica de um estudante ou de um pesquisador não escapa, no transcurso de sua carreira, da contaminação que exerce a posição que ele ocupa nas hierarquias instituídas. Manter a coesão institucional é meta que ainda perdura 50 anos após a fundação do instituto, assim como o acesso restrito apenas aos talentosos e de alto nível intelectual. O espírito corporativo foi sempre uma constante entre os pesquisadores do Impa, procurando manter um status de instituição de elite e evitando que professores, sem o reconhecimento dos pares, fizessem parte do seu quadro de docentes ou pesquisadores. O conselho orientador da instituição, dirigido por um seleto grupo de pesquisadores, zelava, e talvez ainda zele, para que essas normas sejam cumpridas e mantidas. Pertencer ao quadro de pesquisadores desse instituto é quase uma garantia de se alcançar entre a comunidade de matemáticos do país um lugar de destaque.
Recebido em: junho 2006
Aprovado para publicação em: janeiro 2008
Pesquisa financiada pelo Conselho Nacional de Desenvolvimento Científico e Tecnológico - CNPq
- ARQUIVO DA ACADEMIA BRASILEIRA DE CIÊNCIAS. Rio de Janeiro.
- ANDRADE, A. M. R. Físicos, mesons e política: a dinâmica da ciência na sociedade. São Paulo: Hucitec; Rio de Janeiro: Museu de Astronomia e Ciências Afins, 1999.
- BOURDIEU, P. O Campo científico. In: ORTIZ, R. (org.) Sociologia São Paulo: Ática, 1983. p.122-155.
- CARMO, M. P. Pesquisa em geometria diferencial no Brasil. Matemática Universitária, n. 26/27, p.1-27, jun./dez. 1999.
- CASTELLUBER, A. Os Currículos de matemática em universidades públicas da região sudeste e os professores egressos do Impa Vitória, 2003. Dissert. (mestr.) Universidade Federal do Espírito Santo.
- CONSELHO NACIONAL DE PESQUISAS. Conselho Deliberativo. Ata 112: reunião de 17/10/1952. Rio de Janeiro. Disponível em: centrodememoria.cnpq.br/atas-cd52-112-03.html Acesso em: maio 2006.
- ______. Ata 117: reunião de 15/10/1952. Rio de Janeiro: Arquivo CNPq, t.6.3.002 (Mast).
- CONSELHO NACIONAL DE PESQUISAS TECNOLÓGICAS. Arquivo Museu de Astronomia e Ciências Afins. Rio de Janeiro.
- DIAS, C. S. Cientistas do Brasil: depoimentos. São Paulo, 1998. Entrevista concedida a Vera Rita da Costa, por Candido da Silva Dias, p.693-701.
- ERNEST, P. The Philosophy of mathematics education London: Falmer, 1991.
- GROTHENDIECK, A. Cosenhas y siembras: reflexiones y testimonios sobre un pasado de matemático. Disponível em: http://kolmogorov.unex.es/~navarro/res/ Acesso em: 20 ago. 2006.
- HABERMAS, J. Conhecimentos e interesse Rio de Janeiro: Zahar, 1982.
- HARDY, G. H. Em defesa de um matemático São Paulo: Martins Fontes, 2000.
- INSTITUTO DE MATEMÁTICA PURA E APLICADA. Doutores e mestres do Impa: resumo de teses. Rio de Janeiro [199-?]
- ______. Relatório de atividades do Impa Rio de Janeiro, 1972. [Arquivo]
- INSTITUTO NACIONAL DE MATEMÁTICA PURA E APLICADA. Relatório de atividades do Impa Rio de Janeiro, 1979. [Arquivo]
- LIMA, E. L.; NACHBIN, L. O Ensino da matemática nas faculdades de ciências e nas escolas de engenharia do Brasil. Boletim da Sociedade Paranaense de Matemática, v. 4, n.1, p.8-18, 1961.
- LIMA, E. L. Entrevista: Elon Lages Lima comenta sua vocação de matemático e divulgador da matemática. Matemática Universitária, n.9/10, p.33-50, 1989.
- MENINO, F. S. A Escola de Engenharia de São Carlos e a criação de um curso de matemática 2001. Rio Claro, 2001. Dissert. (mestr.) Universidade Estadual de São Paulo.
- MERTON, R. La Sociologia da ciencia, 2: Investigaciones teóricas y empiricas. Madrid: Alianza, 1985.
- O'CONNOR, J. J.; ROBERTSON, E. F. Biografias de matemáticos na internet: Disponível em: http://www-history.mcs.st-and.ac.uk/history/Mathematicians Acesso em: 10 mar. 2003.
- PALIS, J.; CAMACHO, C.; LIMA, E. L. (orgs.) Impa 50 anos Rio de Janeiro, 2003.
- PICCININI, R. Entrevista concedida a Circe Mary Silva da Silva, 16 jan. 2003. por e-mail.
- PYENSON, L.; SHEETS-PYENSON, S. Servants of nature: a history of scientific institutions, enterprises and sensibilities. Londres: Fontana, 1999.
- SILVA, C. M. S. A Construção de um instituto de pesquisas matemáticas nos trópicos: o Impa. Revista Brasileira de História da Matemática, v.4, n.7, p.37-67, 2004.
- ______. Entrevista Elon Lages Lima. Matemática Universitária, n.16, p.1-18, jul. 1994.
- ______. Formação de professores e pesquisadores de matemática na Faculdade Nacional de Filosofia. Cadernos Pesquisas, n.117, p.103-126, nov. 2002.
- ______. O Impa e a formação de pesquisadores em matemática no Brasil. In: COLÓQUIO BRASILEIRO DE HISTÓRIA DA MATEMÁTICA, 1. Anais.. Natal, 2005. p.81-105.
- ______. Lélio Itapuambyra Gama e a modernização do ensino da matemática no Brasil. In: SEMINÁRIO NACIONAL DE HISTÓRIA DA CIÊNCIA E DA TECNOLOGIA, 7. Anais.. São Paulo: Edusp; Ed da Unesp; Imprensa Oficial, 2000. p.369-377.
- ______. Some german contributions to mathematics research in Brazil. In: HOFFMANN, M.; LENHARD, J.; SEEGER F. (orgs.) Activity and sign: grounding mathematics education. New York: Springer, 2005a.
- SMALE, S. Uma ferradura nas praias do Rio de Janeiro. Ciência Hoje, v. 26, n.156, p.34-41, 1999.
- THE MATHEMATICS GENEALOGY PROJECT. Disponível em: http://www.genealogy.ams.org/html Acesso em: 15 ago. 2004.
Datas de Publicação
-
Publicação nesta coleção
27 Maio 2010 -
Data do Fascículo
Dez 2009
Histórico
-
Aceito
Jan 2008 -
Recebido
Jun 2006