Resumen
The present review summarizes the most relevant results of our research group obtained recently in the field of unimolecular reaction dynamics. The following processes are specifically analyzed: the isomerization, dissociation and elimination in methyl nitrite, the fragmentation reactions of the mercaptomethyl cation, the C-CO dissociation in the acetyl and propionyl radicals, and the decomposition of vinyl fluoride. In all the cases, only state- or energy-selected systems are considered. Special emphasis is paid to the possibility of systems exhibiting non-statistical behavior.
reaction dynamics; classical trajectories; RRKM calculations
reaction dynamics; classical trajectories; RRKM calculations
REVISÃO
DINÁMICA DE REACCIONES UNIMOLECULARES EN FASE GAS. DESVIACIONES DEL COMPORTAMIENTO ESTADÍSTICO
Emilio Martínez-Núñez
Departamento de Química Física, Facultad de Ciencias Lagoas, Marcosende, 36200 Vigo - España
Saulo A. Vázquez*
Departamento de Química Física, Facultad de Química, Universidad de Santiago de Compostela, 15706 Santiago de Compostela - España
*e-mail: qfsaulo@usc.es
Recebido em 26/3/01; aceito em 19/9/01
DYNAMICS OF UNIMOLECULAR REACTIONS IN GAS PHASE. DEVIATIONS FROM STATISTICAL BEHAVIOR. The present review summarizes the most relevant results of our research group obtained recently in the field of unimolecular reaction dynamics. The following processes are specifically analyzed: the isomerization, dissociation and elimination in methyl nitrite, the fragmentation reactions of the mercaptomethyl cation, the C-CO dissociation in the acetyl and propionyl radicals, and the decomposition of vinyl fluoride. In all the cases, only state- or energy-selected systems are considered. Special emphasis is paid to the possibility of systems exhibiting non-statistical behavior.
Keywords: reaction dynamics; classical trajectories; RRKM calculations.
INTRODUCCIÓN
La evolución de los estudios experimentales en el campo de las reacciones unimoleculares presenta tres etapas bien definidas. Los trabajos más antiguos involucraban sistemas térmicos en los cuales las moléculas se excitaban mediante calentamiento1-9. La segunda etapa comenzó con la introducción de la técnica de activación química (principios de los años 60), que permite formar una especie altamente excitada que posteriormente puede reaccionar (isomerizar o descomponerse) o bien perder energía mediante colisiones10-13. La tercera etapa comenzó a primeros de los años 70 con el desarrollo de métodos más generales y precisos para preparar moléculas con energías o en estados definidos, así como el desarrollo de bases de tiempo absolutas para la medida de las velocidades de reacción. Hoy en día, mediante láseres, se pueden excitar moléculas por encima de sus límites de disociación con una resolución de números de onda, y seguir la reacción a través del tiempo desde milisegundos hasta femtosegundos.
Desde el punto de vista teórico, con los medios computacionales actuales se puede calcular la geometría, energía y frecuencias vibracionales de la molécula en función de la coordenada de reacción, lo que permite determinar con bastante exactitud las velocidades de reacción mediante modelos teóricos. De forma alternativa, se pueden construir superficies de energía potencial (SEP) y utilizarlas para investigar las reacciones mediante métodos de trayectorias clásicas y dinámica cuántica, los cuales no están inherentemente limitados por las suposiciones de las teorías estadísticas. En particular, la técnica de trayectorias clásicas viene siendo ampliamente utilizada con éxito. Cuatro libros excelentes acerca de las reacciones unimoleculares son los de Forst14, Robinson y Holbrook15, Gilbert y Smith16 y Baer y Hase17.
Estos importantes avances, tanto experimentales como teóricos, en el campo de las reacciones unimoleculares han conducido a la posibilidad de realizar tests críticos de las suposiciones básicas de las teorías estadísticas propuestas ya hace más de 70 años por Rice y Ramsperger18-20. Esta viene siendo en gran medida la actividad desarrollada en nuestro grupo de investigación durante los últimos años. Nuestra intención en este artículo es mostrar algunos de los resultados más relevantes que obtuvimos recientemente mediante cálculos de trayectorias clásicas, cálculos estadísticos y cálculos mecanocuánticos. Más concretamente, una vez presentados los métodos computacionales usados, se resumen los resultados obtenidos en nuestros estudios previos sobre la dinámica del nitrito de metilo (isomerización, disociación y eliminación), catión mercaptometilo, radicales acetilo y propionilo, y fluoroetileno. En todos los casos se investiga la dinámica en fase gas de sistemas excitados a energías seleccionadas, básicamente mediante el cálculo y análisis de las constantes de velocidad específicas de la energía k(E) y/o distribuciones de energías en los productos de reacción, prestando especial atención a posibles efectos no estadísticos.
METODOLOGÍA
Cálculos ab initio
Para cualquier estudio teórico dinámico los cálculos ab initio normalmente suponen un primer paso a llevar a cabo. En muchos casos estos cálculos están encaminados a calcular las propiedades (geometrías, frecuencias vibracionales y energías) de los puntos estacionarios más relevantes del sistema (reactivo, estado de transición y producto/s). Asimismo estos cálculos ab initio pueden englobar el cálculo del camino de mínima energía que une a los reactivos y a los productos21,22.
Con un mayor coste computacional los cálculos ab initio pueden utilizarse para la construcción de una SEP del sistema. Sin embargo, hoy en día, esto sólo es factible para sistemas con un número pequeño de átomos. Como se apuntó anteriormente, los cálculos ab initio también se pueden incorporar en los códigos de trayectorias clásicas para utilizarlos en cálculos de dinámica directa.
Una excelente introducción sobre el uso de cálculos ab initio en la construcción de SEP y su posterior aplicación a la dinámica y cinética de reacciones químicas es el libro de Steinfield, Francisco y Hase23. Un libro más avanzado en el que se describen diversas aproximaciones analíticas para la construcción de una SEP global es el de Murrel, Carter, Farantos, Huxley y Varandas24.
Cálculos de trayectorias
El método de trayectorias clásicas (TC), cuyo pionero fue Bunker a comienzos en los años 6025-28, es el equivalente a un experimento real realizado en un ordenador. Los cálculos de trayectorias han sido usados extensivamente para el estudio de reacciones unimoleculares durante las últimas décadas dado que es un método práctico de calcular constantes de velocidad así como obtener información muy detallada sobre la naturaleza fundamental de la dinámica. Se han publicado uno serie de artículos de revisión acerca de los métodos de trayectorias clásicas29. La revisiones de Truhlar y Muckerman29d y Raff y Thompson29e incluyen discusiones detalladas de los métodos básicos; la última de ellas contiene una discusión profunda de métodos para el tratamiento de reacciones unimoleculares. Además, se pueden destacar los trabajos de revisión de Truhlar30 y Miller31 de la dinámica teórica de reacciones químicas.
Obviamente, hay algunas desventajas en el uso de las simulaciones clásicas para el cálculo de las velocidades de reacciones unimoleculares. Primero, las simulaciones son caras desde del punto de vista computacional; no son, a menudo, factibles a energías cercanas al umbral de reacción ya que el tiempo requerido para la reacción puede ser muy superior al necesario para realizar integraciones numéricas exactas de las ecuaciones del movimiento. Más importante aun es la violación de la energía del punto cero, que es más acusada para aquellas trayectorias que se inician en los reactivos y se siguen hasta los productos, dado que las trayectorias pueden pasar por el estado de transición con una energía inferior a la energía del punto cero en los modos perpendiculares al camino de reacción. Este problema tan importante ha sido muy discutido en la bibliografía durante los últimos años32-36. Afortunadamente, la mayoria de los procesos de interés para los químicos pueden ser descritos clásicamente; sin embargo, fenómenos debidos a los efectos de interferencia, como el efecto túnel, pueden ser importantes en la isomerización, disociación y reacciones bimoleculares (ver por ej. la Ref. 37). El tratamiento apropiado de la dinámica multidimensional y de los efectos cuánticos en sistemas grandes generalmente requiere el uso de aproximaciones semiclásicas. Thompson et al.38 han desarrollado una aproximación práctica para incluir correcciones de túnel en cálculos de trayectorias clásicas.
Cuando el número de átomos del sistema es grande, la construcción de una SEP que describa correctamente todas las regiones de importancia para la dinámica puede resultar impracticable. En estos casos los métodos de dinámica directa pueden tener su relevancia. Entendemos aquí por dinámica directa aquellos cálculos en los que no se usa una SEP analítica sino que a cada paso de la trayectoria se realiza la integración utilizando fuerzas obtenidas directamente de cálculos ab initio o semiempíricos. Esta aproximación comenzó a ser usada con éxito por Hase y colaboradores36,39-41 en una serie de reacciones unimoleculares.
MÉTODOS ESTADÍSTICOS
La premisa fundamental de estas teorías es que todos los estados moleculares son igualmente probables17. Esto significa que la probabilidad de que una molécula excitada reaccione depende enteramente de consideraciones estadísticas. Generalmente esta suposición es cierta si la relajación vibracional intramolecular RVI (o redistribución de la energía vibracional en la molécula) es muy rápida comparada con la velocidad de reacción. Su cumplimiento garantiza un decaimiento monoexponencial de las moléculas excitadas vibracionalmente17,
Esta hipótesis fundamental es la base de una seria de teorías estadísticas como son las teorías RRK18-20, RRKM42,43, SACM44-49, y PST50-53. En muchas ocasiones estas teorías se usan para calcular las constantes de velocidad microcanónicas k(E), que es la magnitud de relevancia para las reacciones unimoleculares. La conversión de la constante de velocidad microcanónica y la constante de velocidad canónica (asociada a una temperatura dada T) requiere un promedio sobre la distribución de energías internas a la temperatura T. De esta manera podemos obtener la constante de velocidad unimolecular canónica en el límite de altas presiones haciendo un promedio sobre las constantes microcanónicas mediante la distribución de Boltzmann. Sin embargo, lo más usual es calcular la constante de velocidad canónica usando la teoría variacional del estado de transición54, que se hace uso del hecho de que la teoría del estado de transición es un límite superior a la verdadera constante de velocidad clásica debido a los recruzamientos del estado de transición.
Un proceso unimolecular que evolucione según la Ec. (2.1) se clasifica como intrínsicamente RRKM. Bunker y Hase17,27 caracterizaron dos tipos de comportamiento no-RRKM: intrínseco y aparente. El primero ocurre cuando la molécula posee un acoplamiento débil entre ciertos estados vibracionales, en otras palabras, cuando existe un "cuello de botella" en el flujo de energía entre estados vibracionales.
En muchos experimentos (como la fotoactivación y la activación química) los estados moleculares vibracionales/rotacionales pueden excitarse de forma no aleatoria. En algunos de estos casos las distribuciones de tiempos de vida pueden seguir la Ec. (2.1). En otros casos la probabilidad de un tiempo de vida corto con respecto a la reacción se puede incrementar o reducir, dependiendo de la localización de la excitación inicial dentro de la molécula. Estos son ejemplos de comportamiento no-RRKM aparente debido a la excitación inicial no aleatoria. Para una revisión de estudios en los que se muestra este tipo de comportamiento véase la Ref. 17.
Una variedad de modelos estadísticos que pueden hacer uso de una SEP realista (como la empleada en los cálculos de TC) son los métodos de Monte Carlo55, en donde las sumas y densidades de estados de la expresión RRKM se determinan mediante las integrales clásicas del espacio de fases. Algunas de las aplicaciones de esta metodología se recogen en una revisión exhaustiva de Thompson56.
RESULTADOS
Los resultados aquí presentados para las reacciones unimoleculares estudiadas en nuestro grupo de investigación aparecen divididos de acuerdo con el sistema objeto de análisis. Primeramente trataremos el nitrito de metilo (reacciones de isomerización, disociación y eliminación), luego se hablara del catión mercaptometilo y finalmente se recogen los resultados para los radicales acetilo y propionilo, y el fluoretileno.
Nitrito de metilo
Isomerización del nitrito de metilo. El nitrito de metilo presenta una barrera de isomerización (syn « anti) baja, en torno a las 11 kcal/mol, con una densidad de estados baja a esa energía crítica. Bajo tales condiciones la reacción puede ser mucho más rápida que la RVI, siendo por tanto una candidata perfecta a mostrar efectos no estadísticos.
La Tabla 1 recoge las constantes de velocidad obtenidas mediante trayectorias clásicas usando tres modelos diferentes de SEP57, así como las constantes de velocidad RRKM (usando las mismas SEP) obtenidas en un estudio separado58. Si la velocidad de RVI fuese muy rápida esperaríamos que los resultados RRKM y los de TC fuesen muy parecidos (las diferencias serían errores numéricos). Por otro lado, la definición del estado de transición en los cálculos TC y RRKM debe ser idéntica para una comparación rigurosa. En los cálculos RRKM, la velocidad está determinada por el primer paso de la trayectoria a través del estado de transición. Sin embargo, en los cálculos dinámicos (TC) las trayectorias pueden volver al reactivo una vez que cruzan el estado de transición (recruzamiento de la superficie divisoria del estado de transición). Por ese motivo realizamos cálculos adicionales de TC, a una energía total de 110 kcal/mol, en los cuales el estado de transición fue considerado como un punto sin retorno. Como se observa en la Tabla 1, las constantes de velocidad resultantes son mucho más parecidos a los RRKM, aunque todavía difieren substancialmente.
Las discrepancias restantes se pueden atribuir a una desviación específica del comportamiento estadístico que puede ser descrita como la existencia de "trayectorias directas". Berblinger y Schlier59 definieron una "trayectorias directa" como aquella que, partiendo de un colectivo microcanónico, cruza el estado de transición directamente y cuyo movimiento por tanto no interacciona fuertemente con el resto de los modos del sistema. En nuestro trabajo58, una trayectoria fue considerada directa si lleva a cabo menos de un número mínimo de oscilaciones (pasos por puntos de retorno) en la coordenada de reacción (que en este caso es el ángulo de torsión). Para corregir las velocidades RRKM hemos empleado la siguiente expresión:
donde Pdir y Pdtis r son las fracciones de trayectorias directas para la molécula de reactivo y el estado de transición, respectivamente, y kRRKM(E) es la constante de velocidad RRKM no corregida. Para una explicación detallada acerca de cómo calcular Pdir y Pdtis r el lector puede consultar la Ref. 53. Las constantes corregidas aparecen también recogidas en la Tabla 1 para una energía total de 110 kcal/mol. Como se muestra en la tabla, las constantes de velocidad corregidas concuerdan bastante bien con las constantes de TC sugiriendo que la mayor fuente de desacuerdo entre las constantes estadísticas y de TC es una especial desviación del comportamiento estadístico: las "trayectorias directas".
Disociación y eliminación del nitrito de metilo. Para este sistema60-64 se encontró que la dinámica es estadística a las energías más bajas para la reacción de disociación (MeONO ® MeO + NO) mientras que la reacción de eliminación (MeONO ® CH2O + HNO) tiene un comportamiento no estadístico a todas las energías estudiadas. En particular, las constantes de velocidad calculadas mediante TC para la disociación se muestran en la Figura 1 (círculos). Las líneas en la figura representan los resultados de varios modelos estadísticos clásicos. El límite armónico clásico (RRK) de la teoría RRKM es17,
donde n viene dado en función de las frecuencias vibracionales del reactivo y del estado de transición17,E0 es la energía crítica para la reacción y s es el número de grados de libertad del sistema. Comúnmente esta expresión se ajusta directamente a los resultados de TC, aun cuando la Ec. (3.2) sólo es válida para un Hamiltoniano separable y armónico. Para introducir anarmonicidad en la expresión RRK, el término n, que es constante en la expresión anterior, se hace dependiente de la energía65,
donde la constante a representa el término armónico (independiente de la energía) y fanh(E) es la corrección anarmónica. Aquí se muestran cuatro esquemas RRK diferentes, tres de ellos introducidos recientemente por Song y Hase65 y el último sugerido por nosotros64. Concretamente, el factor de corrección anarmónico para el esquema 1 es
donde b es un parámetro ajustable. En el esquema 2 se usaron dos parámetros ajustables diferentes b y bts para el reactivo y el estado de transición, respectivamente; el factor de corrección anarmónico para la constante de velocidad microcanónica es por tanto
En el esquema 3 se introduce un parámetro adicional de ajuste d:
Finalmente, en el esquema 4 se considera el factor anarmónico del esquema 2 pero asumiendo que dos modos de vibración (los de menor frecuencia) en el estado de transición son rotores bidimensionales, y por tanto en este caso la constante de velocidad queda
donde B1 y B2 son las constantes rotacionales para los rotores bidimensionales alrededor de ejes perpendiculares a la coordenada de reacción (ver Figura 2).
En todos los ajustes el número de grados de libertad de vibración s y la energía crítica E0 se fijaron en 15 y 41.7 kcal/mol, respectivamente. Como se muestra en la Figura 1, las velocidades de TC (círculos) no se ajustan bien mediante el esquema 1, pero se pueden ajustar mediante los esquemas 2 y 3, y mucho mejor mediante el esquema 4. Para el esquema 2, el ajuste da un valor anormalmente alto (1765) para la el factor anarmónico a la energía crítica. El ajuste con el esquema 3 da un valor mucho más realista para el factor anarmónico (15). Sin embargo, el mejor ajuste se obtiene con el esquema 4. En otras palabras, el tratamiento de varios grados de libertad en el estado de transición como rotores bidimensionales en vez de osciladores armónicos condujo al mejor acuerdo entre la teoría estadística RRK y los resultados de trayectorias.
En estos estudios63,64 también se analizaron los efectos rotacionales. Concretamente se consideraron tres orientaciones diferentes del momento angular, cada una de ellas paralela a los ejes principales de inercia. Las constantes de velocidad [para la disociación (I) y eliminación (II)] aparecen en la Tabla 2 junto con los resultados para la molécula sin rotación (L = 0). Se observa que la rotación molecular aumenta substancialmente la velocidad de descomposición. Concretamente, la rotación alrededor del eje a aumenta las constantes de eliminación, mientras que la excitación alrededor de los ejes b y c conducen a las mayores velocidades de disociación. La dependencia de las constantes de velocidad con la dirección del movimiento rotacional se puede explicar mediante los efectos de las fuerzas centrifugas. Para la excitación alrededor del eje a, la fuerza centrífuga aumenta el momento de inercia de ese eje (Ia), favoreciendo el canal de eliminación (ver Figura 3). Por el contrario, para las excitaciones de los ejes perpendiculares hay una fuerza centrífuga a lo largo del eje O-N, y por tanto el efecto de la rotación es aumentar la velocidad de disociación. Además se han analizado los resultados para una excitación inicial de la flexión CON junto con la rotación. Como se muestra en la Tabla 2, la excitación inicial de ese modo normal junto con la rotación alrededor del eje a condujo a la mayor constante de velocidad para la eliminación (0.059 ps-1), mientras que la excitación de los ejes perpendiculares resultó en la mayor constante de velocidad para la disociación (1.347 ps-1). Las constantes de velocidad para 40 kcal/mol de energía rotacional también se recogen en la Tabla 2. Mientras que la excitación alrededor del eje a condujo a una disminución en las constantes de velocidad para ambos canales, la excitación alrededor del eje b aumentó significativamente la velocidad del canal de disociación y eliminó completamente el canal de eliminación (no se encontraron reacciones de eliminación para un colectivo de 2000 trayectorias). El descenso en la constante de velocidad para la excitación del eje a puede explicarse con la teoría RRKM19.Por otra parte, se comprobó que el colectivo con 40 kcal/mol de energía rotacional en el eje b exhibe un comportamiento biexponencial, lo que sugiere la existencia de un "cuello de botella" para la redistribución de la energía asociado con las rotaciones alrededor de los ejes b y c.
Catión mercaptometilo
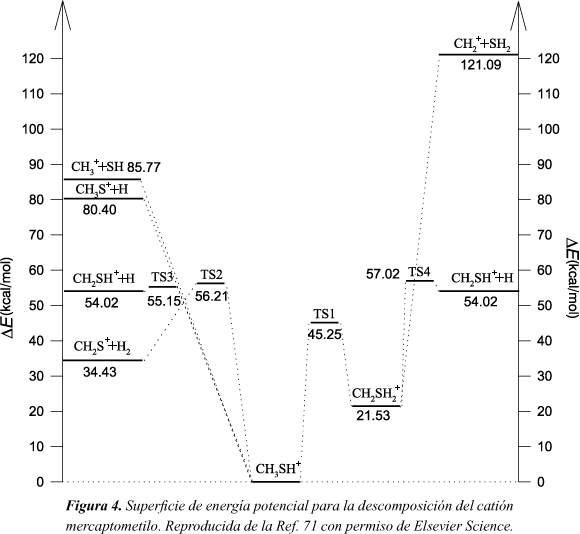
La disociación de este catión es de especial interés debido a la cantidad de datos experimentales disponibles66-70.Un esquema donde se recogen las reacciones de descomposición más relevantes del catión mercaptometilo se muestra en la Figura 4.
Para este sistema se construyó una superficie de energía potencial, basada en nuestros propios cálculos ab initio71, para llevar a cabo un estudio de TC72. Asimismo el método semiempírico AM1 se reparametrizón73 para que modele los procesos de descomposición en concordancia con los resultados ab initio. El método resultante se denominó, siguiendo nomenclatura previa74,36,39-41, AM1-SRP y se usó en un estudio de dinámica directa73 en el que se investigó los canales de menor energía.
La Tabla 3 lista las abundancias relativas72,73 (en tanto por ciento) de los productos calculadas a 170 kcal/mol bajo diferentes condiciones iniciales, así como varios resultados experimentales66-68. Además se muestra el porcentaje de trayectorias reactivas que experimentan isomerización (proceso de menor energía en la Figura 4). Las abundancias calculadas bajo excitación vibracional aleatoria (EMS) concuerdan razonablemente con los resultados experimentales de la Ref. 67 (fragmentación inducida por fotoionización) y de la Ref. 68 (fragmentación inducida por intercambio de carga), en las que el catión mercaptometilo se prepara con una distribución estadística de la energía interna. En la gran mayoría de los casos el producto dominante es CH2SH+ (90%). Bajo excitaciones selectivas de los modos normales de tensión asociados con el grupo metilo (colectivos H-F), la descomposición prácticamente solo dio lugar a CH2SH+. Asimismo, el porcentaje de trayectorias que isomerizan se redujo substancialmente, como es de esperar. Cuando la energía está depositada selectivamente en los modos de bajas frecuencias (torsión, tensión CS y flexión CSH), colectivos L-F, la abundancia relativa de CH2SH+ disminuye drásticamente y la formación de los productos CH3+ + SH se convierte en el canal dominante. Esto concuerda con los resultados experimentales de Fenn et al.66 obtenidos mediante activación por colisiones, corroborando su conclusión de que esta técnica de activación prepara las moléculas con una distribución no aleatoria de la energía (esta se deposita preferentemente en el modo CS de baja frecuencia), conduciendo a un comportamiento no estadístico (no-RRKM aparente). Por otro lado, el porcentaje de trayectorias reactivas que dan lugar a la isomerización (39%) disminuye con respecto al valor alcanzado por el colectivo EMS (57%).
Radicales acetilo y propionilo
Al igual que para la isomerización del nitrito de metilo, las disociaciones de los cationes acetilo y propionilo son buenas candidatas a presentar efectos no estadísticos dado que la escisión del enlace C-CO para formar CH3 (o CH3CH2) y CO presenta una barrera de energía muy baja (menos de 20 kcal/mol)75-77.
Radical acetilo. La disociación de este radical ha sido muy estudiada, sobre todo en los últimos años75-90. En particular, Shibata et al.87 midieron recientemente la velocidad de disociación unimolecular en función de la energía k(E), observando que a energías cercanas al límite de disociación las constantes de velocidad eran un orden de magnitud más pequeñas que las calculadas mediante la teoría RRKM, y sugirieron que la velocidad de RVI y/o el intercambio energético vibración-rotación debía estar restringido. Sus resultados nos llevaron a investigar la dinámica de disociación del radical acetilo a energías internas bajas para corroborar sus conclusiones.
En nuestro estudio teórico90 se analizó el grado de mezcla en el número cuántico Ka (asociado a la proyección del momento angular sobre eje a) a una energía de 23 kcal/mol, lo que proporciona una medida directa del acoplamiento vibración-rotación91. Para este propósito, evaluamos Ka(t) diagonalizando el tensor de inercia a cada paso de integración. Luego, el momento angular fue proyectado sobre el eje a para obtener Ka. Para definir el grado de mezcla en el número cuántico Kaempleamos dos criterios definidos anteriormente por Grebenshchikiv et al.91 En primer lugar
donde
es el promedio de Ka(t) sobre cada una de las trayectorias. En segundo lugar
donde y son los valores máximos y mínimos de Ka a lo largo de la trayectoria. Siguiendo estos dos criterios, la fracción del espacio Ka que se mezcla, f(t) puede ser evaluada de acuerdo con las expresiones
donde se ha tenido en cuenta el hecho de que DK(a1)Î (0,J) y DK(a2)Î (0,2J). En este trabajo se han usado los valores del número cuántico J siguientes: 56, 97 y 140. Para cada uno de los valores del número cuántico se calcularon 5000 trayectorias.
El grado de mezcla en el número cuántico Ka se muestra en la Figura 5 mediante la fracción del espacio K que se mezcla (f) en función del tiempo para J = 56, 97 y 140. Como es de esperar f(2) es mayor para tiempos más pequeños aunque a medida que el tiempo de simulación aumenta la diferencia se hace insignificante. Por otra parte, el grado de mezcla en el número cuántico Ka disminuye al aumentar J. A 6.7 ps (que es el tiempo de vida promedio calculado a 23 kcal/mol) alrededor del 15% del espacio Ka está mezclado para J = 140. Por tanto, a 23 kcal/mol y para valores altos de J, es muy improbable que la rotación cause mezcla en los estados vibracionales y por lo tanto la rotación se puede considerar inactiva. Este resultado está en la línea de las conclusiones de Shibata et al.87.
Radical propionilo. Debido a la existencia de información experimental sobre la disociación del radical propionilo y a cierta controversia sobre su comportamiento estadístico/no-estadístico, hemos estudiado su disociación mediante TC92.
Es bien conocido que la técnica de TC puede dar lugar a distribuciones de energía en los productos (DEP) poco exactas debido al tratamiento incorrecto de la energía del punto cero. Por este motivo, hemos usado en este trabajo una técnica de muestreo cuasiclásico (denominada aquí QCBS)41,que inicia las trayectorias en la barrera y distribuye la energía entre los modos normales de acuerdo con la teoría RRKM cuántica. El método está basado en el muestreo clásico de la barrera93 y selecciona cada estado vibracional con la misma probabilidad, de manera que la distribución de los momentos en la coordenada de reacción está de acuerdo con la teoría RRKM17. Este procedimiento ha sido detallado en la Ref. 41 y por ese motivo aquí sólo daremos una breve descripción del mismo.
Para una comparación con los resultados experimentales, se analizaron las DEP para diferentes colectivos (de trayectorias que parten del reactivo) a una energía total de 67.8 kcal/mol. Asimismo, como comentamos anteriormente y debido al tratamiento incorrecto de la energía del punto cero de las TC, se seleccionó un colectivo adicional (denominado QCBS) en el cual las trayectorias se inician en la barrera de acuerdo con el método que lleva el mismo nombre. Las DEP calculadas se recogen en la Tabla 4 y se comparan con los datos experimentales disponibles94. Los resultados obtenidos para el colectivo QCBS son bastante diferentes de los calculados mediante condiciones iniciales EMS (condiciones microcanónicas partiendo del reactivo). Concretamente, las fracciones de energía correspondientes a la vibración de CH2CH3 son 0.56 y 0.72 para los colectivos QCBS y EMS, respectivamente. En gran medida ese desacuerdo puede deberse a la violación de la energía del punto cero de las trayectorias, aunque como veremos más adelante la causa fundamental está en que el sistema no se comporta estadísticamente, más concretamente, el colectivo EMS exhibe un comportamiento no-RRKM intrínseco. Las diferencias substanciales para las DEP calculadas para los otros colectivos indican una especificidad de modos. Para una discusión más detallada con los resultados experimentales el lector puede consultar la Ref. 92.
Fluoroetileno
La dinámica de descomposición de derivados fluorados del etileno ha sido muy estudiada en la bibliografía95-105. Concretamente, Sato et al.100 usaron espectroscopia de tiempo de vuelo y cálculos ab initio para investigar la disociación del fluoruro de vinilo a 157 nm (182.1 kcal/mol). De acuerdo con sus cálculos MP2/6-31G(d,p), los canales abiertos a la energía experimental son
Las eliminaciones de HF (canal 1) pueden ocurrir a través de un estado de transición de tres centros o bién a través de otro de cuatro centros, como se muestra en la Figura 6. Los cálculos MP2/6-31G(d,p) predicen barreras de 82.2 y 85.3 kcal/mol para las eliminaciones a tres y a cuatro centros, respectivamente. Sin embargo, cálculos más recientes al nivel QCISD(T)/6-311G(2d,2p) predicen valores de 80 kcal/mol para ambos canales106; los otros (canales 2-5) presentan barreras bastante mayores. Sato et al.100 sugirieron que el HF se produce predominantemente mediante el proceso de eliminación a cuatro centros. Sin embargo, cálculos RRKM106 predicen que ambos procesos son probables, estando ligeramente favorecido a 182 kcal/mol el de tres centros.
Por estos motivos realizamos un estudio de dinámica directa para estas dos reacciones107 usando el modelo semiempírico AM1-SRP. La Tabla 5 lista las DEP calculadas a la energía de excitación de 182.1 kcal/mol (y adicionalmente a 111.6 kcal/mol para el colectivo QCBS) así como los valores experimentales96,97,100. La última columna recoge las relaciones N3/N4, donde N3 y N4 son los números de trayectorias que se descomponen a través de los estados de transición de tres y cuatro centros, respectivamente. Se encuentra que para los colectivos EMS, CF/HCH, FCC/CH2 y WAGG (el nombre viene del modo normal excitado inicialmente) el canal a cuatro centros es el preferido, aunque el canal a tres centros es competitivo. Sin embargo, para los colectivos CH y FCH/CH2, la eliminación a tres centros es la más probable. Como se mencionó anteriormente, Sato et al.100 concluyeron que el HF se producía básicamente mediante la eliminación a cuatro centros. Nuestra energía traslacional promedio calculada para el colectivo QCBS-TS1 (43.5 kcal/mol) es similar a su valor promedio (42 kcal/mol). El valor obtenido para QCBS-TS2 es mucho más bajo (27.4 kcal/mol). Estos resultados parecen apoyar su conclusión. Sin embargo, una comparación más rigurosa entre las energías traslacionales calculadas y observadas debe englobar también la forma de las distribuciones.
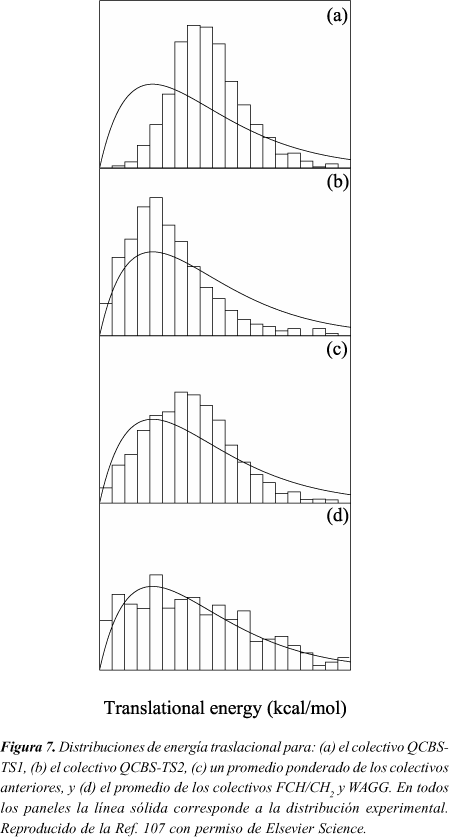
La Figura 7 compara la distribución experimental de energías traslacionales obtenida por Sato et al.100 (línea continua) con la calculada aquí (barras verticales) para los colectivos QCBS-TS1 y QCBS-TS2. Puede observarse que ni la distribución QCBS-TS1 ni la QCBS-TS2 concuerdan con la experimental. La distribución QCBS-TS1 tiene el máximo a una energía traslacional elevada (sobre 40 kcal/mol, muy cerca de su valor medio). La QCBS-TS2 tiene el máximo en un valor similar a la energía traslacional experimental más probable (20 kcal/mol) pero las poblaciones de trayectorias con energías traslacionales elevadas son menores que las mostradas en la distribución experimental. Por tanto, aunque los resultados QCBS-TS1 concuerdan mejor con la energía traslacional media determinada experimentalmente, hay desacuerdo para la energía traslacional más probable. Por el contrario, para el colectivo QCBS-TS2 la energía traslacional más probable concuerda muy bien con el valor experimental pero los valores promedio difieren considerablemente. Una comparación más rigurosa, sin embargo, debería englobar una media ponderada de los colectivos QCBS-TS1 y QCBS-TS2. Usando como factor de ponderación la relación N3/N4 obtenida para el colectivo EMS, la distribución conjunta (Figura 7c) se ajusta mejor a la experimental que la QCBS-TS1 o la QCBS-TS2 separadamente, aunque la distribución experimental tiene el máximo a una energía más baja y es más ancha que la teórica. Esta comparación sugiere que el porcentaje de eliminaciones de HF que ocurren a través del estado de transición de tres centros podría ser significativo en el experimento.
Asimismo, debemos indicar la influencia que podría ejercer una posible excitación inicial no aleatoria en las DEP. Como mostramos anteriormente, los diferentes esquemas de excitación condujeron a diferentes relaciones N3/N4 y DEP. En la Figura 7d se muestra la distribución de energía traslacional obtenida mediante un promedio de las distribuciones FCH/CH2 y WAGG. Esta distribución concuerda razonablemente bien con la curva experimental. Nuestra intención aquí no es sugerir que estos modos normales están excitados preferentemente en las condiciones iniciales de Sato et al.100, sino hacer notar que no se debe descartar la posibilidad de una excitación inicial no aleatoria en el experimento, lo que podría conducir a un comportamiento no-RRKM aparente17,27.
La energía traslacional en los productos calculada para el colectivo EMS (20.3 kcal/mol) es significativamente menor que el valor experimental y, sorprendentemente, que la calculada para los colectivos QCBS. Este resultado tan sorprendente también fue observado para el radical propionilo como se mostró anteriormente. Las trayectorias iniciadas en el reactivo pueden cruzar el estado de transición sin la energía del punto cero en los modos ortogonales a la coordenada de reacción de manera que es de esperar un aumento de la energía traslacional promedio en comparación con los resultados QCBS. Nuestro resultado nos llevó a concluir que la descomposición es intrínsecamente no-RRKM17,27 , un comportamiento frecuentemente observado en cálculos de trayectorias a altas energías108. Como se muestra en la Tabla 5, la energía vibracional media en el acetileno calculada para el colectivo EMS (109.0 kcal/mol) es mucho mayor que para los colectivos QCBS-TS1 y QCBS-TS2 (67.6 kcal/mol y 81.9 kcal/mol, respectivamente). Para otros colectivos en los que se produce una excitación inicial de algún modo de vibración asociado al fragmento HCCH, tales como CH o CC/HCH, los cálculos también muestran altos contenidos vibracionales para el acetileno. Por tanto, parece que en nuestro modelo uno o varios "cuellos de botella" podrían estar asociados con el fragmento HCCH. Como consecuencia, la excitación efectiva en el colectivo EMS sería menor que la correspondiente a los colectivos QCBS, conduciendo a esta tendencia inesperada.
Por último es de destacar el hecho de que a la energías más baja la energía translacional promedio no varía sustancialmente en la distribución QCBS-TS1 con respecto al valor obtenido a la energía más alta (ver Tabla 5), al contrario de lo que ocurre para la distribución QCBS-TS2. La explicación de este hecho puede estar en la diferencia de la barrera reversa para los canales de eliminación a tres (8.3 kcal/mol) y a cuatro centros (53.2 kcal/mol). Como la energía translacional viene dada por un porcentaje de la barrera reversa y otro de la energía en exceso, es de esperar una variación mayor para la eliminación a tres centros dado que la energía en exceso para este proceso es mucho mayor que la barrera reversa.
CONCLUSIONES Y PERSPECTIVAS FUTURAS
Para una comparación detallada entre los cálculos teóricos y los resultados experimentales es importante utilizar una SEP realista y disponer de técnicas que nos permitan simular las condiciones iniciales del experimento. Si queremos comparar DEP debemos asegurarnos de que las moléculas pasan por el estado de transición con la energía del punto cero en sus modos perpendiculares. Por ese motivo se usan corrientemente técnicas cuasiclásicas de muestreo en la barrera. Esta técnica ha sido muy utilizada en la literatura para el cálculo de las distribuciones de energía en los productos109. Sin embargo estas técnicas están limitadas por el empleo de la aproximación armónica, que si bien no es muy importante para colectivos iniciados en los reactivos puede ser decisiva para muestreos en la barrera. En esa línea hemos recientemente introducido dos modelos de muestreo anarmónico en la barrera110, comprobados en el catión mercaptometilo, que dan lugar a DEP diferentes de las obtenidas usando el modelo armónico tradicional.
En lo referente a las SEP, existen en la bibliografía diversos modelos y aproximaciones para su construcción24, aunque para sistemas con más de tres o cuatro átomos el desarrollo de una SEP realista puede ser muy complicado. Dentro de estas aproximaciones es especialmente intuitiva y útil la expansión doble de multicuerpos (DMBE) con el que uno de los autores y Varandas han desarrollado una SEP para el HSO111. Sin embargo, cuando el número de átomos es mayor resulta más adecuado el empleo de técnicas de dinámica directa. Hoy en día se están haciendo cálculos de trayectorias directas incluso al nivel MP2112.Además, uno de los paquetes de química computacional más usado en el mundo entero, el Gaussian 98113, incluye ya una opción para hacer trayectorias directas. Dentro de nuestro empeño de realizar dinámica en sistemas más grandes hemos recientemente utilizado el método semiempírico PM3 para calcular las DEP para la disociación del dihidrofurano, una molécula con once átomos (cinco de ellos pesados)114.
Recientemente también hemos estado interesados en las teorías semiclásicas de Miller115,116 para el cálculo de las constantes de velocidad canónicas, que permiten incluir efectos cuánticos en cálculos de TC convencionales. Estas teorías se pueden aplicar tanto a procesos bimoleculares como unimoleculares. Concretamente hemos implementado una de estas aproximaciones semiclásicas116 en el código de TC y hemos comprobado su funcionamiento para un proceso bimolecular muy estudiado: CH3 + H2® CH4 + H117. Debido a la utilización exitosa de este método estamos actualmente proyectando su empleo para el estudio de diversas reacciones unimoleculares.
REFERENCIAS
1. Chambers, T. S.; Kistiakowsky, G. B.; J. Am. Chem. Soc. 1934, 56, 399.
2. Schlag, E. W.; Rabinovitch, B. S.; J. Am. Chem. Soc. 1960, 82, 5996.
3. Schneider, F. W.; Rabinovitch, B. S.; J. Am. Chem. Soc. 1962, 84, 4215.
4. Tsang, W.; J. Chem. Phys. 1965, 43, 352.
5. Tsang, W.; J. Phys. Chem. 1972, 76, 143.
6. Tsang, W.; Int. J. Chem. Kin. 1978, 10, 41.
7. Tsang, W. Em Shock Tubes in Chemistry; Lifshitz, A., ed.; Marcel Decker: New York, p. 59-129.
8. Astholz, D. C.; Troe, J.; Wieters, W.; J. Chem. Phys. 1979, 70, 5107.
9. Brouwer, L.; Muller-Markgraf; W.; Troe, J.; Ver. Bunsenges. Phys. Chem. 1983, 87, 1031.
10. Rabinovitch, B. S.; Flowers, M. C.; Quart. Rev. 1964, 18, 122.
11. Rabinovitch, B. S.; Setser, D. W.; Adv. Photochem. 1964, 3, 1.
12. Hassler, J. C.; Setser, D. W.; J. Chem. Soc. 1966, 45, 3237.
13. Simons, J. W.; Taylor, G. W.; J. Phys. Chem. 1969, 73, 1274.
14. Forst, W.; Theory of Unimolecular Reactions; Academic Press: New York, 1971.
15. Robinson, P. J.; Holbrook, K. A.; Unimolecular Reactions, Wiley-Interscience: London, 1972.
16. Gilbert, R. G.; Smith, S. C.; Theory of Unimolecular and Recombination Reactions, Blackwell Scientific: Oxford, 1990.
17. Baer, T.; Hase, W. L.; Unimolecular Reaction Dynamics. Theory and Experiments, Oxford University Press: New York, 1996.
18. Rice, O. K.; Ramsperger H. C.; J. Am. Chem. Soc. 1927, 49, 1617.
19. Rice, O. K.; Ramsperger H. C.; J. Am. Chem. Soc. 1928, 50, 617.
20. Kassel, L. S.; J. Phys. Chem. 1928, 32, 225.
21. Fukui, K.; Pure Appl. Chem. 1992, 54, 1825.
22. Truhlar, D. G.; Kuppermann, A. J.; J. Am. Chem. Soc. 1971, 93, 1840.
23. Steinfield, J. I.; Franciso, J. S.; Hase, W: L.; Chemical Kinetics and Dynamics, 2nd ed., Prentice Hall: New Yersey, 1999.
24. Murrell, J. N; Carter, S.; Farantos, S. C.; Huxley, P.; A. J. C. Varandas; Molecular Potential Energy Functions, John Wiley: Chichester, 1984.
25. Bunker, D. L.; J. Chem. Phys. 1962, 37, 393; Bunker, D. L. J.; Chem. Phys. 1964, 40, 1946; Bunker, D. L.; Theory of Elementary Gas Reaction Rates., Pergamon Press: New York, 1966; Bunker, D. L.; Proceedings of the International School of Physics Enrico Fermi Course XLIV: Molecular Beam and Reaction Kinetics, Schlier, C., ed., Academic Press: New York, 1970, p. 315-319.
26. Bunker, D. L.; Pattengill, M. J.; Chem. Phys. 1968, 48, 772.
27. Bunker, D. L.; Hase, W. L.; J. Chem. Phys. 1973, 54, 4621.
28. Harris, H. H.; Bunker, D. L.; Chem. Phys. Lett. 1971, 11, 433.
29. Porter, R. M.; Ann. Rev. Phys. Chem. 1974, 25, 317; Bunker, D. L.; Method. Comp. Phys. 1971, 10, 287; Porter, R. M.; Raff, L. M. Em Modern Theoretical Chemistry: Dynamics of Molecular Collisions, Miller, W. H., ed.; Plenum Press: New York, 1976, vol. 2, part B, p. 1; Truhlar, D. G.; Muckerman, J. T. Em Atom-Molecule Collision Theory: A Guide for the Experimentalist, Bernstein, R. B., ed., Plenum Pess: New York, 1979, p. 505; Raff, L. M.; Thompson, D. L. Em The Theory of Chemical Reaction Dynamics, Baer, M., ed., CRC, Boca Raton: FL, 1985, v. 3, p. 1; Benito, R. M.; Aoiz, F. J.; Computational Chemistry: Structure, Interactions and Reactivity; Franga, S., ed., 1992, 562; Mayne, H. R.; Dynamics of Molecules and Chemical Reactions; Wyatt, R. E.; Zhang, Z. H., eds., Marcel Dekker: New York, 1996, p. 589; Sewell, T. D.; Thompson, D. L.; Int. J. Mod. Phys. B 1997, 11, 1067.
30. Truhlar, D. G.; Comp. Phys. Comm. 1994, 84, 78.
31. Miller, W. H. Em Frontiers of Chemical Dynamics, Yurtsever, E., ed., Kluwer Academic: Dordrecht, 1995, p. 1.
32. Varandas, A. J. C.; Brandão, J.; Pastrana, M. R.; J. Chem. Phys. 1992, 96, 5137; Varandas, A J. C.; Marques, J. M. C.; J. Chem. Phys. 1992, 97, 4050; Marques, J. M. C.; Varandas, A. J. C.; An. Fis. 1994, 90, 284; Varandas, A. J. C.; J. Chem. Phys. 1993, 99, 1076.
33. Bowman, J. M.; Gazdy, B.; Sun, Q.; J. Chem. Phys. 1989, 91, 2859; Miller, W. H.; Hase, W. L.; Darling, C. L.; J. Chem. Phys. 1989, 91, 2863; Varandas, A. J. C.; Marques, J. M. C.; J. Chem. Phys. 1994, 100, 1908; Ben-Nun, M.; Levine, R. D.; J. Chem. Phys. 1994, 101, 8768; Kumar, S.; Sathyamurthy, N.; Ramaswamy, R.; J. Chem. Phys. 1995, 103, 6021; Ben-Nun, N.; Levine, R. D.; J. Chem. Phys. 1996, 105, 8136.
34. Truhlar, D. G.; J. Phys. Chem. 1979, 83, 188.
35. Guo ,Y.; Thompson, D. L.; Sewell, T. D.; J. Chem. Phys. 1996, 104, 576.
36. Milliam, J. M.; Bakken, V.; Chen, W.; Hase, W. L.; Schlegel, H. B.; J. Chem. Phys. 1999, 111, 3800.
37. Benderskii, V. A.; Makarov, D. E.; Wight, C. A.; Adv. Chem. Phys. 1994, 88.
38. Guo, Y.; Thompson, W. L., Em Modern Methods for Multidimensional Dynamics Computations in Chemistry; Thompson, D. L., ed., World Scientific: Singapore, 1998.
39. Bolton, K.; Hase, W. L.; Peslherbe, G. H.; Ref. 38, p. 143.
40. Doubleday Jr., C.; Bolton, K.; Hase, W. H.; J. Phys. Chem. A 1998, 102, 3648.
41. Doubleday Jr., C.; Bolton, K.; Peslherbe, G. H.; Hase, W. H.; J. Am. Chem. Soc. 1996, 118, 9922.
42. Marcus, R. A.; Rice, O. K.; J. Phys. Colloid. Chem. 1951, 55, 894.
43. Rosenstock, H. M.; Wallenstein, M. B.; Wahrhaftig, A. L.; Eyring; H. Proc. Nat. Acad. Sci. 1952, 38, 667.
44. Eliason, M. A.; Hirschfelder, J. O.; J. Chem. Phys. 1959, 30, 1426.
45. Hofacker, L.; Z. Naturforsch., A. Phys. Sci. 1963, 18, 607.
46. Mies, F. H.; J. Chem. Phys. 1969, 51, 798.
47. Marcus, R. A.; J. Chem. Phys. 1966, 45, 4493.
48. Quack, M.; Troe J.; Ver. Bunsenges. Phys. Chem. 1974, 78, 240; Quack, M.; Troe, J.; Int. Rev. Phys. Chem. 1981, 1, 97.
49. Troe, J.; J. Chem. Phys. 1983, 79, 6017.
50. Pechukas, P.; Light, J. C.; J. Chem. Phys. 1965, 42, 3281.
51. Pechukas, P.; Light, J. C.; Rankin, C.; J. Chem. Phys. 1966, 44, 794.
52. Nikitin, E.; Theor. Exp. Chem. 1965, 1, 90.
53. Klots, C. E.; J. Phys. Chem. 1971, 75, 1526; Klots, C. E.; Z. Naturforsch., A. Phys. Sci. 1972, 27, 553.
54. Truhlar, D. G.; Isaacson, A. D.; Garret, B. C., Em Theory of Chemical Reaction Dynamics, Baer, M., ed., CRC Boca Raton: FL, 1985, v. 4; p. 65-137.
55. Doll, J. D.; J. Chem. Phys. 1981, 74, 1074.
56. Thompson, D. L.; Int. Rev. Phys. Chem. 1998, 17, 547.
57. Martínez-Núñez, E.; Vázquez, S. A.; J. Chem. Phys. 1997, 107, 5393.
58. Martínez-Núñez, E.; Vázquez, S. A.; Chem. Phys. Lett. 1999, 310, 209.
59. Berblinger, M.; Schlier, C.; J. Chem. Phys. 1994, 101, 4750.
60. Fernández-Ramos, A.; Martínez-Núñez, E.; Ríos, M. A.; Rodríguez-Otero J.; Vázquez, S. A.; Estévez, C. M.; J. Am. Chem. Soc. 1998, 120, 7594.
61. Batt, L.; Milne, R. T.; McCulloch, R. D.; Int. J. Chem. Kinet. 1977, 9, 567.
62. He, Y.; Sanders, W. A.; Lin, M. C.; J. Phys. Chem. 1988, 92, 5474.
63. Martínez-Núñez, E.; Vázquez, S. A.; J. Chem. Phys. 1998, 109, 8907.
64. Martínez-Núñez, E.; Vázquez, S. A.; J. Chem. Phys. 1999, 111, 10501.
65. Song, K.; Hase, W. L.; J. Chem. Phys. 1999, 110, 6198.
66. Fenn, P. T.; Chen, Y.-T.; Stimson, S.; Ng, C. Y.; J. Phys. Chem. A 1997, 101, 6513.
67. Kutina, R. E.; Edwards, A. K.; Berkowitz, J.; J. Chem. Phys. 1974, 77, 5508.
68. Jonsson, B.-Ö; Lind, J.; J. Chem. Soc. Faraday Trans. 1974, 2, 1399.
69. Nourbaksh, S.; Norwood, K.; Yin, H.-M.; Liao, C. L.; Ng, C. Y.; J. Chem. Phys. 1991, 95, 945.
70. Cheung, Y.-S.; Hsu, C.-W.; Huang, J.-C.; Li, W.-K.; Chiu, S.-W.; Int. J. Mass Spectrom. Ion Process 1996, 13, 159.
71. Martínez-Núñez, E.; Vázquez, S. A.; TEOCHEM 2000, 505, 109.
72. Martínez-Núñez, E.; Vázquez, S. A.; J. Phys. Chem. A 1999, 103, 9783.
73. Martínez-Núñez, E.; Peña-Gallego, A.; Rodríguez-Fernández, R.; Vázquez, S. A.; Chem. Phys. Lett. 2000, 324, 88.
74. González-Lafont, A.; Truong, T.; Truhlar, D. G.; J. Phys. Chem. 1991, 95, 4618.
75. North, S. W.; Blanck, D. A.; Lee, Y. T.; Chem. Phys. Lett. 1994, 224, 381.
76. North, S. W.; Blanck, D. A.; Gezelter, J. D.; Longfelow, C. A.; Lee, Y. T.; J. Chem. Phys. 1995, 102, 4447.
77. Martínez-Núñez, E.; Vázquez, S. A.; J. Mol. Struct. 2000, 556, 123.
78. North, S. W.; Ph. D. Thesis, University of California, USA, 1995.
79. Kroger, P. M.; Riley, S. J.; J. Chem. Phys. 1977, 67, 4483.
80. Hall, G. E.; Bont, D.; Sears, T. J.; J. Chem. Phys. 1991, 94, 4182.
81. Kim, S. K.; Pedersen, S.; Zewail, A. H.; J. Chem. Phys. 1995, 102, 477.
82. Buzza, S. A.; Snyder, E. M.; Castleman Jr., A. W.; J. Chem. Phys. 1996, 104, 5040.
83. Kim, S. K.; Zewail, A. H.; Chem. Phys. Lett. 1996, 250, 279.
84. Trentleman, K. A.; Kable, S. H.; Moss, D. B.; Houston, P. L.; J. Chem. Phys. 1989, 91, 7498.
85. Owrutsky, J. C.; Baranavski, A. P.; J. Chem. Phys. 1998, 108, 6652.
86. Kim, S. K.; Guo, J.; Baskin, J. S.; Zewail, A. H.; J. Phys. Chem. 1996, 100, 9202.
87. Shibata, T.; Li, H.; Katayanagi, H.; Suzuki, T.; J. Phys. Chem. A 1998, 102, 3643.
88. Zhong, Q.; Poth, L.; Castleman Jr., A. W.; J. Chem. Phys. 1999, 110, 192.
89. Peña-Gallego, A.; Martínez-Núñez, E.; Vázquez, S. A.; J. Chem. Phys. 1999, 110, 11323.
90. Martínez-Núñez, E.; Vázquez, S. A.; Chem. Phys. Lett. 2000, 316, 471.
91. Grebenshchikov, S. Y.; Flothmann, H.; Schinke, R.; Bezel, I.; Witig, C.; Kato, S.; Chem. Phys. Lett. 1998, 285, 410.
92. Martínez-Núñez, E.; Peña-Gallego, A; Vázquez, S. A.; J. Chem. Phys. 2001, 114, 3546.
93. Hase, W. L.; Buckowski, D. G.; Chem. Phys. Lett. 1980, 74, 284.
94. Hall, G. E.; Metzler, H. W.; Muckerman, J. T.; Preses, J. M.; Weston Jr., R. E.; J. Chem. Phys. 1995, 102, 6660.
95. Berry, M. J.; Pimentel, G. C.; J. Chem. Phys. 1969, 51, 2274.
96. Quick Jr., C. R.; Wittig, C.; J. Chem. Phys. 1980, 72, 1694.
97. Watanabe H.; Horiguchi H.; Tsuchiya S.; Bull. Chem. Soc. Jpn. 1980, 53, 1530.
98. Donaldson, D. J.; Watson, D. G.; Sloan, J. J.; Chem. Phys. 1982, 68, 95.
99. Kato, S.; Morokuma, K.; J. Chem. Phys. 1980, 74, 6285.
100. Sato, K.; Tsunashima, S.; Takayanagi, T.; Fijisawa, G.; Yokoyama, A.; Chem. Phys. Lett. 1995, 242, 401.
101. Takayanagi, T.; Yokoyama, A.; Bull. Chem. Soc. Jpn. 1995, 68, 2245.
102. Hall, G. E.; Muckerman, J. T.; Preses, J. M.; Weston Jr., R. E.; Flynn, G. W.; Persky, A.; J. Chem. Phys. 1994, 101, 3679.
103. Balko, B. A.; Zhang, J.; Lee, Y. T.; J. Phys. Chem. A 1997, 101, 6611.
104. Lin, S.-R; Lee, Y.-P.; J. Chem. Phys. 1999, 111, 9233.
105. da Silva, A. M.; Arbilla, G.; da Silva, E. C.; J. Phys. Chem. A 2000, 104, 9535.
106. Martínez-Núñez, E.; Vázquez, S. A.; Struct. Chem. 2001, 12, 95.
107. Martínez-Núñez, E.; Vázquez, S. A.; Chem. Phys. Lett. 2000, 332, 583.
108. Shalashilin, D. V.; Thompson, D. L.; J. Chem. Phys. 1996, 105, 1833.
109. Li, X.; Milliam, J. M.; Schlegel, H. B.; J. Chem. Phys. 2001, 114, 8897; Doubleday, C.; 2001, 105, 6333; Li, X.; Milliam, J. M.; Schlegel, H. B.; J. Chem. Phys. 2000, 113, 10062; Bolton, K.; Schlegel, H. B.; Hase, W. L.; Song, K.; Phys. Chem. Chem. Phys. 1999, 1, 999; Bolton K.; Hase, W. L.; Schlegel H. B.; Song, K.; Chem. Phys. Lett 1997, 288, 621; Chang, Y.-T.; Minichino, C.; Miller, W. H.; J. Chem. Phys. 1992, 96, 4341; Uggerud, E.; Helgaker, T.; J. Am. Chem. Soc. 1992, 114, 4265.
110. Martínez-Núñez, E.; Vázquez, S. A.; J. Phys. Chem. A 2001, 105, 4808.
111. Martínez-Núñez, E.; Varandas, A. J. C.; J. Phys. Chem. A 2001, 105, 5923.
112. Li X.; Millam J. M.; Schlegel H. B.; J. Chem. Phys. 2000, 113, 10062.
113. Gaussian 98 (Revision A.7), Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Zakrzewski, V. G.; Montgomery, J. A.; Stratmann, R. E.; Burant, J. C.; Dapprich, S.; Millam, J. M.; Daniels, A. D.; Kudin, K. N.; Strain, M. C.; Farkas, O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennucci, B.; Pomelli, C.; Adamo, C.; Clifford, S.; Ochterski, J.; Petersson, G. A.; Ayala, P. Y.; Cui, Q.; Morokuma, K.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Cioslowski, J.; Ortiz, J. V.; Stefanov, B. B. Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Gomperts, R.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Gonzalez, C.; Challacombe, M.; Gill, P. M. W.; Johnson, B. G.; Chen, W.; Wong, M. W.; Andres, J. L.; Head-Gordon, M.; Replogle, E. S.; Pople, J. A., Gaussian Inc.: Pittsburgh PA, 1998.
114. Martínez-Núñez, E.; Marques, J. M. C.; Vázquez, S. A.; J. Chem. Phys. 2001, 115, 7872.
115. Miller, W. H.; J. Phys. Chem. A 1998, 102, 793.
116. Wang, H.; Sun, X.; Miller, W. H.; J. Chem. Phys. 1998, 108, 9726.
117. Fernández-Ramos, A.; Martínez-Núñez, E.; Smedarchina, Z.; Vázquez, S. A.; Chem. Phys. Lett. 2001, 341, 351
- 1. Chambers, T. S.; Kistiakowsky, G. B.; J. Am. Chem. Soc. 1934, 56, 399.
- 2. Schlag, E. W.; Rabinovitch, B. S.; J. Am. Chem. Soc. 1960, 82, 5996.
- 3. Schneider, F. W.; Rabinovitch, B. S.; J. Am. Chem. Soc. 1962, 84, 4215.
- 4. Tsang, W.; J. Chem. Phys. 1965, 43, 352.
- 5. Tsang, W.; J. Phys. Chem 1972, 76, 143.
- 6. Tsang, W.; Int. J. Chem. Kin 1978, 10, 41.
- 7. Tsang, W. Em Shock Tubes in Chemistry; Lifshitz, A., ed.; Marcel Decker: New York, p. 59-129.
- 8. Astholz, D. C.; Troe, J.; Wieters, W.; J. Chem. Phys 1979, 70, 5107.
- 9. Brouwer, L.; Muller-Markgraf; W.; Troe, J.; Ver. Bunsenges. Phys. Chem. 1983, 87, 1031.
- 10. Rabinovitch, B. S.; Flowers, M. C.; Quart. Rev. 1964, 18, 122.
- 11. Rabinovitch, B. S.; Setser, D. W.; Adv. Photochem. 1964, 3, 1.
- 12. Hassler, J. C.; Setser, D. W.; J. Chem. Soc. 1966, 45, 3237.
- 13. Simons, J. W.; Taylor, G. W.; J. Phys. Chem. 1969, 73, 1274.
- 14. Forst, W.; Theory of Unimolecular Reactions; Academic Press: New York, 1971.
- 15. Robinson, P. J.; Holbrook, K. A.; Unimolecular Reactions, Wiley-Interscience: London, 1972.
- 16. Gilbert, R. G.; Smith, S. C.; Theory of Unimolecular and Recombination Reactions, Blackwell Scientific: Oxford, 1990.
- 17. Baer, T.; Hase, W. L.; Unimolecular Reaction Dynamics. Theory and Experiments, Oxford University Press: New York, 1996.
- 18. Rice, O. K.; Ramsperger H. C.; J. Am. Chem. Soc. 1927, 49, 1617.
- 19. Rice, O. K.; Ramsperger H. C.; J. Am. Chem. Soc. 1928, 50, 617.
- 20. Kassel, L. S.; J. Phys. Chem. 1928, 32, 225.
- 21. Fukui, K.; Pure Appl. Chem. 1992, 54, 1825.
- 22. Truhlar, D. G.; Kuppermann, A. J.; J. Am. Chem. Soc. 1971, 93, 1840.
- 23. Steinfield, J. I.; Franciso, J. S.; Hase, W: L.; Chemical Kinetics and Dynamics, 2nd ed., Prentice Hall: New Yersey, 1999.
- 24. Murrell, J. N; Carter, S.; Farantos, S. C.; Huxley, P.; A. J. C. Varandas; Molecular Potential Energy Functions, John Wiley: Chichester, 1984.
- 25. Bunker, D. L.; J. Chem. Phys. 1962, 37, 393;
- Bunker, D. L. J.; Chem. Phys. 1964, 40, 1946;
- Bunker, D. L.; Theory of Elementary Gas Reaction Rates., Pergamon Press: New York, 1966;
- Bunker, D. L.; Proceedings of the International School of Physics Enrico Fermi Course XLIV: Molecular Beam and Reaction Kinetics, Schlier, C., ed., Academic Press: New York, 1970, p. 315-319.
- 26. Bunker, D. L.; Pattengill, M. J.; Chem. Phys. 1968, 48, 772.
- 27. Bunker, D. L.; Hase, W. L.; J. Chem. Phys. 1973, 54, 4621.
- 28. Harris, H. H.; Bunker, D. L.; Chem. Phys. Lett. 1971, 11, 433.
- 29. Porter, R. M.; Ann. Rev. Phys. Chem 1974, 25, 317;
- Bunker, D. L.; Method. Comp. Phys 1971, 10, 287;
- Porter, R. M.; Raff, L. M. Em Modern Theoretical Chemistry: Dynamics of Molecular Collisions, Miller, W. H., ed.; Plenum Press: New York, 1976, vol. 2, part B, p. 1;
- Truhlar, D. G.; Muckerman, J. T. Em Atom-Molecule Collision Theory: A Guide for the Experimentalist, Bernstein, R. B., ed., Plenum Pess: New York, 1979, p. 505;
- Raff, L. M.; Thompson, D. L. Em The Theory of Chemical Reaction Dynamics, Baer, M., ed., CRC, Boca Raton: FL, 1985, v. 3, p. 1;
- Benito, R. M.; Aoiz, F. J.; Computational Chemistry: Structure, Interactions and Reactivity; Franga, S., ed., 1992, 562;
- Mayne, H. R.; Dynamics of Molecules and Chemical Reactions; Wyatt, R. E.; Zhang, Z. H., eds., Marcel Dekker: New York, 1996, p. 589;
- Sewell, T. D.; Thompson, D. L.; Int. J. Mod. Phys. B 1997, 11, 1067.
- 30. Truhlar, D. G.; Comp. Phys. Comm 1994, 84, 78.
- 31. Miller, W. H. Em Frontiers of Chemical Dynamics, Yurtsever, E., ed., Kluwer Academic: Dordrecht, 1995, p. 1.
- 32. Varandas, A. J. C.; Brandão, J.; Pastrana, M. R.; J. Chem. Phys. 1992, 96, 5137;
- Varandas, A J. C.; Marques, J. M. C.; J. Chem. Phys. 1992, 97, 4050;
- Marques, J. M. C.; Varandas, A. J. C.; An. Fis. 1994, 90, 284;
- Varandas, A. J. C.; J. Chem. Phys. 1993, 99, 1076.
- 33. Bowman, J. M.; Gazdy, B.; Sun, Q.; J. Chem. Phys. 1989, 91, 2859;
- Miller, W. H.; Hase, W. L.; Darling, C. L.; J. Chem. Phys. 1989, 91, 2863;
- Varandas, A. J. C.; Marques, J. M. C.; J. Chem. Phys. 1994, 100, 1908;
- Ben-Nun, M.; Levine, R. D.; J. Chem. Phys. 1994, 101, 8768;
- Kumar, S.; Sathyamurthy, N.; Ramaswamy, R.; J. Chem. Phys. 1995, 103, 6021;
- Ben-Nun, N.; Levine, R. D.; J. Chem. Phys. 1996, 105, 8136.
- 34. Truhlar, D. G.; J. Phys. Chem. 1979, 83, 188.
- 35. Guo ,Y.; Thompson, D. L.; Sewell, T. D.; J. Chem. Phys. 1996, 104, 576.
- 36. Milliam, J. M.; Bakken, V.; Chen, W.; Hase, W. L.; Schlegel, H. B.; J. Chem. Phys. 1999, 111, 3800.
- 37. Benderskii, V. A.; Makarov, D. E.; Wight, C. A.; Adv. Chem. Phys. 1994, 88
- 38. Guo, Y.; Thompson, W. L., Em Modern Methods for Multidimensional Dynamics Computations in Chemistry; Thompson, D. L., ed., World Scientific: Singapore, 1998.
- 39. Bolton, K.; Hase, W. L.; Peslherbe, G. H.; Ref. 38, p. 143.
- 40. Doubleday Jr., C.; Bolton, K.; Hase, W. H.; J. Phys. Chem. A 1998, 102, 3648.
- 41. Doubleday Jr., C.; Bolton, K.; Peslherbe, G. H.; Hase, W. H.; J. Am. Chem. Soc. 1996, 118, 9922.
- 42. Marcus, R. A.; Rice, O. K.; J. Phys. Colloid. Chem. 1951, 55, 894.
- 43. Rosenstock, H. M.; Wallenstein, M. B.; Wahrhaftig, A. L.; Eyring; H. Proc. Nat. Acad. Sci. 1952, 38, 667.
- 44. Eliason, M. A.; Hirschfelder, J. O.; J. Chem. Phys. 1959, 30, 1426.
- 45. Hofacker, L.; Z. Naturforsch., A. Phys. Sci. 1963, 18, 607.
- 46. Mies, F. H.; J. Chem. Phys. 1969, 51, 798.
- 47. Marcus, R. A.; J. Chem. Phys. 1966, 45, 4493.
- 48. Quack, M.; Troe J.; Ver. Bunsenges. Phys. Chem. 1974, 78, 240;
- Quack, M.; Troe, J.; Int. Rev. Phys. Chem. 1981, 1, 97.
- 49. Troe, J.; J. Chem. Phys. 1983, 79, 6017.
- 50. Pechukas, P.; Light, J. C.; J. Chem. Phys. 1965, 42, 3281.
- 51. Pechukas, P.; Light, J. C.; Rankin, C.; J. Chem. Phys. 1966, 44, 794.
- 52. Nikitin, E.; Theor. Exp. Chem. 1965, 1, 90.
- 53. Klots, C. E.; J. Phys. Chem. 1971, 75, 1526;
- Klots, C. E.; Z. Naturforsch., A. Phys. Sci. 1972, 27, 553.
- 54. Truhlar, D. G.; Isaacson, A. D.; Garret, B. C., Em Theory of Chemical Reaction Dynamics, Baer, M., ed., CRC Boca Raton: FL, 1985, v. 4; p. 65-137.
- 55. Doll, J. D.; J. Chem. Phys. 1981, 74, 1074.
- 56. Thompson, D. L.; Int. Rev. Phys. Chem. 1998, 17, 547.
- 57. Martínez-Núñez, E.; Vázquez, S. A.; J. Chem. Phys. 1997, 107, 5393.
- 58. Martínez-Núñez, E.; Vázquez, S. A.; Chem. Phys. Lett. 1999, 310, 209.
- 59. Berblinger, M.; Schlier, C.; J. Chem. Phys. 1994, 101, 4750.
- 60. Fernández-Ramos, A.; Martínez-Núñez, E.; Ríos, M. A.; Rodríguez-Otero J.; Vázquez, S. A.; Estévez, C. M.; J. Am. Chem. Soc. 1998, 120, 7594.
- 61. Batt, L.; Milne, R. T.; McCulloch, R. D.; Int. J. Chem. Kinet. 1977, 9, 567.
- 62. He, Y.; Sanders, W. A.; Lin, M. C.; J. Phys. Chem. 1988, 92, 5474.
- 63. Martínez-Núñez, E.; Vázquez, S. A.; J. Chem. Phys. 1998, 109, 8907.
- 64. Martínez-Núñez, E.; Vázquez, S. A.; J. Chem. Phys. 1999, 111, 10501.
- 65. Song, K.; Hase, W. L.; J. Chem. Phys. 1999, 110, 6198.
- 66. Fenn, P. T.; Chen, Y.-T.; Stimson, S.; Ng, C. Y.; J. Phys. Chem. A 1997, 101, 6513.
- 67. Kutina, R. E.; Edwards, A. K.; Berkowitz, J.; J. Chem. Phys. 1974, 77, 5508.
- 68. Jonsson, B.-Ö; Lind, J.; J. Chem. Soc. Faraday Trans. 1974, 2, 1399.
- 69. Nourbaksh, S.; Norwood, K.; Yin, H.-M.; Liao, C. L.; Ng, C. Y.; J. Chem. Phys. 1991, 95, 945.
- 70. Cheung, Y.-S.; Hsu, C.-W.; Huang, J.-C.; Li, W.-K.; Chiu, S.-W.; Int. J. Mass Spectrom. Ion Process 1996, 13, 159.
- 71. Martínez-Núñez, E.; Vázquez, S. A.; TEOCHEM 2000, 505, 109.
- 72. Martínez-Núñez, E.; Vázquez, S. A.; J. Phys. Chem. A 1999, 103, 9783.
- 73. Martínez-Núñez, E.; Peña-Gallego, A.; Rodríguez-Fernández, R.; Vázquez, S. A.; Chem. Phys. Lett. 2000, 324, 88.
- 74. González-Lafont, A.; Truong, T.; Truhlar, D. G.; J. Phys. Chem. 1991, 95, 4618.
- 75. North, S. W.; Blanck, D. A.; Lee, Y. T.; Chem. Phys. Lett. 1994, 224, 381.
- 76. North, S. W.; Blanck, D. A.; Gezelter, J. D.; Longfelow, C. A.; Lee, Y. T.; J. Chem. Phys. 1995, 102, 4447.
- 77. Martínez-Núñez, E.; Vázquez, S. A.; J. Mol. Struct. 2000, 556, 123.
- 78. North, S. W.; Ph. D. Thesis, University of California, USA, 1995.
- 79. Kroger, P. M.; Riley, S. J.; J. Chem. Phys. 1977, 67, 4483.
- 80. Hall, G. E.; Bont, D.; Sears, T. J.; J. Chem. Phys. 1991, 94, 4182.
- 81. Kim, S. K.; Pedersen, S.; Zewail, A. H.; J. Chem. Phys. 1995, 102, 477.
- 82. Buzza, S. A.; Snyder, E. M.; Castleman Jr., A. W.; J. Chem. Phys. 1996, 104, 5040.
- 83. Kim, S. K.; Zewail, A. H.; Chem. Phys. Lett. 1996, 250, 279.
- 84. Trentleman, K. A.; Kable, S. H.; Moss, D. B.; Houston, P. L.; J. Chem. Phys. 1989, 91, 7498.
- 85. Owrutsky, J. C.; Baranavski, A. P.; J. Chem. Phys. 1998, 108, 6652.
- 86. Kim, S. K.; Guo, J.; Baskin, J. S.; Zewail, A. H.; J. Phys. Chem. 1996, 100, 9202.
- 87. Shibata, T.; Li, H.; Katayanagi, H.; Suzuki, T.; J. Phys. Chem. A 1998, 102, 3643.
- 88. Zhong, Q.; Poth, L.; Castleman Jr., A. W.; J. Chem. Phys. 1999, 110, 192.
- 89. Peña-Gallego, A.; Martínez-Núñez, E.; Vázquez, S. A.; J. Chem. Phys. 1999, 110, 11323.
- 90. Martínez-Núñez, E.; Vázquez, S. A.; Chem. Phys. Lett. 2000, 316, 471.
- 91. Grebenshchikov, S. Y.; Flothmann, H.; Schinke, R.; Bezel, I.; Witig, C.; Kato, S.; Chem. Phys. Lett. 1998, 285, 410.
- 92. Martínez-Núñez, E.; Peña-Gallego, A; Vázquez, S. A.; J. Chem. Phys. 2001, 114, 3546.
- 93. Hase, W. L.; Buckowski, D. G.; Chem. Phys. Lett. 1980, 74, 284.
- 94. Hall, G. E.; Metzler, H. W.; Muckerman, J. T.; Preses, J. M.; Weston Jr., R. E.; J. Chem. Phys. 1995, 102, 6660.
- 95. Berry, M. J.; Pimentel, G. C.; J. Chem. Phys. 1969, 51, 2274.
- 96. Quick Jr., C. R.; Wittig, C.; J. Chem. Phys. 1980, 72, 1694.
- 97. Watanabe H.; Horiguchi H.; Tsuchiya S.; Bull. Chem. Soc. Jpn. 1980, 53, 1530.
- 98. Donaldson, D. J.; Watson, D. G.; Sloan, J. J.; Chem. Phys. 1982, 68, 95.
- 99. Kato, S.; Morokuma, K.; J. Chem. Phys. 1980, 74, 6285.
- 100. Sato, K.; Tsunashima, S.; Takayanagi, T.; Fijisawa, G.; Yokoyama, A.; Chem. Phys. Lett. 1995, 242, 401.
- 101. Takayanagi, T.; Yokoyama, A.; Bull. Chem. Soc. Jpn. 1995, 68, 2245.
- 102. Hall, G. E.; Muckerman, J. T.; Preses, J. M.; Weston Jr., R. E.; Flynn, G. W.; Persky, A.; J. Chem. Phys. 1994, 101, 3679.
- 103. Balko, B. A.; Zhang, J.; Lee, Y. T.; J. Phys. Chem. A 1997, 101, 6611.
- 104. Lin, S.-R; Lee, Y.-P.; J. Chem. Phys. 1999, 111, 9233.
- 105. da Silva, A. M.; Arbilla, G.; da Silva, E. C.; J. Phys. Chem. A 2000, 104, 9535.
- 106. Martínez-Núñez, E.; Vázquez, S. A.; Struct. Chem. 2001, 12, 95.
- 107. Martínez-Núñez, E.; Vázquez, S. A.; Chem. Phys. Lett. 2000, 332, 583.
- 108. Shalashilin, D. V.; Thompson, D. L.; J. Chem. Phys. 1996, 105, 1833.
- 109. Li, X.; Milliam, J. M.; Schlegel, H. B.; J. Chem. Phys. 2001, 114, 8897;
- Doubleday, C.; 2001, 105, 6333;
- Li, X.; Milliam, J. M.; Schlegel, H. B.; J. Chem. Phys. 2000, 113, 10062;
- Bolton, K.; Schlegel, H. B.; Hase, W. L.; Song, K.; Phys. Chem. Chem. Phys. 1999, 1, 999;
- Bolton K.; Hase, W. L.; Schlegel H. B.; Song, K.; Chem. Phys. Lett 1997, 288, 621;
- Chang, Y.-T.; Minichino, C.; Miller, W. H.; J. Chem. Phys. 1992, 96, 4341;
- Uggerud, E.; Helgaker, T.; J. Am. Chem. Soc. 1992, 114, 4265.
- 110. Martínez-Núñez, E.; Vázquez, S. A.; J. Phys. Chem. A 2001, 105, 4808.
- 111. Martínez-Núñez, E.; Varandas, A. J. C.; J. Phys. Chem. A 2001, 105, 5923.
- 112. Li X.; Millam J. M.; Schlegel H. B.; J. Chem. Phys. 2000, 113, 10062.
- 113. Gaussian 98 (Revision A.7), Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Zakrzewski, V. G.; Montgomery, J. A.; Stratmann, R. E.; Burant, J. C.; Dapprich, S.; Millam, J. M.; Daniels, A. D.; Kudin, K. N.; Strain, M. C.; Farkas, O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennucci, B.; Pomelli, C.; Adamo, C.; Clifford, S.; Ochterski, J.; Petersson, G. A.; Ayala, P. Y.; Cui, Q.; Morokuma, K.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Cioslowski, J.; Ortiz, J. V.; Stefanov, B. B. Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Gomperts, R.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Gonzalez, C.; Challacombe, M.; Gill, P. M. W.; Johnson, B. G.; Chen, W.; Wong, M. W.; Andres, J. L.; Head-Gordon, M.; Replogle, E. S.; Pople, J. A., Gaussian Inc.: Pittsburgh PA, 1998.
- 114. Martínez-Núñez, E.; Marques, J. M. C.; Vázquez, S. A.; J. Chem. Phys. 2001, 115, 7872.
- 115. Miller, W. H.; J. Phys. Chem. A 1998, 102, 793.
- 116. Wang, H.; Sun, X.; Miller, W. H.; J. Chem. Phys. 1998, 108, 9726.
- 117. Fernández-Ramos, A.; Martínez-Núñez, E.; Smedarchina, Z.; Vázquez, S. A.; Chem. Phys. Lett. 2001, 341, 351
Fechas de Publicación
-
Publicación en esta colección
26 Ago 2002 -
Fecha del número
Jul 2002
Histórico
-
Acepto
19 Set 2001 -
Recibido
26 Mar 2001