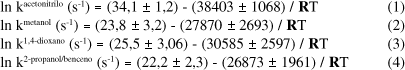Resumen
The thermal decomposition reaction of trans-3,6-dimethyl-3,6-diphenyl-1,2,4,5-tetraoxacyclohexane (acetophenone cyclic diperoxide, DPAF), in different solvents (methanol, 1,4-dioxane, acetonitrile and 2-propanol/benzene mixtures) in the initial concentration and temperature ranges of (4.2-10.5) x 10-3 M and 140.0 to 185.0 ºC, respectively, follows a pseudo first order kinetic law up to at least 70% DPAF conversion. An important solvent effect on the rate constant values, activation parameters (DH# and DS#) and reaction products obtained in different solvents is detected, showing that the reaction is accelerated in alcohols.
kinetics in solution; solvent effect; acetophenone cyclic diperoxide
kinetics in solution; solvent effect; acetophenone cyclic diperoxide
ARTIGO
Efecto de solvente sobre la descomposición térmica de trans-3,6-dimetil-3,6-difenil-1,2,4,5-tetraoxaciclohexano en solución
Solvent effects on the thermal decomposition of trans-3,6-dimethyl-3,6-diphenyl-1,2,4,5-tetraoxacyclohexane in solution
Gladys N. Eyler; Adriana I. Cañizo; Carmen M. Mateo* * e-mail: cmateo@fio.unicen.edu.ar
Facultad de Ingeniería, Universidad Nacional del Centro de la Provincia de Buenos Aires, Avenida del Valle 5737, (B7400JWI) Olavarría, Buenos Aires - Argentina
ABSTRACT
The thermal decomposition reaction of trans-3,6-dimethyl-3,6-diphenyl-1,2,4,5-tetraoxacyclohexane (acetophenone cyclic diperoxide, DPAF), in different solvents (methanol, 1,4-dioxane, acetonitrile and 2-propanol/benzene mixtures) in the initial concentration and temperature ranges of (4.2-10.5) x 10-3 M and 140.0 to 185.0 ºC, respectively, follows a pseudo first order kinetic law up to at least 70% DPAF conversion. An important solvent effect on the rate constant values, activation parameters (DH# and DS#) and reaction products obtained in different solvents is detected, showing that the reaction is accelerated in alcohols.
Keywords: kinetics in solution; solvent effect; acetophenone cyclic diperoxide.
INTRODUCCIÓN
En general, los peróxidos orgánicos son compuestos de naturaleza inestable y explosivos. Su síntesis y manipulación requieren de estrictos cuidados para evitar accidentes1. Sin embargo, las temperaturas necesarias para efectuar la descomposición térmica de peróxidos orgánicos cíclicos en solución indican que los mismos son relativamente estables2,3 en esas condiciones. Numerosos estudios previos realizados en este laboratorio han permitido comprobar que los miembros de la familia de los 1,2,4-trioxaciclohexanos4, de los 1,2,4,5-tetraoxaciclohexanos5-8 y de los 1,2,4,5,7,8-hexaoxaciclononanos8-10 se descomponen témicamente a través de un mecanismo de reacciones en etapas, en el cual la etapa determinante de la velocidad se asigna a la homólisis unimolecular de la unión peroxídica. La energía de disociación determinada para la ruptura O-O de diferentes compuestos peroxídicos es cercana a las 45 kcal/mol11, sin embargo, el valor de dicha energía puede verse afectado por efectos estéricos provocados por los diferentes sustituyentes del anillo5 o por el cambio de propiedades fisicoquímicas del solvente utilizado para llevar a cabo los estudios cinéticos4,6.
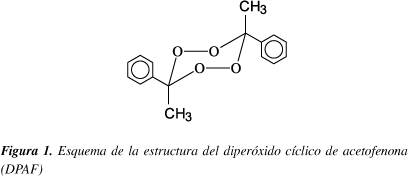
En este trabajo se presenta la descomposición térmica del diperóxido cíclico de acetofenona (DPAF, 3,6-dimetil-3,6-difenil-1,2,4,5-tetraoxaciclohexano, Figura 1) en 1,4-dioxano, metanol, acetonitrilo y mezclas 2-propanol-benceno. Se estudia el efecto de solvente producido en la termólisis de este diperóxido incluyendo datos obtenidos previamente en solución de benceno7. Las conclusiones que de aquí se desprendan serán de gran utilidad para posteriores estudios relacionados con la utilización de este peróxido como iniciador polifuncional de polimerización radicálica de estireno12 u otros monómeros (p. ej. Metacrilato de metilo) o como agente oxidante de compuestos orgánicos13.
RESULTADOS Y DISCUSIÓN
La descomposición térmica del trans-3,6-dimetil-3,6-difenil-1,2,4,5-tetraoxaciclohexano (DPAF), ha sido estudiada en acetonitrilo, metanol, 1,4-dioxano y mezclas de 2-propanol/benceno 1:1 (V/V), para concentraciones iniciales comprendidas en el intervalo 4,2-10,5 x 10-3 M, y en un amplio rango de temperaturas 140,0-185,0 °C (Tabla 1).
El DPAF muestra un comportamiento que está de acuerdo con una ley cinética de pseudo-primer orden hasta conversiones del diperóxido ca. 70%, por lo cual se descarta que en estas condiciones de trabajo existan reacciones inducidas de segundo orden que aceleren la descomposición térmica del mismo. Algunos peróxidos cíclicos suelen descomponerse simultáneamente por el ataque de radicales libres generados in situ a partir del propio peróxido mostrando un comportamiento que sólo responde a una ley de pseudo-primer orden a bajas conversiones14, sin embargo esto no se observa para el DPAF.
El efecto de la temperatura sobre las constantes de velocidad puede ser representado a través de las ecuaciones (1-4) donde las energías de activación están expresadas en cal mol-1 y los errores corresponden a las desviaciones estándar derivadas de un tratamiento de los datos cinéticos por un método de cuadrados mínimos.
La linealidad de estas ecuaciones de Arrhenius en un amplio rango de temperaturas (ca. 30 °C, Tabla 1) sugiere que los parámetros de activación que de allí se derivan para el DPAF en los diferentes solventes corresponden a un proceso simple, el cual podría representarse por la ruptura homolítica unimolecular del enlace O-O de la molécula del diperóxido tal como ha sido postulado para la descomposición térmica de este peróxido cíclico en benceno7 (ec. 5).
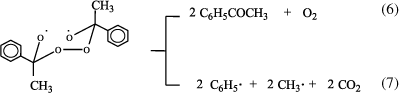
El birradical inicialmente formado sufre posterior descomposición a través de rupturas C-O dando acetofenona (ec. 6) como principal producto derivado del DPAF en los distintos solventes (Tabla 2), para un 100% de conversión del peróxido. Puede observarse que un aumento en la polaridad del solvente también aumenta el rendimiento de la acetofenona. Como se indica en la ecuación 7, el birradical también puede descomponerse a través de rupturas C-C, dando lugar a los otros productos observados. Esto permite postular que si bien la primera etapa es común en todos los solventes, las posteriores etapas que involucran la ruptura de enlaces C-O para la formación de la cetona son influenciadas por las características del solvente.
Los estudios realizados en solución de benceno7 muestran la presencia de otros productos como fenol, oxígeno, dióxido de carbono, metano, metanol y trazas de etano, todos ellos identificados por cromatografía gaseosa utilizando detectores de conductividad térmica o de ionización de llama. Para el presente trabajo, si bien el análisis de productos no fue exhaustivo, pudo detectarse cualitativamente la presencia de productos minoritarios derivados del ataque de radicales CH3. sobre el solvente (p.ej.: propanonitrilo en acetonitrilo) o productos de oxidación originados a partir de la formación de oxígeno en el medio como fenol en mezcla 2-propanol/benceno (ecs. 8, 9) o 1,2-bencenodiol en acetonitrilo.
Si se analizan los valores de kexp a 160,0 °C en todos los solventes (Tabla 3), puede observarse una alta reactividad del DPAF en solventes próticos, como metanol o 2-propanol, detectándose constantes de velocidad de reacción aproximadamente 10 veces mayores que en solventes apróticos o de baja polaridad como benceno o 1,4-dioxano. En particular, a 160 ºC, la constante de velocidad de reacción aumenta 11,5 veces cuando se cambia de un solvente hidrocarbonado como benceno puro a una mezcla 1:1 V/V de 2-propanol-benceno. Este efecto del solvente sobre las constantes de velocidad de la reacción de descomposición térmica de DPAF también se pone en evidencia en los valores de los parámetros de activación correspondientes, los cuales fueron calculados a partir de la ecuación de Eyring (ec. 10) (Tabla 3).
La complejidad de las diferentes interacciones intermoleculares soluto-solvente presentes en las reacciones en solución dificultan la tarea de decidir cuales de las propiedades del solvente afectan realmente las velocidades de reacción. Por otro lado, tampoco es tarea fácil definir qué características de la molécula reaccionante deben considerarse cuando se ha determinado la existencia de un efecto de solvente sobre su reactividad. La polaridad del solvente no puede medirse adecuadamente por ciertas constantes físicas vinculadas con interacciones no específicas como son el momento dipolar, la constante dieléctrica, el índice de refracción, entre otras. En la literatura15 se ha propuesto el uso del término "polaridad" para definir en forma general la capacidad de solvatación como un resultado de la suma de interacciones específicas y no específicas, excluyendo aquellas que provocan reacciones químicas entre soluto y solvente. Parámetros empíricos de polaridad del solvente como el denominado ET(30), definido por Reichardt y Dimroth15,16 describen de manera más completa todas las interacciones presentes en solución. En la Figura 2 se ilustra el efecto del solvente sobre las constantes de velocidad de reacción en función del ET(30). Dado que en la literatura no figura el valor de este parámetro para mezclas 2-propanol-benceno, el correspondiente valor de constante de velocidad no se incluye en el gráfico. Si bien la correlación mostrada no es buena, la tendencia es evidente. La constante de velocidad aumenta con la polaridad del solvente medida a través de este parámetro. En general, se ha observado que un aumento en la polaridad del solvente produce a todas las temperaturas experimentales un aumento en la velocidad de la reacción de descomposición térmica del DPAF.
El efecto de solvente puede analizarse también sobre los valores de los parámetros de activación de la reacción de descomposición térmica del DPAF aunque este tratamiento suele resultar más complejo que el análisis de las constantes de velocidad. Sin embargo, se detectan cambios importantes en los valores de los mismos cuando se establecen comparaciones entre solventes hidrocarbonados y alcoholes, tal como ocurre con los valores de las constantes de velocidad. Por ejemplo, la entalpía de activación desciende 10,9 kcal mol-1 y la entropía de activación 20,1 cal mol-1 K-1 cuando la reacción se lleva a cabo en mezclas 2-propanol-benceno en lugar de realizarla en benceno puro, mientras que en el mismo sentido la disminución observada en la energía libre de Gibbs (ec. 11) está dentro del error experimental y es de 2,7 kcal mol-1. Puede observarse en todos los sistemas estudiados (Tabla 3) que una modificación en DH# va siempre acompañada de un cambio en el mismo sentido del DS# correspondiente, sin embargo prácticamente no se observan efectos sobre la energía libre. El hecho de que los valores de DG# sean prácticamente constantes, permite considerar que si bien la descomposición térmica de DPAF está influenciada por el solvente de reacción, en todos los casos la reacción en estudio es la misma. Este efecto puede ser evaluado en términos de solvatación preferencial del reactivo o del complejo activado. Un complejo activado con carácter más polar que el estado inicial y estructuralmente más parecido al birradical (ec. 5) estará más solvatado en solventes de mayor polaridad y por consiguiente, la reacción transcurrirá a mayores velocidades observándose una disminución en los valores de DG# (Tabla 3).
En general, cuando el cambio de solvente afecta la velocidad de la reacción considerada en el sentido de provocar un aumento de la misma, los correspondientes parámetros de activación disminuyen. Este fenómeno fue descrito por Leffler17 como Ley de Compensación o Relación Isocinética y se representa por la ecuación (12) donde DH0# es la ordenada al origen y no tiene sentido físico, b es la pendiente de la recta determinada por la representación gráfica de DH# en función de DS# (Figura 3) y se conoce como la temperatura isocinética expresada en Kelvin (K). A esta temperatura no habría efecto de solvente ya que la reacción transcurriría en cualquier solvente con la misma velocidad. En la mayoría de los casos descritos en la bibliografía el valor de b está alejado del intervalo de temperaturas experimentales y es mayor que la temperatura media experimental.
La representación gráfica de la ec. 10 con los datos obtenidos para este trabajo, es prácticamente lineal (Figura 3, r2 = 0,995). La variación de los parámetros de activación supera ampliamente los errores cometidos en la determinación de los mismos (DDH # = 12 kcal mol-1 y DDS # = 23,3 cal mol-1 K-1) y el valor de b es de 510,1 K (237,1 °C), el cual resulta superior a las temperaturas experimentales (135,5-185,0 °C). Esta correlación es consistente con el tratamiento propuesto por Exner18 años más tarde quien sugiere la representación en el plano de Arrhenius de los datos cinéticos obtenidos en los diferentes solventes estudiados (Figura 3). La existencia de una zona o un punto donde las rectas se intercepten hace posible el cálculo del valor de la temperatura isocinética, la cual debe ser comparable con el valor obtenido a partir de la pendiente de la recta (según ec. 12) para que la correlación se considere válida. La aplicación de un tratamiento estadístico a los datos cinéticos19 (Figura 4) permite calcular la función Su (suma residual de cuadrados) cuyo mínimo representa la inversa de la temperatura isocinética (b-1) mientras que su valor máximo coincide con la zona de temperaturas experimentales. El valor de b calculado por este método es 497,5 K (224,5 °C) el cual no difiere demasiado con el obtenido de acuerdo al tratamiento de Leffler (ec. 12 y Figura 3). La concordancia entre estos dos tratamientos apoyan la existencia de un efecto de solvente que opera tanto sobre los valores de las constantes de velocidad como sobre los parámetros de activación. Así, se puede definir al conjunto de reacciones estudiadas como una serie de reacciones para las cuales puede postularse un mecanismo común en etapas iniciado por la ruptura homolítica unimolecular (ec. 5) de la molécula del DPAF. Sin embargo, no podría aseverarse que en dicha serie de reacciones actúe un único mecanismo de interacción ya que los solventes utilizados son de naturaleza muy diferente, en consecuencia, se pondrían de manifiesto distintos mecanismos específicos de interacción solvente-DPAF.
CONCLUSIONES
La descomposición térmica unimolecular del diperóxido cíclico de acetofenona (DPAF) en solución sigue una cinética de pseudo-primer orden, comprobándose la existencia de un efecto de solvente sobre las constantes de velocidad, los parámetros de activación y los productos de la reacción considerada, de modo que un aumento en la polaridad del solvente acelera la reacción a la vez que genera mayor cantidad de acetofenona. Los cambios observados en las constantes de velocidad en los diferentes medios de reacción están causados por modificaciones tanto en la entalpía como en la entropía de activación, de manera tal que tienden a compensarse y en consecuencia los valores de la energía libre de activación resultan prácticamente constantes.
La aplicación de diferentes criterios con respecto al tratamiento de los datos cinéticos obtenidos para la descomposición térmica de DPAF en solución permiten postular un mecanismo común de termólisis iniciado por la ruptura homolítica de un enlace O-O con diferentes mecanismos de interacción con el solvente.
Los resultados obtenidos en esta investigación resultan de interés para estudios relacionados con procesos de polimerización radicálica, donde algunos compuestos de esta familia de peróxidos cíclicos polifuncionales han demostrado ser eficientes iniciadores de dichos procesos.
PARTE EXPERIMENTAL
Reactivos
El trans-3,6-dimetil-3,6-difenil-1,2,4,5-tetraoxaciclohexano fue sintetizado de acuerdo con el método de preparación descrito en la literatura20.
Los solventes utilizados en la reacción han sido purificados según técnicas standard21 excepto el 2-propanol y el metanol que fueron tratados, previo a su destilación, con la sal disódica del ácido etilendiaminotetraacético a fin de eliminar trazas de metales22 que podrían catalizar la descomposición del DPAF.
Métodos cinéticos
Las soluciones de DPAF se prepararon en solventes puros, excepto en 2-propanol, debido a la baja solubilidad del peróxido en este alcohol.
Las determinaciones cinéticas correspondientes a la termólisis del DPAF en los distintos solventes se llevaron a cabo cargando la respectiva solución inicial en ampollas de vidrio Pyrex (diámetro interno: 6 mm), las que se degasifican en una línea para vacío, son enfriadas a 196 °C con nitrógeno líquido y finalmente se cierran a la llama de un soplete. Posteriormente, las ampollas se colocan en un baño termostático a la temperatura elegida (±0,1 °C), se extraen a tiempos de reacción convenientemente predeterminados deteniendo la reacción por inmersión de las mismas en un baño a 0 °C.
Las determinaciones cuantitativas del DPAF remanente en las soluciones y de la acetofenona producto de reacción, se realizan por cromatografía líquida de alta resolución (H.P.L.C), en un instrumento Hewlett-Packard serie 1050 C, utilizando una columna de fase reversa (ODS Hypersil, 5 µm, 100 x 4,6 mm) y detector UV de longitud de onda variable. La separación de la acetofenona y el DPAF se realiza de modo isocrático, con fase móvil 40% Metanol: 40% Acetonitrilo: 20% Agua, en las siguientes condiciones:
- En solución de Metanol, Acetonitrilo y 1,4 Dioxano, se usó un flujo de 0,5 mL/min y l constante = 254 nm.
- En solución de 2-propanol- Benceno 1:1 (V/V), se usó un flujo de 0,8 mL/min y l variable: de 0-4,5 min, l = 270 nm, y de 4,5-15 min, l = 254 nm.
Los solventes utilizados son calidad HPLC.
Los parámetros de activación se calculan a partir de la ecuación de Eyring (ec. 10), y los errores de los mismos usando un método de cuadrados mínimos23.
AGRADECIMIENTOS
El presente trabajo fue subsidiado por la Facultad de Ingeniería y la Secretaría de Ciencia y Técnica de la Universidad Nacional del Centro de la Provincia de Buenos Aires.
Recebido em 2/2/04; aeito em 25/5/04; publicado na web em 27/8/04
- 1. Noller, D. C.; Bolton, D. J.; Anal. Chem. 1963, 35, 887.
- 2. Nonhebel, D. C.; Walton, J. C.; Free Radical Chemistry, Cambridge UP: London, 1974, cap. 13.
- 3. Jefford, C. W.; Jaber, A.; Boukoubalas, J.; Tissot, P. O.; Thermochim. Acta 1991, 188, 337.
- 4. Eyler, G. N.; Cañizo, A. I.; Mateo, C. M.; Alvarez, E. E.; Cafferata, L. F. R.; J. Org. Chem. 1999, 64, 8457.
- 5. Cafferata, L. F. R.; Eyler, G. N.; Svartman, E. L.; Cañizo, A. I.; Borkowski, E. J.; J. Org. Chem. 1990, 55, 1058.
- 6. Cafferata, L. F. R.; Eyler, G. N.; Svartman, E. L.; Cañizo, A. I.; Alvarez, E. E.; J. Org. Chem. 1991, 56, 411.
- 7. Cafferata, L. F. R.; Mirífico, M. V.; An. Asoc. Quím. Argent. 1982, 74, 501.
- 8. Cañizo, A. I.; Eyler, G. N.; Mateo, C. M.; Alvarez, E. E.; Nesprías, R. K.; Heterocycles, en prensa.
- 9. Mateo, C. M.; Eyler, G. N.; Alvarez, E. E.; Cañizo, A. I.; J. Org. Chem. 2000, 65, 2319.
- 10. Eyler, G. N.; Cañizo, A. I.; Alvarez, E. E.; Cafferata, L. F. R.; An. Asoc. Quím. Argent. 1994, 82, 175.
- 11. Bach, R. D.; Ayala, P. Y. ; Schlegel, H. B.; J. Chem. Soc. 1996, 118, 12758.
- 12. Cerna, J.; Morales, G.; Eyler, G. N.; Cañizo, A. I.; J. Appl. Polym. Sci. 2002, 83, 1.
- 13. Cañizo, A. I.; Nesprias, R. K.; Mateo, C. M.; Eyler, G. N.; trabajo no publicado.
- 14. Cañizo, A. I.; Eyler, G. N.; Mateo, C. M.; Alvarez, E. E.; Cafferata, L. F. R.; Afinidad 2002,59, 684.
- 15. Reichardt, C.; Chem. Int. Ed. Engl. 1965, 4, 29.
- 16. Reichardt, C.; Dimroth, K.; Fortschr. Chem. Forsch. 1968, 2,1. (CA 70:31979a)
- 17. Leffler, J. E.; J. Org. Chem 1955, 20, 1202.
- 18. Exner, O.; Nature 1970, 227, 366.
- 19. Exner, O.; Collect. Czech. Chem. Commun. 1972, 37, 1425.
- 20. Mc Cullough, K. J.; Morgan, A. R.; Nonhebel, D. C.; Pauson, P. L.; White, G. J.; J Chem. Res., Synop. 1980, 34, M 0601.
- 21. Riddick, J. A.; Bunger, W. B. En Organic Solvent; Weissberger, A., ed.; Wiley Interscience: New York, 1970.
- 22. Wilson, T.; Landis, M. E.; Baumstark, A. L.; Bartlett, P. D.; J. Am. Chem. Soc. 1973, 95, 4765.
- 23. Huyberechts, S.; Halleux, A.; Kruys, P.; Bull. Soc. Chim. Belg. 1955, 64, 203.
Fechas de Publicación
-
Publicación en esta colección
02 Dic 2004 -
Fecha del número
Dic 2004
Histórico
-
Recibido
02 Feb 2004 -
Acepto
25 Mayo 2004